Dispersive treatment of $K_S\rightarrow \gamma \gamma$ and $K_S\rightarrow \gamma \ell ^+\ell ^-$

Abstract

We analyse the rare kaon decays $K_S \rightarrow \gamma \gamma$ and $K_S \rightarrow \gamma \ell ^+\ell ^-$ $(\ell = e \text{ or } \mu )$ in a dispersive framework in which the weak Hamiltonian carries momentum. Our analysis extends predictions from lowest order $SU(3)_L\times SU(3)_R$ chiral perturbation theory ($\chi$PT$_3$) to fully account for effects from final-state interactions, and is free from ambiguities associated with extrapolating the kaon off-shell. Given input from $K_S \rightarrow \pi \pi$ and $\gamma \gamma ^{(*)}\rightarrow \pi \pi$, we solve the once-subtracted dispersion relations numerically to predict the rates for $K_S \rightarrow \gamma \gamma$ and $K_S \rightarrow \gamma \ell ^+\ell ^-$. In the leptonic modes, we find sizeable corrections to the $\chi$PT$_3$ predictions for the integrated rates.

1 Introduction

In the study of kaon decays, our ability to obtain precise predictions from the Standard Model (SM) depends on whether the underlying physics is predominantly of short- or long-distance nature. At one end of a broad spectrum of possible decay channels, there are “golden modes” like $K\rightarrow \pi \nu \bar{\nu }$, where the amplitude factorises into a hadronic form factor and perturbative corrections—both of which are under excellent theoretical control [1]. In such cases, the resulting prediction can be at a level of precision that competes with (or even surpasses) current experimental measurements. This state of affairs can lead to powerful constraints on physics beyond the SM and drives much of the theoretical and experimental interest in these modes.

By contrast, non-leptonic decays such as $K\rightarrow \pi \pi$ and $K\rightarrow \pi \pi \pi$ are dominated by long-distance contributions involving hadronic matrix elements of four-quark operators. The evaluation of these matrix elements is a notoriously difficult non-perturbative problem, and this hinders the comparison of theory with experiment.

In between these extremes lies a range of decay modes in which a clean separation of the short- and long-distance physics can be achieved with varying degrees of success.

Since kaon decays occur at low energies, a systematic analysis can be undertaken within $SU(3)_L\times SU(3)_R$ chiral perturbation theory ($\chi$PT$_3$), where amplitudes are expanded as an asymptotic series in powers of $O(m_{K})$ momentum and light quark masses $m_{u,d,s} = O(m_{K}^2)$. The application of $\chi$PT$_3$ to kaon decays is covered in a comprehensive review [2]; here we recall two important features that determine the quality of predictions arising from the 3-flavour expansion:

• 1. hadronic uncertainties are parametrised in terms of low-energy constants (LECs), whose values are not fixed by chiral symmetry alone. For several purely leptonic and semi-leptonic kaon decays, the corresponding LECs can be extracted from a combination of experimental data and input from lattice QCD. However, the situation for non-leptonic and weak radiative decays is far less certain, with many of the LECs essentially unconstrained at next-to-lowest-order (NLO) in the chiral expansion;

• 2. at energies above the $\pi \pi$ threshold, final-state interactions (FSI), especially in the $0^{++}$ channel [3–6], can spoil the convergence of the $\chi$PT$_3$ expansion. These effects are related to the broad $f_0(500)$ resonance [7], whose $O(m_{K})$ mass [8] implies a lack of scale separation between the Goldstone $\pi ,K,\eta$ and non-Goldstone $f_0,\rho ,\omega ,\ldots$ sectors. In these cases, chiral-perturbative methods must be abandoned in favour of non-perturbative methods based on unitarity, analyticity, and crossing symmetry.¹

Dispersion relations offer a means to address items 1 and 2 within a model-independent framework. These methods have been mostly applied in the context of pure strong processes such as pion form factors [11, 12], $\pi \pi$-scattering [13–17], $\pi K$-scattering [18], $\gamma \gamma ^{(*)} \rightarrow \pi \pi$ [19–21], $\pi N$ scattering [22–24], semi-leptonic kaon decays $K_{\ell 3}$ [25–30] and $K_{\ell 4}$ [31–33], or decays not involving kaons, e.g. $\eta \rightarrow \pi \pi \pi$ [34–39].

In view of current high-statistics kaon experiments such as NA62 [40], we believe it is timely to consider extending the scope of dispersive methods to $\Delta S=1$ processes involving the effective weak Hamiltonian ${\mathscr {H}}_w$, and in particular to two-body decays. Such an extension was proposed sometime ago by Büchler et al. [41, 42], who treated the decay $K\rightarrow \pi \pi$ dispersively by allowing ${\mathscr {H}}_w$ to carry momentum, thereby overcoming the difficulty that the kinematics in two-body decays are completely fixed. The advantage of this approach over $\chi$PT$_3$ is that (a) only a few subtraction constants are required as input, and (b) $\pi \pi$ rescattering effects are fully accounted for in terms of Omnès factors and calculable dispersive integrals in crossed channels. Moreover, by allowing ${\mathscr {H}}_w$ to carry momentum, the ambiguities associated with taking the kaon off-shell [42, 43] are entirely avoided.

In this article, we extend the dispersive framework developed in [41] to the rare decays $K_S \rightarrow \gamma \gamma$ and $K_S\rightarrow \gamma \ell ^+\ell ^-$ $(\ell = e \text{ or } \mu )$. In lowest-order (LO) $\chi$PT$_3$, the amplitudes for $K_S\rightarrow \gamma \gamma ^{(*)}$ possess the well known feature of ultraviolet finite $\pi ^\pm$, $K^\pm$ one-loop diagrams coupled to the external photons. For the pure radiative decay, the chiral prediction [2, 44, 45] for the rate

$$\begin{aligned} \mathrm {BR}(K_S \rightarrow \gamma \gamma )_{\chi \mathrm {PT}_3} = 2.0 \times 10^{-6} \end{aligned}$$

(1)

is in reasonable agreement with the experimental average [46]

$$\begin{aligned} \mathrm {BR}(K_S \rightarrow \gamma \gamma ) = (2.63\pm 0.17)\times 10^{-6}, \end{aligned}$$

(2)

while the predictions [47] for the leptonic modes are typically expressed in terms of the ratios

$$\begin{aligned} \left. \frac{\Gamma (K_S\rightarrow \gamma \ell ^+\ell ^-)}{\Gamma (K_S\rightarrow \gamma \gamma )} \right| _{\chi \mathrm {PT}_3} = \left\{ \begin{array}{cl} 1.6\times 10^{-2} &{} \quad (\ell = e) \\ 3.8\times 10^{-4} &{} \quad (\ell =\mu ) \end{array} \right. . \end{aligned}$$

(3)

Although these decays have not yet been measured, they may lie within reach of the KLOE-2 experiment at DA$\mathrm {\Phi }$NE [48], which is projected to be sensitive down to $K_S$ branching ratios of $O(10^{-9})$. Given these projections, it is clearly of interest to determine what impact $\pi \pi$ rescattering effects have on the $\chi$PT$_3$ predictions (3).

The outline of this paper is as follows. In Sect. 2 we introduce the general formalism needed to analyse $K_S\rightarrow \gamma \gamma ^*$ dispersively, and derive the decomposition of the decay amplitude into a basis of scalar functions that are free from kinematic zeros and singularities. In particular, we use this basis to extend the LO $\chi$PT$_3$ calculation [47] to the case where ${\mathscr {H}}_w$ carries non-zero momentum. Section 3 reviews the dispersive framework developed for $K_S\rightarrow \pi \pi$ [41], which forms a key input in our analysis of $K_S\rightarrow \gamma \gamma ^*$. In Sect. 4 we examine $K_S\rightarrow \gamma \gamma$ and find that the inclusion of effects from FSI improves the agreement between theory and experiment. We also comment on how our results compare with previous work [49] based on extrapolating the kaon off-shell. Section 5 concerns $K_S\rightarrow \gamma \ell ^+\ell ^-$, where we observe that FSI and the pion vector form factor lead to sizeable corrections of the LO $\chi$PT$_3$ predictions. Our summary is given in Sect. 6.

2 Preliminaries

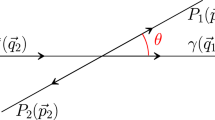
We begin by considering the radiative decay

$$\begin{aligned} K_S(k) \rightarrow \gamma (q_1)\gamma ^*(q_2)\,, \end{aligned}$$

(4)

whose amplitude is given by

$$\begin{aligned} M(K_S\rightarrow \gamma \gamma ^*) = e^2\varepsilon ^{\mu *}_1(q_1,\lambda _1)\varepsilon ^{\nu *}_2(q_2,\lambda _2) A_{\mu \nu }(k,q_1,q_2)\,, \end{aligned}$$

(5)

where $\varepsilon _{1,2}$ are the polarization vectors of the photons. The tensor $A_{\mu \nu }$ is defined in terms of the pure $\Delta I =1/2$ matrix element²

$$\begin{aligned} A_{\mu \nu }(k,q_1,q_2)&=- \int \!\! \mathrm{d}^4x\, \mathrm{d}^4y\, e^{i(q_1 \cdot x + q_2 \cdot y)}\nonumber \\&\quad \times \langle \mathrm {vac} | T\{ J_\mu (x)J_\nu (y) {\mathscr {H}}_w^{1/2}(0)\}|K_S(k)\rangle , \end{aligned}$$

(6)

where $J_\mu$ is the electromagnetic current of the light quarks u, d, s, and we allow the weak Hamiltonian ${\mathscr {H}}_w$ to carry non-zero momentum $h_\mu \ne 0$. Then the decay amplitude (5) becomes a function of the three Mandelstam variables

$$\begin{aligned} s = (q_1 + q_2)^2, \quad t = (k-q_1)^2, \quad u = (k-q_2)^2, \end{aligned}$$

(7)

which satisfy

$$\begin{aligned} s+t+u = m_{K}^2 + q_2^2 + h^2. \end{aligned}$$

(8)

In what follows it is convenient to set $h^2=0$, while keeping $h_\mu \ne 0$ in general. Doing so does not result in a loss of generality, but does simplify several expressions derived in this paper. To recover the physical decay amplitude, one simply takes the limit $h_\mu \rightarrow 0$, in which case the kinematic variables become fixed at the values

$$\begin{aligned} s = m_{K}^2, \quad t=q_2^2, \quad u=0. \end{aligned}$$

(9)

2.1 Tensor decomposition

To set up a dispersive framework for $K_S\rightarrow \gamma \gamma ^*$, the first step is to decompose $A_{\mu \nu }$ in a basis of independent tensors, whose scalar coefficients are free from kinematic singularities and zeros. This can be achieved by applying the prescription of Bardeen and Tung [50], and Tarrach [51]; our approach resembles the tensor decomposition of $\gamma ^*\gamma ^*\rightarrow \pi \pi$ discussed in [52–54].

Let $q_i = \{q_1,\,q_2,\,h-k\}$ label the three independent momenta and observe that Lorentz covariance and CP-invariance implies a decomposition in terms of ten tensors³

$$\begin{aligned} A_{\mu \nu } = g_{\mu \nu } A_1 + \sum _{i,j=1}^3 q_{i\mu }q_{j\nu } A_2^{ij}\,. \end{aligned}$$

(10)

The scalar functions $\{A_1,\, A_2^{ij}\}$ are not all independent since $A_{\mu \nu }$ is constrained by the electromagnetic Ward identities

$$\begin{aligned} q_1^\mu A_{\mu \nu } = q_2^\nu A_{\mu \nu } = 0\,. \end{aligned}$$

(11)

A convenient way to impose the constraint (11) is to introduce the gauge projector

$$\begin{aligned} P_{\mu \nu } = g_{\mu \nu } - \frac{q_{2\mu }q_{1\nu }}{q_1\cdot q_2}\,, \end{aligned}$$

(12)

and let it act on both indices of $A_{\mu \nu }$:

$$\begin{aligned} A_{\mu \nu } = P_{\mu \alpha } P_{\beta \nu } A^{\alpha \beta } = \sum _{i=1}^5 \bar{T}_{\mu \nu }^i \bar{A}_i\,. \end{aligned}$$

(13)

By definition, this leaves the physical tensor $A_{\mu \nu }$ invariant and removes contributions that do not satisfy the Ward identities; with this procedure the set of scalar functions reduces to five. The new basis functions $\bar{A}_i$ are free from kinematic singularities, but contain zeros because the tensors $\bar{T}_{\mu \nu }^i$ contain single and double poles in $q_1\cdot q_2$. As shown in [52–54], the removal of these poles can be performed by adding suitable linear combinations of $\bar{T}_{\mu \nu }^i$ with non-singular coefficients, followed by a rescaling in powers of $q_1\cdot q_2$. In our case, contraction with $\varepsilon _1$ and setting $q_1^2=0$ imposes two additional constraints, so the final result is

$$\begin{aligned} A_{\mu \nu }(k,q_1,q_2) = \sum _{i=1}^3 T_{\mu \nu }^i\, B_i(s,t,u,q_2^2)\,, \end{aligned}$$

(14)

where the scalar functions $B_i$ are free from kinematic zeros and singularities, and the corresponding tensors are

$$\begin{aligned} \begin{aligned} T^1_{\mu \nu }&= (q_1 \cdot q_2) g_{\mu \nu } - q_{2\mu } q_{1\nu } \,, \\ T^2_{\mu \nu }&= (q_1 \cdot q_2) q_{3\mu } q_{2\nu } - q_2^2 q_{3\mu } q_{1\nu } \\&\quad +\tfrac{1}{2}\left[ (t-u)-m_{K}^2\right] (q_2^2 g_{\mu \nu }-q_{2\mu } q_{2\nu }),\\ T^3_{\mu \nu }&= (q_1 \cdot q_2) q_{3\mu } q_{3\nu } - \tfrac{1}{4} \left[ (t-u)^2 - m_{K}^4 \right] g_{\mu \nu } \\&\quad +\, \tfrac{1}{2} \left[ (t-u) +m_{K}^2 \right] q_{3\mu } q_{1\nu }\\&\quad -\, \tfrac{1}{2} \left[ (t-u) -m_{K}^2 \right] q_{2\mu } q_{3\nu }. \end{aligned} \end{aligned}$$

(15)

At the physical point (9) there are only two independent momenta, so $A_{\mu \nu }$ reduces to $T_{\mu \nu }^1$ times the coefficient

$$\begin{aligned}&B_1\left( m_{K}^2,q_2^2\right) - q_2^2\, B_2\left( m_{K}^2,q_2^2\right) + \tfrac{1}{2}\left( q_2^2+m_{K}^2\right) \nonumber \\&\quad \times B_3\left( m_{K}^2,q_2^2\right) . \end{aligned}$$

(16)

Evidently, the determination of the scalar functions $B_i$ completely fixes the prediction for the $K_S \rightarrow \gamma \gamma ^*$ amplitude (5).

2.2 $K_S\rightarrow \gamma \gamma ^{*}$ in lowest-order $\chi$PT$_{\mathbf 3}$

Fig. 1

Lowest-order $\chi$PT$_3$ graphs for $K_S\rightarrow \gamma \gamma ^*$, where the weak Hamiltonian ${\mathscr {H}}_w$ carries momentum

Before discussing our dispersive treatment of the scalar functions $B_i$, it is instructive to extend the LO $\chi$PT$_3$ calculation of $K_S\rightarrow \gamma \gamma ^*$ [47] to the case where ${\mathscr {H}}_w$ carries momentum. In the conventions of [2], the graphs shown in Fig. 1 yield

$$\begin{aligned} A_{\mu \nu }\big |_{{\chi \mathrm {PT}_3}}= & {} -iG_8 F_\pi \left( 3s +m_{K}^2 -4m_{\pi }^2\right) I_{\mu \nu }\nonumber \\&-\big \{m_{\pi }^2 \rightarrow m_{K}^2\big \}, \end{aligned}$$

(17)

where $G_8 = 9.1 \times 10^{-6}$ GeV$^{-2}$ is the octet coupling at $O(p^2)$, $F_\pi = 92.2$ MeV is the pion decay constant [46], and the loop integral is

$$\begin{aligned} I_{\mu \nu } = \int \!\!\! \frac{\mathrm{d}^{4}\ell }{(2\pi )^4} \frac{g_{\mu \nu }(\ell ^2-m_\phi ^2) - (2\ell +q_1)_\mu (2\ell -q_2)_\nu }{\left[ (\ell +q_1)^2-m_\phi ^2\right] \left[ (\ell -q_2)^2-m_\phi ^2\right] \left[ \ell ^2-m_\phi ^2\right] }, \end{aligned}$$

(18)

where $\phi = \pi ^\pm$ or $K^\pm$. The integral is ultraviolet finite and can be evaluated in terms of Feynman parameters:

$$\begin{aligned} I_{\mu \nu } = \frac{i}{16\pi ^2}\int _0^1 \mathrm{d}u \int _0^{1-u} \mathrm{d}v \frac{4uv T_{\mu \nu }^1 - 2v(1-2v) T_{\mu \nu }^4}{D(u,v,m_\phi ^2)}, \end{aligned}$$

(19)

where the denominator is given by

$$\begin{aligned} D(u,v,m_\phi ^2) = m_\phi ^2 - suv - v(1-u-v) q_2^2 - i\varepsilon . \end{aligned}$$

(20)

In (19), the second tensor

$$\begin{aligned} T_{\mu \nu }^4 = (q_1\cdot q_2) q_{1\mu }q_{2\nu } - q_2^2 q_{1\mu }q_{1\nu } \end{aligned}$$

(21)

vanishes upon contraction with $\varepsilon _1$, so we find that only $B_1$ contributes to $M(K_S\rightarrow \gamma \gamma ^*)$ at LO, with

$$\begin{aligned} B_{1}(s,q_2^2)\big |_{\chi \mathrm {PT}_3}= & {} \frac{G_8 F_\pi }{4\pi ^2} \bigg ( \frac{3s +m_{K}^2 -4m_{\pi }^2}{s}\bigg ) H(s,m_{\pi }^2,q_2^2)\nonumber \\&- \big \{m_{\pi }^2\rightarrow m_{K}^2\big \}. \end{aligned}$$

(22)

Here, the quantity

(23)

is defined [2] in terms of the one-loop functions

$$\begin{aligned} F(a)&= \left\{ \begin{array}{lll} 1 - \dfrac{4}{a}\arcsin ^2\left( \sqrt{a}/2\right) &{} \quad &{} a \le 4 , \\ 1 + \dfrac{1}{a}\left( \ln \dfrac{1-\sqrt{1-4/a}}{1+\sqrt{1-4/a}}+i\pi \right) ^2 &{} \quad &{} a> 4, \end{array}\right. \\ G(a)&= \left\{ \begin{array}{lll} \sqrt{4/a-1}\arcsin \big (\sqrt{a}/2\big ) &{} \quad &{} a \le 4, \\ \dfrac{1}{2}\sqrt{1-4/a}\bigg (\ln \dfrac{1+\sqrt{1-4/a}}{1-\sqrt{1-4/a}} - i\pi \bigg ) &{} \quad &{} a>4. \end{array}\right. \nonumber \end{aligned}$$

(24)

At the physical point (9), the expression in (22) agrees with the original $\chi$PT$_3$ result [47], as it should.

As emphasised in [55], tadpole cancellation completely eliminates the weak mass operator at $O(p^2)$ in the $\chi$PT$_3$ expansion. The argument can be extended to $O(p^4)$ [56] and remains valid when ${\mathscr {H}}_w$ carries momentum.

Fig. 2

Unitarity relation for the $\pi \pi$ intermediate state in $K_S\rightarrow \gamma \gamma ^*$, where the weak Hamiltonian carries momentum $h_\mu \ne 0$. The dashed line indicates the cutting of the pion propagators, while the grey blobs refer to the respective $K_S\rightarrow \pi \pi$ and $\gamma \gamma ^*\rightarrow \pi \pi$ sub-amplitudes

2.3 Unitarity and $\pi \pi$ intermediate states

Let us now analyse the unitarity relation due to the intermediate $\pi \pi$ state. In the s-channel, this contribution reads (Fig. 2)

$$\begin{aligned} \mathrm {disc}_s A_{\mu \nu } =\,&\frac{1}{2} \int \!\!\! \frac{\mathrm{d}^{3}p_1}{(2\pi )^32E_1} \frac{\mathrm{d}^{3}p_2}{(2\pi )^32E_2}(2\pi )^4\nonumber \\&\times \delta ^4(q_1+q_2- p_1 - p_2) A_{\pi \pi }(s,t',u')\nonumber \\&\times W_{\mu \nu }^*(q_1,q_2,p_1) , \end{aligned}$$

(25)

where $A_{\pi \pi }$ and $W_{\mu \nu }$ are the amplitudes for the subprocesses $K_S\rightarrow \pi \pi$ and $\gamma \gamma ^*\rightarrow \pi \pi$ respectively. On the left-hand side of the cut, the Mandelstam variables are

$$\begin{aligned} t' = (k-p_1)^2, \quad u' = (k-p_2)^2 , \end{aligned}$$

(26)

while on the right-hand side, $W_{\mu \nu }$ can be decomposed into a basis of three independent tensors [21, 52–54]:

$$\begin{aligned} W_{\mu \nu }(q_1,q_2,p_1) = \sum _{i=1}^3 t_{\mu \nu }^i W_i(s,t'',u'',q_2^2)\,, \end{aligned}$$

(27)

where

$$\begin{aligned} t''= (q_1 - p_1)^2, \quad u'' = (q_1 - p_2)^2, \end{aligned}$$

(28)

and

$$\begin{aligned} t_{\mu \nu }^1&= (q_1\cdot q_2)g_{\mu \nu } - q_{2\mu }q_{1\nu }\,, \nonumber \\ t_{\mu \nu }^2&= (q_1\cdot q_2)\Delta _\mu (q_{2\nu } - q_2^2 q_{1\nu })\nonumber \\&\quad + \tfrac{1}{2}(t''-u'')(q_2^2 g_{\mu \nu } - q_{2\mu }q_{2\nu })\,, \nonumber \\ t_{\mu \nu }^3&= (q_1\cdot q_2) \Delta _\mu \Delta _\nu - \tfrac{1}{4}(t''-u'')^2g_{\mu \nu } \nonumber \\&\quad + \tfrac{1}{2}(t''-u'')(\Delta _\mu q_{1\nu } - q_{2\mu }\Delta _\nu ), \quad \Delta = p_2 - p_1\,. \end{aligned}$$

(29)

The phase space integration (25) must project each of the tensors $t_{\mu \nu }^i$ onto linear combinations of $T_{\mu \nu }^{i}$. However, the integration is trivial if contributions from D waves and higher are neglected. This is because in this approximation, $A_{\pi \pi }$ is independent of $t'$ and $u'$, while the scalar functions $W_i$ can be expressed in terms of a single helicity partial wave [53, 54],

$$\begin{aligned} W_1&= -\frac{2}{s-q_2^2}h_{++}^0\left( s,q_2^2\right) , \quad W_2 = W_3 = 0. \end{aligned}$$

(30)

Since $W_{1}$ is independent of the pion momenta, the tensor $t_{\mu \nu }^{1}$ can be pulled under the phase space integral (25). Equating the scalar coefficients then gives the analytical result

$$\begin{aligned} \mathrm {disc}_s\, B_1(s,q_2^2)&=\frac{1}{32\pi ^2} \int _0^\infty \!\!\! dp \frac{p^2}{m_{\pi }^2+p^2} \nonumber \\&\quad \times \delta \left( q_1^0+q_2^0 - 2\sqrt{m_{\pi }^2+p^2}\right) \nonumber \\&\quad \times \int \!\! d\Omega '' A_{\pi \pi }(s) W_1^*(s,q_2^2) \nonumber \\&= -\frac{\sigma _\pi (s)}{8\pi }\, \frac{A_{\pi \pi }(s)[h_{++}^0(s,q_2^2)]^*}{s-q_2^2}\,, \end{aligned}$$

(31)

where we have introduced the kinematic factor

$$\begin{aligned} \sigma _\phi (s) = \sqrt{1-4m_\phi ^2/s}. \end{aligned}$$

(32)

At higher energies, other intermediate states like $4 \pi$, $K \bar{K}$ etc. will contribute to the s-discontinuity of $A_{\mu \nu }$. Moreover, for a complete dispersive treatment one should also consider discontinuities in the t- and u-channels. We will not consider any of these contributions to the dispersion relation for $A_{\mu \nu }$, and we explain below on what grounds these approximations can be justified.

3 Dispersive framework for $K\rightarrow \pi \pi$

The construction of a dispersion relation for $K_S\rightarrow \gamma \gamma ^{(*)}$ requires input from $K_S\rightarrow \pi \pi$ and $\gamma \gamma ^{(*)}\rightarrow \pi \pi$. It is well known that one-loop chiral corrections to the $K_S\rightarrow \pi \pi$ amplitude are substantial, and largely due to significant rescattering effects of pions in the final state [57–59]. An understanding of FSI is thus essential in order to make sense of puzzles such as the $\Delta I =1/2$ rule or the SM prediction for $\varepsilon '/\varepsilon$. As noted in Sect. 1, dispersive techniques are well suited to addressing FSI; here we review the dispersive framework [41, 42] developed for $K\rightarrow \pi \pi$.

We begin with the standard isospin decomposition for the $K^0\rightarrow \pi \pi$ amplitude [2]

$$\begin{aligned} \frac{A_{\pi \pi }}{\sqrt{2}}&= A_{1/2}\,, \end{aligned}$$

(33)

where $A_{1/2}$ is generated by the $\Delta I= 1/2$ component of ${\mathscr {H}}_w$, and we have omitted a term involving $\Delta I=3/2$.$^2$ As in Sect. 2, we allow the effective weak Hamiltonian ${\mathscr {H}}_w$ to carry momentum $h_\mu \ne 0$, so the amplitude reads

$$\begin{aligned} A_{1/2}(s,t',u') = \langle (\pi (p_1)\pi (p_2))_{I=0} | {\mathscr {H}}_w^{1/2}(0)| K^0(k) \rangle , \end{aligned}$$

(34)

where the corresponding Mandelstam variables are given in (26), and satisfy

$$\begin{aligned} s+t'+u' = 2m_{\pi }^2 + m_{K}^2. \end{aligned}$$

(35)

The physical $K^0\rightarrow \pi \pi$ decay amplitude is then obtained by taking the limit $h_\mu \rightarrow 0$, at which point we have

$$\begin{aligned} s=m_{K}^2 \quad \text{ and } \quad t'=u'=m_{\pi }^2. \end{aligned}$$

(36)

If contributions from the imaginary parts of D waves and higher are neglected, it is possible to decompose $A_{1/2}$ in terms of single-variable functions

$$\begin{aligned} A_{1/2}(s,t',u') = M_0(s) + C(s,t',u'), \end{aligned}$$

(37)

where the angular dependence is contained in

$$\begin{aligned} C(s,t',u')&= \frac{1}{3} \left[ N_0(t') + 2 R_0(t') \right] \nonumber \\&\quad + \frac{1}{2} \left[ s-u' - \frac{m_{\pi }^2(m_{K}^2-m_{\pi }^2)}{t'} \right] N_1(t')\nonumber \\&\quad + \{t' \leftrightarrow u'\} , \end{aligned}$$

(38)

and the explicit expressions for $N_i$ and $R_i$ can be found in [41].

As a result of this simplification, the dispersive treatment of the full amplitude $A_{1/2}$ is reduced to solving a coupled set of dispersion relations of the single-variable functions appearing in the right-hand side of (37). As shown in [41], these relations can be solved numerically, with a minimum of two subtraction constants⁴ needed to ensure convergence of the dispersive integrals. One of these constants $a_{\pi \pi }$ can be determined at the soft-pion point

$$\begin{aligned} s=u'=m_{\pi }^2 \quad \text{ and } \quad t'=m_{K}^2\,, \end{aligned}$$

(39)

where $A_{1/2}$ is related to the on-shell $K\rightarrow \pi$ amplitude $A_\pi$:

$$\begin{aligned} -\frac{A_\pi }{2F_\pi }&= A_{1/2}\left( m_{\pi }^2,m_{K}^2,m_{\pi }^2\right) \nonumber \\&= a_{\pi \pi } +\frac{1}{3}\left[ N_0(m_{K}^2)+2R_0(m_{K}^2)\right] + O(m_{\pi }^2). \end{aligned}$$

(40)

Note that with both K and $\pi$ on-shell, the weak operator ${\mathscr {H}}_w$ in $A_\pi$ necessarily carries momentum. The relevance of lattice calculations of $A_\pi$ in connection with the $\Delta I=1/2$ rule has recently been discussed in [62].

On the other hand, the second constant $b_{\pi \pi }$ can be obtained by considering e.g. the derivative $\partial A_{1/2}/\partial s$ at the soft-pion point (39). Ideally, lattice techniques would be used to determine $a_{\pi \pi }$ and $b_{\pi \pi }$, although such calculations remain to be undertaken. Thus the approach taken in [41] was essentially pragmatic: to illustrate the role of FSI, the value of $b_{\pi \pi }$ was fixed by applying $\chi$PT$_3$, so that

$$\begin{aligned} b_{\pi \pi } = \frac{3a_{\pi \pi }(1+X)}{m_{K}^2-m_{\pi }^2(4+3X)} + O(m_{K}^4)\,, \end{aligned}$$

(41)

where the dimensionless parameter X controls the size of the expected NLO corrections; on the basis of the 3-flavour expansion it can be varied between $X=\pm 0.3$. We note that the relation (41) is not affected by the weak mass term in ${\mathscr {H}}_w$; see Sect. 2.2.

From the solutions to the dispersion relations, it is a straightforward matter to reconstruct the $K\rightarrow \pi \pi$ amplitude. For $u'$ fixed near the physical value ${m_{\pi }^{2}}$, it has been shown [63] that the contribution due to $C(s,t',u')$ is negligible relative to $M_0$ in the low-energy region $s \lesssim 1.5$ GeV$^2$. Thus to a good approximation, we can write

$$\begin{aligned}&A_{1/2}\left( s,m_{K}^2+m_{\pi }^2-s,m_{\pi }^2\right) \nonumber \\&\quad \simeq a_{\pi \pi }\left[ 1 + E(X) s/m_{K}^2 \right] \Omega _0^0(s), \end{aligned}$$

(42)

where the quantity

$$\begin{aligned} E(X) = \frac{3m_{K}^2(1+X)}{m_{K}^2-m_{\pi }^2(4+3X)} \end{aligned}$$

(43)

parametrises the NLO corrections, and

$$\begin{aligned} \Omega _0^0(s) = \exp \left( \frac{s}{\pi } \int _{4m_{\pi }^2}^{\infty }\! \mathrm{d}z\, \frac{\delta _0^0(z)}{z(z-s-i\epsilon )} \right) . \end{aligned}$$

(44)

is the Omnès function [64] subtracted at $s=0$, with $\delta _0^0$ the $\pi \pi$ scattering phase shift in the $I=\ell =0$ channel.

The $K\rightarrow \pi \pi$ amplitude in (42) can be determined up to the unknown subtraction constant $a_{\pi \pi }$, modulo chiral corrections parametrised by X. As a result, a first principles prediction for $K\rightarrow \pi \pi$ is not currently possible within this framework. Fortunately, this does not pose a problem for $K_S\rightarrow \gamma \gamma ^*$ since we can eliminate the dependence on $a_{\pi \pi }$ by matching to $A_{1/2}=A_0e^{i\delta _0}$ at the physical point (36):

$$\begin{aligned} |a_{\pi \pi }| = \frac{A_0}{|\Omega _0^0(m_{K}^2)| \left[ 1 + E(X) \right] }, \end{aligned}$$

(45)

where

$$\begin{aligned} A_0 = (2.704\pm 0.001)\times 10^{-7} \text{ GeV } \end{aligned}$$

(46)

is the empirical value of the $I=0$ amplitude [2]. In this way, the dispersive representation of $K_S\rightarrow \gamma \gamma ^*$ is largely determined in terms of measurable quantities, and as we show in Sects. 4 and 5 this leads to rather small uncertainties in our final results.

4 Dispersion relations for $K_S \rightarrow \gamma \gamma$

As a first application of our dispersive framework, here we consider the case where both photons are on-shell. A complete dispersive treatment of $K_S \rightarrow \gamma \gamma$ (with ${\mathscr {H}}_w$ carrying momentum) would require an analysis of all possible intermediate states in all three channels s, t and u—clearly a daunting task. A simplification which has proven to be particularly effective for other scattering processes at low energies is to neglect the contributions to discontinuities coming from D waves and higher. This leads to a dispersive representation of the scattering amplitude in terms of single-variable functions, much like in the case of the $K \rightarrow \pi \pi$ amplitude discussed in Sect. 3. As in that case, we expect that at the physical point (9), the contributions to the S wave coming from discontinuities in the t and u channels are negligible, and so will not consider them. Effectively this means that we construct a dispersion relation of the form-factor type (i.e. with a right-hand cut only), and only for the S wave. Moreover, we will explicitly consider only the effect of $\pi \pi$ rescattering, which at low energies should be by far the most important one. Indeed, this expectation is borne out by the LO $\chi$PT$_3$ result discussed in Sect. 2.2.

Let us define $A_{\gamma \gamma }(s) = e^2 B_1(s)$, whose imaginary part coincides with the s-discontinuity in (31) once we set $q_2^2=0$:

$$\begin{aligned}&\mathrm {Im}_s\, A_{\gamma \gamma }(s)\nonumber \\&=-\alpha \frac{\sigma _\pi (s)}{\sqrt{2}s} \frac{\Omega _0^0(s)A_0}{|\Omega _0^0(m_{K}^2)|} \frac{\left[ 1 + E(X)s/m_{K}^2 \right] }{\left[ 1 + E(X) \right] }[h_{0,++}^{0}(s)]^*\,. \end{aligned}$$

(47)

Here $\alpha = e^2 /4\pi$ is the fine-structure constant, and $h_{0,++}^0$ is the projection of $h_{++}^0$ onto the $I=0$ channel. The real part then follows from a once-subtracted dispersion relation at $s=s_0$:

$$\begin{aligned} A_{\gamma \gamma }(s) = a_{\gamma \gamma } + \frac{s-s_0}{\pi }\int _{4m_{\pi }^2}^\infty \mathrm{d}z \frac{\mathrm {Im}_s\, A_{\gamma \gamma }(z)}{(z-s_0)(z -s - i\epsilon )}, \end{aligned}$$

(48)

where $a_{\gamma \gamma }$ is the subtraction constant. The subtraction is necessary because the $\pi ^\pm ,K^\pm$ loop contribution to the $\chi$PT$_3$ amplitude vanishes at the point

$$\begin{aligned} s_0=-0.098 \text{ GeV }^{2}, \end{aligned}$$

(49)

and, moreover, to ensure convergence of the dispersive integral. This feature can be deduced from the explicit form of the $\chi$PT$_3$ amplitude in (22), with $q_2^2=0$. It follows that matching $A_{\gamma \gamma }(s_0)$ onto LO $\chi$PT$_3$ fixes $a_{\gamma \gamma }=0$, although in general, $a_{\gamma \gamma }$ will receive SU(3) corrections due to terms at $O(p^6)$ in the chiral expansion. It is important to note that by matching below the $\pi \pi$ threshold, we make use of $\chi$PT$_3$ only in a kinematic region where the typically large corrections due to FSI are entirely absent, i.e. where the 3-flavour expansion should behave as expected.

To compute the integral in (48), we require input for $h^0_{0,++}$ and the S wave of the $K_S \rightarrow \pi \pi$ amplitude which, in our representation, is given by $\Omega _0^0$. Concerning the latter, the dispersive representation of the single-variable functions in (37) is only valid in the elastic scattering region $4 m_{\pi }^2< s < 16m_{\pi }^2$, even though the first significant inelastic contribution is due to the $K\bar{K}$ intermediate state when $s > 4 m_K^2$. Taking this into account would require a coupled-channel analysis of $K_S\rightarrow \pi \pi$ and $K_S\rightarrow KK$, which is beyond the scope of this work. Moreover, it is unclear whether this would lead to better precision, because there are no sources of experimental information on $K_S \rightarrow KK$, and we would have to rely completely on $\chi$PT$_3$ to determine the subtraction constants, with correspondingly large uncertainties.

We will thus stick to a single-channel treatment and only consider the contribution to the imaginary part of the S wave specified in (47). This implies that the phases of $h^0_{0,++}$ and $\Omega _0^0$ have to match exactly in order for $\mathrm {Im}_s\, A_{\gamma \gamma }$ to be real, as it should be in a single-channel treatment. This is guaranteed in the elastic region, which effectively extends up to $s=4 m_K^2$, but above that threshold an ambiguity arises: do the phases of the $K_S\rightarrow \pi \pi$ partial waves continue to behave like the elastic scattering phase shifts $\delta _\ell ^I$, or do they exhibit a sharp “dip” like the one observed [12] in the scalar form factor of the pion?⁵ This ambiguity affects both quantities: $h^0_{0,++}$ as well as $\Omega _0^0$. We take a pragmatic approach to the problem and follow Moussallam [21], who constructs a phase with the property

$$\begin{aligned} \phi _0^0(s) = \left\{ \begin{array}{lcc} \delta _0^0(s)\,, &{} \qquad &{} s \le s_\pi \\ \delta _0^0(s) - \pi \,, &{} \qquad &{} s > s_\pi \end{array} \right. \,, \end{aligned}$$

(50)

where $s_\pi$ lies near the $K\bar{K}$ threshold and is the point where $\delta _0^0$ crosses $\pi$. The corresponding Omnès function $\Omega _0^0[\phi ]$ thus displays a “dip” across the inelastic region. Another option is to evaluate the Omnès function with the phase of $h^0_{0,++}$,

$$\begin{aligned} \psi _0^0(s) = \arg h_{0,++}^0(s)\,, \end{aligned}$$

(51)

as input. Watson’s theorem ensures $\phi _0^0 = \psi _0^0$ in the elastic region, and leads to two representations for $\Omega _0^0$ which are in very close agreement at low energy. A comparison of the two phases and corresponding Omnès factors is shown in Fig. 3.

Fig. 3

Energy dependence of phase shift inputs (top) and magnitude of the corresponding Omnès functions (bottom)

As argued by Moussallam [21] and earlier by Morgan and Pennington [65] (see also the discussion in [12]), unless the operator which is responsible for the creation of the pion pair has a large overlap with the $f_0(980)$, one expects a weak coupling to the $f_0(980)$, and correspondingly a dip in the amplitude. The only known example of an operator whose amplitude would have a peak instead of a dip is that of the $\bar{s} s$ operator.

We thus conclude that our preferred phase is the one given in Eq. (50) and with this we will obtain our central results. The phase in (51) will be used to estimate our systematic uncertainty. More extreme behaviours—like “Solution 1” in [33]—are deemed to be very unlikely and will not be considered.

Regarding the input for $h_{0,++}^0$, we use data from the coupled-channel analysis of $\gamma \gamma \rightarrow \pi \pi$ performed by García–Martín and Moussallam (GMM) [19]. Since the determination of $h_{0,++}^0$ in this analysis is expected to be reliable up to $s \lesssim 2$ GeV$^2$,⁶ it is necessary to impose a cutoff $\Lambda$ in our dispersion integral (48). At the physical point $s=m_{K}^2$, a comparison of the cutoff dependence is shown in Fig. 4, where $|\text{ Re } A_{\gamma \gamma }|$ is seen to exhibit a very mild sensitivity to variations in $\Lambda$.

Fig. 4

Cutoff dependence of the dispersive amplitude $|\text{ Re } A_{\gamma \gamma }|$ at the physical point (9), where the blue band corresponds to the systematic uncertainty. For comparison, the PDG value of $|\text{ Re } A_{\gamma \gamma }|$ and its $1\sigma$ uncertainties is shown by the green band, while the lowest-order prediction from $\chi$PT$_3$ is shown by the dashed red line

Taking $\Lambda = 1.2$ as a benchmark value, the energy dependence of the real and imaginary parts of $A_{\gamma \gamma }$ is shown in Figure 5. As expected, the dispersive representation agrees with LO $\chi$PT$_3$ below the $\pi \pi$ threshold. However, for $s > 4m_{\pi }^2$, the effects from FSI distort the amplitude, producing a significant enhancement (suppression) of the real (imaginary) part. These effects lead to an enhanced prediction for the branching ratio

$$\begin{aligned} \mathrm {BR}(K_S \rightarrow \gamma \gamma )&= \frac{m_{K}^3}{64\pi } \frac{|A_{\gamma \gamma }(m_{K}^2)|^2}{\Gamma (K_S)_\mathrm {tot}} \nonumber \\&=(2.34 \pm 0.31) \times 10^{-6} \end{aligned}$$

(52)

which brings the SM and experiment (2) into much better agreement. The uncertainty has been determined by considering the variation $X=\pm 0.3$, shifting the value of $s_0$ by 30%, the comparison of the two Omnès inputs (Fig. 3), and an estimate of contributions from the high-energy region $\Lambda > 1.2$ GeV, where the phase of $\Omega _0^0$ is guided to $\pi$ and the helicity partial wave is fixed to a constant value $|h_{0,++}| \approx 4$. Combined in quadrature, the final uncertainty has turned out to be remarkably modest.

Fig. 5

Energy dependence of the real and imaginary parts of the $K_S\rightarrow \gamma \gamma$ amplitude. The blue band in the dispersive result corresponds to the systematic uncertainty

4.1 Comparison to the literature

As shown in Fig. 5, the real part of $A_{\gamma \gamma }$ receives a significant enhancement in absolute value at $s=m_{K}^2$ due to FSI. A similar observation has been made by Kambor and Holstein (KH) [49], who estimated the effects of $\pi \pi$ rescattering in $K_S\rightarrow \gamma \gamma$ and $K_L\rightarrow \pi ^0\gamma \gamma$ by extrapolating the kaon mass off-shell. Focusing on the former process, we can adapt their notation to ours by defining

$$\begin{aligned} A_{\gamma \gamma }^\mathrm {KH}(s) = - 2\alpha F_\pi B(s) / s, \end{aligned}$$

(53)

where B(s) is a scalar function whose definition is given in [49]. In our comparison, we have updated the input used in [49] to account for improved determinations [19] of the Omnès factor and helicity partial wave. The resulting predictions at the benchmark value of $\Lambda =1.2$ GeV are shown in Table 1, where we also list the pure octet$^2$ predictions from $\chi$PT$_3$. We note that although the KH formalism produces a branching ratio consistent with experiment, it relies on the assumption that one can extrapolate the kaon mass off the mass shell. As discussed in [42, 43], this procedure suffers from an inherent ambiguity as there is no unique way in which to perform the off-shell extrapolation. By contrast, our framework always involves on-shell states, and is free from such ambiguities.

Table 1 Determinations of the $K_S\rightarrow \gamma \gamma$ amplitude $A_{\gamma \gamma }$ and branching ratio at the physical point $s=m_{K}^2$. The numbers in the row labelled “This work” have been obtained with input from GMM

5 Dispersion relations for $K_S \rightarrow \gamma \ell ^+\ell ^-$

We now consider the case where the photon momentum in $K_S\rightarrow \gamma \gamma ^*$ can remain off-shell $q_2^2\ne 0$. As in Sect. 4, we focus on contributions from S waves and define $A_{\gamma \gamma ^*}(s,q_2^2) = e^2 B_1(s,q_2^2)$.

In the presence of $\pi \pi$ rescattering in the $I=0$ channel, the s-discontinuity reads

$$\begin{aligned} \mathrm {disc}_s \, A_{\gamma \gamma ^*}(s,q_2^2)&=-\alpha \frac{\sigma _\pi (s)}{\sqrt{2}}\frac{\Omega _0^0(s)A_0}{|\Omega _0^0(m_{K}^2)|}\\&\quad \times \frac{\left[ 1 + E(X)s/m_{K}^2 \right] }{\left[ 1 + E(X) \right] } \frac{\left[ h_{0,++}^{0}(s,q_2^2)\right] ^*}{s-q_2^2}, \nonumber \end{aligned}$$

(54)

so the corresponding dispersion integral is given by⁷

$$\begin{aligned} A_{\gamma \gamma ^*}(s,q_2^2) = a_{\gamma \gamma ^*}(q_2^2) + \frac{s}{\pi } \int _{4m_{\pi }^2}^{\infty } dz \, \frac{\mathrm {disc}_s \,A_{\gamma \gamma ^*}(z,q_2^2)}{z(z-s-i\epsilon )}, \end{aligned}$$

(55)

where we have subtracted at $s_0=0$ to ensure convergence of the dispersive integral, and fixed the subtraction constant by matching to the $\chi$PT$_3$ amplitude (22):

$$\begin{aligned} a_{\gamma \gamma ^*}(q_2^2) = e^2B_1(0,q_2^2)\big |_{{\chi \mathrm {PT}_3}} \equiv A_{\gamma \gamma ^*}(0,q_2^2)\big |_{{\chi \mathrm {PT}_3}}\,. \end{aligned}$$

(56)

To evaluate (55), we begin by decomposing the helicity partial wave

$$\begin{aligned} h_{0,++}^0(s,q_2^2) = h_{0,++}^{0,\mathrm {Born}}(s,q_2^2) + h_{0,++}^{0,\mathrm {scatt}}(s,q_2^2)\,, \end{aligned}$$

(57)

noting that Low’s theorem [67] implies the Born-subtracted partial wave $h_{0,++}^{0,\mathrm {scatt}}$ has a zero at $s=q_2^2$ (i.e. when the on-shell photon becomes soft $q_1 \rightarrow 0$).

The Born contribution to the helicity partial wave⁸

$$\begin{aligned} h_{0,++}^{0,\mathrm {Born}}\left( s,q_2^2\right) = -\sqrt{\frac{4}{3}}\frac{F_\pi ^V(q_2^2)}{s-q_2^2} \left[ \frac{4 m_{\pi }^2}{\sigma _\pi (s)} \ln \dfrac{1+\sigma _\pi (s)}{1-\sigma _\pi (s)} - 2q_2^2 \right] \end{aligned}$$

(58)

produces a double pole $\sim (s-q_2^2)^2$ in $\mathrm {disc}_s\, A_{\gamma \gamma ^*}$, so a decomposition of the integrand,

$$\begin{aligned} \frac{1}{(z-s)(z-q_2^2)^2}&= \frac{1}{(s-q_2^2)^2} \left[ \frac{1}{z-s} - \frac{1}{z-q_2^2}\right] \nonumber \\&\quad - \frac{1}{s-q_2^2} \frac{1}{\left( z-q_2^2\right) ^2}, \end{aligned}$$

(59)

is required in order to evaluate the dispersive integral numerically. In the above, $F_\pi ^V$ denotes the vector form factor of the pion, and is set to unity in LO $\chi$PT$_3$. Using the identity in (59), we get the Born part of the $K_S\rightarrow \gamma \gamma ^*$ amplitude

$$\begin{aligned}&A_{\gamma \gamma ^*}^\mathrm {Born}(s,q_2^2) \\&\quad = \frac{s}{\pi }\left\{ \frac{Q(s,q_2^2) - Q(q_2^2,q_2^2)}{(s-q_2^2)^2} - \frac{1}{s-q_2^2} \left[ \frac{\partial }{\partial \lambda } Q(\lambda ,q_2^2) \right] _{\lambda =q_2^2} \right\} , \nonumber \end{aligned}$$

(60)

where we have defined

$$\begin{aligned} Q(s,q^2)&= \int _{4m_{\pi }^2}^{\infty } \mathrm{d}z \frac{(z-q^2)^2\, \mathrm {disc}_s \, A_{\gamma \gamma ^*}^\mathrm {Born}(z,q^2)}{z(z-s-i\epsilon )}. \end{aligned}$$

(61)

Similarly, for the rescattering contribution, we use the identity

$$\begin{aligned} \frac{1}{(z-s)(z-q_2^2)} = \frac{1}{s-q_2^2} \left[ \frac{1}{z-s} - \frac{1}{z-q_2^2} \right] \end{aligned}$$

(62)

so that

$$\begin{aligned} A^{\mathrm {scatt}}_{\gamma \gamma ^*}(s,q_2^2) = \frac{s}{\pi } \left\{ \frac{R(s,q_2^2)-R(q_2^2,q_2^2)}{s-q_2^2}\right\} \,, \end{aligned}$$

(63)

where

$$\begin{aligned} R(s,q^2)&= \int _{4m_{\pi }^2}^{\infty } \mathrm{d}z \frac{(z-q^2)\,\mathrm {disc}_s \, A_{\gamma \gamma ^*}^\mathrm {scatt}(z,q^2)}{z(z-s-i\epsilon )}, \end{aligned}$$

(64)

Fig. 6

Energy dependence of helicity partial waves obtained from dispersive analyses of $\gamma \gamma ^{(*)}\rightarrow \pi \pi$ [19, 21]

In the evaluation of (60) and (63), we use the two Omnès inputs discussed in Sect. 4, as well as the pion form factor and helicity partial waves $h_{0,++}^{0}$ obtained from Moussallam’s single-channel analysis of $\gamma \gamma ^*\rightarrow \pi \pi$ [21]. The range of validity of $h_{0,++}^{0}$ can be inferred by comparing the result from the single-channel analysis at $q_2^2=0$ with that from GMM’s coupled-channel analysis of $\gamma \gamma \rightarrow \pi \pi$ [19]. As shown in Fig. 6, the real parts begin to differ for $\sqrt{s}\gtrsim 0.8$ GeV, while the imaginary parts differ for $\sqrt{s} \gtrsim 0.5$ GeV. The reason⁹ why the imaginary part differs at relatively small energies is because it is related to the real part via Watson’s theorem

$$\begin{aligned} \mathrm {Im}\, h_{0,++}^0(s) = \pm \mathrm {Re}\, h_{0,++}^0(s) \times \tan \delta _0^0(s)\,. \end{aligned}$$

(65)

Fig. 7

Energy dependence of the real and imaginary parts of the $K_S\rightarrow \gamma \gamma ^*$ amplitude $A_{\gamma \gamma ^*}$ for fixed values of $q_2^2$. Colour coding as in Fig. 5

Near $\sqrt{s}=0.8$, the phase is close to $\pi /2$, so small variations in the zero of $\mathrm {Re}\, h_{0,++}^0$ can lead to a large variation in $\mathrm {Im}\, h_{0,++}^0$. From a conservative viewpoint, this suggests that the cutoff be fixed to $\Lambda \simeq 0.8$ GeV. However, we have checked that increasing the cutoff to $\Lambda = 1.2$ GeV does not lead to a difference of more than $\approx 7\%$ in the resulting predictions for $A_{\gamma \gamma ^*}$. Note that this $7\%$ is the effect of a $100\%$ uncertainty on our input between 0.8 and 1.2 GeV. Since this small change is covered by our estimate of the systematic uncertainty, we take the larger cutoff as a benchmark value in our numerics and stress that only a coupled-channel analysis for this process would allow one to better assess this source of uncertainty and push the cutoff to yet higher energies. As noted in Sect. 4, however, there are non-trivial difficulties in performing a coupled-channel analysis for two-body K decays.

By combining (60) and (63), we obtain the desired result for the total $K_S\rightarrow \gamma \gamma ^*$ amplitude:

$$\begin{aligned} A_{\gamma \gamma ^*}(s,q_2^2) = a_{\gamma \gamma ^*}(q_2^2) + A_{\gamma \gamma ^*}^\mathrm {Born}(s,q_2^2) + A_{\gamma \gamma ^*}^\mathrm {scatt}(s,q_2^2). \end{aligned}$$

(66)

For fixed values of $q_2^2$, we first compare the predictions arising from (66) against those of $\chi$PT$_3$. In Fig. 7, we show the energy dependence of the amplitude for three values of $q_2^2$. As shown in the figure, when $q_2^2 < 4m_{\pi }^2$, the effect of FSI resembles that previously seen in $K_S\rightarrow \gamma \gamma$ (Fig. 5), with the real (imaginary) parts enhanced (suppressed) relative to $\chi$PT$_3$. However, as $q_2^2$ increases above the $\pi \pi$ threshold, the pion form factor $F_\pi ^V$ becomes progressively more important, and both real and imaginary parts in the dispersive amplitude are enhanced relative to LO $\chi$PT$_3$. This feature can be clearly seen in Fig. 8, where we keep $s=m_{K}^2$ fixed and vary $q_2^2$ within the physical region

$$\begin{aligned} 4m_\ell ^2 \le q_2^2 \le m_{K}^2 \end{aligned}$$

(67)

of the three-body decay. The effect of including the pion form factor in the $\chi$PT$_3$ amplitude shows a moderate enhancement at large $q_2^2$, especially for the real part. We also note that even for small values of $q_2^2$, the dispersive amplitude differs from $\chi$PT$_3$ due to the effects of FSI.

We now consider the predictions for the $K_S \rightarrow \gamma \ell ^+\ell ^-$ decay rates. Here the differential decay rate is [47]

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{\gamma \ell \ell }}{\mathrm{d}q_2^2} = \frac{m_K^3}{32\pi q_2^2} \left( 1-\frac{q_2^2}{m_{K}^2}\right) ^3\big |A_{\gamma \gamma ^*}(m_K^2,q_2^2)\big |^2 \frac{1}{\pi } \Pi (q_2^2), \end{aligned}$$

(68)

where the electromagnetic spectral function is given by

$$\begin{aligned} \frac{1}{\pi }\Pi (q_2^2) = \frac{\alpha }{3\pi } \left( 1 + 2\frac{m_\ell ^2}{q_2^2} \right) \sqrt{1-4m_\ell ^2/q_2^2} \,\theta (q_2^2-4m_\ell ^2). \end{aligned}$$

(69)

In Fig. 9, we compare the $\chi$PT$_3$ prediction [47] for the differential decay rate involving muons against our dispersive result. Evidently, the corrections are large for $q_2^2 \gtrsim 0.05$: again, this can be inferred from the $q_2^2$ behaviour shown in Fig. 8. We also see that, for this mode, the dominant source of the enhancement is due to the pion form factor.

Fig. 8

Dependence of the $K_S\rightarrow \gamma \gamma ^*$ amplitude on the photon momentum $q_2^2$ for fixed $s=m_{K}^2$. The real parts are denoted by the solid curves, while the imaginary parts are dashed. The bands on the dispersive results correspond to the systematic uncertainty

Fig. 9

Differential decay width for $K_S \rightarrow \gamma \mu ^+\mu ^-$, normalised to the total $K_S$ rate. Colour coding as in Fig. 8

The integrated rates (normalised to the total $K_S$ decay width) are shown in Table 2, where the uncertainties are determined as in Sect. 4, except for the subtraction constant: here we keep the subtraction point fixed and vary the $\chi$PT$_3$ amplitude by 30%. In both cases, the corrections are sizeable: for the electron mode we see a shift of $O(50\%)$, while in the muon mode we have a shift of $O(100\%)$. The origin of these shifts are different in each case. For the electron mode, the phase space is peaked near the origin $q_2^2=0$, so the role of $F_\pi ^V$ is suppressed and the dominant effect is due to FSI. On the other hand, the enhancement in the muon mode is predominantly due to the form factor (Fig. 9).

Table 2 Predictions for the branching ratio of $K_S\rightarrow \gamma \ell ^+\ell ^-$. The second row indicates the effect of including the pion vector form factor $F_\pi ^V$ in the $\chi$PT$_3$ amplitude

6 Summary

Current and near-future searches for rare kaon decays are reaching sensitivities where a better control over the long-distance contribution to the relevant amplitudes is needed. Chiral perturbation theory and lattice QCD are two of the main tools which allow a systematic calculation of these contributions, but getting FSI under good control in either of these approaches is challenging. Dispersion relations offer a different, complementary methodology to the previous two, which addresses specifically the treatment of FSI. If one can match the dispersive and the chiral representation, and solve the dispersion relation, one can usually obtain much better control over FSI effects. In this paper, we have taken a first step in this direction by introducing a dispersive framework for $K_S\rightarrow \gamma \gamma$ and $K_S\rightarrow \gamma \ell ^+\ell ^-$.

A key feature of our analysis is that by allowing the weak Hamiltonian to carry momentum, there is no need to extrapolate the kaon mass off-shell. Moreover, the input for the sub-amplitudes $K_S \rightarrow \pi \pi$ and $\gamma \gamma ^{(*)}\rightarrow \pi \pi$ provide a strong constraint on the dispersive amplitude, and when expressed in terms of measurable quantities we find relatively small uncertainties in our final predictions. In particular, the Born contribution to $\gamma \gamma ^*\rightarrow \pi \pi$ has a negligible uncertainty because the pion vector form factor is known to high precision: for this particular contribution, going off-shell in the photon momentum does not lead to larger uncertainties.

In general, we find that the effects due to FSI provide sizeable corrections to the predictions from LO $\chi$PT$_3$. For $K_S\rightarrow \gamma \gamma$, these effects distort the amplitude such that the relative size of the real and imaginary parts are interchanged. That LO $\chi$PT$_3$ predicts too large an imaginary part can be concluded on the basis of unitarity alone and by taking as input the experimental measurements of $K_S \rightarrow \pi \pi$ and $\gamma \gamma \rightarrow \pi \pi$ at $s=m_K^2$: LO $\chi$PT$_3$ overshoots the correct value by 21%. As for the real part, we need to rely on analyticity and on a dispersive treatment of both $K_S \rightarrow \pi \pi$ as well as $\gamma \gamma \rightarrow \pi \pi$, where the latter is also well constrained by data. The uncertainties involved here are larger, but still allow us to firmly conclude that the prediction of LO $\chi$PT$_3$ has the correct sign (negative), but substantially underestimates the absolute value: we obtain an enhancement of about 70%. This feature has been observed earlier by Kambor and Holstein [49], who noted that the reasonable agreement between the rates from LO $\chi$PT$_3$ and experiment should be not be viewed as a success of the effective theory, since unitarization methods produce nearly identical results. Our results confirm this observation and places it on a stronger footing since we do not rely on off-shell extrapolations.

For $K_S\rightarrow \gamma \ell ^+\ell ^-$, we found that the pion vector form factor produces an additional source of enhancement over LO $\chi$PT$_3$. Since the form factor is well known experimentally in both the timelike and the spacelike region, we can evaluate this particular correction very reliably, which is an important outcome of this analysis. Although less pronounced in the electron mode due to phase space suppression, we observed a particularly large increase in the rate for the muon mode. In view of this result, we believe the muon mode has good prospects of being observed at the projected sensitivities of KLOE-2.

In our analysis, we have restricted ourselves to the case where at most one photon is off-shell. It would be interesting to extend our dispersive framework to the doubly off-shell amplitude $K_S \rightarrow \gamma ^*\gamma ^*$, which provides the dominant contribution to the rare decay $K_S \rightarrow \ell ^+\ell ^-$. For the muon mode, LHCb [68] has recently placed an upper bound on the rate $\mathrm {BR}(K_S\rightarrow \mu ^+\mu ^-) < 9 \times 10^{-9}$, and future upgrades are expected to improve the sensitivity down to $O(10^{-10})$ [69]. Given that a signal well above $10^{-11}$ has been claimed [70] to be clear evidence of physics beyond the SM, determining the role of FSI in this mode will be essential in order to draw definite conclusions regarding the SM background. Work in this direction is currently in progress.