Excited state mass spectra of doubly heavy baryons ${\Omega _{cc}}$, ${\Omega _{bb}}$, and ${\Omega _{bc}}$

Abstract

We discuss the mass spectrum of $\Omega$ baryon with two heavy quarks and one light quark (ccs, bbs, and bcs). The main goal of the paper is to calculate the ground state masses and after that, the positive and negative parity excited states masses are also obtained within a hypercentral constituent quark model, using Coulomb plus linear potential framework. We also added a first order correction to the potential. The mass spectra up to 5S for radial excited states and 1P–5P, 1D–4D, and 1F–2F states for orbital excited states are computed for $\Omega _{cc}$, $\Omega _{bb}$, and $\Omega _{bc}$ baryons. Our obtained results are compared with other theoretical predictions, which could be a useful complementary tool for the interpretation of experimentally unknown heavy baryon spectra. The Regge trajectory is constructed in both the ($n_r$, $M^{2}$) and the (J, $M^{2}$) planes for $\Omega _{cc}$, $\Omega _{bb}$, and $\Omega _{bc}$ baryons and their slopes and intercepts are also determined. Magnetic moments of doubly heavy $\Omega '$s are also calculated.

1 Introduction

The doubly heavy $\Omega$ baryons represent a unique part of three-quark systems because they contain a strange light quark. Experiments and theoretical calculations have been diversely used in studying the heavy hadrons in the last few years. So far singly heavy baryons have been discovered and the quantum numbers of most of the observed states have been assigned. Many experiments, LHCb, BELLE, BABAR, FOCUS, are planning to detect doubly and triply heavy baryons [1, 2]. The future project PANDA experiment at GSI is expected to give fruitful results in the heavy baryon sector; especially the charm sector. In fact, $\Xi _{cc}^{+}$ has been discovered [3] but none of the double/triple heavy $\Omega$ baryons have been discovered. Predictions for the masses of doubly heavy baryons have been presented by many authors so far. Indeed, this gives additional ground for new theoretical and experimental investigations of doubly as well as triply heavy baryonic properties. Much theoretical work has focused on doubly heavy baryons, like the relativistic three-quark model [4, 5], the Salpeter model [6], heavy-quark effective theory [7], QCD sum rule [8–12], semiempirical mass formulas [13], the Hamiltonian model [14], the variational approach [15], the three-body Faddeev method [16], the hypercentral constituent quark model [17, 18], lattice QCD [19–24], etc. Recently, Wei et al. used Regge phenomenology, and with the quadratic mass relations, they obtained doubly and triply charmed and bottom baryon masses [25, 26].

In this paper we shall study baryons containing two heavy quarks; charm–charm, bottom–bottom, and charm–bottom with a light strange quark. First of all, the mass spectra of these baryons ($\Omega _{cc}^{+}$, $\Omega _{bb}^{-}$, and $\Omega _{bc}^{0}$) are determined in the framework of hypercentral constituent quark model (HCQM) [17, 18, 27–33]. In this paper we use coloumb plus linear potential and solve six-dimensional hyperradial Schrödinger equation numerically. Second, the first order correction is taken into account in the potential. So, the purpose of our new investigation with an alternative calculation scheme of the baryon mass spectrum are elaborated as compared with the earlier performed investigations through the variational approach in Ref. [17, 18]. The quantum numbers of the doubly heavy ground state baryons are as follows:

• Strangeness $S=-1$ and isospin $I=0$

• Spin-parity $J^{P}$=$\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$

• Quark content ccs, bbs, bcs

The calculations have been performed for the radial excited states (up to 5S) and orbital excited states (1P–5P, 1D–4D, and 1F–2F) at $\nu$=1.0¹ for $\Omega _{cc}, \Omega _{bb}$ and $\Omega _{bc}$ systems. To obtain the excited states of these doubly heavy baryons, we follow the same methodology as used in previous calculations for singly charm baryons [27, 28]. Ground states were studied by various theoretical approaches for $\Omega _{cc}$, $\Omega _{bb}$, and $\Omega _{bc}$ and are listed in Table 1.

The paper is organized as follows. After the introduction, we briefly describe our hypercentral constituent quark model in Sect. 2. In Sect. 3 we present our results and draw Regge trajectories for $\Omega _{cc}$, $\Omega _{bb}$, and $\Omega _{bc}$ baryons. We also calculate the magnetic moments for each baryons. In the last section, we draw our conclusions.

2 The HCQM model

Table 1 The quark model parameters

The baryons are made of three quarks and they are related to the Jacobi co-ordinates given as [34]

$$\begin{aligned} \mathbf {\rho }= & {} \frac{1}{\sqrt{2}}(\mathbf {r_{1}} - \mathbf {r_{2}}),\end{aligned}$$

(1)

$$\begin{aligned} \mathbf {\lambda }= & {} \frac{m_1\mathbf {r_1}+m_2\mathbf {r_2}-(m_1+m_2)\mathbf {r_3}}{\sqrt{m_1^2+m_2^2+(m_1+m_2)^2}}. \end{aligned}$$

(2)

Table 2 Ground state masses of $\Omega _{cc}^{+}$, $\Omega _{bb}^{-}$, and $\Omega _{bc}^{0}$

Here $m_i$ and $\mathbf {r_i}$ (i = 1, 2, 3) denote the mass and coordinate of the ith constituent quark. Quarks masses are shown in Table 1. The respective reduced masses are given by

$$\begin{aligned} m_{\rho }= & {} \frac{2 m_{1} m_{2}}{m_{1}+ m_{2}},\end{aligned}$$

(3)

$$\begin{aligned} m_{\lambda }= & {} \frac{2 m_{3} (m_{1}^2 + m_{2}^2+m_1m_2)}{(m_1+m_2)(m_{1}+ m_{2}+ m_{3})}. \end{aligned}$$

(4)

The hyperradius $x= \sqrt{\rho ^{2} + \lambda ^{2}}$ and hyperangle $\xi = arctan (\frac{\rho }{\lambda })$ are given in terms of the absolute values $\rho$ and $\lambda$ of the Jacobi coordinates [35–37]. In the center of mass frame ($R_{c.m.} = 0$), the kinetic energy operator can be written as

$$\begin{aligned} -\frac{\hbar ^2}{2m}(\bigtriangleup _{\rho } + \bigtriangleup _{\lambda })= -\frac{\hbar ^2}{2m}\left( \frac{\partial ^2}{\partial x^2}+\frac{5}{x}\frac{\partial }{\partial x}+\frac{L^2(\Omega )}{x^2}\right) \end{aligned}$$

(5)

where $L^2(\Omega )=L^2(\Omega _{\rho },\Omega _{\lambda },\xi )$ is the quadratic Casimir operator of the six-dimensional rotational group O(6) and its eigen functions are the hyperspherical harmonics,

$$\begin{aligned} Y_{[\gamma ]l_{\rho }l_{\lambda }}(\Omega _{\rho },\Omega _{\lambda },\xi ), \end{aligned}$$

satisfying the eigenvalue relation

$$\begin{aligned} L^2Y_{[\gamma ]l_{\rho }l_{\lambda }}(\Omega _{\rho },\Omega _{\lambda },\xi )=-\gamma (\gamma +4) Y_{[\gamma ]l_{\rho }l_{\lambda }}(\Omega _{\rho },\Omega _{\lambda },\xi ). \end{aligned}$$

Here, $\gamma$ is the grand angular momentum quantum number. In the present paper, the confining three-body potential is chosen within a string-like picture, where the quarks are connected by gluonic strings and the potential strings increase linearly with the collective radius $r_{3q}$ as mentioned in [38]. Accordingly the effective two-body interactions can be written as

$$\begin{aligned} \sum _{i<j}V(r_{ij})=V(x)+\cdots \end{aligned}$$

(6)

In the hypercentral approximation, the potential only depends on the hyperradius (x). More details can be found in Refs. [38, 39]. The hyperradius x is a collective coordinate and therefore the hypercentral potential contains also the three-body effects. The Hamiltonian of the three-body baryonic system in the hCQM is then expressed as

$$\begin{aligned} H=\frac{P_{x}^{2}}{2m} +V(x) \end{aligned}$$

(7)

Table 3 Radial excited states masses of $\Omega _{cc}$, $\Omega _{bb}$, and $\Omega _{bc}$ baryons (in GeV)

where $m=\frac{2 m_{\rho } m_{\lambda }}{m_{\rho } + m_{\lambda }}$ is the reduced mass and x is the six-dimensional radial hypercentral coordinate of the three-body system. The hyperradial Schrödinger equation corresponding to the above Hamiltonian can be written

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}}{\mathrm{d} x^{2}} \!+\! \frac{5}{x} \frac{\mathrm{d}}{\mathrm{d}x} - \frac{\gamma (\gamma +4)}{x^{2}} \right] \Psi _{ \gamma }(x) \!=\! -2m[E- V(x)]\Psi _{ \gamma }(x) \end{aligned}$$

(8)

where $\Psi _{\gamma }$(x) is the hypercentral wave function and $\gamma$ is the grand angular quantum number. We consider a reduced hypercentral radial function, $\phi _{\gamma }(x) = x^{\frac{5}{2}}\Psi _{ \gamma }(x)$. Thus, the six-dimensional hyperradial Schrödinger equation reduces to

$$\begin{aligned} \left[ \frac{-1}{2m}\frac{\mathrm{d}^{2}}{\mathrm{d} x^{2}} + \frac{\frac{15}{4}+ \gamma (\gamma +4)}{2mx^{2}}+ V(x)\right] \phi _{ \gamma }(x)= E\phi _{\gamma }(x). \end{aligned}$$

(9)

For the present study we consider the hypercentral potential V(x) as the color Coulomb plus linear potential with first order correction [46–51],

$$\begin{aligned} V(x) = V^{0}(x) + \left( \frac{1}{m_{\rho }}+ \frac{1}{m_{\lambda }}\right) V^{(1)}(x)+V_{SD}(x) \end{aligned}$$

(10)

where $V^{0}(x)$ is given by

$$\begin{aligned} V^{(0)}(x)= \frac{\tau }{x}+ \beta x \end{aligned}$$

(11)

and the first order correction is similar to the one given by [46],

$$\begin{aligned} V^{(1)}(x)= - C_{F}C_{A} \frac{\alpha _{s}^{2}}{4 x^{2}}. \end{aligned}$$

(12)

Table 4 Orbitally excited states masses of $\Omega _{cc}$ baryons (in GeV)

Here, $\tau$ is the hyper-Coulomb strength corresponding to the strong running coupling constant $\alpha _{s}$ [27, 28]. $\beta$ is the string tension of the confinement part of potential. $C_{F}$ and $C_{A}$ are the Casimir charges of the fundamental and adjoint representation. If we compare Eq. (9) with the usual three-dimensional radial Schrödinger equation, the resemblance between angular momentum and hyper angular momentum is given by [52], ${l(l+1)\rightarrow \frac{15}{4}+ \gamma (\gamma +4)}$. The spin-dependent part, $V_{SD}(x)$ of Eq. (10) contains three types of interaction terms [53],

$$\begin{aligned} V_{SD}(x)= V_{SS}(x)(\mathbf {S_{\rho }}.\mathbf {S_\lambda }) + V_{\gamma S}(x) (\mathbf {\gamma } \cdot \mathbf {S})&\nonumber \\ + V_{T} (x) \left[ S^2-\frac{3(\mathbf {S }\cdot \mathbf {x})(\mathbf {S} \cdot \mathbf {x})}{x^{2}} \right] . \end{aligned}$$

(13)

The spin–spin term $V_{SS} (x)$ gives the spin singlet triplet splittings, the spin–orbit term $V_{\gamma S}(x)$ and tensor term $V_{T}(x)$ describe the fine structure of the states. The details of the terms are given in [27, 28]. We numerically solve the six-dimensional Schrödinger equation using the Mathematica notebook [54]. We have followed the $^{(2S+1)} {\gamma }_{J}$ notations for spectra of baryons.

Table 5 Orbitally excited states masses of $\Omega _{bb}$ baryons (in GeV)

3 Results and discussions

3.1 Mass spectra

The ground and excited states of doubly heavy $\Omega$ baryons are still experimentally unknown to us. Therefore, we have calculated the ground as well as excited state masses of doubly heavy baryons $\Omega _{cc}$, $\Omega _{bb}$, and $\Omega _{bc}$ (see Tables 2, 3, 4, 5 and 6). Such kind of theoretical study is very much useful to obtain their experimental states ($J^{P}$ values), masses, and other properties. These mass spectra of doubly heavy baryons are obtained by using Coulomb plus linear potential in the hypercentral constituent quark model. Our computed ground states with $J^{P}=\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$ are compared with different theoretical approaches in Table 2. Our estimated ground state masses of $\Omega _{cc}^{+}$ have a difference in the range of $\approx$ 100 MeV with other predictions, whereas the $\Omega _{bb}^{-}$ and $\Omega _{bc}^{0}$ masses are higher than others.

Lattice QCD calculations for excited states of $\Omega _{cc}$ have been performed by Padmanath et al. up to $\frac{7}{2}^{+}$ and $\frac{7}{2}^{-}$ parities [55]. They use a variational approach in which they try to write down the eigen states in terms of the operators and determine the energies from the evolution of the correlators of the eigenstates. The energy splittings of the $\Omega _{cc}$ states are from the mass of the $\eta _c$ meson. Reference [56] estimates the ground state mass of $\Omega _{cc}$ to be around 3.726 GeV in chiral perturbation theory.

The radial excited state masses for these three baryons are computed from 2S–5S and are compared with Refs. [5, 6, 14–16] in Table 3. We can observe that our 2S and 3S states show a smaller difference in MeV, see Ref. [5], than other references for $\Omega _{cc}^{+}$ and $\Omega _{bb}^{-}$. Next, in the case of $\Omega _{bc}$ only Ref. [6] has calculated radial excited states up to 3S. We noticed that our 2S and 3S state masses (A(B)) with $J^{P}$=$\frac{1}{2}^{+}$ are 76(69) and 225(211), while 80(73) and 224(210) (with $J^{P}$=$\frac{3}{2}^{+}$) are lower, respectively. Note that A are masses without first order correction and B are masses by adding a first order correction in Tables 3, 4, 5, and 6.

The orbital excited states are calculated for 1P–5P, 1D–4D, and 1F–2F mentioned in Tables 4, 5, and 6. Isospin splittings were also considered, which means that we have considered all possible combinations of total spin S and total angular momentum J to obtain orbital states mass spectra. We can observe that the total combinations for P, D, and F states number 5, 6, and 6, respectively. Other theoretical approaches have also calculated these orbital excited states but they have not considered all (S, J) combinations. We have compared our outcomes with other models in Tables 4, 5, and 6.

Our obtained orbital excited masses (A) are compared and discussed with other predictions in the following paragraph. For $\Omega _{cc}$, our 1P state $J^{P}=\frac{1}{2}^{-}$ shows 38 MeV (with [5]), $J^{P}=\frac{3}{2}^{-}$ shows 38 MeV and $J^{P}=\frac{5}{2}^{-}$ show 123 MeV (with [25]) difference. Our 2P state $J^{P}=\frac{1}{2}^{-}$ shows 10 MeV (with [5]), $J^{P}=\frac{3}{2}^{-}$ shows 27 MeV (with [14]) difference. Our 1D state $J^{P}=\frac{5}{2}^{+}$ shows 40 MeV and $J^{P}=\frac{3}{2}^{-}$ shows 199 MeV difference with [25]. For the 2D–3D states the difference is 79 and 4 MeV for $J^{P}=\frac{5}{2}^{+}$ with Ref. [14]. Our 1F state values are 119($J^{P}=\frac{7}{2}^{-}$) and 272($J^{P}=\frac{9}{2}^{-}$) MeV lower than Ref. [25].

Table 6 Orbitally excited states masses of $\Omega _{bc}$ baryons (in GeV)

For $\Omega _{bb}$, our 1P state $J^{P}=\frac{1}{2}^{-}$ and $J^{P}=\frac{3}{2}^{-}$ are 18 and 10 MeV higher than Ref. [15]. Reference [14] has masses for $J^{P}=\frac{1}{2}^{-}$, $J^{P}=\frac{3}{2}^{-}$, and $J^{P}=\frac{5}{2}^{-}$ which are 85, 80, and 154 MeV lower than our prediction. Our 3P state shows 39 MeV difference with [14]. Our 1D state $J^{P}=\frac{5}{2}^{+}$ shows 48 and 57 MeV difference with [14, 15], respectively. We have also compared our results with the recent paper [26] for 1P, 1D, and 1F states. Their values are higher than ours. The orbital mass spectra of the third doubly heavy baryon, $\Omega _{bc}$, is not calculated in any approach. References [5, 44] stated that excited levels are not possible for $\Omega _{bc}$ because the excited states of diquarks $\lbrace bc\rbrace$ are not stable due to the emission of soft gluons. We have not considered the diquark mechanism in our approach, so that we calculated orbital mass spectra for the $\Omega _{bc}$ baryon. We guess that we are the first to calculate these spectra.

3.2 Regge trajectory

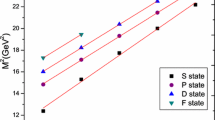
We calculated both radial and orbital excited states masses up to L = 3. Using them we are able to construct Regge trajectories in the (n, $M^{2}$) and (J, $M^{2}$) planes. n is the principal quantum number and J is the total spin. The Regge trajectories are presented in Figs. 1, 2, 3, 4, and 5. Straight lines were obtained by the linear fitting in all figures. The ground and radial excited states S ($J^{P}=\frac{1}{2}^{+}$) and the orbital excited state P ($J^{P}= \frac{1}{2}^{-}$), D ($J^{P}= \frac{5}{2}^{+}$), and F ($J^{P}= \frac{7}{2}^{-}$) are plotted in Figs. 1, 2, and 3 from bottom to top. We use

$$\begin{aligned} n_r=\beta M^2+ \beta _{0} \end{aligned}$$

(14)

Fig. 1

Regge trajectory ($M^{2}$ $\rightarrow$ n) for $\Omega _{cc}$ baryon

Fig. 2

Regge trajectory ($M^{2}$ $\rightarrow$ n) for $\Omega _{bb}$ baryon

Fig. 3

Regge trajectory ($M^{2}$ $\rightarrow$ n) for $\Omega _{bc}$ baryon

Fig. 4

Regge trajectory ($M^{2}$ $\rightarrow$ J) for $\Omega _{cc}$ baryon

Fig. 5

Regge trajectory ($M^{2}$ $\rightarrow$ J) for $\Omega _{bb}$ baryon

where $\beta$ and $\beta _{0}$ are the slope and intercept, respectively, and $n_{r}$= n-1. The fitted slopes and intercepts are given in Table 7.

Table 7 Fitted slopes and intercepts of the Regge trajectories in the (n, $M^{2}$) plane

Table 8 Fitted parameters $\alpha$ and $\alpha _0$ are slope and Intercept of parent and daughter Regge trajectories. Columns 3, 4 are for natural parities and 5, 6 are for unnatural parities

Table 9 Magnetic moment (in nuclear magnetons) of $J^{P}$: $\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$ doubly heavy baryons

We use the natural ($J^{P}=\frac{1}{2}^{+}$, $J^{P}=\frac{3}{2}^{-}$, $J^{P}=\frac{5}{2}^{+}$, $J^{P}=\frac{7}{2}^{-}$) and unnatural ($J^{P}=\frac{3}{2}^{+}$, $J^{P}=\frac{5}{2}^{-}$, $J^{P}=\frac{7}{2}^{+}$, $J^{P}=\frac{9}{2}^{-}$) parity masses and plotted graphs for $\Omega _{cc}$ and $\Omega _{bb}$ (see Figs. 4, 5). For that reason we use

$$\begin{aligned} J=\alpha M^2+ \alpha _{0} \end{aligned}$$

(15)

where $\alpha$ and $\alpha _{0}$ are the slope and intercept, respectively. The fitted slopes and intercepts for both natural and unnatural parities are given in Table 8. We observe that the squares of the calculated masses fit very well to the linear trajectory and yield almost parallel states, equidistant in S, P, D, and F. We can determine the possible quantum numbers and prescribe them to particular Regge trajectory with the help of our obtained results.

3.3 Magnetic moments

The magnetic moment of baryons are obtained in terms of the spin, charge, and effective mass of the bound quarks as [18, 29–33]

$$\begin{aligned} \mu _{B}=\sum _{i}\langle \phi _{sf}\vert \mu _{iz}\vert \phi _{sf}\rangle ) \end{aligned}$$

where

$$\begin{aligned} \mu _{i}=\frac{e_i \sigma _i}{2m_{i}^{eff}} \end{aligned}$$

(16)

$e_i$ is the charge and $\sigma _i$ is the spin of the respective constituent quark corresponding to the spin flavor wave function of the baryonic state. The effective mass for each of the constituting quark $m_{i}^{eff}$ can be defined as

$$\begin{aligned} m_{i}^{eff}= m_i\left( 1+ \frac{\langle H \rangle }{\sum _{i} m_i} \right) \end{aligned}$$

(17)

where $\langle H \rangle$ = E + $\langle V_{spin} \rangle$. Using these equations, we calculated the magnetic moments of the $\Omega _{cc}^{+}$, $\Omega _{bb}^{-}$, and $\Omega _{bc}^{-}$ baryons. The spin flavor wave function [57] and magnetic moments are given in Table  9. Our obtained ground state magnetic moments are also compared with others and the results are reasonably close.

4 Conclusions

The ground state as well as excited state masses are obtained for doubly heavy $\Omega$ baryons in hCQM; they are tabulated in Tables 2, 3, 4, 5, and 6. We have compared our results with other approaches and they are not in mutual agreement. Moreover, all are unknown experimentally. Due to that fact, we cannot single out any model. It is very important to compare results with lattice QCD but for most of them have calculated only ground state masses of these baryons [21–23]. We have also constructed the Regge trajectories from the masses obtained. This study will help future experiments to identify the baryonic states from resonances. In addition, we have calculated the magnetic moments and they are fairly in agreement with other calculations. We have successfully employed this model to study doubly heavy $\Omega$ baryons. Now, we would like to calculate the properties of $\Xi$ baryons in the future.