1 Introduction

One of the recently discovered concepts that has impacted the theoretical physics community in the most significant way is most likely the idea of a noncommutative (NC) spacetime, which led to a NC generalization of quantum mechanics and field theory. The idea of noncommutativity of spacetime was first discussed in the work by Snyder [1] and Connes [2, 3]. The above concept (NC) spacetime allows one to find a possible solution to ultraviolet divergencies in quantum field theory [4, 5]. The NC physics also arises as a possible scenario for the short-distance behavior of physical theories (at the Planck scale). At this scale, the universal constants \(c, \hbar \), and G appear naturally equivalent. Below the Planck length, the distance loses its meaning [4–6] and the physical phenomena are believed to be nonlocal. NC geometry could be realized by introducing the noncommutativity through the coordinates which satisfy the commutation relations \([ x^\mu , x^\nu ]=i\theta ^{\mu \nu }\), where \(\theta ^{\mu \nu }\) is a skew-symmetric matrix characterizing the deformation of the spacetime. This leads to a new Heisenberg uncertainty relation, given on the spacetime coordinates by \(\Delta x^\mu \Delta x^\nu \ge \theta ^{\mu \nu }\), and this makes this spacetime a quantum space [6, 7]. The important implications of noncommutativity are the loss of Lorentz invariance in the dispersion relations and the loss of causality [8–13]. Intuitive arguments involving quantum mechanics in NC space are realized by imposing the commutation relations, now between coordinates and momenta, as

$$\begin{aligned}{}[ x^\mu , x^\nu ]=i\theta ^{\mu \nu },\quad [p^\mu ,p^\nu ]=i\gamma ^{\mu \nu },\quad [x^\mu , p^\nu ]=i\hbar \kappa ^{\mu \nu }\nonumber \\ \end{aligned}$$
(1)

where \(\gamma ^{\mu \nu }\) are also skew-symmetric matrices. In this paper we restrict ourself to the case where \(\gamma ^{\mu \nu }=0\), this implies that \(\kappa ^{\mu \nu }=\delta ^{\mu \nu }\), the Kronecker symbol. We also assume that the tensor \(\theta ^{\mu \nu }\) is chosen to have the dimension of length \(\cdot \) time, i.e., \(\theta ^{0j}=\theta ^j\in \mathbb {R}, \,\,\theta ^{ij}=0,\,\, \,\,i, j=1,2,\ldots , D.\) The noncommutative variables can be expressed in terms of commutative coordinates as \(x^j=x_c^j-i\theta ^j\partial _0=( x ),\) and \( p^j=p^j_c,\,\, p^0=i\hbar \partial _0=E\), where the index c is used to specify the commutative variables and where E is the energy of the system. The Hamiltonian of quantum system on NC space can be expressed with the commutative coordinates \(H(x,p)\equiv H_c(x_c,p_c,\theta )\), where the parameter \(\theta =\theta ^j\) is showed to have the fundamental limit \(\theta \preceq 1.6\cdot 10^{-27}\mathrm{m}\cdot \mathrm{s}\approx 0.3 \mathrm{(keV)}^{-2}\), which is smaller than the one obtained by the theory of quantum gravity [14, 15].

The compactified extra dimension is motivated by string theory, which predicts the existence of extra dimensions and noncommutativity between coordinates. Our idea is to understand how the eigenvalue problem changes if we periodically identify one of the NC coordinates \(x^j=(x^1,x^2,x^3,x^4)\) in the target space, say \([-\pi R,\pi R]\ni w, \text {such that}\,\, x^4=w - 2\pi R k,\,\, k\in \mathbb {Z}\), and R is the radius of the circle. The wave function \(\psi (x^0,x^{\bar{\ell }},x^4),\,\bar{\ell }=1,2,3\), can be expanded in the Fourier mode as [16]

$$\begin{aligned} \psi (x^0,x^{\bar{\ell }},x^4)=\frac{1}{\sqrt{2\pi R}}\sum _{n=-\infty }^\infty \, \psi _n(x^0,x^{\bar{\ell }})\exp \left( \frac{i n\, x^4}{R}\right) .\nonumber \\ \end{aligned}$$
(2)

Note that the orthonormalized functions \((2\pi R)^{-1/2}\exp \big (i x^4 n/R\big )\) are eigenfunctions of the operator \(\nabla ^2_{x^4}\) with eigenvalues \(E_{n0}=-n^2/R^2\). This means that the spectrum of a quantum system defined with one dimension compactified is in the form \(E_{nl}=E_{n0}+E'_{nl}\), where l is a positive integer, \(E'_{nl}\) depends on the potential associated to the system which is required to be computed. In the following paper we investigate the spectrum of the Coulomb and Yukawa Hamiltonian on \((4+1)\)-dimensional NC spacetime. Using the first order approximation of the deformation parameter \(\theta \) and by compactifying one extra dimension \(x^4\) we have the resulting topology \(\mathbb {R}^{3+1}\times S^1\) (see [17] and [18] for the essential reviews), the spectrum may be given exactly. We prove that in the case of space \(\cdot \) time noncommutativity, the correction of the energy spectrum does not depend on the NC deformation parameter \(\theta \) but rather on the parameter associated to the compactified dimension.

Our paper is organized as follows. In Sect. 2, we focus on the hydrogen atom in \((D+1)\)-dimensional noncommutative space with non-compactified extra dimension. We discuss the particular case where \(D= 4\) in which the solution of the spectral problem can be solved. The Yukawa potential is also discussed in this section. In Sect. 3 the same problem is solved with compactified extra dimensions. The discussion and conclusion are given in Sect. 4.

2 Hydrogen atom in noncommutative space with non-compactified extra dimension

In this section we focus on the hydrogen atom problem defined in \((D+1)\) dimensional NC spacetime (we consider the particular case where \(D=4\)). To be specific, the model is given with the spherical potential of the form

$$\begin{aligned} V(\vec r_{nc})=-\frac{q_e^2}{|\vec r_{nc}|^{D-2}}, \end{aligned}$$
(3)

where \(q_e\) is related to the atomic charge and where we use the following notation: \(\vec {r}_{nc}=\vec {r}-i\vec \theta \partial _0\), i.e., the NC coordinates are \(\vec r_{nc}=(x)\) and the commutative coordinates are \(\vec r=(x_c)\). It would be advisable to work in a spherical coordinates system, \(\vec r=(r,\alpha _1,\alpha _2,\alpha _3)\), such that \(r\in \mathbb {R}_+\), \(0<\alpha _{\bar{\ell }}<\pi ,\,\, \bar{\ell }=1,2\), and \(0<\alpha _{3}<2\pi \). It thus follows that the Hamiltonian of the system is

$$\begin{aligned} H=-\frac{\hbar ^2}{2m}\Big [\frac{\partial ^2}{\partial r^2} + \frac{D-1}{r}\frac{\partial }{\partial r}-\frac{\mathcal {L}^2(D-1)}{r^2}\Big ]+V(\vec {r}_{nc}),\nonumber \\ \end{aligned}$$
(4)

where \(\mathcal {L}^2(D-1)\) is the Laplace–Beltrami operator on the \((D-1)\)-sphere. Hence the potential (3), using the first order Taylor expansion on \(\vec \theta \), is

$$\begin{aligned} V(\vec r_{nc})= & {} -\frac{ q_e^2}{|\vec r-i\vec \theta \partial _0|^{D-2}}\\\approx & {} - \frac{q_e^2}{r^{D-2}}\Big (1 + i(D-2)\frac{\vec {r}.\vec {\theta }}{r^2}\partial _0 \Big ). \end{aligned}$$
(5)

We consider the adequate choice, such that the vector \(\vec \theta \) is transformed in the spherical coordinates to \(\vec {r}.\vec {\theta }\equiv r \theta \) [14]. Furthermore, the spherical functions \( \mathcal {Y}_\ell ^{(D-1)}(\alpha _1,\alpha _2, \ldots , \alpha _{D-1})\), which are the eigenfunctions of the operator \(\mathcal L(D-1)\) are considered:

$$\begin{aligned} \mathcal {L}^2 (D-1) \mathcal {Y}_\ell ^{(D-1)} = \ell (\ell +D-2) \mathcal {Y}_\ell ^{(D-1)} = \lambda _D \mathcal {Y}_\ell ^{(D-1)},\nonumber \\ \end{aligned}$$
(6)

where \(\ell \) is the orbital angular momentum quantum number.

Note that the Hamiltonian (4) depends on the partial derivative with respect to the time t, due to the relation (5). But one can show that the wave function \(\psi (\vec r,t)\), namely the solution of the Schrödinger equation is expressed as \(\psi (\vec {r},t) = \mathcal {Y}_\ell ^{(D-1)}\psi (r)f(t)\), where the time dependent function is \( f(t) = \exp \big ({-\frac{i}{\hbar }Et}\big ) \) and where \(\psi (r)\) satisfies the radial equation

$$\begin{aligned}&\Bigg [\frac{\mathrm{d}^2 }{\mathrm{d}r^2} + \frac{D-1}{r}\frac{\mathrm{d}}{\mathrm{d}r}-\Big (\frac{\lambda _D}{r^{2}} - \frac{\nu ^2}{r^{D-2}} - \frac{\mu _D}{r^{D-1}} - \alpha ^2\Big )\Bigg ]\psi (r) = 0,\nonumber \\ \end{aligned}$$
(7)

with \( \alpha ^2 = \frac{2m E}{\hbar ^2},\,\, \nu ^2 = \frac{2m q_e^2}{\hbar ^2} ,\,\,\mu _D = (D-2) \nu ^2 \theta \, E/\hbar . \) Now for \(D=4\), this equation turns to become

$$\begin{aligned} \Bigg [\frac{\mathrm{d}^2 }{\mathrm{d}r^2} + \frac{3}{r}\frac{\mathrm{d}}{\mathrm{d}r}-\Big (\frac{\lambda _4-\nu ^2}{r^{2}} - \frac{\mu _4}{r^{3}} - \alpha ^2\Big )\Bigg ]\psi (r) = 0. \end{aligned}$$
(8)

However, in this case (unlike for the commutative case discussed in [17, 18]), such an equation seems to be non-solvable. We provide an algebraic method, which will allow us to derive the solution of this equation. For this purpose, let us reparameterize the function \(\psi (r)\) as \(\psi (r):=\psi ( r, \theta \,)\). Then \(\psi (r,0)\) corresponds to the solution of Eq. (8) in the case where \(\theta =0\). The first order Taylor expansion on \(\theta \) of the function \(\psi (r,\theta )\) takes the form

$$\begin{aligned} \psi (r,\theta \,)= & {} \psi (r,0) + \theta \, \frac{\mathrm{d}\psi (r,\theta \,)}{\mathrm{d}\theta \,}\Big |_{\theta \, = 0} + \mathcal {O}(\theta \,^2). \end{aligned}$$
(9)

We get simply

$$\begin{aligned} \psi (r,0) = \frac{{ c}}{r}{ J}_{\nu }(\alpha r)+ \frac{{ c'}}{r}{Y}_{\nu }( \alpha r),\quad c, \,c'\in \mathbb {R}, \end{aligned}$$
(10)

where \({ J}_{\nu }(\alpha r)\) and \({Y}_{\nu }(\alpha r)\) are, respectively, the first and second kind Bessel functions (see [18] for more details). By replacing the solution (9) in the partial differential equation (8), we get

$$\begin{aligned} \Bigg [\frac{\mathrm{d}^2 }{\mathrm{d}r^2} + \frac{3}{r}\frac{\mathrm{d}}{\mathrm{d}r} + \Big (\alpha ^2 - \frac{\lambda _4-\nu ^2}{r^{2}}\Big )\Bigg ]\tilde{\chi }(r) = -\frac{2\nu ^2E}{\hbar r^3}\psi (r,0),\nonumber \\ \end{aligned}$$
(11)

where \( \tilde{\chi }(r) = \frac{\mathrm{d}\psi (r,\theta \,)}{\mathrm{d}\theta \,}\Big |_{\theta \, = 0}\). This equation corresponds to a nonhomogeneous differential equation, which can be solved easily. For \(\epsilon =(1+\lambda _4-\nu ^2)^{1/2}\) and \(g(r)=-2\nu ^2E\psi (r,0)/\hbar r^3\), by using the Wronskian method, the solution of Eq. (11) takes the form

$$\begin{aligned} \tilde{\chi }(r)= & {} cJ_\epsilon (\alpha r)+c'Y_\epsilon (\alpha r)\\&- \frac{\pi }{2r}J_\epsilon (\alpha r)\int _1^r x^2 Y_\epsilon (\alpha x) g(x)\mathrm{d}x\\&+\frac{\pi }{2r}Y_\epsilon (\alpha r)\int _1^r x^2 J_\epsilon (\alpha x) g(x)\mathrm{d}x,\; c, \,c'\in \mathbb {R}.\; \end{aligned}$$
(12)

Note that there are some difficulties, however. One defect of this method (in the commutative and NC case) is that the energy spectrum can only be determined numerically, and we do not deal here with a numerical method to provide this spectrum. In more than \((4+1)\) dimensions, the differential equations (7) are much more complicated.

Now let us discuss the case of a Yukawa potential:

$$\begin{aligned} V(\vec r_{nc}) = -V_0 \frac{e^{-\eta r_{nc}}}{|\vec r_{nc}|^{D-2}}, \end{aligned}$$
(13)

where \(V_0 \) and \(\eta \) depend on the constant of the neutral atom. In order to probe this potential, we write the expression (13) at the first order in \(\theta \) as

$$\begin{aligned} V(\vec r_{nc},t)= -\frac{V_0 e^{-\eta r}}{r^{D-2}}\Big [1+i\big (\eta r+D-2\big )\frac{\theta }{r}\partial _0 \Big ]. \end{aligned}$$
(14)

After separation variables in the Schrödinger equation, it become easy to show that the radial equation is given by the following:

$$\begin{aligned}&\Big [\frac{\partial ^2}{\partial r^2} + \frac{D-1}{r}\frac{\partial }{\partial r}+s_D(r)\Big ]\psi (r) = 0. \end{aligned}$$
(15)

where

$$\begin{aligned} s_D(r)= & {} \frac{2m V_0 e^{-\eta r}}{\hbar ^3 r^{D-2}}\Big (D-2+ \eta r \Big )\frac{E\theta }{r} \\&+ \frac{2m E}{\hbar ^2} -\frac{\lambda _D}{r^2} + \frac{2m V_0 e^{-\eta r}}{\hbar ^2 r^{D-2}} ,\nonumber \end{aligned}$$
(16)

In the particular case where \(D = 4\), this equation is reduced to

$$\begin{aligned}&\frac{\mathrm{d}^2 \psi (r)}{\mathrm{d} r^2} + \frac{3}{r}\frac{\mathrm{d} \psi (r)}{\mathrm{d} r}+s_4(r)\psi (r) = 0. \end{aligned}$$
(17)

This equation (including now the occurrence of the exponential factor \(e^{-\eta r}\)) has the same shape as (8), and therefore the same conclusion with (12) will be made.

3 Hydrogen atom in noncommutative space with compactified extra dimension

In this section we consider \((D+1)\) NC spacetime, where one dimension \(x^D\) is compactified on a circle of radius R. This means that \(\mathbb {R}^{D+1}\) is reduced to \(\mathbb {R}^{D-1+1}\times [-\pi R,\pi R]\) and \(x^D=\omega -2\pi nR\), \(n\in \mathbb {Z}\). The interaction potential (5) written now with the required coordinates \(\vec r= (r, \alpha _1,\ldots , \alpha _{D-2}) \) and the compactify coordinate w is

$$\begin{aligned} V(\vec r, w)= & {} -q_e^2\sum _{n=-\infty }^{\infty }\left\{ \frac{1}{\big (r^2 + (w-2\pi n R)^{2}\big )^{\frac{D-2}{2}}} \right. \\&\left. + \frac{i(D-2) r\theta }{\big (r^2 + (w-2\pi n R)^{2}\big )^{\frac{D}{2}}} \partial _0\right\} , \end{aligned}$$
(18)

where r is now the radial coordinates in \((D-1)\)-dimensional space, and the extra dimension \(x^D\) satisfy the condition \(\vert x^D -2\pi n R\vert \le \pi R\). For \(D=4\), we get

$$\begin{aligned} V(\vec r,w)= & {} -q_e^2 \sum _{n \in \mathbb {Z}}\left\{ \frac{1}{r^2 + (w-2\pi n R)^{2}} \right. \\&\left. +\frac{2ir \theta }{\big (r^2 + (w-2\pi n R)^{2}\big )^{2}} \partial _0\right\} . \end{aligned}$$
(19)

Then we can compute the following identities:

$$\begin{aligned} \sum _{n \in \mathbb {Z}}\frac{1}{r^2 + (w-2\pi n R)^{2}} = \frac{1}{2R r}\frac{\sinh (r/R)}{\cosh (r/R)-\cos (w/R)}\nonumber \\ \end{aligned}$$
(20)

and

$$\begin{aligned} \sum _{n \in \mathbb {Z}}\frac{2 r}{\big (r^2 + (w-2\pi n R)^{2}\big )^2} =G(r) +F(r) \end{aligned}$$
(21)

where

$$\begin{aligned}&G(r)= -\frac{1}{2R r^2}\frac{\sinh (r/R)}{\cosh (r/R)-\cos (w/R)}, \\&F(r)= \frac{1}{2R^2 r}\frac{1-\cosh (r/R) \cos (w/R)}{\big (\cosh (r/R)-\cos (w/R)\big )^2}. \end{aligned}$$
(22)

The potential \(V(\vec r,w)\) is periodic with respect to the w-direction, and it can be expanded in a Fourier series as follows:

$$\begin{aligned} V(\vec r,w) = \sum _{n \in \mathbb {Z}} a_n(r)e^{inw/R} + i\theta \,\sum _{n \in \mathbb {Z}} b_n(r)e^{inw/R} \partial _0, \end{aligned}$$
(23)

where

$$\begin{aligned}&a_n(r) = -\frac{q_e^2}{2rR}e^{-|n|r/R},\\&b_n(r) = -\frac{q_e^2}{2Rr^2}\Big [ 1+ |n|\Big ]e^{-|n|r/R}, \end{aligned}$$
(24)

such that

$$\begin{aligned}&V(\vec r,w) = -\frac{q_e^2}{2rR} \sum _{n \in \mathbb {Z}} \Big [1 + i\theta \Big (\frac{1}{r} + \frac{|n|}{R}\Big )\partial _0 \Big ]e^{-(|n|r - inw)/R}.\nonumber \\ \end{aligned}$$
(25)

The separation of the variables in the Schrödinger equation shows that the radial function \(\psi (r)\) satisfies

$$\begin{aligned} \Big (\frac{\mathrm{d}^2}{\mathrm{d} r^2} + \frac{2}{r}\frac{\mathrm{d}}{\mathrm{d} r}- \frac{n^2}{R^2} + \alpha ^2+ \frac{\zeta }{r} - \frac{\nu ^2_\theta }{r^2}\Big ) \psi _n(r) = 0 , \end{aligned}$$
(26)

with \( \alpha ^2 = \frac{2m E}{\hbar ^2},\, \nu _\theta ^2 = \lambda _4 - \zeta E \theta /\hbar ,\,\zeta = \nu ^2/(2R),\,\nu ^2 = \frac{2m q_e^2}{\hbar ^2}. \)

The solution of the above equation is expressed as

$$\begin{aligned} \psi _n(r)= & {} \Big [ \frac{(2 \zeta )^{a+2} \; l!}{(2l+1+a)^{a+3} \Gamma (l+1+a)}\Big ]^{\frac{1}{2}} \, r^{\frac{1}{2}(a-1)}e^{-\frac{\zeta r}{2l+a+1}} \\&\times \, L_{l}^{a}\Big (\frac{2 \zeta r}{2l+a+1} \Big ), \quad a = \sqrt{4 \nu _\theta ^2+1}, \end{aligned}$$
(27)

where we have used the normalization condition \( \int _0^{\infty }e^{-z} z^{a+1} [L_{l}^{a}(z)]^2 \mathrm{d}z = \frac{(2l+1+a) \Gamma (l+1+a)}{l!} \), and where \(L_l^a\) stands for the generalized Laguerre polynomial. The quantum number l is a positive integer, which corresponds to the physical situation. This integer is given by

$$\begin{aligned} l = -\frac{1}{2}-\frac{1}{2}\sqrt{4 \nu _\theta ^2+1}+\frac{\zeta R}{2\sqrt{n^2-\alpha ^2 R^2}}. \end{aligned}$$
(28)

Two energy contributions appear from Eq. (28):

$$\begin{aligned} E_{nl}^{(1)}=\frac{\hbar ^2}{2m}\Big ( \frac{n^2}{R^2} - \frac{\zeta ^2}{(2l + 1 +\sqrt{1+4\lambda _4})^2}\Big ) \end{aligned}$$
(29)

and

$$\begin{aligned} E_{nl}^{(2)}= & {} \frac{\hbar ^2}{2m}\frac{\zeta ^2}{(2l+1+\sqrt{1+4\lambda _4})^2}\\&+\frac{\hbar \sqrt{1+4\lambda _4}}{4\theta \zeta }(2l+1+\sqrt{1+4\lambda _4}). \end{aligned}$$
(30)

Let us discuss the energy spectrum (30). In the limit where \(\theta \rightarrow 0\), \(E_{nl}^{(2)}\) is not well defined. Also as expected in our introduction the eigenfunctions of the operator \(\nabla ^2_{x^4}\) with eigenvalues \(E_{n0}=-n^2/R^2\) are not recovered. Finally this expression cannot be taking into account as a solution of the eigenvalue problem. Then the energy spectrum becomes

$$\begin{aligned} E_{nl} = \frac{\hbar ^2}{2m}\Big ( \frac{n^2}{R^2} - \frac{\zeta ^2}{(2l + 1 +\sqrt{1+4\lambda _4})^2}\Big ). \end{aligned}$$
(31)

Remark 1

  • Our result shows that the energy spectrum (31) does not depend on the NC parameter \(\theta \) if we consider the first order approximation in this parameter. The solution of the eigenvalue problem of the hydrogen atom with one compactified dimension is solved numerically in [17, 18] (see also [19, 20] in the case where no dimensions are compactified). Due to the fact that \(\lim _{\theta \rightarrow 0} E_{nl}=E_{nl}\), the expression (31) can be considered as a solution of the hydrogen atom in \(4+1\)-dimensional spacetime for both the NCFootnote 1 and the commutative cases, where one dimension is compactified.

  • The quantity

    $$\begin{aligned} E_{nl}'=-\frac{\hbar ^2\zeta ^2}{2m(2l + 1 +\sqrt{1+4\lambda _4})^2} \end{aligned}$$
    (32)

    corresponds to the reduced dimension energy spectrum and is discussed in the introduction of our paper.

We consider now the case of a Yukawa potential (13) for \(D = 4\). On shell, and with the compactified \(x^4\) direction on the circle we get the reduced potential

$$\begin{aligned} V(\vec r,w)= & {} i V_0 \theta \, \Bigg [-\frac{1}{2R r^2}\frac{\sinh (r/R)}{\cosh (r/R)-\cos (w/R)} \\&+ \frac{1}{2R^2 r}\frac{1-\cosh (r/R) \cos (w/R)}{\Big (\cosh (r/R)-\cos (w/R)\Big )^2}\Bigg ] \partial _0 \\&-\frac{V_0}{2R r}\frac{\sinh (r/R)}{\cosh (r/R)-\cos (w/R)}. \end{aligned}$$
(33)

Let us briefly give the proof of this relation. The goal of this proof is to compute the integral \(\int _{\Gamma }\, f(z)\mathrm{d}z\), where \(\Gamma \) is a closed contour on the complex plane and f(z) is a holomorphic function given by

$$\begin{aligned} f(z) = \frac{\cot (\pi z)\exp \big [-c\big ((a-z)^2 + b^2\big )^{1/2}\big ]}{(a-z)^2 + b^2}, \end{aligned}$$
(34)

where a, b, c are three real numbers. The poles of f(z) are \(z_n = n, n \in \mathbb {Z}\), \( z_I = a+ib \), and \(z_{II} = a-ib\). Using the residue theorem,

$$\begin{aligned} \int _{\Gamma }\, f(z)\mathrm{d}z=2i\pi \sum \mathcal {R}es [f(z)]=0, \end{aligned}$$
(35)

with

$$\begin{aligned}&\underset{z_n \quad \quad }{\mathcal {R}es[f(z)]} = \frac{\exp \big [-c\big ((a-n)^2 + b^2\big )^{\frac{1}{2}}\big ]}{\pi [(a-n)^2 + b^2]},\\&\underset{z_I \quad \quad }{\mathcal {R}es[f(z)]} = -\frac{i}{2b}\cot [\pi (a+i b)] , \quad \text{ and } \\&\underset{z_{II} \quad \quad }{\mathcal {R}es[f(z)]} = \frac{i}{2 b}\cot [\pi (a-i b)]. \end{aligned}$$
(36)

Hence,

$$\begin{aligned}&\sum _{n \in \mathbb {Z}}\frac{\exp \big [-c\big ((a-n)^2 + b^2\big )^{1/2}\big ]}{(a-n)^2 + b^2} \\&\quad = \frac{\pi }{b} \frac{\sinh (2\pi b)}{\cosh (2\pi b) - \cos (2\pi a)}. \end{aligned}$$
(37)

The first term on the right hand side of (33) is

$$\begin{aligned}&\sum _{n \in \mathbb {Z}}\frac{\exp \big [-\zeta \big (r^2 +(w -2\pi n R)^2 \big )^{1/2}\big ]}{r^2 + (w-2\pi n R)^2} \\&\quad = \frac{1}{2 R r} \frac{\sinh (r/R)}{\cosh (r/R) - \cos (w/R)}. \end{aligned}$$
(38)

The second term on the right hand side of Eq. (33) is the first order derivative of Eq. (38) respect to r. Then Eq. (33) is straightforwardly obtained.

Now using the fact that the function \(V(\vec r ,w)\) is periodic, the Fourier series can be given by

$$\begin{aligned} V(\vec r,w) = \sum _{n \in \mathbb {Z}} \Big (a_n(r) + i\theta b_n(r) \partial _0\Big )e^{inw/R}, \end{aligned}$$
(39)

where the Fourier coefficients are

$$\begin{aligned} a_n(r)= & {} -\frac{V_0}{2rR}e^{-|n|r/R}, \\b_n(r)= & {} -V_0 \Big [\frac{1}{2Rr^2} + \frac{|n|}{2R^2 r}\Big ]e^{-|n|r/R} \end{aligned}$$
(40)

Finally we arrive at

$$\begin{aligned} V(\vec r,w) =- & {} \frac{V_0}{2rR} \sum _{n \in \mathbb {Z}} \Big [1 + i\theta \Big (\frac{1}{r} + \frac{|n|}{R}\Big )\partial _0 \Big ]\\\times & {} e^{-(|n|r - inw)/R}. \end{aligned}$$
(41)

Equation (33) can also be expanded using the Fourier series as follows:

$$\begin{aligned} V(\vec r,w) =- & {} \frac{V_0}{2rR} \sum _{n \in \mathbb {Z}} \Big [1 + i\theta \Big (\frac{1}{r} + \frac{|n|}{R}\Big )\partial _0 \Big ]\\\times & {} e^{-(|n|r - inw)/R}, \end{aligned}$$
(42)

and the radial equation takes the form

$$\begin{aligned} \Big [\frac{\mathrm{d}^2}{\mathrm{d} r^2} + \frac{2}{r}\frac{\mathrm{d}}{\mathrm{d} r}- \frac{n^2}{R^2} + \alpha ^2+ \frac{u}{r} - \frac{v}{r^2}\Big ] \psi _n(r) = 0, \end{aligned}$$
(43)

where \(\alpha ^2 = \frac{2m E}{\hbar ^2}\); \(v = \lambda _4 -\frac{m V_0 E \theta }{\hbar ^3 R}\), \(u = \frac{m V_0}{\hbar ^2 R}\). The solution of this equation leads to the same results as given in (27) and (31).

4 Discussion and conclusion

In this paper we have found that the noncommutativity of spacetime can help to compute the exact expression of the energy spectrum of the hydrogen atom in \((4+1)\) dimensions with one compactified extra dimension. Unfortunately, it is clear that this method cannot be used in higher dimensions. To be more precise, let us consider the particular case where \(D=6\), the compactified one dimension \(x^6\) gives the potential

$$\begin{aligned} V(\vec r,w)= & {} -\frac{q_e^2}{(2 R r)^{2}} \Bigg (\frac{R}{r} \frac{\sinh (r/R)}{\cosh (r/R) - \cos (w/R)} \\&+ \frac{\cosh (r/R) \cos (w/R) - 1}{[\cosh (r/R) - \cos (w/R)]^2} \Bigg ) \\&+ \frac{i \theta \,q_e^2}{8 r^4 R^3 \big (\cos (w/R)-\cosh (r/R)\big )^3} \\&\times \Bigg [ (r^2+3 R^2) \sinh (r/R) \cos (2w/R) \\&+ \cos (w/R) \Big ((r^2-6 R^2) \sinh (2r/R) \\&+ 3 r R (\cosh (2r/R)+3)\Big )\\&+ 3 \sinh (r/R) \Big (R^2 \cosh (2r/R)+2 R^2 -r^2\Big ) \\&- 3 r R \cosh (r/R) \Big (\cos (2w/R)+3\Big )\Bigg ]\partial _0. \end{aligned}$$
(44)

This relation can be expanded in a Fourier series as

$$\begin{aligned} V(\vec r,w)= & {} -\frac{q_e^2}{(2 R r)^{2}}\sum _{n \in \mathbb {Z}} \Bigg [\Big (\frac{R}{r} + |n| \Big )\\&+i\theta \, \Big (\frac{3R}{r^2} + \frac{3|n|}{r} + \frac{n^2}{R} \Big ) \partial _0\Bigg ] e^{-|n|r/R} e^{inw/R},\nonumber \\ \end{aligned}$$
(45)

in which the radial part of the Schrödinger equation becomes

$$\begin{aligned}&\Bigg (\frac{\mathrm{d}^2}{\mathrm{d} r^2} + \frac{2}{r}\frac{\mathrm{d}}{\mathrm{d} r}-\frac{\lambda _4}{r^2} - \frac{n^2}{R^2} + \alpha ^2 + \frac{2m q_e^2}{4\hbar ^2r^3 R} + \frac{3m q_e^2E \theta }{2\hbar ^3 r^4 R} \Bigg ) \psi _n(r) =0.\nonumber \\ \end{aligned}$$
(46)

The solution of this equation is not yet understood. Surprisingly, we have also shown that, despite this noncommutativity, the energy spectrum does not depend on the deformation parameter \( \theta \) and therefore might be considered as the energy solution of commutative space, with one compactified extra dimension, solved in [17] and [18]. Finally let us mention that in the case of higher dimensions higher than \(4+1\) the compactified several extra dimensions may be considered.

Let us examinate the case of the Klein–Gordon (KG) equation:

$$\begin{aligned}&\Big (i\hbar \partial _0 - V(\vec {r}_{nc})\Big )^2 \psi (\vec {r}_{nc}, t) \\&\quad = m^2 c^4 \psi (\vec {r}_{nc}, t)- \hbar ^2 c^2 \Delta \psi (\vec {r}_{nc}, t), \end{aligned}$$
(47)

where the potential \(V(\vec {r}_{nc})\) is

$$\begin{aligned} V(\vec {r}_{nc})=-\wp \frac{\hbar c}{|\vec r_{nc}|^{D-2}}. \end{aligned}$$
(48)

\(\wp \) is related to the fine structure constant and c is the light speed. For \(D=4\), by taking into account the fact that \(\vec {r}_{nc}=\vec {r}-i\vec \theta \partial _0\), and writing the extra dimension \(x^4=w - 2\pi R k,\,\, k\in \mathbb {Z}\), we get

$$\begin{aligned} V(r, w)= & {} -\wp \hbar c \sum _{n=-\infty }^{\infty }\Bigg \{\frac{1}{r^2 + (w-2\pi n R)^{2}} \\&+ \frac{2i r\theta }{\big (r^2 + (w-2\pi n R)^{2}\big )^{2}} \partial _0\Bigg \}. \end{aligned}$$
(49)

The left hand side of Eq. (47), using (49), gives

$$\begin{aligned}&\Big (i\hbar \frac{\partial }{\partial t} - V({r}, w)\Big )^2\psi (\vec r,t) \\&\quad =\Bigg [ -\hbar ^2 \partial _0^2 + \wp \hbar ^2 c \Big (2i A (r,w) \partial _0 + 3\theta \frac{\partial A(r,w)}{\partial r} \partial _0^2\Big ) \\&\qquad + \wp ^2 \hbar ^2 c^2 \Big ( A^2(r,w) - i\theta \frac{\partial A^2(r,w)}{\partial r} \partial _0\Big )\Bigg ]\psi (\vec r,t) \end{aligned}$$
(50)

where A(r, w) is written as

$$\begin{aligned} A (r,w) = \frac{1}{2 R r} \frac{\sinh (r/R)}{\cosh (r/R) - \cos (w/R)}, \end{aligned}$$
(51)

with the Fourier series

$$\begin{aligned} A (r,w) = \frac{1}{2rR} \sum _{n \in \mathbb {Z}} e^{inw/R} e^{inw/R}. \end{aligned}$$
(52)

After some technical handling, we can show that the quantity \(A^2(r,w)\) is expanded as

$$\begin{aligned} A^2(r,w) = \frac{1}{(2 R r)^2} \sum _{n \in \mathbb {Z}} \Big [|n| + \coth \Big (\frac{r}{R}\Big ) \Big ] e^{-\frac{|n|r}{R}} e^{\frac{inw}{R}}.\nonumber \\ \end{aligned}$$
(53)

By replacing (52) and (53) in (50) and separating variables as \(\psi (\vec {r}, t) = \Psi (\vec {r}) e^{- i E t/\hbar } \) and \(\Psi (\vec {r}) = \Psi (r) \mathcal {Y}_\ell ^{(3)}\) such that \(\hat{l}^2 \mathcal {Y_\ell }^{(3)} = \ell (\ell \,{+}\, 2)\mathcal {Y_\ell }^{(3)} \,{=}\,\lambda _4 \mathcal {Y_\ell }^{(3)} \) we find the radial equation:

$$\begin{aligned}&\Big [\frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d}r}\Big (r^2\frac{\mathrm{d}}{\mathrm{d}r}\Big )+V_\mathrm{eff}(r) + \frac{E^2}{\hbar ^2 c^2} - \frac{m^2 c^2}{\hbar ^2} - \frac{n^2}{R^2}\Big ] \Psi _{n}(r) = 0,\\&\end{aligned}$$
(54)

where the effective potential \(V_\mathrm{eff}(r)\) is

$$\begin{aligned} V_\mathrm{eff}(r)= & {} -\frac{\lambda _4}{r^2} + \frac{3\theta \wp E^2}{2r^2R\hbar ^2 c} + \frac{\wp E}{rR\hbar c}+ \frac{\wp ^2 }{(2 R r)^2} \coth (r/R)\\&+ \frac{\theta \wp ^2 E}{(2 R r)^2 \hbar } \Bigg (\frac{2}{r}\coth (r/R) + \frac{ r}{\sinh ^2(r/R)}\Bigg ). \end{aligned}$$
(55)
Fig. 1
figure 1

Plot of the potential \(V_\mathrm{eff}(r)\), with \(R=0.01\), \(\theta =0.01\), \(\hbar =c=1,\) \(\wp =1/137\), \(E=1\), \(\ell =1\)

Full size image

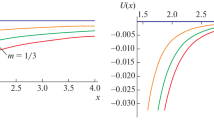
Equation (54) can be solved numerically using the approximation method (Fig. 1). Consider the Taylor expansion of \(V_\mathrm{eff}\) by using the fact that

$$\begin{aligned}&\coth (r/R) = \frac{R}{r} + \frac{r}{3R} + \cdots \\&\sinh (r/R) = \frac{r}{R} + \cdots . \end{aligned}$$
(56)

Then (54) becomes

$$\begin{aligned}&\frac{\mathrm{d}^2 \Psi _{n}(r)}{\mathrm{d} r^2} + \frac{2}{r}\frac{\mathrm{d} \Psi _{n}(r)}{\mathrm{d} r}+\sum _{j=0}^4\,\frac{b_j}{r^j} \Psi _{n}(r) = 0, \;\;\; \end{aligned}$$
(57)

with \( b_4 = \frac{\theta \wp ^2 E}{2 R \hbar }, \,\, b_3= \frac{\theta \wp ^2 E}{4 \hbar } + \frac{\wp ^2 }{4 R},\,\, b_2 = \frac{\theta \wp ^2 E}{6 R^3 \hbar } + \frac{3\theta \wp E^2}{2 R\hbar ^2 c} - \lambda _4, \,\, b_1 = \frac{\wp ^2 }{12 R^3} + \frac{\wp E}{R\hbar c} ,\,\, b_0 = \frac{E^2}{\hbar ^2 c^2} - \frac{m^2 c^2}{\hbar ^2} - \frac{n^2}{R^2}. \)

We shall first examine the wave functions \(\Psi _n(r)\) in the asymptotic range, \(r\rightarrow \infty \). The potential \(V_\mathrm{eff}(r)\) vanishes, in this limit, i.e.,

$$\begin{aligned} V_\mathrm{eff}(r_\infty )\rightarrow 0. \end{aligned}$$
(58)

In the region \(r_\infty \) Eq. (57) gives the solution of the form

$$\begin{aligned} \Psi ^\infty _n(r)=U\frac{e^{-\sqrt{-b_0}r}}{r},\quad U\in \mathbb {R}. \end{aligned}$$
(59)

The general solution of Eq. (57) takes the form

$$\begin{aligned} \Psi _n(r)=U(r)\frac{e^{-\sqrt{-b_0}r}}{r}, \end{aligned}$$
(60)

where U(r) satisfies the differential equation

$$\begin{aligned} U''(r)-2\sqrt{-b_0}U'(r)+\sum _{j=1}^4\,\frac{b_j}{r^j} U(r) = 0. \end{aligned}$$
(61)

The investigation of the numerical solution of this equation can be made in forthcoming work.