Abstract
Based on current CERN infrastructure, an electron–proton collider is proposed at a centre-of-mass energy of about 9 TeV. A 7 TeV LHC bunch is used as the proton driver to create a plasma wakefield which then accelerates electrons to 3 TeV, these then colliding with the other 7 TeV LHC proton beam. Although of very high energy, the collider has a modest projected integrated luminosity of 10–100 pb\(^{-1}\). For such a collider, with a centre-of-mass energy 30 times greater than HERA, parton momentum fractions, x, down to about \(10^{-8}\) are accessible for photon virtualities, \(Q^2\), of 1 GeV\(^2\). The energy dependence of hadronic cross sections at high energies, such as the total photon–proton cross section, which has synergy with cosmic-ray physics, can be measured and QCD and the structure of matter better understood in a region where the effects are completely unknown. Searches at high \(Q^2\) for physics beyond the Standard Model will be possible, in particular the significantly increased sensitivity to the production of leptoquarks. These and other physics highlights of a very high energy electron–proton collider are outlined.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The HERA electron–proton accelerator was the first and so far only lepton–hadron collider worldwide. With its centre-of-mass energy of about 300 GeV, HERA dramatically extended the kinematic reach [1] for the deep inelastic scattering process compared to fixed-target experiments. A broad range of physics processes were studied and new insights were gleaned from HERA which complemented the \(p\bar{p}\) and \(e^+e^-\) colliders, the Tevatron and LEP. The LHeC project [2, 3] is a proposed ep collider with significantly higher energy and luminosity than HERA with a programme to investigate Higgs physics and QCD, to search for new physics, etc. This will use significant parts of the LHC infrastructure at CERN with different configurations, such as eA, also possible. In this article, the possibility of having a very high energy electron–proton collider (VHEeP) is considered with an ep centre-of-mass energy of about 9 TeV, a factor of six higher than proposed for the LHeC and a factor of 30 higher than HERA.
The VHEeP machine would strongly rely on the use of the LHC beams and the technique of plasma wakefield acceleration to accelerate electrons to 3 TeV over relatively short distances. Given such an acceleration scheme, the luminosity will be relatively modest with \(10{-}100~\mathrm{pb}^{-1}\) expected over the lifetime of the collider. With such an increase in centre-of-mass energy, the VHEeP collider will probe a new regime in deep inelastic scattering and QCD in general. The kinematic regime accessible will be extended by three orders of magnitude compared to that measured at HERA. This article puts forward the physics case for such a collider, highlighting some of the measurements most sensitive to unveiling new physics. Complementary studies of high energy ep colliders have been performed elsewhere [4–6], considering both the accelerator design [4, 5] and physics potential [6].
The article is organised as follows. In Sect. 2, the kinematics and basic properties of deep inelastic scattering are defined. In Sect. 3, the scheme of plasma wakefield acceleration is briefly explained and a basic accelerator design for VHEeP is outlined, including justification of the centre-of-mass energy and estimate of the achievable luminosity. The basic kinematics and properties of the final state at these new energies are discussed and also their effect on the choice of detector design are described in Sect. 4. In Sects. 5 and 6, the headline physics areas in QCD and beyond the Standard Model are outlined. These include measuring the total photon–proton cross section, the deep inelastic scattering cross section at the lowest possible x values and the search for leptoquarks. In Sect. 7, the broad spectrum of other possible areas of study in high energy electron–proton collisions is briefly given. In Sect. 8, the physics case is summarised and an outlook for the VHEeP project given.
2 Deep inelastic scattering
Deep inelastic scattering [7] can be classified as either neutral current (NC) or charged current (CC), depending on whether the exchanged boson is a photon or \(Z^0\) boson (NC) or a \(W^\pm \) boson (CC). The NC reaction, which dominates the cross section for the processes considered here, in electron–proton collisions can be written as \(e^- (k) + p(p) \rightarrow e^-(k^\prime ) + X(p^\prime )\) with the four vectors given in the brackets and X referring to a hadronic final state. In the case of CC, the final state electron is replaced by a neutrino. The four-momentum of the exchanged boson, q, is given by \(q=k-k^\prime \). The events can be described by the following quantities: the squared centre-of-mass energy, s, is given by
the virtuality, \(Q^2\), of the exchanged boson is given by
the Bjorken-x variable, interpreted as the fraction of proton’s momentum carried by the struck quark in the proton’s infinite-momentum frame, is given by
the inelasticity, y, interpreted in the proton rest frame as the fraction of energy transferred from the lepton to the proton, is given by
The above variables are related, \(Q^2 = s\,x\,y\), where particle masses can be ignored at the very high energies considered here. Another quantity of importance is the exchanged-boson–proton centre-of-mass energy, W, which is given by
The neutral current cross section for \(e^- p\) scattering, \(\frac{d^2\sigma ^{e^- p}_\mathrm{NC}}{dx\,dQ^2}\), can be written in terms of these variables and the structure functions of the proton as
where \(\alpha \) is the fine structure constant and \(Y_\pm = 1 \pm (1-y)^2\). The structure function \(F_2\) is sensitive to the quark and antiquark distributions in the proton and dominates at low \(Q^2\); the structure function \(xF_3\) is sensitive to the difference in the quark and antiquark distributions in the proton and arises due to the interference of the photon- and \(Z^0\)-exchange contributions at \(Q^2\) values around the mass of the W and Z bosons. The longitudinal structure function \(F_\mathrm{L}\) is sensitive to the gluon distribution in the proton and becomes important at high values of y.
The double-differential cross section can also be written in terms of the photon–proton cross section, \(\sigma ^{\gamma p}\), and the photon flux, \(\phi \). The equivalent photon approximation [8–10] relates these as
where all quantities depend on both \(Q^2\) and y.
The event kinematics are calculated using the initial beam energies and the kinematics of the scattered electron and hadronic final state. Of particular importance are the scattered electron energy, \(E_e^\prime \), and polar angle, \(\theta _e\), and the hadronic angle, \(\gamma _\mathrm{had}\), where both angles are measured with respect to the proton beam direction.
3 VHEeP accelerator complex
Tajima and Dawson first proposed that plasmas can sustain very large electric fields capable of accelerating bunches of particles [11]. Using a laser pulse or electron bunch to drive the plasma “wakefield”, accelerating gradients of up to, respectively, 100 GV m\(^{-1}\) [12] and 50 GV m\(^{-1}\) [13] have been measured. This acceleration concept can also make use of bunches of protons [14], given high energy proton bunches are available and hence the possibility to have the acceleration performed in one stage. Simulation has shown that the plasma wakefield created by the LHC proton bunches can accelerate a trailing bunch of electrons to 6 TeV in 10 km [15]. The concept of proton-driven plasma wakefield acceleration will be tested by the AWAKE collaboration at CERN which aims to demonstrate the scheme for the first time [16–18]. The initial aims of the AWAKE experiment are to demonstrate GeV acceleration of electrons within 10 m of plasma [16–18]. Following this, the AWAKE collaboration proposes to accelerate bunches of electrons to 10 GeV in about 10 m of plasma [19].
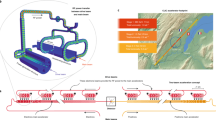
The very high energy electron–proton collider (VHEeP) is based on current LHC infrastructure and a new tunnel to house the plasma accelerator. The facility uses one of the LHC proton beams to generate wakefields and accelerate a trailing electron bunch which then collides with the other proton beam. This is shown in a simple schematic in Fig. 1 in which the electron beam is chosen to have an energy of 3 TeV, achieved in a plasma accelerator of \(\lesssim \)4 km, and the proton beams have an energy of 7 TeV. Separation of the drive proton beam and witness electron beam will be needed to avoid pp collisions; as well as the temporal difference, the beams will need to be separated transversely by O (mm). Further study of this important issue is needed.
Simple schematic of the VHEeP accelerator complex, showing the LHC ring. Protons from the LHC are extracted into the VHEeP plasma accelerator and used to accelerate bunches of electrons. Proton bunches rotating in the other direction in the LHC are extracted into the VHEeP tunnel and collided with electrons. Both proton and electron dumps could be used for fixed-target (beam-dump) experiments
Although the energy of VHEeP will be very high, obtaining high luminosities will be, as with all plasma wakefield acceleration schemes, a challenge. In these initial studies, an integrated luminosity over the lifetime of VHEeP of \(10{-}100\) pb\(^{-1}\) is considered [20, 21], based on the expected capabilities of the LHC and pre-accelerators. The lower limit will be sufficient for measurements at low x where the cross section is expected to rise with decreasing x. A higher integrated luminosity will aid the search for physics beyond the Standard Model, typically at high \(Q^2\).
Distributions of scattered electron energy, \(E_e^\prime \), scattered electron angle, \(\theta _e\), \(E_e^\prime \) versus \(\pi - \theta _e\), and hadronic angle, \(\gamma _\mathrm{had}\), generated using the Ariadne Monte Carlo programme for \(Q^2 > 1\) GeV\(^2\), \(W^2 > 5\) GeV\(^2\) and \(x > 10^{-7}\) for a luminosity of 0.01 pb\(^{-1}\). The hadronic angle is also shown for different requirements on x
4 VHEeP kinematics and basic detector design
In order to investigate the kinematic distributions of events at these high energies, a small sample of deep inelastic scattering events was generated using the Ariadne Monte Carlo programme [22, 23] with requirements \(Q^2 > 1\) GeV\(^2\), \(W^2 > 5\) GeV\(^2\) and \(x > 10^{-7}\) for a luminosity of about 0.01 pb\(^{-1}\). The CTEQ2L [24] set of proton parton distribution functions was used as this gave a reasonable and continuous distribution at low x. The cut on x was required because of technical difficulties generating events down to \(x = 10^{-8}\), the kinematic limit for \(Q^2 > 1\) GeV\(^2\), as the parton density functions in CTEQ2L are not valid at these very low values.
The basic kinematic distributions of deep inelastic scattering events are shown in Fig. 2, focusing on the low-x and low-\(Q^2\) region. In this region, a high luminosity will not be needed due to the high cross section, with e.g. 10s of million of events in the region \(10^{-7}< x < 10^{-6}\) for \(Q^2 > 1\) GeV\(^2\) and an integrated luminosity of 10 pb\(^{-1}\). It should be noted that the lowest value of \(Q^2\) measured at HERA was \(Q^2 = 0.045\) GeV\(^2\), which at VHEeP corresponds to a minimum x value of \(5 \times 10^{-10}\). At this \(Q^2\), a significantly larger number of events is expected.
Total \(\gamma p\) cross section versus photon–proton centre-of-mass energy, W, shown for data compared to various models. The data is taken from the PDG [25], with references to the original papers given therein. The VHEeP data point is shown at the same W value relative to \(\sqrt{s}\) as the HERA results. The VHEeP cross section is assumed to be double the ZEUS value and the same uncertainties are assumed. The ZEUS measurement is at \(\sqrt{s} =209\) GeV and used a luminosity of 49 nb\(^{-1}\). The Regge fits shown are those of Donnachie–Landshoff (1992 [26] and 2004 [27]). The \(\ln ^2(W^2)\) form is based on [28]
Kinematic distributions of the electron and hadron final state are shown in Fig. 3. The scattered electron energy, \(E_e^\prime \), is strongly peaked at the initial electron beam energy of 3 TeV, but with a tail down to a few GeV. The angle of the scattered electron, \(\theta _e\), measured with respect to the proton beam, is shown to strongly peak at 180\(^\circ \), with the higher the energy, the stronger the peak, as shown in the correlation between \(E_e^\prime \) and \(\pi - \theta _e\). The angle of produced hadrons, \(\gamma _\mathrm{had}\), is distributed over 0\(^\circ \) to 180\(^\circ \), but with a peak at 0\(^\circ \) and even stronger peak at 180\(^\circ \). The events at low angles are due to events at high x, whereas the events with hadrons at high angles are dominated by events at low x.
The distributions in Fig. 3 have consequences for the detector design with a central detector needed as well as instrumentation close to the beamline to measure both electrons and hadrons. A simple schematic of the detector needed for VHEeP is shown in Fig. 4. A central detector, which is expected to be similar to other colliding-beam experiments, will be needed to reconstruct the hadronic final state and, in particular, events at high \(Q^2\). Additionally, long spectrometer arms will be required in the electron direction to measure the hadronic final state at low x and the scattered electron. A spectrometer in the direction of the proton beam will be required to measure the hadronic final state at high x. The systems will possibly consist of dipole magnets to extract the particles from the beamline and low-angle detector systems. Clearly, an understanding of the radiation created by the beams as well as possible radiation from the plasma acceleration will need detailed study.
5 QCD physics at VHEeP
Electron–proton collisions at \(\sqrt{s} \sim 9\) TeV give access to a completely new kinematic regime for deep inelastic scattering with, in particular, a reach in x a factor of about 1000 lower than at HERA and, depending on the luminosity, a similar increase in the reach at high \(Q^2\). The energy dependence of hadronic cross sections, such as the total photon–proton cross section, are poorly understood. Predictions calculated from first principles are often not available and so phenomenological models are used to describe the dependence. Being able to measure the energy dependence, particularly with the long lever arm presented by VHEeP, will deepen our understanding of QCD and the structure of matter. In this section, some highlight physics measurements which particularly benefit from this extended kinematic regime are discussed.
5.1 Total photon–proton cross section
Measurements of the total \(\gamma p\) cross section are shown in Fig. 5 compared to phenomenological models. A projection for a measurement at the expected maximum W at VHEeP is also shown; further measurements of similar precision at lower W are also expected. The many cross sections at low energies can be fitted in Regge phenomenology in which the dominant contributions arise from Reggeon exchange, which falls with increasing centre-of-mass energy, and Pomeron exchange, which rises. As an example, two such fits from Donnachie and Landshoff [26, 27] are shown in the figure. The 1992 fit predates HERA data and is made over the range \(6< W < 20\) GeV. It has a single Pomeron term and a single Reggeon term. The 2004 fit includes HERA data (photoproduction, as well as DIS data for \(Q^2 < 45\) GeV\(^2\)) and allows an additional second Pomeron term. Up to the highest HERA energies, both fits give good descriptions of the data. At higher energies, the second Pomeron term starts to become dominant and the cross-section predictions differ significantly. Also shown is an extrapolation based on the Froissart bound [28], \(\sigma _{\gamma p} \propto \ln ^2(s)\). Assuming measurements from VHEeP up to \(W \sim 6\) TeV, even with very low luminosities (\({\mathcal {L}} = 49\) nb\(^{-1}\), as used in the ZEUS measurement [29]), the data will be able to strongly constrain the energy dependence of the total cross section and hence provide a clearer picture of QCD. It should be noted that the multi-TeV energies and hence large lever arm attainable at VHEeP are necessary to do this.
A photon–proton collision of \(W = 6\) TeV, corresponding to photon and proton energies of, respectively, 1.3 and 7 TeV, is equivalent to a 20 PeV photon on a fixed target. This extends significantly into the region of ultra high energy cosmic rays. Therefore VHEeP data could be used to constrain cosmic-ray air-shower simulations and so will be of benefit to understanding the nature of cosmic rays at the highest energies (for example, see [30]).
5.2 Vector meson production
Vector meson production is dependent on the partonic distributions in the proton and given the need for two gluons from the proton to create a vector meson, see Fig. 6, is particularly sensitive to saturation of the parton densities or other effects. For high vector meson masses, QCD calculations are expected to be more reliable and so measurements of \(J/\psi \) production can constrain the gluon density in a complementary way to fits to inclusive cross section in deep inelastic scattering (see [31, 32] and references therein).
Vector meson production has been measured extensively at HERA and fixed-target experiments [33, 34] and the cross sections are shown in Fig. 7 as a function of the photon–proton centre-of-mass energy, W. Photoproduction cross sections extracted from LHC data [35–38] are also shown, which extend up to the TeV scale. The cross sections all rise with increasing W or equivalently decreasing x. These cross section dependences, as well as the total cross section from Fig. 5 which is also shown, can be parametrised in terms of a power of W, as also shown in Fig. 7. The simple power-law behaviour of W with particle mass describe well the data from fixed-target, HERA and LHC experiments. However, such functions lead to non-sensical results at VHEeP energies, also indicated, in which e.g. \(\sigma _{J/\psi }\) approaches \(\sigma _\omega , \sigma _\phi \) and will at some point be larger. Clearly, the cross sections must take on another form and start to level out, be it through saturation or some other mechanism. As shown, data from VHEeP will be able to determine this behaviour.
The total \(\gamma p\) cross section compared to the cross sections for exclusive vector meson production. The data in each of the reactions is shown along with a function depending on a power of W. The ALICE and LHCb data are extracted from measurements of vector meson production in \(p-Pb\) and pp collisions, respectively [35–38]. The reach of VHEeP is shown with simulated points for \(J/\psi \) production up to the centre-of-mass energy, indicated as the vertical dashed line
Measurements (open points) of \(\sigma ^{\gamma p}\) versus W for \(0.25< Q^2 < 120\) GeV\(^2\) from HERA and fixed-target experiments. The blue lines show fits to the data, performed separately for each \(Q^2\) value, of the form given in Eq. 8. The red lines show fits of the form given in Eq. 9. The reach of VHEeP is shown as projected data points (closed points). The points are placed on the red curve. The uncertainties are assumed to be of order 1 %, given the increased cross section expected and similar systematics to those at HERA and are not visible as error bars on this plot
5.3 Physics at low Bjorken x
As discussed above, the energy dependence of the total photoproduction cross section at high energies is of great interest, both on fundamental grounds and for understanding cosmic-ray events in the atmosphere. The energy dependence of scattering cross sections for virtual photons on protons is also of fundamental interest, and its study at different virtuality is expected to bring insight into the processes leading to the observed universal behaviour of cross sections at high energies.
In deep inelastic scattering of electrons on protons at HERA, the strong increase in the proton structure function \(F_2\) with decreasing x for fixed, large, \(Q^2\) is usually interpreted as an increasing density of partons in the proton, providing more scattering targets for the electron. This interpretation relies on choosing a particular reference frame to view the scattering—the Bjorken frame. In the frame where the proton is at rest, it is the state of the photon or weak boson that differs with varying kinematic parameters. For the bulk of the electron–proton interactions, the scattering process involves a photon, and we can speak of different states of the photon scattering on a fixed proton target. What is seen is that the photon–proton cross section rises quickly with W for fixed \(Q^2\) [39]. In the proton rest frame, we interpret this as follows: as the energy of the photon increases, time dilation allows shorter lived fluctuations of the photon to become active in the scattering process, thereby increasing the scattering cross section.
Figure 8 shows the results of extrapolation of fits to the energy dependence of the photon–proton cross section for different virtualities as given in the caption [40], for two different assumptions on the energy behaviour. In one instance (blue curves), the energy dependence is assumed to follow a simple behaviour at small values of x:
while in the second instance a form inspired by double asymptotic scaling [41] was used
The simple behaviour is what has been used in most fits to HERA data [1] to date, and it deviates strongly from the expectations of double asymptotic scaling in the VHEeP kinematic range. It is found that this simple behaviour cannot continue to ever smaller values of x as this would result in large-\(Q^2\) cross sections becoming larger than small-\(Q^2\) cross sections. A change of the energy dependence is therefore expected to become visible in the VHEeP kinematic range. This should yield exciting and unique information on the fundamental underlying physics at the heart of the high energy dependence of hadronic cross sections.
6 Physics beyond the Standard Model
We now switch to a discussion of prospects for the discovery of new physics beyond the Standard Model (BSM). The key features of VHEeP are the very large centre-of-mass energy and the unique combination of electron and proton scattering. We therefore focus on new physics where these features are essential. Two topics were chosen for this initial study: the search for quark substructure, and the search for production of leptoquarks. This is by no means an exhaustive list of topics, but is intended to show the capabilities of VHEeP for BSM physics.
6.1 Quark substructure
In order to look for quark substructure, an effective finite radius of the quark can be assigned. The Standard Model prediction, \(\frac{d\sigma ^\mathrm{SM}}{dQ^2}\), is modified using a semi-classical form-factor approach [42]:
where \(R_e^2\) and \(R_q^2\) are the mean-square radii of the electron and quark radius, respectively. As has been done in a recent analysis of HERA data [43], the radius of the electron is assumed to be zero, i.e. the electron is point-like.
The existence of a finite quark radius primarily changes the \(Q^2\) distribution; in a more complete analysis, the full \(x-Q^2\) dependence of the cross section must be analysed to separate the effects of a finite quark radius from effects due to uncertain parton density distributions. For this first study, it was assumed that the parton densities were known with negligible uncertainty, and only the modification of the \(Q^2\) dependence was considered. The effect of the finite quark radius grows with \(Q^2\), as seen in Eq. 10 but this is counterbalanced by the rapidly falling cross section with \(Q^2\). Deep inelastic scattering events were generated with the Ariadne Monte Carlo programme, corresponding to a luminosity of 100 pb\(^{-1}\). The event distribution as a function of \(Q^2\) for the range \(10^5< Q^2 < 10^7\) GeV\(^2\) was analysed and an upper limit on \(R_q\) was determined by reweighting the known cross section using Eq. 10 and performing a fit to the simulated data using the BAT package [44]. The limits correspond to 68 % credibility upper limits where a flat prior was taken for \(0\le R_q<5 \times 10^{-19}\) m.
The extracted limit on \(R_q\) is \(R_q\le 1 \times 10^{-19}\) m, which can be compared with the 95 % Confidence Level limit extracted from HERA data [43], \(R_q<4 \times 10^{-19}\) m. The limit extracted from the HERA data was the result of a much fuller analysis; it is expected that the limits from VHEeP would become considerably stronger if lower \(Q^2\) data were included in the analysis, but this would require a much more complete analysis using detailed information on systematic uncertainties. The limit would also improve by about a factor 3 for a factor 10 increase in luminosity.
6.2 Leptoquark production
Electron–proton collisions are particularly sensitive to leptoquark production as the leptoquark is produced resonantly in the s-channel. This is shown pictorially in Fig. 9, where an electron and quark fuse, with a coupling \(\lambda \). The leptoquark subsequently decays to a lepton–quark system, again with a coupling \(\lambda \), and this effect can be searched for by reconstructing the invariant mass of the final states or looking for a resonant deviation from the Standard Model in the x distribution which is related to the mass of the leptoquark.
a Simulated deep inelastic scattering data with a luminosity of 100 pb\(^{-1}\) (points) and the expectation, both generated with the Ariadne Monte Carlo programme with \(Q^2 > 10\,000\) GeV\(^2\) and \(y>0.1\). b Upper limits on the number of events, \(\nu \), and leptoquark coupling parameter, \(\lambda \), versus mass of the leptoquark, \(M_\mathrm{LQ}\)
In this analysis, deep inelastic scattering events were generated with the Ariadne Monte Carlo programme and the x distribution plotted. This is the same sample as used to extract the limit on \(R_q\), corresponding to a luminosity of 100 pb\(^{-1}\), with events up to about \(x \sim 0.5\), see Fig. 10a. Cuts \(Q^2 > 10\,000\) GeV\(^2\) and \(y>0.1\) were applied to enhance the possible signal over background. A much larger independent sample was generated, again using Ariadne, and used as the Standard Model prediction, also shown in Fig. 10a. The 90 % probability upper limit on the number of signal events, \(\nu \), above the Standard Model prediction was then extracted based on this pseudo-data sample and is shown as a function of the leptoquark mass in Fig. 10b.
In order to extract a signal or limit on leptoquark production, the Standard Model prediction is convoluted with the prediction for leptoquark production according to the Buchmüller–Rückl–Wyler (BRW) model [45]. The Born-level cross section for resonant s-channel leptoquark production in the narrow-width approximation (NWA), \(\sigma ^\mathrm{NWA}\), is
where \(q(x_0,M^2_\mathrm{LQ})\) is the initial-state quark (or antiquark) parton-density function in the proton for a Bjorken-x value of \(x_0=M^2_\mathrm{LQ}/s\), where \(M_\mathrm{LQ}\) is the mass of the leptoquark, and J is the spin of the leptoquark. Given the limit on \(\nu \), a limit on the coupling \(\lambda \) as a function of the mass of scalar leptoquarks was extracted and is shown in Fig. 10.
These results show that VHEeP has sensitivity up to the kinematic limit of 9 TeV. The HERA limits are \(\lambda =0.01\) just below the kinematic limit of 0.3 TeV, rising rapidly to \(\lambda =1\) at about 1 TeV [46, 47]. Limits from the LHC experiments are also \(\lambda =1\) at about \(1{-}2\) TeV for pp collisions at \(\sqrt{s} = 8\) TeV for \({\mathcal {L}} \sim 20\) fb\(^{-1}\) [48, 49]. Given the increased centre-of-mass energy and higher luminosities the sensitivity to leptoquark production at the LHC will extend to \(2{-}3\) TeV. Hence VHEeP has a sensitivity to leptoquark production significantly beyond the HERA limits and LHC limits, both measured and expected.
7 Further physics areas
As well as the areas discussed in the previous sections, many other areas, in particular in QCD, will be open to investigation at VHEeP. Standard tests of QCD, performed at HERA and other colliders, will be possible in this new kinematic regime, such as measurements of the strong coupling constant, jet and heavy flavour production and properties of the hadronic final state. The structure of the proton and photon can be further investigated and fits of the parton densities to the data performed. The results will be related to the measurements above, sensitive to effects such as saturation, but more conventional determinations of the inclusive deep inelastic scattering cross section can be made in a region less sensitive to the more exotic QCD effects. In particular, given the possibility to change the beam energy and to also vary this as widely as possible, the longitudinal structure function can be well measured, which was done with only limited precision at HERA given the relatively small lever arm in centre-of-mass energy [50, 51]. Given the possibility to run with other heavy ions as well as protons in the LHC, VHEeP will also be able to investigate the properties of electron–ion, eA, scattering. Finally, diffraction, an area of QCD re-invigorated at HERA, and particularly sensitive to low-x dynamics can be studied.
8 Summary and outlook
The concept of proton-driven plasma wakefield acceleration will be tested in the next few years in the AWAKE experiment at CERN, with first results expected already this year. Recent simulations of the scheme indicate that acceleration of electrons with 7 TeV LHC proton bunches could be used to bring electrons to 3 TeV with an average gradient of about 1 GeV/m. This opens up tremendous opportunities for considering very high energy colliders; in this paper, we consider the possibility of colliding 3 TeV electrons accelerated in this way with 7 TeV protons from the LHC. This will allow an extension of the kinematic reach of the HERA electron–proton collider by three orders of magnitude, albeit with moderate luminosities.
It is wise to decouple achieving very high energies in a particle collider from the requirement for very high luminosities. While cross sections for standard s-channel physics lead to extremely high luminosity requirements for TeV and beyond energy scales, there are physics questions which can be probed with lower luminosities. Since achieving high luminosities with realistic power consumption could be technologically much more difficult than achieving high energies, it is important that the physics case for a high energy but low luminosity collider be investigated. We consider just such an option in this paper—a very high energy electron–proton collider, VHEeP. We have investigated a number of physics topics that could be addressed by VHEeP and found that indeed very fundamental particle physics questions could be addressed by such a collider. These range from clarifying the underlying physics leading to the energy dependence of cross sections at very high energies, including unraveling the mechanisms for a saturation of the cross section growth, to opening new windows for physics beyond the reach of the LHC, such as leptoquark production with masses beyond 3 TeV. The studies presented in this paper are just a small first step in understanding the physics possibilities of such a collider, and we heartily encourage our colleagues to consider other topics. While we believe that the collider parameters given in this paper are achievable, there is a long road ahead to realise such a machine. New ideas could well arise along the way that would allow for higher luminosities than we have assumed here. Clearly, serious studies of the accelerator and detector will be needed. We believe these are warranted by the exciting physics that a collider such as VHEeP would provide.
References
H1 and ZEUS Collaborations, H. Abramowicz et al., Eur. Phys. J. C 75, 580 (2015) and references therein
P. Newman, A. Stasto, Nat. Phys. 9, 448 (2013)
LHeC Study Group, J.L. Abelleira Fernandez et al., J. Phys. G 39, 075001 (2012)
Y.C. Acar et al., (2016). arXiv:1602.03089
G. Xia et al., Nucl. Instrum. Methods A 740, 173 (2014)
Y.C. Acar et al., (2016). arXiv:1605.08028
See, for example, A. Cooper-Sarkar, R. Devenish, Deep Inelastic Scattering (Oxford University Press, Oxford, 2004). ISBN: 0 19 8506716
E.J. Williams, Phys. Rev. 45, 729 (1934)
C.F. von Weizsäcker, Z. Phys. 88, 612 (1934)
V.N. Gribov et al., Sov. Phys. JETP 14, 1308 (1962)
T. Tajima, J.M. Dawson, Phys. Rev. Lett. 43, 267 (1979)
W.P. Leemans et al., Nat. Phys. 2, 696 (2006)
I. Blumenfeld et al., Nature 445, 741 (2007)
A. Caldwell et al., Nat. Phys. 5, 363 (2009)
A. Caldwell, K. Lotov, Phys. Plasmas 18, 103101 (2011)
AWAKE Collaboration, A. Caldwell et al., Nucl. Instrum. Methods A 829, 3 (2016)
AWAKE Collaboration, R. Assmann et al., Plasma Phys. Control. Fusion 56, 084013 (2014)
AWAKE Collaboration, Design Report, CERN-SPSC-2013-013
E. Adli (on behalf of the AWAKE Collaboration), in Proceedings of IPAC2016, Busan, Korea, p. 2557
A. Caldwell, M. Wing, Presented at XXIII international workshop on deep-inelastic scattering, Dallas, Texas, 2015, Proc. of Science (DIS2015), p. 240
A. Caldwell, M. Wing, Presented at XXIV international workshop on deep-inelastic scattering, Hamburg, Germany, 2016
L. Lönnblad, Comput. Phys. Commun. 71, 15 (1992)
L. Lönnblad, Z. Phys. C 65, 285 (1995)
CTEQ Collaboration, J. Botts et al., Phys. Lett. B 304, 159 (1993)
W.-M. Yao et al. (Particle Data Group), J. Phys. G 33, 1 (2006). Data from http://pdg.lbl.gov/2006/hadronic-xsections/hadron.html
A. Donnachie, P.V. Landshoff, Phys. Lett. B 296, 227 (1992)
A. Donnachie, P.V. Landshoff, Phys. Lett. B 595, 393 (2004)
M. Froissart, Phys. Rev. 123, 1053 (1961)
ZEUS Collaboration, S. Chekanov et al., Nucl. Phys. B 627, 3 (2002)
F. Cornet et al., Phys. Rev. D 92, 114011 (2015)
ZEUS Collaboration, S. Chekanov et al., Eur. Phys. J. C 24, 345 (2002)
H1 Collaboration, C. Alexa et al., Eur. Phys. J. C 73, 2466 (2013)
See, for example, L. Favart et al., Eur. Phys. J. A 52, 158 (2016)
I.P. Ivanov, N.N. Nikolaev, A.A. Savin, Phys. Part. Nucl. 37, 1 (2006) and references therein
LHCb Collaboration, R. Aaij et al., J. Phys. G 40, 045001 (2013)
LHCb Collaboration, R. Aaij et al., J. Phys. G 41, 055002 (2014)
LHCb Collaboration, R. Aaij et al., JHEP 1509, 084 (2015)
ALICE Collaboration, B.B. Abelev et al., Phys. Rev. Lett. 113, 232504 (2014)
ZEUS Collaboration, J. Breitweg et al., Phys. Lett. B 407, 432 (1997)
A. Caldwell, New J. Phys. 18, 073019 (2016)
S. Forte, R.D. Ball, Phys. Lett. B 335, 77 (1994)
G. Kopp et al., Z. Phys. C 65, 545 (1995)
ZEUS Collaboration, H. Abramowicz et al., Phys. Lett. B 757, 468 (2016)
A. Caldwell, D. Kollar, K. Kroninger, Comput. Phys. Commun. 180, 2197 (2009)
W. Buchmüller, R. Rückl, D. Wyler, Phys. Lett. B 191, 442 (1987) [Erratum, ibid B 448, 320 (1999)]
H1 Collaboration, F.D. Aaron et al., Phys. Lett. B 704, 388 (2011)
ZEUS Collaboration, H. Abramowicz et al., Phys. Rev. D 86, 012004 (2012)
ATLAS Collaboration, G. Aad et al., Eur. Phys. J. C 76, 5 (2016)
CMS Collaboration, V. Khachatryan et al., Phys. Rev. D 93, 032005 (2016)
H1 Collaboration, V. Andreev et al., Eur. Phys. J. C 74, 2814 (2014)
ZEUS Collaboration, H. Abramowicz et al., Phys. Rev. D 90, 072002 (2014)
Acknowledgments
L. Lönnblad is gratefully acknowledged for discussions using the Ariadne Monte Carlo programme in this new kinematic regime. E. Shaposhnikova is also gratefully acknowledged for discussions on the LHC beam parameters. R. McNulty is gratefully acknowledged for assistance with the LHCb data on vector meson production. M. Wing acknowledges the support of STFC, DESY and the Alexander von Humboldt Stiftung.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Caldwell, A., Wing, M. VHEeP: a very high energy electron–proton collider. Eur. Phys. J. C 76, 463 (2016). https://doi.org/10.1140/epjc/s10052-016-4316-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4316-1