The longitudinal and transverse distributions of the pion wave function from the present experimental data on the pion–photon transition form factor

Abstract

The low-energy and high-energy behavior of the pion–photon transition form factor $F_{\pi \gamma }(Q^2)$ are sensitive to the transverse and longitudinal distributions of the pion wave function, respectively. A careful study of $F_{\pi \gamma }(Q^2)$ shall thus provide helpful constraints on the properties of the pion wave function. In this paper, we present a combined analysis of the data on $F_{\pi \gamma }(Q^2)$ reported by the CELLO, the CLEO, the BABAR, and the BELLE Collaborations. It is performed by using the method of least squares. By using the combined measurements of the BELLE and CLEO Collaborations, the pion wave function longitudinal and transverse behavior can be fixed to a certain degree, i.e. we obtain $\beta \in [0.691,0.757]$ GeV and $B \in [0.00,0.235]$ for $P_{\chi ^2} \ge 90\,\%$, where $\beta$ and B are two parameters of a convenient pion wave function model. It is noted that the distribution amplitude of such a pion wave function can mimic various longitudinal behaviors, as suggested in the literature under a proper choice of parameters. We observe that the CELLO, CLEO, and BELLE data are consistent with each other, all of which prefer the asymptotic-like distribution amplitude; while the BABAR data prefers a more broad distribution amplitude, such as the CZ-like one.

1 Introduction

The pion–photon transition form factor (TFF) $F_{\pi \gamma }(Q^2)$ provides a simplest example for the perturbative QCD (pQCD) application to exclusive processes, where $Q^2$ stands for the momentum transfer. The TFF relates two photons with the lightest meson (pion) and provides a good platform for studying longitudinal and transverse properties of the pion wave function.

The pion–photon TFF $F_{\pi \gamma }(Q^2)$ is measured via the process, $e^+ e^- \rightarrow e^+ e^- \pi ^0$, in a single-tagged mode. It was first measured in a low-energy region $Q^2 < 3\,\mathrm{GeV}^2$ by the CELLO Collaboration [1]. Later on, it was measured by the CLEO Collaboration [2, 3] in the energy region $Q^2 \in [1.5,9.2]\,\mathrm{GeV}^2$, and by the BABAR Collaboration [4] and the BELLE Collaboration [5] in the widest energy region $Q^2 \in [4,40]\,\mathrm{GeV}^2$. On the other hand, it has been predicted by using the pQCD approach, the QCD light-cone sum rules, or some of the phenomenological models such as the semi-bosonized Nambu–Jona-Lasinio model and the nonlocal chiral-quark model [6–28]. For example, Lepage and Brodsky studied the pion–photon TFF by neglecting the transverse distributions ($\mathbf k _\perp$-distribution) of the constituent quarks, and this resulted in the well-known asymptotic prediction [6], i.e., $Q^2 F_{\pi \gamma }(Q^2)$ tends to be a constant ($\sqrt{2}f_\pi$) for the asymptotic pion DA $\phi ^\mathrm{as}_\pi (x,Q^2)|_{Q^2 \rightarrow \infty } = 6x(1-x)$. The pion decay constant $f_\pi = 130.41 \pm 0.03 \pm 0.20\,\mathrm{MeV}$ [29].

When $Q^2$ $\sim$ a few $\mathrm{GeV}^2$, one should take the $\mathbf k _\perp$-terms into account so as to achieve a reliable prediction of $F_{\pi \gamma }(Q^2)$ [7–15]. The experimental data in this $Q^2$ region is then helpful for determining the transverse behavior of the pion wave function. When $Q^2$ is large enough, the $\mathbf k _\perp$-terms become less important, and the TFF $F_{\pi \gamma }(Q^2)$ shall be dominated by the longitudinal behavior of the pion wave function,which is related to the pion distribution amplitude (DA). At present, there is no definite conclusion on the pion DA due to the different trends indicated by the BABAR and BELLE data. The experimental data in large $Q^2$ region is thus helpful for determining the longitudinal behavior of the pion wave function.

In the present paper, we shall study the pion–photon TFF $F_{\pi \gamma }(Q^2)$ by using a convenient pion wave function model. This pion wave function is constructed from the revised light-cone harmonic oscillator model and its DA can conveniently mimic the asymptotic-like to more broad longitudinal behavior via proper choices of input parameters. Then we perform a combined analysis of the experimental data reported by the CELLO, the CLEO, the BABAR and the BELLE Collaborations, with an attempt to extract useful information of the pion wave function. For the purpose, we shall adopt the analytical expression of $F_{\pi \gamma }(Q^2)$ suggested in our previous paper [16] as its basic fitting function. The pion wave function parameters shall then be fitted by comparing the experimental data with the help of the method of least squares such that to achieve the best goodness-of-fit.

The remaining parts of the paper are organized as follows. In Sect. 2, we give a short review on the pion–photon TFF $F_{\pi \gamma }(Q^2)$ and a brief introduction of the method of least squares. A combined analysis for the experimental data reported by the CELLO, the CLEO, the BABAR, and the BELLE Collaborations is presented in Sect. 3. In Sect. 4, we analyze the TFF $F_{\pi \gamma }(Q^2)$ in detail by using the BELLE and the CLEO data as an attempt to find more accurate information on the pion wave function. Section 5 is reserved for a summary.

2 A brief review of the pion–photon TFF and the method of least squares

The pion–photon TFF can be divided into two parts

$$\begin{aligned} F_{\pi \gamma }(Q^2) = F_{\pi \gamma }^{(V)}(Q^2) + F_{\pi \gamma }^{(NV)}(Q^2). \end{aligned}$$

(1)

$F_{\pi \gamma }^{(V)}(Q^2)$ stands for the contribution from the valence-quark part, which is pQCD calculable. The analytical expression of $F_{\pi \gamma }^{(V)}(Q^2)$ can be found in Ref. [16], in which the next-to-leading order contributions [11, 30, 31] and the $\mathbf k _\perp$-dependence has been kept explicitly, i.e.

$$\begin{aligned} F^{(V)}_{\pi \gamma }(Q^2)= & {} \frac{1}{4\sqrt{3}\pi ^2}\int _0^1\int _0^{x^2 Q^2}\frac{\mathrm{d}x}{x Q^2}\left[ 1-\frac{C_\mathrm{F} \alpha _s(Q^2)}{4\pi } \right. \nonumber \\&\times \left. \left( \ln \frac{\mu _f^2}{xQ^2+k_\perp ^2} +2\ln {x} +3- \frac{\pi ^2}{3} \right) \right] \nonumber \\&\times \Psi _{q\bar{q}}(x,k_\perp ^2) \mathrm{d}k^2_\perp , \end{aligned}$$

(2)

where $[\mathrm{d}x]=\mathrm{d}x\mathrm{d}x'\delta (1-x-x')$, $C_\mathrm{F}=4/3$ and $k_\perp =|\mathbf {k}_\perp |$. $\mu _\mathrm{f}=Q$ stands for the factorization scale. $F_{\pi \gamma }^{(NV)}(Q^2)$ stands for the nonvalence-quark part contribution, which is related to the higher Fock states of the pion, which can be estimated via a proper phenomenological model [15],

$$\begin{aligned} F^{(NV)}_{\pi \gamma }(Q^2)=\frac{\alpha }{(1+Q^2/\kappa ^2)^2}. \end{aligned}$$

(3)

The two phenomenological parameters $\alpha$ and $\kappa$ can be determined from the asymptotic behavior at $Q^2\rightarrow 0$, i.e. $\alpha =\frac{1}{2}F_{\pi \gamma }(0)$ and $\kappa = \sqrt{-\frac{F_{\pi \gamma }(0)}{\frac{\partial }{\partial Q^2} F^{(NV)}_{\pi \gamma }(Q^2)|_{Q^2\rightarrow 0}}}$. Here the value of $\alpha$ is determined by the fact that $F^{(NV)}_{\pi \gamma }(0) = F^{(V)}_{\pi \gamma }(0)$; and the value of $\kappa$ is fixed by the asymptotic behavior $\frac{\partial }{\partial Q^2} F^{(NV)}_{\pi \gamma }(Q^2)|_{Q^2\rightarrow 0}$, where the differential expression of ${\partial } F^{(NV)}_{\pi \gamma }(Q^2)/{\partial Q^2}$ can be found in Ref. [15]. The model (3) for the nonvalence-quark part contribution is reasonable, which satisfies the usual power counting: $F^{(NV)}_{\pi \gamma }(Q^2)$ should be at least $1/Q^2$-suppressed to $F^{(V)}_{\pi \gamma }(Q^2)$ in the large $Q^2$ region.

Table 1 The wave function parameters which are fixed by using the method of least squares for the CELLO, the CLEO, the BABAR, and the BELLE data, respectively

The pion–photon TFF $F_{\pi \gamma }(Q^2)$ is a convolution of the hard scattering amplitude with the $\mathbf k _\perp$-correction and the pion wave function. By taking the BHL-prescription [32–34], the pion wave function can be constructed over the light-cone harmonic oscillator model [16], i.e.

$$\begin{aligned} \Psi _{q\bar{q}}(x,\mathbf{{k}}_\perp ) = \frac{m_\mathrm{q}}{\sqrt{\mathbf{{k}}_\perp ^2 + m_\mathrm{q}^2}} A \varphi (x) \exp \left[ -\frac{\mathbf{{k}}^2_\perp + m_\mathrm{q}^2}{8\beta ^2 x(1-x)} \right] ,\nonumber \\ \end{aligned}$$

(4)

where $m_\mathrm{q}$ is the mass of constituent quark, A is the normalization constant. The spin-space part $\frac{m_\mathrm{q}}{\sqrt{\mathbf{{k}}_\perp ^2 + m_\mathrm{q}^2}}$ is from the Wigner–Melosh rotation [35], and the spatial part wave function is further divided into a x-dependent part $\varphi (x)$ and a $\mathbf{{k}}_\perp$-dependent part. The $\mathbf{{k}}_\perp$-dependent part, with the harmonic parameter $\beta$, is constructed from the BHL-prescription. The x-dependent part can be expanded as a Gegenbauer polynomial, $\varphi (x) = 1 + B \times C^{3/2}_2(2x-1)+\cdots$. As will be found later, the determined parameter B is close to the second Gegenbauer moment $a_2$, thus the function $\varphi (x)$ dominantly determines the longitudinal distribution of the pion wave function. After integrating over the transverse momentum dependence, we obtain the pion DA

$$\begin{aligned} \phi _{q\bar{q}}(x,\mu ^2_0)= & {} \frac{\sqrt{3}A m_\mathrm{q} \beta }{2\pi ^{3/2}f_\pi } \sqrt{x(1-x)} \varphi (x) \nonumber \\&\times \left\{ \mathrm{Erf} \left[ \sqrt{\frac{m_\mathrm{q}^2 + \mu _0^2}{8\beta ^2 x(1-x)}} \right] \right. \nonumber \\&- \left. \mathrm{Erf} \left[ \sqrt{\frac{m_\mathrm{q}^2}{8\beta ^2 x(1-x)}} \right] \right\} , \end{aligned}$$

(5)

where the initial scale $\mu _0 \sim 1$ GeV, the error function $\mathrm{Erf}(x) = \frac{2}{\sqrt{\pi }} \int ^x_0 e^{-t^2} \mathrm{d}t$. The pion DA satisfies the normalization condition, $\int ^1_0 \mathrm{d}x \phi _{q\bar{q}}(x,\mu ^2_0) = 1$. The input model parameters can be fitted from the known experimental data. In addition, one extra constraint from the sum rules of $\pi ^0 \rightarrow \gamma \gamma$ shall be adopted, which states $\int ^1_0 \mathrm{d}x \Psi _{q\bar{q}}(x,\mathbf k _\perp = 0) = \frac{\sqrt{6}}{f_\pi }$. We can adopt this and the normalization condition to fix the values of A and $\beta$, leaving $m_\mathrm{q}$ and B as the two free parameters to be determined from the data. Reference [16] has observed that on setting $m_\mathrm{q}$ to be the usually choosing 300 MeV, the pion DA (5) shall change from the asymptotic-like form [6] to the CZ-like form [36] by simply shifting the parameter B from 0.00 to 0.60. In the present paper, to be more general, we shall adopt a broader range, $m_\mathrm{q} \in [200, 400]\,\mathrm{MeV}$ and $B \in [0.00,0.60]$, to do our fit.

The data fit shall be done by using the method of least squares. Considering a set of N independent measurements $y_i$ with the known variance $\sigma _i$ and the mean $\mu (x_i;\mathbf {\theta })$ at known points $x_i$. The measurements $y_i$ are assumed to be in the Gaussian distribution. The goal of the method of least squares is to get the preferable value of $\mathbf {\theta }$ by minimizing the likelihood function [29],

$$\begin{aligned} \chi ^2(\mathbf {\theta }) = \sum ^N_{i=1} \frac{(y_i - \mu (x_i,\mathbf {\theta }))^2}{\sigma _i^2}. \end{aligned}$$

(6)

As for the present case, the function $\mu (x_i;\mathbf {\theta })$ stands for the pion–photon TFF function defined by (1) and $\mathbf {\theta } = (m_\mathrm{q}, B)$; The value of $y_i$ and its variance $\sigma _i$ for the pion–photon TFF can be read from the measurements of the CELLO, the CLEO, the BABAR, and the BELLE Collaborations [1–5], respectively. The goodness-of-fit is judged by the magnitude of the probability

$$\begin{aligned} P_{\chi ^2} = \int ^\infty _{\chi ^2} f(y;n_\mathrm{d}) \mathrm{d}y, \end{aligned}$$

(7)

where $f(y;n_\mathrm{d}) = \frac{1}{\Gamma (\frac{n_\mathrm{d}}{2}) 2^{n_\mathrm{d}/2}} y^{\frac{n_\mathrm{d}}{2}-1} e^{-\frac{y}{2}}$ is the probability density function of $\chi ^2$, and $n_\mathrm{d}$ is the number of degrees of freedom. The probability $P_{\chi ^2}$ is within the range of [0, 1]; when its value is closer to 1, a better fit is assumed to be achieved.

3 Best fit of the CELLO, the CLEO, the BABAR, and the BELLE data on $F_{\pi \gamma }(Q^2)$

Fig. 1

The pion–photon TFFs $Q^2 F_{\pi \gamma }(Q^2)$ for the experimental data measured by the BABAR, the BELLE, the CLEO and the CELLO Collaborations, respectively. The fitted curves are obtained by using the method of least squares

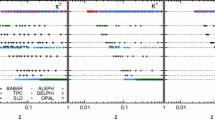
We adopt Eq. (1) as the basic input function to achieve a best fit of the pion wave function parameters by using the known experimental data on the TFF $F_{\pi \gamma }(Q^2)$. More specifically, the values of the two free parameters $(m_\mathrm{q}, B)$ are fixed by requiring them to achieve the minimum value of $\chi ^2(m_\mathrm{q}, B)$, which indicates a best fit of the experimental data within the allowable parameter spaces. The determined pion wave function parameters for the data of the BABAR, the BELLE, the CLEO and the CELLO Collaborations are presented in Table 1, where the values of $\chi ^2_\mathrm{min}/n_\mathrm{d}$ and the probability $P_{\chi ^2_\mathrm{min}}$ are also presented. The pion–photon TFFs under those parameters are put in Fig. 1. Figure 1 shows that the BELLE, the CLEO, and the CELLO data result in a similar trend of the pion–photon TFF, while the BABAR data leads to a quite different TFF behavior in larger $Q^2$ region, i.e. $Q^2 > 10\;\mathrm{GeV}^2$.

Table 1 shows a better fit with better confidence level can be achieved from the CLEO and the BELLE data, whose probabilities are 0.986 and 0.958, respectively. The low probability of the CELLO data is reasonable due to the small number of data. The probability of the BABAR data is less than 0.50, indicating there may have some questionable points. This conclusion agrees with the arguments of Refs. [20–25]. By using the EKHARA event generator [37], a Mont Carlo simulation of the pion–photon TFF on the BESIII platform within the energy region $Q^2 < 3.1\, \mathrm{GeV}^2$ has been given in Ref. [38]. Those simulation data lead to: $m_\mathrm{q} = 272$ MeV, $B = 0.058$, $A=22.118 \,\mathrm{GeV}^{-1}$, $\beta = 0.656$ GeV, $\chi ^2_\mathrm{min}/n_\mathrm{d} = 4.521/16$ and $P_{\chi ^2_\mathrm{min}} = 0.998$, which is also consistent with the above BELLE, CELLO and CLEO predictions.

4 The pion wave function from the BELLE and the CLEO data

In the above section, the pion wave function parameters are fixed by minimizing the likelihood function $\chi ^2$. In present section, we shall adopt a weaker constraint from the probability $P_{\chi ^2}$ to present a more detailed discussion of possible constraints on the pion wave function. We will take a bigger enough probability $P_{\chi ^2}$ to constrain the allowable ranges for the model parameters and extract the information on the pion leading-twist DA. Moreover, we shall only adopt the BELLE and CLEO data to present the discussion, since they are at a higher confidence level. The future more precise data shall lead to stricter constraints on those parameters.

Fig. 2

The allowable $(m_\mathrm{q},B)$ region versus the probability $P_{\chi ^2}$ from the BELLE data for $Q^2\in [4,40]\,\mathrm{GeV}^2$. The four shaded bands from inside to outside are for $P_{\chi ^2}\ge 95\,\%$, $90\,\% \le P_{\chi ^2} < 95\,\%$, $70\,\% \le P_{\chi ^2} < 90\,\%$ and $50\,\%\le P_{\chi ^2}< 70\,\%$, respectively

Fig. 3

The allowable $(m_\mathrm{q},B)$ region versus the probability $P_{\chi ^2}$ from the CLEO data for $Q^2 \in [1.5,9.2]\,\mathrm{GeV}^2$. The four shaded bands from inside to outside are for $P_{\chi ^2}\ge 95\,\%$, $90\,\% \le P_{\chi ^2} < 95\,\%$, $70\,\% \le P_{\chi ^2} < 90\,\%$, and $50\,\%\le P_{\chi ^2}< 70\,\%$, respectively

Figures 2, 3 show the allowable $(m_\mathrm{q},B)$ region versus the probability $P_{\chi ^2}$ from either the BELLE or CLEO data, where the four shaded bands from inside to outside are for $P_{\chi ^2}\ge 95\,\%$, $90\,\% \le P_{\chi ^2} < 95\,\%$, $70\,\% \le P_{\chi ^2} < 90\,\%$, and $50\,\%\le P_{\chi ^2}< 70\,\%$, respectively. Figures 2, 3 show that a stricter constraint to the pion wave function parameters can be achieved by requiring a higher probability $P_{\chi ^2}$.

Fig. 4

The allowable $(m_\mathrm{q},B)$ region from both the BELLE and the CLEO data, where the light-color band is for $P_{\chi ^2} \ge 90\,\%$ and the fuscous band is for $70\,\% \le P_{\chi ^2} < 90\,\%$

As a combination, we put the allowable $(m_\mathrm{q},B)$ region from both the BELLE and the CLEO data in Fig. 4. If requiring $P_{\chi ^2}\ge 90\,\%$, we obtain $B \in [0,0.235]$ and $m_\mathrm{q} \in [227,265]\,\mathrm{MeV}$, which then lead to the first two Gegenbauer moments of the pion DA, $a_2(1\,\mathrm{GeV}) = [0.087,0.348]$ and $a_4(1\,\mathrm{GeV}) = [-0.007,0.015]$. The predicted $a_2$ agrees with the ones determined in the literature from other approaches or other processes, i.e. $a_2(1\,\mathrm{GeV}) = 0.26^{+0.21}_{-0.09}$ [39] and $0.19 \pm 0.06$ [40, 41] by QCD sum rules on the pion–photon TFFs; $0.24 \pm 0.14 \pm 0.08$ [42, 43], $0.20 \pm 0.03$ [44], and $0.19 \pm 0.05$ [45] by QCD LCSRs on the pion form factors; $0.19 \pm 0.19 \pm 0.08$ [46], $0.17^{+0.15}_{-0.17}$ [47, 48], and $0.112 \pm 0.073$ [49] by LCSRs analysis on the $B/D \rightarrow \pi l\nu$.

It is noted that $a_2 \sim B$, indicating that the longitudinal behavior of the pion wave function is dominantly determined by the parameter B. The BELLE data provides a strong constraint for both B and $m_\mathrm{q}$, especially for $P_{\chi ^2}\ge 90\,\%$. On the other hand, Fig. 3 shows by using the lower $Q^2$-data alone, one cannot determine the pion wave function’s longitudinal behavior, because in the low $Q^2$ region, the TFF is insensitive to the choice of the parameter B.¹ However, as will be shown later, the low-energy data is helpful for determining the transverse behavior of the pion wave function.

Fig. 5

The allowable $(\beta ,B)$ region versus the probability $P_{\chi ^2}$ from the BELLE data, where $Q^2 \in [4,40]\,\mathrm{GeV}^2$. The four shaded bands from inside to outside are for $P_{\chi ^2}\ge 95\,\%$, $90\, \% \le P_{\chi ^2} < 95\,\%$, $70\,\% \le P_{\chi ^2} < 90\,\%$, and $50\,\%\le P_{\chi ^2}< 70\,\%$, respectively

Fig. 6

The allowable $(\beta ,B)$ region versus the probability $P_{\chi ^2}$ from the CLEO data, where $Q^2 \in [1.5,9.2]\,\mathrm{GeV}^2$. The four shaded bands from inside to outside are for $P_{\chi ^2}\ge 95\,\%$, $90\,\% \le P_{\chi ^2} < 95\,\%$, $70\,\% \le P_{\chi ^2} < 90\,\%$, and $50\,\%\le P_{\chi ^2}< 70\,\%$, respectively

The transverse behavior of the pion wave function is dominated by the harmonic parameter $\beta$ [50]. To show how the experimental data affect the transverse behavior, we take the parameters (B, $\beta$) as the two free input parameters. Following the same fit procedures, we can obtain the allowable ranges for the parameters (B, $\beta$). The results are presented in Figs. 5, 6, which are for the BELLE and the CLEO data, respectively. Here the four shaded bands from inside to outside are for $P_{\chi ^2}\ge 95\,\%$, $90\,\% \le P_{\chi ^2} < 95\,\%$, $70\,\% \le P_{\chi ^2} < 90\,\%$, and $50\,\%\le P_{\chi ^2}< 70\,\%$, respectively.

The BELLE data leads to $\beta \in [0.691,0.933]\,\mathrm{GeV}$ and $B \in [0.00,0.269]$ for $P_{\chi ^2} \ge 90\,\%$. Figure 5 shows the allowed $\beta$ range quickly expands when $P_{\chi ^2}$ becomes smaller. For example, when $B=0.20$, we have $\beta \in [0.721,0.810]$ for $P_{\chi ^2} \ge 90\,\%$, $\beta \in [0.672,0.918]$ for $P_{\chi ^2} \ge 70\,\%$, and $\beta \in [0.651,1.004]$ for $P_{\chi ^2} \ge 50\,\%$. On the other hand, as shown by Fig. 6, the low-energy CLEO data can give a better constraint to the range of $\beta$, whose allowable range slightly increases with the decrement of $P_{\chi ^2}$. For example, we obtain $\beta \in [0.652,0.757]\, \mathrm{GeV}$ for $P_{\chi ^2} \ge 90\,\%$, $\beta \in [0.634,0.789]\, \mathrm{GeV}$ for $P_{\chi ^2} \ge 70\,\%$, and $\beta \in [0.623,0.812]\, \mathrm{GeV}$ for $P_{\chi ^2} \ge 50\,\%$, accordingly.

Fig. 7

The regions of the pion wave function parameters $(\beta ,B)$ from the BELLE and CLEO data under the probability $P_{\chi ^2} \ge 90\,\%$, where the light-color band is for $P_{\chi ^2} \ge 90\,\%$ and the fuscous band is for $70\,\% \le P_{\chi ^2} < 90\,\%$

The allowable $(\beta ,B)$ region from both the BELLE and the CLEO data is presented in Fig. 7. The lower edge of the shaded band is determined by the BELLE data and the upper edge of the shaded band is determined by the CLEO data, which indicates that the low-energy data is important and helpful for determining the pion wave function’s transverse behavior. Figure 7 shows that $B \in [0.00,0.235]$ and $\beta \in [0.691,0.757]\, \mathrm{GeV}$ for $P_{\chi ^2} \ge 90\,\%$.

Fig. 8

The allowable $(\beta ,B)$ region versus the choice of the probability $P_{\chi ^2}$ from the BELLE data in the high-energy region $Q^2\in [10,40]\, \mathrm{GeV}^2$

The importance of the low-energy data can be further explained by Fig. 8, which shows the allowable $(\beta ,B)$ region versus the probability $P_{\chi ^2}$ from the BELLE data in high-energy region $Q^2\in [10,40]\, \mathrm{GeV}^2$. Figure 8 shows that the allowable range of $\beta$ is quickly broadened for a smaller and smaller $P_{\chi ^2}$. For example, when setting $B=0.00$, we shall have $\beta \in [0.818,0.887]$ for $P_{\chi ^2} \ge 90\,\%$, $\beta \in [0.659,1.111]$ for $P_{\chi ^2} \ge 70\,\%$, and $\beta \in [0.613,1.2]$ for $P_{\chi ^2} \ge 50\,\%$. Thus by using the large $Q^2$ data alone, one may not get a definite conclusion on the transverse behavior, unless the goodness-of-fit is high enough.

5 Summary

We have studied the transverse and longitudinal behavior of the pion wave function by fitting the CELLO, the CLEO, the BABAR, and the BELLE data on the pion–photon TFF $F_{\pi \gamma }(Q^2)$. The method of least squares is adopted for such an analysis.

Fig. 9

The pion DAs with the parameters listed in Table 1, which are fit from the TFF data of BABAR, BELLE, CLEO, and CELLO Collaborations, respectively. As a comparison, we also present the asymptotic-DA [6] and the CZ-DA [36] in the figure

Using the best fit parameters that lead to minimized likelihood function which are listed in Table 1, we get useful information on the pion wave function. As an example, we put its distribution amplitude in Fig. 9. It is shown that the best fit of the CELLO, the CLEO, and the BELLE data prefer an asymptotic-like behavior, while the BABAR data prefers a more broad distribution, such as the CZ-like behavior. Table 1 also indicates that a better fit with better confidence level can be achieved from the CLEO and the BELLE data, whose probabilities are close to 1. The low probability of the CELLO data is reasonable due to the small number of data. The probability of the BABAR data is less than 0.50, indicating there may be some questionable points within the measured data.

Fig. 10

The predicted pion–photon TFF $Q^2 F_{\pi \gamma }(Q^2)$ by using the parameters determined from the BELLE and the CLEO data. The BABAR, the BELLE, the CLEO, and the CELLO data are also presented as a comparison

It is noted that the transverse and longitudinal behavior of the pion wave function is dominantly determined by the parameter $\beta$ and B, respectively. The parameter B can precisely be constrained by the $Q^2 F_{\pi \gamma }(Q^2)$ behaviors in high-energy region. For example, the BELLE data can determine the parameter B well. Figures 3 and 6 show that if using the lower $Q^2$-data alone, such as the CLEO data, one cannot determine the pion wave function’s longitudinal behavior. However, as shown by Fig. 6, the low-energy CLEO data is important and helpful for determining the transverse behavior of the pion wave function. However, one still cannot determine the pion wave function precisely due to the different trends indicated by the BABAR and BELLE data in the large $Q^2$ region. Therefore, the future experimental data in the large $Q^2$ region will be crucial for determining the longitudinal behavior of the pion wave function.

Using the BELLE and the CLEO data together and requiring $P_{\chi ^2}\ge 90\,\%$, we obtain $B \in [0,0.235]$, $m_\mathrm{q} \in [227,265]\,\mathrm{MeV}$, and $\beta \in [0.691,0.757]\, \mathrm{GeV}$. Using those parameters, our final prediction on the pion–photon TFF $F_{\pi \gamma }(Q^2)$ are presented in Fig. 10.