Pseudo-scalar Higgs boson production at threshold N$^3$LO and N$^3$LL QCD

Abstract

We present the first results on the production of pseudo-scalar Higgs boson through gluon fusion at the LHC to N$^3$LO in QCD taking into account only soft-gluon effects. We have used the effective Lagrangian that describes the coupling of the pseudo-scalar Higgs boson with the gluons in the large top quark mass limit. We have used quantities that have recently become available, namely the three-loop pseudo-scalar Higgs boson form factor and the third order universal soft function in QCD to achieve this. Along with the fixed order results, we also present the process dependent resummation coefficient for a threshold resummation to N$^3$LL in QCD. Phenomenological impact of these threshold N$^3$LO corrections to pseudo-scalar Higgs boson production at the LHC is presented and their role in the reduction of the renormalization scale dependence is demonstrated.

1 Introduction

The spectacular discovery of the Higgs boson [1, 2] at the Large Hadron Collider (LHC) has put the Standard Model (SM) of elementary particles on a firm footing. Most importantly, the mystery of the electroweak symmetry breaking [3–7] mechanism can now be solved. The consistency of the measured decay rates of the Higgs boson to a pair of vector bosons namely $W^+W^-, ZZ$ and fermions $b \overline{b},\tau \overline{\tau }$ with the precise predictions of the SM for the measured Higgs boson mass of 125 GeV within the experimental uncertainty [8, 9] makes this discovery very robust. In addition, there is a strong evidence that the discovered Higgs boson has spin zero and even parity [10, 11]. The ongoing 13 TeV run at LHC will indeed provide further scope to the study of the properties of the Higgs boson in great detail.

While the SM is complete in the sense that all of its predictions have been tested experimentally, the model suffers from various deficiencies, as it cannot explain the baryon asymmetry in the Universe, dark matter, the neutrino mass etc. There are several extensions of the SM, motivated to address these issues. The minimal version of the Supersymmetric Standard Model (MSSM) [12] is one of the most elegant extensions of the SM and it addresses the above mentioned issues. The Higgs sector of it contains a pair of Higgs doublets which after symmetry breaking gives two CP even Higgs bosons, h, H, and one CP odd (pseudo-scalar) Higgs boson, A, and two charged Higgs bosons H$^{\pm }$ [13–20]. The predicted upper bound on the mass of the lightest Higgs boson (h) up to three-loop level is consistent [21–24] with the recently observed Higgs boson at the LHC. The efforts to test the predictions of MSSM or its variants already are under way and the current run at the LHC will shed more light on them. One of them could be to look for a CP odd Higgs boson in the gluon fusion through heavy fermions as its coupling is appreciable for small and moderate $\tan \beta$, the ratio of vacuum expectation values $v_i, i=1,2$. In addition, a large gluon flux can boost the cross section.

Since the leading order production mechanism of the pseudo-scalar Higgs boson of mass $m_A$ is through heavy quarks, the cross section is not only proportional to $\tan \beta$ but also the square of the strong coupling constant. Like the scalar Higgs boson in the SM, the leading order prediction of the pseudo-scalar Higgs boson production at the hadron colliders suffers from theoretical uncertainties that are large, particularly due to the renormalization scale $\mu _R$ arising from the strong coupling constant, and are mild due to the factorization scale $\mu _F$ in the parton distribution functions. Predictions based on one-loop perturbative Quantum Chromodynamics (pQCD) corrections [25–28] reduce these uncertainties (in the conventional range with the central scale $\mu = m_A/2$ and $m_A=200$ GeV) from about 48 to 35 %, while increasing the LO cross section substantially, by as much as 67 %. The effective theory approach in the large top quark mass limit provides an opportunity to go beyond NLO. Such an approach [28, 29] in the case of scalar Higgs boson production [30–32] turned out to be most successful, as the finite quark mass effects at NNLO level were found to be within 1 % [33–37]. NNLO predictions in the effective theory for the production of pseudo-scalar Higgs boson at the hadron colliders are already available [32, 38, 39]. The calculations were further performed after considering the finite mass of the top quarks in [40, 41]. The NNLO correction increases the NLO cross section by about 15 % and reduces the scale uncertainties to about 15 %. Due to the large gluon flux at the threshold, namely when the mass of pseudo-scalar Higgs boson approaches the partonic center of mass energy, the cross section is dominated by the presence of soft gluons. These contributions often can spoil the reliability of the predictions based on fixed order perturbative computations. Resummation of large logarithms resulting from soft gluons to all orders in perturbation theory provides the solution to this problem. The systematic predictions based on the next-to-next-to-leading log (NNLL) resummed result [42–50] demonstrate the reliability of the approach and also reduce the scale uncertainties.

A complete calculation at NNLO [30–32] and leading logarithms at N$^{3}$LO in the threshold limit [43–47] and NNLL soft-gluon resummation [42] for the scalar Higgs boson production have been known for more than a decade. Recently there have been series of works on predicting inclusive scalar Higgs boson production beyond this level. The computation of the $\delta (1-z)$ contribution at N$^{3}$LO in the threshold limit [51] was the first among them. This was confirmed independently in [52]. Later on, the sub-leading collinear logarithms were computed in [53, 54]. A spin-off of the result presented in [51] is the computation of the N$^{3}$LO prediction for the Drell–Yan production [52, 55, 56] at the hadron colliders in the threshold limit. In addition, one can obtain N$^{3}$LO threshold corrections to the Higgs boson production through bottom quark annihilation [57] and also in association with vector boson [58] at the hadron colliders. Later, along the same direction, the rapidity distribution of the Higgs boson in gluon fusion [59], Drell–Yan [59], and the Higgs boson in bottom quark annihilation [60] were obtained at threshold N$^{3}$LO QCD.

A milestone in this direction was achieved by Anastasiou et al. who have now accomplished the complete N$^{3}$LO prediction [61] of the scalar Higgs boson production through gluon fusion at the hadron colliders in the effective theory. These third order corrections increase the cross section by a few percent, about 2 % and reduce the scale uncertainty by about 2 %. Using these predictions, it is now possible to obtain the soft-gluon resummation at N$^{3}$LL; see [56, 62]. In [63], the SM Higgs resummation is performed for the first time in the soft-collinear effective field theory (SCET) approach to N$^3$LL. We also note that in the exact theory, including the finite top mass effects, the three-loop virtual corrections are already available in [64] and the full result is yet to be computed.

While the next step in the wish list is to obtain the N$^{3}$LO predictions for the pseudo-scalar Higgs boson production through gluon fusion, the first task in this direction is to obtain the threshold enhanced cross section at N$^{3}$LO level. One of the crucial ingredients is the form factor of the effective composite operators that couple to pseudo-scalar Higgs boson, computed between partonic states. One- and two-loop results for them between gluon states were computed for NNLO production cross section [38, 39, 65], the analytical results up to two-loop level can be found in [65]. These were computed in dimensional regularization where the space-time dimension is $d=4+\epsilon$. Threshold corrections to pseudo-scalar Higgs boson production at N$^3$LO level requires the knowledge of the form factors up to three-loop level. We also need to know one- and two-loop corrections computed to desired accuracy in $\epsilon$, namely up to $\epsilon ^2$ for one loop and up to $\epsilon$ at two loops. In [66], we obtained the three-loop form factors of the effective composite operators between quark and gluon states along with the lower order ones to the desired accuracy in $\epsilon$. In the present article we will describe how threshold corrections at N$^3$LO level can be obtained from the formalism developed in [45, 46] using the available information on recently computed three-loop form factor of the pseudo-scalar Higgs boson [66], the universal soft-collinear distribution [55], and the operator renormalization constant [66–68] and the mass factorization kernels [69, 70] known to three-loop level. In addition, we compute a third order correction to the N-independent part of the resummed cross section [71, 72] using our formalism [45, 46]. We also present the numerical impact of our findings with a brief conclusion.

The underlying effective theory is discussed in the Sect. 2. This is followed by a short description of the formalism which has been employed to compute the soft-plus-virtual cross section in Sect. 3. We present the analytical results of these findings in the Sect. 4 up to N$^3$LO in QCD. In Sect. 5, the N-independent parts of the threshold resummed cross section in Mellin space have been presented up to third order in QCD. Before making our concluding remarks, in Sect. 6 we demonstrate the numerical implications of the fixed order soft-plus-virtual cross sections to N$^3$LO at LHC.

2 The effective Lagrangian

A pseudo-scalar Higgs boson couples to gluons only indirectly through a virtual heavy quark loop which can be integrated out in the infinite quark mass limit. The effective Lagrangian [73] describing the interaction between pseudo-scalar Higgs boson $\chi ^{A}$ and the QCD particles in the infinitely large top quark mass limit is given by

$$\begin{aligned} \mathcal{L}^{A}_\mathrm{eff} = \chi ^{A}(x) \left[ -\frac{1}{8} {C}_{G} O_{G}(x) - \frac{1}{2} {C}_{J} O_{J}(x)\right] \end{aligned}$$

(2.1)

where the two operators are defined as

$$\begin{aligned}&O_{G}(x) = G^{\mu \nu }_a \tilde{G}_{a, \mu \nu } \equiv \epsilon _{\mu \nu \rho \sigma } G^{\mu \nu }_a G^{\rho \sigma }_a,\qquad \nonumber \\&O_{J}(x) = \partial _{\mu } \left( \bar{\psi } \gamma ^{\mu }\gamma _5 \psi \right) . \end{aligned}$$

(2.2)

The symbols $G^{\mu \nu }_{a}$ and $\psi$ represent the gluonic field strength tensor and the quark field, respectively. The Wilson coefficients $C_{G}$ and $C_{J}$ of the two operators are the consequences of integrating out the heavy quark loop in the effective theory. $C_{G}$ does not receive any QCD corrections beyond one loop because of the Adler–Bardeen theorem [74], whereas $C_{J}$ starts only at second order in the strong coupling constant. These Wilson coefficients are given by [73]

$$\begin{aligned} C_{G}= & {} -a_{s} 2^{\frac{5}{4}} G_{F}^{\frac{1}{2}} \mathrm{cot}\beta , \nonumber \\ C_{J}= & {} - \left[ a_{s} C_{F} \left( \frac{3}{2} - 3\ln \frac{\mu _{R}^{2}}{m_{t}^{2}} \right) + a_s^2 C_J^{(2)} + \cdots \right] C_{G}.\nonumber \\ \end{aligned}$$

(2.3)

$G_{F}$ stands for the Fermi constant and $\mathrm{cot}\beta$ is the mixing angle in the Two-Higgs-Doublet model. $m_{A}$ and $m_{t}$ symbolize the masses of the pseudo-scalar Higgs boson and top quark (heavy quark), respectively. The strong coupling constant $a_{s} \equiv a_{s} (\mu _{R}^{2})$ is renormalized at the mass scale $\mu _{R}$ and is related to the unrenormalized one, ${\hat{a}}_{s} \equiv {\hat{g}}_{s}^{2}/16\pi ^{2}$, through

$$\begin{aligned} {\hat{a}}_{s} S_{\epsilon } = \left( \frac{\mu ^{2}}{\mu _{R}^{2}} \right) ^{\epsilon /2} Z_{a_{s}} a_{s} \end{aligned}$$

(2.4)

with $S_{\epsilon } = \mathrm{exp} \left[ (\gamma _{E} - \ln 4\pi )\epsilon /2 \right]$ and the scale $\mu$ is introduced to keep the unrenormalized strong coupling constant dimensionless in $d=4+\epsilon$ space-time dimensions. The renormalization constant $Z_{a_{s}}$ up to $\mathcal{O}(a_{s}^{3})$ is given by

$$\begin{aligned} Z_{a_{s}}= & {} 1+ a_s\left[ \frac{2}{\epsilon } \beta _0\right] + a_s^2 \left[ \frac{4}{\epsilon ^2 } \beta _0^2 + \frac{1}{\epsilon } \beta _1 \right] \nonumber \\&+\, a_s^3 \left[ \frac{8}{ \epsilon ^3} \beta _0^3 +\frac{14}{3 \epsilon ^2} \beta _0 \beta _1 + \frac{2}{3 \epsilon } \beta _2 \right] . \end{aligned}$$

(2.5)

$\beta _{i}$’s are the coefficients of the QCD $\beta$ function [75].

3 Threshold corrections

The inclusive cross section for the production of a colorless pseudo-scalar at the hadron colliders can be computed using

$$\begin{aligned} \sigma ^A(\tau ,m_A^2)= & {} \sigma ^{A,(0)}(\mu _{R}^{2}) \sum _{a,b=q,\bar{q},g} \int _{\tau }^{1} \mathrm{d}y ~ \varPhi _{ab}(y,\mu _F^2) \nonumber \\&\varDelta _{ab}^{A}\left( \frac{\tau }{y}, m_A^2, \mu _R^2, \mu _F^2\right) \end{aligned}$$

(3.1)

where the Born cross section at the parton level including the finite top mass dependence is given by

$$\begin{aligned} \sigma ^{A,(0)}(\mu _{R}^{2}) = \frac{\pi \sqrt{2} G_F}{16} a_s^2 \mathrm{cot}^2\beta ~\big | \tau _A f(\tau _A)\big |^2. \end{aligned}$$

(3.2)

Here $\tau _A = 4m_t^2/m_A^2$ and the function $f(\tau _{A})$ is given by

$$\begin{aligned}&f(\tau _{A}) = {\left\{ \begin{array}{ll} \mathrm{arcsin}^{2}\frac{1}{\sqrt{\tau _{A}}} &{} \tau _{A} \ge 1, \\ -\frac{1}{4} \left( \ln \frac{1-\sqrt{1-\tau _{A}}}{1+\sqrt{1-\tau _{A}}} +i \pi \right) ^{2} &{} \tau _{A} < 1, \end{array}\right. } \end{aligned}$$

(3.3)

while the parton flux is given by

$$\begin{aligned} \varPhi _{ab}(y,\mu _F^2) = \int _y^1 {\mathrm{d}x \over x} f_a(x,\mu _F^2) f_b\left( {y \over x},\mu _F^2\right) , \end{aligned}$$

(3.4)

where $f_a$ and $f_b$ are the parton distribution functions (PDFs) of the initial state partons a and b, renormalized at the factorization scale $\mu _{F}$. Here, ${\varDelta }^{A}_{a b} (\frac{\tau }{y}, m_A^2, \mu _{R}^{2}, \mu _F^2)$ are the partonic level cross sections, for the sub-process initiated by the partons a and b, computed after performing the overall operator UV renormalization at scale $\mu _{R}$ and the mass factorization at a scale $\mu _{F}$. The variable $\tau$ is defined as $q^{2}/s$ with $q^{2} = m_{A}^{2}$.

The goal of this article is to study the impact of the soft-gluon contributions to the pseudo-scalar Higgs boson production cross section at hadron colliders. The infrared safe contribution is obtained by adding the soft part of the cross section to the ultraviolet (UV) renormalized virtual part and performing the mass factorization using appropriate counter terms. This combination is often called the soft-plus-virtual (SV) cross section, whereas the remaining portion is known as the hard part. Thus, we write the partonic cross section as

$$\begin{aligned} {\varDelta }^{A}_{a b} (z, q^{2}, \mu _{R}^{2}, \mu _F^2)= & {} {\varDelta }^{A, \text {SV}}_{a b} (z, q^{2}, \mu _{R}^{2}, \mu _F^2)\nonumber \\&+\,{\varDelta }^{A,\text {hard}}_{a b} (z, q^{2}, \mu _{R}^{2}, \mu _F^2) \end{aligned}$$

(3.5)

with $z \equiv q^{2}/\hat{s} = \tau /(x_{1} x_{2})$. The threshold contributions ${\varDelta }^{A,\text {SV}}_{a b} (z, q^{2}, \mu _{R}^{2}, \mu _F^2)$ contain only distributions of the kind $\delta (1-z)$ and $\mathcal{{D}}_{i}$, where the latter one is defined through

$$\begin{aligned} \mathcal{{D}}_{i} \equiv \left[ \frac{\ln ^{i}(1-z)}{1-z} \right] _{+}. \end{aligned}$$

(3.6)

On the other hand, the hard part ${\varDelta }^{A,\text {hard}}_{a b}$ contains all the terms regular in z. The SV cross section in z-space is computed in $d=4+\epsilon$ dimensions, as formulated for the first time in [45, 46], using

$$\begin{aligned} {\varDelta }^{A,\text {SV}}_{g} (z, q^2, \mu _{R}^{2}, \mu _F^2) = \mathcal{C} \exp (\varPsi ^A_{g}(z, q^2, \mu _R^2, \mu _F^2, \epsilon ) )\Big |_{\epsilon = 0}\nonumber \\ \end{aligned}$$

(3.7)

where $\varPsi ^A_{g} (z, q^2, \mu _R^2, \mu _F^2, \epsilon )$ is a finite distribution and $\mathcal{C}$ is the Mellin convolution defined as

$$\begin{aligned} \mathcal{C} e^{f(z)} = \delta (1-z) + \frac{1}{1!} f(z) + \frac{1}{2!} f(z) \otimes f(z) + \cdots .\nonumber \\ \end{aligned}$$

(3.8)

Here $\otimes$ represents Mellin convolution and f(z) is a distribution of the kind $\delta (1-z)$ and $\mathcal{D}_i$. The subscript g signifies the gluon initiated production of the pseudo-scalar Higgs boson. The equivalent formalism of the SV approximation is in the Mellin (or N-moment) space, where instead of distributions in z the dominant contributions come from the meromorphic functions of the variable N (see [71, 72]) and the threshold limit of $z \rightarrow 1$ is translated to $N \rightarrow \infty$. The $\varPsi ^A_{g} (z, q^2, \mu _R^2, \mu _F^2, \epsilon )$ is constructed from the form factors ${\mathcal{F}}^A_{g} (\hat{a}_s, Q^2, \mu ^2, \epsilon )$ with $Q^{2}=-q^{2}$, the overall operator UV renormalization constant $Z^A_{g}(\hat{a}_s, \mu _R^2, \mu ^2, \epsilon )$, the soft-collinear distribution $\varPhi ^A_{g}(\hat{a}_s, q^2, \mu ^2, z, \epsilon )$ arising from the real radiations in the partonic sub-processes and the mass factorization kernels $\varGamma _{gg} (\hat{a}_s, \mu _F^2, \mu ^2, z, \epsilon )$. In terms of the above-mentioned quantities it takes the following form, as presented in [46, 55, 57]:

$$\begin{aligned}&\varPsi ^{A}_{g} (z, q^2, \mu _R^2, \mu _F^2, \epsilon ) =(\ln [ Z^A_{g} (\hat{a}_s, \mu _R^2, \mu ^2, \epsilon ) ]^2\nonumber \\&\quad +\, \ln | {\mathcal{F}}^A_{g} (\hat{a}_s, Q^2, \mu ^2, \epsilon ) |^2 ) \delta (1-z)\nonumber \\&\quad +\, 2 \varPhi ^A_{g} (\hat{a}_s, q^2, \mu ^2, z, \epsilon ) - 2 \mathcal{C} \ln \varGamma _{gg} (\hat{a}_s, \mu _F^2, \mu ^2, z, \epsilon ).\nonumber \\ \end{aligned}$$

(3.9)

In the subsequent sections, we will demonstrate the methodology to get these ingredients to compute the SV cross section of pseudo-scalar Higgs boson production at N$^{3}$LO. In particular, in Sect. 3.1, we show how to obtain the relevant form factor that goes into the computation of pseudo-scalar production through gluon fusion, using the form factors obtained in our earlier work [66]. In Sect. 3.2, we calculate the operator renormalization constant from the relevant UV anomalous dimensions. Mass factorization is discussed very briefly in Sect. 3.3. Finally, we explain the relevant soft-collinear distribution in Sect. 3.4.

3.1 The form factor

The quark and gluon form factors represent the QCD loop corrections to the transition matrix element from an on-shell quark–antiquark pair or two gluons to a color-neutral operator O. For the pseudo-scalar Higgs boson production through gluon fusion, we need to consider two operators $O_{G}$ and $O_{J}$, defined in Eq. (2.2), which yield in total two form factors. The unrenormalized gluon form factors at $\mathcal{O}({\hat{a}}_{s}^{n})$ are defined [66] through

$$\begin{aligned}&{\hat{\mathcal{F}}}^{G,(n)}_{g} \equiv \frac{\langle {\hat{\mathcal{M}}}^{G,(0)}_{g}|{\hat{\mathcal{M}}}^{G,(n)}_{g}\rangle }{\langle {\hat{\mathcal{M}}}^{G,(0)}_{g}|{\hat{\mathcal{M}}}^{G,(0)}_{g}\rangle }, \nonumber \\&{\hat{\mathcal{F}}}^{J,(n)}_{g} \equiv \frac{\langle {\hat{\mathcal{M}}}^{G,(0)}_{g}|{\hat{\mathcal{M}}}^{J,(n+1)}_{g}\rangle }{\langle {\hat{\mathcal{M}}}^{G,(0)}_{g}|{\hat{\mathcal{M}}}^{J,(1)}_{g}\rangle } \end{aligned}$$

(3.10)

where $n=0, 1, 2, 3, \ldots$. In the above expressions $|{\hat{\mathcal{M}}}^{\lambda ,(n)}_{g}\rangle$ $(\lambda = G,J)$ is the $\mathcal{O}({\hat{a}}_{s}^{n})$ contribution to the unrenormalized matrix element described by the bare operator $[O_{\lambda }]_B$. In terms of these quantities, the full matrix element and the full form factors can be written as series expansions in ${\hat{a}}_{s}$:

$$\begin{aligned}&|\mathcal{M}^{\lambda }_{g}\rangle \equiv \sum _{n=0}^{\infty } {\hat{a}}^{n}_{s} S^{n}_{\epsilon } |{\hat{\mathcal{M}}}^{\lambda ,(n)}_{g} \rangle ,\nonumber \\&\mathcal{F}^{\lambda }_{g} \equiv \sum _{n=0}^{\infty } \left[ {\hat{a}}_{s}^{n} \left( \frac{Q^{2}}{\mu ^{2}} \right) ^{n\frac{\epsilon }{2}} S_{\epsilon }^{n} {\hat{\mathcal{F}}}^{\lambda ,(n)}_{g}\right] , \end{aligned}$$

(3.11)

where $Q^{2}=-2\, p_{1}.p_{2}=-q^{2}$ and $p_i$ ($p_{i}^{2}=0$) are the momenta of the external on-shell gluons. Note that $|{\hat{\mathcal{M}}}^{J,(n)}_{g}\rangle$ starts at $n=1$ i.e. from the one-loop level.

The form factor for the production of a pseudo-scalar Higgs boson through gluon fusion, ${\hat{\mathcal{F}}}^{A,(n)}_{g}$, can be written in terms of the two individual form factors, Eq. (3.11), as follows:

$$\begin{aligned} {\mathcal{F}}^{A}_{g} = {\mathcal{F}}^{G}_{g} + \left( \frac{Z_{GJ}}{Z_{GG}} + \frac{4 C_{J}}{C_{G}} \frac{Z_{JJ}}{Z_{GG}}\right) {\mathcal{F}}^{J}_{g} \frac{\langle {\hat{\mathcal{M}}}^{G,(0)}_{g}|{\hat{\mathcal{M}}}^{J,(1)}_{g}\rangle }{\langle {\hat{\mathcal{M}}}^{G,(0)}_{g}|{\hat{\mathcal{M}}}^{G,(0)}_{g}\rangle }.\nonumber \\ \end{aligned}$$

(3.12)

In the above expression, the quantities $Z_{ij} (i,j= G, J)$ are the overall operator renormalization constants which are required to introduce in the context of UV renormalization. These are discussed in our recent article [66] in great detail. The ingredients of the form factor ${\mathcal{F}}^{A}_{g}$, namely, ${\mathcal{F}}^{G}_{g}$ and ${\mathcal{F}}^{J}_{g}$ have been calculated up to three-loop level by some of us and presented in the same article [66]. Using those results we obtain the three-loop form factor for the pseudo-scalar Higgs boson production through gluon fusion. In this section, we present the unrenormalized form factors ${\hat{\mathcal{F}}}^{A,(n)}_{g}$ up to three loops where the components are defined through the expansion

$$\begin{aligned} {\mathcal{F}}^{A}_{g} \equiv \sum _{n=0}^{\infty } \left[ {\hat{a}}_{s}^{n} \left( \frac{Q^{2}}{\mu ^{2}} \right) ^{n\frac{\epsilon }{2}} S_{\epsilon }^{n} {\hat{\mathcal{F}}}^{A,(n)}_{g}\right] . \end{aligned}$$

(3.13)

We present the unrenormalized results for the choice of the scale $\mu _{R}^{2}=\mu _{F}^{2}=q^{2}$ as follows:

$$\begin{aligned}&{\hat{\mathcal{F}}}^{A,(1)}_{g} = {\varvec{C_{A}}} \Bigg \{ - \frac{8}{\epsilon ^2} + 4 + \zeta _2 + \epsilon \Bigg ( - 6 - \frac{7}{3} \zeta _3 \Bigg )\nonumber \\&\qquad +\, \epsilon ^2 \Bigg ( 7 - \frac{\zeta _2}{2} + \frac{47}{80} \zeta _2^2 \Bigg )\nonumber \\&\qquad + \epsilon ^3 \Bigg ( - \frac{15}{2} +\, \frac{3}{4} \zeta _2 + \frac{7}{6} \zeta _3 + \frac{7}{24} \zeta _2 \zeta _3 - \frac{31}{20} \zeta _5 \Bigg )\nonumber \\&\qquad +\, \epsilon ^4 \Bigg ( \frac{31}{4} - \frac{7}{8} \zeta _2 - \frac{47}{160} \zeta _2^2 + \frac{949}{4480} \zeta _2^3 - \frac{7}{4} \zeta _3 - \frac{49}{144} \zeta _3^2 \Bigg ) \nonumber \\&\qquad +\, \epsilon ^5 \Bigg ( - \frac{63}{8} + \frac{15}{16} \zeta _2 + \frac{141}{320} \zeta _2^2 + \frac{49}{24} \zeta _3 - \frac{7}{48} \zeta _2 \zeta _3\nonumber \\&\qquad +\, \frac{329}{1920} \zeta _2^2 \zeta _3 + \frac{31}{40} \zeta _5 + \frac{31}{160} \zeta _2 \zeta _5 -\, \frac{127}{112} \zeta _7 \Bigg ) \nonumber \\&\qquad + \epsilon ^6 \Bigg ( \frac{127}{16} - \frac{31}{32} \zeta _2 - \frac{329}{640} \zeta _2^2 - \frac{949}{8960} \zeta _2^3\nonumber \\&\qquad +\, \frac{55779}{716800} \zeta _2^4 - \frac{35}{16} \zeta _3 + \frac{7}{32} \zeta _2 \zeta _3 \nonumber \\&\qquad +\, \frac{49}{288} \zeta _3^2 + \frac{49}{1152} \zeta _2 \zeta _3^2 - \frac{93}{80} \zeta _5 - \frac{217}{480} \zeta _3 \zeta _5 \Bigg )\nonumber \\&\qquad +\,\epsilon ^7 \Bigg ( - \frac{255}{32} + \frac{63}{64} \zeta _2 + \frac{141}{256} \zeta _2^2 + \frac{2847}{17920} \zeta _2^3 \nonumber \\&\qquad +\, \frac{217}{96} \zeta _3 - \frac{49}{192} \zeta _2 \zeta _3 - \frac{329}{3840} \zeta _2^2 \zeta _3 + \frac{949}{15360} \zeta _2^3 \zeta _3\nonumber \\&\qquad -\, \frac{49}{192} \zeta _3^2 - \frac{343}{10368} \zeta _3^3 + \frac{217}{160} \zeta _5-\frac{31}{320} \zeta _2 \zeta _5 \nonumber \\&\qquad +\, \frac{1457}{12800} \zeta _2^2 \zeta _5 + \frac{127}{224} \zeta _7 + \frac{127}{896} \zeta _2 \zeta _7 - \frac{511}{576} \zeta _{9} \Bigg ) \Bigg \},\nonumber \\&{\hat{\mathcal{F}}}^{A,(2)}_{g}= {\varvec{C_{F} n_{f}}} \Bigg \{ - \frac{80}{3} + 6 \ln \left( \frac{q^2}{m_t^2}\right) + 8 \zeta _3\nonumber \\&\qquad +\, \epsilon \Bigg ( \frac{2827}{36} - 9 \ln \left( \frac{q^2}{m_t^2}\right) - \frac{19}{6} \zeta _2 - \frac{8}{3} \zeta _2^2 \nonumber \\&\qquad -\, \frac{64}{3} \zeta _3 \Bigg ) + \epsilon ^2 \Bigg ( - \frac{70577}{432} + \frac{21}{2} \ln \left( \frac{q^2}{m_t^2}\right) \nonumber \\&\qquad +\, \frac{1037}{72} \zeta _2 - \frac{3}{4} \ln \left( \frac{q^2}{m_t^2} \right) \zeta _2 + \frac{64}{9} \zeta _2^2 + \frac{455}{9} \zeta _3 \nonumber \\&\qquad -\, \frac{10}{3} \zeta _2 \zeta _3 + 8 \zeta _5 \Bigg ) + \epsilon ^3 \Bigg ( \frac{1523629}{5184} - \frac{45}{4} \ln \left( \frac{q^2}{m_t^2}\right) \end{aligned}$$

$$\begin{aligned}&\qquad -\, \frac{14975}{432} \zeta _2 + \frac{9}{8} \ln \left( \frac{q^2}{m_t^2}\right) \zeta _2 \nonumber \\&\qquad -\, \frac{70997}{4320} \zeta _2^2 + \frac{22}{35} \zeta _2^3 - \frac{3292}{27} \zeta _3 + \frac{7}{4} \ln \left( \frac{q^2}{m_t^2}\right) \zeta _3\nonumber \\&\qquad +\, \frac{80}{9} \zeta _2 \zeta _3 + 15 \zeta _3^2 - \frac{64}{3} \zeta _5 \Bigg )\nonumber \\&\qquad +\, \epsilon ^4 \Bigg ( - \frac{30487661}{62208} + \frac{93}{8} \ln \left( \frac{q^2}{m_t^2}\right) + \frac{43217}{648} \zeta _2\nonumber \\&\qquad -\,\frac{21}{16} \ln \left( \frac{q^2}{m_t^2}\right) \zeta _2 + \frac{1991659}{51840} \zeta _2^2 \nonumber \\&\qquad -\, \frac{141}{320} \ln \left( \frac{q^2}{m_t^2}\right) \zeta _2^2 - \frac{176}{105} \zeta _2^3 + \frac{694231}{2592} \zeta _3\nonumber \\&\qquad -\,\frac{21}{8} \ln \left( \frac{q^2}{m_t^2}\right) \zeta _3 - \frac{9757}{432} \zeta _2 \zeta _3 - \frac{1681}{180} \zeta _2^2 \zeta _3 \nonumber \\&\qquad -\, 40 \zeta _3^2 + \frac{8851}{180} \zeta _5 - 2 \zeta _2 \zeta _5 - \frac{127}{8} \zeta _7 \Bigg ) \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A} n_{f}}} \Bigg \{ - \frac{8}{3 \epsilon ^3} + \frac{20}{9 \epsilon ^2} + \Bigg ( \frac{106}{27} + 2 \zeta _2 \Bigg ) \frac{1}{\epsilon } \nonumber \\&\qquad -\, \frac{1591}{81} - \frac{5}{3} \zeta _2 - \frac{74}{9} \zeta _3 + \epsilon \Bigg ( \frac{24107}{486} - \frac{23}{18} \zeta _2\nonumber \\&\qquad +\,\frac{51}{20} \zeta _2^2 + \frac{383}{27} \zeta _3 \Bigg ) + \epsilon ^2 \Bigg ( - \frac{146147}{1458} \nonumber \\&\qquad +\, \frac{799}{108} \zeta _2 - \frac{329}{72} \zeta _2^2 - \frac{1436}{81} \zeta _3 + \frac{25}{6} \zeta _2 \zeta _3 - \frac{271}{30} \zeta _5 \Bigg )\nonumber \\&\qquad +\, \epsilon ^3 \Bigg ( \frac{6333061}{34992} - \frac{11531}{648} \zeta _2 + \frac{1499}{240} \zeta _2^2\nonumber \\&\qquad +\, \frac{253}{1680} \zeta _2^3 + \frac{19415}{972} \zeta _3 - \frac{235}{36} \zeta _2 \zeta _3 - \frac{1153}{108} \zeta _3^2 + \frac{535}{36} \zeta _5 \Bigg )\nonumber \\&\qquad +\, \epsilon ^4 \Bigg ( - \frac{128493871}{419904} + \frac{133237}{3888} \zeta _2 - \frac{21533}{2592} \zeta _2^2 + \frac{649}{1440} \zeta _2^3\nonumber \\&\qquad -\, \frac{156127}{5832} \zeta _3 +\frac{215}{27} \zeta _2 \zeta _3 + \frac{517}{80} \zeta _2^2 \zeta _3 + \frac{14675}{648} \zeta _3^2 \nonumber \\&\qquad -\, \frac{2204}{135} \zeta _5 + \frac{171}{40} \zeta _2 \zeta _5 + \frac{229}{336} \zeta _7 \Bigg ) \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^2}} \Bigg \{ \frac{32}{\epsilon ^4} + \frac{44}{3 \epsilon ^3} +\Bigg ( - \frac{422}{9} - 4 \zeta _2 \Bigg ) \frac{1}{\epsilon ^2} \nonumber \\&\qquad +\Bigg ( \frac{890}{27} -\, 11 \zeta _2 + \frac{50}{3} \zeta _3 \Bigg ) \frac{1}{\epsilon } + \frac{3835}{81} + \frac{115}{6} \zeta _2 \nonumber \\&\qquad - \frac{21}{5} \zeta _2^2+\,\frac{11}{9} \zeta _3 + \epsilon \Bigg ( - \frac{213817}{972} - \frac{103}{18} \zeta _2 + \frac{77}{120} \zeta _2^2\nonumber \\&\qquad +\, \frac{1103}{54} \zeta _3 - \frac{23}{6} \zeta _2 \zeta _3 - \frac{71}{10} \zeta _5 \Bigg ) + \epsilon ^2 \Bigg ( \frac{6102745}{11664} - \frac{991}{27} \zeta _2\nonumber \\&\qquad -\, \frac{2183}{240} \zeta _2^2 + \frac{2313}{280} \zeta _2^3 - \frac{8836}{81} \zeta _3 \end{aligned}$$

$$\begin{aligned}&\qquad -\, \frac{55}{12} \zeta _2 \zeta _3 + \frac{901}{36} \zeta _3^2 + \frac{341}{60} \zeta _5 \Bigg ) + \epsilon ^3 \Bigg ( - \frac{142142401}{139968}\nonumber \\&\qquad +\, \frac{75881}{648} \zeta _2 + \frac{79819}{2160} \zeta _2^2 - \frac{2057}{480} \zeta _2^3 \nonumber \\&\qquad +\, \frac{606035}{1944} \zeta _3 - \frac{251}{72} \zeta _2 \zeta _3 - \frac{1291}{80} \zeta _2^2 \zeta _3 - \frac{5137}{216} \zeta _3^2\nonumber \\&\qquad +\,\frac{14459}{360} \zeta _5 + \frac{313}{40} \zeta _2 \zeta _5 - \frac{3169}{28} \zeta _7 \Bigg ) \nonumber \\&\qquad +\, \epsilon ^4 \Bigg ( \frac{2999987401}{1679616} - \frac{1943429}{7776} \zeta _2 - \frac{15707}{160} \zeta _2^2\nonumber \\&\qquad -\,\frac{35177}{20160} \zeta _2^3 + \frac{50419}{1600} \zeta _2^4 - \frac{16593479}{23328} \zeta _3 \nonumber \\&\qquad +\, \frac{1169}{27} \zeta _2 \zeta _3 + \frac{22781}{1440} \zeta _2^2 \zeta _3 + \frac{93731}{1296} \zeta _3^2 - \frac{1547}{144} \zeta _2 \zeta _3^2\nonumber \\ \end{aligned}$$

$$\begin{aligned}&\qquad -\, \frac{8137}{54} \zeta _5 - \frac{1001}{80} \zeta _2 \zeta _5 + \frac{845}{24} \zeta _3 \zeta _5 \nonumber \\&\qquad -\, \frac{33}{2} \zeta _{5,3} + \frac{56155}{672} \zeta _7 \Bigg ) \Bigg \},\nonumber \\&{\hat{\mathcal{F}}}^{A,(3)}_{g}= {\varvec{n_{f} C^{(2)}_{J}}} \Bigg \{ - 2+3 \epsilon \Bigg \} + {\varvec{C_{F} n_{f}^2}} \Bigg \{ \Bigg ( - \frac{640}{9}\nonumber \\&\qquad +\, 16 \ln \left( \frac{q^2}{m_t^2}\right) + \frac{64}{3} \zeta _3 \Bigg ) \frac{1}{\epsilon } + \frac{7901}{27} \nonumber \\&\qquad -\, 24 \ln \left( \frac{q^2}{m_t^2}\right) - \frac{32}{3} \zeta _2 - \frac{112}{15} \zeta _2^2 - \frac{848}{9} \zeta _3 \Bigg \}\nonumber \\&\qquad +\,{\varvec{C_{F}^2 n_{f}}} \Bigg \{ \frac{457}{6} + 104 \zeta _3 - 160 \zeta _5 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A}^2 n_{f}}} \Bigg \{ \frac{64}{3 \epsilon ^5} - \frac{32}{81 \epsilon ^4} + \Bigg ( - \frac{18752}{243} - \frac{376}{27} \zeta _2 \Bigg ) \frac{1}{\epsilon ^3}\nonumber \\&\qquad + \Bigg (\frac{36416}{243} - \frac{1700}{81} \zeta _2 + \frac{2072}{27} \zeta _3 \Bigg ) \frac{1}{\epsilon ^2} \nonumber \\&\qquad + \Bigg ( \frac{62642}{2187} + \frac{22088}{243} \zeta _2 - \frac{2453}{90} \zeta _2^2 - \frac{3988}{81} \zeta _3 \Bigg ) \frac{1}{\epsilon }\nonumber \\&\qquad -\, \frac{14655809}{13122} - \frac{60548}{729} \zeta _2 + \frac{917}{60} \zeta _2^2 \nonumber \\&\qquad -\, \frac{772}{27} \zeta _3 - \frac{439}{9} \zeta _2 \zeta _3 + \frac{3238}{45} \zeta _5 \Bigg \} + {\varvec{C_{A} n_{f}^2}} \Bigg \{ - \frac{128}{81 \epsilon ^4}\nonumber \\&\qquad +\, \frac{640}{243 \epsilon ^3} + \Bigg ( \frac{128}{27} + \frac{80}{27} \zeta _2 \Bigg ) \frac{1}{\epsilon ^2}\nonumber \\&\qquad + \Bigg ( - \frac{93088}{2187} - \frac{400}{81} \zeta _2 - \frac{1328}{81} \zeta _3 \Bigg ) \frac{1}{\epsilon } + \frac{1066349}{6561}\nonumber \\&\qquad -\, \frac{56}{27} \zeta _2 + \frac{797}{135} \zeta _2^2 + \frac{13768}{243} \zeta _3 \Bigg \}\nonumber \end{aligned}$$

$$\begin{aligned}&\qquad +\, {\varvec{C_{A} C_{F} n_{f}}} \Bigg \{ - \frac{16}{9 \epsilon ^3} + \Bigg ( \frac{5980}{27} - 48 \ln \left( \frac{q^2}{m_t^2}\right) - \frac{640}{9} \zeta _3 \Bigg )\frac{1}{\epsilon ^2}\nonumber \\&\qquad + \Bigg ( - \frac{20377}{81} - 16 \ln \left( \frac{q^2}{m_t^2}\right) + \frac{86}{3} \zeta _2 + \frac{352}{15} \zeta _2^2 + \frac{1744}{27} \zeta _3 \Bigg ) \frac{1}{\epsilon }\nonumber \\&\qquad +\, 72 \ln \left( \frac{q^2}{m_t^2}\right) - \frac{587705}{972} - \frac{551}{6} \zeta _2 \nonumber \\&\qquad +\, 12 \ln \left( \frac{q^2}{m_t^2}\right) \zeta _2 - \frac{96}{5} \zeta _2^2 + \frac{12386}{81} \zeta _3 + 48 \zeta _2 \zeta _3 + \frac{32}{9} \zeta _5 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^3}} \Bigg \{ - \frac{256}{3 \epsilon ^6} - \frac{352}{3 \epsilon ^5} \nonumber \\&\qquad +\, \frac{16144}{81 \epsilon ^4} + \Bigg ( \frac{22864}{243} + \frac{2068}{27} \zeta _2 - \frac{176}{3} \zeta _3 \Bigg ) \frac{1}{\epsilon ^3}\nonumber \\&\qquad + \Bigg ( - \frac{172844}{243} - \frac{1630}{81} \zeta _2 + \frac{494}{45} \zeta _2^2 \nonumber \\&\qquad -\, \frac{836}{27} \zeta _3 \Bigg ) \frac{1}{\epsilon ^2} + \Bigg ( \frac{2327399}{2187} - \frac{71438}{243} \zeta _2 + \frac{3751}{180} \zeta _2^2\nonumber \\&\qquad -\, \frac{842}{9} \zeta _3 + \frac{170}{9} \zeta _2 \zeta _3 + \frac{1756}{15} \zeta _5 \Bigg ) \frac{1}{\epsilon } \nonumber \\&\qquad +\, \frac{16531853}{26244} + \frac{918931}{1458} \zeta _2 + \frac{27251}{1080} \zeta _2^2 - \frac{22523}{270} \zeta _2^3\nonumber \\&\qquad -\, \frac{51580}{243} \zeta _3 + \frac{77}{18} \zeta _2 \zeta _3 - \frac{1766}{9} \zeta _3^2 + \frac{20911}{45} \zeta _5 \Bigg \}. \end{aligned}$$

(3.14)

The results up to two-loop level is consistent with the existing ones [65] and the three-loop result is the new one.

3.2 Operator renormalization constant

The strong coupling constant renormalization through $Z_{a_{s}}$ is not sufficient to make the form factor $\mathcal{F}^{A}_{g}$ completely UV finite; one needs to perform additional renormalization to remove the residual UV divergences. This additional renormalization is called the overall operator renormalization; it is performed through the constant $Z^{A}_{g}$. This is determined by solving the underlying RG equation:

$$\begin{aligned} \mu _{R}^{2} \frac{\mathrm{d}}{\mathrm{d}\mu _{R}^{2}} \ln Z^{A}_{g} ({\hat{a}}_{s}, \mu _{R}^{2}, \mu ^{2}, \epsilon )=\sum _{i=1}^{\infty } a_{s}^{i} \gamma ^{A}_{g,i}. \end{aligned}$$

(3.15)

In the above expression, the $\gamma ^{A}_{g,i}$ are the UV anomalous dimensions where the components are defined through the expansion in powers of $a_{s}$:

$$\begin{aligned} \gamma ^{A}_{g} \equiv \sum \limits _{i=1}^{\infty } a_{s}^{i} \gamma ^{A}_{g,i}. \end{aligned}$$

(3.16)

The $\gamma ^{A}_{g,i}$ are determined by explicitly comparing the results of the form factors, Eq. (3.14), against the universal decomposition [65] of the form factors in terms of soft, cusp, collinear and UV anomalous dimensions. The universal decomposition follows from the property of the form factor that it satisfies the KG-differential equation [76–80]. This is a direct consequence of the facts that QCD amplitudes exhibit the factorization property, and the gauge and renormalization group (RG) invariances. The $\gamma ^{A}_{g,i}$ up to three loops ($i=3$) are obtained:

$$\begin{aligned} \gamma ^{A}_{g,1}= & {} \frac{11}{3} C_{A} - \frac{2}{3} n_{f}, \nonumber \\ \gamma ^{A}_{g,2}= & {} \frac{34}{3} C_{A}^{2} - \frac{10}{3} C_{A} n_{f} - 2 C_{F} n_{f}, \nonumber \\ \gamma ^{A}_{g,3}= & {} \frac{2857}{54} C_{A}^3 - \frac{1415}{54} C_{A}^2 n_{f} - \frac{205}{18} C_{A} C_{F} n_{f}\nonumber \\&+\, C_{F}^2 n_{f} + \frac{79}{54} C_{A} n_{f}^2 + \frac{11}{9} C_{F} n_{f}^2. \end{aligned}$$

(3.17)

Let us emphasize and note that the $\gamma ^{A}_{g,i}$’s are found to satisfy

$$\begin{aligned} \gamma ^{A}_{g} = -\frac{\beta }{a_{s}}\quad \text {up to three loops}, \end{aligned}$$

(3.18)

where $\beta = - \sum _{i=0}^{\infty } \beta _{i} a_{s}^{i+2}$ is the usual QCD $\beta$-function. For a more elaborate discussion, see the recent article [66] (also see [67, 68]). Using the results of $\gamma ^{A}_{g,i}$ from Eq. (3.17) and solving the above RG equation, we obtain the overall renormalization constant up to three-loop level:

$$\begin{aligned} Z^{A}_{g}= & {} 1 + a_s \Bigg [ \frac{22}{3\epsilon } C_{A} - \frac{4}{3\epsilon } n_{f} \Bigg ] +a_s^2 \Bigg [ \frac{1}{\epsilon ^2} \Bigg \{ \frac{484}{9} C_{A}^2\nonumber \\&-\,\frac{176}{9} C_{A} n_{f} + \frac{16}{9} n_{f}^2 \Bigg \} + \frac{1}{\epsilon } \Bigg \{ \frac{34}{3} C_{A}^2 \nonumber \\&-\, \frac{10}{3} C_{A} n_{f} - 2 C_{F} n_{f} \Bigg \} \Bigg ] + a_s^3 \Bigg [ \frac{1}{\epsilon ^3} \Bigg \{ \frac{10648}{27} C_{A}^3\nonumber \\&\,-\frac{1936}{9} C_{A}^2 n_{f}+\frac{352}{9} C_{A} n_{f}^2 - \frac{64}{27} n_{f}^3 \Bigg \} \nonumber \\&+\, \frac{1}{\epsilon ^2} \Bigg \{ \frac{5236}{27} C_{A}^3 - \frac{2492}{27} C_{A}^2 n_{f} - \frac{308}{9} C_{A} C_{F} n_{f}\nonumber \\&+\,\frac{280}{27} C_{A} n_{f}^2 + \frac{56}{9} C_{F} n_{f}^2 \Bigg \}+\frac{1}{\epsilon } \Bigg \{ \frac{2857}{81} C_{A}^3\nonumber \\&-\,\frac{1415}{81} C_{A}^2 n_{f} - \frac{205}{27} C_{A} C_{F} n_{f} + \frac{2}{3} C_{F}^2 n_{f}\nonumber \\&+\, \frac{79}{81} C_{A} n_{f}^2 + \frac{22}{27} C_{F} n_{f}^2 \Bigg \} \Bigg ]. \end{aligned}$$

(3.19)

We emphasize that $Z_{g}^{A}=Z_{GG}$, which is introduced in Eq. (3.12), has been discussed in great detail in [66]. The complete UV finite form factor $[\mathcal{F}^{A}_{g}]_{R}$ in terms of this $Z_{g}^{A}$ is

$$\begin{aligned}{}[\mathcal{F}^{A}_{g}]_{R} = Z^{A}_{g} \mathcal{F}^{A}_{g}. \end{aligned}$$

(3.20)

This is presented in our recent article [66] up to three loops in the form of hard matching coefficients of soft-collinear effective theory.

3.3 Mass factorization kernel

The UV finite form factor contains additional divergences arising from the soft and collinear regions of the loop momenta. In this section, we address the issue of collinear divergences and describe a prescription to remove them. The collinear singularities that arise in the massless limit of partons are removed in the ${\overline{MS}}$ scheme using mass factorization kernel. The kernel contains only the poles in $\epsilon$ and Altarelli–Parisi splitting functions. For the SV cross section only the diagonal parts of the splitting functions and kernels contribute.

3.4 Soft-collinear distribution

The resulting expression from form factor along with operator renormalization constant and mass factorization kernel is not completely finite, it contains some residual divergences which get canceled against the contribution arising from soft-gluon emissions. Hence, the finiteness of $\varDelta _{g}^{A, \text {SV}}$ in the limit $\epsilon \rightarrow 0$ requires that the soft-collinear distribution, $\varPhi ^A_{g} (\hat{a}_s, q^2, \mu ^2, z, \epsilon )$, has a pole structure in $\epsilon$ similar to that of residual divergences. In the articles [45, 46] it was shown that $\varPhi ^{A}_{g}$ must obey a KG type integro-differential equation, which we call the ${\overline{KG}}$ equation [45, 46], to remove the residual divergences. However, due to the universality of the soft-gluon contribution, $\varPhi ^{A}_{g}$ must be the same as that of the Higgs boson production in gluon fusion:

$$\begin{aligned} \varPhi ^{A}_{g} = \varPhi ^{H}_{g} = \varPhi _{g}. \end{aligned}$$

(3.21)

In the above expression, $\varPhi _{g}$ is written in order to emphasize the universality of these quantities i.e. $\varPhi ^{H}_{g}$ can be used for any gluon fusion process, these are independent of the operator insertion. The result up to three-loop level was presented in the article [32, 55]. The three-loop one was obtained by using the results of the Higgs boson production cross section at threshold at N$^{3}$LO QCD [51]. This completes all the ingredients required to compute the SV cross section up to N$^{3}$LO that are presented in the next section.

4 SV cross sections

In this section, we present our findings of the SV cross section at N$^{3}$LO along with the results of previous orders. Expanding the SV cross section ${\varDelta }^{A, \mathrm{SV}}_{g}$, Eq. (3.7), in powers of $a_{s}$, we obtain

$$\begin{aligned} \varDelta _{g}^{A, \mathrm{SV}}(z, q^{2}, \mu _{R}^{2}, \mu _{F}^{2}) = \sum _{i=0}^\infty a_s^i \varDelta _{g,i}^{A, \mathrm{SV}} (z, q^{2}, \mu _R^2, \mu _{F}^{2})\nonumber \\ \end{aligned}$$

(4.1)

where

$$\begin{aligned} \nonumber \varDelta _{g,i}^{A, \mathrm{SV}} = \varDelta _{g,i}^{A, \mathrm{SV}}\left| _\delta \delta (1-z) + \sum _{j=0}^{2i-1} \varDelta _{g,i}^{A, \mathrm{SV}}\right| _{\mathcal{D}_j} \mathcal{D}_j. \end{aligned}$$

Here, we present the results of the pseudo-scalar Higgs boson production cross section up to N$^{3}$LO for the choices of the scale $\mu _{R}^{2}=\mu _{F}^{2}=q^{2}$ for which the Eq. (4.1) reads

$$\begin{aligned} \varDelta _{g}^{A, \mathrm{SV}}(z, q^{2}) = \sum _{i=0}^\infty a_s^i(q^{2}) \varDelta _{g,i}^{A, \mathrm{SV}} (z, q^{2}), \end{aligned}$$

(4.2)

with the following $\varDelta _{g,i}^{A, \mathrm{SV}} (z, q^{2})$:

$$\begin{aligned}&{\varDelta }^{A, \mathrm{SV}}_{g,0} = {\varvec{\delta (1-z)}},\nonumber \\&{\varDelta }^{A, \mathrm{SV}}_{g,1} = {\varvec{\delta (1-z)}} \Bigg [ {\varvec{C_{A}}} \Bigg \{ 8 + 8 \zeta _2 \Bigg \} \Bigg ] + {\varvec{\mathcal{D}_{1}}} \Bigg [ {\varvec{C_{A}}} \Bigg \{ 16\Bigg \} \Bigg ],\nonumber \\&{\varDelta }^{A, \mathrm{SV}}_{g,2} = {\varvec{\delta (1-z)}} \Bigg [{\varvec{C_{A}^2}} \Bigg \{ \frac{494}{3} + \frac{1112}{9} \zeta _2 - \frac{4}{5} \zeta _2^2 - \frac{220}{3} \zeta _3 \Bigg \}\nonumber \\&\qquad +\,{\varvec{C_{A} n_{f}}} \Bigg \{ - \frac{82}{3} - \frac{80}{9} \zeta _2 - \frac{8}{3} \zeta _3 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{F} n_{f}}} \Bigg \{ - \frac{160}{3} + 12 \ln \left( \frac{q^2}{m_t^2}\right) + 16 \zeta _3 \Bigg \}\Bigg ]\nonumber \\&\qquad +\,{\varvec{\mathcal{D}_{0}}} \Bigg [ {\varvec{C_{A} n_{f}}} \Bigg \{ \frac{224}{27} - \frac{32}{3} \zeta _2 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^2}} \Bigg \{ - \frac{1616}{27} + \frac{176}{3} \zeta _2 + 312 \zeta _3 \Bigg \} \Bigg ]\nonumber \\&\qquad +\, {\varvec{\mathcal{D}_{1}}} \Bigg [ {\varvec{C_{A} n_{f}}} \Bigg \{ - \frac{160}{9} \Bigg \} + {\varvec{C_{A}^2}} \Bigg \{ \frac{2224}{9} - 160 \zeta _2 \Bigg \} \Bigg ]\nonumber \\&\qquad +\, {\varvec{\mathcal{D}_{2}}} \Bigg [ {\varvec{C_{A}^2}} \Bigg \{ - \frac{176}{3} \Bigg \} + {\varvec{C_{A} n_{f}}} \Bigg \{ \frac{32}{3} \Bigg \} \Bigg ] + {\varvec{\mathcal{D}_{3}}} \Bigg [ C_{A}^2 \Bigg \{ 128 \Bigg \} \Bigg ],\nonumber \\&{\varDelta }^{A, \mathrm{SV}}_{g,3} = {\varvec{\delta (1-z)}} \Bigg [ {\varvec{n_{f} C_{J}^{(2)}}} \Bigg \{ -4 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{F} n_{f}^2}} \Bigg \{ \frac{1498}{9} - \frac{40}{9} \zeta _2 - \frac{32}{45} \zeta _2^2 - \frac{224}{3} \zeta _3 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^3}} \Bigg \{ \frac{114568}{27} + \frac{137756}{81} \zeta _2 - \frac{61892}{135} \zeta _2^2\nonumber \\&\qquad -\, \frac{64096}{105} \zeta _2^3 - 3932 \zeta _3 + \frac{7832}{3} \zeta _2 \zeta _3 \nonumber \\&\qquad +\, \frac{13216}{3} \zeta _3^2 - \frac{30316}{9} \zeta _5 \Bigg \} + {\varvec{C_{F}^2 n_{f}}} \Bigg \{ \frac{457}{3} + 208 \zeta _3\nonumber \\&\qquad -\, 320 \zeta _5 \Bigg \} + {\varvec{C_{A}^2 n_{f}}} \Bigg \{ - \frac{113366}{81}\nonumber \\&\qquad -\, \frac{10888}{81} \zeta _2 + \frac{21032}{135} \zeta _2^2 + \frac{8840}{27} \zeta _3 - \frac{2000}{3} \zeta _2 \zeta _3\nonumber \\&\qquad +\,\frac{6952}{9} \zeta _5 \Bigg \} + {\varvec{C_{A} n_{f}^2}} \Bigg \{ \frac{6914}{81} - \frac{1696}{81} \zeta _2\nonumber \\&\qquad -\, \frac{608}{45} \zeta _2^2 + \frac{688}{27} \zeta _3 \Bigg \} + {\varvec{C_{A} C_{F} n_{f}}} \Bigg \{ - 1797 - \frac{4160}{9} \zeta _2\nonumber \\&\qquad +\,\frac{176}{45} \zeta _2^2 + \frac{1856}{3} \zeta _3 + 192 \zeta _2 \zeta _3\nonumber \\&\qquad +\, 160 \zeta _5 + 96 \ln \left( \frac{q^2}{m_t^2}\right) + 96 \ln \left( \frac{q^2}{m_t^2}\right) \zeta _2 \Bigg \} \Bigg ]\nonumber \\&\qquad +\, {\varvec{\mathcal{D}_{0}}} \Bigg [ {\varvec{C_{A}^2 n_{f}}} \Bigg \{ \frac{173636}{729} - \frac{41680}{81} \zeta _2 \end{aligned}$$

$$\begin{aligned}&\qquad -\, \frac{544}{15} \zeta _2^2 - \frac{7600}{9} \zeta _3 \Bigg \} + {\varvec{C_{A} C_{F} n_{f}}} \Bigg \{ \frac{3422}{27} - 32 \zeta _2\nonumber \\&\qquad -\,\frac{64}{5} \zeta _2^2 - \frac{608}{9} \zeta _3 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A} n_{f}^2}} \Bigg \{ - \frac{3712}{729} + \frac{640}{27} \zeta _2 + \frac{320}{27} \zeta _3 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^3}} \Bigg \{ - \frac{943114}{729} + \frac{175024}{81} \zeta _2 + \frac{4048}{15} \zeta _2^2 \nonumber \\&\qquad +\, \frac{210448}{27} \zeta _3 - \frac{23200}{3} \zeta _2 \zeta _3 + 11904 \zeta _5 \Bigg \} \Bigg ]\nonumber \\&\qquad +\, {\varvec{\mathcal{D}_{1}}} \Bigg [ {\varvec{C_{A}^3}} \Bigg \{ \frac{414616}{81} - \frac{13568}{3} \zeta _2 - \frac{9856}{5} \zeta _2^2 \nonumber \\&\qquad -\, \frac{22528}{3} \zeta _3 \Bigg \} + {\varvec{C_{A}^2 n_{f}}} \Bigg \{ - \frac{79760}{81} + \frac{6016}{9} \zeta _2 + \frac{2944}{3} \zeta _3 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A} n_{f}^2}} \Bigg \{ \frac{1600}{81} - \frac{256}{9} \zeta _2 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A} C_{F} n_{f}}} \Bigg \{ - 1000 + 384 \zeta _3 + 192 \ln \left( \frac{q^2}{m_t^2}\right) \Bigg \} \Bigg ] \nonumber \\&\qquad +\, {\varvec{\mathcal{D}_{2}}} \Bigg [ {\varvec{C_{A} C_{F} n_{f}}} \Bigg \{ 32 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A} n_{f}^{2}}} \Bigg \{ - \frac{640}{27} \Bigg \} + {\varvec{C_{A}^2 n_{f}}} \Bigg \{ \frac{16928}{27} - \frac{2176}{3} \zeta _2 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A}^3}} \Bigg \{ - \frac{79936}{27} + \frac{11968}{3} \zeta _2 \nonumber \\&\qquad +\, 11584 \zeta _3 \Bigg \} \Bigg ] + {\varvec{\mathcal{D}_{3}}} \Bigg [ {\varvec{C_{A}^2 n_{f}}} \Bigg \{ - \frac{10496}{27} \Bigg \} + {\varvec{C_{A} n_{f}^2}} \Bigg \{ \frac{256}{27} \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A}^3}} \Bigg \{ \frac{86848}{27} - 3584 \zeta _2 \Bigg \} \Bigg ] + {\varvec{\mathcal{D}_{4}}} \Bigg [ {\varvec{C_{A}^3}} \Bigg \{ - \frac{7040}{9} \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^2 n_{f}}} \Bigg \{ \frac{1280}{9}\Bigg \} \Bigg ] + {\varvec{\mathcal{D}_{5}}} \Bigg [ {\varvec{C_{A}^3}} \Bigg \{ 512 \Bigg \} \Bigg ]. \end{aligned}$$

(4.3)

The SV cross section up to NNLO are in agreement with the existing ones, computed in the article [32, 38, 39]. The result at N$^{3}$LO i.e. ${\varDelta }^{A, \mathrm{SV}}_{g,3}$ is the new one computed in this article for the first time.

5 Threshold resummation

Despite the spectacular accuracy of the fixed order results which are defined in power series expansions of the strong coupling constant $a_{s}$, it is necessary, in certain cases, to resum the dominant contributions to all orders in $a_{s}$ to get more reliable predictions and to reduce the scale uncertainties significantly. In case of threshold corrections, due to soft-gluon emission the fixed order pQCD calculation may yield large threshold logarithms of the kind $\mathcal{D}_{i}$, defined in Eq. (3.6), hence we must resum these contributions to all orders in $a_{s}$. The resummation of these so-called Sudakov logarithms is usually pursued in Mellin space using the formalism developed in [71, 72, 81, 82]. Alternatively, it is performed in the framework of SCET [83–89]. Here, we will discuss this in the context of Mellin space formalism.

5.1 Mellin space prescription

Under this prescription, the threshold resummation is performed in Mellin-N space where the Nth order Mellin moment is defined with respect to the partonic scaling variable z. In Mellin space, the threshold limit $z\rightarrow 1$ corresponds to $N\rightarrow \infty$ and the plus distributions $\mathcal{D}_{i}$, Eq. (3.6), take the form $\ln ^{i-1} N$. These logarithmic contributions are evaluated to all orders in perturbation theory by performing the threshold resummation through [71, 72, 81, 82]

$$\begin{aligned} {\varDelta }^{A,\mathrm{res}}_{g,N}(q^{2}, \mu _{R}^{2}, \mu _{F}^{2})&= C^{A, \mathrm{th}}_{g}(q^{2}, \mu _{R}^{2}, \mu _{F}^{2}) \varDelta _{g,N}(q^{2})\,. \end{aligned}$$

(5.1)

The component $C^{A, \mathrm{th}}_{g}$ depends on both the initial and the final state particles, though it is independent of the variable N. On the other hand, the remaining part $\varDelta _{g,N}$ does not care about the details of the final state particle, it only depends on the initial state partons and the variable N. Being independent of the nature of the final state, $\varDelta _{g,N}$ can be considered as a universal quantity which is the same for any operator. In addition, it is investigated in the articles [71, 72] that it arises solely from the soft-parton radiation and it resums all the perturbative contributions $a_{s}^{n} \ln ^{m}N$ ($m \ge 0$) to all orders. Our goal is to calculate the threshold resummation factor $C^{A,\mathrm{th}}_{g}$, which encapsulates all the remaining N-independent contributions to the resummed partonic cross section (5.1). Below, we demonstrate the prescription based on our formalism to calculate this quantity $C^{A,\mathrm{th}}_{g}$ order by order in perturbation theory.

In the article [46], it was shown how the soft-collinear distribution $\varPhi ^{A}_{g}(=\varPhi _{g})$ captures all the features of the N-space resummation. In this section, we discuss that prescription briefly in the present context. Using the well-known identity

$$\begin{aligned}&\frac{1}{1-z} [(1-z)^{2}]^{j \frac{\epsilon }{2}}\nonumber \\&\quad = \frac{1}{j\epsilon } \delta (1-z) + \left( \frac{1}{1-z} [ (1-z)^{2}]^{j \frac{\epsilon }{2}} \right) _{+}, \end{aligned}$$

(5.2)

we can express the soft-collinear distribution as

(5.3)

where $A^{A}_{g}$ is the cusp anomalous dimension corresponding to the gluonic operator. All the poles in $\epsilon$ are contained within ${\overline{K}}^{A}_{g}$ and the finite terms are dumped into ${\overline{G}}^{A}_{g}$. The components ${\overline{K}}^{A}_{g,j}(\epsilon )$ are defined through the expansion of ${\overline{K}}^{A}_{g}$ in powers of ${\hat{a}}_{s}$ in the following way:

$$\begin{aligned}&{\overline{K}}^{A}_{g}\left( {\hat{a}}_{s}, \frac{\mu _{R}^{2}}{\mu ^{2}}, z, \epsilon \right) \nonumber \\&\quad = \delta (1-z) \sum _{j=1}^{\infty } {\hat{a}}_{s}^{j} \left( \frac{\mu _{R}^{2}}{\mu ^{2}} \right) ^{j \frac{\epsilon }{2}} S^{j}_{\epsilon } {\overline{K}}^{A}_{g,j}(\epsilon ). \end{aligned}$$

(5.4)

The identification of the first plus distribution part of $\varPhi ^{A}_{g}$, Eq. (5.3), with the factor contributing to the process independent $\varDelta _{g,N}(q^{2})$ has been discussed in the same article [46] which reads

(5.5)

with

$$\begin{aligned} D_{g}( a_{s}(q^{2}(1-z)^{2}))&= 2 {\overline{G}}_{g}\left( a_{s}(q^{2}(1-z)^{2}),\epsilon \right) |_{\epsilon =0}. \end{aligned}$$

(5.6)

Fig. 1

Pseudo-scalar Higgs boson production cross section (left panel) for LHC13 and the corresponding K-factors (right panel). The observed spike at 345 GeV indicates the top quark pair threshold region

In the above expression, the superscript A has been omitted to emphasize the universal nature of these quantities. The remaining part of the Eq. (5.3) along with the other parts, namely, form factor, operator renormalization constant and mass factorization kernel in Eq. (3.9) contribute to $C^{A,\mathrm{th}}_{g}$. Expanding this in powers of $a_{s}$ as

$$\begin{aligned} C^{A,\mathrm{th}}_{g}= 1+\sum _{j=1}^{\infty } a_{s}^{j}\, C^{A,\mathrm{th}}_{g,j}, \end{aligned}$$

(5.7)

we determine $C^{A,\mathrm{th}}_{g,j}$ up to three-loop ($j=3$) order which are provided below (with the choice $\mu _{R}^{2}=\mu _{F}^{2}=q^{2}$):

$$\begin{aligned}&C^{A,\mathrm{th}}_{g,1} = {\varvec{C_{A}}} \{ 8 + 8 \zeta _2\}, \nonumber \\&C^{A,\mathrm{th}}_{g,2} = {\varvec{C_{A}^2}} \Bigg \{ \frac{494}{3} + \frac{1112}{9} \zeta _2 + 12 \zeta _2^2 - \frac{220}{3} \zeta _3 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A} n_{f}}} \Bigg \{ - \frac{82}{3} - \frac{80}{9} \zeta _2 - \frac{8}{3} \zeta _3 \Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{F} n_{f}}} \Bigg \{ - \frac{160}{3} + 12 \ln \left( \frac{q^2}{m_t^2}\right) + 16 \zeta _3 \Bigg \}, \nonumber \\&C^{A,\mathrm{th}}_{g,3} = {\varvec{n_{f} C^{(2)}_{J}}} \Bigg \{ -4 \Bigg \} + {\varvec{C_{F} n_{f}^2}} \Bigg \{ \frac{1498}{9} - \frac{40}{9} \zeta _2\nonumber \\&\qquad -\, \frac{32}{45} \zeta _2^2 - \frac{224}{3} \zeta _3 \Bigg \}+{\varvec{C_{F}^2 n_{f}}} \Bigg \{ \frac{457}{3} + 208 \zeta _3 - 320 \zeta _5 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A}^2 n_{f}}} \Bigg \{ - \frac{113366}{81} - \frac{10888}{81} \zeta _2 + \frac{17192}{135} \zeta _2^2\nonumber \\&\qquad +\,\frac{584}{3} \zeta _3 - \frac{464}{3} \zeta _2 \zeta _3 + \frac{808}{9} \zeta _5\Bigg \} \nonumber \\&\qquad +\, {\varvec{C_{A}^3}} \Bigg \{ \frac{114568}{27} + \frac{137756}{81} \zeta _2 - \frac{4468}{27} \zeta _2^2 - \frac{32}{5} \zeta _2^3\nonumber \\&\qquad -\, \frac{80308}{27} \zeta _3 -\frac{616}{3} \zeta _2 \zeta _3 + 96 \zeta _3^2 + \frac{3476}{9} \zeta _5 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A} n_{f}^2}} \Bigg \{ \frac{6914}{81} - \frac{1696}{81} \zeta _2 -\frac{608}{45} \zeta _2^2 + \frac{688}{27} \zeta _3 \Bigg \}\nonumber \\&\qquad +\, {\varvec{C_{A} C_{F} n_{f}}} \Bigg \{ - 1797 + 96 \ln \left( \frac{q^2}{m_t^2}\right) - \frac{4160}{9} \zeta _2 \nonumber \\&\qquad +\, 96 \ln \left( \frac{q^2}{m_t^2}\right) \zeta _2 + \frac{176}{45} \zeta _2^2 + \frac{1856}{3} \zeta _3 \nonumber \\&\qquad + 192 \zeta _2 \zeta _3 + 160 \zeta _5 \Bigg \}. \end{aligned}$$

(5.8)

The above new result of $C^{A,\mathrm{th}}_{g,3}$ along with the universal factor $\varDelta _{g,N}$ provide the threshold resummed cross section of the pseudo-scalar Higgs boson production at N$^{3}$LL accuracy. A more elaborate discussion of this prescription to perform threshold resummation will be presented elsewhere.

6 Numerical impact of SV cross section

In this section, we present our findings on the numerical impact of threshold N$^3$LO predictions in QCD for the production of a pseudo-scalar Higgs boson at the LHC and also make comparison with the corresponding results for the SM Higgs boson. While we have all the ingredients up to three-loop level, the one of the Wilson coefficients, namely, $C^{(2)}_J$ is known only to two-loop level. Note that $C_{G}$ is exact due to Adler–Bardeen theorem [74]. Due to the unavailability of $C^{(2)}_{J}$ in the literature, we discuss the impact of missing three-loop contribution later on in this section by varying this quantity. As we are interested in quantifying the QCD effects, we assume that pseudo-scalar Higgs boson couples only to top quarks. Hence, the dominant contribution resulting from bottom quark initiated processes can be included in a systematic way in our numerical study but we do not perform it here. Moreover, our predictions are based on the effective theory approach where the top quarks are integrated out and we have only light quarks. Like in the case of predictions for the scalar Higgs boson production in the effective theory, for the pseudo-scalar Higgs boson production we multiply the Born cross section computed using the finite top mass ($m_t=172.5$ GeV) with higher orders which are obtained in the effective theory. Without loss of generality, we normalize the cross section by $\hbox {cot}^2\beta$. The mass of the pseudo-scalar Higgs boson is taken to be $m_A = 200$ GeV. We use MSTW2008 [90] parton distribution functions (PDFs) throughout where the LO, NLO, and NNLO parton level cross sections are convoluted with the corresponding MSTW2208lo, MSTW2008nlo, and MSTW2008nnlo PDFs, while for the N$^3$LO$_\mathrm{SV}$ cross sections we use the MSTW2008nnlo PDFs. The strong coupling constant is provided by the respective PDFs from LHAPDF with $\alpha _s(m_Z)$ = 0.1394(LO), 0.12018(NLO), and 0.11707(NNLO).

To estimate the impact of QCD corrections, we define the K-factors as

$$\begin{aligned} \hbox {K}^{(1)} = \frac{ \sigma ^\mathrm{NLO} }{\sigma ^\mathrm{LO}},\quad \hbox {K}^{(2)} = \frac{ \sigma ^\mathrm{NNLO} }{\sigma ^\mathrm{LO}},\quad \hbox {K}^{(3)} = \frac{ \sigma ^\mathrm{N^3LO_\mathrm{SV}} }{\sigma ^\mathrm{LO}}. \end{aligned}$$

(6.1)

Fig. 2

Same as Fig. 1 but for smaller values of $m_A$

Fig. 3

Pseudo-scalar Higgs boson production cross sections as a function of $\sqrt{S}$ (left panel) and the corresponding K-factors (right panel)

In Fig. 1, for LHC13, we plot the pseudo-scalar Higgs boson production cross section as a function of its mass $m_A$. Since we retain the dependence on the $m_t$ at the Born level, beyond the top pair threshold ($\tau _A > 1$), due to change in the functional dependence of $\tau _A$ one finds a spike at $2m_t$ (left panel). We note here that the effective theory (EFT) formalism formally holds only for the pseudo-scalar masses up to top pair threshold. However, from the knowledge of the QCD corrections to the Higgs boson production up to NNLO, we notice that below the top pair threshold, the difference between the results of EFT and the finite top contributions is about 5 % and is even smaller at NNLO, about 1 %. We assumed the same to hold in the QCD corrections for pseudo-scalar production for scalar masses above the top pair threshold. The corresponding K-factors are given in the right panel and are in general found to increase with $m_A$. The NLO correction enhances the LO predictions by as much as 100 % for $m_A=1$ TeV, whereas the NNLO correction adds about an additional 45 %. On the other hand the $\mathrm{N^3LO}_\mathrm{SV}$ correction is found to be about 1.5 % of LO for small mass region $m_A < 300$ GeV and for higher $m_A$ values the correction at the $\mathrm{N^3LO}_\mathrm{SV}$ level becomes even smaller, about 0.3 % for $m_A=1$ TeV. In either case, these N$^3$LO$_\mathrm{SV}$ effects show a convergence of the perturbation series. In Fig. 2, we present similar results but only for pseudo-scalar masses below the top pair threshold, where the effective theory approximation works very well.

Table 1 K-factors for the Higgs and pseudo-scalar Higgs boson production cross sections up to $\mathrm{N^3LO_\mathrm{SV}}$ for different energies at LHC. Here, $m_H=m_A=125$ GeV

Table 2 Higgs and pseudo-scalar Higgs boson cross sections up to $\mathrm{N^3LO_\mathrm{SV}}$ for LHC13

In Fig. 3, we present the cross sections as a function of the center of mass energy $\sqrt{S}$ of the incoming protons at the LHC. The increase in the cross sections (left panel) with $\sqrt{S}$ is simply because of the increase in the corresponding parton fluxes for any given $m_A$. On the contrary, the corresponding K-factors (right panel) increase with decreasing $\sqrt{S}$ for fixed $m_A$. A similar pattern is shown both in Figs. 1 and 2 where the K-factors increase with $m_A$ for a given $\sqrt{S}$. The guiding principles for the behavior of the K-factors in these two cases are the same, namely, as $m_A$ approaches $\sqrt{S}$, the cross sections are dominated by large soft-gluon effects.

The QCD corrections to pseudo-scalar Higgs boson production are found to be similar to those of the SM Higgs production due to universal infrared structure of the gluon initiated processes. We give a numerical comparison between their K-factors at various orders. We take $m_H=m_A=125$ GeV and ignore bottom as well as other light quarks and electro weak effects for both cases. Although the full N$^3$LO QCD corrections are already available for the SM Higgs boson, for comparison we take into account only the N$^3$LO$_\mathrm{SV}$. Table 1 contains the K-factors, defined in Eq. (6.1) up to N$^3$LO$_\mathrm{SV}$ in QCD for both the Higgs and the pseudo-scalar Higgs boson as a function of $\sqrt{S}$. For this mass region, the QCD corrections are positive and hence the K-factors increase with the order in the perturbation theory. Moreover, these K-factors, following the line of argument given before, are found to decrease with $\sqrt{S}$ but they are identical in both cases. The difference between the Higgs and the pseudo-scalar Higgs boson cross sections in their respective K-factors is noticed at the second decimal place only. At three-loop level, $\mathrm{K^{(3)}}$ is found to be around 2.4 (2.2) for the 7(14) TeV case.

The tiny difference between them can be attributed to the presence of an additional operator present in the effective interaction, namely ${O}_J$, which along with the matching coefficient formally enters from NNLO onwards for the gluon initiated processes. For quark–antiquark initiated processes, this contribution vanishes as the quark flavors are massless. The gluon initiated processes involving only ${O}_J$ can contribute at N$^4$LO and beyond. However, the interference effects of ${O}_G$ and ${O}_J$ will show up in the gluon initiated processes at NNLO. Thus, the operator ${O}_J$ has non-zero contributions at the lowest order namely at two-loop level. However, the presence of such an interference contribution is found to be very small and is the main difference between the SM Higgs and the pseudo-scalar Higgs boson contribution. The QCD corrections through soft- and collinear-gluon emissions for this interference contribution will be of even higher order and hence will contribute at the three-loop level and beyond. In Table 2, we present the Higgs and pseudo-scalar Higgs boson production cross sections up to N$^3$LO$_\mathrm{SV}$ as a function of the scalar mass around 125 GeV. The pseudo-scalar Higgs boson cross section is about twice as big as that of the Higgs boson and the convergence of perturbation series is good and the K-factors are roughly the same for both cases.

We have also studied the impact of missing three-loop contribution to $C_{J}$ i.e. $C^{(2)}_{J}$. At higher orders starting from N$^3$LO$_\mathrm{SV}$ onwards, the second term, $C_J^{(2)}$, in the Wilson coefficient $C_{J}$ can give a non-zero contribution. To estimate the numerical impact of this term, we assume the following form of $C_J^{(2)}$:

$$\begin{aligned} C_J^{(2)} = \left[ a \ln ^2 \frac{\mu _{R}^{2}}{m_{t}^{2}} + b \ln \frac{\mu _{R}^{2}}{m_{t}^{2}} + c \right] , \end{aligned}$$

(6.2)

and we vary the parameters a, b, and c in the range $[-10, 10]$. We found that the contribution of such a $C_J^{(2)}$ term changes the cross sections only at the third decimal place and hence we ignore its contribution in the rest of our phenomenological study.

Table 3 PDF uncertainties in the Higgs and pseudo-scalar Higgs boson production cross sections up to N$^3$LO$_\mathrm{SV}$ for LHC13 and for $m_H=m_A=125$ GeV

Fig. 4

Modified soft-plus-virtual vs. fixed order results for Higgs and pseudo-scalar Higgs boson production cross sections for different energies at LHC

Since the predictions are sensitive to the choice of parton density functions, we have estimated the uncertainty resulting from them by choosing the central fit for various well known PDF sets such ABM11 [91], CT10 [92], MSTW2008 [90] and NNPDF23 [93]. For N$^3$LO$_\mathrm{SV}$ cross sections, however, we use NNLO PDF sets. The corresponding strong coupling constant is directly taken from the LHAPDF [94]. In Table 3, we present the SM Higgs boson and pseudo-scalar Higgs boson production cross sections at NLO, NNLO, and N$^3$LO$_\mathrm{SV}$ for LHC13. We find that for NLO, CT10 gives the lowest cross section, while MSTW2008 gives the highest, whereas for NNLO and N$^3$LO$_\mathrm{SV}$, ABM11 gives the lowest and NNPDF23 gives the highest. The percentage uncertainty arising from PDF sets at any order is defined as $(\sigma ^A_\mathrm{max} - \sigma ^A_\mathrm{min})/\sigma ^A_\mathrm{min} \times 100$ where $\sigma ^A_\mathrm{max}$ and $\sigma ^A_\mathrm{min}$ are the highest and lowest cross sections at any order obtained from the PDFs considered, respectively. These PDF uncertainties in the case of Higgs boson cross sections are about 5.7 % at NLO, 8.6 % at NNLO and 9.2 % at N$^3$LO$_\mathrm{SV}$. For pseudo-scalar Higgs boson production the cross sections are approximately twice the Higgs cross sections, but the percentages of PDF uncertainties are almost the same.

Fig. 5

Scale uncertainties associated with the pseudo-scalar Higgs boson production cross sections for LHC13. Variation with $\mu _R$ keeping $\mu _F=m_A$ fixed (left panel). Variation with $\mu _F$ keeping $\mu _R=m_A$ fixed (right panel)

The SV corrections give a rough estimate of the fixed order (FO) QCD corrections and are often useful in absence of the latter. However, the relative contribution of these SV corrections to the full FO results crucially depends on the kinematic region and in some cases on the process that we study. For the SM Higgs or pseudo-scalar Higgs boson with a mass of about 125 GeV, it is far from the threshold region $\tau = m_H^2/S \rightarrow 1$ for $\sqrt{S}=13$ TeV. Since the parton fluxes corresponding to this mass region are very high, apart from the threshold logarithms the contributions of the regular terms as well as of other sub-processes present in the FO corrections are expected to be reasonably very high. For a Higgs or pseudo-scalar Higgs boson, the prediction at NLO$_\mathrm{SV}$ level differs from the LO by only a few percent, whereas the regular terms at NLO contribute significantly and increase LO prediction by about 70 %. Similar is the case even at NNLO. Thus the SV corrections poorly estimate the FO ones, however, if we redefine the hadron level cross sections without affecting the total cross sections in such a way that the parton fluxes peak near the threshold region [51, 59, 95], then the SV contributions can be shown to dominate over the regular ones. This is due to arbitrariness involved in splitting the parton level cross section in terms of threshold enhanced and regular ones. Using a regular function G(z), we can write the hadronic cross section as

$$\begin{aligned} \sigma ^A(\tau )= & {} \sigma ^{A,(0)} \sum _{a,b=q,\bar{q},g} \int _{\tau }^{1} \mathrm{d}y\nonumber \\&\times G\left( {\tau \over y}\right) \varPhi _{ab}(y) \left( {{\varDelta }^{A}_{ab} \left( \frac{\tau }{y}\right) \over G\left( {\tau \over y}\right) }\right) \end{aligned}$$

(6.3)

where $\varDelta (z)/G(z)$ can be decomposed as

$$\begin{aligned} \varDelta (z)/G(z) = {\varDelta }^\mathrm{SV}(z) + \tilde{\varDelta }^\mathrm{hard}(z). \end{aligned}$$

(6.4)

In the above equation the ${\varDelta }^\mathrm{SV}$ is independent of G(z) (if $\lim _{z \rightarrow 1} G(z) \rightarrow 1$) and contains only distributions, whereas the hard part $\tilde{\varDelta }^\mathrm{hard}$ is modified due to G(z). Hence the SV part of the cross section at the hadron level depends on the choice of G(z). For the peculiar choice $G(z) = z^2$, the ${\varDelta }^\mathrm{SV}$ dominates over $\tilde{\varDelta }^\mathrm{hard}$ in such a way that almost the entire NLO and NNLO corrections (Eq. (6.3)) results from ${\varDelta }^\mathrm{SV}$ alone. As was noted earlier, $G(z)=1$ corresponds to the standard SV contribution. Note that the flux $\varPhi _{ab}$ is modified to $\varPhi ^\mathrm{mod}_{ab}(y)=\varPhi _{ab}(y) G(\tau /y)$, which is responsible for this behavior. We may denote the SV cross sections thus obtained with these modified fluxes as $\mathrm{NLO_{(sv)}}$, $\mathrm{NNLO_{(sv)}}$, and $\mathrm{N^3LO_{(sv)}}$ while those obtained with the normal fluxes as $\mathrm{NLO_{sv}}$, $\mathrm{NNLO_{sv}}$, and $\mathrm{N^3LO_{sv}}$. In Fig. 4, we depict the comparison between the SV cross sections obtained from the modified parton fluxes using $G(z)=z^2$ and the normal fixed order results that are obtained from the standard parton fluxes, for both the SM Higgs boson (left panel) and the pseudo-scalar Higgs boson (right panel). We notice that the SV results are significantly closer to the corresponding fixed order ones. Incidentally, this agreement is good for NLO as well as for NNLO where different sub-processes appear, and also for several values of $\sqrt{S}$ where the integration range over the parton fluxes is different. While this could be purely accidental, this good agreement might hint at some subtle hidden aspect and might be useful in the phenomenology.

Motivated by the above observation, one can convolute the perturbative coefficients $\varDelta _\mathrm{SV}^{(3)}$ with the modified parton fluxes $\varPhi ^\mathrm{mod}_{ab}(y)$ for the choice of $G(z)=z^2$ to get $\mathrm{N^3LO_{(sv)}}$, which could approximate the full $\mathrm N^3LO$ result. This way, we present in Fig. 4 the SV corrections obtained using $G(z)=1$ and $G(z)=z^2$ for Higgs as well as pseudo-scalar Higgs boson productions.

Fig. 6

Scale uncertainties associated with the pseudo-scalar Higgs boson production cross sections for LHC13 with $\mu = \mu _R = \mu _F$

Fig. 7

Renormalization scale ($\mu _R$) uncertainties associated with the Higgs (left panel) and pseudo-scalar Higgs boson (right panel) production cross sections for LHC13, keeping $\mu _F=m_H=m_A$ fixed

Fig. 8

Factorization scale ($\mu _R$) uncertainties associated with the Higgs (left panel) and pseudo-scalar Higgs boson (right panel) production cross sections for LHC13, keeping $\mu _R=m_H=m_A$ fixed

Fig. 9

Scale ($\mu =\mu _R=\mu _F$) uncertainties associated with the Higgs (left panel) and pseudo-scalar Higgs boson (right panel) production cross sections for LHC13

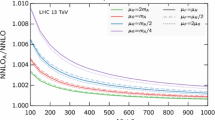
Next, we present the scale ($\mu _R,\mu _F$) uncertainties up to $\mathrm{N^3LO}_\mathrm{SV}$ in Fig. 5 for the choice of $m_A=200$ GeV. In the rest of our numerical analysis for studying the scale uncertainties, we simply use the modified parton fluxes for the choice $G(z)=z^2$ at three-loop level. In the left panel, we vary the renormalization scale $\mu _R$ between $m_A/4$ and $4m_A$, keeping $\mu _F=m_A$ fixed. Unlike the Drell–Yan process, for the pseudo-scalar Higgs boson production the renormalization scale $\mu _R$ enters even at LO through the strong coupling constant $a_s$. This is identical to the SM Higgs boson production in the gluon fusion channel. This is the main source of large scale uncertainty at LO. It gets significantly reduced when we include NLO and NNLO corrections as expected and it continues to do so at N$^3$LO level. In the right panel, we show the factorization scale uncertainties by varying $\mu _F$ from $m_A/4$ to $4m_A$ and fixing $\mu _R=m_A$. Here, the fixed order results show improvement in the reduction of factorization scale uncertainty from NLO to NNLO. However, due to the lack of parton distribution functions at N$^3$LO level and also due to the missing regular contributions from the parton level cross sections, the N$^3$LO$_\mathrm{SV}$ cross sections do not show any improvement of the factorization scale uncertainties. However, we observe that with the modified parton fluxes, the factorization scale uncertainties in N$^3$LO$_\mathrm{(SV)}$ get significantly reduced compared to N$^3$LO$_\mathrm{SV}$. In Fig. 6, we show the combined effect of $\mu _R$ and $\mu _F$ scale uncertainties by varying the scale $\mu$ between $m_A/4$ and $4m_A$, where $\mu =\mu _R=\mu _F$. Here, the NNLO cross sections show a good improvement over the NLO ones against the scale variations, while the N$^3$LO$_\mathrm{(SV)}$ cross sections are found to be more stable than the NNLO ones.

Further, we also study the renormalization and factorization scale variations of both the cross sections for the production of the SM Higgs boson and the pseudo-scalar Higgs boson for $m_H=m_A=125$ GeV by varying them between $m_A/4$ and $4m_A$. In Fig. 7, the renormalization scale uncertainties are given for Higgs boson (left panel) and for pseudo-scalar Higgs boson (right panel), for $\mu _F=m_A=m_H$. In Fig. 8, we present similar results but for the factorization scale uncertainties keeping $\mu _R=m_H=m_A$. Moreover, in Fig. 9, we present the combined effect by varying $\mu =\mu _R=\mu _F$. The pattern of the results for $\mu _R$ and $\mu _F$ and the combined variations are similar to the earlier analysis for $m_A=200$ GeV where the renormalization scale uncertainties get stabilized further after including the third order threshold corrections, while the scale uncertainties due to $\mu =\mu _R=\mu _F$ variation get significantly improved at N$^3$LO$_\mathrm{(SV)}$ than at NNLO.

7 Conclusions

In this paper, using the pseudo-scalar Higgs boson form factors that have recently become available up to three loops and the third order soft function from the real radiations, a complete N$^3$LO threshold correction to the production of a pseudo-scalar Higgs boson at the LHC has been obtained. The computation is performed using the z space representation of the resummed cross section. We have exploited the universal structure of the soft function that appears in scalar Higgs boson production at the LHC. We found that the singularities resulting from soft and collinear regions in the virtual diagrams cancel against those from the universal soft functions as well as from mass factorization kernels. Using our approach, we have also computed the process dependent coefficient that appears in the threshold resummed cross section. This will be useful for resummed predictions at N$^3$LL in QCD. Using threshold corrected N$^3$LO results, we have presented a detailed phenomenological study of the pseudo-scalar Higgs boson production at the LHC for various center of mass energies as a function of its mass. While the third order corrections are small, they play an important role in reducing the theoretical uncertainty resulting from renormalization scale. In addition, we have made a detailed comparison against scalar Higgs boson production and found their corrections are very close to each other confirming the universal behavior of the QCD effects even though the operators responsible for their interactions with gluons are very different.