Two-Higgs-doublet type-II and -III models and $t\rightarrow c h$ at the LHC

Abstract

We study the constraints of the generic two-Higgs-doublet model (2HDM) type-III and the impacts of the new Yukawa couplings. For comparisons, we revisit the analysis in the 2HDM type-II. To understand the influence of all involving free parameters and to realize their correlations, we employ a $\chi$-square fitting approach by including theoretical and experimental constraints, such as the S, T, and U oblique parameters, the production of standard model Higgs and its decay to $\gamma \gamma$, $WW^*/ZZ^*$, $\tau ^+\tau ^-$, etc. The errors of the analysis are taken at 68, 95.5, and $99.7~\%$ confidence levels. Due to the new Yukawa couplings being associated with $\cos (\beta -\alpha )$ and $\sin (\beta -\alpha )$, we find that the allowed regions for $\sin \alpha$ and $\tan \beta$ in the type-III model can be broader when the dictated parameter $\chi _F$ is positive; however, for negative $\chi _F$, the limits are stricter than those in the type-II model. By using the constrained parameters, we find that the deviation from the SM in $h\rightarrow Z\gamma$ can be of $\mathcal{O}(10~\%)$. Additionally, we also study the top-quark flavor-changing processes induced at the tree level in the type-III model and find that when all current experimental data are considered, we get $Br(t\rightarrow c(h, H) )< 10^{-3}$ for $m_h=125.36$ and $m_H=150$ GeV, and $Br(t\rightarrow cA)$ slightly exceeds $10^{-3}$ for $m_A =130$ GeV.

1 Introduction

A scalar boson around 125 GeV was observed in 2012 by ATLAS [1] and CMS [2] at CERN with more than $5\sigma$ significance. The discovery of such particle was based on the analyses of the following channels: $\gamma \gamma$, $WW^*$, $ZZ^*$ and $\tau ^+\tau ^-$ with errors of order of 20–30 % and $b\bar{b}$ channel with an error of order of 40–50 %. The recent updates from ATLAS and CMS with $7\oplus 8$ TeV data [3–7] indicate the possible deviations from the standard model (SM) predictions. Although the errors of the current data are still somewhat large, the new physics signals may become clear in the second run of the LHC at 13–14 TeV.

It is expected that the Higgs couplings to gauge bosons (fermions) at the LHC indeed could reach 4–6 % (6–13 %) accuracy when the collected data are up to the integrated luminosity of 300 fb$^{-1}$ [8–11]. Furthermore, the $e^+ e^-$ Linear Collider (LC) would be able to measure the Higgs couplings at the percent level [12]. Therefore, the goals of LHC at run II are (a) to pin down the nature of the observed scalar and see if it is the SM Higgs boson or a new scalar boson; (b) to reveal the existence of new physics effects, such as the measurement of flavor-changing neutral currents (FCNCs) at the top-quark decays, i.e. $t\rightarrow q h$.

Motivated by the observations of the diphoton, $WW^*$, $ZZ^*$, and $\tau ^+\tau ^-$ processes at the ATLAS and CMS, it is interesting to investigate what sorts of models may naturally be consistent with these measurements and what the implications are for other channels, e.g. $h\rightarrow Z \gamma$ and $t\rightarrow ch$. Although many possible extensions of the SM have been discussed [13–19], it is interesting to study the simplest extension from a one-Higgs doublet to a two-Higgs-doublet model (2HDM) [20–47]. According to the situation of Higgs fields coupling to fermions, the 2HDMs are classified as type-I, -II, and -III models, lepton specific model, and flipped model. The 2HDM type-III is the case where both Higgs doublets couple to all fermions; as a result, FCNCs at the tree level appear. The detailed discussions of the 2HDMs are shown elsewhere [23].

After the scalar particle of 125 GeV was discovered, the implications of the observed $h \rightarrow \gamma \gamma$ in the type-I and -II models were studied [48–54] and the impacts on $h \rightarrow \gamma Z$ are given [55–57]. As is well known, the $\tan \beta$ and angle $\alpha$ are important free parameters in the 2HDMs, where the former is the ratio of two vacuum expectation values (VEVs) of Higgses and the latter is the mixing parameter between the two CP-even scalars. It is found that the current LHC data put rather severe constraints on the free parameters [24–29]. For instance, the large $\tan \beta \sim m_t/m_b$ scenario in the type-I and -II is excluded except if we tune the $\alpha$ parameter to be rather small, $\alpha < 0.02$. Nevertheless, both type-I and type-II models can still fit the data in some small regions of $\tan \beta$ and $\alpha$.

In this paper, we will explore the influence of new Higgs couplings on the $h\rightarrow \tau ^+\tau ^-$, $h\rightarrow gg,\gamma \gamma , WW, ZZ$, and $h\rightarrow Z\gamma$ decays in the framework of the 2HDM type-III. We will show what is the most favored regions of the type-III parameter space when theoretical and experimental constraints are considered simultaneously. FCNCs of the heavy quark such as $t\rightarrow qh$ have been intensively studied both from the experimental and the theoretical points of view [58]. Such processes are well established in the SM and are excellent probes for the existence of new physics. In the SM and 2HDM type-I and -II, the top-quark FCNCs are generated at one-loop level by charged currents and are highly suppressed due to the GIM mechanism. The branching ratio (BR) for $t\rightarrow ch$ in the SM is estimated to be $3 \times 10^{-14}$ [59]. If this decay $t\rightarrow ch$ is observed, it would be an indisputable sign of new physics. Since the tree-level FCNCs appear in the type-III model, we explore if the $Br(t\rightarrow ch)$ reaches the order of $10^{-5}$–$10^{-4}$ [60–62], the sensitivity which is expected by the integrated luminosity of 3000 fb$^{-1}$.

The paper is organized as follows. In Sect. 2, we introduce the scalar potential and the Yukawa interactions in the 2HDM type-III. The theoretical and experimental constraints are described in Sect. 3. We set up the free parameters and establish the $\chi$-square for the best-fit approach in Sect. 6. In the same section, we discuss the numerical results when all theoretical and experimental constraints are taken into account. The conclusions are given in Sect. 7.

2 Model

In this section we define the scalar potential and the Yukawa sector in the 2HDM type-III. The scalar potential in $SU(2)_L\otimes U(1)_Y$ gauge symmetry and CP invariance is given by [69]

$$\begin{aligned}&V(\Phi _1,\Phi _2) = m^2_1 \Phi ^{\dagger }_1\Phi _1+m^2_2 \Phi ^{\dagger }_2\Phi _2 -(m^2_{12} \Phi ^{\dagger }_1\Phi _2+\mathrm{h.c.})\nonumber \\&\quad +\,\frac{1}{2} \lambda _1 (\Phi ^{\dagger }_1\Phi _1)^2 +\frac{1}{2} \lambda _2 (\Phi ^{\dagger }_2\Phi _2)^2\nonumber \\&\quad +\, \lambda _3 (\Phi ^{\dagger }_1\Phi _1)(\Phi ^{\dagger }_2\Phi _2) + \lambda _4 (\Phi ^{\dagger }_1\Phi _2)(\Phi ^{\dagger }_1\Phi _2) \nonumber \\&\quad +\,\left[ \frac{\lambda _5}{2}(\Phi ^{\dagger }_1\Phi _2)^2 + \left( \lambda _6 \Phi ^\dagger _1 \Phi _1 + \lambda _7 \Phi ^\dagger _2 \Phi _2 \right) \Phi ^\dagger _1 \Phi _2+\mathrm{h.c.} \right] ,\nonumber \\ \end{aligned}$$

(1)

where the doublets $\Phi _{1,2}$ have a weak hypercharge $Y=1$, the corresponding VEVs are $v_1$ and $v_2$, and $\lambda _i$ and $m^2_{12}$ are real parameters. After electroweak symmetry breaking, three of the eight degrees of freedom in the two Higgs doublets are the Goldstone bosons ($G^\pm$, $G^0$) and the remaining five degrees of freedom become the physical Higgs bosons: two CP-even h, H, one CP-odd A, and a pair of charged Higgs $H^\pm$. After using the minimized conditions and the W mass, the potential in Eq. (1) has nine parameters, which will be taken as $(\lambda _i)_{i=1,\ldots ,7}$, $m^2_{12}$, and $\tan \beta \equiv v_2/v_1$. Equivalently, we can use the masses as the independent parameters; therefore, the set of free parameters can be chosen to be

$$\begin{aligned} \{m_{h}, m_{H}, m_{A}, m_{H^\pm }, \tan \beta , \alpha , m^2_{12} \}, \end{aligned}$$

(2)

where we only list seven of the nine parameters, the angle $\beta$ diagonalizes the squared-mass matrices of CP-odd and charged scalars and the angle $\alpha$ diagonalizes the CP-even squared-mass matrix. In order to avoid generating spontaneous CP violation, we further require

$$\begin{aligned} m^2_{12} - \frac{\lambda _6 v^2_1}{2} - \frac{\lambda _7 v^2_2}{2} \ge \zeta \lambda _5 v_1 v_2 \end{aligned}$$

(3)

with $\zeta =1(0)$ for $\lambda _5> (< )0$ [69]. It has been well known that by assuming neutral flavor conservation at the tree level [63], we have four types of Higgs couplings to the fermions. In the 2HDM type-I, the quarks and leptons couple only to one of the two Higgs doublets and the case is the same as the SM. In the 2HDM type-II, the charged leptons and down-type quarks couple to one Higgs doublet and the up-type quarks couple to the other. The lepton-specific model is similar to type-I, but the leptons couple to the other Higgs doublet. In the flipped model, which is similar to type-II, the leptons and up-type quarks couple to the same double.

If the tree-level FCNCs are allowed, both doublets can couple to leptons and quarks and the associated model is called 2HDM type-III [23, 64–66]. Thus, the Yukawa interactions for the quarks are written as

$$\begin{aligned} \mathcal{{L}}_{Y} = \bar{Q}_{L} Y^{k} d_{R} \phi _k+ \bar{Q}_{L } \tilde{Y}^{k} u_{R} \tilde{\phi }_k + \hbox {h.c.} \end{aligned}$$

(4)

where the flavor indices are suppressed, $Q^T_L=(u_L, d_L)$ is the left-handed quark doublet, $Y^k$ and $\tilde{Y}^k$ denote the $3\times 3$ Yukawa matrices, $\tilde{\phi _k}=i\sigma _2 \phi ^*_k$, and k is the doublet number. Similar formulas could be applied to the lepton sector. Since the mass matrices of the quarks are combined by $Y^{1} (\tilde{Y}^{1})$ and $Y^2 (\tilde{Y}^{2})$ for down- (up-) type quarks and $Y^{1,2}(\tilde{Y}^{1,2})$ generally cannot be diagonalized simultaneously, as a result, the tree-level FCNCs appear and the effects lead to the oscillations of $K-\bar{K}$, $B_q-\bar{B}_q$ and $D-\bar{D}$ at the tree level. To get naturally small FCNCs, one can use the ansatz formulated by $Y^{k}_{ij},\,\tilde{Y}^k_{ij} \propto \sqrt{m_i m_j}/v$ [64–66]. After spontaneous symmetry breaking, the scalar couplings to the fermions can be expressed as [67, 68]

$$\begin{aligned} \mathcal{L}^{2\mathrm{HDM}\text {-}\mathrm{III}}_Y= & {} \bar{u}_{Li} \left( \frac{\cos \alpha }{\sin \beta }\frac{m_{u_i}}{v} \delta _{ij} - \frac{\cos (\beta -\alpha )}{\sqrt{2}\sin \beta } X^u_{ij} \right) u_{Rj} h \nonumber \\&+\, \bar{d}_{Li} \left( -\frac{\sin \alpha }{\cos \beta }\frac{m_{d_i}}{v} \delta _{ij} + \frac{\cos (\beta -\alpha )}{\sqrt{2}\cos \beta } X^d_{ij} \right) d_{Rj} h \nonumber \\&+\, \bar{u}_{Li} \left( \frac{\sin \alpha }{\sin \beta }\frac{m_{u_i}}{v} \delta _{ij} + \frac{\sin (\beta -\alpha )}{\sqrt{2}\sin \beta } X^u_{ij} \right) u_{Rj} H \nonumber \\&+\, \bar{d}_{Li} \left( \frac{\cos \alpha }{\cos \beta }\frac{m_{d_i}}{v} \delta _{ij} - \frac{\sin (\beta -\alpha )}{\sqrt{2}\cos \beta } X^d_{ij} \right) d_{Rj} H \nonumber \\&-\, i\bar{u}_{Li} \left( \frac{1}{\tan \beta }\frac{m_{u_i}}{v} \delta _{ij} -\frac{X^u_{ij} }{\sqrt{2}\sin \beta } \right) u_{Rj} A \nonumber \\&+\, i\bar{d}_{Li} \left( -\tan \beta \frac{m_{d_i}}{v} \delta _{ij} + \frac{X^d_{ij}}{\sqrt{2}\cos \beta } \right) d_{Rj} A\nonumber \\&+\,\mathrm{h.c.}, \end{aligned}$$

(5)

where $v=\sqrt{v^2_1 + v^2_2}$, $X^q_{ij}=\sqrt{m_{q_i} m_{q_j}}/v \chi ^q_{ij}$ ($q=u,d$) and $\chi ^{q}_{ij}$ are the free parameters. By the above formulation, if the FCNC effects are ignored, the results are returned to the case of the 2HDM type-II, given by

$$\begin{aligned} \mathcal{L}^{2\mathrm{HDM}\text {-}\mathrm{II}}_Y= & {} \bar{u}_{Li} \left( \frac{\cos \alpha }{\sin \beta }\frac{m_{u_i}}{v} \delta _{ij} \right) u_{Rj} h \nonumber \\&+\,\bar{d}_{Li} \left( -\frac{\sin \alpha }{\cos \beta }\frac{m_{d_i}}{v} \delta _{ij} \right) d_{Rj} h + \mathrm{h.c}. \end{aligned}$$

(6)

The couplings of the other scalars to fermions can be found elsewhere [67, 68]. It can be seen clearly that if $\chi ^{u,d}_{ij}$ are of $\mathcal{{O}}(10^{-1})$, the new effects are dominated by heavy fermions and comparable with those in the type-II model. The couplings of the h and H to the gauge bosons $V=W,Z$ are proportional to $\sin (\beta -\alpha )$ and $\cos (\beta -\alpha )$, respectively. Therefore, the SM-like Higgs boson h is recovered when $\cos (\beta -\alpha )\approx 0$. The decoupling limit can be achieved if $\cos (\beta -\alpha )\approx 0$ and $m_h \ll m_H, m_A, m_{H\pm }$ are satisfied [69]. From Eqs. (5) and (6), one can also find that in the decoupling limit, the h couplings to the quarks return to the SM case.

In this analysis, since we take $\alpha$ in the range $-\pi /2 \le \alpha \le \pi /2$, $\sin \alpha$ will have both a positive and a negative sign. In the 2HDM type-II, if $\sin \alpha <0$ then the Higgs couplings to up- and down-type quarks will have the same sign as those in the SM. It is worthwhile to mention that $\sin \alpha$ in minimal supersymmetric SM (MSSM) is negative, unless some extremely large radiative corrections flip its sign [69]. If $\sin \alpha$ is positive, then the Higgs coupling to down quarks will have a different sign with respect to the SM case. This is called the wrong sign Yukawa coupling in the literature [69–71]. Later we will explain whether the type-III model would favor such a wrong sign scenario or not.

3 Theoretical and experimental constraints

The free parameters in the scalar potential defined in Eq. (1) could be constrained by theoretical requirements and the experimental measurements, where the former mainly includes tree-level unitarity and vacuum stability when the electroweak symmetry is broken spontaneously. Since the unitarity constraint involves a variety of scattering processes, we adopt the results [72–75]. We also force the potential to be perturbative by requiring that all quartic couplings of the scalar potential obey $|\lambda _i| \le 8 \pi$ for all i. For the vacuum stability conditions which ensure that the potential is bounded from below, we require that the parameters satisfy the conditions [76–78]

$$\begin{aligned}&\lambda _1> 0,\quad \lambda _2> 0,\quad \lambda _3 + \sqrt{\lambda _1\lambda _2 }> 0, \nonumber \\&\quad \sqrt{\lambda _1\lambda _2 } + \lambda _{3} + \lambda _{4} -|\lambda _{5}| >0,\nonumber \\&{2|\lambda _6 + \lambda _7| \le \frac{1}{2}(\lambda _1 + \lambda _2) + \lambda _3 + \lambda _4 + \lambda _5}. \end{aligned}$$

(7)

In the following we state the constraints from the experimental data. The new neutral and charged scalar bosons in 2HDM will affect the self-energy of W and Z bosons through the loop effects. Therefore, the involved parameters could be constrained by the precision measurements of the oblique parameters, denoted by S, T, and U [79]. Taking $m_h = 125$ GeV, $m_t = 173.3$ GeV, and assuming that $U=0$, the tolerated ranges for S and T are found to be [80]

$$\begin{aligned} \Delta S = 0.06\pm 0.09,\quad \Delta T = 0.10\pm 0.07, \end{aligned}$$

(8)

where the correlation factor is $\rho =+0.91$, $\Delta S = S^{\text {2HDM}} - S^{\text {SM}}$, and $\Delta T = T^{\text {2HDM}} - T^{\text {SM}}$, and their explicit expressions can be found [69]. We note that in the limit $m_{H^\pm }=m_{A^0}$ or $m_{H^\pm }=m_{H^0}$, $\Delta T$ vanishes [81, 82].

The second set of constraints comes from B physics observables. It has been shown recently in Ref. [83] that $Br(\overline{B}\rightarrow X_s \gamma )$ gives a lower limit on $m_{H^\pm }\ge 480$ GeV in the 2HDM type-II at $95~\%$ CL. However, in 2HDM type-III the situation is slightly different. In fact, the charged Higgs–top-quark affects $Br(\overline{B}\rightarrow X_s \gamma )$ via the Wilson coefficients $C_{7,8}$ at leading-order (LO) as well as at the next-to-next LO (NNLO). The $Br(\overline{B}\rightarrow X_s \gamma )$ constraint can get weakened in the 2HDM type-III because of the off-diagonal element that enters in the $H^+t\bar{b}$ coupling. This new term can lead to a destructive interference with the SM and then reduce the 2HDM contribution. It was pointed out that in 2HDM type-III a light charged Higgs boson with a mass around 200 GeV is still allowed at NLO level by the measured $Br(\overline{B}\rightarrow X_s \gamma )$ within 2$\sigma$ [84–86]. While in type-II, such light charged Higgs boson cannot be accommodated.

By precision measurements of $Z\rightarrow b \bar{b}$ and $B_q$–$\bar{B}_q$ mixing, the values of $\tan \beta < 0.5$ have been excluded [87, 88]. In this work we allow $\tan \beta \ge 0.5$. Except for some specific scenarios, $\tan \beta$ cannot be too large due to the requirement of perturbation theory.

By the observation of a scalar boson at $m_h \approx 125$ GeV, the searches for Higgs boson at ATLAS and CMS can give strong bounds on the free parameters. The signal events in the Higgs measurements are represented by the signal strength, which is defined by the ratio of the Higgs signal to the SM prediction and is given by

$$\begin{aligned} \mu ^f_i= \frac{\sigma _i(h) \cdot Br(h\rightarrow f) }{\sigma ^{SM}_i(h) \cdot Br^{SM}(h\rightarrow f) } \equiv \bar{\sigma }_i \cdot \mu _f, \end{aligned}$$

(9)

where $\sigma _i(h)$ denotes the Higgs production cross section by channel i and $Br(h\rightarrow f)$ is the BR for the Higgs decay $h\rightarrow f$. Since several Higgs boson production channels are available at the LHC, we are interested in the gluon fusion production (ggF), $t \bar{t} h$, vector boson fusion (VBF) and Higgs-strahlung Vh with $V=W/Z$; and they are grouped into $\mu ^f_{ggF+t\bar{t} h}$ and $\mu ^f_{VBF+Vh}$. In order to consider the constraints from the current LHC data, the scaling factors which show the Higgs coupling deviations from the SM are defined as

$$\begin{aligned} \kappa _V^{} =\kappa _W = \kappa _Z \equiv \frac{g_{hVV}^{\text {2HDM}}}{g_{hVV}^{\text {SM}}},\quad \kappa _f^{} \equiv \frac{y_{hff}^{\text {2HDM}}}{y_{hff}^{\text {SM}}}, \end{aligned}$$

(10)

where $g_{hVV}$ and $y_{hff}$ are the Higgs couplings to gauge bosons and fermions, respectively, and f stands for top, bottom quarks, and tau lepton. The scaling factors for the loop-induced channels are defined by

$$\begin{aligned} \kappa _\gamma ^2\equiv & {} \frac{\Gamma (h\rightarrow \gamma \gamma )_{\text {2HDM}}}{\Gamma (h\rightarrow \gamma \gamma )_{\text {SM}}},\quad \kappa _g^2 \equiv \frac{\Gamma (h\rightarrow g\,g)_{\text {2HDM}}}{\Gamma (h\rightarrow g\,g)_{\text {SM}}}, \nonumber \\ \quad \kappa _{Z\gamma }^2\equiv & {} \frac{\Gamma (h\rightarrow Z\gamma )_{\text {2HDM}}}{\Gamma (h\rightarrow Z\gamma )_{\text {SM}}},\quad \kappa _{h}^2 \equiv \frac{\Gamma (h)_{\text {2HDM}}}{\Gamma (h)_{\text {SM}}}, \end{aligned}$$

(11)

where $\Gamma (h\rightarrow XY)$ is the partial decay rate for $h\rightarrow XY$. In this study, the partial decay width of the Higgs is taken from [89, 90], where the QCD corrections have been taken into account. In the decay modes $h\rightarrow \gamma \gamma$ and $h\rightarrow Z\gamma$, we have included the contributions of the charged Higgs and the new Yukawa couplings. Accordingly, the ratio of the cross section to the SM prediction for the production channels $ggF+t\bar{t} h$ and VBF+Vh can be expressed as

$$\begin{aligned}&\overline{\sigma }_{ggF+t\bar{t} h} = \frac{\kappa ^2_{g}\sigma _{SM}(ggF) + \kappa ^2_{t}\sigma _{SM}(tth)}{\sigma _{SM}(ggF) + \sigma _{SM}(tth)}, \quad \end{aligned}$$

(12)

$$\begin{aligned}&\overline{\sigma }_{VBF+Vh} \nonumber \\&\quad =\frac{\kappa ^2_{V}\sigma _{SM}(VBF)+\widetilde{\kappa }_{Zh}\widetilde{\sigma }_{SM}(Zh) + \kappa ^2_{V}\sigma _{SM}(Zh) + \kappa ^2_{V}\sigma _{SM}(Wh)}{\sigma _{SM}(VBF)+\widetilde{\sigma }_{SM}(Zh) + \sigma _{SM}(Zh) + \sigma _{SM}(Wh)},\nonumber \\ \end{aligned}$$

(13)

where $\sigma _{SM}(Zh)$ is from the coupling of ZZh and occurs at the tree level, and $\widetilde{\sigma }_{SM}(Zh)\equiv \sigma _{SM} (gg\rightarrow Zh)$ represents the effects of the top-quark loop. With $m_h=125.36$ GeV, the scalar factor $\widetilde{\kappa }_{Zh}$ can be written as [3]

$$\begin{aligned} \widetilde{\kappa }_{Zh}= & {} 2.27\kappa ^2_Z + 0.37\kappa ^2_t - 1.64\kappa _Z\kappa _t. \end{aligned}$$

(14)

In the numerical estimations, we use $m_h = 125.36$ GeV, which is from LHC Higgs Cross Section Working Group [8–10] at $\sqrt{s} = 8$ TeV. The experimental values of the signal strengths are shown in Table 1, where the results of ATLAS [5] and CMS [91] are combined and denoted by $\widehat{\mu }^f_{ggF+t\bar{t} h}$ and $\widehat{\mu }^f_{VBF+Vh}$.

Table 1 Measured signal strengths $\widehat{\mu }_\mathrm{{ggF+tth}}$ and $\widehat{\mu }_\mathrm{{VBF+Vh}}$ that combine the best fit of ATLAS and CMS and correlation coefficient $\rho$ for the Higgs decay mode [5, 91]

4 Parameter setting, global fitting, and numerical results

4.1 Parameters and global fitting

After introducing the scaling factors for displaying the new physics in various channels, in the following we show the explicit relations with the free parameters in the type-III model. By the definitions in Eq. (10), the scaling factors for $\kappa _V$ and $\kappa _f$ in the type-III are given by

$$\begin{aligned} \kappa _V^{}= & {} \sin (\beta -\alpha ), \nonumber \\ \kappa _U^{}= & {} \kappa _t = \kappa _c = \frac{\cos \alpha }{\sin \beta } - \chi _F \frac{\cos (\beta -\alpha )}{\sqrt{2}\sin \beta }, \nonumber \\ \kappa _D^{}= & {} \kappa _b = \kappa _{\tau } = -\frac{\sin \alpha }{\cos \beta } + \chi _F \frac{\cos (\beta -\alpha )}{\sqrt{2}\cos \beta }. \end{aligned}$$

(15)

Although the FCNC processes give strict constraints on the flavor-changing couplings $\chi ^{f}_{ij}$ with $i\ne j$, the constraints are applied to the flavor-changing processes in the K, D, and B meson systems. Since the couplings of the scalars to the light quarks have been suppressed by $m_{q_i}/v$, the direct limit on the flavor-conserved coupling $\chi ^f_{ii}$ is mild. Additionally, since the signals for top-quark flavor-changing processes have not been observed yet, the direct constraint on $X^u_{3i}= \sqrt{m_t m_{q_i}}/v \chi ^u_{3i}$ is from the experimental bound of $t\rightarrow h q_i$. Hence, for simplifying the numerical analysis, in Eq. (15) we have set $\chi ^u_{22}=\chi ^u_{33} = \chi ^{d}_{33} =\chi ^{\ell }_{33}=\chi _F$. Since $X^u_{33} = m_t/v \chi _F$, it is conservative to adopt the value of $\chi _F$ to be $\mathcal{O}(1)$. In the 2HDM, the charged Higgs will also contribute to $h\rightarrow \gamma \gamma$ decay and the associated scalar triplet coupling $hH^+ H^-$ reads

$$\begin{aligned}&\lambda _{hH^{\pm }H^{\mp }} \nonumber \\&\quad =\frac{1}{2m^2_W}\Bigg (\frac{\cos (\alpha +\beta )}{\sin 2\beta }(2m^2_h - 2\lambda _5 v^2)\nonumber \\&\qquad -\,\sin (\beta -\alpha )(m^2_h - 2m^2_{H^\pm })\nonumber \\&\qquad +\,m^2_W\cos (\beta -\alpha )\left( \frac{\lambda _6}{\sin ^2\beta } - \frac{\lambda _7}{\cos ^2\beta }\right) \Bigg ). \end{aligned}$$

(16)

The scaling factors for loop-induced processes $h\rightarrow (\gamma \gamma , Z\gamma , gg)$ can be expressed by

(17)

where we have used $m_h = 125.36$ GeV and taken $m_{H^\pm } = 480$ GeV. It is clear that the charged Higgs contribution to $h\rightarrow \gamma \gamma$ and $h\rightarrow Z\gamma$ is small. In order to study the influence of the new free parameters and to understand their correlations, we perform the $\chi$-square fitting by using the LHC data for Higgs searches [1, 2, 4, 6]. For a given channel $f=\gamma \gamma , W W^*, Z Z^*, \tau \tau$, we define the $\chi ^2_f$ as

$$\begin{aligned} \chi ^2_f= & {} \frac{1}{\hat{\sigma }^2_{1}(1-\rho ^2)}(\mu ^{f}_{1} - \hat{\mu }^{f}_{1})^2 + \frac{1}{\hat{\sigma }^2_{1}(1-\rho ^2)}(\mu ^{f}_{2} - \hat{\mu }^{f}_{2})^2\nonumber \\&-\frac{2\rho }{\hat{\sigma }_{1}\hat{\sigma }_{2}(1-\rho ^2)}(\mu ^{f}_{1} - \hat{\mu }^{f}_{1})(\mu ^{f}_{2} - \hat{\mu }^{f}_{2}), \end{aligned}$$

(18)

where $\hat{\mu }^{f}_{1,2}$, $\hat{\sigma }_{1,2}$ and $\rho$ are the measured Higgs signal strengths, their one-sigma errors, and their correlation, respectively, and for their values one may refer to Table 1. The indices 1 and 2 in turn stand for $\mathrm ggF+tth$ and $\mathrm VBF+Vh$, and $\mu ^{f}_{1,2}$ are the results in the 2HDM. The global $\chi$-square is defined by

$$\begin{aligned} \chi ^2 = \sum _{f}\chi ^2_{f} + \chi ^2_{ST} , \end{aligned}$$

(19)

where the $\chi ^2_{ST}$ is related to the $\chi ^2$ for S and T parameters, the definition can be obtained from Eq. (18) by replacing $\mu ^f_1 \rightarrow S^{2HDM}$ and $\mu ^f_2\rightarrow T^{2HDM}$, and the corresponding values can be found from Eq. (8). We do not include the $b\bar{b}$ channel in our analysis because the errors of the data are still large.

In order to display the allowed regions for the parameters, we show the best fit at 68, 95.5, and $99.7~\%$ confidence levels (CLs), that is, the corresponding errors of $\chi ^2$ are $\Delta \chi ^2 \le 2.3$, 5.99, and 11.8, respectively. For comparing with the LHC data, we require the calculated results in agreement with those shown by ATLAS (Fig. 3 of Ref. [3]) and by CMS (Fig. 5 of Ref. [7]).

5 Numerical results

In the following we present the limits of the current LHC data based on the three kinds of CL introduced in the last section. In our numerical calculations, we set the mass of SM Higgs to be $m_h=125.36$ GeV, and we scan the involved parameters in the chosen regions as

(20)

The main difference in the scalar potential between type-II and type-III is that the $\lambda _{6,7}$ terms appear in the type-III model. With the introduction of the $\lambda _{6,7}$ terms in the potential, not only the mass relations of scalar bosons are modified but also the scalar triple and quartic coupling receives contributions from $\lambda _{6}$ and $\lambda _{7}$. Since the masses of the scalar bosons are regarded as free parameters, the relevant $\lambda _{6,7}$ effects in this study enter the game through the triple coupling h–$H^+$–$H^-$, which contributes to the $h\rightarrow \gamma \gamma$ decay, as shown in Eq. (16) and the first line of Eq. (17). Since the contribution of the charged Higgs loop to the $h\rightarrow \gamma \gamma$ decay is small, expectedly the influence of $\lambda _{6,7}$ on the parameter constraint is not significant. To demonstrate that the contributions of $\lambda _{6,7}$ are not very important, we present the allowed ranges for $\tan \beta$ and $\sin \alpha$ by scanning $\lambda _{6,7}$ in the region of $[-1,1]$ in Fig. 1, where the theoretical and experimental constraints mentioned earlier are included and the plots from left to right in turn stand for $\Delta \chi ^2 =11.8$, 5.99, and 2.3, respectively. Additionally, to understand the influence of $\chi _F$ defined in Eq. (15), we also scan $\chi _F=[-1,1]$ in the plots. By comparing the results with the case of $\lambda _{6,7}\ll 1$ and $\chi _F= 1$, which is displayed in the third plot of Fig. 2, it can be seen that only a small region for positive $\sin \alpha$ is modified and the modifications happen only in the large errors of $\chi ^2$; the plot with $\Delta \chi ^2=2.3$ shows almost no change. However, it can be seen from Fig. 1 (right panel) that for small $\chi ^2$ the values of positive $\sin \alpha$ are excluded by LHC constraints on $h\rightarrow \tau ^+\tau ^-$, which exceed a 20 % deviation from SM values, which is excluded by the LHC data. Therefore, to simplify the numerical analysis and to reduce the scanned parameters, it is reasonable in this study to assume $\lambda _{6,7}\ll 1$. Since the influence of $|\chi _F|\le 1$ should be smaller, to get the typical contributions from the FCNC effects, we illustrate our studies by setting $\chi _F = \pm 1$ in the whole numerical analysis.

Fig. 1

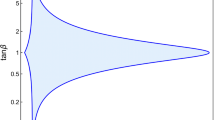
The allowed regions in $(\sin \alpha , \tan \beta )$ constrained by theoretical and current experimental inputs, where we have used $m_h = 125.36$ GeV in the type-III with $-1\le \chi _F\le 1$ and $-1\le \lambda _{6,7}\le 1$. The errors for the $\chi$-square fit are 99.7 $\%$ CL (left panel), 95.5 $\%$ CL (middle panel), and 68 $\%$ CL (right panel)

Fig. 2

The allowed regions in $(\sin \alpha , \tan \beta )$ constrained by theoretical and current experimental inputs, where we have used $m_h = 125.36$ GeV, the left, middle, and right panels stand for the 2HDM type-II, type-III with $\chi _F=-1$ and type-III with $\chi _F=+1$, respectively. The errors for the $\chi$-square fit are 99.7 $\%$ CL (black), 95.5 $\%$ CL (red), and 68 $\%$ CL (green)

With $\lambda _{6,7}\ll 1$, we present the allowed regions for $\sin \alpha$ and $\tan \beta$ in Fig. 2, where the left, middle, and right panels stand for the 2HDM type-II, type-III with $\chi _F= -1$ and type-III with $\chi _F = +1$, respectively, and in each plot we show the constraints at $68~\%$ CL (green), 95.5 $\%$ CL (red), and 99.7 $\%$ CL (black). Our results in type-II are consistent with those obtained by the authors in Refs. [24–29, 48–54] when the same conditions are chosen. By the plots, we see that in type-III with $\chi _F=-1$, due to the sign of the coupling being the same as type-II, the allowed values for $\sin \alpha$ and $\tan \beta$ are further shrunk; especially $\sin \alpha$ is limited values less than 0.1. On the contrary, for type-III with $\chi _F=+1$, the allowed values of $\sin \alpha$ and $\tan \beta$ are broad.

As discussed before, the decoupling limit occurs at $\alpha \rightarrow \beta -\pi /2$, i.e. $\sin \alpha =-\cos \beta < 0$. Since we regard the masses of new scalars as free parameters and scan them in the regions shown in Eq. (20), the three plots in Fig. 2 cover lower and heavier mass of charged Higgs. We further check that $\sin \alpha >0$ could be excluded at 95.5(99.7) $\%$ CL when $m_{H^\pm } \ge 585(690)$ GeV. The main differences between type-II and type-III are the Yukawa couplings as shown in Eq. (5).

Fig. 3

$\kappa _{g}$ as a function of $\sin \alpha$ and $\tan \beta$ in type-II (left) and type-III with $\chi _F=(-1, +1)$ (middle, right), where the solid, dashed, and dotted lines in each plot stand for the decoupling limit (DL) of SM, $15~\%$ deviation from DL and $20~\%$ deviation from DL, respectively. The dotted points are the allowed values of parameters resulting from Fig. 2

Fig. 4

Correlation of $\kappa _D$ and $\kappa _U$, where the left, middle, and right panels represent the allowed values in type-II, type-III with $\chi _F=-1$, and type-III with $\chi _F=+1$, respectively, and the results of Fig. 2 are applied

Fig. 5

The legend is the same as that in Fig. 4, but for the correlation of $\kappa _V$ and $\kappa _D$

In order to see the influence of the new effects of type-III, we plot the allowed $\kappa _g$ as a function of $\sin \alpha$ and $\tan \beta$ in Fig. 3, where the three plots from left to right correspond to type-II, type-III with $\chi _F=-1$, and type-III with $\chi _F=+1$, the solid, dashed, and dotted lines in each plot stand for the decoupling limit (DL) of SM, $15~\%$ deviation from DL and $20~\%$ deviation from DL, respectively. For comparison, we also put the results of $99.7~\%$ in Fig. 2 in each plot. By the analysis, we see that the deviations of $\kappa _g$ from DL in $\chi _F=+1$ are clear and significant, while the influence of $\chi _F=-1$ is small. It is pointed out that a wrong sign Yukawa coupling to down-type quarks could happen in type-II 2HDM [69–71]. For understanding the sign flip, we rewrite the $\kappa _D$ defined in Eq. (15),

$$\begin{aligned} \kappa _{D}= -\frac{\sin \alpha }{\cos \beta } \left( 1- \frac{\chi _F \sin \beta }{\sqrt{2}}\right) + \frac{\chi _F \cos \alpha }{\sqrt{2}}. \end{aligned}$$

(21)

In the type-II case, we know that in the decoupling limit $\kappa _D=1$, but $\kappa _D < 0$ if $\sin \alpha >0$. According to the results in the left panel of Fig. 2, $\sin \alpha >0$ is allowed when the errors of best fit are taken by $2\sigma$ or 3$\sigma$. The situation in type-III is more complicated. From Eq. (21), we see that the factor in the brackets is always positive, therefore, the sign of the first term should be the same as that in type-II case. However, due to $\alpha \in [ -\pi /2, \pi /2]$, the sign of the second term in Eq. (21) depends on the sign of $\chi _F$. For $\chi _F = -1$, even $\sin \alpha < 0$, $\kappa _D$ could be negative when the first term is smaller than the second term. For $\chi _F=+1$, if $\sin \alpha >0$ and the first term is over the second term, $\kappa _D < 0$ is still allowed. In order to understand the available values of $\kappa _D$ when the constraints are considered, we present the correlation of $\kappa _U$ and $\kappa _D$ in Fig. 4, where the panels from left to right stand for type-II, type-III with $\chi _F = -1$ and type-III with $\chi _F=+1$. In each plot, the results obtained by $\chi$-square fitting are applied. The similar correlation of $\kappa _V$ and $\kappa _D$ is presented in Fig. 5. By these results, we find that comparing with type-II model, the negative $\kappa _D$ gets a stricter limit in type-III, although a wider parameter space for $\sin \alpha > 0$ is allowed in type-III with $\chi _F = +1$.

Fig. 6

Correlation of $\kappa _\gamma$ and $\kappa _g$, where the left, middle and right panels represent the allowed values in type-II, type-III with $\chi _F=-1$ and type-III with $\chi _F=+1$, respectively, and the results in Fig. 2 obtained by $\chi$-square fitting are applied

Fig. 7

The allowed regions in the $(\kappa _{\gamma }, \kappa _{Z\gamma })$ plane after imposing theoretical and experimental constraints. Color coding the same as Fig. 2

Fig. 8

Correlation between $\mu ^{\gamma \gamma }_{ggF+tth}$ and $\mu ^{Z\gamma }_{ggF+tth}$ at $\sqrt{s} = 13$ TeV after imposing theoretical and experimental constraints. Left, middle, and right panels represent the allowed values in type-II, type-III with $\chi _F=-1$ and type-III with $\chi _F=+1$, respectively, and the results in Fig. 2 obtained by $\chi$-square fitting are applied

Besides the scaling factors of tree-level Higgs decays, $\kappa _{D,U}$ and $\kappa _V$, it is also interesting to understand the allowed values for loop-induced processes in 2HDM, e.g. $h\rightarrow \gamma \gamma$, gg, and $Z\gamma$, etc. It is well known that the differences in the associated couplings between $h\rightarrow \gamma \gamma$ and gg are the colorless W-, $\tau$-, and $H^\pm$-loop. By Eq. (17), we see that the contributions of $\tau$ and $H^\pm$ are small, therefore, the main difference is from the W-loop in which the $\kappa _V$ is involved. By using the $\chi$-square fitting approach and with the inputs of the experimental data and theoretical constraints, the allowed regions of $\kappa _\gamma$ and $\kappa _g$ in type-II and type-III are displayed in Fig. 6, where the panels from left to right are type-II, type-III with $\chi _F=-1$ and $+1$; the green, red, and black colors in each plot stand for the 68, 95.5, and $99.7~\%$ CL, respectively. We find that except a slightly lower $\kappa _\gamma$ is allowed in type-II, the first two plots have similar results. The situation can be understood from Figs. 4 and 5, where the $\kappa _U$ in both models is similar, while $\kappa _V$ in type-II could be smaller in the region of negative $\kappa _D$; that is, a smaller $\kappa _V$ will lead to a smaller $\kappa _\gamma$. In the $\chi _F=+1$ case, the allowed values of $\kappa _\gamma$ and $\kappa _g$ are localized in a wider region.

It is well known that except for the different gauge couplings, the loop diagrams for $h\rightarrow Z\gamma$ and $h\rightarrow \gamma \gamma$ are exactly the same. One can understand the loop effects by the numerical form of Eq. (17). Therefore, we expect the correlation between $\kappa _{Z\gamma }$ and $\kappa _\gamma$ should behave like a linear relation. We present the correlation between $\kappa _\gamma$ and $\kappa _{Z\gamma }$ in Fig. 7, where the legend is the same as that for Fig. 6. From the plots, we see that in most of the region $\kappa _{Z\gamma }$ is less than the SM prediction. The type-III with $\chi _F=-1$ gets a stricter constraint and the change is within $10~\%$. For $\chi _F=+1$, the deviation of $\kappa _{Z\gamma }$ from unity could be over $10~\%$. From run I data, the LHC has an upper bound on $h\rightarrow Z\gamma$, at run II this decay mode will be probed. We give the predictions at 13 TeV LHC for the signal strength $\mu ^{\gamma \gamma }_{ggF+tth}$ and $\mu ^{Z\gamma }_{ggF+tth}$ in Fig. 8. Hence, with the theoretical and experimental constraints, $\mu ^{Z\gamma }_{ggF+tth}$ is bounded and could be $\mathcal {O}$(10 %) away from SM at 68 $\%$ CL.

6 $t\rightarrow ch$ decay

In this section, we study the flavor-changing $t\rightarrow c h$ process in the type-III model. Experimentally, there have been intensive activities to explore the top FCNCs. The CDF, D0, and LEPII collaborations have reported some bounds on top FCNCs. At the LHC with rather large top cross section, ATLAS and CMS search for top FCNCs and put a limit on the branching fraction, which is $Br(t\rightarrow ch)< 0.82$ % for ATLAS [60, 61] and $Br(t\rightarrow ch)< 0.56$ % for CMS [62]. Note that the CMS limit is slightly better than the ATLAS limit. CMS search for $t\rightarrow ch$ in different channels: $h\rightarrow \gamma \gamma$, $WW^*$, $ZZ^*$, and $\tau ^+\tau ^-$, while ATLAS used only a diphoton channel. With the high luminosity option of the LHC, the above limit will be improved to reach about $Br(t\rightarrow ch)< 1.5 \times 10^{-4}$ [60, 61] for the ATLAS detector.

From the Yukawa couplings in Eq. (5), the partial width for the $t\rightarrow ch$ decay is given by

$$\begin{aligned} \Gamma (t\rightarrow ch)= & {} \left( \frac{\cos (\beta -\alpha )X_{23}^u}{\sin \beta }\right) ^2\frac{m_t}{32\pi } \left( (x_c + 1)^2 - x^2_h\right) \nonumber \\&\times \sqrt{1-(x_h - x_c)^2}\sqrt{1-(x_h + x_c)^2} \end{aligned}$$

(22)

where $x_c = m_c/m_t$, $x_h =m_h/m_t$, and $X_{23}^u$ is a free parameter and dictates the FCNC effect. It is clear from the above expression that the partial width of $t\rightarrow ch$ is proportional to $\cos (\beta -\alpha )$. As seen in the previous section, in the case where h is SM-like, $\cos (\beta -\alpha )$ is constrained by LHC data to be rather small and the $t\rightarrow ch$ branching fraction is limited. As we will see later in 2HDM type-II with flavor conservation the rate for $t\rightarrow ch$ is much smaller than type-III [92–95]. Since we assume that the charged Higgs is heavier than 400 GeV, the total decay width of the top contains only $t\rightarrow ch$ and $t\rightarrow bW$. With $m_h=125.36$ GeV, $m_t=173.3$ GeV, and $m_c=1.42$ GeV, the total width can be written

$$\begin{aligned} \Gamma _t = \Gamma ^{SM}_t + 0.0017 \left( \frac{\cos (\beta -\alpha )X^u_{23}}{\sin \beta }\right) ^2\,\,\mathrm{GeV} \end{aligned}$$

(23)

where $\Gamma ^{SM}_t$ is the partial decay rate for $t\rightarrow Wb$, given by

$$\begin{aligned} \Gamma ^{SM}_t= & {} \frac{G_F m_t^3}{8\pi \sqrt{2}}\left( 1-\frac{m_W^2}{m_t^2}\right) ^2 \left( 1+2 \frac{m_W^2}{m_t^2}\right) \nonumber \\&\times \left( 1-2 \frac{\alpha _s(m_t)}{3 \pi } \left( 2\frac{\pi ^2}{3}-\frac{5}{2}\right) \right) =1.43~\mathrm{GeV},\nonumber \end{aligned}$$

in which the QCD corrections have been included. By the above numerical expressions together with the current limit from ATLAS and CMS, the limit on the tch FCNC coupling is foun:

$$\begin{aligned}&\left( \frac{\cos (\beta -\alpha )X^u_{23}}{\sin \beta }\right)< 2.2 \quad \mathrm{for}\ Br(t\rightarrow ch)< 8.2 \times 10^{-3}, \nonumber \\&\left( \frac{\cos (\beta -\alpha )X^u_{23}}{\sin \beta }\right)< 0.36 \quad \mathrm{for}\ Br(t\rightarrow ch)< 5.6 \times 10^{-3},\nonumber \\ \end{aligned}$$

(24)

in agreement with [96].

We perform a systematic scan over the 2HDM parameters, as depicted in Eq. (20), taking into account LHC and theoretical constraints. Although $X^u_{23}$ is a free parameter, in order to suppress the FCNC effects naturally, as stated earlier we adopt $X^u_{23} = \sqrt{m_t m_c}/v \chi ^u_{23}$. Since the current experimental measurements only give an upper limit on $t\rightarrow h c$, basically $\chi ^u_{23}$ is limited by Eq. (24) and could be as large as $\mathcal{O}(1-10^{2})$, depending on the allowed value of $\cos (\beta -\alpha )$. In order to use the constrained results which are obtained from the Higgs measurements and the self-consistent parametrization $X^u_{33}=m_t /v \chi _F$, which was used before, we assume $\chi ^u_{23} = \chi _F = \pm 1$. In our numerical analysis, the results under the assumption should be conservative. In Fig. 9(left) we illustrate the branching fraction of $t\rightarrow ch$ in 2HDM-III as a function of $\cos (\beta -\alpha )$. The LHC constraints within 1$\sigma$ restrict $\cos (\beta -\alpha )$ to be in the range $[-0.27,0.27]$. The branching fraction for $t\rightarrow ch$ is slightly above $10^{-4}$. The actual CMS and ATLAS constraint on $Br(t\rightarrow ch)<5.6 \times 10^{-3}$ does not restrict $\cos (\beta -\alpha )$. The expected limit from the ATLAS detector with high luminosity 3000 fb$^{-1}$ is depicted as the dashed horizontal line. As one can see, the expected ATLAS limit is somehow similar to LHC constraints within 1$\sigma$. In the right panel, we show the allowed parameters space in the $(\sin \alpha , \tan \beta )$ plane where we apply the ATLAS expected limit $Br(t\rightarrow ch)< 1.5 \times 10^{-4}$. This plot should be compared to the right panel of Fig. 2. It is then clear that this additional constraint only acts on the 3$\sigma$ allowed region from the LHC data.

Fig. 9

Left Branching ratio of Br$(t\rightarrow ch)$ as a function of $\cos (\beta -\alpha )$; the two horizontal lines correspond to LHC actual limit (upper line) and the expected limit from ATLAS with 3000 fb$^{-1}$ luminosity (dashed line). Right panel Allowed parameters space in type-III with the ATLAS expected limit on $Br(t\rightarrow ch)< 1.5 \times 10^{-4}$

Fig. 10

Branching ratios of Br$(t\rightarrow ch)$ (left), Br$(t\rightarrow cH)$(middle), and Br$(t\rightarrow cA)$ (right) as a function of $\kappa _U$ in type-III with $\chi _{F} = +1$. For $m_h=125.36$ GeV, $m_H = 150$ GeV, and $m_A = 130$ GeV

Fig. 11

The legend is the same as Fig. 10, but for $\chi _{F} = -1$

In Figs. 10 and 11, we show the fitted branching fractions for $t\rightarrow ch$ (left), $t\rightarrow cH$ at $m_H=150$ GeV (middle), and $t\rightarrow cA$ at $m_A=130$ GeV (right) as a function of $\kappa _U$, where Fig. 10 is for $\chi _{F} = +1$, while Fig. 11 is $\chi _{F}=-1$. In the case of $\chi _{F} = +1$ the fitted value for $\kappa _U$ at the 3$\sigma$ level is in the range [0.6, 1.18] and the branching fraction for $t\rightarrow ch , cH$ are less than $10^{-3}$, while $Br(t\rightarrow cA)$ slightly exceeds the $10^{-3}$ level. Similarly, for $\chi _{F} = -1$ the fitted value for $\kappa _U$ at the 3$\sigma$ level is in the range [0.85, 1.25] and the branching fraction for $t\rightarrow ch , cH, cA$ are the same size as in the previous case.

7 Conclusions

For studying the constraints of the 8 TeV LHC experimental data, we perform a $\chi$-square analysis to find the most favorable regions for the free parameters in the two-Higgs-doublet models. For comparison, we focus on the type-II and type-III models, in which the latter model not only affects the flavor conserving Yukawa couplings but also generates the scalar-mediated flavor-changing neutral currents at the tree level.

Although the difference between type-II and type-III is the Yukawa sector, however, since the new Yukawa couplings in type-III are associated with $\cos (\beta -\alpha )$ and $\sin (\beta -\alpha )$, the modified couplings tth and $btH^{\pm }$ will change the constraint of the free parameters.

In order to represent the influence of modified Yukawa couplings, we show the allowed values of $\sin \alpha$ and $\tan \beta$ in Fig. 2, where the LHC updated data for $pp\rightarrow h \rightarrow f$ with $f=\gamma \gamma$, $WW^*/ZZ^*$ and $\tau ^+\tau ^-$ are applied and other bounds are also included. By the results, we see that $\sin \alpha$ and $\tan \beta$ in type-III get an even stronger constraint if the dictated parameter $\chi _F = -1$ is adopted; on the contrary, if we take $\chi _F=+1$, the allowed values for $\sin \alpha$ and $\tan \beta$ are wider. It has been pointed out that there exist Yukawa couplings to down-type quarks of the wrong sign in the type-II model, i.e. $\sin \alpha >0$ or $\kappa _D <0$. By the study, we find that except that the allowed regions of parameters are shrunk slightly, the situation in $\chi _F=-1$ is similar to the type-II case. In $\chi _F=+1$, although the $\kappa _D <0$ is not excluded completely yet, the case has a strict limit by current data. We show the analyses in Figs. 4 and 5. In these figures, one can also see the correlations with a modified Higgs coupling to the top quark, $\kappa _U$, and to the gauge boson, $\kappa _V$.

When the parameters are bounded by the observed channels, we show the influence on the unobserved channel $h\rightarrow Z\gamma$ by using the scaling factor $\kappa _{Z\gamma }$, which is defined by the ratio of the decay rate to the SM prediction. We find that the change of $\kappa _{Z\gamma }$ in type-III with $\chi _F=-1$ is less than $10~\%$; however, with $\chi _F=+1$, the value of $\kappa _{Z\gamma }$ could be lower from the SM prediction by over $10~\%$. We also show our predictions for the signal strengths $\mu _{\gamma \gamma }$ and $\mu _{\gamma Z}$ and their correlation at 13 TeV.

The main difference between type-II and -III model is that the flavor-changing neutral currents in the former are only induced by loops, while in the latter they could occur at the tree level. We study the scalar-mediated $t\rightarrow c (h, H, A)$ decays in the type-III model and find that when all current experimental constraints are considered, $Br(t\rightarrow c(h, H) )< 10^{-3}$ for $m_h=125.36$ and $m_H=150$ GeV, and $Br(t\rightarrow cA)$ slightly exceeds $10^{-3}$ for $m_A =130$ GeV. The detailed numerical analyses are shown in Figs. 9, 10, and 11.