Exploring the low $\tan \beta$ region of two Higgs doublet models at the LHC

Abstract

Current interpretations of the LHC results on two Higgs doublet models (2HDM) underestimate the sensitivity due to neglecting higher order effects. In this work, we revisit the impact of these effects using the current cross-section times branching ratio limits of the $A\rightarrow hZ, H \rightarrow VV$ and $H\rightarrow hh$ channels. With a degenerate heavy Higgs mass $m_\varPhi$, we find that the LHC searches gain sensitivity to the small $\tan \beta$ region after including loop corrections, even close to $\cos (\beta -\alpha )=0$ which is not reachable at tree level for all types of 2HDM. For a benchmark point with $m_\varPhi =300$ GeV, $\tan \beta <1.8(1.2)$ can be probed for the Type-I(II) 2HDM model for $\cos (\beta -\alpha )=0$. When the deviation from $\cos (\beta -\alpha )=0$ is larger, the region for which current searches have exclusion potential becomes larger.

1 Introduction and motivation

The discovery of a Standard Model (SM)-like Higgs boson at the Large Hadron Collider (LHC) [1, 2] strongly informs LHC searches for physics beyond-the-SM (BSM), especially for an expanded Higgs sector. Motivations for an extension of the SM arise from both theoretical and observational considerations [3].

Two Higgs doublet models (2HDMs) are well motivated scenarios that provide the simplest generalization of the SM Higgs sector [4]. After electroweak symmetry breaking (EWSB), the general 2HDM will generate 5 mass eigenstates, a pair of charged Higgs boson $H^\pm$, one CP-odd Higgs boson A and two CP-even Higgs bosons, h, H. Here we take the lighter h as the observed SM-like Higgs. The spectrum can be studied through direct heavy Higgs searches at hadron colliders, or indirect, precision measurements of the couplings of the SM-like Higgs bosons at the LHC or future lepton colliders [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Direct search signals are a fruitful area of study because of the interesting variety of heavy Higgs decay channels $H/H^\pm /A \rightarrow f{\bar{f}}^{'}, VV^{'}, Vh, hh$. There are also some exotic decay channels such as $A/H \rightarrow H/A Z$ [21,22,23]. So far, the assessments of the null results at the LHC searching for heavy Higgs include only the tree-level heavy Higgs couplings, under the assumption that electroweak higher-order corrections are not important for the interpretation of the current LHC datasets for the heavy Higgs searches. However, this neglects the fact that, in some special regions, loop corrections can play a key role. For example, in the $A\rightarrow Zh,\ H\rightarrow VV$, and $H\rightarrow hh$ channels, the tree-level couplings are proportional to $\cos (\beta -\alpha )$. They therefore vanish in the “alignment limit” of $\cos (\beta -\alpha )=0$ and, as a result, give no constraint around the $\cos (\beta -\alpha )=0$ region [7,8,9, 11, 24,25,26,27,28]. Loop corrections change this picture substantially, however, and we will find below that with a combination of these channels the region around $\cos (\beta -\alpha )=0$ is no longer unreachable. Our study shows that the searches in these channels are sensitive to small $\tan \beta$ values even for $\cos (\beta -\alpha )=0$ which is unconstrained at tree level, and we present the updated limits on the parameters of two Higgs doublet models for degenerate heavy Higgs masses. The study shows that the small $\tan \beta$ region can be strongly constrained for all four types of 2HDM, where the experimental limits are applicable.

The paper is structured as follows. In Sect. 2, we give a brief introduction to 2HDMs, summarizing the experimental and theoretical results for the four decay channels described above, with the detailed formulae at one-loop level given in Appendix A. We present our individual channel analyses as well as the combined results in Sect. 3. Finally we give our main conclusions in Sect. 4.

2 Two Higgs doublet models

2.1 2HDM Higgs sector

For the general CP-conserving 2HDM, there are two $\mathrm{SU}(2)_L$ scalar doublets $\varPhi _i\ (i=1,2)$ with hyper-charge $Y=+1/2$,

$$\begin{aligned} \varPhi _{i}=\begin{pmatrix} \phi _i^{+} \\ (v_i+\phi ^{0}_i+iG_i)/\sqrt{2} \end{pmatrix}\,. \end{aligned}$$

(1)

where $v_i$ are the vacuum expectation values (vev) of the two doublets after EWSB with $v_1^2+v_2^2 = v^2 = (246\ \mathrm{GeV})^2$ and $\tan \beta \equiv v_2/v_1$.

The Higgs sector Lagrangian of the 2HDM can be written as

$$\begin{aligned} {\mathcal {L}}=\sum _i |D_{\mu } \varPhi _i|^2 - V(\varPhi _1, \varPhi _2) + {\mathcal {L}}_\mathrm{Yuk}\,, \end{aligned}$$

(2)

with a Higgs potential of

$$\begin{aligned} V(\varPhi _1, \varPhi _2)&= m_{11}^2\varPhi _1^\dag \varPhi _1 + m_{22}^2\varPhi _2^\dag \varPhi _2 -m_{12}^2 \nonumber \\&\times (\varPhi _1^\dag \varPhi _2+ h.c.) + \frac{\lambda _1}{2}(\varPhi _1^\dag \varPhi _1)^2\nonumber \\&+ \frac{\lambda _2}{2}(\varPhi _2^\dag \varPhi _2)^2 + \lambda _3(\varPhi _1^\dag \varPhi _1)(\varPhi _2^\dag \varPhi _2)\nonumber \\&+\lambda _4(\varPhi _1^\dag \varPhi _2)(\varPhi _2^\dag \varPhi _1)+\frac{\lambda _5}{2} \Big [ (\varPhi _1^\dag \varPhi _2)^2 + h.c.\Big ]\,, \end{aligned}$$

(3)

where we have assumed CP conservation, and a soft ${\mathbb {Z}}_2$¹ symmetry breaking term $m_{12}^2$.

After EWSB, three Goldstone bosons become the longitudinal component of the SM gauge bosons Z, $W^\pm$, providing their masses. The remaining physical mass eigenstates are h, H, A and $H^\pm$. The usual eight parameters appearing in the Higgs potential are $m_{11}^2$, $m_{22}^2$, $m_{12}^2$, $\lambda _{1,2,3,4,5}$, and can be transformed to a more convenient choice of the mass parameters: v, $\tan \beta$, $\alpha$, $m_h$, $m_H$, $m_A$, $m_{H^\pm }$, $m_{12}^2$, where $\alpha$ is the rotation angle diagonalizing the CP-even Higgs mass matrix.

${\mathcal {L}}_\mathrm{Yuk}$ in the Lagrangian represents the Yukawa interactions of the two doublets. To avoid tree-level flavor-changing neutral currents (FCNC), all fermions with the same quantum numbers are made to couple to the same doublet [29, 30]. By assigning different doublets to different fermions, in general, there are four possible types of Yukawa coupling: Type-I, Type-II, Type-LS (Lepton specific), and Type-FL (Flipped). In this work, the most relevant Yukawa couplings are bottom coupling $y_b$ and top coupling $y_t$, which matter for the $A\rightarrow Zh$ with $h\rightarrow b{\bar{b}}$ process and constitute the dominant loop corrections. Thus we will focus on the Type-I and Type-II 2HDMs. The situation in the Type-LS and Type-FL 2HDMs would be similar:

$$\begin{aligned} \kappa _b&\equiv \frac{y_{b}^\mathrm{2HDM}}{y_{b}^\mathrm{SM}}={\left\{ \begin{array}{ll} \frac{c_\alpha }{s_\beta } &{}\quad \text {Type-I, LS}\\ -\frac{s_\alpha }{c_\beta } &{}\quad \text {Type-II, FL} \end{array}\right. },\nonumber \\ \kappa _t&\equiv \frac{y_t^\mathrm{2HDM}}{y_t^\mathrm{SM}} = {\left\{ \begin{array}{ll} \frac{c_\alpha }{s_\beta } &{}\quad \text {Type-I, LS}\\ \frac{c_\alpha }{s_\beta } &{}\quad \text {Type-II, FL}. \end{array}\right. } \end{aligned}$$

(4)

Here we take $c_x = \cos x$ and $s_x= \sin x$.

2.2 Current constraints

Heavy Higgs loop corrections would involve the Higgs masses, same as various theoretical considerations and experimental measurements, such as vacuum stability, perturbativity and unitarity, as well as electroweak precision measurements. Here are the current status about 2HDM.

• Vacuum stability  In order to have a stable vacuum, the following conditions on the quartic couplings need to be satisfied [31]:

  $$\begin{aligned}&\lambda _1>0, \quad \lambda _2>0,\quad \lambda _3> -\sqrt{\lambda _1\lambda _2},\nonumber \\&\lambda _3+\lambda _4-|\lambda _5|> -\sqrt{\lambda _1\lambda _2}\,. \end{aligned}$$

  (5)

• Perturbativity and unitarity  We adopt a general perturbativity condition of $|\lambda _i| \le 4\pi$ and the tree-level unitarity of the scattering matrix in the 2HDM scalar sector [32]. When taking $m_H=m_A$ or $m_H=m_{H^\pm }$ in our study , these theoretical constraints are meet automatically.

• Higgs precision measurements  The allowed 95% C.L. regions for four types of 2HDMs under the current LHC limit [33] in $\cos (\beta -\alpha )$-$\tan \beta$ are shown in Fig. 2, using the $\varDelta \chi ^2$ statistic with the number of d.o.f$=2$ for the two fitting parameters $\tan \beta$ and $\cos (\beta -\alpha )$,

  $$\begin{aligned} \chi ^2=\sum _i\frac{(\mu _i^\mathrm{{BSM}}-\mu _i^\mathrm{{obs}})^2}{\sigma _{\mu _i}^2}\,, \end{aligned}$$

  (6)

  where $\mu _i^\mathrm{{2HDM}}=(\sigma \times \text {Br}_i)_\mathrm{{2HDM}}/(\sigma \times \text {Br}_i)_\mathrm{{SM}}$ is the signal strength for various Higgs search channels, $\sigma _{\mu _i}$ is the estimated error for each process [33].

For the theoretical constraints, we firstly show its allowed region in the plane of $\lambda v^2 - \tan \beta$, with degenerate heavy Higgs mass, as the blue shaded region in the Fig. 1. Here we define $\lambda v^2=m_H^2-\frac{m_{12}^2}{\sin \beta \cos \beta }$. Our studies confirm that, under $\lambda v^2=m_H^2-\frac{m_{12}^2}{\sin \beta \cos \beta } = 0$ and $\cos (\beta -\alpha )=0$, there is no constraints on $\tan \beta$ [19, 34], which is independent of heavy Higgs masses.

Fig. 1

Allowed regions by and theoretical constraints in the $\lambda v^2$-$\tan \beta$ plane

In Fig. 2, we show the allowed region by Higgs precision measurements at LHC run-II [33]. The 95% C.L. results of Type-I and II are indicated by green regions in the left and right panel respectively, and we also show the theoretical constraints represented by blue region.

Fig. 2

Allowed regions by SM-like Higgs precision measurements (green) and theoretical constraints (blue) in the $\cos (\beta -\alpha )$-$\tan \beta$ plane. The left is for the Type-I and right for the Type-II 2HDM respectively

In our study, we focus on the small $\tan \beta$ regions with tiny region around $\cos (\beta -\alpha )=0$ through the neutral heavy Higgs decays. As shown at Figs. 1 and 2, both the theoretical constraints and Higgs precision measurements at current LHC Run-II can not explore our study region.

Flavor physics consideration usually constrains the charged Higgs mass to be larger than about 600 GeV for the Type-II 2HDM [35]. However, the charged Higgs contributions to various flavor observables could be canceled by other new particles in a specific model [19, 36] and be relaxed consequently. We thus will not pursue the bounds on charged Higgs further.

2.3 Heavy Higgs decay channels

The heavy Higgs decay channels we are interested in and the corresponding tree-level couplings are

$$\begin{aligned} \mathbf{A\rightarrow Zh} g_{AhZ}&= \frac{m_Z}{v}c_{\beta -\alpha }(p_A^\mu - p_h^\mu ) ,\end{aligned}$$

(7)

$$\begin{aligned} \mathbf{H\rightarrow ZZ} g_{HZZ}&= \frac{2m_Z^2}{v}c_{\beta -\alpha } , \end{aligned}$$

(8)

$$\begin{aligned} \mathbf{H\rightarrow WW} g_{HWW}&= \frac{2m_W^2}{v}c_{\beta -\alpha }, \end{aligned}$$

(9)

$$\begin{aligned} \mathbf{H\rightarrow hh} g_{Hhh}&= -\frac{c_{\beta -\alpha }}{4s_{2\beta }v}\Bigg (\frac{4m_{12}^2}{s_\beta c_\beta }(3s_\alpha c_\alpha -s_\beta c_\beta )\nonumber \\&\quad -2(2m_h^2+m_H^2)s_{2\alpha }\Bigg ). \end{aligned}$$

(10)

At the tree-level, all of these couplings vanish in the alignment limit where $c_{\beta -\alpha } = 0$. As a consequence, all are currently thought to be irrelevant for constraining 2HDMs in the tree-level alignment limit.

However, at one-loop level, the definition of the alignment limit will shift channel-by-channel from the previous definition $c_{\beta -\alpha } = 0$. For $c_{\beta -\alpha } = 0$ and $m_{H} = m_{A} = m_{H^\pm } = \sqrt{(m_{12}^2/s_\beta c_\beta )}\equiv m_{\phi }$, the one-loop coupling expressions for the relevant vertices can be simplified and given by

$$\begin{aligned} C_{hAZ}&\approx \frac{3e^3(p_h^\mu -p_A^\mu )}{64\pi ^2s_W^3c_Wm_W^2}\sum _{f=t,b}\xi _fm_f^2\times \Big (\mathcal {PV}_1\Big ),\end{aligned}$$

(11)

$$\begin{aligned} C_{HWW}&\approx \frac{3e^3}{32\pi ^2s_W^3m_W}\sum _{f=t,b}\xi _fm_f^2 \nonumber \\&\quad \times \left( {g^{\mu \nu }\Big (\mathcal {PV}_2\Big )} + {\frac{p_1^\mu p_2^\nu }{m_W^2}\Big (\mathcal {PV}_3\Big )}\right) , \end{aligned}$$

(12)

$$\begin{aligned} C_{HZZ}&\approx \frac{3e^3g^{\mu \nu }}{8\pi ^2s_W^3c_W^2m_W}\sum _{f=t,b}\xi _fm_f^2\left( \left( \left( c_L^f\right) ^2+\left( c_R^f\right) ^2\right) \right. \nonumber \\&\quad \left. \times \left( {g^{\mu \nu }\Big (\mathcal {PV}_4\Big )} + {\frac{p_1^\mu p_2^\nu }{m_Z^2}\Big (\mathcal {PV}_5\Big )}\right) \right. \nonumber \\&\quad \left. +c_L^fc_R^f\times \left( {g^{\mu \nu }\Big (\mathcal {PV}_6\Big )} + {\frac{p_1^\mu p_2^\nu }{m_Z^2}\Big (\mathcal {PV}_7\Big )}\right) \right) ,\end{aligned}$$

(13)

$$\begin{aligned} C_{Hhh}&\approx \frac{3e^3}{32\pi ^2s_W^3m_W^3}\sum _{f=t,b}\xi _fm_f^2\times \Big (\mathcal {PV}_8\Big ), \end{aligned}$$

(14)

where $\xi _t = \cot \beta$ for both the Type-I and Type-II models, while $\xi _b = \cot \beta$ for the Type-I model and $\xi _b = -\tan \beta$ for the Type-II model. $c_L^f=I_f - Q_f s_W^2$ and $c_R^f=-Q_f s_W^2$ are the couplings between fermions and the Z-boson. $(\mathcal {PV}_i)$ represents some combination of Passarino-Veltman functions [37] which only depends on the masses. The full expressions in this limit can be found in A.

In the tree-level alignment limit, the dominant contributions to the above couplings come from the fermion (top and/or bottom) loop. Thus, all of these couplings are related to the Yukawa coupling modifier $\xi _f$. In both the Type-I and Type-II models, $\xi _t = \cot \beta$ which will be significantly enhanced in the low $\tan \beta$ region. Together with the large value of $m_t$, the unexplored region around $c_{\beta -\alpha }=0$ at low $\tan \beta$ can thus be probed by these channels.

We calculated the complete expressions for the amplitudes for all decay channels (ff, VV, SV and SS) of all scalars ($h, H, A, H^\pm$) using FeynArts [38] and FormCalc [39, 40], using the 2HDM model files including full 1-loop counter terms and renormalization conditions. All renormalization constants are determined using the on-shell renormalization scheme, except $m_{12}^2$ which is renormalized by $\overline{\mathrm{MS}}$ using the triple higgs vertex [41]. Note that, for the SVV type couplings, we also include the Lorentz structure $p_1^\mu p_2^\nu /m_V^2$ in the calculation which does not appear in the tree-level calculation. The $\epsilon _{\mu \nu \rho \sigma }$ structure which represents a CP-odd interaction between the scalar and vector bosons can be safely ignored in our calculation, since for the CP-even scalar H, the presence of such structure indicates CP violation which can only come from the CP phase in the CKM matrix in the CP conserving 2HDM. All of these NLO amplitudes are then implemented in 2HDMC [42] to fully determine the branching fractions of different channels and the total width of each particle.

Fig. 3

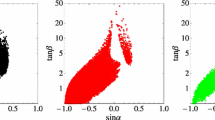
Regions in the $\cos (\beta -\alpha )$-$\tan \beta$ plane excluded by experimental results in the $A\rightarrow Zh$ channel in the Type-I (left panel) and Type-II (right panel) 2HDM. We have assumed degenerate heavy Higgs masses of 300 GeV. The dashed lines in the figures reproduce the tree-level constraints, while the green and red regions are one-loop level results. The green ones are assumed to be excluded by the b-associated production channel, whilst the red regions show the excluded regions by the gluon-fusion production channel. The blue backgrounds represent the points with $\varGamma _A/m_A > 10\%$ or $\varGamma _H/m_H > 10\%$ at one-loop level, which is covered by red and green regions at small $\tan \beta$ region. The blue regions are exactly same to them at Fig. 4

2.4 Heavy Higgs search results at LHC Run-II

A variety of searches for heavy Higgs bosons have been conducted by the ATLAS and CMS collaboration. Here we use the published cross-section times branching ratio limits to directly constrain the 2HDM parameter space, with the SusHi package [43, 44] for the production cross-section at NNLO level, and our own improved 2HDMC code, which adds loop-level effects to the public 2HDMC code [42], for the branching ratios.² For each Higgs production and decay process of interest, there exist both ATLAS and CMS public results, and these are non-trivial to apply in practice due to the assumption of a particular width in the presentation of the final results. Since we are not modelling a continuous likelihood, we do not combine these results but, instead, take the most constraining, or the limit with the widest region of applicability from the perspective of the Higgs boson widths. For points where the heavy Higgs decay widths are larger than those assumed for the derivation of the published limits, we use the largest available $\varGamma _H/m_H$ limit, but overlay plots with a region of applicability to indicate the need for caution in our reinterpretations (a device borrowed from experimental reports such as Fig. 7 of [24]). The analyses that we consider include the following:

• 1. $\mathbf{A}\rightarrow \mathbf{Zh}$: Both the ATLAS [11] and CMS [24] collaborations have presented results with $h\rightarrow b{\bar{b}}$. Here we choose the ATLAS report for reinterpretation, due to the clear statement of decay width $\varGamma _A/m_A \le 10\%$, and it includes both b-associated and gluon fusion production modes.

• 2. $\mathbf{H} \rightarrow \mathbf{ZZ}$: We choose the CMS report [9] for reinterpretation rather than the ATLAS report [8, 25], since it has a clear $\varGamma _H/m_H$ table with an upper limit of $\varGamma _H/m_H=$30%. The report uses all the heavy Higgs production modes at CMS.

• 3. $\mathbf{H} \rightarrow \mathbf{WW}$: We use the ATLAS results [7] rather than the CMS [26] results, since the ATLAS collaboration has published limits on $\sigma \times \mathrm Br$ in terms of different $\varGamma _H/m_H$ assumptions (the narrow width approximation which assumes $\varGamma _H/m_H=$2%, 5%, 10% and 15%). This ATLAS report only consider the gluon fusion production mode for heavy Higgs.

• 4. $\mathbf{H}\rightarrow \mathbf{hh}$: We use the ATLAS [27] results which have a detailed description of the $\varGamma _H/m_H$ assumptions. The results involve a combination of the SM-like Higgs decay channel results, combining $b{\bar{b}} \gamma \gamma$, $b{\bar{b}}b{\bar{b}}$, and $b{\bar{b}} \tau ^+\tau ^-$ for $\varGamma _H/m_H \le 2\%$; $b{\bar{b}}b{\bar{b}}$ and $b{\bar{b}} \tau ^+\tau ^-$ for $2\% \ge \varGamma _H/m_H \le 5\%$; and $b{\bar{b}}$ and $\tau ^+\tau ^-$ for $5\% \le \varGamma _H/m_H \le 10\%$. As in the $H\rightarrow ZZ$ case, the heavy Higgs production here is assumed to include all modes. In the report, the cross section times branching ratio limits are estimated based on the assumption that all SM-like Higgs couplings, except for the triple Higgs coupling itself $g_{hhh}$, are the same as those expected in the SM. We use the acceptance and efficiency information given and then rescale to get the cross section times branching ratio limits for the 2HDM where the SM-like Higgs couplings can depart from their SM values. The CMS results can be found in [28].

Fig. 4

Regions in the $\cos (\beta -\alpha )$-$\tan \beta$ plane excluded by experimental results in the $H \rightarrow VV$ channel, with assumed degenerate heavy Higgs masses of 300 GeV. The red dashed lines in the figures represent the tree-level constrained regions, while the red shadow regions are excluded by the one-loop-level results. In the case of diboson decay, the four types are exactly the same at tree-level and the loop effects do not differ significantly for different types. Here the left panel is for the Type-I 2HDM $H \rightarrow ZZ$ channel and the right is for the Type-II $H\rightarrow WW$ channel. The blue backgrounds represent the regions where $\varGamma _A/m_A > 10\%$ or $\varGamma _H/m_H > 10\%$ at one-loop level

3 Results

To build intuition for the full impact of the one-loop corrections to heavy Higgs decays, we first provide a detailed comparison of the tree-level and one-loop-level results for each channel separately in the $\cos (\beta -\alpha )- \tan \beta$ plane.

3.1 The $A\rightarrow Zh (h \rightarrow b{\bar{b}})$ channel

In  Fig. 3, the constrained parameter space is shown in the $\cos (\beta -\alpha )- \tan \beta$ plane, with the benchmark point $m_A=m_H=m_{H^\pm } = 300 \,\text {GeV}$, $m_{H}^2=m_ {12}^2/(s_\beta c_\beta )$ . The left panel is for the Type-I 2HDM and the right one is for the Type-II. The results are shown separately for the b-associated and gluon fusion production modes, as the green and red shadow regions respectively. In the figures the tree-level results are shown with dashed lines. For the Type-I 2HDM, the effects of the limits within the region of applicability can exclude the $\tan \beta < 8$ region, except for two bands. The central band around $\cos (\beta -\alpha )=0$ has a small tree-level AhZ coupling as in Eq. (7) and the lower left curve band has a small hbb coupling. The green and red regions represent the one-loop level results excluded by the b-associated production and gluon-fusion production channel respectively. We display the regions of $\varGamma _A/m_A >0.1$ or $\varGamma _H/m_H >0.1$ with light blue backgrounds. Generally $\tan \beta <8$ is also strongly constrained, but the loop-level effects shift the the allowed region around $\cos (\beta -\alpha )=0$ in the small $\tan \beta$ region. The $0.2< \tan \beta <2$ allowed region is shifted to the right whilst the $\tan \beta <0.2$ region is shifted to left. For the Type-II 2HDM, the shifted allowed region at small $\tan \beta$ is similar to that seen in the Type-I scenario. The allowed band for $\cos (\beta -\alpha )>0.3$ arises because the hbb coupling becomes small in that region. Meanwhile the constraints in large $\tan \beta$ region are quite different because of the effect of the hbb Yukawa couplings, which affect the b-associated production cross-section.

Fig. 5

Study of the impact of measurements in the $H \rightarrow hh$ channel in the $\cos (\beta -\alpha )$-$\tan \beta$, with degenerate heavy Higgs masses of 300 GeV. As before the dashed red lines in the figure show results based on tree-level calculations, and the excluded region at loop level are red. The left plot is for the Type-I 2HDM and the right for Type-II. Here the Higgs production modes include both gluon fusion and b-associated production, and the latter provides the main difference between the two model types. The blue backgrounds represent the points with $\varGamma _A/m_A > 10\%$ or $\varGamma _H/m_H > 10\%$ at one-loop level

3.2 The $H \rightarrow VV$ channel

As shown in Eqs.  (8), and (9), the tree-level HVV couplings are only proportional to $\cos (\beta -\alpha )$, and they are therefore independent of the 2HDM model type. At one-loop level, the couplings will become type-dependent through fermion corrections. However, the main difference comes from the production which is similar to the $A\rightarrow hZ$ case. Hence, we will only show the results for one type and briefly comment on the difference after that.

In Fig. 4, we show the constrained parameter space in the $\cos (\beta -\alpha )- \tan \beta$ plane for the Type-I 2HDM $H \rightarrow ZZ$ channel (left panel), and for the Type-II $H\rightarrow WW$ channel (right panel), with the benchmark point $m_A=m_H=m_{H^\pm } = 300 \,\text {GeV}$, $m_{12}^2/(s_\beta c_\beta )=m_H^2$. For the tree-level results shown with dashed red lines, in the region the limits are applicable, $\tan \beta <2(1)$ is strongly constrained for the Type-I and Type-II 2HDMs except for the central band around the $\cos (\beta -\alpha )=0$ region. At the one-loop level, the excluded regions represented by red shadow are largely separated into two parts. For the $H\rightarrow ZZ$ channel, one excluded part is at $0.3< \tan \beta<5, \cos (\beta -\alpha )<0$ and the other one has $\tan \beta <2$ around $\cos (\beta -\alpha )=0$. For the Type-II $H\rightarrow WW$ scenario, one is around $\tan \beta =1$ with $\cos (\beta -\alpha )<0$ and the other one has $\tan \beta <0.2$ around $\cos (\beta -\alpha )=0$. The large deviations from the tree-level results in the low $\tan \beta$ region are mainly from the influence of the large triple scalar couplings which give rise to large corrections through Higgs field renormalization as well as the large branching ratio of $H\rightarrow hh$. Similar to Fig. 3, the regions of $\varGamma _A/m_A >0.1$ or $\varGamma _H/m_H >0.1$ are displayed with light blue backgrounds.

The large $\tan \beta$ region is less constrained because the production cross-sections of the heavy Higgs bosons are much smaller. For the $H \rightarrow ZZ$ channel, the report from CMS [9] includes both gluon fusion and b-associated production. As a result, the different types of exclusion limit for the HZZ channel are different at large $\tan \beta$ to the case of the $A\rightarrow Zh$ channel. On the other hand, results are only reported for gluon-fusion production in the case of the HWW channel. Hence the results are quite similar for the different model types. We also note the small red region at large $\tan \beta$, which comes from the noncontinuous cross section times branching ratio limits in that region.

3.3 The $H \rightarrow hh$ channel

As shown in Eq. (10), the Hhh couplings at tree-level are type-independent. At one-loop level, though, the correction is type-dependent. The main differences between types come from the production mode as in previous cases. At large $\tan \beta$, b-associated production makes a big difference for different types.

The results for the $H\rightarrow hh$ channel are shown in Fig. 5, where the left panel is for Type-I and the right panel is for Type-II, with the dashed red lines for tree-level results and red regions for loop-level results. Here the benchmark point is still $m_A=m_H=m_{H^\pm } = 300 \,\text {GeV}$, $m_{12}^2/(s_\beta c_\beta )=m_H^2$. For both of the Yukawa types, there are two allowed regions. One is the region around $\cos (\beta -\alpha )=0$, and the other one is the band starting from $\tan \beta =1.5, \cos (\beta -\alpha )=-1$ to $\tan \beta =0.01, \cos (\beta -\alpha )=0$. The main feature here is that, in the parameter space where reports limits are applicable (non-blue region), there is nearly no allowed region, especially for $\tan <0.3$, at one-loop level, which is still allowed at tree-level.

3.4 Loop effects summary

Our individual analyses of the channels $A\rightarrow hZ, H\rightarrow VV/hh$ have revealed that loop effects can contribute greatly in some regions, especially the small $\tan \beta$ region. Now we display the combined results with the same benchmark point $m_A=m_H=m_{H^\pm } = 300\,\,\text {GeV}$, $m_{12}^2/(s_\beta c_\beta )=m_H^2$.

Fig. 6

Combined study in the $\cos (\beta -\alpha )$-$\tan \beta$ plane, with assumed degenerate heavy Higgs masses of 300 GeV. The dashed lines represent tree-level results and the red represent loop-level constrained regions. The left (right) is for Type-I (Type-II) 2HDM. The blue background represent the points with $\varGamma _A/m_A > 10\%$ or $\varGamma _H/m_H > 10\%$ at one-loop level

In Fig. 6, the combined results are shown in the $\cos (\beta -\alpha )$-$\tan \beta$ plane. In the Type-I 2HDM scenario (left panel), the allowed region is generally around $\cos (\beta -\alpha )=0$. At tree-level, considering the parameter space where the reported limits are applicable, the allowed regions are $\tan \beta >8, |\cos (\beta -\alpha )|<0.6$, $\tan \beta<8, |\cos (\beta -\alpha )|<0.02$ and smaller $\tan \beta$ with smaller $|\cos (\beta -\alpha )|$. At one-loop level, for the non-blue region, the allowed region at $\tan \beta >1.8$ is similar, while the small $\tan \beta$ region is totally excluded, even if $\cos (\beta -\alpha )=0$. The Type-II 2HDM results are displayed in the right panel. The main differences occur at $\cos (\beta -\alpha )>0.3$. At the one-loop level, the region $\tan \beta <1.2$ around $\cos (\beta -\alpha )=0$ is totally excluded except for the blue region. We keep in mind that the blue regions are not currently detectable because of the large heavy Higgs boson decay width in that region.

Further, the combined results are also shown in the $m_\varPhi - \tan \beta$ plane in Fig. 7. Here we take $m_{H}^2=m_{12}^2/(s_\beta c_\beta )$ and $\cos (\beta -\alpha )=0, \pm 0.01$ as the benchmark parameters. We find that the Type-I and Type-LS models have quite similar results because of their similar hbb coupling, shown in the left panel. For the red line with $\cos (\beta -\alpha )=0$, with current published limits the region $m_\varPhi < 2 m_t$ GeV for $\tan \beta <0.5$ can be constrained, and the sensitivity can be extended up to $\tan \beta \sim 3$ with lower masses except for the grey region where the decay width is too large and limits are not applicable any more. When $\cos (\beta -\alpha )$ deviates from exactly 0, such as $\pm 0.01$ (shown by the blue and green lines), we can see that the constraints in the small $\tan \beta$ region become stronger than those for $\cos (\beta -\alpha )=0$. In the right panel, we show the Type-II and Type-FL cases which have similar results. The exclusion limits are also similar to the Type-I and Type LS models, except for the moderately reduced constraints on $\tan \beta$.

With these combined exclusion regions shown in the $\cos (\beta -\alpha )-\tan \beta$ and $m_\varPhi - \tan \beta$ planes, we find that loop effects in the considered channels are important in the small $\tan \beta$ region, especially for the $\cos (\beta -\alpha )=0$ region which is excluded by a loop-level analysis except for the space where the limits are not applicable, while the tree-level analysis has no sensitivity. We also find that, even though the loop corrections are usually type-dependent, the difference between loop- and tree-level results becomes relatively type-independent.

Fig. 7

Study in the $m_\phi$-$\tan \beta$ plane. Here we choose the benchmark parameter $\cos (\beta -\alpha )=$ 0 (red line), 0.01 (blue line) − 0.01 (green line). The left is for the Type-I, LS 2HDM and right for the Type-II, F 2HDM. The grey background represents the points with $\varGamma _A$ or $\varGamma _H$ larger than the values described in Sect. 2.4, with three black lines for $\varGamma _A$ = 10%, 20%, and 30%

4 Conclusions

Studies of extensions of the Higgs sector of the SM are a promising way to try and address various theoretical and experimental questions following the discovery of the SM-like Higgs boson. In the framework of 2HDMs, we have interpreted current LHC experimental limits on the cross section times branching ratio of the $A\rightarrow Zh, H\rightarrow VV$ and $H \rightarrow hh$ channels at the one-loop level. In previous studies, the limits were reported at tree-level, with no limit for the region around $\cos (\beta -\alpha )=0$ because the couplings are proportional to the parameter $\cos (\beta -\alpha )$. At one-loop level, however, we have shown that these results are modified considerably.

Our results for individual channels were displayed in Figs. 3, 4 and 5 in the $\cos (\beta -\alpha )- \tan \beta$ plane, which showed that loop effects can contribute significantly in some regions of parameter space, especially in the small $\tan \beta$ region with $\cos (\beta -\alpha )\sim 0$. Through the combined analysis shown in Fig. 6, we find that the region around $\cos (\beta -\alpha )=0$ with degenerate heavy Higgs masses $m_\varPhi$ is detectable using these channels. Except for the regions of parameter space where current limits are not applicable due to large decay width, $\tan \beta <1.8(1.2)$ can be excluded for the Type-I(II) models, for a benchmark point with $m_\varPhi =300$ GeV. The combined results in the $m_\varPhi - \tan \beta$ plane were also shown in Fig. 7. Generally the sensitive region is $\tan \beta <4$. For $\cos (\beta -\alpha )=0, \pm 0.01$, the sensitive region has $m_\varPhi$ values up to 350 GeV. For large $m_\varPhi$, the $t{\bar{t}}$ decay channel opens, resulting in large heavy Higgs decay widths, and the current reported limits are no longer applicable. Our study also shows that the improvement of the sensitivity through loop corrections is approximately type-independent.

Appendix A: Coupling formula

The more detailed equations of Eqs. (11)–(14) for $m_H=m_A=m_{H^\pm }=\sqrt{m_{12}^2/(s_\beta c_\beta )}\equiv m_\phi$ and $\cos (\beta -\alpha )=0$ are listed in the following:

(A.1)

(A.2)

(A.3)

(A.4)

where $\xi _t = \cot \beta$ for both the Type-I and Type-II models, while $\xi _b = \cot \beta$ for the Type-I model and $\xi _b = -\tan \beta$ for the Type-II model. ${\tilde{f}}$ is the SU(2) partner of f. $B_i^{f_1f_2f_3}\equiv B_i(m_{f_1}^2,m_{f_2}^2,m_{f_3}^2)$, $C_i^{f_1f_2f_3f_4}\equiv C_i(m_{f_1}^2,m_{f_2}^2,m_{f_3}^2,m_{f_4}^2,$$m_{f_4}^2,m_{f_4}^2)$ and $C_i^{f_1f_2f_3f_4f_5f_6}\equiv C_i(m_{f_1}^2,m_{f_2}^2,m_{f_3}^2,m_{f_4}^2,m_{f_5}^2,$$m_{f_6}^2)$ are the Passarino-Veltman scalar function [37] in the convention of LoopTools [39]. $c_L^f=I_f - Q_f s_W^2$ and $c_R^f=-Q_f s_W^2$.