1 Introduction

The theory of polytropes has a significant role to play in studying the inner structure of astrophysical compact objects (CO) very precisely. In Newtonian gravity, various useful physical phenomena have been addressed with polytropic equations of state (EoSs). Chandrasekhar [1] presented the basic theory of Newtonian polytropes emerging through the laws of thermodynamics for polytropic spheres. Tooper [2, 3] provided the basic formalism of polytropes for a compressible fluid under the assumption of quasi-static equilibrium. He extended his work for an adiabatic fluid sphere and provided the fundamental framework to derive the Lane–Emden equation (LEe) for relativistic polytropes. Kovetz [4] redefined some anomalies in the theory of slowly rotating polytropes presented by Chandrasekhar [1]. Abramowicz [5] extended the general form of the LEe for spherical, planar, and cylindrical polytropes for higher dimensional spaces.

In general relativity (GR), polytropes have been discussed by many researchers by means of the LEe which can be derived from the hydrostatic equilibrium configuration of the CO. Cosenza et al. [6] presented a heuristic procedure to construct anisotropic models in GR. Herrera and Santos [7] provided a comprehensive study to discuss the possible causes for the existence of local anisotropy in self-gravitating systems both in the Newtonian and the relativistic regime. Herrera and Barreto [8] investigated relativistic polytropes under the assumption of a post-quasi-static regime and presented a new way to describe various physical variables like pressure, mass, and energy density by means of effective variables. They considered two possible configurations of polytropes in the framework of GR and found that only one was physically viable. Anisotropy plays a very vital role in the theory of GR applied to a discussion of spherical CO. Herrera et al. [9] developed a full set of governing equations for spherically symmetric dissipative fluids with anisotropic stresses to study self-gravitating systems in the framework of GR. Herrera and Barreto [10, 11] used the Tolman mass (measure of active gravitational mass) to find the stability of both Newtonian and relativistic polytropes with an anisotropic inner matter configuration. Herrera et al. [12] analyzed in detail anisotropic polytropes with a conformally flat condition, which was useful in reducing the parameters involved in a relativistic modified LEe. Recently, Herrera et al. [13] discussed the stability of anisotropic polytropes by means of cracking.

The presence of charge on the stars is an important physical ingredient in studying the dynamics of astrophysical objects. To discuss the effect of charge on CO is always of great value in GR. Bekenstein [14] introduced the idea of hydrostatic equilibrium to observe gravitational collapse in charged CO. Bonnor [15, 16] observed that electric repulsion can delay the gravitational collapse in spherically symmetric CO. Bondi has [17] provided a detailed explanation of the contraction in isotropic radiating CO with the help of Minkowski coordinates. Koppar et al. [18] provided a new technique to derive a charge generalization of a known static fluid solution for spherical symmetry. Ray et al. [19] examined the high density CO, which can hold an amount of charge of approximately \( 10^{20}\) coulomb. Herrera et al. [20] analyzed charged dissipative spherical fluids. The physical meaning of structure scalars is analyzed for charged dissipative spherical fluids and for neutral dust in the presence of a cosmological constant. Takisa and Maharaj [21] studied the models of charged polytropic spherical symmetries. Sharif and Sadiq [22] presented a general formalism to study the effects of charge on anisotropic polytropes and developed a modified LEe. Azam et al. [23–26] analyzed different charged CO models to formulate their stability in the scenario of linear and quadratic regimes. It is found that the stability of these objects depends on the electromagnetic field as well as the choice of EoS.

In the development of the CO models the selection of the EoS is a very crucial issue. A polytropic EoS, \(P_r=K \rho _0^{1+\frac{1}{n}}\), has been used by many researchers [5–14] for development and discussion of spherical CO. Chavanis [27] proposed the generalized polytropic EoS \(P_r=\alpha _1\rho _o+K\rho _o^{1+\frac{1}{n}}\) to discuss various cosmological aspects of the universe. He developed a model of the early universe to elaborate the transformation from a pre-radiation era to the radiation era for positive indices \(n>0\). In this continuity, he also produced models which described the late universe by considering negative indices in the case of a generalized polytropic EoS [28]. Freitas and Goncalves [29] used a generalized polytropic EoS to study primordial quantum fluctuations and build a universe with constant density at the origin. In this work, we will use a generalized polytropic EoS to discuss the theory of Newtonian polytropes and relativistic charged polytropes.

The plan of this paper is as follows. In Sect. 2, we shall provide the basics of the Einstein–Maxwell field equation and the hydrostatic equilibrium equation. In Sect. 3, Newtonian polytropes will be discussed and Sect. 4 is devoted to the observation of relativistic polytropes. Energy conditions and the conformally flat condition are discussed in Sect. 5. Section 6 is devoted to a stability analysis of polytropes. In the last section, we shall conclude and present our results.

2 The Einstein–Maxwell field equations

We consider a static spherically symmetric space-time

$$\begin{aligned} \mathrm{d}s^2=e^{\nu }\mathrm{d}t^{2}-e^{\lambda }\mathrm{d}r^{2}-r^2 \mathrm{d}\theta ^{2}-r^2 \sin ^2\theta {\mathrm{d}\phi ^2}, \end{aligned}$$
(1)

where \(\nu ,~\lambda \) are functions of r only. The energy-momentum tensor for an anisotropic matter distribution is given by

$$\begin{aligned} T_{i j}=(P_t+\rho ) V_{i} V_{j} -g_{i j}P_t +(P_r - P_t) S_{i} S_{j}, \end{aligned}$$
(2)

where \(P_t,~P_r\), and \(\rho \), respectively, represent the tangential pressure, the radial pressure, and the energy density of the inner fluid distribution. The four-velocity \(V_{i}\) and four-vector \(S_{i}\) satisfy the following equations:

$$\begin{aligned} V_{i} = e^{\frac{\nu }{2}} \delta ^0_i,\!\quad V^{i}V_{i} = 1,\quad S_{i} = e^{\frac{\lambda }{2}} \delta ^1_i,\quad S^{i}S_{i} =-1,\quad S^{i}V_{i} =0. \end{aligned}$$
(3)

The electromagnetic energy-momentum tensor is defined by

$$\begin{aligned} T^{(\mathrm{em})}_{ij}=\frac{1}{4\pi }\left( F_{i}^{m} F_{j m}-\frac{1}{4} F^{mn} F_{mn} g_{ij}\right) , \end{aligned}$$
(4)

where

$$\begin{aligned} F_{ij}=\psi _{j,i}-\psi _{i,j} \end{aligned}$$
(5)

is the Maxwell field tensor and it satisfies the following relations:

$$\begin{aligned} F^{ij}_{;j}=\mu _0 J^i,\quad F_{[ij;k]}=0, \end{aligned}$$
(6)

where \(\psi _i\) is the four-potential, \(\mu _0\) is the magnetic permeability, and \(J^i\) is the four-current. Also, the four-potential and four-velocity satisfy the following relations in co-moving coordinates:

$$\begin{aligned} \psi _{i}=\psi (r) \delta ^0_i,\quad J^i=\sigma V^i,\quad i=0,1,2,3, \end{aligned}$$
(7)

where \(\psi \) is the scalar potential and \(\sigma \) is the charge density. The Maxwell equation (6) yields

$$\begin{aligned} \psi ^{\prime \prime }+\Big (\frac{2}{r}-\frac{\nu ^\prime }{2} -\frac{\lambda ^\prime }{2}\Big )\psi ^\prime =4 \pi \sigma e^{\frac{\nu +\lambda }{2}}, \end{aligned}$$
(8)

where the prime \(\prime \) denotes differentiation with respect to r. From the above, we have

$$\begin{aligned} \psi ^{\prime }=\frac{q(r)}{r^2}e^{\frac{\nu +\lambda }{2}}, \end{aligned}$$
(9)

where \(q(r)=4 \pi \int _0^r \mu e^{\frac{\lambda }{2}} r^2 \mathrm{d}r \) represents the total charge inside the sphere.

The Einstein–Maxwell field equations for the line element of Eq. (1) are given by

$$\begin{aligned}&\frac{\lambda ^\prime e^{-\lambda }}{r}+\frac{(1-e^{-\lambda })}{r^2}=8\pi \rho -\frac{q^2}{r^4}, \end{aligned}$$
(10)
$$\begin{aligned}&\frac{\nu ^\prime e^{-\lambda }}{r}-\frac{(1-e^{-\lambda })}{r^2}=8\pi P_r -\frac{q^2}{r^4}, \end{aligned}$$
(11)
$$\begin{aligned}&e^{-\lambda } \bigg [\frac{\nu ^{\prime \prime }}{2}-\frac{\nu ^\prime \lambda ^\prime }{4}+\frac{\nu ^{\prime ^2}}{4}+\frac{\lambda ^\prime -\nu ^\prime }{2r}\bigg ] = 8 \pi P_t+\frac{q^2}{r^4}, \end{aligned}$$
(12)

and solving Eqs. (10)–(11) simultaneously leads to the hydrostatic equilibrium equation [22]

$$\begin{aligned} \frac{\mathrm{d} P_r}{\mathrm{d}r}-\frac{2}{r}\Big (\Delta +\frac{q q\prime }{8\pi r^3}\Big )+\frac{(4\pi r^4 P_r-q^2+m r)}{r(r^2-2mr+q^2)}=0, \end{aligned}$$
(13)

where we have used \(\Delta =(P_t-P_r)\).

The junction conditions are commonly used to relate inner and outer regions of the CO over a boundary surface. The choice of the outer geometry totally relies on the inner fluid distribution of the CO. For spherical symmetry, if the matter in the interior of a star is charged and anisotropic, we take the Reissner–Nordsträm space-time as the exterior geometry,

$$\begin{aligned} \mathrm{d}s^2= & {} \Big (1-\frac{2M}{r}+\frac{Q^2}{r^2}\Big )\mathrm{d}t^2- \Big (1-\frac{2M}{r}+\frac{Q^2}{r^2}\Big )^{-1}\mathrm{d}r^2\nonumber \\&-r^2 \mathrm{d}\theta ^{2}-r^2 \sin ^2\theta {\mathrm{d}\phi ^2}. \end{aligned}$$
(14)

Junction conditions play a very significant role in the study of the CO. These conditions determine whether the combination of two space-time metrics provides a physically viable solution or not when a hyper-surface divides the space-time into interior and exterior regions. The smooth matching of interior and exterior regions through the first and second fundamental forms [30–33] yields the following relations on the boundary surface:

$$\begin{aligned} e^{\nu }= & {} e^{-\lambda }=\Big (1-\frac{2M}{r}+\frac{Q^2}{r^2}\Big ),\quad m(r)=M,\quad q(r)=Q,\quad \nonumber \\&P_r=0, \end{aligned}$$
(15)

and the Misner–Sharp mass leads to [34, 35]

$$\begin{aligned} m(r)=\frac{r}{2}\left( 1-e^{-\lambda }+\frac{q^2}{r^2}\right) . \end{aligned}$$
(16)

In spherical symmetry the Misner–Sharp mass can be described as a measure of the total energy within a sphere of a radius r at a time t. The theory of polytropes is based on the assumption of hydrostatic equilibrium and polytropic EoS. In this work, we discuss Newtonian and relativistic polytropes by using a generalized polytropic EoS, which is a combination of linear and polytropic EoSs.

3 Newtonian Polytrope

In the framework of Newtonian gravity, the polytropic EoSs are very useful in describing a huge variety of situations like inner pressure, types of inner fluid distribution etc. In this section, we formulate Newtonian polytropes through a hydrostatic equilibrium equation in the scenario of a generalized polytropic equation of state. Polytropes are supposed to be in hydrostatic equilibrium; we have to keep in mind that the appearance of cracking occurs when the system is taken out of equilibrium. We consider the following basic equations [8]:

$$\begin{aligned} \frac{\mathrm{d} P_r}{\mathrm{d}r}=-\frac{\mathrm{d}\phi }{\mathrm{d}r}\rho _o, \end{aligned}$$
(17)

and in spherical coordinates the Poisson equation is given by

$$\begin{aligned} \frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d}r}\Big (r^2 \frac{\mathrm{d} \phi }{\mathrm{d}r}\Big )=4\pi \rho _o, \end{aligned}$$
(18)

here \(\rho _o\) is the mass density and \(\phi \) is taken to be the Newtonian gravitational potential. Equations (17)–(18), along with the generalized polytropic EoS [27, 28]

$$\begin{aligned} P_r=\alpha _1\rho _o+K\rho _o^{\gamma }=\alpha _1\rho _o+ K\rho _o^{1+\frac{1}{n}}, \end{aligned}$$
(19)

lead to a modified LEe (for \( \gamma \ne 1\)). Here K is the polytropic constant and n is the polytropic index. We take

$$\begin{aligned} \rho _o=\rho _{gc}\theta ^n(r), \end{aligned}$$
(20)

where \(\rho _{gc}\) is the density evaluated at center c, and using Eqs. (19)–(20) in (17), we get

$$\begin{aligned} \frac{n\alpha _1 \theta ^\prime }{\theta }+(n+1)K\rho _{gc}\theta ^\prime =-\frac{\mathrm{d}\phi }{\mathrm{d}r}. \end{aligned}$$
(21)

From Eqs. (18), (20), and (21), we obtain

$$\begin{aligned} -A^2_3\left( \frac{r}{A_2}\right) ^{-2}\frac{\mathrm{d}}{\mathrm{d}r} \left( \frac{r^2 \theta ^\prime }{\theta }\right) -\left( \frac{r}{A_2}\right) ^{-2}\frac{\mathrm{d}}{\mathrm{d}r} \left( r^2 \theta ^\prime \right) =\theta ^n, \end{aligned}$$
(22)

where \(A^2_2\) and \( A^2_3\) are given by

$$\begin{aligned} A^2_2 = \frac{4\pi \rho _{gc}^{1-\frac{1}{n}}}{K(n+1)},\quad A^2_3 = \frac{Kn(n+1)\alpha _1}{16 \pi ^2 \rho _{gc}^{2-\frac{1}{n}}}. \end{aligned}$$
(23)

Inserting \(\xi =\frac{r}{A_2}\) in the above equation, we obtain the modified form of the LEe,

$$\begin{aligned} \Big (\frac{A^2_3+\theta }{\theta }\Big )\frac{\mathrm{d}^2 \theta }{\mathrm{d} \xi ^2}+\frac{2}{\xi }\Big (\frac{A^2_3+\theta }{\theta }\Big )\frac{\mathrm{d} \theta }{\mathrm{d} \xi }-\Big (\frac{A^2_3}{\theta ^2}\Big )\Big (\frac{\mathrm{d} \theta }{\mathrm{d} \xi }\Big )^2+\theta ^n=0, \end{aligned}$$
(24)

with the boundary conditions

$$\begin{aligned} \frac{\mathrm{d} \theta }{\mathrm{d} \xi }(\xi =0)=0,\quad \theta (\xi =0)=1. \end{aligned}$$
(25)

The boundary of the sphere is defined by \(\xi =\xi _n\), such that \(\theta (\xi _n)=0\).

4 The relativistic polytropes

This section deals with the relativistic configuration of polytropes with generalized EoS. The generalized polytropic EoS is the linear combination of the linear EoS ‘\(P_r=\alpha _1\rho _o \)’ and the polytropic EoS ‘\(P_r=K\rho _o^{1+\frac{1}{n}}\)’. The linear EoS describes pressureless \((\alpha _1=0)\) or radiation \((\alpha _1=\frac{1}{3})\) matter. The polytropic part describes the cosmology of the early universe for positive values of the polytropic index, whereas it elaborates the late time universe with negative values of the polytropic index [27, 28]. In order to discuss the cosmic behavior, \(\rho _o\) was taken to be the Planck density, but for relativistic discussion we will consider it as the mass density and total energy density in case 1 and case 2, respectively. Here, we shall present the general formalism for relativistic polytropes with generalized polytropic EoS and investigate the presence of charge in the following two cases.

4.1 Case 1

Here, we consider the generalized polytropic EoS as

$$\begin{aligned} P_r=\alpha _1\rho _o+K\rho _o^{\gamma }=\alpha _1\rho _o+K\rho _o^{1+\frac{1}{n}}, \end{aligned}$$
(26)

so that the original polytropic part remains conserved; also the mass density \(\rho _o\) is related to the total energy density \(\rho \) by [12]

$$\begin{aligned} \rho =\rho _{o}+n P_r. \end{aligned}$$
(27)

Now making the assumptions

$$\begin{aligned}&\alpha =\frac{P_{\mathrm{rc}}}{\rho _{\mathrm{gc}}},\quad \alpha _2 =1+(n+1)(\alpha _1+\alpha \theta ),\quad \alpha _3 =(n+1)\alpha ,\nonumber \\&\alpha _4=\frac{4\pi P_{\mathrm{rc}} q^2}{\alpha \alpha _3},\quad r=\frac{\xi }{A},\quad \rho _{o}=\rho _{\mathrm{gc}}\theta ^n,\nonumber \\&m(r) =\frac{4\pi \rho _{\mathrm{gc}} v({\xi })}{A^3},\quad A^2= \frac{4\pi \rho _{\mathrm{gc}}}{(n+1)\alpha }, \end{aligned}$$
(28)

where \(P_{\mathrm{rc}}\) is the pressure at center of the star, \(\rho _{\mathrm{gc}}\) is the mass density evaluated at the center of the CO, \(\xi \), \(\theta \) and v are dimensionless variables. Using the above assumptions along with the EoS (26), the hydrostatic equilibrium equation Eq. (13) implies

$$\begin{aligned}&\Big (1-2\alpha _3 \frac{v(\xi )}{\xi }+\frac{\alpha _4}{\xi ^2} \Big )\nonumber \\&\,\,\times \left( \frac{n\alpha _1 \theta ^{-1} +\alpha _3}{\alpha _2\alpha _3} \xi ^2 \frac{\mathrm{d}\theta }{\mathrm{d}\xi } -2\frac{\alpha ^2\alpha ^2_3\xi ^3\Delta +2\pi P^2_{\mathrm{rc}} q \frac{\mathrm{d} q}{\mathrm{d}\xi }}{\alpha \alpha _2 \alpha _3^3 P_{\mathrm{rc}}\xi ^2}\theta ^{-n}\right) \nonumber \\&\quad - \frac{\alpha _4}{\alpha _3 \xi }+v(\xi )+(\alpha _1+\alpha \theta )\xi ^3\theta ^n=0. \end{aligned}$$
(29)

Now differentiating Eq. (16) with respect to r and using the assumptions given in Eq. (28), we get

$$\begin{aligned} \frac{\mathrm{d}v(\xi )}{\mathrm{d}\xi }=\xi ^2\theta ^n(1+n\alpha _1+n\alpha \theta ) -\frac{\alpha _4}{\alpha _3\xi ^2}+\frac{\alpha _4}{\alpha _3 \xi q}\frac{\mathrm{d} q}{\mathrm{d}\xi }. \end{aligned}$$
(30)

Thus Eq. (29) coupled with Eq. (30) yields a modified LEe [see the appendix, Eq. (53)] which describes the relativistic polytropes in the presence of charge q with a generalized polytropic EoS.

4.2 Case 2

Here, we consider the generalized polytropic EoS

$$\begin{aligned} P_r=\alpha _1\rho +K\rho ^{1+\frac{1}{n}}, \end{aligned}$$
(31)

where the mass density \(\rho _o\) is replaced by the total energy density \(\rho \) in Eq. (26), and they are related to each other by [12]

$$\begin{aligned} \rho =\frac{\rho _o}{\big (1-K \rho _o^{\frac{1}{n}}\big )^n}. \end{aligned}$$
(32)

We make the following assumptions:

$$\begin{aligned} \alpha =\frac{P_{\mathrm{rc}}}{\rho _{c}},\quad \alpha _5=1+\alpha _1+\alpha \theta , \end{aligned}$$
$$\begin{aligned} r=\frac{\xi }{A},\quad \rho _{o}=\rho _{c}\theta ^n,\quad m(r) =\frac{4\pi \rho _{c} v({\xi })}{A^3},\quad A^2=\frac{4\pi \rho _{c}}{(n+1)\alpha }, \end{aligned}$$
(33)

where c represents the quantity at the center of the star, \(\alpha _2\), \(\alpha _3\), and \(\alpha _4\) obey the same relations as in Eq. (28) with \(\alpha \) defined in Eq. (33). Using the above assumptions along with the EoS (31), the hydrostatic equilibrium equation (13) becomes

$$\begin{aligned}&\Big (1-2\alpha _3 \frac{v(\xi )}{\xi }+\frac{\alpha _4}{\xi ^2} \Big )\nonumber \\&\,\,\times \left( \frac{n\alpha _1 \theta ^{-1} +\alpha _3}{\alpha _3\alpha _5} \xi ^2 \frac{\mathrm{d}\theta }{\mathrm{d}\xi }-2\frac{\alpha ^2\alpha ^2_3\xi ^3\Delta +2\pi P^2_{\mathrm{rc}} q \frac{\mathrm{d} q}{\mathrm{d}\xi }}{\alpha \alpha _3^3 \alpha _5 P_{\mathrm{rc}}\xi ^2}\theta ^{-n}\right) \nonumber \\&\quad - \frac{\alpha _4}{\alpha _3 \xi }+v(\xi )+(\alpha _1+\alpha \theta )\xi ^3\theta ^n=0. \end{aligned}$$
(34)

Now differentiating Eq. (16) with respect to r and using the assumptions given in Eq. (33), we get

$$\begin{aligned} \frac{\mathrm{d}v(\xi )}{\mathrm{d}\xi }=\xi ^2\theta ^n-\frac{\alpha _4}{\alpha _3 \xi ^2}+\frac{\alpha _4}{\alpha _3 \xi q}\frac{\mathrm{d} q}{\mathrm{d}\xi }. \end{aligned}$$
(35)

Equation (34) coupled with Eq. (35) gives the modified LEe [see the appendix, Eq. (54)] representing the relativistic polytropes in the presence of a charge q with a generalized polytropic EoS.

5 Energy conditions and conformally flat condition

The energy conditions in GR are designed to obtain maximum possible information without enforcing a particular EoS. The energy conditions are provided in the sense that energy density cannot be negative because if it allows for random \(+\mathrm{ve}\) and \(-\mathrm{ve}\) energy regions, the empty space would become unstable. The energy conditions satisfied by all the spherically symmetric models are [22, 36]

$$\begin{aligned} \rho +\frac{q^2}{8\pi r^4}>0,\quad \frac{P_{r}}{\rho } \le 1+\frac{q^2}{4\pi \rho r^4},\quad \frac{P_{t}}{\rho }\le 1. \end{aligned}$$
(36)

For case 1 the conditions given in Eq. (36) turn out to be

$$\begin{aligned}&1+n(\alpha +\alpha _1)\theta +\frac{\alpha _4 \theta ^{-n}}{2\alpha _3 \xi ^4}>0,\nonumber \\&1\le n +(\alpha _1+\alpha \theta )^{-1}+\frac{\alpha _4 \theta ^{-n}}{(\alpha _1+\alpha \theta )\alpha _3 \xi ^4}, \nonumber \\&\frac{3 v(\xi )}{\xi ^3}+\frac{2\alpha _4\frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3 q \xi ^3} +\alpha _1 \theta +\alpha \theta ^{n+1}\le \frac{4\alpha _4}{\alpha _3 \xi ^3}, \end{aligned}$$
(37)

and for case 2 the conditions given in Eq. (36) emerge as

$$\begin{aligned}&1+\frac{\alpha _4 \theta ^{-n}}{\alpha _3 \xi ^4}>0,~\alpha _1+\alpha \theta -\frac{\alpha _4 \theta ^{-n}}{\alpha _3 \xi ^4}\le 1,\nonumber \\&\frac{3 v(\xi )}{\xi ^3} +\frac{2\alpha _4\frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3 q \xi ^3} +\alpha _1 +\alpha \theta ^{n+1}\le \frac{4\alpha _4}{\alpha _3 \xi ^4}. \end{aligned}$$
(38)

We observe that the coupled equations (29)–(30) and Eqs. (34)–(35) form a system of differential equations. These systems involve three variables and we want some additional information to study a polytropic CO. We use the conformally flat condition to reduce one variable in the above said system of equations. The electric part of the Weyl tensor is related to the Weyl scalar given by [12, 22]

$$\begin{aligned} W=\frac{r^3 e^{-\lambda }}{6}\Bigg (\frac{e^\lambda }{r^2} +\frac{\lambda ^\prime \nu ^\prime }{4} -\frac{1}{r^2} -\frac{\nu ^{\prime 2}}{4}- \frac{\nu ^{\prime \prime }}{2}-\frac{\lambda ^\prime \nu ^\prime }{2 r}\Bigg ). \end{aligned}$$
(39)

Now using the conformally flat condition, i.e., \(W=0\), along with the field equations, Eqs. (10)–(11), in Eq. (39), we get

$$\begin{aligned} \Delta =P_t-P_r=\frac{e^{-\lambda }}{4\pi }\Bigg (\frac{e^{\lambda }}{r^2} -\frac{\lambda ^\prime }{2r} -\frac{1}{r^2}\Bigg )-\frac{q^2}{4 \pi r^4}. \end{aligned}$$
(40)

The above equation along with Eqs. (28) and (30) for case 1 yields

$$\begin{aligned} \Delta =\rho _{\mathrm{gc}}\left( (1+n\alpha _1+n\alpha \theta ) \theta ^n+3\frac{v(\xi )}{\xi ^3} -4\frac{\alpha _4}{\alpha _3 \xi ^4}+2 \frac{\alpha _4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3 q \xi ^3}\right) . \end{aligned}$$
(41)

Similarly, the anisotropy parameter for case 2 turns out to be

$$\begin{aligned} \Delta =\rho _{c}\left( \theta ^n+3\frac{v(\xi )}{\xi ^3} -4\frac{\alpha _4}{\alpha _3 \xi ^4}+2\frac{\alpha _4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3 q \xi ^3}\right) . \end{aligned}$$
(42)

Using Eqs. (41) in (29), we obtain the first equation of a coupled differential system corresponding to case 1,

$$\begin{aligned}&\left( 1-2\alpha _3 \frac{v(\xi )}{\xi ^2} +\frac{\alpha _4}{\xi ^2} \right) \left( \frac{n\alpha _1 \theta ^{-1}+\alpha _3}{\alpha _2\alpha _3} \xi ^2 \frac{\mathrm{d}\theta }{\mathrm{d}\xi } \right. \nonumber \\&\quad \left. -\frac{2\xi }{\alpha _2\alpha _3} (1+n\alpha _1+n \alpha \theta )\right. \nonumber \\&\quad \left. +\left( -\frac{6\alpha v(\xi )}{\alpha _2\alpha _3 P_{\mathrm{rc}}\xi ^2} +\frac{8\alpha \alpha _4}{\alpha _2\alpha _3^2 P_{\mathrm{rc}} \xi ^3} -\frac{4\alpha \alpha _4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _2\alpha _3^2} +\frac{4\pi P^2_{\mathrm{rc}} q \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha \alpha _2\alpha _3^3 \xi ^2}\right) \theta ^{-n}\right) \nonumber \\&\quad -\frac{\alpha _4}{\alpha _3 \xi }+v(\xi )+(\alpha _1+\alpha \theta )\xi ^3\theta ^n=0. \end{aligned}$$
(43)

The above equation coupled with Eq. (30) provides a modified LEe [see the appendix, Eq. (55)] which describes the conformally flat polytropes for case 1.

In the same way, for case 2, using Eqs. (41) in (34), we obtain

$$\begin{aligned}&\left( 1-2\alpha _3 \frac{v(\xi )}{\xi }+\frac{\alpha _4}{\xi ^2} \right) \left( \frac{n\alpha _1 \theta ^{-1}+\alpha _3}{\alpha _3\alpha _5} \xi ^2 \frac{\mathrm{d}\theta }{\mathrm{d}\xi }-\frac{2\xi }{\alpha _3\alpha _5}\right. \nonumber \\&\quad \left. +\left( -\frac{6 v(\xi )}{\alpha _3\alpha _5 P_{\mathrm{rc}}\xi ^2}+\frac{8\alpha _4}{\alpha _3\alpha _5 P_{\mathrm{rc}} \xi ^3}\right. \right. \nonumber \\&\quad \left. \left. -\frac{4\alpha _4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3^2\alpha _5q \xi ^2} -\frac{4\pi P_{\mathrm{rc}} q \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha \alpha _3^3 \xi ^2}\right) \theta ^{-n}\right) \nonumber \\&\quad -\frac{\alpha _4}{\alpha _3 \xi }+v(\xi )+(\alpha _1+\alpha \theta )\xi ^3\theta ^n=0. \end{aligned}$$
(44)

The above equation coupled with Eq. (35) leads to a modified LEe [see the appendix, Eq. (56)] for conformally flat polytropes (case 2).

6 Stability analysis

The stability of the model can be discussed by means of the Tolman mass, which measures the active gravitational mass of the CO. The important feature of the Tolman mass is that it can be evaluated by integrating over the region occupied by matter or electromagnetic energy [37–39]. The modified form of the Tolman mass for an anisotropic spherically symmetric metric (1) is given by [22]

$$\begin{aligned} m_T=M\frac{r_\Sigma ^3}{r^3}+r^3 \int _r^{r_\Sigma } e^{(\lambda +\nu )/2} \left( \frac{2}{\tilde{r}^4}W-\frac{4\pi \Delta }{\tilde{r}}+\frac{q^2}{16\tilde{r}^5} \right) \mathrm{d}\tilde{r},\nonumber \\ \end{aligned}$$
(45)

where \(\Sigma \) represents the values calculated at the boundary of the CO. In order to get an expression for \(\nu \), we will solve the Einstein–Maxwell field equations (10)–(11) simultaneously; we have

$$\begin{aligned} \frac{\nu ^\prime }{2}=\frac{(4\pi r^4 P_r-q^2+m r)}{r(r^2-2mr+q^2)}. \end{aligned}$$
(46)

The integration of the above equation yields

$$\begin{aligned} \nu =\nu _{\Sigma }-\int _r^{r_\Sigma }2 \frac{(4\pi r^4 P_r-q^2+m r)}{r(r^2-2mr+q^2)}\mathrm{d}r. \end{aligned}$$
(47)

We define the dimensionless variables by

$$\begin{aligned} x=\frac{r}{r_\Sigma }=\frac{\xi }{\tilde{A}},\quad \tilde{A}=A r_\Sigma ,\quad y=\frac{M}{r_\Sigma },\quad \tilde{m}=\frac{m}{M}. \end{aligned}$$
(48)

For case 1, using Eqs. (28), (46), and (48) in (45), we get

$$\begin{aligned} \frac{m_T}{M}= & {} x^3+ \frac{(n+1)\alpha x^3 \tilde{A}^2}{4 \pi y}\int _x^1 \left( \frac{1-2y+Q^2/r_\Sigma ^2}{1-2(n+1)\alpha v/x\tilde{A}+q^2/x^2 r_\Sigma ^2}\right) ^{1/2}\nonumber \\&\times \, \mathrm{exp}\left( \int _x^1 -\frac{4\pi (\alpha _1+\alpha \theta ) \theta ^{n} x^4 r_\Sigma ^4-q^2(n+1)\alpha v x r_\Sigma ^2/\tilde{A}}{r_\Sigma ^3 x^4 -2(n+1) \alpha v r_\Sigma ^4 x^3 /\tilde{A}+ q^2 r_\Sigma ^2 x}\right) \mathrm{d}x\nonumber \\&\times \,\left( \frac{-4\pi \Omega }{x r_\Sigma }+\frac{q^2}{16 x^5 r_\Sigma \rho _{\mathrm{gc}}}\right) \mathrm{d}x, \end{aligned}$$
(49)

where \(y=\frac{(n+1)\alpha \nu _\Sigma }{\xi _\Sigma }\) and \(\Omega \) is given by

$$\begin{aligned} \Omega =\frac{\Delta }{\rho _{\mathrm{gc}}}= & {} \left( (1+n\alpha _1+n\alpha \theta ) \theta ^n+3\frac{v(\xi )}{\xi ^3}-4\frac{\alpha _4}{\alpha _3 \xi ^4}\right. \nonumber \\&\left. +\,2\frac{\alpha _4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3 q \xi ^3}\right) . \end{aligned}$$
(50)

For case 2, inserting Eqs. (33), (46), and (48) in (45), we obtain

$$\begin{aligned} \frac{m_T}{M}= & {} x^3+ \frac{(n+1)\alpha x^3 \tilde{A}^2}{4 \pi y}\int _x^1 \left( \frac{1-2y+Q^2/r_\Sigma ^2}{1-2(n+1)\alpha v/x\tilde{A}+q^2/x^2 r_\Sigma ^2}\right) ^{1/2}\nonumber \\&\times \, \mathrm{exp}\left( \int _x^1 -\frac{4\pi (\alpha _1+\alpha \theta )\theta ^{n} x^4 r_\Sigma ^4-q^2(n+1)\alpha v x r_\Sigma ^2/\tilde{A}}{r_\Sigma ^3 x^4 -2(n+1) \alpha v r_\Sigma ^4 x^3 /\tilde{A}+ q^2 r_\Sigma ^2 x}\right) \mathrm{d}x\nonumber \\&\times \, \left( \frac{-4\pi \Omega }{x r_\Sigma }+\frac{q^2}{16 x^5 r_\Sigma \rho _{c}}\right) \mathrm{d}x \end{aligned}$$
(51)

and \(\Omega \) is given by

$$\begin{aligned} \Omega =\frac{\Delta }{\rho _{\mathrm{gc}}}=\left( \theta ^n+3\frac{v(\xi )}{\xi ^3}-4\frac{\alpha _4}{\alpha _3 \xi ^4}+2\frac{\alpha _4 \frac{\mathrm{d} q}{\mathrm{d} \xi }}{\alpha _3 q \xi ^3}\right) . \end{aligned}$$
(52)
Fig. 1
figure 1

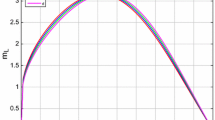
Case 1: \(\frac{m_T}{M}\) as a function of x for \(n=1\), curve a: \(\alpha =8\times 10^{-11}\),  y = 0.3991, Q \(=\) 0.2 \(M_\odot \), curve b: \(\alpha =10^{-10}\),  y = 0.4091, Q = 0.4 \(M_\odot \), curve c: \(\alpha =2 \times 10^{-10}\),  y = 0.3998, Q = 0.6 \(M_\odot \), curve d: \(\alpha =4 \times 10^{-10}\),  y = 0.3858, Q = 0.64 \(M_\odot \)

Full size image
Fig. 2
figure 2

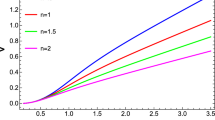
Case 1: \(\frac{v}{\nu _\Sigma }\) as a function of x for \(n=1\), curve a: \(\alpha =8\times 10^{-11}\),  y = 0.3991, Q \(=\) 0.2 \(M_\odot \), curve b: \(\alpha =10^{-10}\),  y = 0.4091, Q = 0.4 \(M_\odot \), curve c: \(\alpha =2 \times 10^{-10}\),  y = 0.3998, Q = 0.6 \(M_\odot \), curve d: \(\alpha =4 \times 10^{-10}\),  y = 0.3858, Q = 0.64 \(M_\odot \)

Full size image
Fig. 3
figure 3

Case 1: \(\Omega \) as a function of x for \(n=1\), curve a: \(\alpha =8\times 10^{-11}\),  y = 0.3991, Q = 0.2 \(M_\odot \), curve b: \(\alpha =10^{-10}\),  y = 0.4091, Q = 0.4 \(M_\odot \), curve c: \(\alpha =2 \times 10^{-10}\),  y = 0.3998, Q = 0.6 \(M_\odot \)

Full size image

In order to study the physical viability of these models, we have calculated the Tolman mass whose behavior describes some physical features of these models, particularly the stability of the model. Figures 1, 2 and 3 have been plotted for case 1 (relativistic polytropes) corresponding to different parametric values n, \(\alpha \), y, Q, and \(\alpha _1=0.5\) [12, 22]. Figure 1 shows that the Tolman mass is gradually decreasing and does not show any abnormal behavior as the value of \(\alpha \) and charge Q increases. The curves become steeper with higher values of \(\alpha \) and charge Q, but they remain positive, which is consistent with the results of Herrera et al. [12] for neutral polytropes. It is noted that for smaller values of y, the sphere gets more compact, which corresponds to an equilibrium configuration. This behavior is shown by the migration of the Tolman mass toward the boundary surface. In terms of stability, it happens due to a sharper reduction of the active gravitational mass in the inner regions of the sphere, which may correspond to more stable configurations for small values of y. The smooth behavior of Fig. 2 describes the solution of Eq. (30) which shows that the stability of the model can be enhanced through decreasing the values of y. Figure 3 represents the anisotropy of the model, which is larger near the center and becomes weaker near the surface. For case 2, the model does not satisfy the energy conditions presented in Eq. (38) for various values of parameters. These results are consistent with [12, 22] for charged and neutral polytropes.

7 Conclusion and discussion

In this work, we have developed the general framework to discuss the Newtonian and relativistic polytropes with a generalized polytropic EoS in the presence of an electromagnetic field under the conformally flat condition. The generalized polytropic EoS \(P_r=\alpha _1\rho _o+K\rho _o^{1+\frac{1}{n}}\) is the union of linear and polytropic EoSs. It is widely used in cosmology to explain different eras of the universe with the help of mathematical models. In the cosmic scenario \(\rho _o\) was taken to be the Planck density but for a relativistic discussion we have taken it as a mass density and the total energy density in case 1 and case 2, respectively. In order to discuss the physical features of Newtonian and relativistic ploytropes, we have formulated the general formalism to obtain a modified LEe. The solutions of the LEe are called polytropes, which depend on the density profile function of the dimensionless radius \(\xi \) and the order of the solution is constrained by the value of the polytropic index n. The LEes are helpful to explain a relativistic CO as they produced a simple solution to describe the internal structure of the CO. But the cost of this simplicity is a power law relationship between the pressure and the density, which should be valid throughout the inner matter of the CO. The LEes have been initially developed for relativistic charged ploytropes with an anisotropic factor involved in them [see Eqs. (53) and (54)], which have three unknown variables. The conformally flat conditions are used to simplify these equations by eliminating anisotropy factor, which corresponds to a modified LEe [see Eqs. (55) and (56)], for charged polytropic spheres in the context of a generalized polytropic EoS. The energy conditions are helpful in order to check the physical viability of the CO in GR without enforcing an EoS. The energy conditions for both cases of relativistic polytropes have been developed in the presence of charge.

The stability of the relativistic polytropes is analyzed with the help of the Tolman mass. For case 1, the model behaved well as shown in Figs. 1, 2 and 3. The models developed here are anisotropic (in pressure) and helped us to discuss highly charged CO solutions. Figure 1 represents the physical behavior of the Tolman mass for different values of charge and model’s parameters [12, 22]. The Tolman mass, which is a measure of the active gravitational mass, gradually shifts toward the boundary surface but remains stable and does not present any fluctuations. Figure 1 represents the slow migration of the Tolman mass toward the boundary as the charge increases, corresponding to higher stability of the model. It is worth mentioning here that our results for the Tolman mass are considerably consistent with work of Herrera et al. [12] for polytropic EoSs.

Figure 2 describes the solution of Eq. (30), which shows that the stability of the model can be enhanced through decreasing the values of y. This figure has been plotted for the indicated values of the triplet \(n,~\alpha ,~Q\) and shows a stable behavior for small values of \(\alpha \). Also, the configurations of the solution remain stable for an increasing value of charge, although the solution curves start bending toward the boundary of the CO, as shown in Fig. 2. It is also evident that the behavior of the parameter shows dispersal in the beginning, i.e., near the center of the CO, and it becomes more consistent as we move toward the boundary with the increase of charge. So, we can say that charge is the stabilizing factor here for relativistic polytropes with generalized polytropic EoS. Thus, the discussion of charge is essential for the study and exploration of relativistic polytropic COs as regards their physical viability.

The inclusion of anisotropy plays a vital role in the study of the astrophysical CO. The inner fluid distribution is assumed to be anisotropic for a spherically symmetric CO. Figure 3 represents the graphs of \(\Omega \), which is the ratio of the anisotropy and the central mass density. The curves remain stable even after an increase of the charge but rapidly move toward the boundary of the sphere, and this phenomenon shows that the anisotropy is affected by the presence of an electromagnetic field. Hence, the presence of anisotropy with charge may lead toward gravitational collapse of the polytropic CO and can also be a source of the cracking phenomenon. The presence of cracking can be tested by means of methods provided by Herrera [40] and Gonzalez [41]. In this work, methods for the development of a generalized LEe have been presented. We observe that in case 2 polytropes are not physically viable due to a violation of the energy conditions.