1 Introduction

The present stage of accelerate expansion of the universe seems to be well established from the analysis of observational data. Besides the supernova Ia data [1–3], the data from the observation of the anisotropy of the cosmic microwave background radiation (CMB) [4, 5], the baryonic acoustic oscillations [6–11], large scale structures [12–14], weak lensing [15] and the differential age of old galaxies (H(z0) [16–21] give strong evidence for the present accelerated expansion phase. Since gravity is attractive, the cosmic acceleration expansion requires some new form of exotic matter, which leads to a violation of the strong energy condition (SEC) [22–24], as far as general relativity (GR) is considered. This exotic component is dubbed dark energy.

The most popular, and most simple, candidate for dark energy is the cosmological constant. Interpreted as a manifestation of the quantum vacuum energy, the cosmological constant faces, however, a huge discrepancy between the observed value and the predicted one. The exact value of this discrepancy depends on many details, but in general it amounts to many dozen orders of magnitude [25].

The incertitude about the dynamical origin of the observed accelerated expansion led to many speculations about possible extensions of GR in such way that the accelerated expansion could be obtained without the introduction of dark energy. In this sense, one of these possible extensions is to generalise the Einstein–Hilbert action including non-linear geometric terms. One of these proposals is the class of f(R) theories [26–30], where the non-linear terms are combinations of the Ricci scalar R. Such theories may give very good results at cosmological scales but must be complemented with a screening mechanism in order not to spoil the achievements of GR at scales of the solar system [31]. There is a long list of other possible, and generally more complex, modifications of GR [32–61].

Another problem concerning the applications of GR to concrete problems is the presence of singularities, as that predicted in the primordial universe and in the end of the life of some massive stars. The presence of such singularities seems to point to the limit of application of GR, requiring perhaps to consider quantum effects in the strong gravitational regime. Some other possibility to cure this singularity problem, yet in the context of a classical theory, is to consider as source of the gravitational equations matter fields that may lead to violation of at least some of the energy conditions. Examples are given by non-linear gauge fields, like the electromagnetic field. Non-linear electromagnetism [64] has been conceived originally to cure singularity problems in Maxwell theory. In theories of gravity, the electromagnetic field appears as one of the sources of the structure of the space-time. In such a context, some success in avoiding singularities has been obtained in implementing such an extension of the classical Maxwell field [65–88].

In Ref. [62] both proposals of extensions of the usual gravitational and gauge field theories were considered. In that paper, the emphasis was on the study of black hole configurations. A very general form of this theory, mixing the f(R) theory and the non-linear electromagnetic Lagrangian \(\mathcal {L}_\mathrm{NED}\), has been considered. A static, spherically symmetric space-time has been used. Particularly, solutions with horizon (thus, candidates to represent a black hole) were found, but without the singularity existing in the usual black hole solutions of GR. This singularity-free black hole solutions imply the violation of the SEC only in certain regions of the space-time. However, the other energy conditions are generally satisfied. We remember that the energy conditions are directly connected with the existence of singularities in GR theory [22–24].

In the present paper, we revisit the problem treated in Ref. [62], and we show that new non-singular solutions are possible. This new solutions emerge from a specific, but very appealing, choice of the mass function M(r), which will be properly defined later. The mass function we will use was constructed in Ref. [63], with GR theory coupled to a non-linear electromagnetic field, in order to satisfy some requirements, like to avoid violation of the weak energy condition (WEC) and to have the Reissner–Nordström asymptotic limit: the mass function M(r) given in Ref. [63] is the most general functional form satisfying the WEC in GR. As found for other mass functions in Ref. [62], the employment of the mass function of Ref. [63] in our general context implies that the violation of SEC occurs only in a limited region of the space-time, the other energy conditions being satisfied in the entire space-time. We will prove a new theorem for the energy conditions for f(R) gravity according to which we must recover the same conditions of GR when the same geometry is simultaneously a solution for the equations of GR and f(R) gravity.

This paper is organised as follows. In the next section, the equations of motion are written down. In Sect. 3, we determine the new non-singular solutions and analyse the fate of the energy conditions for these solutions. The final conclusions are presented in Sect. 4. In the Appendix, it is shown explicitly that the solutions found here are asymptotically regular.

2 The equations of motion in f(R) gravity

f(R) gravity is defined by the action

$$\begin{aligned} S_{f(R)}=\int \mathrm{d}^4x\sqrt{-g}\left[ f(R)+2\kappa ^2\mathcal {L}_m\right] , \end{aligned}$$
(1)

where g stands for the determinant of the metric \(g_{\mu \nu }\), f(R) is a given function of the Ricci scalar R, \(\mathcal {L}_m\) represents the Lagrangian density of the matter and other fields, and \(\kappa ^2=8\pi G/c^4\), with G and c being the Newton gravitational constant and the speed of light, respectively.

There are two main approaches for this theory, the first one supposing the dynamical fields are the metric and the matter field, known as the metric formalism, and the second one, called the Palatini formalism, for which the dynamical fields are the metric, the matter field, but with the Levi-Civita connection independent of the metric. In the following we will use the first approach.

Applying the variational principle in terms of the metric to the action (1), we find the following field equations:

$$\begin{aligned} f_RR^{\mu }_{\;\;\nu }-\frac{1}{2}\delta ^{\mu }_{\nu }f+\left( \delta ^{\mu }_{\nu } \square -g^{\mu \beta }\nabla _{\beta }\nabla _{\nu }\right) f_R=\kappa ^2\Theta ^{\mu }_{ \;\;\nu }, \end{aligned}$$
(2)

where \(f_R\!\equiv \!\mathrm{d}f(R)/\mathrm{d}R\), \(R^{\mu }_{\;\;\nu }\) is the Ricci tensor, \(\nabla _{\nu }\) stands for the covariant derivative, \(\square \equiv g_{\alpha \beta }\nabla _{\alpha }\nabla _{\beta }\) is the d’Alembertian, and \(\Theta _{\mu \nu }\) is the matter energy–momentum tensor.

In the present work, we will analyse the coupling of the f(R) gravity with a non-linear electrodynamic theory (NED), given by \(\mathcal {L}_m\equiv \mathcal {L}_\mathrm{NED}(F)\), where \(F=(1/4)F^{\mu \nu }F_{\mu \nu }\), and with \(F_{\mu \nu }\) being the Maxwell tensor, and \( \mathcal {L}_\mathrm{NED}(F)\) is an arbitrary function of F. A similar structure was exploited in Ref. [62]. We will first review the methodology employed in that reference, which will be applied in the present paper in order to find new regular black hole solutions.

Considering the NED coupling, the energy–momentum tensor for matter in (2) is given by

$$\begin{aligned}&\Theta ^{\mu }_{\;\;\nu }=\delta ^{\mu }_{\nu }\mathcal {L}_\mathrm{NED}-\frac{ \partial \mathcal {L}_\mathrm{NED}(F)}{\partial F}F^{\mu \alpha }F_{\nu \alpha }. \end{aligned}$$
(3)

In the particular case of the Maxwell Lagrangian \(\mathcal {L}_\mathrm{NED}\equiv F\), the energy–momentum tensor of the linear Maxwell electrodynamics is re-obtained.

Defining the Maxwell tensor in terms of the four-potential \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\), the variation of the functional (1) with respect to the potential can be performed, leading to the generalised Maxwell equation,

$$\begin{aligned} \nabla _{\mu }\left[ F^{\mu \nu }\mathcal {L}_F\right] \equiv \partial _{\mu }\left[ \sqrt{-g}F^{\mu \nu }\mathcal {L}_F\right] =0, \end{aligned}$$
(4)

where \(\mathcal {L}_F=\partial \mathcal {L}_\mathrm{NED}/\partial F\).

We then consider a spherically symmetric and static space-time, whose line element, in Schwarzschild coordinates, reads

$$\begin{aligned} \mathrm{d}s^2=e^{a(r)}\mathrm{d}t^2-e^{b(r)}\mathrm{d}r^2-r^2\left[ \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2\right] , \end{aligned}$$
(5)

where a(r) and b(r) are arbitrary functions of the radial coordinate r. We will consider the particular case where there is only electric field, the components connected with the magnetic field of the Maxwell tensor \(F_{\mu \nu }\) being zero. Imposing spherical symmetry, through the Killing vectors and the equation \(\mathcal {L}_{\zeta ^{\mu }}F^{\alpha \beta }(t,r,\theta ,\phi )\equiv 0\), we can show that the only non-null component of the Maxwell tensor is \(F^{10}(r)\) [89, 90]. The generalised Maxwell equation (4) for \(\nu =0\) is

$$\begin{aligned} F^{10}(r)=\frac{q}{r^2}e^{-[a(r)+b(r)]/2}\mathcal {L}_F^{-1} (r) , \end{aligned}$$
(6)

where \(q\in \mathfrak {R}\) is an integration constant representing the electric charge of the source.

The equations of motion for the f(R) gravity coupled to a NED are then found by using the line element (5), the energy–momentum (3), with the only non-null component given by (6), and the field equations (2):

$$\begin{aligned}&\frac{e^{-b}}{4r}\Big \{4r\frac{\mathrm{d}^2f_R}{\mathrm{d}r^2}+ 2\left[ 4-rb'\right] \frac{\mathrm{d}f_R}{\mathrm{d}r}\nonumber \\&\qquad +\big [ra'b'-2ra''-r(a')^2-4a'\big ]f_R+2re^bf\Big \}\nonumber \\&\quad =-\kappa ^2\left[ \mathcal {L}_\mathrm{NED}+ \frac{q^2}{r^4}\mathcal {L}_F^{-1}\right] ,\end{aligned}$$
(7)
$$\begin{aligned}&\frac{e^{-b}}{4r}\Big \{2\left[ 4+ra'\right] \frac{\mathrm{d}f_R}{\mathrm{d}r}\nonumber \\&\qquad + \left[ (4+ra')b'-2ra''-r(a')^2\right] f_R+2re^bf\Big \}\nonumber \\&\quad =-\kappa ^2\left[ \mathcal {L}_\mathrm{NED}+ \frac{q^2}{r^4}\mathcal {L}_F^{-1}\right] ,\end{aligned}$$
(8)
$$\begin{aligned}&\frac{e^{-b}}{2r^2}\Big \{2r^2\frac{\mathrm{d}^2f_R}{\mathrm{d}r^2}\nonumber \\&\quad +[r^2(a'-b')+2r] \frac{\mathrm{d}f_R}{\mathrm{d}r}+[r(b'-a')\nonumber \\&\quad +2(e^b-1)]f_R+r^2e^bf\Big \} =-\kappa ^2\mathcal {L}_\mathrm{NED} , \end{aligned}$$
(9)

where the prime (\('\)) stands for the total derivative with respect to the radial coordinate r.

In the next section, we will use an algebraic methodology to solve these equations and to obtain new regular solutions.

3 New generalisations for regular black holes on GR to f(R) gravity

We will simplify the equations of motion in such a way that a new class of solution can be determined. Subtracting Eq. (8) from Eq. (7) we have

$$\begin{aligned} \frac{e^{-b}}{2r}\left[ 2r\frac{\mathrm{d}^2f_R}{\mathrm{d}r^2}-\left( r\frac{\mathrm{d}f_R}{\mathrm{d}r}+2f_R\right) (a'+b')\right] =0\,. \end{aligned}$$
(10)

We have now a second order differential equation, with variable coefficients, given in terms of the function \(f_R\). This equation does not have an analytical solution in general and we must choose a given restriction in order to solve it. There are two obvious possibilities. The first one corresponds to choosing the quasi-global system of coordinates

$$\begin{aligned} b(r)=-a(r). \end{aligned}$$
(11)

This is an additional requirement to the metric functions since the coordinate system has already been fixed. However, the fact that the functions f(R) and \(\mathcal {L}_\mathrm{NED}\) are, for the moment, arbitrary ensures the possibility to impose such a new condition, as will be verified later. In GR, when the spherical symmetry is fixed, implying \(\Theta ^{0}_{\;\;0}\equiv \Theta ^{1}_{\;\;1}\), the identity (11) comes out directly. But, in f(R) gravity this does not happen, and an extra condition must be imposed to simplify the equations of motion.

The second choice is \(b(r)\ne -a(r)\), which does not lead to a solution of the equations of motion unless there is the relation \(b(r)=-a(r)+b_1(r)\), with \(b_1(r)\) given in such a way that an analytical solution can be determined for (10). An example is given in Ref. [93].

The determination of new solutions for the f(R) gravity, in the case with spherical symmetry, has been studied also in Refs. [94–98].

Imposing the quasi-global coordinate condition for (10), we obtain

$$\begin{aligned} e^{-b}\frac{\mathrm{d}^2f_R}{\mathrm{d}r^2}=0. \end{aligned}$$
(12)

Integrating this expression,

$$\begin{aligned} f_R(r)=c_1r+c_0, \end{aligned}$$
(13)

where the integration constants \(c_0,c_1\in \mathfrak {R}\) appear. Here, we must make the following observations. First, for the particular case \(c_1\equiv 0,c_0=1\), GR is recovered, since the integration of (13) with respect to R leads to \(f(R)=R\). Second, if the line element (5) is considered, the Ricci scalar becomes

$$\begin{aligned} R= & {} e^{-b}\left[ a''+\left( a'-b'\right) \left( \frac{a'}{2} +\frac{2}{r}\right) +\frac{ 2}{r^2} \right] -\frac{2}{r^2}\;\nonumber \\= & {} e^{a}\left[ a''+ 2a'\left( \frac{a'}{2} +\frac{2}{r}\right) +\frac{ 2}{r^2} \right] -\frac{2}{r^2}\;. \end{aligned}$$
(14)

In order to have a better description of the new regular black hole solutions, it is useful to define

$$\begin{aligned} e^{a(r)}=1-\frac{2M(r)}{r}, \end{aligned}$$
(15)

where M(r) is the mass function, which for the regular solutions satisfies the condition \(\lim _{r\rightarrow 0}[M(r)/r]\equiv 0\). The mass function M(r) must coincide with the ADM mass m in the spatial infinity limit, where the radial coordinate r goes to infinity.

Inserting (15) and (11) in (14), the curvature scalar can be rewritten as

$$\begin{aligned} R(r)=-\frac{2}{r^2}[rM''(r)+2M'(r)], \end{aligned}$$
(16)

which, for a given M(r) model, may allow one to invert Eq. (16), to obtain r(R). After integration of (13) it leads to

$$\begin{aligned} f(R)=c_0R+c_1\int r(R)\mathrm{d}R\;. \end{aligned}$$
(17)

It is also possible to obtain f(R) from the expression \(f_R=(\mathrm{d}f/\mathrm{d}r)(\mathrm{d}R/\mathrm{d}r)^{-1}\). After integration and using (16) we obtain

$$\begin{aligned} f(r)=\int f_R(r)\frac{\mathrm{d}R(r)}{\mathrm{d}r}\mathrm{d}r. \end{aligned}$$
(18)

Now, we use the methodology presented in [62] to solve the equations of motion. Taking Eqs. (11), (15), (13) and (18), we can solve Eqs. (7)–(9) to obtain \(\mathcal {L}_\mathrm{NED}\) and \(\mathcal {L}_F\) as

$$\begin{aligned}&\mathcal {L}_\mathrm{NED}=-\frac{1}{2\kappa ^2 r^2}\left[ r^2f(r) +4c_0M'(r)+2c_1r\right] ,\end{aligned}$$
(19)
$$\begin{aligned}&\mathcal {L}_F=-\kappa ^2 \frac{q^2}{r^2}\big [(c_1r+c_0)rM''(r) -(2c_0+c_1r)M'(r)\nonumber \\&\qquad -3c_1M(r)+c_1r\big ]^{-1}\;. \end{aligned}$$
(20)

The solution above satisfies the equations of motion. However, its consistency can be verified through the Lagrangian density \(\mathcal {L}_\mathrm{NED}\) and its derivative with respect to F, \(\mathcal {L}_F\). By definition, we have

$$\begin{aligned} \mathcal {L}_F=\frac{\partial \mathcal {L}_\mathrm{NED}}{\partial F}=\frac{\partial \mathcal {L}_\mathrm{NED}}{\partial r}\frac{\partial r}{\partial F}=\frac{\partial \mathcal {L}_\mathrm{NED}}{\partial r}\left( \frac{\partial F}{\partial r}\right) ^{-1}\;. \end{aligned}$$
(21)

To perform such a verification we must remember that \(F=(1/4)F^{\mu \nu }F_{\mu \nu }=-(1/2)e^{a+b}[F^{10}(r)]^2\), and that the only non-null component of the Maxwell tensor, for this symmetry, is obtained from Eqs. (11), (15) and (20), which, considering (6), leads to

$$\begin{aligned} F^{10}(r)= & {} \frac{1}{q\kappa ^2}\Big \{3c_1M(r)+(2c_0+c_1r)M'(r)\nonumber \\&-r[c_1+(c_0+c_1r)M''(r)]\Big \}\;. \end{aligned}$$
(22)

Now, using Eqs. (11), (13), (15), (16), (18)–(20) and (22), it is possible to verify that the constraint (21) is satisfied. Hence, the solution is consistent.

In order to perform an analysis of the physical properties of this class of solutions, we must take into account the energy condition relations for the f(R) theory. Following the results of Refs. [91, 92], Eq. (2) is rewritten as

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R= & {} f_R^{-1}\big [\kappa ^2\Theta _{\mu \nu } +\frac{1}{2}g_{\mu \nu }\left( f-Rf_R\right) \nonumber \\&-\left( g_{\mu \nu }\square -\nabla _{\mu }\nabla _{\nu }\right) f_R\big ]=\kappa ^{2 } \mathcal {T}_{\mu \nu }^{(\mathrm{eff})}, \end{aligned}$$
(23)

where \(\mathcal {T}^{(\mathrm{eff})}_{\mu \nu }\) is the effective energy–momentum tensor, and the perfect fluid content is identified by the relations \(\mathcal {T}^{0(\mathrm{eff})}_{0}=\rho ^{(\mathrm{eff})},\mathcal {T}^{1(\mathrm{eff})}_{1}=-p^{(\mathrm{eff})}_r,\mathcal {T}^{2(\mathrm{eff})}_{2}=\mathcal {T}^{3(\mathrm{eff})}_{3}=-p^{(\mathrm{eff})}_t\), where \(\rho ^{(\mathrm{eff})}\), \(p^{(\mathrm{eff})}_r\) and \(p^{(\mathrm{eff})}_t\) are the energy density, radial and tangential pressures, respectively. The explicit expressions for the energy–momentum tensor can be found in Ref. [62]. With these expressions, the energy conditions for the f(R) theory can be written as

$$\begin{aligned}&\mathrm{NEC}_{1,2}(r)=\rho ^{(\mathrm{eff})}+p_{r,t}^{(\mathrm{eff})}\ge 0\;,\end{aligned}$$
(24)
$$\begin{aligned}&\mathrm{SEC}(r)=\rho _{(\mathrm{eff})}+p_{r}^{(\mathrm{eff})}+2p_{t}^{(\mathrm{eff})}\ge 0\,,\end{aligned}$$
(25)
$$\begin{aligned}&\mathrm{WEC}_{1,2}(r)=\rho ^{(\mathrm{eff})}+p_{r,t}^{(\mathrm{eff})}\ge 0\;,\end{aligned}$$
(26)
$$\begin{aligned}&\mathrm{DEC}_{1}(r)=\rho ^{(\mathrm{eff})}\ge 0, \end{aligned}$$
(27)
$$\begin{aligned}&\mathrm{DEC}_{2,3}(r)=\rho ^{(\mathrm{eff})}-p_{r,t}^{(\mathrm{eff})}\ge 0\;, \end{aligned}$$
(28)

where, in view of the identity \(\mathrm{WEC}_3(r)\equiv \mathrm{DEC}_1(r)\), one of the conditions was not written.

We call to attention that the effective energy–momentum tensor in (23) is equal to the Einstein tensor, which is in the left hand side of that equation. This means that the energy conditions are related only to the type of geometry for which the solution is written, and they can be the same for two different theories as, in the present case, for GR and f(R) gravity. We can then state the following theorem.

Teorema

Given a solution of Eqs. (7)–(9) of the f(R) gravity, described by \(S_1=\{a(r),b(r),f(R),\mathcal {L}_{NED},F^{10}(r)\}\), if there exists a solution in GR \(S_2=\{a(r),b(r),\bar{\mathcal {L}}_{NED},\bar{F}^{10}(r)\}\), then the energy conditions (24)–(28) are identical for \(S_1\) and \(S_2\).

Proof

If \(S_1=\{a(r),b(r),f(R),\mathcal {L}_\mathrm{NED},F^{10}(r)\}\) is a solution of the equations of motion (7)–(9) then it can be rewritten as in (23), where we have the expression \(G_{\mu \nu }(a,b)=\kappa ^2\mathcal {T}_{\mu \nu }^{(\mathrm{eff})}\). If there exists a similar solution of GR for the geometric part, it can take the form \(G_{\mu \nu }(a,b)=\kappa ^2 T_{\mu \nu }^{GR}\). Using these identities we have the equivalence \(\mathcal {T}_{\mu \nu }^{(\mathrm{eff})}\equiv T_{\mu \nu }^{GR}\), which models the energy–momentum tensor for a perfect fluid, implying that the energy conditions must be the same for the two solutions. \(\square \)

We will verify this theorem for the new solutions we will write down later.

In the next subsection, we will use a specific model for the general mass function M(r), coming from GR, in order to obtain a generalisation of this class of solutions.

3.1 New regular black hole solutions

As it has been shown in Ref. [62], there is no model for the mass function M(r) that leads to a generalisation of a solution of GR to the f(R) gravity theory, with a function f(R) containing non-linear terms. Physically, our motivation is to generalise a given GR model where at most the SEC energy condition is the only one to be violated. Using the energy condition theorem of the previous section, we can determine the most general mass function M(r) which satisfies the WEC in f(R) gravity, as in Ref. [63]. We will use a model obtained by integration of the general mass function satisfying the WEC given by [63], which reads

$$\begin{aligned}&M(r)=\frac{6^3m^4r^3}{q^6}\frac{\Gamma ^3(4/a_1)\Gamma (b_1/a_1)}{\Gamma ^3(a_1^{-1})\Gamma [(b_1-3)/a_1]}\,_{2}\nonumber \\&\quad \times \, F_{1}\left[ \frac{3}{a_1};\frac{b_1}{a_1};\frac{a_1+3}{a_1};-\left( \frac{6\Gamma (4/a_1)}{\Gamma (a_1^{-1})\Gamma [(a_1+3)/a_1]}\frac{m}{q^2}r\right) ^{a_1}\right] , \nonumber \\ \end{aligned}$$
(29)

where \(_2F_1[k_1;k_2;k_3;z]\) is the Gauss hypergeometric function.

This model is, in general, very complicated. It is possible to express the solutions in terms of integrals, which may or may not be analytical. It is more instructive to work with some particular cases. Let us first take the case where \(a_1=2\) and \(b_1=4\), for which the metric functions (11) and (15) are given by

$$\begin{aligned} e^{a}=e^{-b}=1+\frac{32m^2q^2}{\pi ^2q^4+64m^2r^2}-\frac{4m}{\pi r}\arctan \left[ \frac{8mr}{\pi q^2}\right] .\nonumber \\ \end{aligned}$$
(30)

This solution represents a charged, regular black hole, asymptotically flat, with two horizons: \(r_H\) (an event horizon) and \(r_-\) (inner or Cauchy horizon). It is possible to verify that this solution is regular in all space-time by inspecting the Ricci and Kretschmann scalars, which read

$$\begin{aligned} R= & {} -\frac{16384m^4\pi ^2q^6}{(\pi ^2q^4+64m^2r^2)^3},\end{aligned}$$
(31)
$$\begin{aligned} \mathcal {K}= & {} R^{\alpha \beta \mu \nu }R_{\alpha \beta \mu \nu }\nonumber \\= & {} \frac{64m^2}{r^6}\Bigg \{\frac{64m^2q^4r^2}{(\pi ^2q^4+64m^2r^2)^6}\nonumber \\&\times (3\pi ^4q^8+256\pi ^2m^2q^4r^2+20480m^4r^4)\nonumber \\&\times (\pi ^4q^8+256\pi ^2m^2q^4r^2+28672m^4r^4)\nonumber \\&+\frac{1}{\pi ^2}\arctan \left( \frac{8mr}{\pi q^2}\right) \Big [3\arctan \left( \frac{8mr}{\pi q^2}\right) \nonumber \\&-\frac{16m\pi q^2r}{(\pi ^2q^4+64m^2r^2)^3}\nonumber \\&\times (3\pi ^4q^8+512m^2\pi ^2q^4r^2+36864m^4r^4)\Big ]\Bigg \}. \end{aligned}$$
(32)

These scalars are finite in all space-time. The limits in the origin of the radial coordinate and in the spatial infinity are given by \(\lim _{r\rightarrow 0}\{R,\mathcal {K}\}\,{=}\,\{-(16384m^4)/(\pi ^4q^6),(134217728m^8)/(3\pi ^8q^{12})\}\) and \(\lim _{r\rightarrow \infty }\{R,\mathcal {K}\}=\{0,0\}\).

Equation (31) implies

$$\begin{aligned} r(R)=\frac{q}{8m}\sqrt{-\pi ^2q^2+\frac{16(2\pi m^2)^{2/3}}{(-R)^{1/3}}}. \end{aligned}$$
(33)

From (31) it can be verified that \(R\le 0\), which must be taken into account in order to define correctly (33) in the usual limit \(0\le r\le +\infty \).

Now, the function f(R) can be obtained inserting (33) in (17), leading to

$$\begin{aligned}&f(R)=c_0R+\frac{c_1}{8mq^3\pi ^{8/3}}\sqrt{-\pi ^2 q^2+\frac{16(2\pi m^2)^{2/3}}{(-R)^{1/3}}}\nonumber \\&\quad \times \big [192(2m^8)^{1/3}(-R)^{1/3}+4(4\pi ^{4}m^4)^{1/3}(-R)^{2/3}-\pi ^{8/3}q^4 (-R)\big ]\nonumber \\&\quad +\frac{768c_1m^3}{\pi ^3q^4}\arctan ^{-1}\left\{ \pi q\Big [-\pi ^2q^2+\frac{16(2\pi m^2)^{2/3}}{(-R)^{1/3}}\Big ]^{-1/2}\right\} . \end{aligned}$$
(34)

We can now see clearly that the last two terms that multiply the constant \(c_1\) generalise the GR solution to f(R) gravity, including non-linear terms in the Ricci scalar R. In the particular case where \(c_1=0\), GR is recovered.

We perform now a brief analysis of the stability of this solution. Following the results of [99], a small perturbation in the Ricci scalar, \(\tilde{R}=R+\delta R(r,t)\), leads to the following equation after taking the trace of Eq. (2):

$$\begin{aligned} \left[ \frac{\partial ^2}{\partial t^2}-\mathbf {\nabla }^2\right] \delta R(r,t)=-m_R^2\delta R(r,t),\,m_R^2\sim \frac{1}{3f_{RR}}, \end{aligned}$$
(35)

where \(f_{RR}=\mathrm{d}f_R/\mathrm{d}R\). Hence, the stability condition for a static spherically symmetric configuration is given by

$$\begin{aligned} m_R^2\sim \frac{1}{3f_{RR}}>0. \end{aligned}$$
(36)

The second derivative of (34) with respect to R, leads to

$$\begin{aligned} f_{RR}=\frac{2^{2/3}(\pi m)^{1/3}q^2c_1}{3R^{4/3}q\sqrt{-\pi ^{4/3}q^2+\frac{2^{14/3}m^{4/3}}{(-R)^{1/3}}}}. \end{aligned}$$
(37)

From (36) and (37) this solution turns out to be stable for \(c_1 > 0\).

It is not possible to obtain analytically a functional relation between the scalar F and the Lagrangian density \(\mathcal {L}_\mathrm{NED}\). Hence, using (22), with (29), we obtain

$$\begin{aligned}&F^{10}(r)=\frac{1}{\pi q\kappa ^2(\pi ^2q^4+64m^2r^2)^3}\nonumber \\&\quad \times \Bigg \{-\pi r\Big [-524288c_0m^6q^2r^3+c_1\nonumber \\&\quad \times \Big (\pi ^6q^{12}+4096m^4\pi ^2q^4r^2 (2q^2+3r^2)+65536m^6r^4\nonumber \\&\quad \times (-3q^2+4r^2)+48m^2\pi ^4q^8(q^2+4r^2)\Big )\Big ]\nonumber \\&\quad +6c_1m(\pi ^2q^4+64m^2r^2)^3\arctan \left( \frac{8mr}{\pi q^2}\right) \Bigg \}. \end{aligned}$$
(38)

Now, \(\mathcal {L}_\mathrm{NED}\) can be obtained through (19):

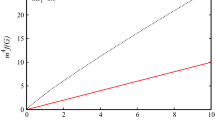
$$\begin{aligned} \mathcal {L}_\mathrm{NED}(r)= & {} -\frac{1}{\kappa ^2}\Bigg \{\frac{c_1}{r}-\frac{8192m^4\pi ^2q^6}{(\pi ^2q^4+64m^2r^2)^3}(c_0+c_1r)\nonumber \\&+\frac{2048m^4q^2}{(\pi ^2q^4+64m^2r^2)^2}(2c_0+c_1r)\nonumber \\&+\frac{3072c_1m^4r}{\pi ^2q^2(\pi ^2q^4+64m^2r^2)}\nonumber \\&+\frac{384c_1m^3}{\pi ^3q^4}\arctan \left( \frac{8mr}{\pi q^2}\right) \Bigg \}. \end{aligned}$$
(39)

It is possible to represent parametrically a graphic \(\mathcal {L}_\mathrm{NED}(F)\times F\), where \(F=(1/4)F^{\mu \nu }F_{\mu \nu }\). This behaviour is displayed in Fig. 1.

Fig. 1
figure 1

Parametric representation \(\{\mathcal {L}_\mathrm{NED},F\}\) of the solution (30), with \(q=10, m=80,c_0=1, c_1=2, \kappa ^2=8\pi \)

Full size image

The energy conditions can now be verified. Taking explicitly the effective density and pressure [62] for our particular case (30), we find the following expressions for the energy conditions:

$$\begin{aligned} \mathrm{NEC}_1(r)= & {} \mathrm{WEC}_1(r)=0, \mathrm{NEC}_2(r)=\mathrm{WEC}_2(r)\nonumber \\= & {} \frac{524288m^6q^2r^2}{\kappa ^2(\pi ^2q^4+64m^2r^2)^3},\end{aligned}$$
(40)
$$\begin{aligned} \mathrm{DEC}_1(r)= & {} \frac{1}{2}\mathrm{DEC}_2(r)=\frac{4096m^4q^2}{\kappa ^2(\pi ^2q^4+64m^2r^2)^2},\mathrm{DEC}_3(r)\nonumber \\= & {} \frac{8192m^4\pi ^2q^6}{\kappa ^2(\pi ^2q^4+64m^2r^2)^3},\end{aligned}$$
(41)
$$\begin{aligned} \mathrm{SEC}(r)= & {} \frac{8192m^4q^2[(8mr)^2-\pi ^2q^4]}{\kappa ^2(\pi ^2q^4+64m^2r^2)^3}. \end{aligned}$$
(42)

The energy conditions NEC, WEC and DEC are satisfied in all space-time. However, the SEC energy condition (42) is violated for \(r<[\pi q^2/(8m)]\), which, for the values \(m=8q,q=10\), represents a region very near the Cauchy horizon (\(\pi q^2/(8m)=0.490874,r_\mathrm{Cauchy}=0.0419174,r_{H}=159.373\)).

Let us stress the main differences between the GR solution given by the mass function (29), with \(a_1=2\) and \(b_1=4\), and our solution for f(R) gravity, obtained for the same mass function and parameters \(a_1\) and \(b_1\). The actions for these theories are completely different: while for GR the geometric part is given by \(S_{EH}=\int \mathrm{d}^4x\sqrt{-g}R\), for the solution we have determined above we have \(S_{f(R)}=\int \mathrm{d}^4x \sqrt{-g}f(R)\), with f(R) given by (34). The actions corresponding to the matter and electromagnetic components are also different: for GR the Lagrangian density behaves asymptotically as the Reissner–Nordström case; for our case we do not have such a restriction.

Let us show a second analytical example for the general mass (29). For the values \(a_1=3\) and \(b_1=4\), using the same procedure as before, the following functions characterise the solutions:

$$\begin{aligned}&e^{a(r)}=e^{-b(r)}=1-\frac{2m}{r}\left[ 1-\frac{q^2}{(q^6+8m^3r^3)^{1/3}}\right] ,R(r)\nonumber \\&\quad =-\frac{64m^4q^8}{(q^6+8m^3r^3)^{7/3}} , \end{aligned}$$
(43)
$$\begin{aligned}&F^{10}(r)=\frac{256c_0m^7q^2r^5}{\kappa ^2 q(q^6+8m^3r^3)^{7/3}}+\frac{c_1}{\kappa ^2 q}\nonumber \\&\qquad \qquad \quad \times \left[ 3m-r+\frac{256m^7q^2r^6}{(q^6+8m^3r^3)^{7/3}}-\frac{8m^4q^2r^3}{(q^6+8m^3r^3)^{4/3}}\right. \nonumber \\&\qquad \qquad \quad \left. -\frac{3mq^2}{(q^6+8m^3r^3)^{1/3}}\right] , \end{aligned}$$
(44)
$$\begin{aligned}&\mathcal {K}=\frac{16m^2}{r^6(q^6+8m^3r^3)^{14/3}}\nonumber \\&\qquad \times \Big [3q^{28}+112m^3q^{22}r^3+1856m^6q^{16}r^6\nonumber \\&\qquad +\,14336m^9q^{10}r^9+57344m^{12}q^4r^{12}-(q^6+8m^3r^3)^{1/3}\times \nonumber \\&\qquad \times \left( 6q^{26}+208m^3q^{20}r^3+2944m^6q^{14}r^6+19456m^9q^8r^9\right. \nonumber \\&\qquad \left. +\,49152m^{12}q^2r^{12}\right) \nonumber \\&\qquad +\,(q^6+8m^3r^3)^{2/3}\Big (3q^{24}+96m^3q^{18}r^3\nonumber \\&\qquad +\,1152m^6q^{12}r^6+6144m^9q^6r^9+12288m^{12}r^{12}\Big )\Big ]\end{aligned}$$
(45)
$$\begin{aligned}&f(R)=c_0R\!+\!\frac{c_1}{2mq^{12}(mq^2)^{16/3}}(-R)^{16/21}[4\times 2^{4/7}(mq^2)^{12/7}\nonumber \\&\qquad \qquad -q^6(-R)^{3/7}]^{4/3}[3\times 2^{4/7}(mq^2)^{12/7}(-R)^{4/7}-q^6R]\,.\nonumber \\ \end{aligned}$$
(46)

In spatial infinity, we have \(\lim _{r\rightarrow +\infty }\{e^{a(r)},e^{b(r)}\}=\{1,1\}\) and \(\lim _{r\rightarrow +\infty }\{R(r),\mathcal {K}\}=\{0,0\}\), showing the regularity in the asymptotical region. When the radial coordinate goes to zero it is necessary to perform an expansion around \(r = 0\) to analyse the behaviour of the solution in this limit. Taking \(e^{a(r)}\) and R(r), (43), \(\mathcal {K}\) inserting in (45), we find the following expansions around \(r=0\):

$$\begin{aligned}&e^{a(r)}\sim 1-\frac{16m^4}{3q^{6}}r^2+O\left( r^3\right) ,\nonumber \\&\quad R(r)\sim -\frac{64m^4}{q^{6}}+O\left( r^3\right) ,\nonumber \\&\quad \mathcal {K}\sim \frac{2048m^8}{3q^{12}}+O\left( r^3\right) . \end{aligned}$$
(47)

When r goes to zero, we have \(\lim _{r\rightarrow 0}\{e^{a(r)},e^{b(r)}\}=\{1,1\}\) and \(\lim _{r\rightarrow 0}\{R(r),\mathcal {K}\}=\{-64m^4/q^{6},2048m^8/q^{12}\}\), showing the regularity in the origin of the radial coordinate. Hence, we have shown that the solution (43) corresponds to a regular black hole in all space-time. This black hole has spherical symmetry, and it is charged and asymptotically flat.

The stability of the solution can be briefly analysed. Taking the second derivative of (46) with respect to R, we find

$$\begin{aligned} f_{RR}=\frac{2^{11/7}q^2c_1}{7R^{10/7}(mq^2)^{9/7}}\left[ \frac{1}{m^3}-\frac{2^{18/7}}{(mq^2)^{9/7}(-R)^{3/7}}\right] ^{-2/3}.\nonumber \\ \end{aligned}$$
(48)

From (48) we see that the stability condition (36) is satisfied for \(c_1>0\), and the solution is stable.

Let us verify now the energy conditions for this case. They read

$$\begin{aligned}&\mathrm{NEC}_1(r)=\mathrm{WEC}_1(r)=0, \mathrm{NEC}_2(r)=\mathrm{WEC}_2(r)\nonumber \\&\quad =\frac{256m^7q^2r^3}{\kappa ^2(q^6+8m^3r^3)^{7/3}},\end{aligned}$$
(49)
$$\begin{aligned}&\mathrm{DEC}_1(r)=\frac{1}{2}\mathrm{DEC}_2(r)=\frac{16m^4q^2}{\kappa ^2(q^6+8m^3r^3)^{4/3}},\nonumber \\&\mathrm{DEC}_3(r)=\frac{32m^4q^8}{\kappa ^2(q^6+8m^3r^3)^{7/3}},\end{aligned}$$
(50)
$$\begin{aligned}&\mathrm{SEC}(r)=\frac{32m^4q^2(8m^3r^3-q^6)}{\kappa ^2(q^6+8m^3r^3)^{7/3}}. \end{aligned}$$
(51)

The conditions NEC, WEC and DEC are satisfied in all space-time. However, the SEC condition, given by (51), is violated for \(r<q^2/(2m)\). For the values \(m=8q,q=10\), this violation occurs in a region very near the Cauchy horizon (\(q^2/(2m)=0.625,r_\mathrm{Cauchy}=0.0676869,r_{H}=159.373\)).

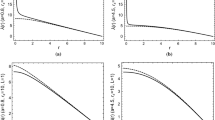
To complete our analysis, we display in Fig. 2 the graphics for the density, the radial and tangential effective pressures for the solutions (30) and (43). We show also the graphics for the relative fractions of these quantities, \(\omega _r=p_{r}^{(\mathrm{eff})}/\rho ^{(\mathrm{eff})},\omega _t=p_{t}^{(\mathrm{eff})}/\rho ^{(\mathrm{eff})},\omega _\mathrm{eff}=(p_{r}^{(\mathrm{eff})}+2p_{r}^{(\mathrm{eff})})/\rho ^{(\mathrm{eff})}\) and \(p_{r}^{(\mathrm{eff})}/p_{t}^{(\mathrm{eff})}\).

Fig. 2
figure 2

Parametric representation of the density and effective pressures of the solution (30) (left up panel) and of the solution (43) (right up panel). Also displayed are the fractions \(\omega _r=p_{r}^{(\mathrm{eff})}/\rho ^{(\mathrm{eff})},\omega _t=p_{t}^{(\mathrm{eff})}/\rho ^{(\mathrm{eff})},\omega _\mathrm{eff}=(p_{r}^{(\mathrm{eff})}+2p_{r}^{(\mathrm{eff})})/\rho ^{(\mathrm{eff})}\) and \(p_{r}^{(\mathrm{eff})}/p_{t}^{(\mathrm{eff})}\). We used \(q=10, m=80, c_0=1, c_1=2, \kappa ^2=8\pi \)

Full size image

It can be seen from Fig. 2 that the radial pressure reveals always the relation \(p_r^{(\mathrm{eff})}=-\rho ^{(\mathrm{eff})}\) for both solutions. The tangential pressure has this behaviour only very near the origin of the radial coordinate. For both solutions, there is a small difference between these two pressures that grows as r increases. This fact reveals the anisotropy of the effective matter content for the theory.

Again the main differences between the solution coming from GR and our solution are in the geometric and matter parts of the total action, as commented on before for the first solution.

4 Conclusion

In this paper, we have investigated the existence of regular black hole structures for a general f(R) theory, sourced by non-linear electromagnetic terms expressed by the Lagrangian \(\mathcal {L}_\mathrm{NED}\). Our approach follows very closely the one employed in Ref. [62]: instead of choosing specific forms for the f(R) and \(\mathcal {L}_\mathrm{NED}\) functions, the approach consists in expressing the metric in terms of a mass function M(r) and to choose a mass function that satisfies some requirements. Specifically, we have used the mass function determined in Ref. [63]. Such a mass function was constructed, in the context of GR theory coupled to non-linear electromagnetic field, in order to satisfy the WEC and to have an asymptotic Reissner–Nordström limit. In fact, the chosen mass function M(r) is the most general functional form satisfying the WEC in GR.

Applied to the case of general f(R) and \(\mathcal {L}_\mathrm{NED}\) functions, the mass function of Ref. [63] leads to regular black hole solutions which contain two horizons, the event horizon and the Cauchy horizon. We worked out completely two specific cases of that mass function, by choosing specific values for the free parameters in the model developed in Ref. [63]. The regular character of the solutions is attested by the regular behaviour of the geometric invariants, like the Ricci scalar and the Kretschmann scalar. Asymptotically, as expected, the metric functions reproduces the Reissner–Nordström solution of GR.

The energy conditions are satisfied for the two specific cases studied here, except for the case of the strong energy condition (SEC) which is violated in the vicinity of the Cauchy horizon. Of course, a violation of at least some of the energy conditions must occur if a regular solution must be extracted from the original theory. In this case, the violation is quite mild since it is only the energy condition connected with the convergence of the geodesics that is violated (SEC), and even though in a quite restricted region of the whole space-time.

The stability of the two solutions determined here has been briefly discussed and it has been shown that the two solutions obey the stability condition.

Evidently, there are many open issues related to the problem treated here, like the complete determination of the \(\mathcal {L}_\mathrm{NED}\) function corresponding to the configurations found, and the stability problem. We postpone such a new analysis to future works.