Abstract
A major new release of the Monte Carlo event generator Herwig++ (version 3.0) is now available. This release marks the end of distinguishing Herwig++ and HERWIG development and therefore constitutes the first major release of version 7 of the Herwig event generator family. The new version features a number of significant improvements to the event simulation, including: built-in NLO hard process calculation for virtually all Standard Model processes, with matching to both angular-ordered and dipole shower modules via both subtractive (MC@NLO-type) and multiplicative (Powheg-type) algorithms; QED radiation and spin correlations in the angular-ordered shower; a consistent treatment of perturbative uncertainties within the hard process and parton showering. Several of the new features will be covered in detail in accompanying publications, and an update of the manual will follow in due course.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Herwig is a multi purpose particle physics event generator. It is based on the experience gained with both the HERWIG [1] and the Herwig++ [2] event generators. The latest version of Herwig++, 3.0, marks the point at which the physics capabilities of the HERWIG version 6 series are fully superseded, and thus the last point at which their development is distinguished. Herwig++ 3.0 will henceforth be known as Herwig 7.0. It replaces any prior HERWIG or Herwig++ versions.
Herwig provides highly improved and extended physics capabilities compared to both its predecessors, in particular the ability to perform simulations at next-to-leading order in QCD, while keeping the key physics motivations such as coherent parton showers (including both angular-ordered and dipole evolution), the cluster hadronization model, an eikonal multiple interaction model, and highly flexible BSM capabilities.
The last major public version (2.7) of Herwig++ is described in great detail in [2–7]. This release note summarizes the major changes and improvements introduced since then, which constitute the base for the Herwig 7 series. The physics questions addressed by the capabilities of Herwig 7 will be covered in detail in accompanying publications, as well as comparisons with the other well-known general-purpose event generators, Pythia [8, 9] and Sherpa [10]. A detailed manual covering all technical aspects will be prepared in due course. Please refer to [2] and the present paper if using Herwig 7.0.
1.1 Availability
The new program version, together with other useful files and information, can be obtained from the web site https://herwig.hepforge.org/. In order to improve our response to user queries, all problems and requests for user support should be reported via the bug tracker on our wiki. Requests for an account to submit tickets and modify the wiki should be sent to herwig@projects.hepforge.org.
Herwig is released under the GNU General Public License (GPL) version 2 and the MCnet guidelines for the distribution and usage of event generator software in an academic setting, which are distributed together with the source, and can also be obtained from http://www.montecarlonet.org/.
1.2 Prerequisites
Herwig 7.0 is based on ThePEG 2.0, which is available along with the Herwig installation sources at https://herwig.hepforge.org/downloads. Further requirements are BOOST [11], gsl [12], fastjet [13] and LHAPDF [14], while a number of other dependencies are necessary in order to fully exploit the program’s capabilities. Amongst these are HepMC and/or Rivet [15] to analyze simulated events, as well as some or all of the external amplitude libraries discussed in Sect. 2.2.
In order to simplify the installation process, we provide a bootstrap script to facilitate a consistent build and installation of Herwig in a convenient way. The script requires a python installation, and is available from https://herwig.hepforge.org/herwig-bootstrap.
1.3 Documentation
A significant new feature is the online documentation, which has been completely rewritten and greatly extended to reflect the major changes introduced with this version and replaces the wiki pages. It can be found at https://herwig.hepforge.org/tutorials/. An update of the more detailed physics and manual will be made available in a similar format in due course. Code snippets are provided for a wide variety of control functions for easy inclusion into input files. Detailed documentation of the source code and input file interfaces generated with doxygen is available at https://herwig.hepforge.org/doxygen/.
2 NLO event simulation
A key ingredient in the design and development of Herwig 7.0 was to provide event simulation at next-to-leading order (NLO) accuracy in the strong coupling by default for as many Standard Model processes as possible in an automated way. The program, with the help of external libraries used for amplitude calculation, is now able fully automatically to assemble NLO QCD corrections to virtually all Standard Model processes, including matching to both of its parton-shower algorithms [16, 17], via methods inspired by either the MC@NLO [18] or Powheg [19] type algorithms, which we refer to as subtractive and multiplicative matching, respectively.
Based on extensions of the previously developed Matchbox module [20], NLO event simulation is now possible without the requirement of separately running external codes and/or dealing with intermediate event sample files. Slight changes have been made to improve Herwig’s steering at the level of input files, and significant improvements are provided to integration and unweighting, including parallelization to meet the requirements of more complex processes.
2.1 The matchbox module
The design of the Matchbox modules closely resembles the structure of the NLO QCD cross section calculated within a subtraction paradigm, including the matching subtractions required to consistently combine such calculations with parton showering downstream. Subtraction terms are available in a flexible way, though only Catani–Seymour dipoles [21, 22] are provided so far, including both massless and massive QCD as well as the subtraction terms required for supersymmetric QCD corrections.
Parton-shower matching subtractions are provided on an equally flexible footing, including those required for the angular-ordered shower [16], the dipole shower [17], as well as matrix-element corrected showers forming the basis of Powheg-type matching. For the latter, we provide additional functionality to sample the matrix-element correction Sudakov using the adaptive method outlined in [23]. In order to simplify the calculation of matching subtractions for the angular-ordered shower, the kinematics reconstruction used to work out the final shower kinematics has been changed to avoid additional Jacobian factors when compared to the dipole parameterization in the case of a single (or in general, the hardest) emission.
2.2 External amplitude providers
In order to set up the full calculation of a cross section, Matchbox requires plug-ins to provide the respective tree and one-loop amplitudes. These plug-ins can be interfaced either at the level of matrix elements squared (or tree-loop interferences, respectively), or at the level of helicity, colour-ordered subamplitudes with both trace- and colour flow bases provided within the Matchbox core through adapted versions of the ColorFull [24] and CVolver [25] libraries.Footnote 1 While we provide built-in amplitudes for a limited number of processes, the bulk of Standard Model processes can be simulated using external amplitude plug-ins.
Based on extensions of the BLHA standard [26, 27], Herwig currently supports interfaces to GoSam [28], MadGraph [29], NJet [30], OpenLoops[31] and VBFNLO [32, 33]. Amplitudes for a limited number of LHC relevant processes are directly provided along with the release, and amplitudes for electroweak Higgs plus jets production are available from the Matchbox plug-in HJets++, which is available in the Contrib section of the Herwig 7.0 release.
2.3 Electroweak corrections to VV production
Electroweak corrections to the production of heavy vector boson pairs have been computed [34, 35] and implemented into the program, as outlined in [36]. The corrections are applied as an event reweighting factor \(K(\hat{s}, \hat{t})\). In order to apply this correction in a meaningful way one has to ensure that additional QCD corrections are not too large and apply reasonable cuts to the final state, as detailed in [36]. The reweighting is straightforward when applied together with Powheg-matched QCD corrections. If subtractive QCD matching is going to be applied one should rather apply the matching on information extracted directly from the leptons in the final state, this is detailed as an alternative method in [36]. In order to apply the method, one has to download grid files for the actual K factors from a public archive at hepforge.
3 Improvements to the angular-ordered parton shower
This release includes a number of improvements, which finally bring the default angular-ordered parton shower to the same level of accuracy as that in HERWIG 6.
3.1 QED showering
The emission of QED radiation was not included in Herwig++. In Herwig 7.0 it is included in the following way:
-
A maximum scale is selected for QED radiation in the same way as for QCD radiation, although selecting from the other charged particles in the process rather than the colour partner in order to determine the scale. This scale need not be the same as the maximum scale for QCD radiation.
-
Trial QCD and QED emissions are generated and the one with the higher scale selected, as required by the competition algorithm. This branching is generated as before and then any subsequent emissions of the same type are required to be angular orderedFootnote 2 while those of a different type are only required to be ordered. For example if we generate a \(q\rightarrow q g \) emission at an evolution scale \(\tilde{q}_1\) and the quark has light-cone momentum fraction \(z_1\) then any subsequent \(q\rightarrow q g\) emissions must occur at a scale \(\tilde{q}_2<z\tilde{q}_1\), as required by angular ordering. However, any QED \(q\rightarrow q \gamma \) branchings need not be angular ordered and therefore can occur at an evolution scale \(\tilde{q}_2<\tilde{q}_1\).
3.2 Spin correlations in the shower
There are correlations between the azimuthal angle of a branching and both the hard scattering process and any previous branchings that occurred in the parton shower. There are two types of correlation:
-
1.
The soft correlation from the eikonal current, which correlates the direction of the emitted gluon and the colour partner.
-
2.
Spin correlations in the collinear limit between the azimuthal angle of the branching and the hard process and any previous emissions.
Both of these effects are included in Herwig 7.0 using the algorithm of [37–39]. Now that the full spin correlations are incorporated in the parton shower there is no requirement that unstable decays are generated before the parton shower in order to generate the spin correlations between the production and decay of the particles as described in [40, 41]. The decays of unstable fundamental particles are now handled as part of the parton-shower stage of the event generation including all the spin correlations, both between the production of particles and the parton-shower emissions, the production and decay of particles, and the decay of particles and any parton-shower emissions. The spin correlations are switched on by default and can be switched off using

While the soft correlations can be switched off using

we do not recommend this as the soft correlations affect the cluster mass spectrum and therefore this change requires a retuning of the parton-shower and hadronization parameters.
As the spin correlations are currently not implemented in the shower subtraction terms used at next-to-leading order the spin correlations are switched off by default when using NLO matching. However, as we use the same formalism internally as MadGraph for the calculation of helicity amplitudes [42] the interface to MadGraph can fill the spin-density matrices used in the spin-correlation algorithm and therefore the correlations can be correctly generated at leading order.
3.3 \(g\rightarrow q\bar{q}\)
The branching \(g\rightarrow q\bar{q}\) is only singular in the collinear limit for massless quarks and does not have a soft singularity. It therefore should not be angular ordered in the parton shower, although given the nature of the parton shower algorithm it must continue to be ordered in the evolution variable. We therefore relax the constraint on this branching so that if a gluon is produced at a scale \(\tilde{q}_1\) with light-cone momentum fraction \(z_1\) the maximum scale of a subsequent \(g\rightarrow q\bar{q}\) branching is now \(\tilde{q}_1\), the maximum allowed by ordering of the evolution variable, rather than \(z_1\tilde{q}_1\) as required by angular ordering. The maximum evolution scale for other branchings remains unchanged.
Similarly, the arguments presented in [2, 43] that the scale used in the strong coupling for a branching should be the relative transverse momentum, \(p_\perp \), do not apply, and therefore we have changed this scale to be the invariant mass of the \(q\bar{q}\) pair for this branching only.Footnote 3
4 Perturbative and shower uncertainties
Perturbative uncertainties in all of the hard processes provided by the Matchbox module can be assessed by variation of the renormalization and factorization scales, respectively. When fixed-order predictions at leading or next-to-leading order are combined with subsequent parton showering, variations of the renormalization and factorization scales in the parton shower ( i.e. variations of the scale arguments of \(\alpha _s\) and the parton distribution functions) should be performed in a correlated way along with variations in the hard process. While independent variations are technically possible to assess patterns of scale compensation, the default uncertainty settings will perform a consistent variation.
In addition to estimating unknown higher-order corrections by variation of the renormalization and factorization scale, genuine parton-shower uncertainties due to missing higher logarithmic orders and phase-space constraints can also be estimated by varying the hard scale in the parton shower. There is no unique definition of such a scale, and the relevant quantity is a specific detail of the parton-shower algorithm and varies considerable between different approaches. We provide variations of the relevant scale in both the angular-ordered and the dipole shower algorithms, which can be used to assess these uncertainties, which are expected to be reduced by use of NLO matched simulations. Specifically for this purpose, easily usable settings of strict leading-order simulation to be compared to improved NLO simulation are provided within the new steering formalism summarized in Sect. 6.
5 Tuning
The improvements to both shower modules, as well as the inclusion of next-to-leading order cross sections, have required a new tune to \(e^+e^-\) data; this tune has been carried out using standard methods based on the Professor framework [44] using a representative set of \(e^+e^-\) data as previously described in [2]. Similar parameters and an overall reasonable description of the data have been obtained for both the angular-ordered and the dipole shower. The results of these tuning efforts are the default for the Herwig 7.0 release.
5.1 Tuning of the multi-parton interaction model
It was shown in Ref. [45] that a good description of both underlying event and double parton scattering data [46] can be obtained if one includes the latter in the data being fit to with a sufficiently high weight. We followed the procedure described in Ref. [45] using the MMHT2014 LO parton distribution function [47]Footnote 4 and obtained a tune consistent with double parton scattering data (\(\sigma _{\!{eff}}\approx 15\,\mathrm {mb}\)) that also gives a good description of the underlying event data from the Tevatron’s lowest analysed energy point [50], \(\sqrt{s}=300\,\mathrm {GeV}\) to the LHC’s highest [51], \(\sqrt{s}=7\,\mathrm {TeV}\).
Herwig 7.0 is released together with the tune H7-UE-MMHT, which it uses by default. More information and other related tunes can be obtained from the Herwig tunes page.
6 Steering, integration and run modes
Owing to the complexity of the processes that can be simulated with Herwig, this version introduces some new run modes as well as highly simplified input files to ease steering the event generator. Two alternative integrator modules are provided in addition to the old default, ACDC of ThePEG, providing superior performance especially for more complex processes. One of the algorithms is based on the standard sampling algorithm contained in the ExSample library [23], while the other is based on the MONACO algorithm, a VEGAS [52] variant, used by VBFNLO [32, 33].
Since both of these algorithms require an integration grid to be set up prior to generating events, two levels of run mode have been introduced in addition to the old read and run steps, to meet the requirements of more complex processes. The new integrate step performs the grid adaptation; it is possible to parallelize this step in a way that does not require inter-process communication and the individual tasks in this parallelization can easily be submitted to standard batch or grid queues. The integrate step is to be preceded by a build step,Footnote 5 which will assemble the full fixed-order or matched cross section, including subtraction terms and the possibility of external amplitude libraries generating dedicated code for the process of interest. As this step may also require considerable computational resources, the integrate and run steps both support reading in additional input files, so-called setup files, to modify run parameters independently of the process of building an event generator object. Detailed examples of these various new work-flows are given in the new documentation.
Event generation itself can be parallelized either through submitting runs with explicitly set random seeds or through the newly introduced feature of forking several event generation jobs on multicore nodes.
7 Herwig contrib projects
A number of related codes have been developed along with the main Herwig 7.0 development; while these libraries are not supported at the same level as the core Herwig release, they are provided along with it. Amongst other tools, the new program version provides the following plug-ins:
7.1 Electroweak Higgs plus jets production
A dedicated Matchbox plug-in providing amplitudes for the calculation of electroweak Higgs plus jets production at NLO QCD is available along with the release. This library has been used in the calculation reported in [53]. It provides a full calculation of \(pp\rightarrow h + n\) jets at \(\mathcal{O}(\alpha ^3\alpha _s^{n-2})\) for \(n=2,3,4\) at leading, and \(n=2,3\) at next-to-leading order QCD. All relevant topologies of either VBF or Higgs-Strahlung type are taken into account along with all interferences. The technical details of the library will be described elsewhere; its use is the same as for all other Matchbox-based calculations and a corresponding input file snippet to enable this class of processes is provided.
7.2 FxFx merging support
Herwig 7.0 contains interface support for FxFx merging [54], a method for merging multi-jet NLO samples with a parton shower. The interface allows usage of samples generated from MadGraph 5/aMC@NLO [55]. The module has been tested for \(\mathrm {W+jets}\) and \(\mathrm {Z+jets}\) events, and compared against LHC data at 7 and 8 TeV [56]. Other processes will be supported in future releases.
7.3 Higgs boson pair production
The HiggsPair and HiggsPairOL packages offer production of Higgs boson pairs via gluon fusion. The former uses code from HPAIR [57, 58] whereas the latter uses the OpenLoops one-loop generator for the matrix elements [31].
HiggsPair describes leading-order Higgs boson pair production, either in the Standard Model or in its \(D=6\) effective field theory extension. The original implementation was described in [7] and its \(D=6\) EFT extension was examined in detail in [59].
HiggsPairOL describes SM Higgs boson pair production, with the optional use of Higgs–Higgs+one jet matrix elements merged to the parton shower via the MLM method. See [60] for a detailed description.
8 Sample results
With so many new features, it is impossible to show the full spectrum of results that have been improved, but in Figs. 1, 2, 3 and 4 we show a small sample.
The thrust distribution in \(\mathrm {e^+e^-}\) annihilation at \(\sqrt{s}=M_z\), in comparison with ALEPH data [61]
The Monte Carlo results shown are from Herwig++ version 2.7 using leading-order plus parton shower simulation and from Herwig 7.0 with the angular-ordered parton shower (LO \(\oplus \) PS), the angular-ordered parton shower supplemented by the internally implemented Powheg correction, which includes QCD and QED corrections for the case of \(e^+e^-\rightarrow q\bar{q}\) (QCD \(\otimes \) QED \(\otimes \) PS), by the automatically calculated by Matchbox subtractive (MC@NLO-type) matching (NLO \(\oplus \) PS) and multiplicative (Powheg-type, NLO \(\otimes \) PS) corrections and, finally, the dipole shower supplemented by a subtractive matching to NLO cross sections (NLO \(\oplus \) Dipoles).
In Fig. 1, we show the most well-studied event shape from the LEP era, the thrust distribution, in comparison with data from the ALEPH collaboration [61]. A long-standing problem of Herwig++ producing too many very hard events, whether or not NLO matching was used, is seen to have been solved by the improvements to the angular-ordered shower algorithm. All of the variants of NLO matching then give a similar description of the data, with the dipole shower giving a somewhat better overall description.
The distribution of photon-jet energy fraction in three-jet \(\mathrm {e^+e^-}\) events at \(\sqrt{s}=M_z\) defined with a cutoff in the \(k_\perp \) algorithm of \(y=0.1\) in comparison with ALEPH data [62]
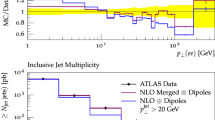
The distribution of separation in azimuthal angle between the \(\mathrm {Z}\) boson and the hardest jet in \(\mathrm {Z+jets}\) events in \(\mathrm {pp}\) collisions at \(\sqrt{s}=7\,\mathrm {TeV}\) in comparison with CMS data [63]
In Fig. 2, the effect of the inclusion of photon emission in the angular-ordered parton shower is shown. Events at \(z_\gamma =1\) are isolated photons (“jets” for which all of the jet energy is carried by a single photon), while events at lower \(z_\gamma \) come from hard collinear photon emission from the final state quark jets. We see clearly that the results from Herwig++ have no component at large \(z_\gamma \) at all, while all of the Herwig 7.0 variants are much closer to the data with that including matching to NLO QED as well as QCD giving the best agreement. QED radiation within the dipole shower is subject to ongoing development and will be available in a future release.
In Fig. 3 we turn to results for \(\mathrm {Z+jets}\) events at the LHC. We show the distribution of separation in azimuthal angle between the \(\mathrm {Z}\) boson and the hardest jet. The region \(\Delta \phi \sim \pi \) corresponds to leading order kinematics, in which the \(\mathrm {Z}\) boson gains its transverse momentum by recoiling against a single hard parton, whereas the broad spectrum of events down to \(\Delta \phi =0\) corresponds to events in which the \(\mathrm {Z}\) boson recoils against two or more jets. The need for NLO corrections is clearly seen. An important cross-check of the two different automated NLO matching schemes and the two different shower algorithms both using subtractive matching can also be seen.
The fraction of events that have less than \(Q_\mathrm{{sum}}\) transverse energy in the rapidity region \(|y|<2.1\) in top quark–antiquark events in \(\mathrm {pp}\) collisions at \(\sqrt{s}=7\,\mathrm {TeV}\) in comparison with ATLAS data [64]
Finally, in Fig. 4 we show the jet activity in \(\mathrm {t\bar{t}}\) events at the LHC, as revealed by the gap fraction, i.e. the fraction of events for which the sum of the transverse momenta of all additional jets in the prescribed rapidity region is less than \(Q_{\mathrm {sum}}\). Herwig++ 2.7 is seen to have far too little jet activity (too many gap events). While Herwig 7.0 with the shower alone is somewhat closer to the data at small \(Q_\mathrm{{sum}}\), a clear deficit is seen for hard jet events at high \(Q_\mathrm{{sum}}\), while both the NLO matching schemes describe the data well.
This is of course just a very small selection of the large number of distributions that have been checked against data in the final preparations of Herwig version 7.0, and more will be shown for specific processes in a series of forthcoming papers.
9 Summary and outlook
We have presented version 7.0 of the Herwig event generator, based on previous Herwig++ development and the experience gained with the HERWIG event generator. The new program features significant improvements as compared to both the Herwig++ 2.x series and the HERWIG 6 event generator, amongst them a powerful framework for NLO calculations and a number of improvements to both shower modules. Several accompanying publications containing detailed coverage of both physics and technical aspects will follow in due course, as well as an updated large and detailed manual to replace [2]. A completely new documentation system is already in place for Herwig 7 to allow the user to exploit the full capability of the new program. The methods and code developed within this release will also form the basis for ongoing and future development such as multijet merging at both leading and next-to-leading order, and electroweak corrections.
Notes
Other choices of colour bases are straightforward to implement through a very transparent interface.
With the proviso discussed below for \(g\rightarrow q\bar{q}\) branchings or in the QED case \(\gamma \rightarrow f\bar{f}\) splittings.
A similar change has been introduced in the dipole shower.
The old read step is still available, representing the subsequent execution of both the build and the integrate steps in one step.
References
G. Corcella et al., HERWIG 6: an event generator for hadron emission reactions with interfering gluons (including supersymmetric processes). JHEP 01, 010 (2001). arXiv:hep-ph/0011363
M. Bähr et al., Herwig++ physics and manual. Eur. Phys. J. C 58, 639–707 (2008). arXiv:0803.0883
M. Bähr et al., Herwig++ 2.2 Release Note. arXiv:0804.3053
M. Bähr et al., Herwig++ 2.3 Release Note. arXiv:0812.0529
S. Gieseke et al., Herwig++ 2.5 Release Note. arXiv:1102.1672
K. Arnold et al., Herwig++ 2.6 Release Note. arXiv:1205.4902
J. Bellm et al., Herwig++ 2.7 Release Note. arXiv:1310.6877
T. Sjöstrand, S. Mrenna, P.Z. Skands, A. Brief, Introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852–867 (2008). arXiv:0710.3820
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten, S. Mrenna, S. Prestel, C.O. Rasmussen, P.Z. Skands, An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). arXiv:1410.3012
T. Gleisberg, S. Hoeche, F. Krauss, M. Schönherr, S. Schumann, F. Siegert, J. Winter, Event generation with SHERPA 1.1. JHEP 02, 007 (2009). arXiv:0811.4622
M. Galassi et al., GNU Scientific Library Reference Manual. Network Theory Limited (2006)
M. Cacciari, G.P. Salam, G. Soyez, FastJet user manual. Eur. Phys. J. C 72, 1896 (2012). arXiv:1111.6097
A. Buckley et al., LHAPDF6: parton density access in the LHC precision era. Eur. Phys. J. C 75, 132 (2015). arXiv:1412.7420
A. Buckley et al., Rivet user manual. Comput. Phys. Commun. 184, 2803–2819 (2013). arXiv:1003.0694
S. Gieseke, P. Stephens, B. Webber, New formalism for QCD parton showers. JHEP 12, 045 (2003). arXiv:hep-ph/0310083
S. Plätzer, S. Gieseke, Coherent parton showers with local recoils. JHEP 01, 024 (2011). arXiv:0909.5593
S. Frixione, B.R. Webber, Matching NLO QCD computations and parton shower simulations. JHEP 06, 029 (2002). arXiv:hep-ph/0204244
P. Nason, A new method for combining NLO QCD with shower Monte Carlo algorithms. JHEP 11, 040 (2004). arXiv:hep-ph/0409146
S. Plätzer, S. Gieseke, Dipole showers and automated NLO matching in Herwig++. Eur. Phys. J. C 72, 2187 (2012). arXiv:1109.6256
S. Catani, M.H. Seymour, A general algorithm for calculating jet cross-sections in NLO QCD. Nucl. Phys. B 485, 291–419 (1997). hep-ph/9605323 (erratum: Nucl. Phys. B 510, 503, 1998)
S. Catani, S. Dittmaier, M.H. Seymour, Z. Trocsanyi, The dipole formalism for next-to-leading order QCD calculations with massive partons. Nucl. Phys. B 627, 189–265 (2002). arXiv:hep-ph/0201036
S. Plätzer, ExSample: a library for sampling Sudakov-type distributions. Eur. Phys. J. C 72, 1929 (2012). arXiv:1108.6182
M. Sjödahl, ColorFull—a C++ library for calculations in SU(Nc) color space. Eur. Phys. J. C 75, 236 (2015). arXiv:1412.3967
S. Plätzer, Summing large-\(N\) towers in colour flow evolution. Eur. Phys. J. C 74, 2907 (2014). arXiv:1312.2448
T. Binoth et al., A proposal for a standard interface between Monte Carlo tools and one-loop programs. Comput. Phys. Commun. 181, 1612–1622 (2010). arXiv:1001.1307
S. Alioli et al., Update of the Binoth Les Houches Accord for a standard interface between Monte Carlo tools and one-loop programs. Comput. Phys. Commun. 185, 560–571 (2014). arXiv:1308.3462
G. Cullen et al., GoSam-2.0: a tool for automated one-loop calculations within the Standard Model and beyond. Eur. Phys. J. C74, 3001 (2014). arXiv:1404.7096
J. Alwall, M. Herquet, F. Maltoni, O. Mattelaer, T. Stelzer, MadGraph 5: going beyond. JHEP 1106, 128 (2011). arXiv:1106.0522
S. Badger, B. Biedermann, P. Uwer, V. Yundin, Numerical evaluation of virtual corrections to multi-jet production in massless QCD. Comput. Phys. Commun. 184, 1981–1998 (2013). arXiv:1209.0100
F. Cascioli, P. Maierhofer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206
K. Arnold et al., VBFNLO: a parton level Monte Carlo for processes with electroweak bosons. Comput. Phys. Commun. 180, 1661–1670 (2009). arXiv:0811.4559
J. Baglio et al., Release Note—VBFNLO 2.7.0. arXiv:1404.3940
A. Bierweiler, T. Kasprzik, J.H. Kühn, Vector-boson pair production at the LHC to \({\cal O}(\alpha ^3)\) accuracy. JHEP 1312, 071 (2013). arXiv:1305.5402
A. Bierweiler, T. Kasprzik, J.H. Kühn, S. Uccirati, Electroweak corrections to W-boson pair production at the LHC. JHEP 11, 093 (2012). arXiv:1208.3147
S. Gieseke, T. Kasprzik, J.H. Kühn, Vector-boson pair production and electroweak corrections in HERWIG++. Eur. Phys. J. C 74, 2988 (2014). arXiv:1401.3964
I.G. Knowles, Spin correlations in parton–parton scattering. Nucl. Phys. B 310, 571 (1988)
I.G. Knowles, A linear algorithm for calculating spin correlations in hadronic collisions. Comput. Phys. Commun. 58, 271–284 (1990)
J.C. Collins, Spin correlations in Monte Carlo event generators. Nucl. Phys. B 304, 794 (1988)
P. Richardson, Spin correlations in Monte Carlo simulations. JHEP 11, 029 (2001). arXiv:hep-ph/0110108
M. Gigg, P. Richardson, Simulation of beyond Standard Model physics in Herwig++. Eur. Phys. J. C 51, 989–1008 (2007). arXiv:hep-ph/0703199
H. Murayama, I. Watanabe, K. Hagiwara, HELAS: HELicity amplitude subroutines for Feynman diagram evaluations. KEK-91-11
A. Buckley et al., General-purpose event generators for LHC physics. Phys. Rep. 504, 145–233 (2011). arXiv:1101.2599
A. Buckley, H. Hoeth, H. Lacker, H. Schulz, J.E. von Seggern, Systematic event generator tuning for the LHC. Eur. Phys. J. C 65, 331–357 (2010). arXiv:0907.2973
M.H. Seymour, A. Siódmok, Constraining MPI models using \(\sigma _{\!{effective}}\) and recent Tevatron and LHC underlying event data. JHEP 10, 113 (2013). arXiv:1307.5015
M. Bähr, M. Myska, M.H. Seymour, A. Siódmok, Extracting \(\sigma _{\!{effective}}\) from the CDF gamma+3jets measurement. JHEP 1303, 129 (2013). arXiv:1302.4325
L.A. Harland-Lang, A.D. Martin, P. Motylinski, R.S. Thorne, Parton distributions in the LHC era: MMHT 2014 PDFs. Eur. Phys. J. C 75, 204 (2015). arXiv:1412.3989
S. Dulat et al., The CT14 Global Analysis of Quantum Chromodynamics. arXiv:1506.0744
NNPDF Collaboration, R.D. Ball et al., Parton distributions for the LHC Run II. JHEP 04, 040 (2015). arXiv:1410.8849
CDF Collaboration, T. Aaltonen et al., A Study of the Energy Dependence of the Underlying Event in Proton–Antiproton Collisions. arXiv:1508.0534
ATLAS Collaboration, G. Aad et al., Measurement of underlying event characteristics using charged particles in pp collisions at\(\sqrt{s} = 900 GeV\) and 7 TeV with the ATLAS detector. Phys. Rev. D 83, 112001 (2011). arXiv:1012.0791
G.P. Lepage, VEGAS: An Adaptive Multi-Dimensional Integration Program, CLNS-80/447 (1980)
F. Campanario, T.M. Figy, S. Plätzer, M. Sjödahl, Electroweak Higgs boson plus three jet production at next-to-leading-order QCD. Phys. Rev. Lett. 111, 211802 (2013). arXiv:1308.2932
R. Frederix, S. Frixione, Merging meets matching in MC@NLO. JHEP 12, 061 (2012). arXiv:1209.6215
J. Alwall et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301
R. Frederix, S. Frixione, A. Papaefstathiou, S. Prestel, P. Torrielli, A study of multi-jet production in association with an electroweak vector boson. arXiv:1511.0084
S. Dawson, S. Dittmaier, M. Spira, Neutral Higgs boson pair production at hadron colliders: QCD corrections. Phys. Rev. D 58, 115012 (1998). arXiv:hep-ph/9805244
T. Plehn, M. Rauch, The quartic higgs coupling at hadron colliders. Phys. Rev. D 72, 053008 (2005). arXiv:hep-ph/0507321
F. Goertz, A. Papaefstathiou, L.L. Yang, J. Zurita, Higgs boson pair production in the \(D=6\) extension of the SM. JHEP 04, 167 (2015). arXiv:1410.3471
P. Maierhöfer, A. Papaefstathiou, Higgs Boson pair production merged to one jet. JHEP 03, 126 (2014). arXiv:1401.0007
ALEPH Collaboration, R. Barate et al., Studies of quantum chromodynamics with the ALEPH detector. Phys. Rep. 294, 1–165 (1998)
ALEPH Collaboration, D. Buskulic et al., First measurement of the quark to photon fragmentation function. Z. Phys. C 69, 365–378 (1996)
C.M.S. Collaboration, S. Chatrchyan et al., Event shapes and azimuthal correlations in \(Z\) + jets events in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Phys. Lett. B 722, 238–261 (2013). arXiv:1301.1646
ATLAS Collaboration, G. Aad et al., Measurement of\(t \bar{t}\) production with a veto on additional central jet activity in pp collisions at sqrt(s) = 7 TeV using the ATLAS detector. Eur. Phys. J. C 72, 2043 (2012). arXiv:1203.5015
Acknowledgments
We are grateful to the authors of the predecessor HERWIG and Herwig++ programs for their many inputs into the development of Herwig and to the many users whose feedback has led to its improvement. We are especially indebted to Leif Lönnblad for his authorship of ThePEG, on which Herwig is built, and his close collaboration, and also to the authors of Rivet and Professor. We would like to thank Terrance Figy for numerous discussions, testing and feedback. We are also grateful to Malin Sjödahl for providing the ColorFull library for distribution along with Herwig. This work was supported in part by the European Union as part of the FP7 Marie Curie Initial Training Network MCnetITN (PITN-GA-2012-315877). It was also supported in part by the Lancaster–Manchester–Sheffield Consortium for Fundamental Physics under STFC Grant ST/L000520/1 and the Institute for Particle Physics Phenomenology under STFC Grant ST/G000905/1. AP and SP acknowledge support by FP7 Marie Curie Intra European Fellowships (PIEF-GA-2013-622071 and PIEF-GA-2013-628739 respectively). CR acknowledges support by the German Federal Ministry of Education and Research (BMBF). SP is grateful to DESY Hamburg and KIT for kind hospitality while part of this work was completed, as well as for providing computing resources. We are also grateful to the Cloud Computing for Science and Economy project (CC1) at IFJ PAN (POIG 02.03.03-00-033/09-04) in Cracow and the U.K. GridPP project whose resources were used to carry out some of the numerical calculations for this project. Thanks also to Mariusz Witek and Miłosz Zdybał for their help with CC1 and Oliver Smith for his help with grid computing.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Bellm, J., Gieseke, S., Grellscheid, D. et al. Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 76, 196 (2016). https://doi.org/10.1140/epjc/s10052-016-4018-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4018-8