1 Introduction

The large body of experimental data on soft interactions at high energy [1–14], presently, cannot be comprehended in terms of theoretical high energy QCD (see [15] for the review).

In this paper we continue our effort [16–18] to comprehend such interactions, by constructing a model that incorporates the advantages of two theoretical approaches to high energy QCD.

The first one is the CGC/saturation approach [19–38], which provides a clear picture of multi particle production at high energy that proceeds in two stages. The first stage is the production of a mini-jet with a typical transverse momentum \(Q_s\). Here \(Q_s\), the saturation scale, is much larger than the soft scale. This stage is under full theoretical control. The second stage is when the mini-jet decays into hadrons, which we have to treat phenomenologically, using data from hard processes. Such an approach leads to a good description of the experimental data on inclusive production, both for hadron–hadron, hadron–nucleus, and nucleus–nucleus collisions, and the observation of some regularities in the data, such as geometric scaling behavior [39–54]. The shortcoming of this approach is the fact that it is disconnected from diffractive physics.

On the other hand, there exists a different approach to high energy QCD: the BFKL Pomeron [55–58] and its interactions [19, 59–79], which is suitable to describe diffractive physics. The BFKL Pomeron calculus turns out to be close to the old Reggeon theory [80], so, for calculating the inclusive characteristics of multiparticle production, we can apply the Mueller diagram technique [81]. The relation between these two approaches has not yet been established, but they are equivalent [74–77] for the rapidities (\(\ln \left( s/s_0\right) \)), such that

$$\begin{aligned} Y \le \frac{2}{\Delta _{\text{ BFKL }}}\ln \left( \frac{1}{\Delta ^2_{\text{ BFKL }}}\right) \end{aligned}$$
(1.1)

where \(\Delta _\mathrm{BFKL}\) denotes the intercept of the BFKL Pomeron. As we have discussed [16], the parameters of our model are such that for \(Y\, \le \,36\), we can trust our approach, based on the BFKL Pomeron calculus.

This paper is the next step in our program to build a model for high energy soft scattering, based on an analytical calculation, without using a Monte Carlo simulation. We discuss the correlation function:

$$\begin{aligned} R\left( y_1, y_2; Y\right) = \frac{1}{\sigma _{NSD}}\frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \mathrm{d}y_2}\bigg /\left( \frac{1}{\sigma _{NSD}}\frac{\mathrm{d} \sigma }{\mathrm{d} y_1} \frac{1}{\sigma _{NSD}}\frac{\mathrm{d} \sigma }{ \mathrm{d} Y_2}\right) - 1 \end{aligned}$$
(1.2)

where Y denotes the total rapidity (\(Y = \ln \left( s/s_0\right) \) and \(s = W^2\), W is the energy in c.m.f.) and \(y_1\) and \(y_2\) are the rapidities of the produced hadrons. \(\sigma _{NSD} = \sigma _{\mathrm{tot}} - \sigma _{\mathrm{el}} - \sigma _{\mathrm{sd}} - \sigma _{\mathrm{dd}}\) where \( \sigma _{\mathrm{tot}}(\sigma _{\mathrm{el}}, \sigma _{\mathrm{sd}}, \sigma _{\mathrm{dd}} )\) are the total, elastic, single, and double diffraction cross sections.

The paper is organized as follows. In the following section we discuss the main features of our approach, concentrating on the description of diffractive processes. In Sect. 3, we derive the main formulas for the correlation functions in our approach, while in Sect. 4 we compare our predictions with the available experimental data.

2 Our model: generalities, elastic amplitude, and inclusive production

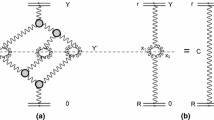
In this section we briefly review our model, which successfully describes diffractive [16, 17] and inclusive cross sections [18]. The main ingredient of our model is the BFKL Pomeron Green’s function, which we determined using the CGC/saturation approach [16, 78]. We determined this function from the solution of the non-linear Balitsky–Kovchegov equation [25, 26, 29], using the MPSI approximation [79, 82–85] to sum enhanced diagrams shown in Fig. 1a. It has the following form:

$$\begin{aligned}&G^{\text{ dressed }}\left( T\right) = a^2 (1 - \exp \left( -T\right) ) + 2 a (1 - a)\frac{T}{1 + T}\nonumber \\&\quad + (1 - a)^2 G\left( T\right) \text{ with }\nonumber \\&\quad \! G\left( T\right) = 1 - \frac{1}{T} \exp \left( \frac{1}{T}\right) \Gamma _0\left( \frac{1}{T}\right) \end{aligned}$$
(2.1)
$$\begin{aligned}&T\left( s, b\right) = \phi _0 S\left( b, m\right) e^{0.63\lambda \ln (s/s_0)} \quad \text{ with }\nonumber \\&\quad S\left( b , m \right) = \frac{m^2}{2 \pi } e^{ - m b} \end{aligned}$$
(2.2)

In these formulas we take \(a=0.65\); this value was chosen so as to obtain the analytical form for the solution of the BK equation. The parameters \(\lambda \) and \(\phi _0\) can be estimated in the leading order of QCD, but due to large next-to-leading order corrections we treat them as parameters of the fit. m is a non-perturbative parameter, which characterizes the large impact parameter behavior of the saturation momentum, as well as the typical sizes of the dipoles that take part in the interactions. The value of \(m =5.25\,\mathrm{GeV}\) in our model justifies our main assumption that BFKL Pomeron calculus based on a perturbative QCD approach is able to describe soft physics, since \(m \gg \mu _{\mathrm{soft}}\), where \(\mu _{\mathrm{soft}}\) denotes the natural scale for soft processes (\( \mu _{\mathrm{soft}} \sim \Lambda _{\mathrm{QCD}}\) and/or the pion mass).

Unfortunately, since the confinement problem is far from being solved, we assume a phenomenological approach for the structure of the colliding hadron. We use a two channel model, which also allows us to calculate the diffractive production in the region of small masses. In this model, we replace the rich structure of the diffractively produced states by a single state with the wave function \(\psi _D\), à la Good and Walker [86]. The observed physical hadronic and diffractive states are written in the form

$$\begin{aligned}&\psi _h= \alpha \psi _1+\beta \psi _2;\quad \psi _D = -\beta \psi _1+\alpha \psi _2;\nonumber \\&\quad \text{ where }\quad \alpha ^2+\beta ^2 =1. \end{aligned}$$
(2.3)

The functions \(\psi _1\) and \(\psi _2\) form a complete set of orthogonal functions \(\{ \psi _i \}\) which diagonalize the interaction matrix \({\mathbf T}\)

$$\begin{aligned} A^{i'k'}_{i,k}=\langle \psi _i\,\psi _k|\mathbf {T}|\psi _{i'}\,\psi _{k'}\rangle = A_{i,k}\,\delta _{i,i'}\,\delta _{k,k'}. \end{aligned}$$
(2.4)

The unitarity constraints take the form

$$\begin{aligned} 2\,\text{ Im }\,A_{i,k}\left( s,b\right) =|A_{i,k}\left( s,b\right) |^2 +G^{\mathrm{in}}_{i,k}(s,b), \end{aligned}$$
(2.5)

where \(G^{\mathrm{in}}_{i,k}\) denotes the contribution of all non-diffractive inelastic processes, i.e. it is the summed probability for these final states to be produced in the scattering of a state i off a state k. In Eq. (2.5) \(\sqrt{s}=W\) denotes the energy of the colliding hadrons, and b the impact parameter. A simple solution to Eq. (2.5) at high energies, has the eikonal form with an arbitrary opacity \(\Omega _{ik}\), where the real part of the amplitude is much smaller than the imaginary part. We have

$$\begin{aligned} A_{i,k}(s,b)&=i \left( 1 -\exp \left( - \Omega _{i,k}(s,b)\right) \right) ,\end{aligned}$$
(2.6)
$$\begin{aligned} G^{\mathrm{in}}_{i,k}(s,b)&=1-\exp \left( - 2\,\Omega _{i,k}(s,b)\right) . \end{aligned}$$
(2.7)

Equation (2.7) implies that \(P^S_{i,k}=\exp \left( - 2\,\Omega _{i,k}(s,b) \right) \), is the probability that the initial projectiles (i, k) reach the final state interaction unchanged, regardless of the initial state re-scatterings.

Table 1 Fitted parameters of the model. The values are taken from Ref. [17]
Full size table
Fig. 1
figure 1

a The set of the diagrams in BFKL Pomeron calculus. The wavy double lines denote the resulting (dressed) Green’s function of the Pomeron in the framework of high energy QCD, while the single wavy lines describe the BFKL Pomerons. b We show the net diagrams that include the interaction of BFKL Pomerons with colliding hadrons

Full size image

Note that there is no factor 1 / 2; its absence stems from our definition of the dressed Pomeron.

In the eikonal approximation we replace \( \Omega _{i,k}(s,b)\) by

$$\begin{aligned} \Omega _{i,k}(s,b)&=\int \mathrm{d}^2 b'\,\mathrm{d}^2 b''\, g_i\big (\vec {b}'\big )\,G^{\text{ dressed }}\big (T\big (s, \vec {b}''\big )\big )\nonumber \\&\quad \times g_k\big (\vec {b} - \vec {b}'- \vec {b}''\big ). \end{aligned}$$
(2.8)

We propose a more general approach, which takes into account new small parameters, which come from the fit to the experimental data (see Table 1 and Fig. 1):

$$\begin{aligned} G_{3{\mathbb {P}}}\Big / g_i(b = 0 ) \ll 1;\quad m \gg m_1\quad \text{ and }\quad m_2. \end{aligned}$$
(2.9)

The second equation in Eq. (2.9) leads to the fact that \(b''\) in Eq. (2.8) is much smaller than b and \( b'\); therefore, Eq. (2.8) can be re-written in a simpler form:

$$\begin{aligned} \Omega _{i,k}(s,b)&= \left( \int \mathrm{d}^2 b''\,G^{\text{ dressed }}\big ( T\big (s, \vec {b}''\big )\big )\right) \nonumber \\&\quad \times \int \mathrm{d}^2 b' g_i\big (\vec {b}'\big )\,g_k\big (\vec {b} - \vec {b}'\big )\nonumber \\&=\tilde{G}^{\text{ dressed }}\big (\bar{T}\big )\, \int \mathrm{d}^2 b' g_i\big ( \vec {b}'\big ) \,g_k\big (\vec {b} - \vec {b}'\big ). \end{aligned}$$
(2.10)

Selecting the diagrams using the first equation in Eq. (2.9) indicates that the main contribution stems from the net diagrams shown in Fig. 1b. The sum of these diagrams [17] leads to the following expression for \(\Omega _{i,k}(s,b)\):

$$\begin{aligned}&\Omega \left( Y; b\right) \nonumber \\&\quad = \int \mathrm{d}^2 b'\,\frac{ g_i\big (\vec {b}'\big )\,g_k\big (\vec {b} - \vec {b}'\big )\,\tilde{G}^{\text{ dressed }}\left( T\right) }{1+G_{3{\mathbb {P}}}\,\tilde{G}^{\text{ dressed }}\left( T\right) \left[ g_i\big (\vec {b}'\big ) + g_k\big (\vec {b} - \vec {b}'\big )\right] };\end{aligned}$$
(2.11)
$$\begin{aligned}&g_i\left( b \right) = g_i \,S_p\left( b; m_i \right) , \end{aligned}$$
(2.12)

where

$$\begin{aligned}&S_p\left( b,m_i\right) = \frac{1}{4 \pi } m^3_i \,b \,K_1\left( m_i b \right) \\&\tilde{G}^{\text{ dressed }}\left( \bar{T}\right) = \int \mathrm{d}^2 b \,G^{\text{ dressed }}\left( T\left( s, b\right) \right) \end{aligned}$$

where \( T\left( s, b\right) \) is given by Eq. (2.2).

Note that \(\tilde{G}^{\text{ dressed }}(\bar{T})\) does not depend on b and is a function of \( \bar{T} =T\left( s, b=0 \right) = \phi _0 \,e^{0.63\,\lambda Y}\).

In all previous formulas, the value of the triple BFKL Pomeron vertex is known: \(G_{3 {\mathbb {P}}} = 1.29\,\mathrm{GeV}^{-1}\).

To simplify the further discussion, we introduce the notation

$$\begin{aligned} N^{\mathrm{BK}}(G^i_{\mathbb {P}}(Y,b))&= a(1 - \exp (- G^i_{\mathbb {P}}(Y, b)))\nonumber \\&\quad +(1 - a)\frac{ G^i_{\mathbb {P}}(Y, b)}{1 + G^i_{\mathbb {P}}(Y, b)}, \end{aligned}$$
(2.13)

with \(a = 0.65\). It should be stressed that Eq. (2.13) with this value of a is an analytical approximation to the numerical solution for the BK equation [16, 17, 78]. Therefore, a is not a fitting parameter, as it has been determined from CGC/saturation effective theory. We have \( G^{i}_{\mathbb {P}}(Y, b) = g_i(b)\,\tilde{G}^{\text{ dressed }}(\bar{T})\). We recall that the BK equation sums the ‘fan’ diagrams shown in Fig. 2.

Fig. 2
figure 2

A typical example of ‘fan’ diagrams that are summed in Eq. (2.13)

Full size image
Fig. 3
figure 3

Mueller diagram for the single inclusive cross section. The double wavy lines describe the resulting Green function of the BFKL Pomerons (\(\tilde{G}^{\text{ dressed }}\)). The blobs stand for the vertices which are the same as in Fig. 1

Full size image
Fig. 4
figure 4

The Mueller diagram for the rapidity correlation between two particles produced in two parton showers. a The first Mueller diagram, while b indicates the structure of general diagrams. The double wavy lines describe the dressed BFKL Pomerons. The blobs stand for the vertices as shown in the legend

Full size image

For the elastic amplitude we have

$$\begin{aligned} a_{\mathrm{el}}(b) = \big (\alpha ^4 A_{1,1} + 2 \alpha ^2\,\beta ^2\,A_{1,2} + \beta ^4 A_{2,2}\big ). \end{aligned}$$
(2.14)

To determine the correlation function (given in Eq. (1.2)), we need to know the single inclusive cross sections. We have discussed these cross sections in Ref. [18]; for the sake of completeness we give the formula that describes the Mueller diagram of Fig. 3.

We have

$$\begin{aligned} \frac{\mathrm{d} \sigma }{\mathrm{d}y}&= \int \mathrm{d}^2 p_T\,\frac{\mathrm{d} \sigma }{\mathrm{d} y \,\mathrm{d}^2 p_T} = a_{{\mathbb {P}}{\mathbb {P}}}\,\ln \left( W/W_0\right) \nonumber \\&\quad \times \left\{ \alpha ^4 \,In^{(1)}\left( \frac{1}{2}Y + y\right) \, In^{(1)}\left( \frac{1}{2}Y - y\right) \right. \nonumber \\&\quad +\left. \alpha ^2\beta ^2 \left( In^{(1)}\left( \frac{1}{2}Y + y\right) \, In^{(2)}\left( \frac{1}{2}Y - y\right) \right. \right. \nonumber \\&\quad +\left. \left. \, In^{(2)}\left( \frac{1}{2}Y + y\right) \, In^{(1)}\left( \frac{1}{2}Y - y\right) \right) \,\right. \nonumber \\&\quad +\left. \beta ^4 \,In^{(2)}\left( \frac{1}{2}Y + y\right) \, In^{(2)}\left( \frac{1}{2}Y - y\right) \right\} \end{aligned}$$
(2.15)

where Y denotes the total rapidity of the colliding particles, and y is the rapidity of produced hadron. \(In^{(i)}\) is given by

$$\begin{aligned} In^{(i)}\left( y\right) = \int \mathrm{d}^2 b \,N^{\mathrm{BK}}\left( \,\tilde{G}^i_{\mathbb {P}}\left( y, b \right) \right) . \end{aligned}$$
(2.16)

\(a_{{\mathbb {P}}{\mathbb {P}}}\) is a fitted parameter that was determined in Ref. [18] (see Table 1).

3 Two particle correlations

3.1 Correlations between two parton showers

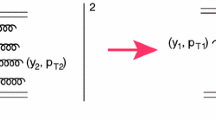
The Mueller diagram for the correlations between two parton showers is shown in Fig. 4. Examining this diagram, we see that the contribution to the double inclusive cross section differs from the product of two single inclusive cross sections. There are two reasons for this; the first is that in the expression for the double inclusive cross section, we integrate the product of the single inclusive cross sections, over b, at fixed b. The second is that the summation over i and k for the product of single inclusive cross sections is for fixed i and k.

Introducing the following new function enables us to write the analytical expression:

$$\begin{aligned}&I^{(i,k}(y, b ) = a_{{\mathbb {P}}{\mathbb {P}}}\,\ln \left( W/W_0\right) \nonumber \\&\quad \times \int \mathrm{d}^2 b' \,N^{\mathrm{BK}}\left( g^{(i)}\,S\left( m_i,b'\right) \tilde{G}^{\text{ dressed }}\left( \frac{1}{2}Y + y \right) \right) \nonumber \\&\quad \times N^{\mathrm{BK}}\left( g^{(k)}\,S\big (m_k, \vec {b} - \vec {b}^{'}\big ) \tilde{G}^{\text{ dressed }}\left( \frac{1}{2}Y- y \right) \right) . \end{aligned}$$
(3.1)

Using Eq. (3.1) we can write the double inclusive cross section in the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{2 } \text{ parton } \text{ showers }}}{ \mathrm{d}y_1\, \mathrm{d}y_2}\nonumber \\&\quad =\int \mathrm{d}^2 b \left\{ \alpha ^4 \,I^{(1,1)}\left( y_1, b \right) \,I^{(1,1)}\left( y_2, b \right) \right. \nonumber \\&\qquad \times \left. \alpha ^2\,\beta ^2\,\left( I^{(1,2)}\left( y_1, b \right) \,I^{(1,2)}\left( y_2, b \right) \right. \right. \nonumber \\&\qquad +\left. \left. I^{(2,1)}\left( y_1, b \right) \,I^{(2,1)}\left( y_2, b \right) \right) \right. \nonumber \\&\qquad +\left. \beta ^4\,I^{(2,2)}\left( y_1, b \right) \,I^{(2,2)}\left( y_2, b \right) \right\} . \end{aligned}$$
(3.2)

Comparing Eq. (3.2) with Eq. (2.15) squared, we note the different powers of \(\alpha \) and \(\beta \), which reflect the different summation over i and k, as well as different integration over b.

3.2 Correlations in one parton shower: semi-enhanced diagrams

The main theoretical assumption that we make in calculating the correlation in a one parton shower, is that the Mueller diagram technique [81], and the AGK cutting rules [87] are valid. We should note, however, that even if the Mueller diagrams provide the correct description of inclusive processes in QCD, the AGK cutting rules are not valid for calculations of the correlations in QCD [88–90]. Nevertheless, we believe that we can neglect the AGK cutting rules violating contributions since, first, they do not lead to long range rapidity correlations, which are the main subject of our concern, and second, as we will show below, the correlations in one parton shower turn out to be negligibly small.

It is instructive to write the expression for the first Mueller diagram in the following form (see Fig. 6a):

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{ one } \text{ parton } \text{ shower }}_{senh}}{\mathrm{d}y_1\,\mathrm{d}y_2} = \left( a_{{\mathbb {P}}{\mathbb {P}}}\,\ln \left( W/W_0\right) \right) ^2\nonumber \\&\quad \times \sum _{i=1,k=1}^2\alpha ^2_i\,\alpha ^2_k\,\int ^Y_{\max \left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2\right) }\!\!\!\!\!\mathrm{d}Y'\nonumber \\&\quad \times \int \mathrm{d}^2 b \,g_i\left( b \right) \tilde{G}\left( Y - Y'\right) \,G_{3 {\mathbb {P}}}\,\tilde{G}\nonumber \\&\quad \times \left( Y' - \frac{1}{2}Y - y_1\right) \,\tilde{G}\left( Y' - \frac{1}{2}Y - y_2\right) \nonumber \\&\quad \times \int \mathrm{d}^2 b' N^{\mathrm{BK}}\left( g^k\left( b \right) \tilde{G}\left( \frac{1}{2}Y - y_1\right) \right) \nonumber \\&\quad \times \int \mathrm{d}^2 b' N^{\mathrm{BK}}\left( g^k\left( b \right) \tilde{G}\left( \frac{1}{2}Y - y_2\right) \right) . \end{aligned}$$
(3.3)

The expression for the first Mueller diagram for two parton showers correlation (see Fig. 4a) has the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{2 } \text{ parton } \text{ showers }}_{senh}}{\mathrm{d}y_1\,\mathrm{d}y_2}\nonumber \\&\quad = \int \mathrm{d}^2 b \frac{\mathrm{d}^2 \sigma ^{\text{2 } \text{ parton } \text{ showers }}}{\mathrm{d} y_1\,\mathrm{d} y_2\,\mathrm{d}^2 b} \nonumber \\&\quad =\left( a_{{\mathbb {P}}{\mathbb {P}}}\,\ln \left( W/W_0\right) \right) ^2\sum _{i=1, k=1}^2\alpha ^2_i\,\alpha ^2_k\,\int \mathrm{d}^2 b \,\left( g_i\left( b \right) \right) ^2 \tilde{G}\nonumber \\&\qquad \times \left( Y' - \frac{1}{2}Y - y_1\right) \,\tilde{G}\left( Y' - \frac{1}{2}Y - y_2\right) \nonumber \\&\qquad \times \int \mathrm{d}^2 b' N^{\mathrm{BK}}\left( g^k\left( b \right) \tilde{G}\left( \frac{1}{2}Y - y_1\right) \right) \nonumber \\&\qquad \times \int \mathrm{d}^2 b' N^{\mathrm{BK}}\left( g^k\left( b \right) \tilde{G}\left( \frac{1}{2}Y - y_2\right) \right) . \end{aligned}$$
(3.4)

Comparing Eq. (3.3) with Eq. (3.4) one can see that

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{ one } \text{ parton } \text{ shower }}_{senh}}{\mathrm{d} y_1\,\mathrm{d} y_2} = \mathcal{H}\left( Y,y_1,y_2\right) \nonumber \\&\quad \times \int \mathrm{d}^2 b \,\frac{G_{3 {\mathbb {P}}}}{g_1\left( b\right) } \frac{\mathrm{d}^2 \sigma ^{\text{2 } \text{ parton } \text{ showers }}}{\mathrm{d} y_1\,\mathrm{d} y_2\,\mathrm{d}^2 b} \nonumber \\&\mathcal{H}\left( Y,y_1,y_2\right) = \int ^Y_{\max (\frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2)}\!\!\!\!\!\mathrm{d}Y' \nonumber \\&\quad \times \frac{ \tilde{G}\left( Y - Y'\right) \,\tilde{G}\left( Y' - \frac{1}{2}Y - y_1\right) \,\tilde{G}\left( Y' - \frac{1}{2}Y - y_2\right) }{\tilde{G}\left( \frac{1}{2}Y - y_1\right) \, \tilde{G}\left( \frac{1}{2}Y - y_2\right) }. \end{aligned}$$
(3.5)

For large values of y \(\tilde{G}\left( y\right) \rightarrow \text{ Const }\) and \( \mathcal{H}\left( Y,y_1,y_2\right) \) are proportional to \(\frac{1}{2}Y - y_1\)(\(y_1 > y_2\)). At small y \(\tilde{G}\left( y\right) \rightarrow \tilde{T}\left( y \right) = \phi _0 \int \mathrm{d}^2 b\, S\left( b,m\right) \,\exp \left( \Delta y\right) \), and the ratio of the \(\tilde{G}\) in Eq. (3.5) is equal to \(\phi _0 \int d^2\, S\left( b, m \right) \,\int \mathrm{d}Y ' \,\exp \left( \Delta \left( Y' - Y\right) \right) = \int \mathrm{d}^2 b \,T\left( Y=0, b \right) /\Delta \) where \( \Delta = 0.63 \lambda \) (see Eq. (2.2)). Therefore, we could expect that the semi-enhanced diagrams give a larger contribution to the double inclusive cross section than the production from two parton showers. However, Fig. 5 shows that both the value and the increase turn out to be small in the kinematic region accessible to experiment. Even at ultra high energies, shown in Fig. 5b, \( \mathcal{H}\left( Y,y_1,y_2\right) \le 0.012\).

Fig. 5
figure 5

a The function \(\mathcal{H}\left( Y,y_1,y_2\right) \) versus \(Y = \ln \left( W^2/W^2_0\right) \) for \(y_1 = y_2=0\). The curve 1 shows \(\mathcal{H}\left( Y,y_1,y_2\right) \) in which all \(\tilde{G}\) are replaced by the first order of its expansion with respect to \(T\left( Y, b\right) \); line 2 is the exact calculation. b is the same as a but for a large region of Y. c \(\mathcal{H}\left( Y,y_1,y_1\right) \) is plotted versus Y at different values of \(y_1\). \(\mathcal{H}\left( Y,0,y_2\right) \) is shown in d as a function of \(|y_2|\) at different energies W

Full size image
Fig. 6
figure 6

Mueller diagrams for the rapidity correlation between two particles produced in one parton showers: semi-enhanced diagrams. a Shows the first Mueller diagram, while b gives the structure of general diagrams. The double wavy lines describe dressed BFKL Pomerons. The blobs stand for the vertices shown in the legend

Full size image

On the other hand, the contribution of Eq. (3.5) is small and is proportional to \(G_{3{\mathbb {P}}}/g_i\,\ll \,1\). Bearing in mind that \(G_{3 {\mathbb {P}}} = 1.29 \) in our approach, one can see that the maximum value for \( \text{ max }\left( \mathcal{H}\right) \approx 0.012\) and we have the values of

$$\begin{aligned}&\max \left( \mathcal{H}\right) \frac{G_{3 {\mathbb {P}}}}{g_1\left( 0 \right) } \approx 1.4 \,10^{-4};\nonumber \\&\quad \max \left( \mathcal{H}\right) \frac{G_{3 {\mathbb {P}}}}{g_2\left( 0 \right) } \approx 1.4 \,10^{-3}. \end{aligned}$$
(3.6)

Therefore, we expect that the contribution of the correlations due semi-enhanced diagrams is negligibly small.

The general expression for the double inclusive cross section (see Fig. 6b) can be written using two new functions \(S^i\left( y_1,y_2\right) \) and \(S_k\left( y_1, y_2\right) \) defined as

$$\begin{aligned}&S^i\left( y_1,y_2\right) \nonumber \\&\quad =\int \mathrm{d}^2 b' \,N^{\mathrm{BK}}\left( g^{(i)}\,S\left( m_i,b'\right) \tilde{G}^{\text{ dressed }}\left( \frac{1}{2}Y + y_1 \right) \right) \nonumber \\&\qquad \times N^{\mathrm{BK}} \left( g^{(i)}\,S\left( m_i, b'\right) \tilde{G}^{\text{ dressed }}\left( \frac{1}{2}Y + y_2 \right) \right) \nonumber \\&\qquad \times \left( \frac{G_{3 {\mathbb {P}}}}{ g^{(i)} \,S\left( m_i,b'\right) }\right) \end{aligned}$$
(3.7)
$$\begin{aligned}&S_i\left( y_1,y_2\right) \nonumber \\&\quad = \int \mathrm{d}^2 b' \,N^{\mathrm{BK}}\left( g^{(i)}\,S\left( m_i,b'\right) \tilde{G}^{\text{ dressed }}\left( \frac{1}{2}Y- y_1 \right) \right) \nonumber \\&\qquad \times N^{\mathrm{BK}}\left( g^{(i)}\,S\left( m_i, b'\right) \tilde{G}^{\text{ dressed }}\left( \frac{1}{2}Y - y_2 \right) \right) . \end{aligned}$$
(3.8)
Fig. 7
figure 7

Mueller diagrams for the rapidity correlation between two particles produced in one parton showers: enhanced diagrams. a shows the first Mueller diagram, while b indicates the structure of general diagrams. The double wavy lines describe dressed BFKL Pomerons. The blobs stand for the vertices which are shown in the legend

Full size image

It takes the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{1 } \text{ parton } \text{ shower }}_{\text{ semi-enhanced }}}{ \mathrm{d}y_1\, \mathrm{d}y_2} = \mathcal{H}\left( Y,y_1,y_2\right) \left( a_{{\mathbb {P}}{\mathbb {P}}}\,\ln \left( W/W_0\right) \right) ^2\nonumber \\&\quad \times \left\{ 2\, \alpha ^4 \,S^1\left( y_1, y_2 \right) \,S_1\left( y_1, y_2 \right) + \alpha ^2\,\beta ^2(S^1(y_1, y_2)\right. \nonumber \\&\quad \qquad \times \left. S_2( y_1 y_2 ) + S_1(-y_1,-y_2)\,S^2( - y_1,- y_2 )\right. \nonumber \\&\quad \qquad +\left. 2\,\beta ^4\,S^2\left( y_1, y_2 \right) \,S_2\left( y_1, y_2 \right) \right\} . \end{aligned}$$
(3.9)

3.3 Correlations in one parton shower: enhanced diagrams

The first Mueller diagram for the correlations from the enhanced diagram is shown in Fig. 7a, and it has the following form:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{ one } \text{ parton } \text{ shower }}_{\mathrm{enh}}}{\mathrm{d}y_1\,\mathrm{d}y_2} = \left( a_{{\mathbb {P}}{\mathbb {P}}}\,\ln \left( W/W_0\right) \right) ^2\nonumber \\&\quad \times \sum _{i=1,k=1}^2\alpha ^2_i\,\alpha ^2_k\,\int ^Y_{\max \left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2\right) }\!\!\!\!\!\mathrm{d}Y'\,\int ^{\min \left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2\right) }_0\!\!\!\!\!\mathrm{d}Y'' \nonumber \\&\quad \times \int \mathrm{d}^2 b \,g_i\left( b \right) \tilde{G}\left( Y - Y'\right) \,G_{3 {\mathbb {P}}}\,\tilde{G}\nonumber \\&\quad \times \left( Y' - \frac{1}{2}Y - y_1\right) \,\tilde{G}\left( Y' - \frac{1}{2}Y - y_2\right) \nonumber \\&\quad \times \int \mathrm{d}^2 b' \,g_k\left( b' \right) \tilde{G}\left( \frac{1}{2}Y + y_2 -Y''\right) \,\tilde{G}\nonumber \\&\quad \times \left( \frac{1}{2}Y + y_1 - Y''\right) \,G_{3 {\mathbb {P}}}\,\tilde{G}\left( Y''\right) ; \end{aligned}$$
(3.10)

this can be re-written as

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{ one } \text{ parton } \text{ shower }}_{\mathrm{enh}}}{\mathrm{d}y_1\,\mathrm{d}y_2}\nonumber \\&\quad = \int \mathrm{d}^2 b \,\frac{G_{3{\mathbb {P}}}}{g_i\left( b\right) } \frac{G_{3 {\mathbb {P}}}}{g_k\left( b\right) } \frac{\mathrm{d}^2 \sigma ^{\text{2 } \text{ parton } \text{ showers }}}{\mathrm{d}y_1\,\mathrm{d}y_2\,\mathrm{d}^2 b}. \end{aligned}$$
(3.11)

An example of typical diagrams is shown in Fig. 7. The formula, summing all diagrams shown in Fig. 7b takes the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{\text{1 } \text{ parton } \text{ shower }}_{\text{ enhanced }}}{ \mathrm{d}y_1\,\mathrm{d}y_2}=\mathcal{K} \left( a_{{\mathbb {P}}{\mathbb {P}}} \,\ln \left( W/W_0\right) \right) ^2\nonumber \\&\quad \times \mathcal{H}\left( Y,y_1,y_2\right) \,\mathcal{H}\left( Y,-y_1,-y_2\right) \,\end{aligned}$$
(3.12)
$$\begin{aligned}&\big \{\alpha ^4 \,S^1\left( y_1, y_2 \right) \,S^1\left( -y_1, -y_2 \right) + \alpha ^2\,\beta ^2\big [S^1\left( y_1, y_2 \right) \nonumber \\&\quad \times S^2\left( -y_1 ,- y_2 \right) + S^2\left( y_1, y_2 \right) \,S^1\left( -y_1 ,- y_2 \right) \big ]\nonumber \\&\quad +\beta ^4\,S^2\left( y_1, y_2 \right) \,S^2\left( -y_1, -y_2 \right) \big \} \end{aligned}$$
(3.13)

where

$$\begin{aligned} \mathcal{K}=\int \mathrm{d}^2 b (G^{\text{ dressed }}(Y,b))^2\Big /\left( \int \mathrm{d}^2 b \,G^{\text{ dressed }}(Y,b)\right) ^2 \end{aligned}$$
(3.14)

where \(G^{\text{ dressed }}\left( Y,b\right) \) is determined by Eqs. (2.1) and (2.2). The contributions of enhanced diagrams are proportional to the square of the ratios given by Eq. (3.6) and, therefore, they are negligibly small.

3.4 Correlation function

The correlation function \(R\left( y_1,y_2\right) \) is defined as

$$\begin{aligned}&R\left( y_1,y_2\right) =\sigma _{NSD}\,\nonumber \\&\quad \times \left\{ \frac{\mathrm{d}^2 \sigma ^{\text{2 } \text{ parton } \text{ showers }}}{ \mathrm{d}y_1\,\mathrm{d}y_2}+\frac{\mathrm{d}^2 \sigma ^{\text{1 } \text{ parton } \text{ shower }}_{\text{ semi-enhanced }}}{ \mathrm{d}y_1\,\mathrm{d}y_2}\right. \nonumber \\&\qquad +\left. \frac{\mathrm{d}^2 \sigma ^{\text{1 } \text{ parton } \text{ shower }}_{\text{ enhanced }}}{ \mathrm{d}y_1\,\mathrm{d}y_2}\right\} \Bigg / \left\{ \frac{\mathrm{d} \sigma }{\mathrm{d}y_1}\,\frac{\mathrm{d} \sigma }{\mathrm{d}y_2}\right\} -1. \end{aligned}$$
(3.15)

3.5 Kinematic corrections

In all our previous equations we assumed that \(Y = \ln \left( W^2/W^2_0\right) \) with \(W_0 = 1\,\mathrm{GeV}\). This assumption appears natural for the elastic amplitude and the cross section of the single inclusive production, but it should be re-examined for the correlation function. For this observable, the definition of Y has to be modified to account for the fact that the energy of the parton shower is not equal to \(W = \sqrt{s}\) (\(s = W^2\)) but smaller than or equal to \(\tilde{s}= \tilde{W}^2 =x_1 x_2 s=x_1 x_2 W^2\) (see Fig. 8, where we show the diffractive cut of the Mueller diagram of Fig. 4a). The simplest way to find \(x_1\) and \(x_2\) is to assume that both \(p^2_1 = p^2_2 = - \bar{Q}^2 \gg \mu ^2_{\text{ soft }}\), where \(\mu _{\text{ soft }}\) is the scale of the soft interactions, \(\mu _{\text{ soft }} \sim \Lambda _{QCD}\). In our approach the scale of the hardness for the BFKL Pomeron is \(\bar{Q} = m \gg \mu _{\text{ soft }}\). Bearing this in mind, the energy variable \(x_1\) (\(x_2\)) for gluon–hadron scattering is equal to

$$\begin{aligned}&0 = (x_1\,P_1 + p_1)^2 = - \bar{Q}^2 + x _1\,2\, p_1\cdot P_1;\nonumber \\&p^2_1 = - \bar{Q}^2\quad x_1 = \frac{\bar{Q}^2}{ M^2 + \bar{Q}^2}. \end{aligned}$$
(3.16)

\(p_1\), \(P_1\), and \(x_1P_1\) are the momenta of the gluon, the hadron, and the parton (quark or gluon) with which the initial gluon interacts. From Eq. (3.16) one has

$$\begin{aligned} \tilde{s}=x_1 x_2 s =\frac{s \,\bar{Q}^4}{M^4} \end{aligned}$$
(3.17)
Fig. 8
figure 8

The Mueller diagram for the rapidity correlation between two particles produced in two parton showers: the diffractive cut of the diagram. The double wavy lines describe dressed BFKL Pomerons. The blob stands for \(a_{{\mathbb {P}}{\mathbb {P}}}\)

Full size image
Fig. 9
figure 9

\(R\left( Y,0,0\right) \) versus \(x_1\) for \(Y =\ln \left( x^2_1W^2/W^2_0\right) \) for different energies W. The red line indicates the moment \(C_2=\langle |n^2|\rangle /\left( \langle |n^2|\rangle \right) = 2\) for the window in rapidity \(-0.5 <y < + 0.5\), measured by the CMS experiment [13]

Full size image

where M denotes the mass of produced hadron in the diffractive process. Equation (3.17) is written for small \(x_i\), where \(M^2 \gg \bar{Q}^2\). For the two channel model, it is the mass of the diffractive state. We can use the quark structure function to estimate the typical value of \(x_1 = x_2\), as is suggested in Ref. [91, 92]. Using the structure functions at \(Q^2 \approx 25\,\mathrm{GeV}^2\), one finds that \(\langle |x_1|\rangle \approx 0.3 \div 0.5\). In Fig. 9 the values of \(R\left( Y,0,0\right) \) are plotted for \(Y = \ln \left( x^2_1W^2/W^2_0\right) \) as a function of \(x_1\).

3.6 Correlation in one parton shower: emission from one BFKL Pomeron

In addition to the sources of correlation that have been discussed above, we need to take into account the correlation between two gluons emitted from one BFKL Pomeron (see Fig. 10). At large \( y_{12} = |y_1 - y_2|\) the diagram of Fig. 10 induces long range correlations in rapidity, however, at small \(y_{12}\) this emission is suppressed, and we do not expect a large contribution from this source.

The contribution of this diagram can be written in the form

$$\begin{aligned} C^{\text{ BFKL }}\left( y_1,y_2\right) =\sigma _{NSD}\frac{\sum ^2_{i,k =1} \alpha _i \alpha _k \Gamma _i\left( \frac{1}{2}Y - y_1\right) \tilde{G}^{\text{ dressed }}\left( y_{12}\right) \Gamma _k\left( \frac{1}{2}Y + y_2\right) }{\sum ^2_{i,k =1}\,\alpha _i \alpha _k\Gamma _i\left( \frac{1}{2}Y - y_1\right) \, \Gamma _k\left( \frac{1}{2}Y + y_1\right) \sum ^2_{i,k =1}\,\alpha _i \,\alpha _k \Gamma _i\left( \frac{1}{2}Y - y_2\right) \, \Gamma _k\left( \frac{1}{2}Y + y_2\right) } \end{aligned}$$
(3.18)

where

$$\begin{aligned} \Gamma _{i}\left( y \right) =\int \mathrm{d}^2 b \,N^{\mathrm{BK}}\big (g_i(b) \tilde{G}^{\text{ dressed }}(y)). \end{aligned}$$
(3.19)
Fig. 10
figure 10

Mueller diagram for emission of particles from one BFKL Pomeron

Full size image

For small values of the argument \( \Gamma _{i}\left( y \right) \, \xrightarrow {y \ll 1}\,\int \mathrm{d}^2 b \, g_i\left( b \right) \tilde{G}^{\text{ dressed }}\left( y\right) \) Eq. (3.18), has no dependence on \(y_{12}\), leading to long range rapidity correlations. However, it turns out that the exact computation, leads to very small values of \( C^{\text{ BFKL }}\left( y_1,y_2\right) \): approximately 0.2 \(\div \) 0.4 % of the contributions from the sources discussed above.

Fig. 11
figure 11

Mueller diagram for the short range rapidity correlations. Wavy double lines denote BFKL Pomerons, zigzag lines describe the exchange of the secondary Reggeon trajectory

Full size image

3.7 Short range rapidity correlation

Besides long range rapidity correlations, the emission from one BFKL Pomeron, as well as the hadronization in one gluon jet, can lead to short range correlations in rapidity. Unfortunately, at present, this contribution cannot be treated on pure theoretical grounds, as it involves confinement effects. To estimate this contribution, we introduce the Mueller diagram shown in Fig. 11, where we describe this correlation by the phenomenological constant \(a_{{\mathbb {P}}{\mathbb {R}}}\), and introduce the correlation length \(\Delta \approx 2\). In the diagram of Fig. 11 for the zigzag line we have \(a^2_{{\mathbb {P}}{\mathbb {R}}}\exp \left( - \frac{y_{12}}{\Delta }\right) \) (\(y_{12} = | y_1 = y_2|\)). Our estimate for \(\Delta \) stems from Reggeon phenomenology, in which the zigzag line describes the contribution of the secondary Reggeon, with a propagator \(\exp \left( - ( 1 - \alpha _{\mathbb {R}}(0)) y_{12}\right) \) and \(\alpha _{\mathbb {R}}(0) \approx 0.5\). At first sight such a parametrization of the short range correlations neglects the contributions of resonances, which are an essential part of these correlations. Due to the duality between the Reggeon exchange and the resonance contributions, we believe that the Reggeon description of the short range correlations takes in consideration the main part of the resonance contributions. However, a more detailed description of the short range correlation should include the production of resonances.

The contribution of this diagram takes the form

$$\begin{aligned} C^{\text{ short } \text{ range }}\left( y_1,y_2\right) = \left( \frac{a_{{\mathbb {P}}{\mathbb {R}}}}{a_{{\mathbb {P}}{\mathbb {P}}}}\right) ^2\,\sigma _{NSD} \frac{\sum ^2_{i,k=1} \alpha _i \,\alpha _k\,\Gamma _i\left( \frac{1}{2}Y - y_1\right) e^{- \frac{y_{12}}{\Delta }}\, \Gamma _k\left( \frac{1}{2}Y + y_2\right) }{\sum ^2_{i,k=1} \alpha _i \,\alpha _k\,\Gamma _i\left( \frac{1}{2}Y - y_1\right) \, \Gamma _k\left( \frac{1}{2}Y + y_1\right) \, \sum ^2_{i,k=1} \alpha _i \,\alpha _k\,\Gamma _i\left( \frac{1}{2}Y - y_2\right) \, \Gamma _k\left( \frac{1}{2}Y + y_2\right) }. \end{aligned}$$
(3.20)

4 Predictions and comparison with the experiment

Figure 9, shows that the correlation function increases with energy and becomes rather large (of the order of 1) at \(W = 7\,\mathrm{TeV}\). This qualitative feature is in agreement with the experimental data from the LHC. The first set of data is the multiplicity distribution measured by the CMS collaboration [13]. In particular, the value of \(C_2=\langle |n^2|\rangle /\left( \langle |n^2|\rangle \right) \) turns out to be very close to 2, for the window in rapidities \(-0.5 < \eta < 0.5\). Since \(C_2 = R\left( 0,0\right) + 1 + 1/\mathrm{d}N/\mathrm{d}\eta |_{\eta =0}\) where \(\mathrm{d}N /\mathrm{d} \eta _{\eta =0}\) denotes the multiplicity at \(\eta =0\), and at \(W = 7\, \mathrm{TeV}\), it is equal to 5.8, while \(R\left( 0, 0\right) = 0.82\).Footnote 1

The second set of the data is the measurement of the double parton interaction (DPI) [93–98]. In the LHC experiments, the double inclusive cross sections of two pairs of back-to-back jets with momenta \(p_{T,1}\) and \(p_{T,2}\) were measured with rapidities of two pairs (\(y_1\) and \(y_2\)) close to each other (\(y_1 \approx y_2\)). These pairs can only be produced from two different parton showers. The data were parameterized in the form

$$\begin{aligned} \frac{\mathrm{d} \sigma }{\mathrm{d}y_1 \mathrm{d}^2 p_{T,1} \mathrm{d}y_2 \mathrm{d}^2 p_{T,2}} =\frac{m}{2 \sigma _{\mathrm{eff}}}\,\frac{\mathrm{d} \sigma }{\mathrm{d}y_1 \mathrm{d}^2 p_{T,1}}\frac{\mathrm{d} \sigma }{\mathrm{d}y_2 \mathrm{d}^2 p_{T,2}}\nonumber \\ \end{aligned}$$
(4.1)

where \(m =2 \) for pairs of different jets, and \(m=1\) for identical pairs. One can calculate the rapidity correlation function using Eq. (4.1),

$$\begin{aligned} R\left( y_1, y_2,p_{T,1},p_{T,2}\right)&=\frac{\frac{1}{\sigma _{\mathrm{in}}}\frac{\mathrm{d} \sigma }{\mathrm{d}y_1 \mathrm{d}^2 p_{T,1} \mathrm{d}y_2 \mathrm{d}^2 p_{T,2}}}{\frac{1}{\sigma _{\mathrm{in}}}\frac{\mathrm{d} \sigma }{\mathrm{d}y_1 \mathrm{d}^2 p_{T,1}}\,\frac{1}{\sigma _{\mathrm{in}}}\frac{\mathrm{d} \sigma }{\mathrm{d}y_2 \mathrm{d}^2 p_{T,2}} }- 1 \nonumber \\&=\frac{\sigma _{\mathrm{in}}}{\sigma _{\mathrm{eff}}} - 1 \approx 2. \end{aligned}$$
(4.2)

For the above the estimates we use \(\sigma _{\mathrm{eff}} = 12 - 15\) mb (see Refs. [93–98]) and \(\sigma _{\mathrm{in}} = \sigma _{\mathrm{tot}} - \sigma _{\mathrm{el}} - \sigma _{\mathrm{sd}} - \sigma _{\mathrm{dd}} \approx 50\) mb for the energy \(W = 7\,\mathrm{TeV}\) (see Ref. [17] and references therein). These data confirm that at high energies we are dealing with a system of partons that have a large mutual attraction. The fact that we predict a smaller correlation than we have in this experiment does not discourage us, since the correlation function in Eq. (4.2) differs from the one that we calculate (see Eq. (1.2)).

Fig. 12
figure 12

\(\sigma _n/\sigma \) versus multiplicity \(n/\bar{n}\) at different energies W in the rapidity window \(-0.5 < y < 0.5\). The curves are normalized by \(\sum _n \frac{\sigma _n}{\sigma }= \bar{n} \sum _{n/ \bar{n}} (\frac{\sigma _n}{\sigma }) = 1\). Hence, at fixed \(n/\bar{n}\), the data at \(W = 13\) TeV with higher multiplicity is above the data at \(W = 7\) TeV

Full size image

The forward–backward correlation has been measured by the ATLAS collaboration in Ref. [14]. The observable that was used in Ref. [14] differs from the correlation function \(R\left( \eta _1,\eta _2\right) \), and it can be re-written as

$$\begin{aligned} \rho ^n_{f b}=\frac{R\left( \eta _1,\eta _2\right) }{\sqrt{R\left( \eta _1,\eta _1\right) \,R\left( \eta _2,\eta _2\right) }}. \end{aligned}$$
(4.3)

The value of \(\rho ^n_{f b} \sim 0.666\) [14] indicates large correlations, but it is difficult to compare \(\rho ^n_{f b}\) with our estimates, since ATLAS introduced a specific selection: the \(p_T\) of all produced particles should be larger than 100 MeV, while \(R\left( \eta _1,\eta _2\right) \) is defined as integrated over all momenta.

Using \(R\left( 0,0\right) \), we estimate the values for \(C_2\) for \(W=13\,\mathrm{TeV}\), and using the formula for the negative binomial distribution,

$$\begin{aligned} \frac{\sigma _n}{\sigma }=\left( \frac{r}{\bar{n} + r}\right) ^r \frac{\Gamma \left( n + r\right) }{n!\,\Gamma \left( r \right) }\left( \frac{\bar{n}}{\bar{n} + r}\right) ^n, \end{aligned}$$
(4.4)

we obtain the multiplicity distribution in the rapidity window \(-0.5 < \eta < 0.5\) shown in Fig. 12. In Eq. (4.4) \(\bar{n} = \mathrm{d}N/\mathrm{d}\eta |_{\eta = 0}\), which was calculated in Ref. [18]. From Fig. 12 we expect a violation of the KNO scaling behavior [99]. Accordingly to KNO scaling \(\sigma _n/\sigma = F\left( n/\bar{n}\right) \) with \(\bar{n} = \int ^{0.5}_{-0.5}\, \mathrm{d} \eta \, \mathrm{d}N/\mathrm{d}\eta = \mathrm{d}N/\mathrm{d} \eta |_{\eta =0}\).

It turns out that \(R\left( y_1,y_2\right) \) at fixed energy depends neither on \(y_1\) nor on \(y_2\), giving a perfect example of long range correlations in rapidity. To understand why we have these features, it is instructive to start from Fig. 4a at small values of Y. In this kinematic region we can replace \(\tilde{G}^{\text{ dressed }} \rightarrow \tilde{G}^{\text{ bare }} =\tilde{T}\left( Y\right) \) and \(N^{\mathrm{BK}}\left( Y, b \right) \rightarrow g_i\left( b\right) \,\tilde{G}^{\text{ bare }}\). After simple algebra, the correlation function is equal to

$$\begin{aligned} R\left( y_1, y_2\right)&=\frac{1}{\alpha ^4}\, \sigma _{NSD}\,\nonumber \\&\quad \times \frac{\int \mathrm{d}^2 b\left( \int \mathrm{d}^2 b' g_1\big (\vec {b}\big )\, g_1\big ( \vec {b} - \vec {b}'\big )\right) ^2}{ \left( \int \mathrm{d}^2 b\, \mathrm{d}^2 b'\, g_1\big ( \vec {b}\big )\, g_1\big (\vec {b} - \vec {b}'\big )\right) ^2} - 1. \end{aligned}$$
(4.5)

In Eq. (4.5) we use the fact that in our model \(g_1 \gg g_2\). Equation (4.5) leads to a correlation function that does not depend on \(y_1\) and \(y_2\).

On the other hand, at very large Y, \(N^{\mathrm{BK}}\left( Y, b \right) \rightarrow \Theta \left( R\left( Y\right) - b\right) \), where \(\Theta \left( b\right) \) is a step function. Plugging in this simple expression, we obtain

$$\begin{aligned}&R\left( y_1, y_2\right) = \sigma _{NSD}\nonumber \\&\qquad \times \frac{\int \mathrm{d}^2 b\, \Theta \left( R\left( \frac{1}{2}Y - y_2\right) - b\right) \,\Theta \left( R\left( \frac{1}{2}Y - y_1\right) - b\right) \,R^2\left( \frac{1}{2}Y - y_1\right) \,R^2\left( \frac{1}{2}Y - y_2\right) }{\pi ^2\,R^4\left( \frac{1}{2}Y - y_1\right) \,R^4\left( \frac{1}{2}Y - y_2\right) } - 1\nonumber \\&\quad \rightarrow \frac{ \sigma _{NSD}}{\pi R^2\left( \frac{1}{2}Y - y_1\right) \Big |_{y_1 < y_2} } - 1. \end{aligned}$$
(4.6)

\(R\left( Y\right) \) in Eq. (4.6) denotes a typical impact parameter at large Y, which is proportional to Y.Footnote 2 Recall that at high energies, all components of the wave functions in the two channel model, give the same contribution. This is the reason why we do not have an extra factor, depending on \(\alpha \) and \(\beta \).

Equation (4.6) shows the logarithmic dependence on \(y_1\). Using Eq. (4.6) we can estimate the \(y_1\)(\(y_2\)) dependence of \(R\left( y_1,y_2\right) )\), calculating

$$\begin{aligned} \langle |b^2\left( Y\right) |\rangle =\frac{\int b^2 \,\mathrm{d}^2 b \,N^{\mathrm{BK}}\left( g_i\left( b\right) \,\tilde{G}^{\text{ dressed }}\left( Y\right) \right) }{\int \,\mathrm{d}^2 b \,N^{\mathrm{BK}}\left( g_i\left( b\right) \,\tilde{G}^{\text{ dressed }}\left( Y\right) \right) }. \end{aligned}$$
(4.7)

From Fig. 13, in which we plot the results of our calculation, one can see that only at large \(Y > 11\) does \( \langle |b^2\left( Y\right) | \rangle \) start showing visible Y dependence. Two vertical dotted lines mark the widow in rapidity, which is essential in the calculation of the correlation function at \(W = 7 \,\mathrm{TeV}\) for \(-2 <y_1,y_2 < 2\). We can expect a change of R by 2 %. The actual calculation gives even less. Using \(N^{\mathrm{BK}}\left( Y, b \right) \rightarrow \Theta \left( R\left( Y\right) - b\right) \) gives \(R^2\left( Y\right) =2 \langle |b^2\left( Y\right) |\rangle \). Using this relation, we estimate \(R\left( y_1,y_2\right) \) as

$$\begin{aligned} R\left( y_1, y_2\right) =\frac{1}{\alpha ^4}\,\frac{ \sigma _{NSD}}{2 \pi \langle |b^2\left( \frac{1}{2}Y - y_1\right) |\rangle } - 1. \end{aligned}$$
(4.8)

At \(W = 7\,\mathrm{TeV}\) from Eq. (4.8) we find that \(R\left( y_1, y_2\right) =1.647\), while the exact calculation give 1.437 (see Fig. 9). At \(W = 13\,\mathrm{TeV}\) this simple formula leads to \(R\left( y_1, y_2\right) = 1.72\), versus 1.64 from the exact calculations (see Fig. 9).

Fig. 13
figure 13

\(\langle |b^2\left( Y\right) |\rangle \), defined in Eq. (4.7), versus Y

Full size image

The correlations, measured by the ATLAS collaboration [14], at first sight contradict both our estimate and the CMS data, regarding the multiplicity distribution. We first check Eq. (4.3). The measured observable has the form [14]

$$\begin{aligned} \rho ^n_{f b}=\frac{\langle \left( n_f - \langle n_f\rangle \right) \,\left( n_b - \langle n_b\rangle \right) \rangle }{\sqrt{\langle \left( n_f - \langle n_f\rangle \right) ^2\rangle \,\langle \left( n_b- \langle n_b\rangle \right) ^2\rangle }}. \end{aligned}$$
(4.9)

The numerator of Eq. (4.9) can be written as \(R\left( y_1,y_2\right) \Delta y_1 \Delta y_2\), where \(\Delta y_i\) is the interval of rapidities where the hadrons are measured. However, at the same value of rapidity \(R\left( y_1,y_1\right) ( \Delta y_1)^2\) corresponds to \(\langle n ( n - 1)\rangle - \langle n \rangle ^2\). Therefore, we have the expression

$$\begin{aligned} \langle \left( n_f - \langle n_f\rangle \right) ^2\rangle =\left( R\left( y_1,y_1\right) + \frac{1}{ \frac{\mathrm{d} N}{\mathrm{d}y_1} \,\Delta y_1}\right) \left( \Delta y_1\right) ^2, \end{aligned}$$

which leads to the following formula for \(\rho ^n_{f b}\):

$$\begin{aligned} \rho ^n_{f b}=\frac{R\left( y_1, y_2\right) }{\sqrt{ \left( R\left( y_1,y_1\right) + \frac{1}{ \frac{\mathrm{d} N}{\mathrm{d}y_1} \,\Delta y_1}\right) \, \left( R\left( y_2,y_2\right) + \frac{1}{ \frac{\mathrm{d} N}{\mathrm{d}y_2} \,\Delta y_2}\right) }}.\nonumber \\ \end{aligned}$$
(4.10)

Taking \(\Delta y_1 = 0.5\), we see that the first element of the Table 2 is equal to 0.7, which is in good agreement with the experimental value \(0.666 \pm 0.011\).

Table 2 Multiplicity correlations for events at \(\sqrt{s} = 7\) TeV for events with a minimum of two charged particles in the kinematic interval \(p_{T} > 100\) MeV and \(|\eta | < 2.5\) for different combinations of forward and backward pseudorapidity interval. The data is take from Ref. [14]. The numbers in parentheses are our estimates
Full size table

To describe our results given in Table 2, we also need to take short range rapidity correlations into account. In this table, in parentheses we have our estimates, which we obtain describing the correlation function in the form

$$\begin{aligned}&R\left( y_1,y_2\right) =R^{\text{ long } \text{ range }}\left( y_1,y_2\right) \,\nonumber \\&\quad +\big (C^{\text{ short } \text{ range }}\left( y_1,y_2\right) - C^{\text{ short } \text{ range }}(0, 0)\big );\nonumber \\&C^{\text{ short } \text{ range }}\left( y_1,y_2\right) = a\nonumber \\&\quad \times \frac{\Gamma _1\left( \frac{1}{2}Y - y_1\right) e^{- \frac{y_{12}}{\Delta }} \Gamma _1\left( \frac{1}{2}Y + y_2\right) }{\Gamma _1\left( \frac{1}{2}Y - y_1\right) \, \Gamma _1\left( \frac{1}{2}Y + y_1\right) \, \Gamma _1\left( \frac{1}{2}Y - y_2\right) \, \Gamma _1\left( \frac{1}{2}Y + y_2\right) } \end{aligned}$$
(4.11)

with \(a =0.7\) and \(\Delta = 2\). In Eq. (4.11) \(y_{12} = | y_1 - y_2|\) and we restrict ourselves to the contribution of the state ”1” in Eq. (3.20), since \(g_1 \gg g_2\). We assumed that \( C^{\text{ short } \text{ range }}(0,0)=0\) since at \(y_{12}=0\) Eq. (3.20) leads to the long range correlations which we have calculated in Sect. 3.4. One can see that the agreement is not perfect, but it demonstrates that the ATLAS data can be reproduced, by including the short range correlations.

5 Conclusions

The main result of this paper, is that in our model, which is based on the CGC/saturation approach, we have discovered a mechanism that produces large, long range rapidity correlations at high energies. The large values of the correlation function \(R\left( y_1,y_2\right) \ge 1\) at high energies, lends strong support to the idea that at high energies the system of partons that is produced, is not only dense, but also has strong attractive forces acting between the partons.

Another interesting result is that this mechanism, leads to long range rapidity correlations that are independent of \(y_{1,2}\), and stems from the correlation between two parton showers, i.e., we found that in our approach the contribution from enhanced and semi-enhanced diagrams that describe the interaction inside a single parton shower, turns out to be negligibly small. It should be stressed that the contribution of the same diagrams in the process of diffraction dissociation in the region of large mass is essential, as they are responsible for the experimental measured diffraction in the region of large mass [17]. This feature, is in direct contradiction to the soft Pomeron-based models for the soft scattering amplitude, suggest should cancel (see Ref. [92]). In these models, the correlations from one parton shower are larger than from two parton showers, and they led to the \(y_{1,2}\) dependence. In other words, in the soft Pomeron based model, the contribution of semi-enhanced and enhanced Pomeron diagrams that describe large mass diffraction, is sufficiently large to induce considerable (actually dominant) contributions to the two particle correlation. Scrutinizing our formulas, we found that the main reason for the small size of the correlation in one parton showers that we observed in our approach, stems from the most theoretically reliable part of our model: from the expression for the dressed BFKL Pomeron Green function.

Another result, our model predicts is the probability of two parton showers production without introducing new phenomenological parameters,Footnote 3 which is able to describe the long range rapidity correlations.

We demonstrated that our model is able to describe the LHC data, eminating from the CMS and ATLAS collaborations. These data are certainly insufficient for a thorough analysis of the details of our approach, but they confirm that the long range rapidity correlations are large at high energies. Our prediction for \(W=13\,\mathrm{TeV}\) is shown in Fig. 9. The correlations should increase with the energy, and the measurements at \(W = 13\,\mathrm{TeV}\) should clarify the situation.

It worthwhile mentioning that the main contributions to the correlation function in terms of Mueller diagrams, has been known from 1970s, as well as the fact that non-enhanced diagrams (production of two and more parton showers) led to long range rapidity correlations, and were needed to describe the correlation at ISR and TEVATRON energies. However, the problem of the contributions of semi-enhanced and enhanced diagrams in the framework of the soft Pomeron calculus, has not been solved theoretically. This, as well as the estimates of the value of the contribution of these diagrams from the experimental data, are very dependent on the model of the Pomeron interactions. From the first paper on CGC/saturation approach [19], it became clear that hard processes could give a considerable contribution to the correlation function. However, it was not clear whether such correlations will be enough to reproduce the experimental data.

It was already appreciated in 1987 that taking into account the perturbative QCD sub-collisions in the Monte Carlo models is not sufficient to reproduces the correlation data from the UA5 experiment [100], and that multiple sub-collisions should be added. In the language of Ref. [100], our main result can be formulated as the statement that only hard and soft processes from two sub-collisions contribute to the correlation function.

In closing, we suggest that the investigation of short range rapidity correlations in MC models, which do not depend on Pomeron interactions and on the contributions of the enhanced and semi-enhanced diagrams, can provide more insight, as such estimates will be complementary to our Reggeon motivated description of short range rapidity correlations.