Extension of minimal fermionic dark matter model: a study with two Higgs doublet model

Abstract

We explore a fermionic dark matter model with a possible extension of Standard Model of particle physics into two Higgs doublet model. Higgs doublets couple to the singlet fermionic dark matter through a non-renormalisable coupling providing a new physics scale. We explore the viability of such dark matter candidate and constrain the model parameter space by collider serach, relic density of DM, direct detection measurements of DM-nucleon scattering cross-section and with the experimentally obtained results from indirect search of dark matter.

1 Introduction

The satellite borne experiments like Planck, WMAP etc. which study the anisotropies of cosmic microwave background radiations predict that more than a quarter of the constituents of the Universe is made of unknown dark matter. The recent Planck data suggest that the relic abundance for dark matter is within the range $\Omega _\mathrm{DM} \mathrm{h}^2 = 0.1199 \pm 0.0027$ [1], where $\mathrm h$ is the Hubble parameter normalised to 100 km s$^{-1}$ Mpc$^{-1}$. There are also several ongoing terrestrial experiments for direct detection of dark matter. Although no dark matter is convincingly detected but there are claims of the observance of three potential dark matter signals by CDMS direct dark matter search experiment [2, 3]. In addition DAMA/NAI [4–6] dark matter direct search experiment had also claimed to have observed the signature of the annual modulation of dark matter signal $-$ a phenomenon that the dark matter direct search signal should exhibit due to the revolution of earth around the sun. The ongoing direct search experiments such as XENON100 [7] and LUX [8] give an upper bound in $m_{\chi }-\sigma _\mathrm{scat}$ plane where $\sigma _\mathrm{scat}$ is the dark matter elastic scattering cross-sections off the target detector and $m_{\chi }$ is the dark matter mass. The XENON100 [7] and LUX [8] experiments provide stringent bounds on DM-nucleon scattering cross-section for different Dark matter masses. Dark matter particles can also be trapped in a highly gravitating astrophysical objects and can eventually undergo annihilation to produce $\gamma$’s or fermion anti-fermion pairs. Such events should show up as excesses over the expected abundance of these particles in the cosmos (for instance in cosmic rays). Indirect searches of dark matter by detecting their annihilation products can be realised by looking for these excesses in the Universe. In fact the satellite borne experiments such as Fermi-Lat [9] (also known as Fermi gamma-ray space telescope or FGST), Alpha Magnetic Spectrometer AMS [10] on board International Space Station (ISS) or the earth bound experiment H.E.S.S. [11], MAGIC [12] as also the Antarctica balloon-borne experiment ATIC [13] study the cosmic gamma ray, positron or antimatter excesses, origin of which could be annihilation of dark matter at the regions of astrophysical interest such as Galactic Centre (GC), Galactic halo etc.

Although the dark matter (DM) searches are being vigorously persued, the particle constituent of dark matter is not known at all. Various particle physics models for cold dark matter (CDM) are available in literature that include the popular candidate neutralino which is supersymmetry motivated, Kaluza Klein dark matter from theories of extra dimensions or particles in some other proposed theories where simple extensions of Standard Model (SM) are considered (such as adding a scalar singlet or an inert doublet and then imposing a discrete $\mathrm{Z}_2$ symmetry that ensures the stability of the dark matter candidate [14–34]). In the present work we consider an extension of SM where a second Higgs doublet is introduced in addition to the SM Higgs doublet. Though the recent findings of CMS [35] and ATLAS [36] have confirmed the existence of a SM like scalar with mass 125 GeV, possibility of having a second Higgs doublet accompanied by the SM sector Higgs doublet is not ruled out. Such an extension of SM sector including a second Higgs doublet is preferably known as two Higgs doublet model or THDM [37]. The two Higgs doublet model is the most general non supersymmetric extension of SM when another complex doublet of same hypercharge is added to the SM. Also a discrete symmetry is introduced between the Higgs doublets of THDM to avoid flavour changing neutral current (FCNC) processes [38]. In this work, we consider a singlet fermionic dark matter candidate in THDM framework. Possibility of a singlet scalar appearing in THDM to provide a feasible DM candidate has been studied extensively in Refs. [39–46]. The case of low mass scalar DM in the framework of THDM has been presented in a recent work by [44]. Thus, the dark matter candidate is the singlet fermion in our model. We then explore the viability of this singlet fermion for being a candidate of cold dark matter in the framework of THDM. In a previous work [47], a minimal model of singlet fermionic dark matter is proposed which is formulated by adding a Lagrangian for the fermion to Standard Model Lagrangian. The fermionic dark matter particle in this minimal model couples with the SM Higgs doublet through a dimension five interaction term and a new physics scale $\Lambda$ is introduced. However this minimal model of fermionic dark matter requires UV completion which can be achieved by adding a singlet scalar to the minimal model. Phenomenologies of such renormalisible singlet fermionic dark matter models with additional singlet scalar are explored in literatures [48, 49]. In the present work, however, we consider a THDM with an additional singlet fermion which is treated as the DM candidate. Previous work including fermionic dark matter in THDM Ref. [41], is based on an ad-hoc assumption that the singlet dark matter couples to the SM Higgs (h) and does not couple to the other scalar H involved in THDM. Based on this simple assumption the work by Cai et al. [41] only explores the low mass dark matter region ($m_\mathrm{DM}\le 20$ GeV). But in our case, the singlet fermion, which is the DM candidate in the present model, couples to both the Higgs doublets through a dimension five coupling when a new physics scale $\Lambda$ is introduced. Hence, DM candidate in present scenario couples to both the scalar bosons h and H of THDM. In addition the work by Cai et al. [41] considered only type II THDM without exploring the THDM parameter space in the model and indirect detection of DM candidate is not taken into account. However, in the present work both THDM phenomenology and indirect DM detection for type I and type II THDM are explored. The stability of such a dark matter is ensured either by assigning a discrete $\mathrm{Z}_2'$ symmetry under which the singlet fermion is odd and the THDM sector is even or by assigning the baryon and lepton charge of the singlet fermion to be zero as taken in Ref. [47]. In this work we explore the possibility that within the framework of this model, the fermion (added to the THDM) is a viable candidate for cold dark matter. We evaluate its direct detection cross-section and relic density and compare them with the experimentally obtained results. The paper is organised as follows. In Sect. 2, we introduce the model and describe the model parameters. The aspect of possible collider physics phenomenology for the model is addressed in Sect. 3. In Sect. 4 we calculate the relic density of the dark matter candidate in our proposed model. The model parameters are constrained by comparing the calculated relic density with observational dark matter relic density data obtained from PLANCK experiments. Results for the allowed parameter space obtained from the relic density calculation are presented in Sect. 5. In Sect. 5.1, we calculate the spin independent direct detection scattering cross-section for different masses of the present dark matter candidate. The model parameters are then further constrained by results obtained from dark matter direct detection experiments. Using the model parameter space thus constrained, we study the indirect DM search for chosen benchmark points (BPs) in our model and compare them with the FGST (Fermi-LAT) results in Sect. 5.2. In Sect. 6 we summarise the work with concluding remarks and discussions.

2 The model

In the present work we add a singlet fermion $\chi$ with two Higgs doublet model. The singlet fermion $\chi$ in the resulting model, is the dark matter candidate. The Lagrangian for $\chi$ can be written as

$$\begin{aligned} \mathcal{L}_{\chi }= & {} \bar{\chi }i \gamma ^{\mu }{\partial _{\mu }} \chi - m_0\bar{\chi }\chi . \end{aligned}$$

(1)

As mentioned earlier, the stability of $\chi$ can be confirmed either by assigning zero lepton number and zero baryon number to the singlet fermion [47] or by assuming a $\mathrm{Z}_2'$ symmetry under which $\chi$ is odd and the SM sector is even. The total Lagrangian of the model in THDM framework can be written as

$$\begin{aligned} \mathcal{L}= & {} \mathcal{L}_\mathrm{THDM} + \mathcal{L}_{\chi } + \mathcal{L}_\mathrm{int}, \end{aligned}$$

(2)

where $\mathcal{L}_\mathrm{int}$ denotes the interaction Lagrangian. The two Higgs doublet model potential is expressed as

(3)

where both the doublet Higgs fields $\Phi _1$ and $\Phi _2$ have non zero vacuum expectation values and a discrete symmetry ($\mathrm{Z}_2$) is imposed between the doublet fields in order to avoid FCNC processes. We consider a CP conserving two Higgs doublet model potential where all the parameters expressed in Eq. (3) are assumed to be real. In addition, the imposed discrete symmetry $\mathrm{Z}_2$ will result in mainly four types of THDM namely type I, type II, lepton specific and flipped THDM according to the nature of the coupling of fermions with the doublet fields. In the present work we consider type I and type II THDM and construct the model. Thus the two scenarios that we consider in this work are type I THDM $+$ one singlet fermion and type II THDM $+$ one singlet fermion. Both the scenarios will give rise to two charged Higgs fields ($H^{\pm }$), two CP even scalar fields (h, H), one CP odd scalar (A) and three Goldstone bosons ($G^{\pm },G$). The Higgs doublets $\Phi _1$ and $\Phi _2$ expressed in terms of physical states of the particles are written as [50],

$$\begin{aligned} \Phi _1= & {} \left( \begin{array}{c} c_{\beta }G^+ - s_{\beta }H^+ \\ \frac{1}{\sqrt{2}}(v_1+c_{\alpha }H-s_{\alpha }h+ic_{\beta }G-is_{\beta }A) \end{array} \right) ,\end{aligned}$$

(4)

$$\begin{aligned} \Phi _2= & {} \left( \begin{array}{c} s_{\beta }G^+ + c_{\beta }H^+ \\ \frac{1}{\sqrt{2}}(v_2+s_{\alpha }H+c_{\alpha }h+is_{\beta }G+ic_{\beta }A) \end{array} \right) , \end{aligned}$$

(5)

where $\tan {\beta } (= \frac{v_2}{v_1})$, is the ratio of the vacuum expectation values $v_2$ and $v_1$ of the doublets $\Phi _1$ and $\Phi _2$ and $\alpha$ is the measure of mixing between two CP even scalars. The terms $c_x$ and $s_x$ ($x = \alpha , \beta$) denote $\cos x$ and $\sin x$ respectively. The scalar potential for the THDM as expressed in Eq. (3) must be bounded from below for the stability of vacuum. The conditions for a stable vacuum of THDM are

$$\begin{aligned}&\lambda _1,\,\lambda _2 > 0, \quad \lambda _3 + 2\sqrt{\lambda _1\lambda _2} > 0, \\&\quad \lambda _3 +\lambda _4 -|\lambda _5| + 2\sqrt{\lambda _1\lambda _2} > 0. \end{aligned}$$

Perturbative unitarity constraints for the THDM are also taken into account. Bounds from the unitarity limits on THDM parameters are adopted from [37].

The interaction Lagrangian, $\mathcal{L}_\mathrm{int}$ of dark matter fermion [Eq. (2)] with $\Phi _1$ and $\Phi _2$ doublet fields is given by

$$\begin{aligned} \mathcal{L}_\mathrm{int}=-\frac{g_1}{\Lambda }(\Phi _1^{\dagger }\Phi _1)\bar{\chi } \chi -\frac{g_2}{\Lambda }(\Phi _2^{\dagger }\Phi _2)\bar{\chi } \chi , \end{aligned}$$

(6)

where $\Lambda$ is a high energy scale and $g_{1,2}$ are dimensionless couplings with the doublet fields $\Phi _{1,2}$. Interaction of THDM sector with the DM candidate can now be obtained easily from Eqs. (2)–(6). Dark matter fermion couples to both the physical Higgs particles h and H which are given by

$$\begin{aligned} \begin{aligned}&g_{\bar{\chi }\chi h} = \frac{v}{\Lambda }(-g_1\sin \alpha \cos \beta +g_2\cos \alpha \sin \beta ), \\&g_{\bar{\chi }\chi H} = \frac{v}{\Lambda }(g_2\cos \alpha \cos \beta +g_2\sin \alpha \sin \beta ), \end{aligned} \end{aligned}$$

(7)

with $\Lambda$ being a very large scale with respect to v. Hence the couplings $g_{\bar{\chi }\chi h}$ and $g_{\bar{\chi }\chi H}$ are expected to be small. Using Eqs. (1)–(7), mass of the singlet is expressed as

$$\begin{aligned} m_{\chi }=m_0 + v^2\left( \frac{g_1}{2\Lambda }\cos ^2\alpha + \frac{g_2}{2\Lambda }\sin ^2\alpha \right) , \end{aligned}$$

where $v (= \sqrt{v_1^2 + v_2^2 })$, is 246 GeV. Note that the new physics scale $\Lambda$ determines the coupling of DM particle to THDM sector and contributes significantly to the singlet fermion mass. As mentioned earlier, the discrete $\mathrm{Z}_2$ symmetry imposed between the Higgs doublets will result in four different types of THDM. In this work we consider THDM of type I and type II. In type I THDM, only one scalar doublet (say $\Phi _2$) couples to the SM particles whereas in type II THDM, up type quarks couple to one Higgs doublet and down type quarks and leptons couple to the other. Higgs couplings to up type quarks, down type quarks and leptons in case of type I THDM are given as [38]

$$\begin{aligned} g_{\bar{f} f h}=-i\frac{gm_f}{2M_W}\frac{\cos \alpha }{\sin \beta },\quad g_{\bar{f} f H}=-i\frac{gm_f}{2M_W}\frac{\sin \alpha }{\sin \beta }, \end{aligned}$$

(8)

where f denotes all SM fermions (up quarks, down quarks and leptons) respectively. In case of type II THDM, Yukawa couplings are

$$\begin{aligned} \begin{aligned}&g_{\bar{u} u h}=-i\frac{gm_u}{2M_W}\frac{\cos \alpha }{\sin \beta },\quad g_{\bar{u} u H}=-i\frac{gm_u}{2M_W}\frac{\sin \alpha }{\sin \beta },\\&g_{\bar{d} d h}=-i\frac{gm_d}{2M_W}\frac{-\sin \alpha }{\cos \beta },\quad g_{\bar{d} d H}=-i\frac{gm_d}{2M_W}\frac{\cos \alpha }{\cos \beta },\\&g_{\bar{l} l h}=-i\frac{gm_l}{2M_W}\frac{-\sin \alpha }{\cos \beta },\quad g_{\bar{l} l H}=-i\frac{gm_l}{2M_W}\frac{\cos \alpha }{\cos \beta }. \end{aligned} \end{aligned}$$

(9)

In the above, u corresponds to up type quarks (u, c, t), d correspondns to down type quarks (d, s, b) and l represents three families of leptons ($e,\mu , \tau$) respectively. Couplings to the gauge bosons ($V=W,Z$) for THDM I and THDM II are same and given by [38]

$$\begin{aligned} \begin{aligned}&g_{W W h}=igM_W\sin (\beta -\alpha )g^{\mu \nu },\\&g_{W W H}=igM_W\cos (\beta -\alpha )g^{\mu \nu }, \\&g_{Z Z h}=ig\frac{M_Z}{\cos \theta _W}\sin (\beta -\alpha )g^{\mu \nu },\\&g_{Z Z H}=ig\frac{M_Z}{\cos \theta _W}\cos (\beta -\alpha )g^{\mu \nu }. \end{aligned} \end{aligned}$$

(10)

In Eqs. (8)–(10), $m_x$ ($x = u,~d,~l$ etc) represents the mass of quarks or leptons and $M_W$ and $M_Z$ denote the masses of W and Z bosons respectively. In the present framework with type I and type II THDM, we consider h to be SM like Higgs boson with mass $m_h=125$ GeV and H as the non-SM Higgs with mass $m_H$.

3 Collider physics phenomenology

The existence of a scalar boson of mass 125 GeV has been confirmed by Large Hadron Collider (LHC) [35, 36]. In this work we treat the new found scalar boson to be equivalent to one of the CP even scalars (h) appearing in THDMs. We further extend the model by including a possible fermionic dark matter (FDM) candidate. This may necessarily affect the phenomenology of collider physics. If the dark matter mass is small ($m_{\chi }\le m_{h}/2$) then one would expect an invisible decay of SM like Higgs boson (h) and the total decay width will change depending on the coupling constant $g_{\bar{\chi }\chi h}$ and other THDM parameters $\alpha ,~\beta$. Since both the scalar bosons in THDM couple with the DM fermion in the present framework, it may change the standard bounds on THDM sector. The signal strength of SM like Higgs boson (h) to a specific channel for type I and type II THDM are given by

$$\begin{aligned} R_{\mathrm{I}} = \frac{\sigma ^\mathrm{I}_h}{\sigma ^\mathrm{SM}} \frac{\mathrm{BR}^\mathrm{I}}{\mathrm{BR}^\mathrm{SM}},\quad R_{\mathrm{II}} = \frac{\sigma ^\mathrm{II}_h}{\sigma ^\mathrm{SM}} \frac{\mathrm{BR}^\mathrm{II}}{\mathrm{BR}^\mathrm{SM}}, \end{aligned}$$

(11)

where $\frac{\sigma ^\mathrm{I,II}_h}{\sigma ^\mathrm{SM}}$ represents the ratio of Higgs production cross-section in type I as also in type II THDM with respect to that for SM ($\sigma ^\mathrm{SM}$ is the SM Higgs production cross-section). The branching ratio ($\mathrm BR$) to any specific channel for the chosen model and for SM are given by ${\mathrm{BR}^\mathrm{X}}~,X=I,II$ and ${\mathrm{BR}^\mathrm{SM}}$. The ratio $\frac{\sigma ^\mathrm{X}_h}{\sigma ^\mathrm{SM}}$ ($X=I,II$) in Eq. (11) for 125 GeV Higgs boson can be expressed as

$$\begin{aligned} \frac{\sigma ^X_h}{\sigma ^\mathrm{SM}}=\frac{\sigma _{tt}f^2_t+\sigma _{bb}f^2_b+\sigma _{tb}f_t f_b}{\sigma ^\mathrm{SM}}, \end{aligned}$$

(12)

where $\sigma _{tt}$, $\sigma _{bb}$ are the Higgs production cross-sections from top and bottom quarks respectively and $\sigma _{tb}$ is the contribution from top-bottom interference. For the calculation of SM Higgs signal strength, we have adopted the leading order (LO) production cross-sections obtained from [51]. The factors $f_t,~f_b$ in Eq. (11) are the Yukawa couplings of SM like Higgs (h) with top and bottom quarks for the specific model normalised with respect to SM. For type I THDM, $f_t=f_b=\frac{\cos \alpha }{\sin \beta }$ and for type II THDM these factors are given as $f_t= \frac{\cos \alpha }{\sin \beta }$ and $f_b= \frac{-\sin \alpha }{\cos \beta }$. As defined earlier, $\alpha$ is the mixing angle between the CP even scalars h and H and $\beta$ is given by the ratio of the VEVs $v_2$ and $v_1$ of Higgs doublets $\Phi _2$ and $\Phi _1$ respectively ($\tan \beta =\frac{v_2}{v_1}$). ATLAS and CMS experiments have measured the signal strengths of SM Higgs (h) boson to different production channels such as $b\bar{b}, \tau \bar{\tau },\gamma \gamma ,WW^*,ZZ^*$. The mean signal strengths of SM Higgs to these channels measured by ATLAS and the best fit value of combined signal strength of h given by CMS experiment are found to be [52, 53]

$$\begin{aligned} R_\mathrm{ATLAS} = 1.23 \pm {0.18},\quad R_\mathrm{CMS} = 0.8\pm {0.14}. \end{aligned}$$

(13)

In the present scenario with THDM, we have a non-SM Higgs (H) in addition to the SM scalar h. The signal strengths of non-SM Higgs boson for type I and type II THDM are given as

$$\begin{aligned} R'_{\mathrm{I}} = \frac{\sigma ^\mathrm{I}_H}{\sigma '^\mathrm{SM}} \frac{\mathrm{BR'}^\mathrm{I}}{\mathrm{BR'}^\mathrm{SM}} \quad \mathrm{and} \quad R'_{\mathrm{II}} = \frac{\sigma ^\mathrm{II}_H}{\sigma '^\mathrm{SM}} \frac{\mathrm{BR'}^\mathrm{II}}{\mathrm{BR'}^\mathrm{SM}}\end{aligned}$$

(14)

respectively, where $\sigma ^\mathrm{X}_H$ ($\mathrm { X=I,~II}$ depending on the nature of THDM considered) is the non-SM Higgs production cross-section and $\mathrm{BR'}^X$ is the branching ratio of H to any specific channel. In Eq. (14), $\sigma '^\mathrm{SM}$ and $\mathrm{BR'}^\mathrm{SM}$ represent the production cross-section and branching ratio of the non-SM Higgs boson (H) with mass $m_H$. The modified non-SM Higgs production cross-section ratio can be given as

$$\begin{aligned} \frac{\sigma ^X_H}{\sigma '^\mathrm{SM}}=\frac{\sigma '_{tt}f'^2_t+\sigma '_{bb}f'^2_b+\sigma '_{tb}f'_t f'_b}{\sigma '^\mathrm{SM}}. \end{aligned}$$

(15)

Similar to Eq. (11), in Eq. (15) also, the factors $f'_t,~f'_b$ are the SM normasiled Yukawa couplings of non-SM Higgs H with top and bottom quarks. For the case of type I THDM, $f'_t=f'_b=\frac{\sin \alpha }{\sin \beta }$, whereas those for type II THDM are $f'_t=\frac{\sin \alpha }{\sin \beta }$ and $f'_b=\frac{\cos \alpha }{\cos \beta }$. In the present work we consider two values of non-SM Higgs mass and they are chosen as $m_H=$ 150 and 200 GeV. The calculations are performed for each of these chosen masses. We use the leading order production cross-section ($\sigma '_{tt},~\sigma '_{bb},~\sigma '_{tb}$ and $\sigma '^{SM}$) obtained from Ref. [51] for the chosen $m_H$ values in the work. Invisible decay of the non-SM Higgs (for $m_\chi \le m_H/2$) has also been taken into account. Since no signature of additional Higgs has been reported by ATLAS and CMS experiment, it is likely to assume that the non-SM Higgs signal strength is negligibly small compared to that of SM Higgs. Hence, throughout the work, we restrict the signal strength for non-SM scalar satisfying the condition $R'_X\le 0.2~(X=I,II)$. SM branching ratios for specific decay modes of SM Higgs ($\mathrm{BR}^\mathrm{SM}$ with mass $m_h=125$ GeV) and non-SM Higgs ($\mathrm{BR'}^\mathrm{SM}$ for $m_H=150$ and 200 GeV) are adopted from Ref. [54]. It is to be mentioned that in this work we do not consider any ad-hoc condition, e.g. by setting $g_{\bar{\chi }\chi h}=0$ or $g_{\bar{\chi }\chi H} =0$ [41] for the SM like scalar (assuming $\sin (\beta -\alpha )=\pm 1$ when h is SM like or $\sin (\beta -\alpha )=0$ when H is SM like). In the present formalism we consider the total allowed range of available parameter space independent of these conditions and restrict them by using limits on SM Higgs signal strength from CMS and ATLAS [Eq. (13)].

4 DM annihilation and relic density

In order to evaluate the relic density of the fermionic dark matter candidate proposed in this work one requires to solve the Boltzmann equation [55]

$$\begin{aligned} \frac{d n}{d t} + 3 \mathrm{H}n= & {} - \langle \sigma v \rangle (n^{2}-n_{eq}^{2}) \end{aligned}$$

(16)

where n is the actual number density of the particle species, $\mathrm H$ is the Hubble parameter and $n_{eq}$ is the number density at thermal equilibrium. An approximate expression for relic density $\Omega$ or $\Omega \mathrm{h}^2$ ($\mathrm{h} = \mathrm{H}/(100\, \mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{Mpc}^{-1})$) that can be obtained from Eq. (16) is given by

$$\begin{aligned} \Omega _\mathrm{DM}\mathrm{h}^2= & {} \frac{1.07\times 10^9 x_F}{\sqrt{g_*}M_\mathrm{Pl}\langle \sigma v\rangle } \end{aligned}$$

(17)

where $x_F=m_{\chi }/T_F$, $g_*$ is the effective degrees of freedom and $M_\mathrm{Pl}=1.22\times 10^{19}$ is the Planck mass. The particle physics input to Eqs. (16)–(17) is the thermal averaged annihilation cross-section $\langle \sigma v \rangle$ and one needs to calculate this quantity for the present fermionic dark matter candidate in our model. The freeze out temperature $T_F$ (or $x_F$) in Eq. (17) can be computed by iteratively solving the equation

$$\begin{aligned} x_F= & {} \ln \left( \frac{m_{\chi }}{2\pi ^3}\sqrt{\frac{45M_{Pl}^2}{2g_*x_F}} \langle \sigma v \rangle \right) . \end{aligned}$$

(18)

The freeze out temperature thus obtained is then used to evaluate the relic density of the dark matter candidate $\chi$ in our model. In order to solve for the freeze out temperature, it is therefore essential to calculate the annihilation cross-section of the dark matter candidate. Dark matter candidates in the present model annihilate to SM particles through h or H mediated s-channel processes. The total annihilation cross-section $\sigma v$ can be expressed as a sum of the three terms

$$\begin{aligned} \sigma v= & {} (s-4m_{\chi }^2) \left[ A\frac{1}{(s-m_h^2)^2+m_h^2\Gamma _h^2}\right. \nonumber \\&+B\frac{1}{(s-m_H^2)^2+m_H^2\Gamma _H^2} \nonumber \\&\left. +C\frac{2(s-m_h^2)(s-m_H^2)+2m_hm_H\Gamma _h\Gamma _H}{[(s-m_h^2)^2+m_h^2\Gamma _h^2][(s-m_H^2)^2+m_H^2\Gamma _H^2]} \right] .\nonumber \\ \end{aligned}$$

(19)

In Eq. (19), $\Gamma _h$ and $\Gamma _H$ are decay widths of light Higgs (h) and heavy Higgs particle (H) respectively. We set the light Higgs mass $m_h$ to be 125 GeV and consider each of the two values of non-SM Higgs mass $m_H=$ 150 and 200 GeV. Thus we assume $m_H > m_h$ in the present work. The terms A,  B and C in the expression for $\sigma v$ [Eq. (19)] in case of THDM I are given as (with summation convention imposed on quarks and leptons)

$$\begin{aligned} A= & {} g_{\bar{\chi }\chi h}^2\frac{G_F}{4\pi \sqrt{2}} \left[ \frac{c_{\alpha }^2}{s_{\beta }^2}(N_cm_{u_i}^2\gamma _{u_i}^3 +N_cm_{d_i}^2\gamma _{d_i}^3+ m_{l_i}^2\gamma _{l_i}^3) \right. \nonumber \\&+\frac{1}{2}s_{\beta -\alpha }^2s\left( 1-x_W+\frac{3}{4}x_W^2\right) \gamma _W\nonumber \\&\left. + \frac{1}{4}s_{\beta -\alpha }^2s\left( 1-x_Z+\frac{3}{4}x_Z^2\right) \gamma _Z \right] ,\end{aligned}$$

(20)

$$\begin{aligned} B= & {} g_{\bar{\chi }\chi H}^2\frac{G_F}{4\pi \sqrt{2}} \left[ \frac{s_{\alpha }^2}{s_{\beta }^2}(N_cm_{u_i}^2\gamma _{u_i}^3 +N_cm_{d_i}^2\gamma _{d_i}^3+ m_{l_i}^2\gamma _{l_i}^3) \right. \nonumber \\&+ \frac{1}{2}c_{\beta -\alpha }^2s\left( 1-x_W+\frac{3}{4}x_W^2\right) \gamma _W\nonumber \\&\left. + \frac{1}{4}c_{\beta -\alpha }^2s\left( 1-x_Z+\frac{3}{4}x_Z^2\right) \gamma _Z\right] , \end{aligned}$$

(21)

and

$$\begin{aligned} C= & {} g_{\bar{\chi }\chi h}g_{\bar{\chi }\chi H}\frac{G_F}{4\pi \sqrt{2}} \left[ \frac{c_{\alpha }s_{\alpha }}{s_{\beta }^2}(N_cm_{u_i}^2\gamma _{u_i}^3 +N_cm_{d_i}^2\gamma _{d_i}^3 \right. \nonumber \\&+ m_{l_i}^2\gamma _{l_i}^3) + \frac{1}{2}s_{\beta -\alpha }c_{\beta -\alpha }s\left( 1-x_W+\frac{3}{4}x_W^2\right) \gamma _W\nonumber \\&+\left. \frac{1}{4}s_{\beta -\alpha }c_{\beta -\alpha }s\left( 1-x_Z+\frac{3}{4}x_Z^2\right) \gamma _Z \right] . \end{aligned}$$

(22)

For type II THDM, the expressions for A,  B and C are

$$\begin{aligned} A= & {} g_{\bar{\chi }\chi h}^2\frac{G_F}{4\pi \sqrt{2}} \left[ N_cm_{u_i}^2\frac{c_{\alpha }^2}{s_{\beta }^2}\gamma _{u_i}^3 +N_cm_{d_i}^2\frac{s_{\alpha }^2}{c_{\beta }^2}\gamma _{d_i}^3+ m_{l_i}^2\frac{s_{\alpha }^2}{c_{\beta }^2}\gamma _{l_i}^3 \right. \nonumber \\&+ \frac{1}{2}s_{\beta -\alpha }^2s\left( 1-x_W+\frac{3}{4}x_W^2\right) \gamma _W\nonumber \\&+ \left. \frac{1}{4}s_{\beta -\alpha }^2s\left( 1-x_Z+\frac{3}{4}x_Z^2\right) \gamma _Z \right] ,\end{aligned}$$

(23)

$$\begin{aligned} B= & {} g_{\bar{\chi }\chi H}^2\frac{G_F}{4\pi \sqrt{2}} \left[ N_cm_{u_i}^2\frac{s_{\alpha }^2}{s_{\beta }^2}\gamma _{u_i}^3 +N_cm_{d_i}^2\frac{c_{\alpha }^2}{c_{\beta }^2}\gamma _{d_i}^3+m_{l_i}^2\frac{c_{\alpha }^2}{c_{\beta }^2}\gamma _{l_i}^3 \right. \nonumber \\&+\frac{1}{2}c_{\beta -\alpha }^2s\left( 1-x_W+\frac{3}{4}x_W^2\right) \gamma _W\nonumber \\&+ \left. \frac{1}{4}c_{\beta -\alpha }^2s\left( 1-x_Z+\frac{3}{4}x_Z^2\right) \gamma _Z\right] ,\end{aligned}$$

(24)

$$\begin{aligned} C= & {} g_{\bar{\chi }\chi h}g_{\bar{\chi }\chi H}\frac{G_F}{4\pi \sqrt{2}} \left[ N_cm_{u_i}^2\frac{s_{\alpha }}{s_{\beta }}\frac{c_{\alpha }}{s_{\beta }}\gamma _{u_i}^3\right. \nonumber \\&-N_cm_{d_i}^2\frac{c_{\alpha }}{c_{\beta }}\frac{s_{\alpha }}{c_{\beta }}\gamma _{d_i}^3- m_{l_i}^2\frac{c_{\alpha }}{c_{\beta }}\frac{s_{\alpha }}{c_{\beta }} \gamma _{l_i}^3 \nonumber \\&+\frac{1}{2}c_{\beta -\alpha }s_{\beta -\alpha }s\left( 1-x_W+\frac{3}{4}x_W^2\right) \gamma _W\nonumber \\&\left. +\frac{1}{4}c_{\beta -\alpha }s_{\beta -\alpha }s\left( 1-x_Z+\frac{3}{4}x_Z^2\right) \gamma _Z\right] . \end{aligned}$$

(25)

In all the above expressions [Eqs. (20)–(25)] $\gamma _a= \left( 1-\frac{4m_a^2}{s}\right) ^{\frac{1}{2}}$ ($a = u,~d,~l,~W,~Z$), $X_B=\frac{4m_B^2}{s}$ and $N_c = 3$ for quarks. Thermal average of pair annihilation cross-section of DM to SM particles is given by

$$\begin{aligned} \langle \sigma v \rangle= & {} \frac{1}{8m_{\chi }^4T_FK_2^2(m_{\chi }/T_F)}\nonumber \\&\times \int _{4m_{\chi }^2}^\infty \hbox {d}s~\sigma (s)~(s-4m_{\chi }^2) \sqrt{s} K_1(\sqrt{s}/T_F) , \end{aligned}$$

(26)

where $K_1$ and $K_2$ are modified Bessel function. Using Eqs. (19)–(26), the annihilation cross-section $\langle \sigma v \rangle$ of DM candidate into SM particles is evaluated for both type I and type II THDM. We first solve for the freeze out temperature $T_F$ using Eq. (18). The relic density $\Omega _\mathrm{DM}\mathrm{h}^2$ of dark matter is obtained by solving Eq. (17) in order to satisfy dark matter relic density obtained from PLANCK experimental value $\Omega _\mathrm{DM}\mathrm{h}^2=0.1199\pm 0.0027$ [1]. The DM relic density is computed with the chosen model parameters such that¹

$$\begin{aligned} \begin{aligned}&m_{\chi }\le 300~\mathrm{GeV}, \\&10^{-4}\le |g_{\bar{\chi }\chi h}| \le 0.1, \\&10^{-4}\le |g_{\bar{\chi }\chi H}| \le 0.1, \\&-\pi /2\le \alpha \le \pi /2, \\&1\le \tan \beta < 30. \end{aligned} \end{aligned}$$

(27)

As mentioned earlier, the calculation of dark matter relic density is performed for two values of non-SM scalar mass $m_H$ taken to be 150 and 200 GeV. We further constrain the model parameter space using the bounds for SM Higgs signal strength as obtained from ATLAS and CMS experiments (Sect. 3) as also using the bounds on the signal strength of H ($R'_{I,II}\le 0.2$).

5 Results

In this section we present the results for our fermionic dark matter in type I and type II THDM. We first obtain the relic density of the DM candidate by solving the Boltzmann equation [Eq. (16)]. The Boltzmann equation is solved by using the range of parameter space given in Eq. (27) and the relic density of the fermionic dark matter in the present model is then calculated. The comparison with the PLANCK’s result for DM relic density, constrains the parameter space of the model considered in this work. The signal strength $R_X$ ($X=\hbox {I},~\hbox {II}$; I, II correspond to type I and type II THDM respectively) for the SM Higgs h is computed with the parameter space restricted by PLANCK results. As mentioned earlier, we also compute the signal strength $R'_X$, the signal strength of the other Higgs H and its value is kept in the limit $R'_X\le 0.2$. The calculated values of both $R_I$ and $R_{\mathrm{II}}$ are compared with the CMS and ATLAS limits for the SM signal strength. Thus the parameter space is further constrained by the CMS and ATLAS results. In Fig. 1a–c we show the allowed parameter space in $\sin \alpha$-$\tan \beta$ plane for fermionic dark matter for each of type I and type II THDM scenarios extended with FDM. The plots in Fig. 1 are obtained for two values of H mass namely $m_H=$ 150 and 200 GeV. In Fig. 1a the variations of $\sin \alpha$ with $\tan \beta$ for FDM extended type I THDM are shown.We found that for type I THDM along with FDM fails to satisfy the combined signal strength as predicted by ATLAS ($R_\mathrm{ATLAS}$). Hence in Fig. 1a, only the constraints from CMS experimental results (for signal strength, i.e. $R_\mathrm{CMS}$) are imposed. The blue and green scattered regions in Fig. 1a–c represent the respective allowed parameter space when $m_H$ is chosen to be 150 and 200 GeV respectively. It can also be observed from Fig. 1a that increase in the mass of the other scalar H associated with the model results in considerable reduction in the overall allowed THDM parameter space. In Fig. 1b we plot the available region of $\sin \alpha$-$\tan \beta$ plane for the case of fermionic dark matter in type II THDM consistent with the PLANCK relic density as also SM Higgs signal strength $R_\mathrm{CMS}$ given in Eq. (13) with $R'_{\mathrm{II}}\le 0.2$. Similar allowed regions but $R_\mathrm{CMS}$ replaced with $R_\mathrm{ATLAS}$ (ATLAS bound) are shown in Fig. 1c for type II THDM scenario. For type II THDM, we use the same colour convention as used in the case of type I THDM (Fig. 1a) to show the valid region of parameter space for $m_H=150$ and 200 GeV. Comparison of the plots in Fig. 1b, c with the type I THDM case (Fig. 1a) clearly shows that there is less allowed parameter space available for type II THDM. It is to be noted that for type II THDM involving FDM is in agreement with both the combined (for all five channels namely $b\bar{b}, \tau \bar{\tau },\gamma \gamma ,WW^*,ZZ^*$) signal strengths $R_\mathrm{CMS}$ and $R_\mathrm{ATLAS}$ as predicted independently by CMS and ATLAS experimental results. Note that, for the case of type II THDM shown in Fig. 1b, c too, the available region of $\sin \alpha$-$\tan \beta$ plane decreases with increase of the mass of H which is similar to the trend observed for type I THDM formalism (Fig. 1a).

Fig. 1

Allowed $\sin \alpha$-$\tan \beta$ parameter space for type I THDM consistent with $R_\mathrm{CMS}$ within the framework of present DM model (a). Green and blue coloured regions are for $m_H=$ 150 and 200 GeV respectively. Similar plots for the case of type II THDM is shown in b. Valid parameter space in type II THDM satisfying $R_\mathrm{ATLAS}$ only is depicted in c. The computation for all the plots are performed with the constrained range of model parameter space values which produce required DM relic density consistent with PLANCK results. For all the plots the constrained $R'_{I,II}$ is respected

5.1 Direct detection measurements

We further restrict the allowed parameter space of our model with the direct detection experimental bounds on DM-nucleon scattering cross-section. Direct detection of dark matter utilises the phenomenon of a possible elastic scattering off a nucleus of detecting material. In order to enable a uniform comparison of experimental results from different dark matter experiments with different detecting materials, the experimentally obtained DM-nucleus elastic scattering cross-section ($\sigma _\mathrm{scat}$) is reduced to DM-nucleon scattering cross-section. The experimental results are then expressed as the allowed region in $m_{\chi }-\sigma _\mathrm{scat}^\mathrm{nucleon}$ plane. This elastic scattering cross-section can be spin independent (SI) or spin dependent (SD), depending on the ground state spin of detector nucleus. The elastic scattering of the dark matter particle off the target causes the recoil of the target nucleus. This recoil energy is measured in the experiment and allowed region in the plane of scattering cross-section and dark matter mass is then obtained. The spin independent dark matter-nucleon elastic scattering cross-section for in the present model is given as

$$\begin{aligned} \sigma _\mathrm{{SI}}\simeq \frac{m_r^2}{\pi } \left( \frac{g_{\bar{\chi }\chi h}g_{NNh}}{m_h^2}+ \frac{g_{\bar{\chi }\chi H}g_{NNH}}{m_H^2} \right) ^2. \end{aligned}$$

(28)

In the above, $m_r$ is the reduced mass $= \frac{m_{\chi }m_N}{m_{\chi }+m_{N}}$, where $m_N$ is the mass of the scattering nucleon (proton or neutron) and $g_{NNx}$ ($x= h$ or H) denotes the effective Higgs nucleon couplings expressed as [56]

$$\begin{aligned} \begin{aligned}&g_{NNh}\simeq (1.217k_d^h+0.493k_u^h)\times 10^{-3},\\&g_{NNH}\simeq (1.217k_d^H+0.493k_u^H)\times 10^{-3}. \end{aligned} \end{aligned}$$

(29)

For the case of THDM I, parameters $k_u^h$ and $k_d^h$ in Eq. (29) are given as

$$\begin{aligned} k_u^h=k_d^h=\frac{\cos \alpha }{\sin \beta },\quad k_u^H=k_d^H=\frac{\sin \alpha }{\sin \beta }. \end{aligned}$$

(30)

and for the case of THDM II these parameters are

$$\begin{aligned} k_u^h=\frac{\cos \alpha }{\sin \beta },\quad k_d^h=-\frac{\sin \alpha }{\cos \beta },\quad k_u^H=\frac{\sin \alpha }{\sin \beta },\quad k_d^H=\frac{\cos \alpha }{\cos \beta }.\nonumber \\ \end{aligned}$$

(31)

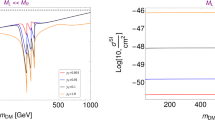
Using Eqs. (28)–(31), we compute $\sigma _\mathrm{SI}$ for the DM candidate within the framework of our chosen specific model in this work and compare them with the latest limits for $\sigma _\mathrm{SI}$ and $m_{\chi }$ (in $\sigma _\mathrm{SI}-m_{\chi }$ plane) given by recent dark matter direct detection experiments namely XENON100 [7] and LUX [8].² In Fig. 2a–f we plot the variation of DM-nucleon scattering cross-section $\sigma _\mathrm{SI}$ with DM mass ($m_{\chi }$) for the cases of both type I and type II THDM. The red and blue lines shown in Fig. 2a–f are the limits on DM-nucleon cross-section obtained from XENON100 and LUX. The calculations are performed with the parameter space (such as couplings etc.) of the present model which has already been constrained by PLANCK results and collider bounds (Fig. 1a–c). Thus the resulting $m_{\chi }-\sigma _\mathrm{SI}$ parameter space is in agreement with the bounds from Higgs signal strength ($R_\mathrm{CMS,ATLAS}$), limits on the signal strength on extra Higgs scalar of THDM ($R'_{\mathrm{I}, \mathrm{II}}\le 0.2$) and also satisfies DM relic density predicted by PLANCK. Shown in Fig. 2a, b are the $m_{\chi }-\sigma _\mathrm{SI}$ parameter space of DM candidate in type I THDM framework for $m_{H}=$ 150 and 200 GeV respectively. Needless to mention, parameters used in these two plots are restricted by $R_{CMS}$, $R'_{\mathrm{I}}$ and PLANCK. It is to be noted from Fig. 1a that observational results of Higgs signal strength (Fig. 1a) indicate that there is no valid parameter space in type I THDM associated with our fermionic dark matter that corresponds to $R_\mathrm{ATLAS}$. It is clear from Fig. 2a, b that due to the presence of an extra scalar in the model along with SM Higgs, an extra pole is likely to appear in the mass range $m_{\chi }\sim m_{H}/2$ with the normal SM Higgs pole occurring near $m_{\chi }\sim m_{h}/2$. This scenario also holds for the case of type II THDM as well. Study of the plots in Fig. 2a, b reveals that the fermionic DM particle $\chi$ in type I THDM can serve as a viable candidate of dark matter with a sufficient allowed parameter space that is in agreement with latest DM direct detection experimental results of XENON100 and LUX. Similarly using the allowed parameter space obtained in Fig. 1b, c (constrained by DM relic density, combined Higgs signal strength ($R_\mathrm{CMS,ATLAS}$) and bound on additional Higgs signal ($R'_{\mathrm{II}}$)), we plot the viable parameter space in $m_{\chi }-\sigma _\mathrm{SI}$ plane for DM in type II THDM (Fig. 2c–f). In Fig. 2c, d, the available $m_{\chi }-\sigma _\mathrm{SI}$ spaces for two values of the scalar mass H, $m_H=$ 150 and 200 GeV respectively are shown. Each of these plots satisfies the model parameter space constrained by PLANCK, $R_\mathrm{CMS}$ and $R'_{\mathrm{II}}$. Analogous plots are obtained in Fig. 2e, f but here only $R_\mathrm{ATLAS}$ is taken into account instead of $R_\mathrm{CMS}$. It is obvious from Fig. 2c–f, that the region of allowed $m_{\chi }-\sigma _\mathrm{SI}$ space depends on the mass of the additional scalar H. Figure 2c–f also shows that a considerable portion of DM-nucleon scattering cross-section $\sigma _\mathrm{SI}$ of the DM candidate $\chi$ in type II THDM lies in the allowed region set by XENON100 and LUX direct detection experiments. Hence, fermionic dark matter $\chi$ appearing in type II THDM can be treated as a potential candidate for dark matter. It is also seen from Fig. 2a–f that as we do not involve any condition on DM-Higgs coupling [such as $g_{\bar{\chi }\chi h}=0$ or $g_{\bar{\chi }\chi H}=0$ [41]] for SM like scalar, the low mass region of dark matter appearing in [41] ($m_{\chi }\le 40$ GeV) is excluded.

Fig. 2

a and b shows the $m_{\chi }-\sigma _\mathrm{SI}$ parameter space for FDM in type I THDM is allowed by PLANCK relic density and collider bounds plotted using $R_\mathrm{CMS}$ for $m_{H}=$ 150 and 200 GeV. Similar plots in $m_{\chi }-\sigma _\mathrm{SI}$ plane with type II THDM are shown in c and d whereas the plots in e and f are in agreement with $R_\mathrm{ATLAS}$. All the results in a–f also satisfy the bounds from DM relic density and $R'_{I,II}\le$ 0.2. The red and blue lines are respective bounds on DM-nucleon scattering cross-section from XENON100 and LUX DM direct search experiments

5.2 Indirect search of dark matter: gamma-ray flux calculation

In indirect detection of dark matter, the experiments look for excess signature of $\gamma$-ray, neutrino, positron and anti-proton flux that might have originated from the annihilation of dark matter candidate into SM particles. In this section, we study such excess $\gamma$-ray flux from the Galactic Centre (GC) region observed by Fermi-LAT (or FGST) [57] assuming that the excess $\gamma$-ray is produced by the process of dark matter pair annihilation at GC. We consider the particle dark matter candidate is the fermionic dark matter $\chi$ in the present framework. In previous works [58, 59] this $\gamma$-ray is reported to be in the range 1–10 GeV and it was explained by considering the annihilation of 10 GeV dark matter at GC. In order to investigate whether our proposed fermionic DM candidate $\chi$ in both type I and type II THDM can account for the observed $\gamma$-ray excess originating from the inner galaxy ($5^0$ surrounding the GC), we first calculate the $\gamma$ flux in inner galactic region produced from the annihilation of DM candidate $\chi$. We then add to it the $\gamma$-ray flux arising out of the known sources present in the inner galaxy (galactic ridge and point source emission) and compare the resultant $\gamma$ flux with the FGST observations of GC gamma-ray flux within the inner $5^0$ region. The flux for the galactic ridge and point sources of $\gamma$-ray emission are obtained from Refs. [60–63]. The differential gamma-ray flux produced at GC from the annihilation of DM particles in a direction that subtends a solid angle $d\Omega$ is given as [64]

$$\begin{aligned} \frac{\hbox {d}\Phi _{\gamma }}{\hbox {d}\Omega dE_{\gamma }}= \frac{r_\odot \rho ^2_{\odot }}{8\pi m_{\chi }^2} J\sum _f {\langle \sigma v \rangle }_f \frac{\hbox {d}N}{\hbox {d}E_{\gamma }}, \end{aligned}$$

(32)

where $r_{\odot }=8.5$ kpc is the distance of the Sun from GC and $\rho _{\odot }=0.3$ GeV cm$^{-3}$ is the local DM density at solar neighbourhood. In Eq. (32), $\frac{\hbox {d}N}{\hbox {d}E_{\gamma }}$ is the photon spectrum per annihilation of DM into final state f with annihilation cross-section ${\langle \sigma v \rangle }_f$. The astrophysical factor J for annihilating DM, is given by the relation (with $\rho (r)$) denoting halo density profile)

$$\begin{aligned} J=\int _{\mathrm{l.o.s.}} \frac{\hbox {d}s}{r_{\odot }} \frac{\rho ^2(r(s,\theta ))}{\rho ^2_{\odot }}, \end{aligned}$$

(33)

In the above, the line of sight integral has been performed over an angle $\theta$. In Eq. (33), $\theta$ is the angle between the line from earth to GC and the direction of line of sight at a distance r $\left( r=\sqrt{r_{\odot }^2+s^2-2r_{\odot }s\cos \theta }\right)$ from GC. The gamma-ray flux originating from an extended region with solid angle $\Delta \Omega$ takes the form

$$\begin{aligned} \frac{d\Phi _{\gamma }}{dE_{\gamma }}= \frac{r_\odot \rho ^2_{\odot }}{8\pi m_{\chi }^2} \bar{J} \Delta \Omega \sum _f {\langle \sigma v \rangle } \frac{dN}{dE_{\gamma }}, \end{aligned}$$

(34)

where $\bar{J}$ is the J factor averaged over a soild angle $\Delta \Omega$ and is expressed as

$$\begin{aligned} \bar{J}=\frac{2\pi }{\Delta \Omega } \int \hbox {d}\theta \sin \theta J(\theta ), \end{aligned}$$

(35)

with

$$\begin{aligned} \Delta \Omega =\int _{\theta _{\min }}^{\theta _{\max }}\,\hbox {d}\theta \sin \theta . \end{aligned}$$

(36)

In the present work we consider two different DM halo density profiles namely Navarro–Frenk–White (NFW) [65] profile and Einasto (Ein) [66] profile. These density profiles are written in the form

$$\begin{aligned}&\rho _{NFW}(r)=\rho _s\frac{r_s}{r}\left( 1+\frac{r}{r_s}\right) ^{-2},\nonumber \\&\rho _{Ein}=\rho _s \mathrm{exp}\left( -\frac{2}{\alpha }\left[ \left( \frac{r}{r_s}\right) ^{\alpha }-1\right] \right) . \end{aligned}$$

(37)

Fig. 3

Comparison of the observed gamma-ray flux obtained from FGST with the resultant gamma-ray flux as generated using the BPs in Table 1 for the case of fermionic dark matter in type I and type II THDM

Table 1 Benchmark points (BPs) for type I and type II THDM associated with FDM used to produce the plots in Fig. 3a–d. BP1 and BP2 correspond to type I THDM for $m_{H}=150$ and 200 GeV respectively while BP3 and BP4 signify the adopted benchmark points for type II THDM with $m_{H}=150$ and 200 GeV respectively

We have used the numerical values of parameters $r_s$ and $\rho _s$ for the above halo profiles from Ref. [64]. The chosen values for $\rho _s$in Eq. (37) are normalised to produce local DM density $\rho _{\odot }=0.3$ GeV cm$^{-3}$ at $r=r_{\odot }$. For the case of Einasto profile, a steeper halo profile with $\alpha =0.11$ (instead of usual value ($\alpha =0.17$)) is recommended [67] when contribution from baryons are also taken into account. This modified Einasto profile with $\alpha =0.11$ (more generally known as EinastoB or EiB) is chosen in this work. Using Eqs. (32)–(37), we calculate the gamma-ray flux resulting from the annihilation of DM candidate $\chi$ in our model (type I and type II THDM) from the inner $5^0$ of GC for a chosen set of benchmark points (BPs) given in Table 1. We consider two benchmark points for each of the type I and type II THDM cases with $m_H=150$ and 200 GeV. These BPs are in agreement with the bounds from DM relic density given by PLANCK experiment, signal strength of SM scalar from LHC, the adopted bound on the signal strength of non-SM scalar ($R'_{x}\le ~0.2$) and direct detection constraints from LUX. We now calculate the gamma-ray flux for the benchmark points considered in Table 1 and compare with the observed gamma-ray flux obtained from FGST data [57].³ The calculated $\gamma$-ray flux for the benchmark points considered are plotted in Fig. 3a–d. As mentioned earlier, the calculations are performed for both NFW and EiB dark matter density profiles. The total $\gamma$-ray flux are then obtained by adding the calculated flux for dark matter annihilation in GC region (either with NFW or with EiB profile) with the galactic ridge and point source data. Therefore, for each plots (a–d) of Fig. 3 we show two results for total $\gamma$-ray flux (from DM annihilation $+$ galactic ridge $+$ point sources) that correspond to NFW and EiB profiles and compare both of them with the Fermi-LAT experimental data points (with error bars) in Fig. 3a–d. Also plotted in Fig. 3a, b the contribution to the $\gamma$-ray flux from galactic ridge and point sources separately. The calculational results shown in Fig. 3a, b correspond to the first set of benchmark points BP1 and BP2 respectively chosen for type I THDM. Figure 3a, b shows the results for $m_{H}=$ 150 and 200 GeV respectively. For type II THDM the set of benchmark points BP3 ($m_{H}=$ 150 GeV) and BP4 ($m_{H}=$ 200 GeV) are adopted and the corresponding results are shown in Fig. 3c, d respectively (Table 1, lower part). Comparison of the plots a and b of Fig. 3 reveals that in case of our proposed fermionic dark matter in type I THDM scenario, the experimental data are best satisfied when we choose the non-SM Higgs mass $m_{H}$ to be 150 GeV and consider Einasto B (EiB) profile in our calculations. For the choice of $m_{H}=$ 200 GeV in type I THDM case however the total flux calculated with either of the NFW or EiB profiles do not agree at all with the experimental data. Similar plots with BP 3 and BP 4 that correspond to type II THDM are shown in Fig. 3c, d. Plots in Fig. 3c, d show that in the case of our fermionic dark matter in type II THDM too, total $\gamma$-ray flux generated using EiB profile is in good agreement with the observed data when compared to those calculated using NFW profile. Finally, $\gamma$-ray produced by the annihilation of our proposed fermionic dark matter in the mass range $\sim$ 50–90 GeV (in type I and type II THDM) can best explain the experimentally observed $\gamma$-ray excess from GC. In Table 1 we tabulate the thermally averaged annihilation cross-section for DM annihilating into $b\bar{b}$, $W^+W^-$ and ZZ channels along with model parameters. From BPs in Table 1 one observes that for BP1 and BP3, DM mainly annihilates into $b\bar{b}$. For the case of BP2 (with $m_{\chi }=90$ GeV) the $W^+W^-$ channel dominates over other annihilation channels thereby reducing the $\gamma$-ray flux produced for BP2. For BP4 ($m_{\chi }=85$ GeV), DM annihilating into $b\bar{b}$ is dominant although $W^+W^-$ channel also contributes (nearly 10 % of $\langle \sigma v\rangle _{b\bar{b}}$). Study of annihilation channels shows that for DM with smaller masses (BP1 and BP3) primarily tends to annihilate into $b\bar{b}$ but with the increase in DM mass other annihilation channels will open up and contributes significantly.

We also like to add that recent analysis of Fermi-LAT data for gamma rays from inner galaxy has reported an excess of $\gamma$-rays from Galactic Centre region [68–77] in the energy range 1–3 GeV. Since no astrophysical phenomena can explain this excess, the annihilation of DM at the GC region could be responsible for the same [77–85]. Many different particle physics models for dark matter candidate have been proposed and explored in order to explain this 1–3 GeV $\gamma$-ray excess [86–99]. In this work, we also explore in the framework of our model, whether the present singlet fermionic dark matter in type I and type II THDM can explain this GC gamma ray excess. We calculate the GC $\gamma$-ray flux obtained from the annihilation of our fermionic DM in this present framework. In doing this we use the benchmark points for the fermionic dark matter discussed earlier. The two dark matter halo profiles namely the NFW and EiB halo profiles as mentioned above are also used in order to explain the 1–3 GeV $\gamma$-ray excess from GC. Shown in Fig. 4a–d, the results and their comparisons with data points. In the plots of Fig. 4a–d, the experimental data points are shown in red whereas the green and blue lines represent the calculational results for the benchmark points for the cases with NFW and EiB halo profile respectively.⁴ In Fig. 4a, b we plot $\gamma$-ray flux produced due to DM annihilation using BP’s adopted for type I THDM scenario (i.e., BP1 and BP2) with $m_H=$ 150 and 200 GeV. From Fig. 4a, b, it can be observed that for type I THDM the excess of $\gamma$-ray produced using BP1 is in better agreement with the experimental results compared to the case with BP2 when EiB profile is considered. Similar plots for the case of type II THDM are shown in Fig. 4c, d. In case of type II THDM, we found that the excess in $\gamma$-ray obtained for BP3 with EiB halo profile is in good agreement with the experimental results of Fermi-LAT in comparison to the results when BP4 is chosen. For both type I and type II THDM framework with singlet fermion the calculated gamma flux using NFW profile with BP’s are not compatible with the observed results of Fermi-LAT.

6 Discussions and conclusions

In this work we consider a singlet fermion dark matter in a framework of two Higgs doublet model. We have explored the viability of such a fermionic dark matter in two different types of THDMs namely THDM I and THDM II and assumed that the new found scalar boson at LHC is one of the two CP even Higgs appearing in THDM. The fermionic dark matter candidate $\chi$ in our model couples to the CP even Higgs-scalars appearing in THDM with a non-renormalisable dimension five interaction. Hence, DM in the present model can undergo the process of annihilation into SM particles through Higgs mediated channels. We solve the Boltzmann equation for the DM candidate $\chi$ to calculate the DM relic density for the case of type I and type II THDM. We have constrained the model parameter space by PLANCK relic density criterion for dark matter, bounds on the SM Higgs signal strength obtained from LHC experiments (CMS and ATLAS) and latest direct detection limits on DM-nucleon scattering cross-section from XENON100 and LUX results. Since both the models (type I and type II THDM) involve an extra Higgs boson (H), additional bounds on the signal strength of non-SM scalar due to its non-observance are also taken into account. Study of the model parameters reveals that an increase in the mass of H ($m_H$) will result in a decrease in the valid parameter space for both the THDM’s considered. The present analysis indicates that the fermionic DM $\chi$ in THDM I and II framework (as considered in the work) can be treated as a possible dark matter candidate satisfying the bounds on DM relic density, direct detection and Higgs signal strength results from CMS and ATLAS. We further test the viability of our model by investigating whether the DM in present mechanism can produce the observed GC gamma-ray flux predicted by FGST. We have chosen two sets of benchmark points, each of one for type I and type II THDM scenarios. We also consider two dark matter halo profiles namely NFW and Einasto B. We calculate the $\gamma$-ray flux originating from DM annihilation for these chosen benchmark points. Comparison of the observed FGST $\gamma$-ray flux with those obtained from the BPs in our model suggests that the fermionic DM candidate $\chi$ in our framework can better explain the GC $\gamma$-ray if Einasto B halo profile is considered. The present framework of THDM excludes the low mass regime explored in the work [41] when the ad-hoc assumption on the DM-Higgs coupling is relaxed. This also holds for the case of scalar or vector dark matter candidate explored in the work [41]. We have found that instead of a low mass DM $\sim$10 GeV, the fermionic DM in the present scenario in the mass range $50\le m_{\chi }\le 90~\mathrm{GeV}$ can also provide a plausible explanation to the GC $\gamma$-ray observed by Fermi-LAT.

Throughout the work we have considered an effective theory approach of dark matter in THDM farmework assuming a dimension five non-renormalisable interaction of DM candidate $\chi$ with the THDM scalar doublets. This non renormalisable interaction invokes a new physics scale $\Lambda$ similar to the case of minimal fermionic dark matter model [47]. Hence, the present model is not UV complete. UV completion of this model can simply be obtained by removing the dimension five couplings within the model and introducing a singlet scalar making the theory renormalisable (as illustrated in literatures [48, 49]). However, adding a singlet scalar to the THDM will change the scalar potential of the model. This new model of THDM with scalar singlet and fermionic dark matter will provide three Higgs like particles and also an extra resonance region apart from the THDM scalar resonances for the DM candidate. Direct detection of DM candidate in this model will also include all three Higgs likes states and will be modified accordingly. Integrating out the newly introduced scalar field is inconvenient as the information about the scalar resonance region will be lost and direct detection results of DM-nucleon scattering will change. Hence the study of fermionic dark matter in THDM with additional singlet scalar will lead to a different Higgs and DM phenomenology compared to the present framework (fermionic DM in THDM) and is not considered in this work. Detailed study of the model (THDM with singlet scalar and fermionic dark matter) is interesting and may provide other perspectives of DM phenomenology.