Abstract
We consider a fermionic dark matter (DM) in the left–right symmetric framework by introducing a pair of vector-like (VL) doublets in the particle spectrum. The stability of the DM is ensured through an unbroken \(\mathcal {Z}_2\) symmetry. We explore the parameter space of the model compatible with the observed relic density and direct and indirect detection cross sections. The presence of charged dark fermions opens up an interesting possibility for the doubly charged Higgs signal at LHC and ILC. The signal for the doubly charged scalar decaying into the dark sector is analyzed in multilepton final states for a few representative parameter choices consistent with DM observations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The new era of search for particles or hints of new physics has been facing its challenges since the discovery of the Higgs boson [1, 2]. While direct searches at experiments at the Large hadron Collider (LHC) have not revealed anything new yet, the irrevocable hints for the existence of tiny neutrino mass and dark matter (DM) in the Universe has led to new efforts in non-collider experiments to establish signals for new phenomenon which may point to an extension of the Standard Model (SM) and more crucially provide information about DM. Left–right symmetric models (LRSM) [3,4,5,6,7,8] are one of the most well motivated and widely studied extensions of the SM as it is able to address several phenomena which are not very well understood in the framework of SM, be it Parity or the tiny neutrino masses which have their origin very naturally in the model. The Parity symmetry (P) prevents one from writing Parity and Charge-Parity (CP) violating terms in the Quantum Chromodynamics (QCD) Lagrangian thus resolving the strong CP problem naturally without the need to introduce a global Peccei-Quinn symmetry. The gauge structure of these models force us to have a right-handed neutrino in the lepton multiplet. This right-handed neutrino can generate a light neutrino mass through the seesaw mechanism. Moreover left–right symmetry is also favored by many scenarios of gauge-unification.
We have also established that a significant part of the Universe (\({\sim }26\%\) of total energy budget) which is made of non-luminous, non-baryonic matter and interacts via gravity, popularly known as dark matter (DM) is one of the most fundamental concerns in current days particle physics and cosmology [9, 10]. There are several astrophysical evidences like the rotational curve of the galaxy, bullet cluster, gravitational lensing, anisotropy in cosmic microwave background (CMB), etc. [11,12,13,14], which indicate the existence of stable DM in the present Universe. However we do not know much about it, the only information so far we know about DM is its relic abundance measured by WMAP and PLANK to be \(\Omega _\mathrm{DM} h^2=0.120\pm 0.001\) [15]. Apart from this the nature of the DM e.g. its spin, non-gravitational interaction and mass still remain an open question. Depending on the production mechanism in the early Universe, DM particles are broadly classified based on its interaction strengths into WIMP [16,17,18], SIMP [19], FIMP [20], etc. Among these the weakly interacting massive particle (WIMP) is one of the popular DM candidates due to its detection possibility in direct (XENON1T [21], PANDAX 4T [22] etc.), indirect (FERMI LAT and MAGIC [23, 24]) and collider (LHC [25] and ILC) search experiments. The weak interaction between WIMP like DM and the visible sector can lead to thermal equilibrium in the early universe at temperatures above the mass scale and freezes out from the thermal bath when the temperature falls below its mass [16]. Many theoretical extension of SM have been formulated to accommodate the particle nature of DM over the past several decades. A novel possibility would be its existence in the framework of left–right symmetric theories. While the supersymmetric versions of the LRSM [26, 27] naturally incorporate a WIMP (through conserved R-parity) in the form of the lightest supersymmetric particle, it is rather challenging to invoke a DM candidate in the minimal setup of LRSM. Therefore a natural extension could be to include new particles in the set-up in the non-supersymmetric model [28,29,30,31,32,33,34]. To accommodate DM in LRSM, we consider two vector-like fermion doublets, \(\psi _1\) and \(\psi _2\) which belong to the \(SU(2)_L\) and \(SU(2)_R\) respectively and both carry a discrete \(\mathcal {Z}_2\) charge of \(-1\) to ensure the stability of the lightest state. The vector-like doublets are introduced in pair to adhere to the left–right Parity requirement of the LRSM Lagrangian where any field (\(O_{L/R}\)) transforms under \(SU(2)_{L/R}\) as \(O_L \leftrightarrow O_R\). This induced dark sector in the LRSM would have enhanced interactions including its participation in both left-handed and right-handed charged currents as well as neutral currents mediated by the electroweak (EW) and new heavy gauge bosons and the numerous scalars present in the model. Thus one expects the DM phenomenology to be very interesting and illuminating in several regions of the model parameter space. A crucial hint of LRSM is the presence of two doubly charged scalars which independently couple to the gauge bosons of \(SU(2)_L\) and \(SU(2)_R\) and therefore have different production strengths. With the inclusion of the dark sector which contains new fermions, the search for these exotics can be a lot different at collider experiments. We shall consider this interesting possibility in our work by studying the signal for the doubly charged scalars at LHC as well as the proposed International Linear Collider (ILC) [35,36,37,38] while highlighting the DM phenomenology of the model in more detail.
The rest of our work is organized as follows. We first briefly describe the proposed model in Sect. 2. In Sect. 3, we discuss possible theoretical and experimental constraints on the model parameters which would be applicable for our analysis. In Sect. 4 we discuss the DM phenomenology where we demonstrate the allowed parameter space compatible with current relic density, direct and indirect search constraints. The collider signature of the doubly charged Higgs in the presence of DM at LHC and ILC in this setup are discussed in Sects. 5 and 6 respectively. Finally, we summarize our findings in Sect. 7.
2 Left–right model with dark doublets
The model is an extension of the popular left–right symmetry model (LRSM) [3, 4] where the only addition is the introduction of two vector-like (VL) fermion doublets [34] in the particle spectrum, viz. \(\psi _1^T= \left( \begin{matrix} \psi _1^0&\psi _1^- \end{matrix}\right) _{L,R}\) and \(\psi _2^T= \left( \begin{matrix} \psi _2^0&\psi _2^- \end{matrix}\right) _{L,R}\) where under left–right parity symmetry \(\psi _1 \leftrightarrow \psi _2\). The new fermions are a replication of the lepton doublets with the only difference being the VL character such that \(\psi _1\) is a VL doublet under \(SU(2)_L \otimes U(1)_{B-L}\) while \(\psi _2\) is a VL doublet under \(SU(2)_R \otimes U(1)_{B-L}\). A discrete \(\mathcal {Z}_2\) symmetry is included in the model under which the new VL doublets are odd, that makes the lightest neutral component of each VL doublet stable. However, after gauge symmetry is spontaneously broken, the neutral components of \(\psi _1\) and \(\psi _2\) will mix leading to only one neutral component to remain stable and act as the DM candidate in the model. Note that all the remaining fields in the model are even under the \(\mathcal {Z}_2\) symmetry. The charge assignment of all fermions including dark fields and scalar fields in the extended LRSM are tabulated in Tables 1 and 2, respectively. It is important to note here that the VL nature of the new fields do not lead to any chiral anomaly, keeping the model anomaly free.
The Lagrangian for this model can be written in two separate components:
The first part of the Lagrangian in Eq. 1 represents the \(\mathcal {Z}_2\) even LRSM Lagrangian while the second part of the Lagrangian represents the proposed dark sector in this setup. Since the left–right symmetric Lagrangian, \(\mathcal {L}^\mathrm{LRSM}\) has been comprehensively studied in the literature we do not discuss it in great detail here and refer the readers to Refs. [3,4,5,6,7,8, 39,40,41,42,43,44,45]. Our main motivation in this work is to study the phenomenology of DM in the extended LRSM setup. We, therefore, restrict ourselves to only the relevant part of the Lagrangian of LRSM for our analysis.
The scalar potential of LRSM
The most general \(\mathcal {C} \, (\mathrm charge)-\mathcal {P} \, (\mathrm parity)\) invariant scalar potential in the LRSM, invariant under the gauge symmetry \(SU(3)_C \otimes SU(2)_R \otimes SU(2)_L \otimes U(1)_{B-L}\) reads as [6, 39]
The neutral scalar fields in the multiplets acquire non-zero vacuum expectation value (vev) leading to the symmetry breaking pattern: \(SU(3)_C \otimes SU(2)_R \otimes SU(2)_L \otimes U(1)_{B-L} \rightarrow SU(3)_C \otimes SU(2)_L \otimes U(1)_Y \rightarrow SU(3)_C \otimes U(1)_Q\) [6, 39] as:
The vevs of the scalar fields are parametrized as:
where v can be identified as SM vev and is given by \(v=\sqrt{v_1^2+ v_2^2}=246\) GeV, with \(v_L \ll v~(v_2 \ll v_1) \ll v_R\). The parity symmetry implies \(g_L=g_R\). Without any loss in generality of the BSM phenomenology, the above scalar potential can be simplified by considering \(\beta _i=0,~\alpha _2=0 ,~\lambda _4 =0~\mathrm{and} ~v_L \rightarrow 0\). Under these assumptions, the masses and corresponding eigenstates of the scalar and the gauge bosons are tabulated in Table 3. Here we have categorized the different scalar types according to their \(\mathcal{CP}\mathcal{}\) properties and electric charge without going into the details, as these have been discussed in the literature [8].
We shall work in the limit of parameter choices in the scalar sector which helps us with a favorable DM phenomenology. This will be obvious when we calculate the observables relevant for DM abundance and its correlation with the scalar spectrum.
Dark Sector Lagrangian:
In this set-up the lightest neutral state which is an admixture of the neutral component of \(SU(2)_L\) fermion doublet (\(\psi _1\)) and \(SU(2)_R\) fermion doublet (\(\psi _2\)) after symmetry breaking, gives rise to a viable candidate of DM due to the unbroken discrete symmetry \(\mathcal {Z}_2\). The Lagrangian of the dark sector in the extended LRSM can be written as,
A very similar extension of the LRSM was studied in Ref. [34]. Although our model is the same with similar particle content, our study differs in how the Yukawa structure of the model has been assigned. We chose a uniform Yukawa coupling strength between the VL fermion doublets with the scalar sector. It is worth noting that while the earlier work treats the individual left-handed and right-handed projections of the \(SU(2)_L\) VL doublet differently and therefore invoke more Yukawa couplings in the model, we keep \(Y_1 = Y_2\) in most our analysis (Eq. 5). A similar structure is assumed for the \(SU(2)_R\) VL doublet. While the \(Y_1 \ne Y_2\) choice remains a viable phenomenological option since it does not alter the VL doublet’s gauge interactions, it does give additional freedom to treat the dark sector fermions independently. A more stark difference with Ref. [34] is in their choice of different Yukawa couplings for the components of the same fermion doublet after symmetry breaking. This is somewhat an unnatural choice and difficult to arrange starting from the symmetry of the model. We consider a more natural and aesthetic approach by choosing the Yukawa couplings to be identical for the up and down components of the same fermion doublet, leading to mass of these fermions in dark sector to be related by same parameters. Hence the mass gap of the particles cannot be made arbitrarily large as assumed in Ref. [34]. This can lead to significant differences in the phenomenological implications since it allows us to correlate the nature of the DM based on its composition unlike their study. We note that this also allows a more interesting signature for the doubly charged scalar in the model. Our choice also leads to a very different DM analysis and allowed parameter space for the model.
In the above Lagrangian (in Eq. 5) \(M_L\) and \(M_R\) are the bare masses of \(\psi _1\) and \(\psi _2\) respectively and \(Y_1\) and \(Y_2\) are the Dirac Yukawa couplings. The other two Majorana type Yukawa couplings, \(y_L\) and \(y_R\) are responsible for generating the mass splitting between the physical eigenstates after mixing. In addition the non-zero values of both \(y_L\) and \(y_R\) lead to interesting collider signatures of the doubly charged scalars (\(H_{L,R}^{\pm \pm }\)) in the model that can affect the search strategies at LHC and ILC which forms a major motivation to study this model.
After symmetry breaking, the dark sector Lagrangian in Eq. 5 leads to mixing between the neutral components \(\psi _1^0\) and \(\psi _2^0\) and also leads to the mixing among the charged components \(\psi _1^\pm \) and \(\psi _2^\pm \) because of the Yukawa interactions with the bidoublet. The mass matrices of the neutral and charged fermion states can be expressed in the interactions basis of \(X_N= \left( \begin{matrix} (\psi _{1L}^0)^c&\psi _{1R}^0&(\psi _{2L}^0)^c&\psi _{2R}^0 \end{matrix} \right) ^T\) and \(X_C =\left( \begin{matrix} \psi _1^-&\psi _2^- \end{matrix} \right) ^T\) respectively as,
where \(\alpha =\frac{Y_1 v_1+ Y_2 v_2}{\sqrt{2}} \simeq \frac{Y_1 v_1}{\sqrt{2}} \) and \(\alpha ^\prime =\frac{Y_1 v_2+ Y_2 v_1}{\sqrt{2}} \simeq \frac{Y_2 v_1}{\sqrt{2}}\) in the limit of \(\tan \beta \rightarrow 0\). The phenomenology of DM depends on the following parameters in dark sector:
along with the free parameters of LRSM. The nature of DM i.e. whether the DM is \(SU(2)_L\) type or \(SU(2)_R\) type or an admixture of them is mainly decided by the choice of the above parameters. Depending on these parameter choices, the model offers three different type of DM scenarios which we shall discuss now.
\({SU(2)_L {\hbox {like DM}}}\) (\(M_L \ll M_R)\)
For the given mass hierarchy, \(M_L \ll M_R\), the light neutral states, \(\chi _{_{1,2}}\) and the light charged state, \(\chi _{_1}^\pm \) dominantly behave like the fermion doublet, \(\psi _1\). The presence of Majorana type Yukawa interaction with \(\psi _1\) \((y_L \overline{\psi _1} \Delta _L^\dagger i\sigma _2 \psi _1^c ~)\), leads to the mass splittings (generated after symmetry breaking) between the light neutral and charged fermion states, \(\chi _{_{1,2}}\) and \(\chi _{_1}^\pm \) as:
whereas the remaining physical states \(\chi _{_{3,4}}\) and \(\chi _{_2}^\pm \) are very heavy \(\left( \mathcal {O}(M_R)\right) \) and do not play any role in contributing to number density of DM. Note here that the light neutral and charged states are nearly degenerate \(\left( \mathcal {O}(M_L)\right) \) as \(v_L\) is small (\( \lesssim 2.6\) GeV, constrained from \(\rho \) parameter: \(1.00038\pm 0.00020\) [46]). In this setup the light dark states interact mostly with the \(SU(2)_L\) fields of LRSM.
\({ SU(2)_R {\hbox {like DM}}}\) (\(M_L \gg M_R)\)
Unlike the previous case, here the right triplet (\(\Delta _R\)) vev, \(v_R\) plays a significant role. In addition, for the reversed case where \(M_L \gg M_R\), the light neutral and charged physical states, \(\chi _{_1,_2}\) and \(\chi _{_1}^\pm \) mostly behave like the second fermion doublet, \(\psi _2\) belonging to \(SU(2)_R\). Similar to the previous scenario, \(\psi _2\) interacts with the \(SU(2)_R\) triplet (\(\Delta _R\)) with the Majorana type Yukawa interactions: \(y_{_R} \overline{\psi _2} \Delta _R^\dagger i\sigma _2 \psi _2^c ~\) which leads to the mass splitting between light neutral and charged physical states, \(\chi _{_1},~\chi _{_2}\) and \(\chi _{_1}^\pm \) as:
whereas the remaining physical states \(\chi _{_{3,4}}\) and \(\chi _{_2}^\pm \) are much heavier (\(\mathcal {O}(M_L)\)), which mostly decay into light states before the time of DM freeze-out from thermal bath. Hence they do not affect todays DM density. It is important to mention here that the right triplet vev, \(v_R\), can easily generate a large mass splitting between the light physical states, obvious from the mass expressions in Eq. 9. The light physical states in this case are \(SU(2)_R\) like in nature and dominantly interact with \(SU(2)_R\) fields.
Mixed DM (\(M_L \sim M_R \))
When both \(M_L\) and \(M_R\) are of similar order of magnitude and the Yukawa couplings, \(y_{_R},Y_{_1}\) and \(Y_{_2}\) have non-zero values, the physical dark states are admixture of both \(\psi _1\) and \(\psi _2\). We henceforth refer this as mixed DM scenario. In order to obtain the physical neutral states, \(\chi _{_i} (i=1,2,3,4)\) one needs to diagonalize the mass matrix \(\mathcal {M}^N\) in Eq. 6 by a unitarity matrix, \({\mathcal {U}_N}_{4\times 4}\). The mass diagonalization leads to a relation between the physical and interactions states given by
where \(\chi _{_1},~\chi _{_2},~\chi _{_3}\) and \(\chi _{_4}\) are the physical eigenstates with mass \(M_1,~M_2,~M_3\) and \(M_4\) respectively following the mass hierarchy \(|M_1|< |M_2|< |M_3| < |M_4|\). Thus the lightest neutral state, \(\chi _{_1}\) of mass \(M_1\) \((\equiv m_\mathrm{DM})\) is the stable DM candidate in this setup. The mass eigenvalues of the mass matrix, \(\mathcal {M}^N\) are given in the limit of \(v_L \rightarrow 0,~\tan \beta \rightarrow 0\) as
The order of magnitude of the above eigenvalues depend on the model parameters. Here all the neutral physical states, \(\chi _{_i}~(i=1,2,3,4)\) behave like Majorana states and are defined as \(\chi _{_i}=\frac{1}{2} \left( \chi _{_i} + \chi _{_i}^c \right) \). Similarly the mass matrix, \(\mathcal {M}^C\) for the charged fermion states mentioned in Eq. 6 can be diagonalized by a unitarity matrix, \({\mathcal {U}_C}_{2\times 2}\). The corresponding mass diagonalization relation and the relation between physical and interaction states are expressed as
Here \(\chi _{_1}^\pm \) and \(\chi _{_2}^\pm \) are the physical charged eigenstates with mass \(M_1^\pm \) and \(M_2^\pm \) respectively with mass hierarchy \(|M_1^\pm | < |M_2^\pm |\). The eigenvalues of the mass matrix, \(\mathcal {M}^C\) in the limit of \(v_L \rightarrow 0,~\tan \beta \rightarrow 0\) are given as
In our analysis we have used the numerical tool SPheno [47] to diagonalize the mass matrices and generate the mass spectrum.
3 Constraints
In this section we briefly address the existing theoretical and experimental constraints on the model parameters which become relevant for our analysis.
Perturbativity: The quartic couplings in the scalar potential, gauge couplings and the Yukawa couplings are bounded from above as:
Relic and Direct Search: The current observation from PLANCK [15] puts a stringent bound on DM number density in the Universe :
We will implement this constraint on our model parameter space. Along with this astrophysical observation, the DM-nucleon scattering cross-section also faces severe constraints from non-observation of DM at direct search experiments like XENON 1T [21] and PANDAX 4T [22]. We also include this limit on the model parameter space when we scan over the free parameters.
Higgs invisible decay: When the DM mass is below \(M_h/2\), the SM Higgs can decay to DM. The invisible decay width of the SM Higgs is measured at LHC [48] which gives a constraint on the parameter space that leads to \(m_\mathrm{DM} < \frac{M_h}{2}\) as well as the coupling strength of DM with the SM like Higgs boson through an upper bound:
LEP constraint: LEP has excluded exotic charged fermion masses below \(\sim 102.7\) GeV [49]. We implement this constraint on the dark charged fermions (\(\chi _{_{1,2}}^\pm \)) mass \(M_{1,2}^{\pm } > 102.7\) GeV.
FCNC constraint: The bi-doublet structure of the scalar gives rise to tree-level flavor changing neutral current (FCNC) interactions with SM quark in LRSM which is mediated by the heavy neutral scalars H, A and can contribute to flavor observables such as \(K_0-\overline{K_0}\), \(B_d-\overline{B_d}\) and \(B_s-\overline{B_d}\) mixings [8, 50]. The flavor observable data puts very stringent lower bound on heavy neutral scalars in the model given by \(M_{H,A} > rsim 15\) TeV. This upper bound further translates on to the quartic coupling \(\alpha _3\) in the scalar potential and on the triplet scalar vev \(\langle \Delta _R^0 \rangle = v_R\). Using the approximate form of the heavy neutral scalar mass \(M_{H}\), the FCNC constraint can be expressed as:
Collider constraint on \(M_{W_R}\): The dominant bound on heavy charged gauge boson \(W^\prime \) come from its decay to dijet. However, in the LRSM model the presence of a heavy right-handed neutrino leads to the possibility of \(W_R\) decay to a charged lepton and a heavy \(N_R\) when kinematically allowed. This leads to a final state with same-sign leptons and jets, which has suppressed SM background and leads to stronger bounds. The decay of \(W_R\) into a boosted right handed neutrino \(N_R\) yields same-sign lepton pair plus jets final states at collider as \(W_R \rightarrow N_R~ \ell ~ \rightarrow ~\mathrm{jets} +2\ell \). The current search by ATLAS [51] with integrated luminosity of \(80 ~\mathrm{fb}^{-1}\) for \(\sqrt{s}=13\) TeV, excludes \(M_{W_R}\) smaller than 5 TeV. This lower bound can be also expressed in terms of \(v_R\) as:
In addition the doubly charged scalars, \(H_{L,R}^{\pm \pm }\) are also constrained from existing searches at LHC which we discuss in detail in the collider analysis section. For our analysis we pick up a set of benchmark points (BPs) which are consistent with the above mentioned constraints. The BPs are tabulated in Tables 4 and 5.
4 DM phenomenology
We now discuss the phenomenology of our proposed fermionic dark matter in the extended LRSM. The lightest neutral Majorana state \(\chi _{_1}\) which can be an admixture of \(SU(2)_L\) like fermion (\(\psi _1\)) and \(SU(2)_R\) like fermion (\(\psi _2\)) or purely \(SU(2)_L\) like fermion \(\psi _1\) or purely \(SU(2)_R\) like fermion \(\psi _2\), is the stable DM candidate under the extended symmetry group \(\mathcal {G}\). In this section we review the region of parameter space which is allowed by observed DM density from WMAP-PLANCK data [14, 15], latest upper bound on DM-nucleon scattering cross-section from direct search experiments [21, 22] and also from indirect search constraints [23, 24].
The lightest neutral Majorana state, \(\chi _{_1}\) assumed to be the viable candidate of DM can be produced at early time of the Universe via thermal freeze-out mechanism [16]. The dark sector particles were connected with visible sector via gauge and scalar mediated interactions of the LRSM and freezes out when the interaction rate (\(\Gamma =\langle \sigma v \rangle n_\mathrm{DM}\)) falls below the expansion rate of the universe (\(\mathcal {H}\)). Apart from \(\chi _{_1}\) the dark sector also has heavy neutral and charged fermion states, \(\chi _{_i} (i=2,3,4)\) and \(~\chi _{_j}^\pm (j=1,2)\) respectively. When the mass of these heavy states lie close to the DM mass, the number density of DM also gets affected by the number changing processes due to these heavy states. So the relic density of DM, \(\chi _{_1}\) is guided by the different type of gauge and Higgs mediated number changing processes as:
where X and Y are the light states in LRSM. The evolution of DM number density with time can be described by solving the Boltzmann equation given by [16]:
where \(n_{_\mathrm{DM}} \simeq n_{\chi _{_1}}\) denotes the number density of DM and \(n_\mathrm{eq}= g_{_\mathrm{DM}}(\frac{m_{_\mathrm{DM }} T}{2\pi })^{3/2}\exp (-m_{_\mathrm{DM}}/T)\) is the equilibrium density. The mass of DM is defined as \(m_\mathrm{DM}\) (i.e \(m_\mathrm{DM}= M_1\)). \(\langle \sigma v\rangle _\mathrm{eff}\) denotes the effective thermal averaged cross-section where all annihilation and co-annihilation type number changing processes are taken into account [52, 53] and which can be expressed as follows:
where
\(i,j=2,3,4\); \(k,l=1,2\); \(\delta _i=\frac{M_i-M_1}{M_1}\) and \(\delta ^{\pm }_k=\frac{M_k^\pm -M_1}{M_1}\). The \(g_{_1}\), \(g_{_i}\) and \(g_{_k}^\pm \) are the internal degrees of freedom of \(\chi _{_1},~\chi _{_i}\) and \(\chi _{_k}^\pm \) state respectively. The parameter x is defined as \(x=\frac{m_\mathrm{DM}}{T} \equiv \frac{M_1}{T}\) where T is the thermal bath temperature. Using the above expression of \(\langle \sigma v\rangle _\mathrm{eff}\), one can express the number density of DM approximately as [52, 53]:
where the SM degrees of freedom \(g_{*}=106.7\) and \(x_f= \frac{m_{_\mathrm{DM}}}{T_f} \simeq 20-25\) [16]. \(T_f\) denotes here the freeze-out temperature of DM. The first term of Eq. 20 represents the standard DM annihilation while the rest of the terms are part of DM co-annihilation. Note that the co-annihilation contribution reduces with large mass splitting, \(\Delta M= M_i- M_1, M_i^\pm -M_1\), due to the Boltzmann suppression of \(\mathrm{exp}(-\Delta M/ T)\). It is worth mentioning here the different tools/packages that have been used for our study. We first implement the model in the public code SARAH [54] for generating numerical modules for SPheno [47] and model files for MicrOmegas [55]. We then use SPheno to compute the mass spectrum and branching ratios which is passed on to MicrOmegas to calculate DM relic density as well as obtain the direct and indirect search cross-section.
We shall now illustrate the behavior of DM number density with the following independent free parameters in the dark sector which are relevant for DM phenomenology:
The phenomenology of DM also significantly depends on the free parameters like mass of the light states which behave as mediator between dark and visible sector, vevs of the scalar fields \(v_R\), \(v_L\) and \(\tan \beta \) in LRSM. It is difficult to study the role of all the free parameters at a time. In addition varying all the parameters at the same time makes it difficult to determine the physics implications of any particular set. We therefore choose to fix the well studied LRSM model parameters which simplifies things but allows us to study the DM phenomenology based on the dark sector parameters. We first fix the LRSM sector as mentioned in BP1 listed in Table 4 which is consistent with existing theoretical and experimental constraints. The dark sector particles speak with the visible sector via light scalars (h, \(H_L\), \(A_L, H_L^\pm , H_L^{\pm \pm }, H_{R}^{\pm \pm }\) ) and the SM gauge bosons (\(Z, W, \gamma \)). While the model possesses many more particles in the spectrum, other heavy state mediated diagrams are suppressed by the mass and they give negligible contribution to DM density. We now consider the DM phenomenology of all three possible scenarios.
\({ SU(2)_L {\hbox {like DM}}}\) (\(M_L \ll M_R)\)
As stated earlier in Sect. 2, the DM (\(\chi _{_1}\)) along with heavier components \(\chi _{_2}\) and \(\chi _{_1}^\pm \) behave like the \(SU(2)_L\) doublet dark fermion (\(\psi _1\)) for the mass parameter \(M_L \ll M_R\). Since the physical states belong to the \(SU(2)_L\) doublet, the relic density of DM is mainly governed by SM gauge boson mediated interactions along with the new scalar triplet \(\Delta _L\) involved through the Yukawa interaction: \( y_{_L} \overline{\psi _1} \Delta _L^\dagger i\sigma _2 \psi _1^c\) which is also responsible for generating the small mass splittings between \(\chi _{_1}\), \(\chi _{_2}\) and \(\chi _{_1}^\pm \). Note here that all other states, \({\chi _{_3,_4}} , \chi _2^\pm \) have mass \(\mathcal {O}(M_R)\) and do not play any relevant role in the DM density.
In the left panel of Fig. 1 we show the variation of relic density as a function of the DM mass \(m_{_\mathrm{DM}} (\equiv M_1\)) for different values of \(y_{_L}\). Correct observed relic density bound measured by WMAP-PLANCK, \((\Omega _\mathrm{DM}h^2=0.120 \pm 0.001)\) is shown by grey dashed line in the same plane. The parameters in LRSM sector are kept fixed as listed in Table 4 for the benchmark BP1. The mass splitting between the light dark states are very small leading to nearly degenerate states with splitting \(\sim y_L \, v_L\). As the vev of the left triplet, \(v_L\) is constrained from the \(\rho \) parameter as \(v_L \lesssim 2.6\) GeV [46], hence the maximum splitting available for this type of scenario is \(\sim 2.6\) GeV for \(y_{_L}=1\). As a result the relic becomes under abundant due to the large gauge mediated co-annihilation cross-sections (\(\chi _{_1} ~\chi _{_2},~\chi _{_i} ~\chi _{_1}^\pm \rightarrow \) X Y) as depicted in the left panel of Fig. 1. The co-annihilation contribution will get suppressed with increase in DM mass and we find that the correct density is obtained when the DM mass is around 1.2 TeV. As we further increase \(y_{_L}\), the light scalars, \(H_L \, (505~\mathrm{GeV}),~A_L \, (505~ \mathrm{GeV}),~H_L^\pm \, (555~ \mathrm{GeV}),~H_L^{\pm \pm } \, (600~ \mathrm{GeV})\) mediated diagrams start contributing. Therefore the relic becomes more under abundant which is shown using the orange line for \(y_{_L}=1\). Different kind of resonance dips are visible near high DM mass, \(m_{_\mathrm{DM}} \sim {M_{H_L}}/{2},~{M_{A_L}}/{2}\); \(~{M_{H_L^\pm }}/{2}\) and \(~{M_{H_L^{\pm \pm }}}/{2}\) and these become more prominent for large values of \(y_{_L}\) due to the Yukawa interaction: \( y_{_L} \overline{\psi _1} \Delta _L^\dagger i\sigma _2 \psi _1^c\). There are two more dips observed in the low DM mass region, around \(m_{_\mathrm{DM}} \sim {M_Z}/{2}\) and \(\sim {M_h}/{2}\). Note that, when the DM mass becomes larger than the light triplet scalars, DM can annihilate and co-annihilate to triplet final states which further reduce the DM density. This effect is observed for large value of \(y_{_L}\) as depicted in the left panel of Fig. 1 by the orange line for \(m_{_\mathrm{DM}} > rsim 500\) GeV.
The spin-independent (SI) DM-nucleon scattering cross-section with DM mass is shown in the right panel of Fig. 1 for different values of \(y_{_L}\). Due to Majorana nature of DM, the \(\chi _{_1} \chi _{_1} Z\) interaction leads to a vanishing contribution to DM-nucleon scattering cross-section. However the presence of the Yukawa interaction \( y_{_L} \overline{\psi _1} \Delta _L^\dagger i\sigma _2 \psi _1^c\) can still lead to SI DM-nucleon scattering through \(\Phi -\Delta _L\) mixed t-channel diagrams which depend on the coupling \(y_L\). The DD cross-section increases with increase of \(y_{_L}\) which can be easily seen in the right panel of Fig. 1.
\({ SU(2)_R {\hbox {like DM}}}\) (\(M_L \gg M_R)\)
With the mass parameter hierarchy \(M_L \gg M_R\), the DM (\(\chi _{_1}\)) along with \(\chi _{_2}\) and \(\chi _{_1}^\pm \) now behave like the \(SU(2)_R\) dark doublet fermion, \(\psi _2\). The relic density in this case is mainly governed by right handed gauged mediated interactions along with scalar triplet \(\Delta _R\) via the Yukawa interaction: \( y_{_R} \overline{\psi _2} \Delta _R^\dagger i\sigma _2 \psi _2^c\). The Yukawa interaction splits the state, \(\psi _2^0\) into two physical Majorana states \(\chi _{_{1,2}}\) and generates a much larger mass splitting between \(\chi _{_1}\), \(\chi _{_2}\) and \(\chi _{_1}^\pm \), thanks to the large \(v_R\). The other heavy states, \(\chi _{_3,_4}\) and \(\chi _{_2}^\pm \) which are \(SU(2)_L\) like with mass \(\mathcal {O}(M_L)\) decay into the less heavier dark states much before DM freeze-out and do not alter the observed DM density.
In the left panel of Fig. 2 we have shown the variation of relic density as a function of DM mass, \(m_\mathrm{DM} (\equiv M_1\)) with different choices of \(y_{_R}\) shown by different colored lines. The black dashed line shows the observed relic density measured by WMAP-PLANCK. The vev of right triplet (\(\Delta _R\)) responsible for the \(SU(2)_R\) breaking is taken to be quite large (\(v_R=12\times 10^3\) GeV for BP1) which corresponds to larger mass splitting between the dark states of around \(\sim ~y_R ~v_R\). For a fixed value of \(v_R\) the mass difference between the light dark states increases with increase of \(y_R\). Therefore the co-annihilation contribution becomes diluted with increase of \(y_R\) due to the Boltzmann suppression (\(\sim \) exp\((-\Delta M/T)\)). This results in a DM which is mediated mostly by the right-handed sector which is very heavy and therefore the relic density becomes over abundant as shown in the left panel of Fig. 2. In addition, due to the \(SU(2)_R\) like nature, the light dark states are dominantly connected with the thermal bath via the right handed heavy gauge fields (\(W_R, Z_R\)) and right scalar fields. The effective cross-section is suppressed due to large mediator mass unlike the \(SU(2)_L\) like DM scenario. However for \(y_R=0.0001\) which corresponds to small mass splitting (\(y_R v_R = 1.2\) GeV) one achieves dominant co-annihilation contributions resulting in under abundance. The density increases slowly with increase of DM mass and satisfies correct density for \(m_\mathrm{DM} \sim 500\) GeV. For larger value of \(y_R= 0.01\) which corresponds to a large mass splitting (\(y_R v_R = 120\) GeV) one again gets over abundance due to suppressed co-annihilation contribution. Now let us try to understand the peculiar behavior of DM density observed when the DM mass is around 80 GeV for \(y_R= 0.01\). This can be understood from the DM mass formula which is defined as \(M_1=M_R-\sqrt{2} y_R v_R\). When \(M_R < \sqrt{2} y_R v_R \, (\sim 169 ~\mathrm{GeV})\) the mass eigenvalue of DM decreases with increase of \(M_R\) while simultaneously increasing the mass splitting between \(\chi _{_1}\) and \(\chi _{_1}^\pm \). An outcome of this is that the relic density increases because co-annihilation get suppressed. This behavior is depicted by the solid black line in left panel of Fig. 2 if one looks at lower DM mass from \(m_{_\mathrm{DM}}\sim 80\) GeV. Again for \(M_R = \sqrt{2} y_R v_R~(\sim 169 ~\mathrm{GeV})\), the DM mass eigenvalue becomes zero and starts increasing with increase of \(M_R\) (\( > \sqrt{2} y_R v_R~\sim 169 ~\mathrm{GeV}\)) which is shown by the dotted line starting from low DM mass (\(M_1 > 0\)).
Similar to the \(SU(2)_L\) like case, the \(\chi _{_1} \chi _{_1} Z\) interaction again leads to vanishing DM-nucleon scattering cross-section due to the Majorana nature of \(\chi _{_1}\). But the presence of Yukawa interaction with \(\Delta _R\): \( y_{_R} \overline{\psi _2} \Delta _R^\dagger i\sigma _2 \psi _2^c\) can lead to spin-independent (SI) DM-nucleon scattering through \(\Phi -\Delta _R\) mixed t-channel diagrams. Due to small mixing between \(\Phi \) and \(\Delta _R\) and large mass suppression due to heavy \(H_R\) the direct search cross-section is much suppressed and almost independent of \(y_{_R}\) which is shown in the right panel of Fig. 2, where we have plotted the SI DM-nucleon scattering cross-section against DM mass for different values of \(y_R\).
Mixed DM (\(M_L \sim M_R\)) Let us now discuss the mixed scenario where the dark states, \(\chi _{_{i}}\) and \(\chi _{_{j}}^\pm \) are an admixture of both \(SU(2)_L\) type doublet (\(\psi _1\)) and \(SU(2)_R\) type doublet (\(\psi _2\)). The mixing between the neutral states, \(\chi _{_{i}} ~(i=1,2,3,4)\) are characterized by the parameters: \(M_L,~M_R,~Y_1~,y_{_R}\) and \(v_{_R}\) whereas for the charged states, \(\chi _{_{j}}^\pm ~(j=1,2)\), it is defined by the parameters \(M_L,~M_R\) and \(Y_2\). When both the bare masses, \(M_L\) and \(M_R\) are of similar order in magnitude, the mixing between the neutral dark states is mainly controlled by the terms, \(Y_{1} v_{_1}\) and \(y_{_R} v_{_R}\). For \(y_{_R} \rightarrow 0\), the mixing between the neutral component of \(\psi _1^0\) and \(\psi _2^0\) increases with increase of \(Y_1\) and it is maximal when \(Y_1 > rsim 0.1\). Keeping \(Y_{1} = 0.1\) fixed if we increase \(y_{_R}\), the contribution of \(\psi _2^0\) becomes dominant in DM \(\chi _{_1}\) which denotes the DM becoming more \(SU(2)_R\) like and the interaction strength with left like scalars and gauge fields are suppressed. The effect of \(y_{_R}\) on DM becomes prominent when \( y_{_R} v_{_R} > rsim Y_1 v_{_1}\). On the other hand, the mixing between the charged dark states simply depend on \(Y_2\) when \(M_L \sim M_R\).
Relic density and spin-independent DM-nucleon scattering cross-section are plotted against DM mass for the mixed DM scenario (\(M_L \sim M_R\)) with different values of \(y_{_R}\) keeping \(y_{_L}\) fixed (top panel) and with different values of \(y_{_L}\) keeping \(y_{_R}\) fixed (bottom panel). Other parameters are kept fixed as mentioned inset of each figure. In the right top and bottom panels, the solid lines correspond to \(Y_1=0.1\) whereas the dotted lines correspond to \(Y_{1,2}=0.6\). The current upper bound on the SI DD cross-section from XENON 1T [21] and PANDAX 4T [22] data are shown in the same plane for comparison
The mixed DM behavior is illustrated in Fig. 3 where we have considered \(M_R-M_L=5\) GeV. In the top-left panel of Fig. 3, we have shown the variation of relic density as a function of \(m_{_\mathrm{DM}}\) with different values of \(y_{_R}\) mentioned in the figure inset. Other dark parameters are kept fixed as mentioned inset of the figure. As stated earlier, for small values of \(y_{_R}\) (\(\rightarrow 0\)), the DM, \(\chi _{_1}\) has maximal \(\psi _1^0\) and \(\psi _2^0\) mixing and the \(SU(2)_R\) composition increases with the increase of \(y_{_R}\) for a fixed value of \(v_{_R}\). As a consequence of that, the DM becomes more \(\psi _2^0\) dominant. Similarly with the increase of \(y_{_R}\), the splitting between DM and heavy state increases which corresponds to less co-annihilation contribution to DM density. Therefore the relic density spans the region between under abundance to over abundance with increase in \(y_{_R}\) as shown in the left top panel Fig. 3. This is because the co-annihilation contribution becomes subdued and the DM interactions with the light mediators available in LRSM for BP1 are suppressed. This can be also understood from the resonance behavior near lower DM mass \(\sim 45\) GeV. When DM has enough \(SU(2)_L\) component \(\psi _1^0\) contribution, we observe dips near \(m_{_\mathrm{DM}} \sim M_W/2, M_Z/2\) which are prominent but disappear with the increase of \(y_{_R}\). However the resonance dip due to SM Higgs, h near \(m_{_\mathrm{DM}} \sim M_h/2\) becomes more prominent with increase of \(y_{_R}\). Apart from the standard resonances we can also see few dips near DM mass: \(m_{_\mathrm{DM}} \sim {M_{H_L}}/{2},~{M_{A_L}}/{2}\); \(~{M_{H_L^\pm }}/{2},~{M_{H_L^{\pm \pm }}}/{2}\) and \(~{M_{H_R^{\pm \pm }}}/{2}\) for the given benchmark point (BP1).
In the bottom left panel of Fig. 3 we have shown the variation of relic density against DM mass with different values of \(y_{_L}\) keeping \(y_{_R}\) fixed (\(=0.001\)) as quoted in the figure inset. For a fixed value of \(y_{_L}=0.01\) and \(M_R-M_L=5\) GeV, the mixing between the \(SU(2)_L\) component, \(\psi _1^0\) and \(SU(2)_R\) component, \(\psi _2^0\) is almost constant in \(\chi _{_1}\). With the increase of \(y_{_L}\), the mass splitting between the light-dark states slightly increases which results in large DM density due to less co-annihilation contribution. The effect of DM annihilation to light triplet states start contributing for large values of \(y_{_L}\) (\( > rsim 1.0\)) with \(m_\mathrm{DM} > m_{X} ~(X=H_L,~A_L,~H_L^\pm ,~H_{L,R}^{\pm \pm })\).
In the right top and bottom panels of Fig. 3, we have shown the SI DM-nucleon scattering cross-section as a function of DM mass with different choices of Yukawa couplings as mentioned inset of both figures. The spin-independent cross-section in the mixed scenario is strongly dependent on the Dirac like Yukawa couplings \(Y_{1,2}\) with the bi-doublet which can be seen from the right top and bottom panels of Fig. 3 where we have considered two different values of \(Y_{1,2}\) keeping \(y_{_L}\) and \(y_{_R}\) fixed respectively. It is also observed from the figures that for non-zero values of \(Y_{1,2}\) the SI DM-nucleon scattering cross-section is almost independent of the other two Yukawa couplings \(y_{_L}\) and \(y_{_R}\) due to the small scalar mixing between \(\Phi -\Delta _L\) and \(\Phi -\Delta _R\) respectively.
Before going into the detail of parameter scans, we briefly point out the important outcomes that emerge from the three scenarios. As we have seen, due to the relatively larger contributions from gauge interactions and dominant co-annihilation due to small mass splittings in the \(SU(2)_L\) like scenario when \(M_L \ll M_R\), the relic density is always under-abundant for DM mass below a TeV. On the other hand for \(SU(2)_R\) like DM with \(M_R \ll M_L\), the observed relic density can only be achieved for small values of \(y_R\) which leads to degenerate dark states. But the mixed DM scenario has rich phenomenological aspects due to its mixed nature. It can open up a large region of parameter space which can satisfy both relic and direct search constraints.
We have discussed here two distinct scenarios, one with \(M_L<< M_R\) where co-annihilation plays a big role in reducing relic abundance because the mass gap between the dark sector fermions is very small and \(M_L>>M_R\) where the mass gap between the dark matter and other dark sector fermions is much larger, which suppresses the co-annihilation mechanisms. We note that it is difficult to resolve such distinctions in the earlier work in Ref. [34] as there, the mass of the neutral dark sector particles and that of the charged dark sector particles are not correlated and could be independently chosen.
4.1 Parameter space scan
Here we investigate the allowed region of DM parameter space for the mixed scenario. We perform a numerical scan over the following region :
while the remaining parameters in LRSM are kept fixed as specified in BP1. Note here that the choices of \(Y_1=Y_2\) and \(y_{_L}=y_{_R}\) does not affect much in DM phenomenology but it does matter for the collider study which we will discuss in detail in a later section.
4.2 Relic density
Relic density as a function of DM mass with two different choices: \(M_L > M_R\) (red points) and \(M_R > M_L\) (blue points). The black dotted line corresponds to the observed DM relic density from WMAP-PLANCK. We fixed \(y_{_R}=0.001\) for left panel figure and \(y_{_R}=0.01\) for the right panel figure
The variation of DM relic density as a function of DM mass is shown in Fig. 4 for two different choices of \(y_{_R}=0.001\) (left) and 0.01 (right). Two different mass hierarchies : \(M_L > M_R\) (red points) and \(M_R > M_L\) (blue points) are considered for each case. The black dotted line corresponds to the central value of observed DM density [15]. For a small value of \(y_{_R}\) (\(=0.001\)), the mixing between the DM component of \(SU(2)_L\) and \(SU(2)_R\) is maximal when the bare mass parameter \(M_L\) and \(M_R\) are of the same order. When \(M_L > M_R\) the \(SU(2)_R\) component of the DM gets enhanced depending on their relative mass separation. Similarly, for the other mass hierarchy, \(M_R > M_L\), the \(SU(2)_L\) part of the DM gets increased. This phenomenon is exactly depicted in left panel of Fig. 4 for \(y_{_R}=0.001\). When DM becomes more \(SU(2)_R\) like (\(M_L > M_R\)) relic density gets enhanced due to suppressed interaction of DM with mediator fields in LRSM. Whereas for the reverse case (\(M_R > M_L\)) when DM becomes more \(SU(2)_L\) like, the interaction between DM and the mediators get enhanced resulting in less density as it is seen from the left panel of Fig. 4 (blue points). If we increase the couplings \(y_{_R}\) and \(y_{_L}\) to 0.01, the mass splitting between dark sector particles increase which leads to a comparably smaller co-annihilation contribution. As a result, relic density of DM increases which is shown in the right panel of Fig. 4. Due to co-annihilation suppression for \(y_{_R}=0.01\), the correct relic density can be achieved throughout the DM mass region for the case \(M_R > M_L\) while for the other hierarchy it only satisfies the near resonance region. There are few dips in the relic density plots which are essentially due to resonances corresponding to the gauge boson (Z), SM like Higgs (h), and the additional light scalars (\(H_L, ~A_L,~H_L^\pm ,~H_L^{\pm \pm }\) and \(H_R^{\pm \pm }\)) available in LRSM for BP1.
4.3 Direct search constraint
Non-observation of DM signal at direct search experiments like XENON-1T [21], PANDAX 4T [22] has set a stringent constraint on DM-nucleon scattering cross-section for WIMP like DM. Here we will apply those constraints on our model parameters space which satisfy the observed relic density constraint.
Relic density satisfied points are shown in spin-independent (SI) direct search cross-section against DM mass for \(y_{_R}=0.001\) (red points) and \(y_{_R}=0.01\) (blue points). The direct search bounds from PANDAX-4T (black dotted line) and XENON-1T (purple dotted line) are shown in the same plane for comparison purposes. The bottom shaded orange region corresponds to the neutrino floor
In Fig. 5 we show SI DM-nucleon cross-section for the model as a function of DM mass for the relic satisfied parameters space. The red points correspond to \(y_{_R}=0.001\) while the blue points are for \(y_{_R}=0.01\). The latest exclusion limits on DM-nucleon scattering cross-section against DM mass from PANDAX-4T [22] and XENON 1T [21] are shown in the same plane by black dashed line and purple dashed line respectively. It is worth mentioning here that the parameter space below the dashed line (PANDAX-4T and XENON 1T) can be allowed from the corresponding direct search experiments. We note here that more number of data points lie below the direct search exclusion limit from recent PANDAX-4T with the increase of \(y_R\) from 0.001 (red points) to 0.01 (blue points). With the increase of \(y_R\), DM becoming more \(SU(2)_R\) dominated resulting in a smaller DD cross-section. The orange shaded region in Fig. 5 corresponds to the neutrino floor due to neutrino-nucleon coherent elastic scattering. In the neutrino floor region, the direct search DM signal is not distinguishable from the neutrino background.
The SI DM-nucleon scattering cross-section in the mixed scenario takes place dominantly via t-channel scalar-mediated diagrams through the Yukawa interactions with the bi-doublets. So the DM-nucleon scattering cross-section directly depends on the Yukawa coupling strength \(Y_1\) and \(Y_2\) which are considered equal here. Therefore the large values of \(Y_1\) are strongly constrained from the recent PANDAX 4T data except the scalars resonance regions as shown in Fig. 6.
4.4 Indirect search constraint
Parameter space satisfying relic density and direct search constraint is shown in the plane of indirect search cross-section as a function of \(m_\mathrm{DM}\) for DM annihilating to WW (left) and DM annihilating to \(\overline{b} b\) (right) final states. The indirect search cross-section is compared with the latest exclusion bound of the corresponding channel from Fermi-LAT and MAGIC [23, 24] shown as shaded regions
DM can also be probed at various indirect search experiments via the production of SM particles either through DM annihilation or via decay in the local Universe. Neutral stable particles like photons, neutrinos which are produced via DM annihilation or decay, can reach indirect search detectors without getting affected much by intermediate regions between the source and the detector. These photons and neutrinos are ideal messengers of DM indirect detection. Due to the WIMP nature of the DM (\(m_\mathrm{DM} \sim \mathcal {O}(\mathrm{GeV-TeV})\)), the photons emitted during DM annihilations or decay lie in the gamma-ray regime, which can be probed at ground-based telescopes of MAGIC (Major Atmospheric Gamma-ray Imaging Cherenkov) [24] and the space-based telescopes of Fermi-LAT (Fermi Large Area Telescope) [23]. It is important to note here that DM cannot interact directly with photons. But the gamma rays can be produced via DM annihilation into different SM charged final states like \(\mu ^+~\mu ^-,~\tau ^+~\tau ^-,~b~\overline{b}\) and \(W^+~W^+\) which finally decay into photons. No signal for DM in indirect search experiments like Fermi-LAT and MAGIC put a strong constraint on the annihilation cross-section of DM into \(\mu ^+~\mu ^-,~\tau ^+~\tau ^-,~b~\overline{b}\) and \(W^+~W^+\). The most stringent constraint comes from the annihilation channel, DM DM \(\rightarrow W^+~W^-\) for \(m_\mathrm{DM} > M_{W^\pm }\) and DM DM \(\rightarrow b~ \overline{b}\) as compared to other two channels, \(\mu ^+~\mu ^-,~\tau ^+~\tau ^-\). In our analysis, we compare the indirect search cross-section for \(W^+W^-\) and \(b\overline{b}\) final state with the corresponding indirect search bounds arising from the Fermi-LAT and MAGIC observations. In Fig. 7, we show both relic density and direct search constraint(PANDAX 4T) satisfied points in \(m_\mathrm{DM}-\langle \sigma v \rangle \) for annihilation of DM to WW (left panel) and to \(b\overline{b}\) (right panel) final states. We find that most of the parameter space shown in blue points for \(y_{_R}=0.001\) and red points for \(y_{_R}=0.01\) are consistent with indirect search constraints except the light scalar resonance region of DM mass around \(\sim \frac{M_{h}}{2}\) and \(~\sim \frac{m_{\Delta _L}}{2}\) with large \(Y_1\).
Relic density, direct and indirect search constraint allowed parameter space is summarized in the \(m_{DM}\) versus \(\Delta M=M_1^\pm -m_{DM}\) plane for \(y_R\) \(=0.001\) (red points) and \(=0.01\) (blue points). The grey shaded region is excluded by LEP (\(M_1^\pm < 102.7\)). The black dotted horizontal line corresponding to \(\Delta M= M_W\) which divides the parameter space into two regions: \(\Delta M > M_W\) (light purple) and \(\Delta M < M_W\) (light green)
Finally, we put together all the constraints coming from relic density, direct and indirect searches and show the allowed region of parameter space in the plane of \(m_\mathrm{DM}-\Delta M (=M_1^\pm - m_\mathrm{DM})\) of Fig. 8. The red and blue points correspond to the Yukawa couplings \(y_{_R}=0.001\) and 0.01 respectively. One should note here that the large \(\Delta M=M_1^\pm -m_{DM}\) is only available near the Higgs resonance: \(m_\mathrm{DM} \sim M_h/2\) and the light scalar resonances: \(\sim m_{\Delta _L}/2\). Apart from resonances the correct relic density only relies on the co-annihilation resulting in the small mass splitting as is shown in the figure. Again the large mass splitting is only available for the large Yukawa coupling \(y_{_R}=0.01\) which is absent for \(y_{_R}=0.001\). This is because the DM, \(\chi _1\) becomes more \(SU(2)_R\) dominated and the interactions between DM and left like fields in LRSM are suppressed with the increase of \(y_{_R}\). The grey shaded region in the bottom left corner of Fig. 8 which corresponds to \(M_1^\pm > 102.7\) GeV is excluded by the LEP data [49]. We separate the parameter space in two regions along the \(\Delta M\) direction with \(\Delta M= M_W\) (black dashed line). The light purple region with \(\Delta M > M_W\), the light charged dark fermion, \(\chi _{_1}^\pm \) (of mass \(M_1^\pm \)) can decay to DM, \(\chi _{_1}\) via on shell W. Whereas the region with \(\Delta M < M_W\) is shown by light green shaded region, the light charged dark fermion, \(\chi _{_1}^\pm \) can decay to DM (\(\chi _{_1}\)) via off-shell W. Depending on the on-shell or off-shell decay of the charged dark fermion to DM, the collider phenomenology will be different which we will discuss in the next section. So far throughout our analysis, we have only considered fixed particle spectrum in LRSM as mentioned in BP1. Now the obvious question arises, what will be the DM parameter space if one considers different particle spectrums in LRSM? The answer is that the DM phenomenology is almost the same except for the second resonance region which depends on the spectrum of the light scalars available in LRSM for a given benchmark point. That’s why we do not repeat the DM analysis for different benchmark points in the LRSM sector. However for the collider analysis where we focus on the doubly charged scalar, we shall choose a different set of BP in the LRSM sector which we discuss in the next section.
5 Collider signatures of \(H^{\pm \pm }\) in presence of dark fermion doublets
The LRSM gives us some unique collider signatures in the form of new gauge bosons, a right-handed charged current interaction, heavy Majorana neutrino production, lepton number violations, etc. Thus each of them can be a test of the model. In addition to the above, the presence of doubly charged scalars in the theory which when produced give a smoking gun signal in terms of resonances in the same sign dilepton final state. In fact, this signal is one of the well studied cases at LHC [56,57,58] which leads to very strong bounds on the mass of the doubly charged scalar. This signal is however shared with other models which also predict doubly charged scalars, for example the Higgs Triplet model which leads to Type-II seesaw for neutrino masses. A significant part of the parameter space for sub-TeV doubly charged scalar is ruled out, when it decays dominantly in the leptonic mode. In LRSM, we have two copies of the doubly charged Higgs where one predominantly couples to the Z while the other couples to the \(Z_R\). This in turn affects the production rates for the two incarnates at LHC. However, in the process, both could have a significantly off-shell Z or \(Z_R\) and conspire to give a cross section of nearly similar strengths for a given mass. The case where the Yukawa couplings that dictate the branching ratios in the leptonic mode being very small for the \(H_L^{\pm \pm }\) and \(H_R^{\pm \pm }\) makes the diboson mode (WW) as the other possibility. Since the \(W_R\) is relatively heavy, the \(H_R^{++}\) decays mostly via the Yukawa coupling to charged leptons. For the \(H_L^{++}\) the decay is to on-shell W boson. Thus, we get the possibility of 4W or  signal from the doubly charged scalar pair production at LHC. It is noteworthy that this decay mode also relaxes the bound on the doubly charged scalars significantly [56, 58]. In this work, we point out an additional channel that may open up for the \(H^{\pm \pm }\) signal giving us hints of the dark sector. As the Yukawa coupling of the Higgs triplets to the new VL doublets are constrained only through the allowed mass spectrum for the DM and its annihilation rates (as discussed in the previous sections), the doubly charged scalar can have its most dominant decay to the VL fermions. We focus on this signal by choosing a few representative points in the model parameter space which are consistent with DM observations and neutrino mass. Our choice of benchmark points shown in Table 5 for the collider study, are allowed from DM relic, direct search, indirect search and others constraints as discussed earlier.
signal from the doubly charged scalar pair production at LHC. It is noteworthy that this decay mode also relaxes the bound on the doubly charged scalars significantly [56, 58]. In this work, we point out an additional channel that may open up for the \(H^{\pm \pm }\) signal giving us hints of the dark sector. As the Yukawa coupling of the Higgs triplets to the new VL doublets are constrained only through the allowed mass spectrum for the DM and its annihilation rates (as discussed in the previous sections), the doubly charged scalar can have its most dominant decay to the VL fermions. We focus on this signal by choosing a few representative points in the model parameter space which are consistent with DM observations and neutrino mass. Our choice of benchmark points shown in Table 5 for the collider study, are allowed from DM relic, direct search, indirect search and others constraints as discussed earlier.
The production of doubly charged scalar at LHC yields the attractive collider signature in presence of DM in our model. The doubly charged scalar decays promptly to a pair of charged component of the dark doublets (\(\chi _{_i}^\pm \)) which then further decay to DM (\(\chi _{_1}\)) and \(W^\pm \). This yields a \(W^+ W^+ W^- W^-\) plus DM final state from a pair produced doubly charged scalar. The very weakly interacting DM particles escape the detector leaving their imprint in the form of missing energy. We look at the following signal subprocesses:
The \(W^\pm \) decays to leptons and/or jets giving rise to the following different final states:
We note that the most promising signal would involve the larger multiplicity of charged leptons in the final state which will also be suggestive of the doubly charged scalar as the parent particle. The final states with increasing jet multiplicities would provide complementary signals, hitherto with reduced sensitivity as the SM background would be large compared to an all lepton final state. We therefore restrict ourselves to the first two channels involving \(n \ge 3\) charged leptons in the final state for our analysis. We also note that this signal overlaps with the 4W final state coming from pair produced doubly charged Higgs when the \(H^{\pm \pm } \rightarrow W^\pm W^\pm \) is the dominant decay channel, which could give us an idea on the improvement of the signal over that of the traditional 4W signal.
We use the publicly available package SARAH [59] to write the model files and create the Universal Feynman Object (UFO) [60] files. The mass spectrum and mixings are generated using SPheno [61, 62]. We have used the package MadGraph5@aMCNLO (v2.6.7) [63, 64] to calculate the scattering process and generate parton-level events at LHC with \(\sqrt{s}=14\) TeV which were then showered with the help of Pythia 8 [65]. We simulate detector effects using the fast detector simulation in Delphes-3 [66] and have used the default ATLAS card. The reconstructed events were finally analyzed using the analysis package MadAnalysis5 [67].
5.1
 signal
signal
The  is one of the cleanest signal because of the low SM background. In our study this signal will appear when all four W bosons produced in the cascade decay of the pair of double charged Higgs, decays leptonically as shown in Fig. 9. The dominant background for the above final state would come from the SM subprocesses producing \(t\overline{t}Z\), ZZ and VVV [68]. Additional sources of background events could also emerge from \(t\overline{t}\) and WZ production, where additional charged leptons can come from misidentification of jets. Although such events would be small, the sheer size of the cross section of the aforementioned processes could lead to significant events mimicking the signal. However, these backgrounds can be eliminated by choosing specific selection cuts. The signal and the background process are generated using the same Monte Carlo event generator and then the cross section of the backgrounds are scaled with their respective k-factors. The k-factor for ZZ , \(t\bar{t}Z\), VVV and WZ considered here are \(\simeq \) 1.72, 1.38, 2.27 and 2.01 respectively [69,70,71,72]. Here the k-factor for ZZ scales it to next-to-next-to-leading order (NNLO), while the rest of the backgrounds are at next-to-leading order (NLO) cross section.
is one of the cleanest signal because of the low SM background. In our study this signal will appear when all four W bosons produced in the cascade decay of the pair of double charged Higgs, decays leptonically as shown in Fig. 9. The dominant background for the above final state would come from the SM subprocesses producing \(t\overline{t}Z\), ZZ and VVV [68]. Additional sources of background events could also emerge from \(t\overline{t}\) and WZ production, where additional charged leptons can come from misidentification of jets. Although such events would be small, the sheer size of the cross section of the aforementioned processes could lead to significant events mimicking the signal. However, these backgrounds can be eliminated by choosing specific selection cuts. The signal and the background process are generated using the same Monte Carlo event generator and then the cross section of the backgrounds are scaled with their respective k-factors. The k-factor for ZZ , \(t\bar{t}Z\), VVV and WZ considered here are \(\simeq \) 1.72, 1.38, 2.27 and 2.01 respectively [69,70,71,72]. Here the k-factor for ZZ scales it to next-to-next-to-leading order (NNLO), while the rest of the backgrounds are at next-to-leading order (NLO) cross section.
To consider the four charged lepton final state coming from the 4W we choose events which have exactly \(N_l = 4\) isolated charged leptons (\(l = e, \mu \)) in the final state. As the final state will still be littered with jets coming from initial state radiations, we therefore choose a more inclusive final state where all jets are vetoed with a relatively large transverse momenta of 40 GeV. As basic acceptance cuts, we therefore demand that all reconstructed objects are isolated (\(\Delta R_{ab} > 0.4\)). In addition,
-
All charged leptons must have \(p_{T_l} > 10\) GeV and lie within the rapidity gap satisfying \(|\eta _l| < 2.5\).
-
We impose additional conditions to demand a hadronically quite environment by putting veto on events with light jets and b jets with \(p_{T_{b/j}} > 40\) GeV and \(|\eta _{b/j}| < 2.5\). This helps in suppressing a significant part of the background coming from \(t \, \bar{t} (Z)\) production.
The kinematic distribution of signal and background events after the basic acceptance cuts to help us define our selection cuts for further analysis. We show the missing transverse energy ( ) distribution in Fig. 10, invariant mass distribution of opposite-sign charged leptons (\(M_{e^+e^-},M_{\mu ^+\mu ^-}\)) in Fig. 13, transverse momentum (\(p_T\)) distributions of leading and sub-leading charged leptons in Fig. 11 and the invariant mass distribution of same-sign charged leptons (\(M_{l^\pm \, l^\pm }\)) in Fig. 12 for the benchmark points BPC1 and BPC2 (tabulated in Table 5) along with the total SM background as discussed before. Following the distinctive features of the signal distributions we use the following set of cuts as discussed below:
) distribution in Fig. 10, invariant mass distribution of opposite-sign charged leptons (\(M_{e^+e^-},M_{\mu ^+\mu ^-}\)) in Fig. 13, transverse momentum (\(p_T\)) distributions of leading and sub-leading charged leptons in Fig. 11 and the invariant mass distribution of same-sign charged leptons (\(M_{l^\pm \, l^\pm }\)) in Fig. 12 for the benchmark points BPC1 and BPC2 (tabulated in Table 5) along with the total SM background as discussed before. Following the distinctive features of the signal distributions we use the following set of cuts as discussed below:
-
The largest contribution to the SM background comes from ZZ. To suppress it and bring it down, we choose a missing
 GeV selection cut. Since the ZZ decaying to give four leptons will have very little missing energy in the final state the cut will throw away a significant part of the background events. This cut does not affects our signal much since it has decay products consisting of dark matter and neutrinos leading to a larger
GeV selection cut. Since the ZZ decaying to give four leptons will have very little missing energy in the final state the cut will throw away a significant part of the background events. This cut does not affects our signal much since it has decay products consisting of dark matter and neutrinos leading to a larger 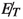 in the signal events. Hence this cut becomes very efficient in improving the signal sensitivity.
in the signal events. Hence this cut becomes very efficient in improving the signal sensitivity. -
To reduce the background further, which may produce final state charged leptons (i.e WZ, VVV and ZZ) from Z decay but have some missing transverse energy which lets them escape the
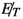 cut, we put a cut on the invariant mass of same flavor opposite charge leptons around the Z mass pole (\(82 {~\mathrm GeV}< M_{\ell ^+\ell ^-} < 100~ \mathrm{GeV} \)). In our signal the leptons come from the \(W^\pm \) decay and no resonant feature can be attributed in the decay as the charged leptons come from different parent particles. So the signal is not affected by a cut used to remove the resonant Z peak in the background.
cut, we put a cut on the invariant mass of same flavor opposite charge leptons around the Z mass pole (\(82 {~\mathrm GeV}< M_{\ell ^+\ell ^-} < 100~ \mathrm{GeV} \)). In our signal the leptons come from the \(W^\pm \) decay and no resonant feature can be attributed in the decay as the charged leptons come from different parent particles. So the signal is not affected by a cut used to remove the resonant Z peak in the background. -
At this point the background is almost at a comparable level with the signal and most of the remaining SM background contribution is from the WZ channel where additional jets/photons can be misidentified as an additional charged lepton. But the events from WZ will give softer decay products and we find the use a strong \(p_T\) cut helpful in suppressing them significantly. In our case the sub-leading lepton with \(p_T[l_2]\) separates the signal from background when compared to the same observable for other charged leptons. Thus we choose a \(p_T[l_2]>30\) GeV selection cut to help reduce the WZ background.
 signal analysis for BPC1 & BPC2 benchmark points at 3000 fb\(^{-1}\) integrated luminosity
signal analysis for BPC1 & BPC2 benchmark points at 3000 fb\(^{-1}\) integrated luminosity-
There is one more kinematic variable of interest which can be used to distinguish the signal from the background. It is the invariant mass of same-sign (SS) charged lepton pairs which can be used to reduce the background even further. Even though the doubly charged scalar does not decay directly to SS leptons, we expect that in the all lepton channel the SS leptons would come from the same primary scalar. As the SS leptons in our signal come from the decay of same parent particle (\(H_L^{\pm \pm }\)), we expect a maximum invariant mass for such lepton pair dictated by the difference in mass of \(H_L^{\pm \pm }\) and the DM pair. But in the background there is no clear possibility of a kinematic edge and therefore the tail of this observable (\(M_{l_i^\pm l_j^\pm }\)) for the background will be much broader compared to the signal. We can remove this tail in the observable for the SM background without rejecting any significant signal events.
All the cuts used above have been shown through a cut-flow chart in Table 6. The final surviving events (after the selection cuts) are shown in Table 7 for an integrated luminosity of 3000 fb\(^{-1}\) and the signal significance is estimated using
where \(\mathcal {B}\) stands for the SM background and \(\mathcal {S}\) represents the new physics signal events respectively.
5.2
 signal
signal
The  is the next cleanest signal for our model after
is the next cleanest signal for our model after  but its features can be studied with lower integrated luminosity compared to the
but its features can be studied with lower integrated luminosity compared to the  case. This is because we allow any one of the W boson to decay hadronically (which has a larger branching ratio over the leptonic channel). Hence the effective cross-section of this signal is much larger than the
case. This is because we allow any one of the W boson to decay hadronically (which has a larger branching ratio over the leptonic channel). Hence the effective cross-section of this signal is much larger than the  case. The prominent SM subprocesses contributing as background to our signal are \(t\bar{t}\), WZ, VVV, \(t \bar{t}Z\) and ZZ. For our analysis of the final state we choose only those events as signals which have exactly three charged leptons (\(e^\pm \) and \(\mu ^\pm \)) and exactly two jets. Similar to the
case. The prominent SM subprocesses contributing as background to our signal are \(t\bar{t}\), WZ, VVV, \(t \bar{t}Z\) and ZZ. For our analysis of the final state we choose only those events as signals which have exactly three charged leptons (\(e^\pm \) and \(\mu ^\pm \)) and exactly two jets. Similar to the  case we consider the basic acceptance cuts for all isolated objects (i.e., \(\Delta R_{ab} >0.4\)) as given below:
case we consider the basic acceptance cuts for all isolated objects (i.e., \(\Delta R_{ab} >0.4\)) as given below:
-
all charged leptons must have \(p_{T_\ell } > 5\) GeV and lie within the rapidity gap satisfying \(|\eta _\ell | < 2.5\).
-
We impose additional conditions and demand no b-tagged jets by putting veto on events with b jets with \(p_{T_{b}} > 40\) GeV and \(|\eta _{b}| < 2.5\). This helps in suppressing a significant part of the background coming from \(t \bar{t}\) and \(t \, \bar{t} (Z)\) production.
At this stage the background coming from WZ and \(t\bar{t}\) is massive compared to other background sources and signal. Hence to suppress these two, we divide our event data set for both signal and background in two mutually exclusive sets.
SetA: This corresponds to events which have two positively charged leptons and one negatively charged lepton. SetB: This set consists of events with one positively charged lepton and two negatively charged leptons.
The distribution of signal events (BPC1 and BPC2) along with dominant SM background with respect to the  , invariant mass of \(e^+e^-\) pair (\(M_{e^+e^-}\)), invariant mass of \(\mu ^-\mu ^+\) pairs \((M_{\mu ^+\mu ^-})\), invariant mass of lepton-jet configuration and invariant mass of same-sign leptons are shown in Figs. 14, 15, 16, 17, 18 and 19 respectively. Two mutually exclusive sets (SetA and SetB) are shown in each case. In order to supress the SM background, we choose a set of cuts on distribution observables as given below:
, invariant mass of \(e^+e^-\) pair (\(M_{e^+e^-}\)), invariant mass of \(\mu ^-\mu ^+\) pairs \((M_{\mu ^+\mu ^-})\), invariant mass of lepton-jet configuration and invariant mass of same-sign leptons are shown in Figs. 14, 15, 16, 17, 18 and 19 respectively. Two mutually exclusive sets (SetA and SetB) are shown in each case. In order to supress the SM background, we choose a set of cuts on distribution observables as given below:
-
To reduce background sources which do (may) not have any
 , such as ZZ and VVV in contrast to our signal which has both neutrinos and dark matter as source for missing transverse energy, we use a selection cut of
, such as ZZ and VVV in contrast to our signal which has both neutrinos and dark matter as source for missing transverse energy, we use a selection cut of  GeV. We also use as before, a rejection cut on the invariant mass of opposite sign same flavor lepton pairs near the Z mass pole to further suppress the background events.
GeV. We also use as before, a rejection cut on the invariant mass of opposite sign same flavor lepton pairs near the Z mass pole to further suppress the background events. -
In our signal two same sign leptons come from same parent doubly charged Higgs via the W bosons while the other doubly charged Higgs gives the opposite sign lepton and two jets in its decay chain. Hence a strong correlation in invariant mass shows up for decay products of these two doubly charged Higgs. So we can put a rejection cut on SetA, with \(M(l^+ l^+)\) , \(M(l^- j_1 j_2)\) \( > rsim (m_{H^{\pm \pm }} - 2 m_{DM})\) and similarly cuts with leptons of opposite polarity on SetB. This cut is very effective in reducing the background coming from \(t\bar{t}\) and WZ.
-
At this stage we still have significant amount of background events left, mostly from the WZ+jets subprocess, because of it’s huge cross-section compared to the signal and other background subprocesses. Since our signal gets two primary jets from the decay of an onshell W while the jets coming in WZ are most likely radiative jets as W and Z both decay to leptons, we use a selection cut on the dijet invariant mass around the W mass pole which helps reduce the WZ background.
With the above choice of cuts the events are tabulated in Table 8 and using Eq. 25 for the signal significance we show our results for the two benchmark points in Table 9.
 signal analysis for BPC1 and BPC2 benchmark points at 1000 fb\(^{-1}\) luminosity
signal analysis for BPC1 and BPC2 benchmark points at 1000 fb\(^{-1}\) luminosityWe therefore conclude that with high enough integrated luminosity we can discover a doubly charged Higgs of mass around 300 GeV in the multi-lepton final state with at least \(N_l=3\) leptons. As the lepton multiplicity decreases we find that the large SM background is more difficult to suppress and give enough sensitivity to observe a doubly charged Higgs decaying to the dark fermions. In addition, a similar analysis of 4l and 3l final states for the third benchmark point (BPC3) shown in Table 5, which represents a compressed mass spectrum for the lighter states in the dark fermion sector, yields a very low (\(< 1\sigma \)) signal significance for a 300 GeV doubly charged scalar. The 3-body decay of the \(\psi ^\pm \) leads to softer final states which make it more difficult to distinguish from the SM background leading to lower signal sensitivity.
6 Signal comparison at ILC
It is quite clear from the analysis shown in the previous section that signals for a doubly charged Higgs become difficult to observe at LHC if they do not decay directly to charged leptons. As is the case for the \(H^{\pm \pm }\) of Type-II seesaw model where the doubly charged scalar has very limited sensitivity if it decays dominantly to a pair of W bosons and where the current limits from LHC give a mass bound as low as between 230–350 GeV [58], the modified decay modes in our model lead to a much weaker sensitivity at current integrated luminosities. Even with the full high luminosity LHC (HL-LHC), we find that a discovery of such a doubly charged scalar would still be limited to sub-400 GeV masses. It would therefore seem that while the LHC energies would probe a much higher energy scale of models such as LRSM and restrict very heavy \(W_R\) and \(Z_R\), it would lack in efficiency for these doubly charged exotics. It would be interesting to find out the sensitivity for such particles at the proposed ILC which may be restricted by its energy reach but would prove beneficial for such particles in general which become more elusive at LHC as they develop newer decay channels in their fold. We choose to highlight just a simple comparison with one of the signals studied at the LHC here and leave a more dedicated ILC study for later work. We however present a slight variation in the spectrum to include a compressed scenario, which has very clear challenges in LHC searches.
 signal at integrated luminosity of 1000 fb\(^{-1}\)
signal at integrated luminosity of 1000 fb\(^{-1}\)6.1
 signal analysis for BPC3 at ILC
signal analysis for BPC3 at ILC
The benchmark point BPC3 is chosen as it represent a scenario where the mass gap between \(\chi ^{\pm }_{1}\) and dark matter (\(\chi _{_1}\)) is less than the mass of W such that the decay \(\chi ^{\pm }_{1} \rightarrow W^\pm \, \chi _{_1}\) is energetically forbidden. Here \(\chi ^{+}_1\) has a three-body decay to \(l_i^{+} \, \nu _j \, \chi _{_1}\) or \( 2j \, \chi _{_1}\). In this case the leptons and jets will be soft and one can no longer put a strong requirement on the \(p_T\) of jets as required to avoid large hadronic debris that can affect any analysis at LHC. This makes an analysis for such a compressed spectrum leading to soft final states at LHC very challenging. Since ILC has a much cleaner environment the jets can be triggered upon with much lower energies and we can put weaker jet tagging conditions (\(P_T(j)>10\) GeV), better suited for benchmarks such as BPC3.
For analyzing this signal at ILC we consider the dominant background coming from WWZ which gives us  final state where one W decays hadronically while the other W and Z decay leptonically producing three leptons and missing energy. As before, our signal comes from \(H^{++}_L H^{--}_L\) pair production via photon or Z mediator (the heavy \(Z_R\) contribution is negligible). Each \(H^{\pm \pm }_L\) then decays to two \(\chi ^{\pm }_{1}\) followed by one \(\chi ^{\pm }_{1}\) decaying to \(\chi _{_1}\) and 2 j and rest of the dark charged fermion decaying leptonically via the W boson. For the analysis we choose only those events as signals which have exactly three charged leptons (i.e., e and \(\mu \)) and exactly two jets. The basic acceptance cuts for all isolated objects (i.e., \(\Delta R_{ab} >0.2\)) are chosen similar to that for LHC.
final state where one W decays hadronically while the other W and Z decay leptonically producing three leptons and missing energy. As before, our signal comes from \(H^{++}_L H^{--}_L\) pair production via photon or Z mediator (the heavy \(Z_R\) contribution is negligible). Each \(H^{\pm \pm }_L\) then decays to two \(\chi ^{\pm }_{1}\) followed by one \(\chi ^{\pm }_{1}\) decaying to \(\chi _{_1}\) and 2 j and rest of the dark charged fermion decaying leptonically via the W boson. For the analysis we choose only those events as signals which have exactly three charged leptons (i.e., e and \(\mu \)) and exactly two jets. The basic acceptance cuts for all isolated objects (i.e., \(\Delta R_{ab} >0.2\)) are chosen similar to that for LHC.
 signal analysis for BPC3 benchmark points at ILC with \(\sqrt{s}=1\) TeV with 1000 \(fb^{-1}\) integrated luminosity
signal analysis for BPC3 benchmark points at ILC with \(\sqrt{s}=1\) TeV with 1000 \(fb^{-1}\) integrated luminosityWe list the selection cuts for the signal and background events in Table 10 along with the events surviving each cut. Here the first cut is on invariant mass of opposite sign same flavor lepton at Z mass pole which suppresses the background significantly because WWZ has one Z always decaying leptonically. The next cut is on the invariant mass of SS leptons which is a prominent characteristic of the signal (as discussed earlier) since these lepton pairs come from the decay chain of the same doubly charged Higgs. The final cut is on the invariant mass of visible decay product of one doubly charged Higgs where one \(\chi ^{\pm }_{1}\) decays hadronically while the other decays to give a charged lepton.
We find that for a mass of \(H^{++}\) similar to BPC1 and a compressed spectrum in the dark sector which gives a 3-body decay for the charged dark fermion, HL-LHC gives a signal sensitivity of less than \(1\sigma \) for BPC3 while the same final state is able to achieve a much higher sensitivity at ILC with \(\sqrt{s}=1\) TeV for a much smaller luminosity, and gives a \( > rsim 4.5\sigma \) signal with an integrated luminosity of 1000 fb\(^{-1}\).Note that unpolarized incoming beams were used for this study. One can use polarized electron-positron beams at ILC which would help in supressing the SM background further compared with the signal leading to similar significances acheived with lower integrated luminosity. In fact, the cleaner environment at ILC would open up the same benchmark for a hadronic rich final state with much larger effective cross section. As a multi-particle final state with hadrons improves the size of signal events and one can effectively control the background easily since all processes will be through electroweak interactions, ILC will give a much higher significance in the final states with smaller lepton multiplicity. The same-sign lepton pairs however provide a symbolism of the produced doubly charged scalar and therefore to establish its presence, the channel with  would be a more appropriate channel for the study at ILC.
would be a more appropriate channel for the study at ILC.
7 Conclusions
In this work we have used the well motivated left–right symmetry model and invoke a dark matter candidate in the model by including a pair of vector-like lepton doublets which preserve the left–right symmetry but are odd under a discrete \(\mathcal {Z}_2\) symmetry. This extended model therefore has its own dark sector which speaks with the SM matter fields via gauge and Yukawa interactions. The dark fermions of the model are neutral and some also carry electric charge, where the lightest neutral state which is an admixture of the neutral components of the two VL doublets after symmetry breaking, acts as the DM candidate. The model gives the DM several characteristics to choose from depending upon its composition and the type of gauge interactions it prefers. This opens up an interesting DM phenomenology where the different composition of the DM will lead to different regions of parameter space that satisfy the observed DM experimental data in the form of relic density, direct-detection experiments and indirect detection experiments. We explore the available parameter space of the model in all different scenarios where the DM is dominantly \(SU(2)_L\) like, \(SU(2)_R\) like or an admixture of all chiralities of the VL doublet pair in the LRSM model. We show the region of parameter space of the mixed DM scenario which is consistent with relic density observations and also satisfy direct detection constraints as well as indirect detection constraints.
The dark sector also contains charged states which on one hand can play a major role in DM phenomenology by contributing to the number density through co-annihilations with the DM when the mass splitting is very low between them, while they could be directly produced at experiments through gauge interactions. Their phenomenology would be very similar to a pair produced VLL that decays to a W boson and a DM. We are however more interested in the signal for the more unique doubly charged Higgs present in the model in the presence of a dark fermion sector which couples to it directly. As in the case of the lepton doublets having a Majorana interaction with the triplet scalars of the model leading to a seesaw mechanism for neutrinos, the dark fermion sector would also have a similar seesaw mechanism. Thus in a significant region of parameter space consistent with DM observations, the doubly charged scalar can decay to the pair of charged dark fermions. We consider this interesting possibility in our work and perform a detailed collider analysis of its signal at the LHC in multi-lepton final state. We find that the bounds on the doubly charged scalar become weaker compared to the more standard leptonic and bosonic decay modes and LHC sensitivity for a doubly charged Higgs in such case would be sub-400 GeV even with an integrated luminosity of 3000 fb\(^{-1}\). We then show how this reach can be improved at the proposed ILC with a center of mass energy of 1 TeV by comparing a similar final state which gives less than \(1\sigma \) sensitivity at LHC but an improved \(\simeq 4.8 \sigma \) sensitivity at ILC.
DataAvailability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The experimental data we used in our manuscript to compare with our estimations are already public from the experiments like: WMAP, PLANCK, XENON-1T, PANDA X, MAGIC and FERMI-LAT data for DM constraints and ATLAS, CMS and LEP data for the collider constraints.]
References
CMS Collaboration, S. Chatrchyan et al., Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). https://doi.org/10.1016/j.physletb.2012.08.021. arXiv:1207.7235
ATLAS Collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). https://doi.org/10.1016/j.physletb.2012.08.020. arXiv:1207.7214
R.N. Mohapatra, J.C. Pati, “Natural’’ left–right symmetry. Phys. Rev. D 11, 2558–2561 (1975). https://doi.org/10.1103/PhysRevD.11.2558
G. Senjanovic, R.N. Mohapatra, Exact left–right symmetry and spontaneous violation of parity. Phys. Rev. D 12, 1502–1505 (1975). https://doi.org/10.1103/PhysRevD.12.1502
R.N. Mohapatra, G. Senjanović, Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys. Rev. D 23, 165–180 (1981). https://doi.org/10.1103/PhysRevD.23.165
N.G. Deshpande, J.F. Gunion, B. Kayser, F. Olness, Left–right-symmetric electroweak models with triplet Higgs field. Phys. Rev. D 44, 837–858 (1991). https://doi.org/10.1103/PhysRevD.44.837
C.S. Aulakh, A. Melfo, G. Senjanović, Minimal supersymmetric left–right model. Phys. Rev. D 57, 4174–4178 (1998). https://doi.org/10.1103/physrevd.57.4174
Y. Zhang, H. An, X. Ji, R.N. Mohapatra, General CP violation in minimal left–right symmetric model and constraints on the right-handed scale. Nucl. Phys. B 802, 247–279 (2008). https://doi.org/10.1016/j.nuclphysb.2008.05.019. arXiv:0712.4218
WMAP Collaboration, D.N. Spergel et al., Wilkinson Microwave Anisotropy Probe (WMAP) three year results: implications for cosmology. Astrophys. J. Suppl. 170, 377 (2007). https://doi.org/10.1086/513700. arXiv:astro-ph/0603449
L. Roszkowski, E.M. Sessolo, S. Trojanowski, WIMP dark matter candidates and searches-current status and future prospects. Rep. Prog. Phys. 81, 066201 (2018). https://doi.org/10.1088/1361-6633/aab913. arXiv:1707.06277
V.C. Rubin, W.K. Ford Jr., Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 159, 379–403 (1970). https://doi.org/10.1086/150317
W. Hu, S. Dodelson, Cosmic microwave background anisotropies. Ann. Rev. Astron. Astrophys. 40, 171–216 (2002). https://doi.org/10.1146/annurev.astro.40.060401.093926. arXiv:astro-ph/0110414
G. Bertone, D. Hooper, J. Silk, Particle dark matter: evidence, candidates and constraints. Phys. Rep. 405, 279–390 (2005). https://doi.org/10.1016/j.physrep.2004.08.031. arXiv:hep-ph/0404175
WMAP Collaboration, G. Hinshaw et al., Nine-year Wilkinson microwave anisotropy probe (WMAP) observations: cosmological parameter results. Astrophys. J. Suppl. 208, 19 (2013). https://doi.org/10.1088/0067-0049/208/2/19. arXiv:1212.5226
Planck Collaboration, N. Aghanim et al., Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020). https://doi.org/10.1051/0004-6361/201833910. arXiv:1807.06209
E.W. Kolb, M.S. Turner, The early universe. Front. Phys. 69, 1–547 (1990)
G. Jungman, M. Kamionkowski, K. Griest, Supersymmetric dark matter. Phys. Rep. 267, 195–373 (1996). https://doi.org/10.1016/0370-1573(95)00058-5
G. Bertone, D. Hooper, J. Silk, Particle dark matter: evidence, candidates and constraints. Phys. Rep. 405, 279–390 (2005). https://doi.org/10.1016/j.physrep.2004.08.031
Y. Hochberg, E. Kuflik, T. Volansky, J.G. Wacker, Mechanism for thermal relic dark matter of strongly interacting massive particles. Phys. Rev. Lett. 113, 171301 (2014). https://doi.org/10.1103/PhysRevLett.113.171301
L.J. Hall, K. Jedamzik, J. March-Russell, S.M. West, Freeze-in production of fimp dark matter. J. High Energy Phys. (2010). https://doi.org/10.1007/jhep03(2010)080
XENON Collaboration, E. Aprile et al., Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. 121, 111302 (2018). https://doi.org/10.1103/PhysRevLett.121.111302. arXiv:1805.12562
Y. Meng, Z. Wang, Y. Tao, A. Abdukerim, Z. Bo, W. Chen et al., Dark matter search results from the pandax-4t commissioning run. Phys. Rev. Lett. (2021). https://doi.org/10.1103/physrevlett.127.261802
M. Ackermann, A. Albert, B. Anderson, W. Atwood, L. Baldini, G. Barbiellini et al., Searching for dark matter annihilation from milky way dwarf spheroidal galaxies with six years of fermi large area telescope data. Phys. Rev. Lett. (2015). https://doi.org/10.1103/physrevlett.115.231301
MAGIC and Fermi-LAT Collaborations, M.L. Ahnen et al., Limits to dark matter annihilation cross-section from a combined analysis of magic and fermi-lat observations of dwarf satellite galaxies. J. Cosmol. Astropart. Phys. 2016, 039–039 (2016). https://doi.org/10.1088/1475-7516/2016/02/039
D. Abercrombie et al., Dark matter benchmark models for early LHC Run-2 Searches: report of the ATLAS/CMS Dark Matter Forum. Phys. Dark Univ. 27, 100371 (2020). https://doi.org/10.1016/j.dark.2019.100371. arXiv:1507.00966
M. Frank, B. Fuks, K. Huitu, S.K. Rai, H. Waltari, Resonant slepton production and right sneutrino dark matter in left–right supersymmetry. J. High Energy Phys. (2017). https://doi.org/10.1007/jhep05(2017)015
A. Chatterjee, M. Frank, B. Fuks, K. Huitu, S. Mondal, S.K. Rai et al., Multileptonic signals of co-annihilating left–right supersymmetric dark matter. Phys. Rev. D (2019). https://doi.org/10.1103/physrevd.99.035017
W.-L. Guo, L.-M. Wang, Y.-L. Wu, C. Zhuang, Dark matter constraints on the left–right symmetric model withz2symmetry. Phys. Rev. D (2008). https://doi.org/10.1103/physrevd.78.035015
W.-L. Guo, Y.-L. Wu, Y.-F. Zhou, Searching for dark matter signals in the left–right symmetric gauge model with cp symmetry. Phys. Rev. D (2010). https://doi.org/10.1103/physrevd.82.095004
J. Heeck, S. Patra, Minimal left–right symmetric dark matter. Phys. Rev. Lett. (2015). https://doi.org/10.1103/physrevlett.115.121804
P.-H. Gu, Left–right symmetric model for neutrino masses, baryon asymmetry, and dark matter. Phys. Rev. D (2010). https://doi.org/10.1103/physrevd.81.095002
E. Ma, Dark-matter fermion from left–right symmetry. Phys. Rev. D (2012). https://doi.org/10.1103/physrevd.85.091701
M. Nemevšek, G. Senjanović, Y. Zhang, Warm dark matter in low scale left–right theory. J. Cosmol. Astropart. Phys. 2012, 006–006 (2012). https://doi.org/10.1088/1475-7516/2012/07/006
S. Bahrami, M. Frank, D.K. Ghosh, N. Ghosh, I. Saha, Dark matter and collider studies in the left–right symmetric model with vectorlike leptons. Phys. Rev. D (2017). https://doi.org/10.1103/physrevd.95.095024
D.K. Ghosh, N. Ghosh, I. Saha, A. Shaw, Revisiting the high-scale validity of the type II seesaw model with novel LHC signature. Phys. Rev. D 97, 115022 (2018). https://doi.org/10.1103/PhysRevD.97.115022. arXiv:1711.06062
S. Ashanujjaman, K. Ghosh, Revisiting type-II see-saw: present limits and future prospects at LHC. arXiv:2108.10952
P. Agrawal, M. Mitra, S. Niyogi, S. Shil, M. Spannowsky, Probing the type-II seesaw mechanism through the production of Higgs bosons at a lepton collider. Phys. Rev. D 98, 015024 (2018). https://doi.org/10.1103/PhysRevD.98.015024. arXiv:1803.00677
B. Barman, S. Bhattacharya, P. Ghosh, S. Kadam, N. Sahu, Fermion dark matter with scalar triplet at direct and collider searches. Phys. Rev. D 100, 015027 (2019). https://doi.org/10.1103/PhysRevD.100.015027. arXiv:1902.01217
C. Bonilla, M.E. Krauss, T. Opferkuch, W. Porod, Perspectives for detecting lepton flavour violation in left–right symmetric models. J. High Energy Phys. (2017). https://doi.org/10.1007/jhep03(2017)027
J. Chakrabortty, J. Gluza, T. Jelinski, T. Srivastava, Theoretical constraints on masses of heavy particles in left–right symmetric models. Phys. Lett. B 759, 361–368 (2016). https://doi.org/10.1016/j.physletb.2016.05.092. arXiv:1604.06987
P.S.B. Dev, R.N. Mohapatra, Y. Zhang, Probing the Higgs sector of the minimal left–right symmetric model at future hadron colliders. JHEP 05, 174 (2016). https://doi.org/10.1007/JHEP05(2016)174. arXiv:1602.05947
G. Chauhan, P.S.B. Dev, R.N. Mohapatra, Y. Zhang, Perturbativity constraints on \(U(1)_{B-L}\)and left–right models and implications for heavy gauge boson searches. JHEP 01, 208 (2019). https://doi.org/10.1007/JHEP01(2019)208. arXiv:1811.08789
P. S. Bhupal Dev, R. N. Mohapatra, W. Rodejohann, X.-J. Xu, Vacuum structure of the left–right symmetric model. JHEP 02, 154 (2019). https://doi.org/10.1007/JHEP02(2019)154. arXiv:1811.06869
G. Chauhan, Vacuum stability and symmetry breaking in left–right symmetric model. JHEP 12, 137 (2019). https://doi.org/10.1007/JHEP12(2019)137. arXiv:1907.07153
T. Mondal, U.K. Dey, P. Konar, Implications of unitarity and charge breaking minima in a left–right symmetric model. Phys. Rev. D 92, 096005 (2015). https://doi.org/10.1103/PhysRevD.92.096005. arXiv:1508.04960
Particle Data Group Collaboration, P.A. Zyla et al., Review of particle physics. PTEP 2020, 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
W. Porod, F. Staub, Spheno 3.1: extensions including flavour, cp-phases and models beyond the mssm. Comput. Phys. Commun. 183, 2458–2469 (2012). https://doi.org/10.1016/j.cpc.2012.05.021
M. Aaboud, G. Aad, B. Abbott, O. Abdinov, B. Abeloos, D. Abhayasinghe et al., Search for invisible Higgs boson decays in vector boson fusion at s =13 TeV with the atlas detector. Phys. Lett. B 793, 499–519 (2019). https://doi.org/10.1016/j.physletb.2019.04.024
DELPHI Collaboration, M. Aaboud et al., Searches for supersymmetric particles in e + e- collisions up to 208 gev and interpretation of the results within the mssm. Eur. Phys. J. C 31, 421–479 (2003). https://doi.org/10.1140/epjc/s2003-01355-5
A. Maiezza, M. Nemevsek, F. Nesti, G. Senjanovic, Left–right symmetry at LHC. Phys. Rev. D 82, 055022 (2010). https://doi.org/10.1103/PhysRevD.82.055022. arXiv:1005.5160
ATLAS Collaboration, M. Aaboud et al., Search for a right-handed gauge boson decaying into a high-momentum heavy neutrino and a charged lepton in \(pp\) collisions with the ATLAS detector at \(\sqrt{s}=13\)TeV. Phys. Lett. B 798, 134942 (2019) (2019). https://doi.org/10.1016/j.physletb.2019.134942. arXiv:1904.12679
K. Griest, D. Seckel, Three exceptions in the calculation of relic abundances. Phys. Rev. D 43, 3191–3203 (1991). https://doi.org/10.1103/PhysRevD.43.3191
J. Edsjö, P. Gondolo, Neutralino relic density including coannihilations. Phys. Rev. D 56, 1879–1894 (1997). https://doi.org/10.1103/physrevd.56.1879
F. Staub, Sarah 4: a tool for (not only susy) model builders. Comput. Phys. Commun. 185, 1773–1790 (2014). https://doi.org/10.1016/j.cpc.2014.02.018
G. Bélanger, F. Boudjema, A. Goudelis, A. Pukhov, B. Zaldivar, micrOMEGAs5.0: freeze-in. Comput. Phys. Commun. 231, 173–186 (2018). https://doi.org/10.1016/j.cpc.2018.04.027. arXiv:1801.03509
ATLAS Collaboration, M. Aaboud et al., Search for doubly charged Higgs boson production in multi-lepton final states with the ATLAS detector using proton–proton collisions at \(\sqrt{s}=13\,\text{TeV}\). Eur. Phys. J. C 78, 199 (2018). https://doi.org/10.1140/epjc/s10052-018-5661-z. arXiv:1710.09748
CMS collaboration, A search for doubly-charged Higgs boson production in three and four lepton final states at \(\sqrt{s}=13~{\text{ TeV }}\)
ATLAS Collaboration, G. Aad et al., Search for doubly and singly charged Higgs bosons decaying into vector bosons in multi-lepton final states with the ATLAS detector using proton-proton collisions at \(\sqrt{s}\) = 13 TeV. JHEP 06, 146 (2021). https://doi.org/10.1007/JHEP06(2021)146. arXiv:2101.11961
F. Staub, SARAH 4: a tool for (not only SUSY) model builders. Comput. Phys. Commun. 185, 1773–1790 (2014). https://doi.org/10.1016/j.cpc.2014.02.018. arXiv:1309.7223
C. Degrande, C. Duhr, B. Fuks, D. Grellscheid, O. Mattelaer, T. Reiter, UFO—the universal FeynRules output. Comput. Phys. Commun. 183, 1201–1214 (2012). https://doi.org/10.1016/j.cpc.2012.01.022. arXiv:1108.2040
W. Porod, SPheno, a program for calculating supersymmetric spectra, SUSY particle decays and SUSY particle production at e+ e- colliders. Comput. Phys. Commun. 153, 275–315 (2003). https://doi.org/10.1016/S0010-4655(03)00222-4. arXiv:hep-ph/0301101
W. Porod, F. Staub, SPheno 3.1: extensions including flavour, CP-phases and models beyond the MSSM. Comput. Phys. Commun 183, 2458–2469 (2012). https://doi.org/10.1016/j.cpc.2012.05.021. arXiv:1104.1573
J. Alwall, M. Herquet, F. Maltoni, O. Mattelaer, T. Stelzer, MadGraph 5: going beyond. JHEP 06, 128 (2011). https://doi.org/10.1007/JHEP06(2011)128. arXiv:1106.0522
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). https://doi.org/10.1007/JHEP07(2014)079. arXiv:1405.0301
T. Sjöstrand, S. Ask, J. R. Christiansen, R. Corke, N. Desai, P. Ilten, An introduction to PYTHIA 8.2. Comput. Phys. Commun 191, 159–177 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012
DELPHES 3 Collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens et al., DELPHES 3, a modular framework for fast simulation of a generic collider experiment. JHEP 02, 057 (2014). https://doi.org/10.1007/JHEP02(2014)057. arXiv:1307.6346
E. Conte, B. Fuks, G. Serret, MadAnalysis 5, a user-friendly framework for collider phenomenology. Comput. Phys. Commun. 184, 222–256 (2013). https://doi.org/10.1016/j.cpc.2012.09.009. arXiv:1206.1599
F. del Aguila, J.A. Aguilar-Saavedra, Distinguishing seesaw models at LHC with multi-lepton signals. Nucl. Phys. B 813, 22–90 (2009). https://doi.org/10.1016/j.nuclphysb.2008.12.029. arXiv:0808.2468
F. Cascioli, T. Gehrmann, M. Grazzini, S. Kallweit, P. Maierhöfer, A. von Manteuffel et al., ZZ production at hadron colliders in NNLO QCD. Phys. Lett. B 735, 311–313 (2014). https://doi.org/10.1016/j.physletb.2014.06.056. arXiv:1405.2219
A. Kardos, Z. Trocsanyi, C. Papadopoulos, Top quark pair production in association with a Z-boson at NLO accuracy. Phys. Rev. D 85, 054015 (2012). https://doi.org/10.1103/PhysRevD.85.054015. arXiv:1111.0610
H. Wang, R.-Y. Zhang, W.-G. Ma, L. Guo, X.-Z. Li, S.-M. Wang, NLO QCD + EW corrections to ZZZ production with subsequent leptonic decays at the LHC. J. Phys. G 43, 115001 (2016). https://doi.org/10.1088/0954-3899/43/11/115001. arXiv:1610.05876
M. Grazzini, S. Kallweit, D. Rathlev, M. Wiesemann, \(W^{\pm }Z\) production at hadron colliders in NNLO QCD. Phys. Lett. B 761, 179–183 (2016). https://doi.org/10.1016/j.physletb.2016.08.017. arXiv:1604.08576
Acknowledgements
The authors would like to acknowledge the support from DAE, India for the Regional Centre for Accelerator based Particle Physics (RECAPP), Harish Chandra Research Institute.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Dey, S., Ghosh, P. & Rai, S.K. Confronting dark fermion with a doubly charged Higgs in the left–right symmetric model. Eur. Phys. J. C 82, 876 (2022). https://doi.org/10.1140/epjc/s10052-022-10778-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10778-z

















 signal
signal
 ) for signal (BPC1 and BPC2) and total SM background
) for signal (BPC1 and BPC2) and total SM background


 GeV selection cut. Since the ZZ decaying to give four leptons will have very little missing energy in the final state the cut will throw away a significant part of the background events. This cut does not affects our signal much since it has decay products consisting of dark matter and neutrinos leading to a larger
GeV selection cut. Since the ZZ decaying to give four leptons will have very little missing energy in the final state the cut will throw away a significant part of the background events. This cut does not affects our signal much since it has decay products consisting of dark matter and neutrinos leading to a larger 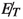 in the signal events. Hence this cut becomes very efficient in improving the signal sensitivity.
in the signal events. Hence this cut becomes very efficient in improving the signal sensitivity.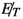 cut, we put a cut on the invariant mass of same flavor opposite charge leptons around the Z mass pole (
cut, we put a cut on the invariant mass of same flavor opposite charge leptons around the Z mass pole (
 ) for both SetA [left] and SetB [right] signal events and the total SM background
) for both SetA [left] and SetB [right] signal events and the total SM background




 signal
signal , such as ZZ and VVV in contrast to our signal which has both neutrinos and dark matter as source for missing transverse energy, we use a selection cut of
, such as ZZ and VVV in contrast to our signal which has both neutrinos and dark matter as source for missing transverse energy, we use a selection cut of  GeV. We also use as before, a rejection cut on the invariant mass of opposite sign same flavor lepton pairs near the Z mass pole to further suppress the background events.
GeV. We also use as before, a rejection cut on the invariant mass of opposite sign same flavor lepton pairs near the Z mass pole to further suppress the background events. signal analysis for BPC3 at ILC
signal analysis for BPC3 at ILC