Exploring the low redshift universe: two parametric models for effective pressure

Abstract

Astrophysical observations have put unprecedentedly tight constraints on cosmological theories. The $\Lambda$CDM model, mathematically simple and fits observational data sets well, is preferred for explaining the behavior of universe. But many basic features of the dark sectors are still unknown, which leaves room for various nonstandard cosmological hypotheses. As the pressure of the cosmological constant dark energy is unvarying, ignoring contributions from radiation and curvature terms at low redshift, the effective pressure keeps constant. In this paper, we propose two parametric models for a non-constant effective pressure in order to study the tiny deviation from $\Lambda$CDM at low redshift. We recover our phenomenological models in the scenarios of quintessence and phantom fields, and we explore the behavior of the scalar field and potential. We constrain our model parameters with SNe Ia and BAO observations, and we detect subtle hints of $\omega _{\mathrm{de}}<-1$ from the data-fitting results of both models, which indicates possibly a phantom dark energy scenario at present.

1 Introduction

Since the discovery of the current acceleration of our universe expansion in 1998, maybe the greatest mystery in cosmology is the deceptive nature of the dark energy. Recent observational results [1] have put tight constraints on the properties of dark energy, but there is still no theoretical or observational indication pinning down its nature. On the one hand, although the simple cosmological constant $\Lambda$ can accommodate the accelerating expansion, it encounters two serious problems. The first one is the fine tuning problem: the measured energy of the vacuum is so much smaller than the estimated value $\rho _{\mathrm{vac}}^{\mathrm{obs}}\ll \rho _{\mathrm{vac}}^{\mathrm{theo}}$, the famous 120-orders-of-magnitude discrepancy that makes the vacuum explanation suspect. On the other hand we may ask why there is dominance of the cosmological constant over the matter component at the present epoch. These two basic problems prompt us to propose some alternatives, which include an evolving scalar field called quintessence [2–8], a noncanonical scalar field (such as K-essence [9–11], phantom [7, 8, 12–18]), modified gravity [7, 8, 19–23], coupled dark energy [8, 24, 25] or decaying dark energy [26] models, and so on. On the other hand, the equation of state (EoS) parameter of the cosmological constant is precisely $\omega _{\mathrm{de}}=-1$. Recent observations show that the EoS parameter of modeled dark energy is $\omega _{\mathrm{de}}=-1.006\pm 0.045$, which slightly favors $\omega _{\mathrm{de}}<-1$. Anyhow, the small deviations from the cosmological constant $\Lambda$ allow one to consider models with $\omega _{\mathrm{de}}\ne -1$. So one can make efforts to construct new models to explain the deviations which may be detectable at the precision of current and future observations.

Parameterization is an useful tool toward a more complete characterization of dark energy modeling and has been routinely employed to analyze data sets. Most parameterizations for dark energy models involve the EoS parameter $\omega _{\mathrm{de}}$ for the dark energy behavior. Several well-known parameterizations for the EoS of dark energy have been proposed so far. We can write the parameterizations in polynomial form $\omega _{\mathrm{de}}(z)=\sum \nolimits _{n=0}\omega _nx_n(z)$ generally, where the expansions can be given in the following ways: (i) by redshift $x_n(z)=z^n$, (ii) by scale factor $x_n(z)=(1-\frac{a}{a_0})^n=(\frac{z}{1+z})^n$, (iii) logarithmic $x_n(z)=[\ln (1+z)]^n$. Parameterization (i) was proposed by Huterer and Turner [27] and Weller and Albrecht [28] with $n\le 1$. Parameterization (ii) with $n\le 1$ was introduced by Chevalier, Polarski and Linder [29, 30], the famous Chevallier–Polarski–Linder (CPL) parameterization. $\omega _{\mathrm{de}}=\omega _0+\omega _1(1-a)=\omega _0+\omega _1\frac{z}{1+z}$ behaves as $\omega _{\mathrm{de}}\rightarrow \omega _0+\omega _1$ for $z\rightarrow \infty$ and $\omega _{\mathrm{de}}\rightarrow \omega _0$ for $z\rightarrow 0$. A more general form with $\omega _{\mathrm{de}}=\omega _0+\omega _1\frac{z}{(1+z)^p}$ was later proposed by Jassal et al. [32]. Parameterization (iii) with $n\le 1$ was introduced by Efstathiou [31]. In recent years, some new parameterizations have been proposed, such as using Padé parameterizations for the EoS of dark energy [33], namely $\omega _{\mathrm{de}}=\frac{\omega _0+\omega _a(1-a)}{1+\omega _b(1-a)}$, and $\omega _{\mathrm{de}}=\frac{\omega _0+\omega _1\ln a}{1+\omega _2\ln a}$. It is worth mentioning that Sen proposed a parameterization for the pressure of the dark energy model [34, 35], $P_\Lambda =-P_0+P_1(1-a)+\cdot \!\cdot \!\cdot \cdot$, in order to study small deviations from the cosmological constant. Different from parameterizations which focused on the EoS of the dark energy mentioned above, in this paper we aim to make parameterizations for the relation between redshift and effective pressure of all energy components in the universe. In the following we propose two parametric models for the effective pressure in order to explore the late-stage evolution of the universe.

This paper is organized as follows: in Sect. 2, we propose two new parametric models for the effective pressure: $P(z)=P_a+P_b z$ and $P(z)=P_c+\frac{P_d}{1+z}$. In Sect. 3, we relate our parametric models with the quintessence and phantom scalar fields, and the behavior of field and potential is then explored. In Sect. 4, we constrain our model parameters with SNe Ia and BAO observations. In Sect. 5, we end with discussions and conclusions.

2 Two parametric models

The Friedmann equations, the equation of energy conservation, and the equation of state constitute a closed system describing the background evolution of the universe. Substituting the EoS by a relation between the effective pressure P and the redshift z is also feasible, as the equation $P=P(z)$ is not linearly dependent on the Friedmann equation and the equation of energy conservation. Also, the EoS can be recovered by inserting the P–z relation into the equation of energy conservation,

$$\begin{aligned} \dot{\mathrm{\rho }}+3 H(P+\rho )=0, \end{aligned}$$

(1)

and integrating out the expression of $\rho$. For example, the effective pressure for $\Lambda$CDM at late stage is nearly constant, say $P_0$; accordingly, we can obtain from Eq. (1)

$$\begin{aligned} \rho (a)=-P_0+C a^{-3} \end{aligned}$$

(2)

where C is an integration constant, and the two terms at the right side represent contributions from the cosmological constant and matter, respectively.

This is just an example of P parameterization; generally, we can have more complicated P–z relations. As the P–z relation is equivalent to the EoS, a parameterization on the effective pressure is equivalent to that of the EoS parameter $\omega _{\mathrm{de}}$. Since $\omega _{\mathrm{de}}$ is the exponential of some component in EoS, the $\omega _{\mathrm{de}}$ parameterization requires a presupposition of the components in EoS; i.e., the physical mechanism of the possible deviation from $\Lambda$CDM has to be dictated; we make parameterizations merely because we actually do not know the concrete mechanism behind the accelerative expansion. To illustrate, a deviation of $\Lambda$CDM might come from the evolution of the EoS of the cosmological constant term, while an additional component might result in the same deviation. However, a parameterization of the effective pressure just circumvents this issue, and no knowledge of the concrete physical mechanism is required. We are able to directly study the deviation from the constant P–z relation without prejudice to a presupposition.

2.1 Model 1

In this subsection, we propose a model which reads

$$\begin{aligned} P(z)=P_a+P_b z, \end{aligned}$$

(3)

where $P_a$ and $P_b$ are free parameters.

For the scale factor a and the redshift z, we have

$$\begin{aligned} a=\frac{a_0}{1+z}=\frac{1}{1+z}, \end{aligned}$$

(4)

where $a_0=1$ corresponds to the value today. Substitute Eqs. (3) and (4) into Eq. (1); then the total energy density can be integrated as

$$\begin{aligned} \rho (a)=-(P_a-P_b)-\frac{3}{2}P_b a^{-1}+C_1 a^{-3}, \end{aligned}$$

(5)

where $C_1$ is an integration constant. If we set $\rho _0$ to be the energy density today, the integration constant is then $C_1=\rho _0+P_a+\frac{1}{2}P_b$. In Eq. (5), we can interpret the inversely cubic term $C_1 a^{-3}$ as dust matter and the constant term $-(P_a-P_b)$ as the cosmological constant in $\Lambda$CDM. The term $-\frac{3}{2}P_b a^{-1}$ does not appear in the $\Lambda$CDM model, whose physical nature will be explored in the next section.

For convenience in data fitting, we introduce some dimensionless parameters. First, we define the dimensionless density and pressure as

$$\begin{aligned} \rho ^*\equiv & {} \frac{\rho }{\rho _0}=\frac{H^2}{H_0^2} , \end{aligned}$$

(6)

$$\begin{aligned} P^*\equiv & {} \frac{P}{\rho _0} . \end{aligned}$$

(7)

The expressions of the total density Eq. (5) and the total pressure Eq. (3) can be rewritten as

$$\begin{aligned} \rho ^*(a)= & {} -(P_a^*-P_b^*)-\frac{3}{2}P_b^*a^{-1}+C_1^*a^{-3} ,\end{aligned}$$

(8)

$$\begin{aligned} P^*(a)= & {} (P_a^*-P_b^*)+P_b^*a^{-1} , \end{aligned}$$

(9)

where $P_a^*\equiv \frac{P_a}{\rho _0}$, $P_b^*\equiv \frac{P_b}{\rho _0}$, and $C^*_1\equiv \frac{C_1}{\rho _0}=1+P_a^*+\frac{1}{2}P_b^*$.

Redefining the two new parameters, $\alpha \equiv -(P_a^*-P_b^*)$ and $\beta \equiv -\frac{3}{2}P_b^*$, we have

$$\begin{aligned} \rho ^*(a)= & {} \alpha +\beta a^{-1}+(1-\alpha -\beta ) a^{-3} ,\end{aligned}$$

(10)

$$\begin{aligned} P^*(a)= & {} -\alpha -\frac{2}{3}\beta a^{-1} . \end{aligned}$$

(11)

As is well known, the dimensionless Hubble parameter is

$$\begin{aligned} E(z)\equiv \frac{H}{H_0} . \end{aligned}$$

(12)

Comparing Eq. (12) with Eq. (6), we obtain

$$\begin{aligned} E(a)= \rho ^*(a)^\frac{1}{2} . \end{aligned}$$

(13)

Then, for model 1, we define

$$\begin{aligned} \Omega _1= & {} \frac{\alpha }{E^2} , \end{aligned}$$

(14)

$$\begin{aligned} \Omega _2= & {} \frac{\beta a^{-1}}{E^2} ,\end{aligned}$$

(15)

$$\begin{aligned} \Omega _m= & {} \frac{\Omega _{m0}a^{-3}}{E^2} , \end{aligned}$$

(16)

where $\Omega _{m0}=1-\alpha -\beta$, hence $\Omega _1+\Omega _2+\Omega _m=1$.

2.2 Model 2

We propose another parameterization as

$$\begin{aligned} P(z)=P_c+\frac{P_d}{1+z}, \end{aligned}$$

(17)

where $P_c$ and $P_d$ are free parameters. Inserting Eqs. (4) and (17) into Eq. (1), we obtain the total energy density for model 2,

$$\begin{aligned} \rho (a)=-P_c-\frac{3}{4}P_d a+C_2 a^{-3}, \end{aligned}$$

(18)

where $C_2$ is an integration constant. Setting the present energy density as $\rho _0$, then $C_2=\rho _0+P_c+\frac{3}{4}P_d$. Still, we can find the term $C_2 a^{-3}$ corresponding to dust matter, and the term $-P_c$ corresponding to the cosmological constant. The difference between model 2 and model 1 rests in the rest term, $-\frac{3}{2}P_b a^{-1}$ for model 2, whereas it is in $-\frac{3}{4}P_d a$ for model 1. Their physical nature will be studied in the next section.

Like model 1, we need to introduce new model parameters in model 2. With Eqs. (6) and (7), we can obtain the expressions of the total density and the total pressure for model 2:

$$\begin{aligned} \rho ^*(a)= & {} -P_c^*-\frac{3}{4}P_d^*a+C_2^*a^{-3} , \end{aligned}$$

(19)

$$\begin{aligned} P^*(a)= & {} P_c^*+P_d^*a , \end{aligned}$$

(20)

where $P_c^*\equiv \frac{P_c}{\rho _0}$, $P_d^*\equiv \frac{P_d}{\rho _0}$, and $C^*_2\equiv \frac{C_2}{\rho _0}=1+P_c^*+\frac{3}{4}P_d^*$.

Redefine two new parameters $\gamma \equiv -P_c^*$ and $\delta \equiv -\frac{3}{4}P_d^*$; then

$$\begin{aligned} \rho ^*(a)= & {} \gamma +\delta a+(1-\gamma -\delta ) a^{-3} ,\end{aligned}$$

(21)

$$\begin{aligned} P^*(a)= & {} -\gamma -\frac{4}{3}\delta a . \end{aligned}$$

(22)

Also, we define for model 2

$$\begin{aligned} \Omega _1= & {} \frac{\gamma }{E^2} , \end{aligned}$$

(23)

$$\begin{aligned} \Omega _2= & {} \frac{\delta a}{E^2} ,\end{aligned}$$

(24)

$$\begin{aligned} \Omega _m= & {} \frac{\Omega _{m0}a^{-3}}{E^2} , \end{aligned}$$

(25)

where $\Omega _{m0}=1-\gamma -\delta$, and we have $\Omega _1+\Omega _2+\Omega _m=1$.

3 Relation with scalar fields

Deviations from the $\Lambda$CDM in our models can be realized through different physical scenarios. Scalar fields are mainstream approaches to explain the acceleration of the universe’s expansion. In the scenarios of scalar fields, dark energy evolves with time. The scalar field dynamics has been studied in great detail (see Refs. [2–18]) and there are lots of issues involved such as (i) choosing the initial conditions for the scalar field; (ii) choosing the potential with solid theoretical motivation; (iii) the existence of the tracker field and so on. Generally, the evolution of a scalar field is studied over the cosmic history, and once the parameters of scalar field models are set they determine the entire cosmological evolution. So a more detailed analysis would involve studying the scalar field dynamics over cosmic history, and then comparing its evolution with that of a pressure parametrization model at low redshift. In this paper, we will merely compare the pressure and the energy density of a field with that of a model of pressure parametrization at low redshift and study the behavior of the field and the potential. The physical realization of the parameterizations through scalar fields means adjusting the behavior of the scalar fields to the dark energy term occurring in the parametric model. Specifically, we write the two equations

$$\begin{aligned}&P_{\mathrm{eff}} = P_{\mathrm{scalar~field}},\end{aligned}$$

(26)

$$\begin{aligned}&\rho _{\mathrm{eff}}-\rho _m = \rho _{\mathrm{scalar~field}}, \end{aligned}$$

(27)

as the mathematical definition of the realization.

In this section, we will take “quintessence” and “phantom” as two examples to realize our models.

Quintessence “Quintessence” denotes a canonical scalar field $\phi$ with a potential $V_1(\phi )$ that does not interact with all the other components except standard gravity, whose EoS parameter $\omega _{\mathrm{de}}>-1$. Quintessence is described by the action

(28)

(29)

where $\kappa ^2=8\pi G$, R is the Ricci scalar, and $S_M$ is the action of matter. The variation of the action Eq. (29) with respect to $\phi$ gives

$$\begin{aligned} \ddot{\phi } + 3 H \dot{\phi } + V^\prime _1(\phi ) = 0, \end{aligned}$$

(30)

where $V_1(\phi )$ is the potential of the quintessence field, the prime denotes the derivative with respect to $\phi$. In a FLRW background, the energy density $\rho _{\mathrm{de}}$ and the pressure $P_{\mathrm{de}}$ of the quintessence field are

$$\begin{aligned} \rho _{\mathrm{de}}= & {} \frac{1}{2}\dot{\phi }^2+V_1(\phi ), \end{aligned}$$

(31)

$$\begin{aligned} P_{\mathrm{de}}= & {} \frac{1}{2}\dot{\phi }^2-V_1(\phi ). \end{aligned}$$

(32)

Then the EoS

$$\begin{aligned} \omega _{\mathrm{de}}=\frac{\frac{1}{2}\dot{\phi }^2-V_1(\phi )}{\frac{1}{2}\dot{\phi }^2+V_1(\phi )}. \end{aligned}$$

(33)

Phantom The minimally coupled phantom model is also a possible realization, whose EoS parameter $\omega _{\mathrm{de}}<-1$. The action of the phantom field minimally coupled to gravity and matter sources is

(34)

(35)

whose variation with respect to $\phi$ gives

$$\begin{aligned} \ddot{\phi } + 3 H \dot{\phi } - V^\prime _2(\phi ) = 0, \end{aligned}$$

(36)

where $V_2(\phi )$ is the potential of the phantom field, and the prime denotes the derivative with respect to $\phi$. The energy density and pressure of the phantom are given by (assuming a flat FRW metric)

$$\begin{aligned} \rho _{\mathrm{de}}= & {} -\frac{1}{2}\dot{\phi }^2+V_2(\phi ) ,\end{aligned}$$

(37)

$$\begin{aligned} P_{\mathrm{de}}= & {} -\frac{1}{2}\dot{\phi }^2-V_2(\phi ) . \end{aligned}$$

(38)

The EoS of the phantom field is then

$$\begin{aligned} \omega _{\mathrm{de}}=-\frac{-\frac{1}{2}\dot{\phi }^2-V_2(\phi )}{-\frac{1}{2}\dot{\phi }^2+V_2(\phi )}. \end{aligned}$$

(39)

So $\omega _{\mathrm{de}}<-1$ for $\frac{1}{2}\dot{\phi }^2<V_2(\phi )$.

3.1 Model 1

The EoS of the scalar fields for model 1 reads

$$\begin{aligned} \omega _{\mathrm{de}}=\frac{ P_{\mathrm{scalar~field}}}{\rho _{\mathrm{scalar~field}}}=-1+\frac{ \frac{1}{3}\beta (1+z)}{\alpha +\beta (1+z)}. \end{aligned}$$

(40)

Note that, in the above equation, there will be a singularity when $z=-\frac{\alpha }{\beta }-1$. In this paper we only consider the universe at low redshift, so we do not need to worry about that situation. Besides, in Sect. 4 data fitting will support our argument.

In the quintessence scenario, assuming the cosmic components consist of matter and quintessence, comparing Eqs. (31) and (32) with Eqs. (3) and (5), we have

$$\begin{aligned}&-(P_a-P_b)-\frac{3}{2}P_b a^{-1} = \frac{1}{2}\dot{\phi }^2+V_1(\phi ) ,\end{aligned}$$

(41)

$$\begin{aligned}&P_a-P_b+P_b a^{-1} = \frac{1}{2}\dot{\phi }^2-V_1(\phi ) . \end{aligned}$$

(42)

Simplify the above two equations, compare to Eqs. (6)–(11), replace model parameters ($P_a$, $P_b$) with the redefined parameters ($\alpha$, $\beta$), and we obtain

$$\begin{aligned} \frac{1}{2}\dot{\phi }^2= & {} \frac{1}{6}\rho _0\beta a^{-1} ,\end{aligned}$$

(43)

$$\begin{aligned} V_1(\phi )= & {} \rho _0\alpha +\frac{5}{6}\rho _0\beta a^{-1} . \end{aligned}$$

(44)

From Eq. (43), it is easy to find that $\beta >0$ in the scenario of quintessence. By Eqs. (43) and (44), one can construct the kinetic energy $\frac{1}{2}\dot{\phi }^2$ and the potential $V_1(\phi )$ of the quintessence field with parameters ($\alpha$, $\beta$) of model 1. In order to solve the above two equations, following [36], we choose the condition $\phi _{a=1}=M_P$, where $M_P$ is the reduced Planck mass. The Friedmann equation can then be rewritten as

$$\begin{aligned} H^2=\frac{1}{3M_P^2}\rho . \end{aligned}$$

(45)

Considering the dark energy domination at the present epoch in the universe, with the density parameter in the dark energy $\Omega _{\mathrm{de}}\sim 0.7$, we define $V_0=\rho _0=3M_P^2H_0^2$. Simplifying Eqs. (43) and (44), we have

$$\begin{aligned}&\frac{\mathrm{d}\phi }{\mathrm{d}a} = \pm M_P\sqrt{\frac{\beta }{\alpha +\beta a^{-1}+(1-\alpha -\beta ) a^{-3}}} a^{-\frac{3}{2}} , \end{aligned}$$

(46)

$$\begin{aligned}&V_1(\phi ) = V_0\left( \alpha +\frac{5}{6}\beta a^{-1}\right) . \end{aligned}$$

(47)

The symbol “$\pm$” in Eq. (46) corresponds to two solutions. Consider $\alpha =0.7, \beta =0.05$ for numerically solving the above two equations; the solutions are represented in Figs. 1 and 2, respectively. From Fig. 1, we find that $\phi$ increases with a, the potential decreases with the increasing $\phi$, Eq. (47), implying that the potential will reach the minimum value $V_1(\phi )=V_0\alpha$ in the future. From Fig. 2, we can see that $\phi$ decreases with a, and the potential decreases with decreasing $\phi$, Eq. (47) implies that the potential will reach the minimum $V_1(\phi )=V_0\alpha$ in the future. By Eqs. (14) and (15), we can obtain the expression of the density parameter $\Omega _\phi$ for model 1:

$$\begin{aligned} \Omega _\phi =\Omega _1+\Omega _2=\frac{\alpha +\beta a^{-1}}{E^2}. \end{aligned}$$

(48)

The evolution of the density parameter $\Omega _\phi$ in the scenario of quintessence is plotted in Fig. 3. From Fig. 3, we can see that until low redshift the energy density in the quintessence field becomes cosmologically dominant. Finally, the field comes to rest at the minimum of the potential $V_1(\phi )=V_0\alpha$, and the universe eventually settles in a de Sitter phase [see Eq. (40)].

Fig. 1

The solution of Eqs. (46) and (47) corresponding to a plus sign in Eq. (46). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_1$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\alpha =0.7,\beta =0.05$

Fig. 2

The solution of Eqs. (46) and (47) corresponding to a minus sign in Eq. (46). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_1$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\alpha =0.7,\beta =0.05$

Fig. 3

Evolution of the density parameters in the quintessence field ($\Omega _\phi$) and matter ($\Omega _m$) for model 1. $\Omega _\phi$ is indicated by solid line, and $\Omega _m$ is indicated by a dashed line. We consider values $\alpha =0.7,\beta =0.05$

In the case of the phantom scenario, assuming the cosmological components to consist of matter and phantom, comparing Eqs. (37) and (38) with Eqs. (5) and (3), then we have

$$\begin{aligned}&-(P_a-P_b)-\frac{3}{2}P_b a^{-1} = -\frac{1}{2}\dot{\phi }^2+V_2(\phi ) ,\end{aligned}$$

(49)

$$\begin{aligned}&P_a-P_b+P_b a^{-1} = -\frac{1}{2}\dot{\phi }^2-V_2(\phi ) . \end{aligned}$$

(50)

Replace the model parameters ($P_a$, $P_b$) with the redefined parameters ($\alpha$, $\beta$), we have

$$\begin{aligned} \frac{1}{2}\dot{\phi }^2= & {} -\frac{1}{6}\rho _0\beta a^{-1} ,\end{aligned}$$

(51)

$$\begin{aligned} V_2(\phi )= & {} \rho _0\alpha +\frac{5}{6}\rho _0\beta a^{-1} . \end{aligned}$$

(52)

From Eq. (51), it is easy to find that in the scenario of phantom, $\beta <0$. By Eqs. (51) and (52), one can construct the kinetic energy $\frac{1}{2}\dot{\phi }^2$ and potential $V_2(\phi )$ of the phantom field with the model parameters ($\alpha$, $\beta$). Equations (51) and (52) can be rewritten as

$$\begin{aligned}&\frac{\mathrm{d}\phi }{\mathrm{d}a} = \pm M_P\sqrt{\frac{-\beta }{\alpha +\beta a^{-1}+(1-\alpha -\beta ) a^{-3}}} a^{-\frac{3}{2}} , \end{aligned}$$

(53)

$$\begin{aligned}&V_2(\phi ) = V_0\left( \alpha +\frac{5}{6}\beta a^{-1}\right) . \end{aligned}$$

(54)

Consider $\alpha =0.7, \beta =-0.05$ for numerically solving the above two equations, the two solutions are represented in Figs. 4 and 5, respectively. From Fig. 4, we can find $\phi$ increases with a, and the potential increases with the increasing $\phi$, Eq. (54) implies that the potential will reach the maximum value $V_2(\phi )=V_0\alpha$ in the future. From Fig. 5, $\phi$ decreases with a, and the potential increases with decreasing $\phi$; in the future the potential will reach the maximum value $V_2(\phi )=V_0\alpha$. In Fig. 6, we plot the evolution of the density parameter $\Omega _\phi$ in the scenario of the phantom. Notice that the energy density in the phantom field becomes cosmologically dominant only in the recent past. In the future, the field comes to rest at the maximum of the potential and the universe eventually settles in a de Sitter phase.

Fig. 4

The solution of Eqs. (53) and (54) corresponding to a plus sign in Eq. (53). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_2$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\alpha =0.7,\beta =-0.05$

Fig. 5

The solution of Eqs. (53) and (54) corresponding to a minus sign in Eq. (53). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_2$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\alpha =0.7,\beta =-0.05$

Fig. 6

Evolution of the density parameters in the phantom field ($\Omega _\phi$) and matter ($\Omega _m$) for model 1. $\Omega _\phi$ is indicated by a solid line, and $\Omega _m$ is indicated by a dashed line. We consider the values $\alpha =0.7,\beta =-0.05$

3.2 Model 2

We write down the EoS of the scalar fields for model 2:

$$\begin{aligned} \omega _{\mathrm{de}}=\frac{ P_{\mathrm{scalar~field}}}{\rho _{\mathrm{scalar~field}}}=-1-\frac{\frac{1}{3}\delta (1+z)^{-1}}{\gamma +\delta (1+z)^{-1}}. \end{aligned}$$

(55)

It is obvious that only when parameters ($\gamma$, $\delta$) have opposite signs, there will be a singularity occurring when $z=-1-\frac{\delta }{\gamma }$. In Sect. 4, data-fitting results will show that such a singularity would not appear at low shift. In the quintessence scenario, compare Eqs. (31) and (32) with Eqs. (18) and (17), and we can obtain

$$\begin{aligned}&-P_c-\frac{3}{4}P_d a = \frac{1}{2}\dot{\phi }^2+V_1(\phi ) ,\end{aligned}$$

(56)

$$\begin{aligned}&P_c+P_d a = \frac{1}{2}\dot{\phi }^2-V_1(\phi ) . \end{aligned}$$

(57)

Simplify the above two equations, referring to Eqs. (6), (7) and  (19)–(22), replace the model parameters ($P_c$, $P_d$) with the redefined parameters ($\gamma$, $\delta$), then

$$\begin{aligned}&\frac{1}{2}\dot{\phi }^2 = -\frac{1}{6}\rho _0\delta a ,\end{aligned}$$

(58)

$$\begin{aligned}&V_1(\phi ) = \rho _0\gamma +\frac{7}{6}\rho _0\delta a . \end{aligned}$$

(59)

From Eq. (58), it is easy to find that in the scenario of quintessence $\delta <0$. By Eqs. (58) and (59), the kinetic energy $\frac{1}{2}\dot{\phi }^2$ and potential $V_1(\phi )$ of the quintessence field are constructed with the parameters ($\gamma$, $\delta$) of model 2. Simplify these two equations, we have

$$\begin{aligned}&\frac{\mathrm{d}\phi }{\mathrm{d}a}= \pm M_P\sqrt{\frac{-\delta }{\gamma +\delta a+(1-\gamma -\delta ) a^{-3}}} a^{-\frac{1}{2}} ,\end{aligned}$$

(60)

$$\begin{aligned}&V_1(\phi ) = V_0\left( \gamma +\frac{7}{6}\delta a\right) , \end{aligned}$$

(61)

where $V_0=\rho _0=3M_P^2H_0^2$. Choose the parameters $\gamma =0.7,\delta =-0.05$ for numerically solving the above two equations, the two solutions are represented in Figs. 7 and 8, respectively. From Fig. 7, we can find that $\phi$ increases with a, and the potential decreases with increasing $\phi$. From Fig. 8, we can find that $\phi$ decreases with a, and the potential decreases with decreasing $\phi$. Notice that since $\delta <0$ in the scenario of quintessence, according to Eqs. (6), (21), and (45), the Friedmann equation is written as $H^2=\frac{1}{3M_P^2}\rho _0[\gamma +\delta a+(1-\gamma -\delta )a^{-3}]$, which will not hold when the scale factor a is very large. Nevertheless at low redshift the relation is still feasible.

Fig. 7

The solution of Eqs. (60) and (61) corresponding to a plus sign in Eq. (60). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_1$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\gamma =0.7,\delta =-0.05$

Fig. 8

The solution of Eqs. (60) and (61) corresponding to a minus sign in Eq. (60). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_1$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\gamma =0.7,\delta =-0.05$

By Eqs. (23) and (24), we can obtain the expression of the density parameter $\Omega _\phi$ for model 2:

$$\begin{aligned} \Omega _\phi =\Omega _1+\Omega _2=\frac{\gamma +\delta a}{E^2}, \end{aligned}$$

(62)

and the evolution curve of density parameter $\Omega _\phi$ in the scenario of quintessence has been plotted in Fig. 9, from which we see that the quintessence field begins to dominate at low redshift.

Fig. 9

Evolution of the density parameters in the quintessence field ($\Omega _\phi$) and matter ($\Omega _m$) for model 2. $\Omega _\phi$ is indicated by a solid line, and $\Omega _m$ is indicated by a dashed line. We consider values $\gamma =0.7,\delta =-0.05$

In order to realize model 2 in a phantom scenario, comparing Eqs. (37) and (38) with Eqs. (18) (17), we can obtain

$$\begin{aligned}&-P_c-\frac{3}{4}P_d a = -\frac{1}{2}\dot{\phi }^2+V_2(\phi ) ,\end{aligned}$$

(63)

$$\begin{aligned}&P_c+P_d a = -\frac{1}{2}\dot{\phi }^2-V_2(\phi ) . \end{aligned}$$

(64)

Simplify and replace the model parameters ($P_c$, $P_d$) with the redefined parameters ($\gamma$, $\delta$), we have

$$\begin{aligned}&\frac{1}{2}\dot{\phi }^2 = \frac{1}{6}\rho _0\delta a , \end{aligned}$$

(65)

$$\begin{aligned}&V_2(\phi ) = \rho _0\gamma +\frac{7}{6}\rho _0\delta a . \end{aligned}$$

(66)

From Eqs. (65) and (66), it is easy to find that in the scenario of phantom $\delta >0$. By the above two equations, one can construct the kinetic energy $\frac{1}{2}\dot{\phi }^2$ and the potential $V_2(\phi )$ of the phantom field with parameters ($\gamma$, $\delta$) of model 2. Equations (65) and (66) can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}a}=\pm M_P\sqrt{\frac{\delta }{\gamma +\delta a+(1-\gamma -\delta ) a^{-3}}} a^{-\frac{1}{2}}, \end{aligned}$$

(67)

$$\begin{aligned} V_1(\phi )=V_0\left( \gamma +\frac{7}{6}\delta a\right) . \end{aligned}$$

(68)

Choose the parameters $\gamma =0.7,\delta =0.05$ for numerically solving the above two equations, the two solutions are represented in Figs. 10 and 11, respectively. From Fig. 10, we can find $\phi$ increases with a, and the potential increases with the increasing $\phi$. In Fig. 11, $\phi$ decreases with a, and the potential increases with decreasing $\phi$. Notice that since $\delta >0$ in the scenario of phantom, the Friedmann equation can be written as $H^2=\frac{1}{3M_P^2}\rho _0[\gamma +\delta a+(1-\gamma -\delta )a^{-3}]$, $H\rightarrow \infty$ as $a\rightarrow \infty$, which means there will be a “rip” in the future.

Fig. 10

The solution of Eqs. (67) and (68) corresponding to a plus sign in Eq. (67). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_2$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\gamma =0.7,\delta =0.05$

Fig. 11

The solution of Eqs. (67) and (68) corresponding to a minus sign in Eq. (67). The field $\phi$ as a function of a is depicted in the top panel, the potential $V_2$ as a function of $\phi$ is depicted in the bottom panel. The arrow indicates the direction of the evolution of the potential with respect to time. We consider values $\gamma =0.7,\delta =0.05$

In Fig. 12, we plot the evolution curve of density parameter $\Omega _\phi$ in the scenario of phantom. Note that the phantom becomes cosmologically dominant only in the recent past, finally the EoS parameter $\omega _{\mathrm{de}}$ is less than $-1$ [$\omega _{\mathrm{de}}=-\frac{4}{3}$; see Eq. (55)] and the universe eventually settles in a “rip”.

Fig. 12

Evolution of the density parameters in the phantom field ($\Omega _\phi$) and matter ($\Omega _m$) for model 2. $\Omega _\phi$ is indicated by a solid line, and $\Omega _m$ is indicated by a dashed line. We consider values $\gamma =0.7,\delta =0.05$

4 Astrophysical data constraints

4.1 Type Ia supernovae

In this paper we use the Union2.1 SNe Ia data sets without systematic errors for data fitting, which compiles 580 SNe Ia covering the redshift range $z=[0.015,1.4]$. To perform the chi-square statistics, the theoretical distance modulus is defined as

$$\begin{aligned} \mu _{\mathrm{th}}(z_i)\equiv 5\log _{10}D_L(z_i)+\mu _0, \end{aligned}$$

(69)

where $\mu _0\equiv 42.39-5\log _{10}h$ with h the Hubble parameter in units of $100\,\mathrm{km/s/Mpc}$,

$$\begin{aligned} D_L= (1+z)\int ^z_0\frac{\mathrm{d}z'}{E(z';\theta )} \end{aligned}$$

(70)

is the Hubble-free luminosity distance in a spatially flat FRW universe, $E(z;\theta )$ is the dimensionless Hubble parameter, and $\theta$ is for the model parameters.

The corresponding $\chi ^2_{\mathrm{SN}}$ function is calculated from

$$\begin{aligned} \chi ^2_{\mathrm{SN}}= \sum ^{580}_{i=1}\frac{[\mu _{\mathrm{obs}}(z_i)-\mu _{\mathrm{th}}(z_i)]^2}{\sigma ^2_i}, \end{aligned}$$

(71)

where $\mu _{\mathrm{obs}}(z_i)$ and $\sigma _i$ are the observed value and the corresponding $1\sigma$ error of the distance modulus for each supernova. The minimization with respect to $\mu _0$ can be made trivially by expanding $\chi ^2_{\mathrm{SN}}$ as

$$\begin{aligned} \chi ^2_{\mathrm{SN}}= A-2\mu _0B+\mu ^2_0C, \end{aligned}$$

(72)

where

$$\begin{aligned} A(\theta )= & {} \sum ^{580}_{i=1}\frac{[\mu _{\mathrm{obs}}(z_i)-\mu _{\mathrm{th}}(z_i;\theta ;\mu _0=0)]^2}{\sigma ^2_i} , \end{aligned}$$

(73)

$$\begin{aligned} B(\theta )= & {} \sum ^{580}_{i=1}\frac{\mu _{\mathrm{obs}}(z_i)-\mu _{\mathrm{th}}(z_i;\theta ;\mu _0=0)}{\sigma ^2_i} , \end{aligned}$$

(74)

$$\begin{aligned} C(\theta )= & {} \sum ^{580}_{i=1}\frac{1}{\sigma ^2_i} . \end{aligned}$$

(75)

Thus $\mu _0$ is minimized as $\mu _0=\frac{B}{C}$ by calculating the following transformed $\chi ^2$:

$$\begin{aligned} \widetilde{\chi }^2_{\mathrm{SN}}(\theta )= A(\theta )-\frac{B(\theta )^2}{C}. \end{aligned}$$

(76)

4.2 Baryon acoustic oscillations

The baryon acoustic oscillation (BAO) data sets are listed in Table 1. We use the parameter A to measure the BAO peak in the distribution of SDSS luminous red galaxies. In the following A is defined as

$$\begin{aligned} A\equiv \sqrt{\Omega _{m0}}E(z_b)^{-\frac{1}{3}}\left[ \frac{1}{z_b}\int ^{z_b}_0\frac{\mathrm{d}z'}{E(z')}\right] ^{\frac{2}{3}}, \end{aligned}$$

(77)

where $z_b=0.35$. The $\chi ^2$ for the BAO data is

$$\begin{aligned} \chi ^2_{\mathrm{BAO}}= \sum ^{6}_{i=1}\frac{[A_{\mathrm{obs}}(z_i)-A_{\mathrm{th}}(z_i;\theta )]^2}{\sigma ^2_A}. \end{aligned}$$

(78)

The total $\chi ^2$ is given by

$$\begin{aligned} \chi ^2 = \widetilde{\chi }^2_{\mathrm{SN}}+\chi ^2_{\mathrm{BAO}}. \end{aligned}$$

(79)

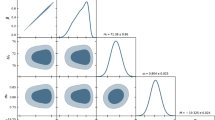
The fitting results and corresponding reduced $\chi ^2$ for model 1 and model 2 are listed in Table 2. The likelihoods of the parameters ($\alpha$, $\beta$) and ($\gamma$, $\delta$) are shown in Figs. 13 and 14, respectively. Besides, the evolution of the EoS parameter $\omega _{\mathrm{de}}$ with respect to the redshift z with $1\sigma$ error propagation from data fitting (Table 2) are shown in Figs. 15 and 16, respectively.

Fig. 13

$1\sigma$ and $2\sigma$ confidence ranges for parameter pair $(\alpha ,\beta )$ of model 1, constrained by SNe Ia and BAO data sets. The dotted straight line ($\beta =0$) corresponds to a $\Lambda$CDM model. The blue dotted line and the red dotted line correspond to $\Omega _{m0}=0.26$ and $\Omega _{m0}=0.32$, respectively

Fig. 14

$1\sigma$ and $2\sigma$ confidence ranges for parameter pair $(\gamma ,\delta )$ of model 2, constrained by SNe Ia and BAO data sets. The dotted straight line ($\delta =0$) corresponds to a $\Lambda$CDM model. The blue dotted line and the red dotted line correspond to $\Omega _{m0}=0.26$ and $\Omega _{m0}=0.32$, respectively

Fig. 15

Evolution of the EoS parameter $\omega _{\mathrm{de}}$ as a function of the redshift z with $1\sigma$ error propagation, constrained by SNe Ia and BAO data sets for model 1. The solid line, the straight dotted line, and the light blue region represent the best-fit, $\omega _{\mathrm{de}}=-1$($\Lambda$CDM), and $1\sigma$ region, respectively

Fig. 16

Evolution of the EoS parameter $\omega _{\mathrm{de}}$ as a function of the redshift z with $1\sigma$ error propagation, constrained by SNe Ia and BAO data sets for model 2. The solid line, the straight dotted line, and the light blue region represent the best-fit, $\omega _{\mathrm{de}}=-1$($\Lambda$CDM), and $1\sigma$ region, respectively

Table 1 Six measurement points of the baryon acoustic oscillation data-sets

Table 2 Parameters of model 1 and model 2 estimated by SNe Ia and BAO data sets with $1\sigma$ errors

5 Conclusion

Since the observational confirmation on late-stage accelerative expansion of the universe many years ago, different models have been proposed to explain its source, among which parameterization is a widely used scheme to better characterize the dark energy and compare with observational results. In this paper, we studied two models parameterizing the effective pressure at low redshift, $P(z)=P_a+P_b z$ and $P(z)=P_c+\frac{P_d}{1+z}$.

Deviations from the $\Lambda$CDM can be realized through different physical scenarios. Roughly speaking, there are two ways. One is to introduce some small but nonzero components besides the cosmological constant $\Lambda$, such as imperfect fluid cosmology [38–41] and cosmic strings [35, 42]; whereas the other is to assume the cosmological constant $\Lambda$ exactly zero and the dark energy characterized by scalar fields evolving with time. In this paper, we pick the second way. We presented two parameterizations in the scenarios of quintessence and phantom fields, and accordingly expressed the kinetic energy term $\frac{1}{2}\dot{\phi }^2$ and the potential term $V(\phi )$ with the model parameters ($\alpha$, $\beta$) and ($\gamma$, $\delta$), respectively. Then we reconstructed the density parameter $\Omega _\phi$ for quintessence and phantom evolving with redshift. In order to obtain a better physical understanding of the field and the potential, we numerically solved the field as a function of the scale factor a and the potential as a function of the field $\phi$.

We constrained the model parameters ($\alpha$, $\beta$) and ($\gamma$, $\delta$) with the SNe Ia and BAO data sets. We reconstructed the evolution of the EoS parameter $\omega _{\mathrm{de}}$ in terms of the redshift z. For model 1, the value for the EoS parameter $\omega _{\mathrm{de}0}$ is $-1.027^{0.043}_{ -0.043}$ at present; for model 2, $\omega _{\mathrm{de}0} =-1.037^{+0.050}_{-0.050}$. These results show that model 1 and model 2 both slightly indicate that the EoS parameter of dark energy $\omega _{\mathrm{de}}<-1$, which corresponds to a phantom dark energy scenario at present. Still, we cannot rule out a quintessence dark energy scenario or a $\Lambda$ dark energy scenario.

Different parameterizations possess their own advantages in addressing some particular problems, but their validity may not be ensured when applied to the explanation of the global evolution. For example, our two parameterizations of the effective pressure can estimate the deviation from the prediction of the standard model at a low redshift with a generality that does not depend on the concrete physical mechanism working in the background.