Cosmological constraints on $f(Q)$ gravity with redshift space distortion data

Abstract

In this paper, we explore one of Einstein’s alternative formulations which involves the non-metricity scalar, Q, within the framework of f(Q) theory. Our study focuses on solving the modified Friedmann equations for the case of dust matter, $\rho =\rho _{m}$, and a form of $f(Q) = \alpha + \beta Q^n$. We investigate the behavior of our model in both linear $(n=1)$ and nonlinear $(n\ne 1)$ scenarios at the background and perturbation levels. By employing the Markov chain Monte Carlo (MCMC) method, we constrain our model using observational datasets including redshift space distortion, cosmic chronometers, and Pantheon$^+$. Without using any parameterization of the growth rate index which quantifies the deviation from the $\Lambda$CDM model, both models exhibit good accuracy in describing the redshift space distortion. We further analyze the dynamics of the Universe using cosmography parameters, where our model exhibits a phase transition between deceleration and acceleration phases at $z=0.789$. Our findings reveal that our model exhibits a phantom-like behavior based on statefinder diagnostic analysis. Interestingly, the model demonstrates a rich variety of behaviors, resembling either a quintessence-like scenario for $(n<1)$ or phantom-like scenario for $(n\ge 1)$. Using the MCMC best fit and parameterizing the growth index, the evolution of the growth index also depends on the parameter n, either remaining constant (in the linear case) or showing a decreasing trend (in the nonlinear case), indicating a weaker growth rate of density perturbations during earlier cosmic times. Finally, we compare our findings of the growth index with the values obtained in the literature.

1 Introduction

Observations evidenced by astronomical probes, such as type Ia supernovae [1,2,3], cosmic microwave background radiation [4, 5], and large-scale structures [6, 7], indicate that the Universe underwent a shift from a decelerating phase in its early history to an accelerating phase in its more recent history. In modern cosmology, one of the most significant and intricate challenges is to pinpoint the agent responsible for the late-time cosmic accelerated expansion. The presence of dark energy with negative pressure is one of the most plausible explanations for this acceleration [8, 9]. Among several dark energy models [10,11,12,13], $\Lambda$CDM has proven to be relatively successful, explaining many cosmological phenomena such as the formation of large-scale structures and accurately describing type Ia supernovae observations. However, its incorporation is impeded by theoretical obstacles related to fine-tuning [14,15,16] and the cosmic coincidence [17, 18].

Another way of approaching the issue of dark energy is to consider alternative theories of gravity that differ from Einstein’s theory of general relativity. These theories may provide an explanation for the accelerating expansion of the Universe without the need for dark energy. Several innovative theories of modified gravity have been suggested, one of which is f(R) gravity [19]. This model relies on a Lagrangian that is dependent on the scalar curvature R and has been successful in elucidating the accelerated expansion of the Universe without invoking the need for dark energy. In addition to the scalar curvature, torsion T and non-metricity Q can also represent affine properties of manifolds. The teleparallel equivalent to GR (TEGR) theory, in which gravity is defined by torsion T with the corresponding action $S=\int \sqrt{-g}T{\text {d}}^{4}x$, is also extended to f(T) gravity [20]. TEGR is an alternative way to describe the geometric concept of gravity, in which the dynamical objects are the four linearly independent tetrads [21,22,23]. Furthermore, TEGR explains the late-time acceleration of the Universe [24, 25], avoiding the Big Bang singularity [26], and provides an alternative to inflation [27]. However, some intrinsic problems arise in TEGR gravity such as the violation of local Lorentz invariance [28]. Furthermore, the symmetric teleparallel equivalent to GR (STEGR) is the underlying gravitational interaction using non-metricity Q without the presence of torsion and curvature. f(Q) gravity is a STEGR theory extension in which the action is defined by $S=\int \sqrt{-g}f(Q){\text {d}}^{4}x$ [29].

Symmetric teleparallel gravity f(Q) is the central focus of this article. So far, constraints have been integrated into the background level by utilizing data from different sources such as the expansion rate from early-type galaxies, supernovae type Ia (SNIa), gamma ray bursts, quasars, cosmic microwave background (CMB), and baryonic acoustic oscillations (BAO). The latter have been used to constrain various f(Q) parameterizations that explicitly depend on the redshift z [30]. Another investigation examines a power law expression for f(Q), specifically $f(Q)=Q+\beta Q^{n}$, which has been studied in terms of cosmological solutions and the evolution of the growth index of matter perturbations [31, 32]. A new proposal suggests an exponential form for the f(Q) function, specifically $f(Q)=Qe^{\lambda \frac{Q_{0}}{Q}}$ [33]. Surprisingly, the combination of cosmic chronometers (CC), type Ia supernovae, and baryon acoustic oscillation datasets, without the use of CMB, shows that this exponential form demonstrates a statistical preference over $\Lambda$CDM, while with the inclusion of CMB data [34], the $\Lambda$CDM model regains its statistical preference.

Moreover, the perturbation level constraints for the f(Q) model have also been obtained using redshift space distortions data (RSD) [35]. This model accurately reproduces the expansion history of the $\Lambda$CDM model. By examining modifications in the evolution of matter density fields, it has been demonstrated that this model has the capability to alleviate the tension associated with $\sigma _{8}$ [36]. Additionally, observable effects such as the characterization of the matter power spectrum, the lensing effect on the CMB angular power spectrum, CMB temperature anisotropy, and the propagation of gravitational waves have been identified in [37].

The motivation behind this article is to explore the form $f(Q) = \alpha + \beta Q^{n}$, which was reconstructed by Capozziello and D’Agostino in [38]. However, this form has only been tested at the background level using a method based on rational Padé approximations [38]. Therefore, the aim of our study is twofold: firstly, to constrain f(Q) gravity by means of Bayesian analysis using redshift space distortion data, and secondly, to investigate whether this model can effectively explain the accelerated phase of the Universe without the need to introduce dark energy. To achieve this aim, we initially solve the modified Friedmann equations under the assumption that the Universe is exclusively composed of dust matter with zero pressure $(p=0)$. We rigorously evaluate the performance of this model by assessing its accuracy at both the background and perturbation levels. To estimate model parameters, we use data from various probes, including redshift space distortion [39,40,41,42,43,44,45,46,47,48,49,50,51], cosmic chronometers [52,53,54,55,56,57,58,59,60,61,62,63], and Pantheon$^+$ datasets [64], in order to constrain f(Q) gravity in linear ($n=1$) and nonlinear ($n\ne 1$) forms. It is worth noting that we numerically solve the evolution of the matter perturbation equation instead of the analytical approximation of the growth factor f. Then, using a Markov chain Monte Carlo (MCMC) analysis [65], we extract the best-fit values of the free parameters for both cases. On the basis of these statistical results, the two f(Q) gravity cases are compared, analyzed, and classified with respect to the standard $\Lambda$CDM model using the corrected Akaike information criterion ($\hbox {AIC}_c$) [66, 67] and the Bayesian information criterion (BIC) [68].

In the next step of this work, we examine how these fitting results impact the current acceleration of the universe by studying the evolution of the equation of state (EoS) and the cosmographic parameters [69,70,71]. The EoS parameter is a commonly used tool for characterizing dark energy in various models, as it describes the relationship between the pressure P and the energy density $\rho$ of the Universe. In the case of an accelerating expanding Universe, it can be classified into two models: (i) quintessence models, where the null energy condition $0 \le \rho +P$ is preserved, resulting in an EoS parameter always greater than −1 but less than −1/3; and (ii) phantom models, where the null energy condition is violated, allowing the EoS parameter to fall below −1 [10]. In this study, we incorporate an effective EoS parameter within the framework of f(Q) gravity to explain the present acceleration of the Universe for both cases. Various cosmographic parameters have been proposed for analyzing the early and late evolution of the Universe, including deceleration (q), jerk (j), and snap (s) [69, 70, 72]. These parameters describe the past history and the evolution of the scale factor a(t) through its derivatives, offering advantages in that they are not dependent on any model-specific assumptions. For geometric comparisons between models, we use the statefinder pairs $\left\{ r,s\right\}$ and $\left\{ r,q\right\}$ introduced by Sahni et al. in [69, 70].

In the last step of this work, we focus on the growth rate index of matter perturbations $\gamma$, which provides an effective approach for estimating the distribution of matter in the Universe and differentiating between modified gravity. The growth rate, f, can be approximated as $\Omega _m^\gamma$. In the $\Lambda$CDM model, the theoretical value of $\gamma$ is approximately $6 / 11 \simeq 0.545$ [73, 74]. However, in various parameterized dark energy models, $\gamma$ is around 0.55 [74], and for the flat DGP (Dvali–Gabadadze–Porrati) model, $\gamma = 11/16 \simeq 0.6875$ [73]. In certain f(R) gravity models, $\gamma$ can range from approximately 0.40 to 0.55 for different parameter values [76, 77], while in Finsler–Randers cosmology, $\gamma \approx 9/14$ [78]. For the f(T) gravity, the growth index $\gamma$ approaches 0.58 [79]. In the present work, the growth index is equal to 0.553 and 0.552 for linear and nonlinear f(Q) gravity, respectively.

The current paper is organized as follows. Firstly, in Sect. 2, we provide an introduction to f(Q) gravity. Next, in Sect. 3, we present the solution of the modified Friedman equations for f(Q). Moving on to Sect. 4, we describe three datasets RSD, CC, and Pantheon$^+$, and we discuss the use of the MCMC method to constrain the f(Q) model parameters. Additionally, in the same section, we present the mean values of cosmological parameters and the results of the information criteria, i.e., the corrected Akaike information criterion and the Bayesian information criterion. In Sect. 5, we examine the effective equation of state and the $\omega _{d}-{\omega _{d}}'$ plane. Section 6 focuses on the cosmography parameters and the statefinder diagnostic, while in Sect. 7 we explore the growth index $\gamma$ of the studied model. Finally, the paper concludes with a summary in Sect. 8.

2 Basic formalism of f(Q) gravity

The main focus of this study is on f(Q) modified gravity models, which are characterized by the non-metricity tensor [80]

$$\begin{aligned} Q_{\alpha \mu \nu }=\nabla _{\alpha }g_{\mu \nu } , \end{aligned}$$

(2.1)

where the non-metricity scalar Q is defined as

$$\begin{aligned} Q=-Q_{\alpha \mu \nu }P^{\alpha \mu \nu }. \end{aligned}$$

(2.2)

The non-metricity conjugate is represented by the tensor $P^{\alpha \mu \nu }$

$$\begin{aligned} P^{\alpha }_{ \mu \nu }=-\frac{1}{2}L_{\mu \nu }^{\alpha }+\frac{1}{4}\left( Q^{\alpha }-\tilde{Q}^{\alpha } \right) g_{\mu \nu }-\frac{1}{4}\delta ^{\alpha }_{(\mu }Q_{\nu )}, \end{aligned}$$

(2.3)

where $L_{\mu \nu }^{\alpha }=\frac{1}{2}Q_{\mu \nu }^{\alpha }-Q_{(\mu \nu )}^{\alpha }$, $Q_{\alpha }=g^{\mu \nu }Q_{\alpha \mu \nu }$ and $\tilde{Q}_{\alpha }=g^{\mu \nu }Q_{ \mu \alpha \nu }$.

The f(Q) modified gravity models under consideration are based on the following action [29]

(2.4)

From now on, we assume that $8\pi G = 1$ and $c=1$. In this expression, represents the Lagrangian for matter fields, G is the Newtonian constant, f(Q) is a general function of the non-metricity scalar, and g is the determinant of the metric tensor $g_{\alpha \beta }$. In flat spacetime, the action (2.4) is equivalent to general relativity for $f(Q)=Q$ [81]. The energy–momentum tensor can be expressed as

(2.5)

By varying the modified Einstein–Hilbert action (2.4) with respect to the metric tensor $g_{\alpha \beta }$, the gravitational field equations can be expressed as

$$\begin{aligned}&\frac{-2}{\sqrt{-g}}\Delta _{\alpha }(\sqrt{-g}f_{Q}P_{\mu \nu }^{\alpha })-\frac{1}{2}g_{\mu \nu }f-f_{Q}(P_{\mu \alpha i}Q_{\nu }^{\alpha i}-2Q_{\alpha i\mu }P^{\alpha i}_{\nu })\nonumber \\&\quad =T_{\mu \nu } , \end{aligned}$$

(2.6)

where $f_{Q}= \frac{\partial f}{\partial Q}$. The variation in the action (2.4) with respect to the connection can be formulated as

$$\begin{aligned} \nabla _{\mu }\nabla _{\nu }(\sqrt{-g}f_{Q}P^{\mu \nu }_{\alpha })=0 . \end{aligned}$$

(2.7)

To incorporate this modified gravity theory into cosmology, we consider the Friedmann–Lemaître–Robertson–Walker (FLRW) line element, which is described as

$$\begin{aligned} {\text {d}}s^2=-{\text {d}} t^2+a^2(t)\left[ {\text {d}} r^2+r^2\left( {\text {d}} \theta ^2+\sin ^2 \theta {\text {d}} \phi ^2\right) \right] , \end{aligned}$$

(2.8)

where a(t) is the scale factor and t represents the cosmic time. The non-metricity invariant Q, as defined in Eq. (2.2), is given by $Q = 6H^{2}$, where $H=\frac{\dot{a}}{a}$ represents the Hubble function and the dot denotes the derivative with respect to the cosmic time. We assume that the energy–momentum tensor is described by a perfect fluid, i.e.,

$$\begin{aligned} T_{\mu \nu }=\left( p+\rho \right) u_{\mu }u_{\nu }+P g_{\mu \nu } , \end{aligned}$$

(2.9)

where P denotes the pressure, and $\rho$ denotes the energy density.

Using Eqs. (2.8) and (2.9), we can derive the modified Friedmann equations for f(Q) gravity

$$\begin{aligned} 6H^{2}f_{Q}-\frac{1}{2}f= & {} \rho , \end{aligned}$$

(2.10)

$$\begin{aligned} \left( 12H^{2}f_{QQ}+f_{Q} \right) \dot{H}= & {} -\frac{1}{2}\left( \rho +P \right) , \end{aligned}$$

(2.11)

where $f_{QQ}= \frac{\partial ^{2} f}{\partial Q^{2}}$.

Within the framework of any dark energy model, including those involving modified gravity, it is widely acknowledged that on sub-horizon scales, the dark energy component is expected to be smooth. Therefore, we focus our consideration solely on perturbations in the matter component of the cosmic fluid. For a thorough analysis of calculations, we recommend referring to the comprehensive details provided in the references [82,83,84]. Moving to the perturbation level, one can derive the evolution equation for the matter overdensity at sub-horizon scales in terms of the cosmic time [36]

$$\begin{aligned} \ddot{\delta } _{m}+2H\dot{\delta } _{m}-\frac{4\pi G}{f_{Q}}\rho _{m}\delta _{m} =0, \end{aligned}$$

(2.12)

where $\delta =\frac{\delta \rho _{m}}{\rho _{m} }$. It is useful to express Eq. (2.12) in terms of the derivative with respect to ln(a), labeled by a prime, and using $\dot{\delta }=H{\delta }'$

$$\begin{aligned} \delta '' _{m}+\left( \frac{{H(x)}'}{H(x)}+2\right) \delta ' _{m}-\frac{\rho _{m}}{2 f_{Q} H(x)^2}\delta _{m}=0. \end{aligned}$$

(2.13)

3 The model solution

In this study, we propose a cosmological form of f(Q) motivated by Capozziello and D’Agostino in [38]

$$\begin{aligned} f(Q)=\alpha +\beta Q^{n}, \end{aligned}$$

(3.1)

where $\alpha$, $\beta$, and n are free parameters of the model. This model exhibits intriguing characteristics that establish connections with both general relativity and $\Lambda$CDM. More specifically, for $\alpha = 0$ and $\beta = n = 1$, the model corresponds to general relativity, while for $n = \beta = 1$ and $\alpha > 0$, it corresponds to the $\Lambda$CDM model. To solve the modified Friedmann equations (2.10) and (2.11), we narrow our focus on the scenario where matter dominates ($\rho =\rho _{m}$ and $P=P_{m}=0$). In this context, the dynamical equation, as presented in Eq. (2.11), describes the model’s dynamics as follows:

$$\begin{aligned} \dot{H}=-\frac{3 H^2}{2n}\left( \frac{\alpha 6^{-n} H^{-2n}}{\beta -2 \beta n}+1\right) . \end{aligned}$$

(3.2)

Indeed, the derivative of the Hubble parameter with respect to the cosmic time can be obtained using the conversion rule,

$$\begin{aligned} \frac{{\text {d}}H}{{\text {d}}t}=-\left( 1+z \right) H(z)\frac{{\text {d}}H}{{\text {d}}z}. \end{aligned}$$

(3.3)

The dynamic of Eq. (3.2) can be transformed to the form

$$\begin{aligned} \frac{{\text {d}}H}{d{\text {d}}z}-\frac{3 H }{2 n (z+1)}\left( \frac{\alpha 6^{-n} H^{-2n}}{\beta -2 \beta n}+1\right) =0. \end{aligned}$$

(3.4)

Using the current value of the Hubble parameter, $H(z =0)= H_{0}$, we derive the following subsequent solution

$$\begin{aligned} H(z)=\left( \frac{(z+1)^3 \left( H_{0}^{2 n} (\beta -2 \beta n)+\alpha 6^{-n}\right) -\alpha 6^{-n}}{\beta -2 \beta n}\right) ^{\frac{1}{2 n}}. \end{aligned}$$

(3.5)

The corresponding normalized Hubble parameter, denoted as $E^{2}\left( z \right) =H^{2}(z)/ H^{2}_{0}$, can be expressed as follows:

$$\begin{aligned} E^{2}\left( z \right) =\left[ \left( \frac{6^{-n} 3 \Omega _{\alpha }}{\beta -2 \beta n}+1\right) (z+1)^3-\frac{6^{-n} 3 \Omega _{\alpha }}{\beta -2 \beta n} \right] ^{1/n}, \end{aligned}$$

(3.6)

where we have defined the dimensionless quantity $\Omega _{\alpha }$ as $\Omega _{\alpha }=\frac{\alpha }{3H_{0}^{2n}}$. In the linear case where $n=1$, and by analogy with the standard model, we can recognize that $\Omega _{m}=1-\frac{\Omega _{\alpha }}{2\beta }$ and $\Omega _{\Lambda }=\frac{\Omega _{\alpha }}{2\beta }$, where $\Omega _{m}$ and $\Omega _{\Lambda }$ represent the critical density of matter and dark energy, respectively. This specific case is referred to as “case I” throughout the article. On the other hand, “case II” represents the nonlinear form of f(Q), expressed as $f(Q) = \alpha + \beta Q^n$.

4 Observational data and likelihood analysis

4.1 Methodology

In this subsection, we provide a brief overview of the Markov chain Monte Carlo (MCMC) technique used to constrain our model. MCMC is frequently used in the field of cosmology for exploring the parameter space of complex models and generating probability distributions for cosmological parameters [65]. The fundamental concept behind MCMC is to create a Markov chain that samples the parameter space of a model based on a probability distribution. This chain comprises a series of parameter values, with each value generated from the preceding one using a set of transition rules that are guided by a proposal distribution [85, 86]. In our analysis, we use three observational datasets, namely the redshift space distortion, the cosmic chronometers, and the Pantheon$^+$ dataset, which consist of 20, 36, and 1701 data points, respectively. Additionally, we perform the fit using various information criteria. The analysis focuses on the following cases:

• Case I: Linear form with the free parameters $\{ \sigma _8, H_{0}, M, \Omega _{\alpha }, \beta \}$.

• Case II: Nonlinear form with the free parameters $\{\sigma _8, H_{0}, M,\Omega _{\alpha }, \beta , n\}$,

where $\sigma _8$ and M represent the amplitude of the matter power spectrum and the absolute magnitudes, respectively. The mean values of the model parameters $\Omega _{\alpha }$, $\beta$, and n are determined by minimizing the chi-square $\chi ^{2}$ or maximizing the likelihood function $\mathcal {L}$. The total likelihood function $\mathcal {L}_{\text {tot}}$ is defined as

$$\begin{aligned} \mathcal {L}_{\text {tot}} \propto e^{-\chi _{tot}^2/2} . \end{aligned}$$

(4.1)

Additionally, the expressions for $\mathcal {L}_{tot}$ and $\chi ^{2}_{\text {tot}}$ are given as

$$\begin{aligned} \mathcal {L}_{\text {tot}}=\mathcal {L}_{\text {RSD}}\times \mathcal {L}_{\text {CC}}\times \mathcal {L}_{\text {Pantheon}^+}, \end{aligned}$$

(4.2)

and

$$\begin{aligned} \chi ^{2}_{\text {tot}}=\chi _{\text {RSD}}^{2}+\chi _{\text {CC}}^{2}+\chi _{\text {Pantheon}^+}^{2} , \end{aligned}$$

(4.3)

respectively.

4.2 Datasets

4.2.1 RSD dataset

Table 1 The data in this table present measurements of $f\sigma _{8}$ obtained from various independent surveys

We consider the more consistent and reliable value derived from redshift surveys, namely the product of the growth rate f(z) and the amplitude of the matter power spectrum $\sigma _8(z)$. This cosmological probe, $f \sigma _8(z) \equiv f(z) \sigma _8(z)$, is almost model-independent and results from the study of distortions in redshift space, where $\sigma _8(z)= \sigma _{8} \delta (z) / \delta _0$ [88,89,90]. In this article, we use $f\sigma _{8}$ data from Table 1 comprising 20 data points. The $\chi ^{2}_{\text {RSD}}$ function is defined as

$$\begin{aligned}&\chi ^{2}_{\text {RSD}}\left( \Omega _{\alpha },\beta ,n,\sigma _{8} \right) \nonumber \\&\quad =\sum _{i=1}^{20}\left( \frac{f\sigma _{8,i}-f\sigma _{8}(z_{i},\Omega _{\alpha },\beta ,n,\sigma _{8})}{\sigma (z_{i})} \right) ^{2}. \end{aligned}$$

(4.4)

In this expression, $\sigma (z_{i})$ represents the standard error associated with the observed value of $f\sigma _{8}$. The terms $f\sigma _{8,i}$ and $f\sigma _{8}(z_i)$ correspond to the observed and theoretical values of $f\sigma _{8}$, respectively. The growth rate is expressed as [87]

$$\begin{aligned} f\sigma _{8}\left( z_{i},\Omega _{\alpha },\beta ,n,\sigma _{8} \right) =\sigma _{8}\frac{\delta '_{m}{\left( z_{i},\Omega _{\alpha },\beta ,n\right) }}{\delta _{m}\left( z=0 \right) } , \end{aligned}$$

(4.5)

where a prime denotes the derivative with respect to $\text {ln(a)}$. The quantity $\sigma _{8}$ stands for the amplitude of the matter power spectrum at the scale of 8 h$^{-1}$ Mpc at the present time, i.e. $z=0$. It is directly connected to the amplitude of the primordial fluctuations and is determined by the growth rate of cosmological fluctuations [91]. The values $\delta '_{m}(z)$ and $\delta _{m}(0)$ are obtained by numerically solving Eq. (2.12) for a given set of cosmological parameters. This theoretical prediction may now be used to constrain, via $f\sigma _{8}$ data, the parameters $\sigma _8$, $\Omega _{\alpha }$, $\beta$, and n in the context of our f(Q) model solution (Eq. 3.5).

Table 2 Measurements of the Hubble expansion, with the corresponding H(z) data used in our analysis expressed in units of km s$^{-1}$ Mpc$^{-1}$

4.2.2 CC dataset

To improve the robustness of our analysis, we incorporate the cosmic chronometers as an additional dataset, imposing more stringent constraints. The Hubble rate can be determined by two methods: detecting baryon acoustic oscillations in the radial direction by examining the clustering of galaxies/quasars, or utilizing the differential age approach, which represents the Hubble parameter as the rate of redshift change.

$$\begin{aligned} H(z)=-\frac{1}{1+z}\frac{{\text {d}}z}{{\text {d}}t} . \end{aligned}$$

(4.6)

By employing the aforementioned methods, a compilation of 36 data points for the Hubble parameter H(z) in the redshift range of $0.07 \le z\le 2.36$ is obtained and is presented in Table 2. The chi-square value for the cosmic chronometers is calculated according to the following definition:

$$\begin{aligned}&\chi ^{2}_{CC}\left( \Omega _{\alpha },\beta ,n,H_{0} \right) \nonumber \\&\quad =\sum _{i=1}^{36}\left[ \frac{H_{obs}\left( z_{i} \right) -H_{th}\left( z_{i},\Omega _{\alpha },\beta ,n,H_{0} \right) }{\sigma \left( z_{i} \right) } \right] ^{2} , \end{aligned}$$

(4.7)

where $H_{\text {obs}}$ and $H_{\text {th}}$ denote the observed and the theoretical value of the Hubble parameter, respectively. On the other hand, $\sigma \left( z_{i} \right)$ corresponds to the error on the observed values of the Hubble parameter H(z).

Table 3 Summary of the mean values and standard deviations of the cosmological parameters for $\Lambda$CDM, case I, and case II

Fig. 1

The $1\sigma$ and $2\sigma$ confidence contours and the posterior distributions obtained from the RSD+CC+Pantheon$^+$ datasets for case I

Fig. 2

The $1\sigma$ and $2\sigma$ confidence contours and the posterior distributions obtained from the RSD+CC+Pantheon$^+$ datasets for case II

4.2.3 Pantheon$^+$ dataset

We include the Pantheon$^+$ compilation supernovae dataset [64] as our final data source. These datasets, comprising 1701 data points, are obtained from 1550 type Ia supernovae spanning a redshift range of $0.001\le z\le 2.3$. The $\chi ^{2}$ function for the supernovae datasets is given by

$$\begin{aligned} \chi _{\text {Pantheon}^+}^{2}\left( \Omega _{\alpha },\beta ,n,M,H_{0}\right) = \vec {F}^T \cdot \textbf{C}_{\text {Pantheon}^+}^{-1} \cdot \vec {F} , \end{aligned}$$

(4.8)

where $\textbf{C}_{\text {Pantheon}^+}$ represents the covariance matrix obtained from the Pantheon$^+$ dataset, accounting for both statistical and systematic uncertainties. In this equation, $\vec {F}=m_{B i}-M-\mu _{\text {model }}$, with $m_{Bi}$ and $\mu _{model}$ denoting the apparent magnitudes and the predicted distance modulus, respectively. The predicted distance modulus is given according to a selected cosmological model, as follows:

$$\begin{aligned}&\mu _{\text {model}}(z_{i},\Omega _{\alpha },\beta ,n,H_{0}) \nonumber \\&\quad =5\log _{10}D_{L}(z_{i},\Omega _{\alpha },\beta ,n,H_{0}) + 25, \end{aligned}$$

(4.9)

where $D_{L}$ denotes the luminosity distance, defined as

$$\begin{aligned}&D_{L}\left( z_{i},\Omega _{\alpha },\beta ,n,H_{0}\right) \nonumber \\&\quad =\left( 1+z\right) \int _{0}^{z}{\frac{c {\text {d}}z'}{H\left( z',\Omega _{\alpha },\beta ,n,H_{0}\right) }}, \end{aligned}$$

(4.10)

where c represents the speed of light. In contrast to the Pantheon dataset, the Pantheon$^+$ dataset introduces a break in the degeneracy between the absolute magnitude M and the Hubble constant $H_{0}$. This is attained by rewriting the vector $\vec {F}$ in Eq. (4.8) in terms of the distance modulus of SNIa in Cepheid hosts. This gives rise to an independent constraint on M, resulting in the following expression:

$$\begin{aligned} \vec {F}_i^{\prime }=\left\{ \begin{array}{ll} m_{B i}-M-\mu _i^{\text {Ceph }} &{} i \in \text { Cepheid hosts } \\ m_{B i}-M-\mu _{\text {model }}\left( z_i\right) &{} \text { otherwise } \end{array}\right. \end{aligned}$$

(4.11)

where $\mu _i^{\text {Ceph }}$ denotes the distance modulus associated with the Cepheid host of the ith SNIa, independently measured by Cepheid calibrators. Consequently, Eq. (4.8) can be rewritten as

$$\begin{aligned} \chi _{\textrm{SN}}^2=\vec {F}^{\prime T} \cdot \textbf{C}_{\text {Pantheon }^+}^{-1} \cdot \vec {F}^{\prime } \end{aligned}$$

(4.12)

4.3 Statistical results

4.3.1 Cosmological parameters

In Table 3, we present the mean values and their associated errors at 1$\sigma$ (68% confidence level, CL) for the studied models, namely $\Lambda$CDM, case I, and case II, using the data combinations RSD, RSD+CC, and RSD+CC+Pantheon$^+$. For the $\Lambda$CDM model, the free parameter vector $P_{\Lambda CDM}$ consists of $(\Omega _{m}, \sigma _8, H_{0}, M)$. In case I, the free parameter vector $P_{I}$ includes $(\Omega _{\alpha },\beta , \sigma _8, H_{0}, M)$, while in case II, the vector $P_{II}$ includes $(\Omega _{\alpha },\beta , n, \sigma _8, H_{0}, M)$. It is worth noting that the number of free parameters $N_{p}$ varies among the three models.

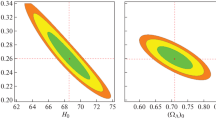
Additionally, Figs. 1 and 2 illustrate the confidence contour plots in two dimensions (2D) for the model parameters in case I and case II, respectively, based on the RSD+CC+Pantheon$^+$ datasets. These plots visually represent the correlations and uncertainties among the parameters within each case, at the 1$\sigma$ and 2$\sigma$ confidence levels. Specifically, we observe a positive correlation between M and $H_{0}$ as well as between $\Omega _{\alpha }$ and $\beta$ in both cases. On the other hand, a negative correlation is found between the parameters n and $\sigma _{8}$ in case II.

Constraining $\Lambda$CDM, case I, and case II with RSD+CC+Pantheon$^+$ datasets, we obtain $\sigma _{8}=0.805\pm 0.025$, $H_{0}= 71.46\pm 0.76$ km/s/Mpc, and $M=-19.320\pm 0.021$ mag for $\Lambda CDM$. In addition, we obtain $\sigma _8=0.804 \pm 0.025$ $(\sigma _8= 0.761\pm 0.027$), $H_{0}=71.38 \pm 0.86$ km/s/Mpc $(H_{0}=71.65 \pm 0.84$ km/s/Mpc), and $M=-19.325\pm 0.024$ mag $(-19.308\pm 0.024$ mag) for case I (case II). In addition, in case I, the parameter values obtained are $\Omega _{\alpha }=0.69_{-0.13}^{+0.27}$ and $\beta =0.484_{-0.095}^{+0.190}$. Moving on to case II, the obtained values are $\Omega _{\alpha }=0.751_{-0.094}^{+0.210}$, $\beta =0.336_{-0.070}^{+0.089}$, and $n=1.167_{-0.063}^{+0.054}$.

4.3.2 Comparison with the data points

We use the mean values obtained previously (Table 3) to assess the alignment of our model’s prediction with observational data in both the background (CC+Pantheon$^+$) and perturbation (RSD) levels.

• Comparison with RSD dataset:

Initially, we compare each case to the 20-redshift-space distortion dataset, along with its $1\sigma$ error bands, and the $\Lambda$CDM model. The results of this comparison are presented in Fig. 3. This figure clearly illustrates the effective alignment of each case with the RSD measurements.

• Comparison with CC dataset:

Then, we compare each case with the 36-cosmic-chronometer dataset and with their 1$\sigma$ error bands, and the $\Lambda$CDM model. The results of this comparison are presented in Fig. 4, where it is clearly demonstrated that each model provides a precise fit to the CC measurements.

• Comparison with Pantheon$^+$ dataset:

Lastly, each case is compared with the 1701 Pantheon$^+$ dataset and with their 1$\sigma$ error bands, and the $\Lambda$CDM model. These comparison findings are shown in Fig. 5. One can see that each case matches the Pantheon$^+$ dataset quite well.

4.3.3 Information criteria

Due to the different numbers of cosmological parameters among the three models, the $\chi ^{2}_{min}$ statistic cannot be regarded as an optimal criterion for selecting the best models. To compare a set of cosmological models based on their theoretical predictions using various observational data, we employ three criteria: the reduced chi-square $\chi _{red}^{2}$, the corrected Akaike information criterion [66], and the Bayesian information criterion [68]. These criteria are respectively defined as follows:

$$\begin{aligned} \chi _{red}^{2}= & {} \frac{-2\ln \mathcal {L}_{max}}{N_{d}-N_{p}}, \end{aligned}$$

(4.13)

$$\begin{aligned} AIC_{c}= & {} -2\ln \mathcal {L}_{max}+2N_{p}+\frac{2N_{p}\left( N_{p}+1 \right) }{N_{d}-N_{p}-1}, \end{aligned}$$

(4.14)

and

$$\begin{aligned} BIC=-2\ln \mathcal {L}_{max}+N_{p}\log \left( N_{d} \right) . \end{aligned}$$

(4.15)

Here, $\chi _{min}^{2}=-2\ln \mathcal {L}_{max}$ corresponds to the maximum likelihood, $N_{d}$ represents the total number of data points, which is equal to 1757, and $N_{p}$ represents the number of free parameters. In practice, when comparing models, the one with the lowest values of $\hbox {AIC}_{c}$ and BIC is considered to be the one preferred by data. The $AIC_{c}$ and BIC values for all studied models can be found in Table 4.

Fig. 3

Error bar plots of 20 data points from the $f\sigma _8$ datasets, showing the fitting of the $f\sigma _8$ function with respect to redshift z for cases I and II, alongside a comparison to the $\Lambda$CDM model

Fig. 4

Error bar plots of 36 data points from the cosmic chronometers datasets, including the fitting of Hubble function H(z) versus redshift z for cases I and II, along with a comparison to the $\Lambda$CDM model

Fig. 5

Error bar plots of 1701 data points from the Pantheon$^+$ datasets, showing the fitting of the $\mu (z)$ function with respect to redshift z for cases I and II, alongside a comparison to the $\Lambda$CDM model

Table 4 Information criteria $\chi _{red}^{2}$, $AIC_{c}$, and BIC for $\Lambda$CDM, case I, and case II, along with the corresponding differences $\Delta AIC=AIC_{c}{_{\text {model}}}-AIC_{c}{_{\Lambda \text {CDM}}}$ and $\Delta BIC=BIC_{\text {model}}-BIC_{\Lambda \text {CDM}}$

In Table 4, we summarize the statistical analysis performed to determine the quality of our fit and the statistical significance of the studied models. The $\hbox {AIC}_{c}$ and BIC must be used as long as the number of free parameters differs from one model to another, i.e. case I ($N_p=5$), case II ($N_p=6$), and $\Lambda$CDM ($N_p=4$). According to the $\hbox {AIC}_{c}$ criterion, case II is the most preferred, followed by $\Lambda$CDM and then case I. On the other hand, the BIC criterion indicates that $\Lambda$CDM is most supported by observations, followed by case II and finally case I. Moreover, in the $\hbox {AIC}_{c}$ analysis, the $\Lambda$CDM model is kept as the reference model even if it does not correspond to the lowest value of $\hbox {AIC}_c$, which explains the negative value $\Delta \hbox {AIC}=-4.49$.

To compare between the two cases, we find that $\Delta \hbox {AIC}_{\text {case II}} <\Delta \hbox {AIC}_{\text {case I}}$ and $\Delta \hbox {BIC}_{\text {case II}}<\Delta \hbox {BIC}_{\text {case I}}$, which means that case II is preferred over the case I model.

5 EoS parameter and $\omega _{d}-{\omega _{de}}'$ plane

The equation of state parameter is a useful tool for investigating the properties of dark energy models. It is defined as $\omega _{de}=\frac{P_{de}}{\rho _{de}}$, where P represents the pressure and $\rho$ represents the energy density of the Universe. For a cosmic acceleration to occur, the value of $\omega _{de}$ needs to be less than $-\frac{1}{3}$, while for the $\Lambda$CDM model, $\omega _{de}=-1$. In the case of dynamical dark energy (DE) models such as quintessence, the range is $-1< \omega _{de} <-\frac{1}{3}$, whereas for phantom energy, $\omega _{de}< -1$.

Observing the form of Eqs. (2.10) and (2.11), we deduce that it is possible to define an effective dark energy sector with energy density and pressure $\rho =\rho _m+\rho _{de}$ and $P=P_m+P_{de}$, respectively.

$$\begin{aligned} 3H^{2}= & {} \rho _{m}+\rho _{de}, \end{aligned}$$

(5.1)

$$\begin{aligned} \dot{H}+H^{2}= & {} -\frac{1}{6}(\rho _{m}+\rho _{de}+3P_{de}), \end{aligned}$$

(5.2)

where $\rho _{de}$ ($P_{de}$) and $\rho _{m}$ ($P_{m}=0$) are the effective dark energy density (effective pressure) and the matter energy density (pressure), respectively. The explicit expressions of $\rho _{de}$ and $P_{de}$ are respectively as follows:

$$\begin{aligned} \rho _{de}= & {} 3 H_{0}^{2}\bigg [ \big ((\Omega _Q+1)(z+1)^3-\Omega _Q\big ){}^{1/n}\nonumber \\{} & {} - \left( \Omega _Q+1\right) (z+1)^3 \bigg ] \end{aligned}$$

(5.3)

and

$$\begin{aligned} P_{de}= & {} 3 H_{0}^{2}\left[ \frac{\left( \Omega _Q+1\right) }{n}(z+1)^3 \left( (\Omega _Q+1)(z+1)^3-\Omega _Q\right) ^{\frac{1}{n}-1}\right. \nonumber \\{} & {} \left. -\left( (\Omega _Q+1)(z+1)^3-\Omega _Q\right) {}^{1/n} \right] , \end{aligned}$$

(5.4)

where $\Omega _{Q}=\frac{3\ \Omega _{\alpha }}{6^{n} \beta (1-2n) }$. Consequently, the effective equation of state can be formulated as

$$\begin{aligned} \omega _{de}=-\frac{2(\dot{H}+H^{2})+\frac{1}{3}\rho _m}{3H^{2}-\rho _{m}}-\frac{1}{3} , \end{aligned}$$

(5.5)

Fig. 6

Evolution of the effective EoS parameter as functions of the redshift variable z

Fig. 7

Evolutionary trajectories of $\omega _{d}-{\omega _{d}}'$ plane

The behavior of the EoS parameter is depicted in Fig. 6 for both case I and case II using the value obtained from RSD+CC+Pantheon$^+$ datasets. It is clear that the EoS parameter of case I exhibits the same behavior as the $\Lambda$CDM model, while in case II, it behaves as a phantom dark energy one with $\omega _{de}=-1.083$ which leads to the current cosmic acceleration. Additionally, to analyze the impact of the parameter n on the model, we also consider the case where $n=0.99$, which is rejected by observational data. This case is shown in the same figure and falls within the quintessence region, with $\omega _{de}=-0.996$.

The $\omega _{de}-{\omega _{de}}'$ plane, which was initially proposed by Caldwell and Linder [93], is depicted in Fig. 7 for both case I and case II, where ${\omega _{de}}'$ represents the first derivative of $\omega _{de}$ with respect to $\text {ln(a)}$. This plane can be divided into two regimes based on the value of ${\omega _{de}}'$: a thawing regime where ${\omega _{de}}'>0$, and a freezing regime where ${\omega _{de}}'<0$. The fixed point $(\omega _{de}=-1,{\omega _{de}}'=0)$ corresponds to the $\Lambda$CDM model, which is also associated with case I and represented by a star. The arrows indicate the time evolution. Notably, case II evolves within the thawing region, while the $n=0.99$ case evolves within the freezing region.

6 Dynamical analysis of the model

6.1 Cosmographic parameters

The goal of this study is to assess a cosmological model that can effectively depict the overall dynamics of the Universe by analyzing its physical and geometric parameters on a large scale. Consequently, it is appropriate to use the Taylor series expansion of a(t) around the present time $t_{0}$.

$$\begin{aligned} \frac{a(t)}{a_{0}}&= 1 + \frac{(t-t_{0})}{1!}\frac{{\text {d}}a}{{\text {d}}t}\Big |_{t_{0}} + \frac{(t-t_{0})^{2}}{2!}\frac{{\text {d}}^{2}a}{{\text {d}}t^{2}}\Big |_{t_{0}}\nonumber \\&\quad + \frac{(t-t_{0})^{3}}{3!}\frac{{\text {d}}^{3}a}{{\text {d}}t^{3}} + \frac{(t-t_{0})^{4}}{4!}\frac{{\text {d}}^{4}a}{{\text {d}}t^{4}} + \ldots \end{aligned}$$

(6.1)

where $a_{0}$ is the current value of the scale factor. The significant terms that define the series expansion above are

$$\begin{aligned} H&= \frac{1}{a}\frac{{\text {d}}a}{{\text {d}}t},&q(t) = -\frac{1}{aH^{2}}\frac{{\text {d}}^{2}a}{{\text {d}}t^{2}} , \end{aligned}$$

(6.2)

$$\begin{aligned} j(t)&= \frac{1}{aH^{3}}\frac{{\text {d}}^{3}a}{{\text {d}}t^{3}},&s(t) = \frac{1}{aH^{4}}\frac{{\text {d}}^{4}a}{{\text {d}}t^{4}}, \end{aligned}$$

(6.3)

which are usually known as the Hubble, deceleration, jerk, and snap parameters, respectively. These four geometrical quantities are sufficient to study the overall dynamics of the Universe. For this purpose, we give the specific expressions of these parameters using the redshift z [94, 95]

$$\begin{aligned} q(z)= & {} -1+(1+z)\frac{{E}'(z)}{E(z)}, \end{aligned}$$

(6.4)

$$\begin{aligned} j(z)= & {} (1+z)^{2}\frac{{E}''(z)}{E(z)}+q^{2}(z), \end{aligned}$$

(6.5)

$$\begin{aligned} s(z)= & {} -(1+z){j}'(z)-2j\left( z \right) -3q(z)j(z). \end{aligned}$$

(6.6)

Fig. 8

Evolution of the deceleration parameter q(z) as functions of the redshift variable z

Fig. 9

Evolution of the jerk parameter j(z) as functions of the redshift variable z

Fig. 10

Evolution of the snap parameter s(z) as functions of the redshift variable z

First, we examine the evolutionary behavior of the cosmography parameters by employing the previously determined mean value, obtained through the combination of RSD+CC+Pantheon$^{+}$ datasets (see Table 3). Figure 8 illustrates the evolution of the deceleration parameter q as a function of redshift z for three scenarios: $\Lambda$CDM, case I, and case II. This parameter measures the rate at which the expansion of the Universe slows. A positive value of q indicates a standard decelerating model, while a negative value suggests accelerating expansion behavior. It is worth noting that case I closely resembles the behavior of $\Lambda$CDM at both high and low redshifts, experiencing a transitional phase at $z=0.718$. Similarly, case II exhibits behavior similar to both $\Lambda$CDM and case I only at low redshifts, with a transition occurring at $z=0.7897$. In all cases, the Universe finally enters a de Sitter phase characterized by $q=-1$. The present values of the deceleration parameter are $q_{0}= -0.576$ $(q_{0}= -0.512$) for case I (case II), respectively.

Figure 9 displays the evolution of the jerk parameter j as a function of redshift z. Notably, in the $\Lambda$CDM model, the jerk parameter remains constant at $j = 1$. Similarly to $\omega _{de}$ and q, both $\Lambda$CDM and case I exhibit identical behavior at both high and low redshifts. However, the trajectory of case II demonstrates a decreasing trend with respect to z. The present values of the jerk parameter are $j_{0}=1$ $(j_{0}= 0.92$) for case I (case II), respectively.

In addition, the redshift evolution of the snap parameter s(z) in case I, case II, and $\Lambda$CDM is plotted in Fig. 10. In the $\Lambda$CDM model, the snap parameter remains fixed at $s=0$. Unlike $\omega _{de}$, q, and j, the snap parameter s breaks the similarity between case I and the $\Lambda$CDM model. The present values of the snap parameter are $s_{0}=-1.273$ ($s_{0}=-1.347$) for case I (case II), respectively.

6.2 Statefinder diagnostic

The so-called statefinder diagnostic technique is widely employed to distinguish and compare different models of dark energy, using higher-order derivatives of the scale factor. This technique involves the use of the cosmological statefinder diagnostic pair $\left\{ r,s \right\}$, which allows for the examination of the cosmic properties of DE in a model-independent way. The statefinder parameters are defined as [69, 70]

$$\begin{aligned} r= & {} {\frac{\dddot{a}}{aH^{3}}}, \end{aligned}$$

(6.7)

$$\begin{aligned} s= & {} \frac{r-1}{3\left( q-\frac{1}{2} \right) }. \end{aligned}$$

(6.8)

Fig. 11

The evolutionary trajectory of the $\left\{ s,r \right\}$ plane for case I, case II, and for $n=0.99$. The statefinder of the $\Lambda$CDM model is a fixed point and is indicated by a star symbol, and the solid points indicate the present values

Fig. 12

The evolutionary trajectory of the $\left\{ q, r \right\}$ plane for case I and case II

The trajectories in the $\left\{ s,r \right\}$ plane play a significant role in classifying distinct cosmological regions. For instance, in this plane, the $\Lambda$CDM model is characterized by the point $(r = 1, s = 0)$, the holographic DE model is represented by $(r = 1, s = \frac{2}{3})$, the phantom region is associated with $(r > 1, s < 0)$, and the quintessence region is identified by $(r < 1, s > 0)$.

Figure 11 shows the evolutionary trajectory for both case I and case II. The star represents the $\Lambda$CDM model, and the arrows indicate the time evolution. In both cases, the evolution starts from the phantom region and moves towards the quintessence region. However, in case II, the evolutionary trajectory eventually returns to the phantom region in the future $(z\longrightarrow -1)$. At the present time, i.e. $z=0$, both cases exhibit behavior within the phantom region. Additionally, the evolutionary trajectory for case $n=0.99$ is depicted in the same figure. It is worth noting that the parameter n can influence the behavior of the model $f(Q)=\alpha +\beta Q^n$, which can exhibit quintessence-like behavior when $n<1$ or phantom-like behavior when $n\ge 1$.

Figure 12 represents the plane $\left\{ r,q \right\}$ for cases I and II. It is evident that in the decelerating phase, case I initiates its evolution from the point $(q = 0.5, r=1)$, representing a matter-dominated Universe. Conversely, during the accelerating phase, both cases I and II end their evolution near the steady-state cosmology at $(q = -1, r = 1)$.

7 Growth index

An alternative method for determining the growth factor f without the need to solve Eq. (2.13) is by employing an approximation, i.e., by specifying a growth index parameterization form, which is defined in relation to $\Omega _m$ as follows [96, 97]:

$$\begin{aligned} f(z)\simeq \Omega _m^{\gamma }(z), \end{aligned}$$

(7.1)

where the fractional energy density of matter is given by

$$\begin{aligned} \Omega _m(z) \equiv \frac{ \rho _m}{3 H^2}=\frac{\Omega _{m 0}(1+z)^3}{E^2(z)}, \end{aligned}$$

(7.2)

and $\gamma$ represents the growth index parameter expressed by a parameterization. In the context of general relativity, when considering dark energy scenarios with a constant equation of state parameter $\omega _{de}$, the growth index can be accurately approximated by $\gamma \simeq \frac{3(\omega _{de}-1)}{6 \omega _{de}-5}$ [32, 98,99,100]. This approximation converges to 6/11 for the specific case of the $\Lambda$CDM model $(\omega _{de}=-1)$. In this study, we examine the widely recognized functional form $\gamma (z) = \gamma _0 + \gamma _1 y(z)$ proposed by Wang and Steinhardt in [100], where the variables y(z), $\gamma _0$, and $\gamma _1$ are defined as

$$\begin{aligned} y(z)= & {} 1-\Omega _m(z), \end{aligned}$$

(7.3)

$$\begin{aligned} \gamma _0= & {} \frac{3\left( 1-\omega _{de}(z)\right) }{5-6 \omega _{de}(z)}, \end{aligned}$$

(7.4)

and

$$\begin{aligned} \gamma _1=\frac{3}{125} \frac{\left( 1-\omega _{de}(z)\right) \left( 1-\frac{3}{2}\omega _{de}(z)\right) }{\left( 1- \frac{6}{5}\omega _{de}(z)\right) ^3}, \end{aligned}$$

(7.5)

respectively.

Table 5 Summary of the present-day values of $\omega _{de}$, $q_{0}$, $j_{0}$, $s_{0}$, and $\gamma$ parameters for case I and case II using the RSD, CC, and Pantheon$^+$ datasets

Fig. 13

The evolution of $\gamma$ for $f(Q)=\alpha +\beta Q^n$ as a function of parameter n; the red line $\gamma =6/11$ corresponds to the $\Lambda$CDM model

Fig. 14

The evolution of growth index $\gamma$ against redshift z for $\Lambda$CDM, case I, and case II

In the last part of this paper, we analyze the growth index using the best-fit value obtained through the numerical resolution of Eq. 2.12 with the RSD+CC+Pantheon+ datasets, as well as by employing the parameterization form of the growth index. We present the results of our analysis by plotting the growth index as a function of a parameter n and comparing it with the theoretical growth index of the $\Lambda$CDM model. Figure 13 illustrates this comparison, demonstrating that for the $f(Q) = \alpha + \beta Q^n$ model, the growth index consistently exhibits greater values relative to the $\Lambda$CDM model only for $0.7<n<1.3$. Notably, when $n=0.7$ or $n=1.3$, the growth index recovers the standard value of 6/11 corresponding to the $\Lambda$CDM model.

To further investigate the behavior of the growth index, we examine its evolution with redshift z for different cases in Fig. 14. Our findings reveal distinct trends between the two cases. In case I, the growth index shows a smooth deviation both in the low redshift region and in the future from the theoretical value of $\Lambda \textrm{CDM}$. However, we observe good agreement between $\Lambda \textrm{CDM}$ and case I at high redshift $\Omega _m(z) \simeq 1$, where $\gamma _{\infty } \simeq \gamma _0 \simeq 6/11$. Additionally, case I closely resembles the behavior of case II in the future. Conversely, in case II, the growth index demonstrates a decreasing trend with increasing redshift, indicating a weaker growth rate of density perturbations at earlier cosmic times.

The present values of the growth index parameter are $\gamma = 0.553$ for case I and $\gamma = 0.550$ for case II. Comparing these results, we find that the values for case I and case II are in good agreement with the $\Lambda$CDM model ($\gamma = 6/11$), with differences of 1.47% and 0.92%, respectively.

8 Conclusions

In this study, we used observational data from RSD, CC, and Pantheon$^+$ datasets to constrain the f(Q) gravity theory. By solving the modified Friedmann equations for the specific scenario of dust matter and considering the form of $f(Q)=\alpha +\beta Q^{n}$, we examined linear $(n=1)$ and nonlinear cases. Our analysis yielded the following values: for case I, $\Omega _{\alpha }=0.69_{-0.13}^{+0.27}$ and $\beta =0.485_{-0.095}^{+0.190}$, while for case II, $\Omega _{\alpha }=0.751_{-0.094}^{+0.210}$, $\beta =0.336_{-0.070}^{+0.089}$, and $n=1.167_{-0.063}^{+0.054}$. Based on the $AIC_{c}$ and BIC criteria, we conclude that the nonlinear form (case II) is preferred over the linear form (case I) using these three datasets.

We also examined the effective equation of state parameter, finding $\omega =-1$ ($\omega =-1.083$) for case I (case II). This indicates that case I aligns with the $\Lambda$CDM value, while case II evolves in the phantom region $(\omega <-1)$. Furthermore, we analyzed the $\omega _{de}-{\omega _{de}}'$ plane and observed that case II evolves in the thawing region.

To gain insight into the dynamics and the behavior of our model, we analyzed cosmography parameters, including deceleration q, jerk j, and snap s. We found that case I behaves similarly to the $\Lambda$CDM model in terms of q and j, but the snap parameter breaks this degeneracy. In contrast, for the model $f(Q)=\alpha +\beta Q^n$ (case II), we observed a transition from a decelerating to an accelerating phase at redshift $z=0.789$. We also employed the statefinder diagnostic to further investigate the behavior of each case, and our analysis demonstrates that both cases exhibit phantom-like behavior in the present epoch. In addition, we explored the impact of the n parameter on the model and found that if $(n\ge 1)$, the model behaves as a phantom, while for $(n<1)$, it behaves as quintessence. The lifting of the degeneracies between case I and $\Lambda$CDM at the snap parameter opens a new perspective to examine other theories of modified gravity in this line.

Finally, we adopted an alternative method to determine the cosmic growth factor f by relating it to $\Omega _m$, i.e., using the best-fit values of the parameters obtained previously. Our results consistently show that in a modified gravity model ($f(Q)=\alpha +\beta Q^{n}$), the growth factor had greater values relative to the $\Lambda$CDM model only for $0.7<n<1.3$. However, when $n=0.7$ or $n=1.3$, the growth index recovered the standard value of 6/11. The evolution of the growth factor with redshift depended on the parameter n: it either remained constant (case I) or exhibited a decreasing trend (case II), indicating a weaker growth rate of density perturbations at earlier cosmic time. We found that the present values of the growth index parameter are $\gamma = 0.553$ ($\gamma = 0.550$) for case I and case II, respectively. For greater precision in determining the $\gamma$ value, future efforts will be dedicated to constraining the $\gamma$ parameter of our f(Q) model by treating it as a free parameter through MCMC analysis. Another research area worth exploring is obtaining the Newtonian and the post-Newtonian approximations of the present f(Q) gravity. Additionally, it is crucial that studies investigate the limitations imposed by local gravity at the solar system level on the theory and determine how these constraints impact the free parameters. Furthermore, assessing the compatibility of these constraints with cosmological observations is an important aspect of this exploration. The Newtonian and the post-Newtonian limits could also be highly valuable for deriving physical constraints from a vast array of astrophysical observations.