Possibility of higher-dimensional anisotropic compact star

Abstract

We provide a new class of interior solutions for anisotropic stars admitting conformal motion in higher-dimensional noncommutative spacetime. The Einstein field equations are solved by choosing a particular density distribution function of Lorentzian type as provided by Nazari and Mehdipour [1, 2] under a noncommutative geometry. Several cases with $4$ and higher dimensions, e.g. $5$, $6$, and $11$ dimensions, are discussed separately. An overall observation is that the model parameters, such as density, radial pressure, transverse pressure, and anisotropy, all are well behaved and represent a compact star with mass $2.27$ $M_{\odot }$ and radius $4.17$ km. However, emphasis is put on the acceptability of the model from a physical point of view. As a consequence it is observed that higher dimensions, i.e. beyond $4D$ spacetime, exhibit several interesting yet bizarre features, which are not at all untenable for a compact stellar model of strange quark type; thus this dictates the possibility of its extra-dimensional existence.

1 Introduction

To model a compact object it is generally assumed that the underlying matter distribution is homogeneous, i.e. we have a perfect fluid, obeying the Tolman–Oppenheimer–Volkoff (TOV) equation. The nuclear matter of density $\rho \sim 10^{15}$ g/cc, which is expected at the core of the compact terrestrial object, becomes anisotropic in nature as was first argued by Ruderman [3]. In the case of anisotropy the pressure inside the fluid sphere can specifically be decomposed into two parts: the radial pressure, $p_r$ and the transverse pressure, $p_t$, where $p_t$ is in the direction perpendicular to $p_r$. Their difference $\Delta =p_t-p_r$ is defined as the anisotropic factor. Now, the anisotropic force ($\frac{2\Delta }{r}$) will be repulsive in nature if $\Delta >0$, or equivalently $p_t>p_r$, and attractive if $p_t<p_r$. So it is reasonable to consider a pressure anisotropy to develop the model under investigation. It is shown that in the case of an anisotropic fluid the existence of a repulsive force helps to construct compact objects [4].

Anisotropy may occur for different reasons in any stellar distribution. It could be introduced by the existence of a solid core or by the presence of a type $3A$ superfluid [5]. Different kinds of phase transitions [6], pion condensation  [7] etc. are also reasonable for anisotropy. It may also occur by the effects of slow rotation in a star. Bowers and Liang [8] showed that anisotropy might have non-negligible effects on such parameters like equilibrium mass and surface redshift. Very recently other theoretical advances also indicate that the pressure inside a compact object is not essentially isotropic in nature [9–15].

In recent years the extension of general relativity to higher dimensions has become a topic of great interest. In particular, along this line of thinking we note that whether the usual solar system tests are compatible with the existence of higher spatial dimensions has been investigated by Rahaman et al. [16]. Some other studies as regards higher dimensions have been done by Liu and Overduin [17] for the motion of a test particle, whereas Rahaman et al. [18] have investigated higher-dimensional gravastars.

One of the most interesting outcomes of string theory is that the target spacetime coordinates become noncommuting operators on the $D$-brane [19, 20]. Now the noncommutativity of a spacetime can be encoded in the commutator $\left[ x^{\mu },x^{\nu }\right] =i \theta ^{\mu \nu }$, where $\theta ^{\mu \nu }$ is an anti-symmetric matrix of dimension $(\mathrm{length})^{2}$, which determines the fundamental cell discretization of spacetime. It is similar to the way the Planck constant $\hbar$ discretizes phase space [21].

In the literature many studies are available on noncommutative geometry; for example, Nazari and Mehdipour [1] used a Lorentzian distribution to analyze Parikh–Wilczek tunneling from noncommutative higher-dimensional black holes. Besides this investigation some other noteworthy work is on galactic rotation curves inspired by a noncommutative-geometry background [22], stability of a particular class of thin-shell wormholes in noncommutative geometry [23], higher-dimensional wormholes with noncommutative geometry [24], noncommutative BTZ black hole [25], noncommutative wormholes [26], and noncommutative wormholes in $f(R)$ gravity with a Lorentzian distribution [27].

It is usual to search for the natural relationship between geometry and matter through the Einstein field equations where it is very convenient to use the inheritance symmetry. The well-known inheritance symmetry is the symmetry under conformal Killing vectors (CKVs), i.e.

$$\begin{aligned} L_{\xi } g_{ik}=\psi g_{ik}, \end{aligned}$$

(1)

where $L$ is the Lie derivative of the metric tensor, which describes the interior gravitational field of a stellar configuration with respect to the vector field $\xi$, and $\psi$ is the conformal factor. It is supposed that the vector $\xi$ generates the conformal symmetry and the metric $g$ is conformally mapped onto itself along $\xi$. It is to be noted that neither $\xi$ nor $\psi$ need to be static, even though one considers a static metric [28, 29]. We also note that: (i) if $\psi =0$, then Eq. (1) gives the Killing vector, (ii) if $\psi =$ constant, then it gives a homothetic vector, and (iii) if $\psi =\psi (\mathbf x ,t)$, then it yields a conformal vector. Moreover, it is to be mentioned that for $\psi =0$ the underlying spacetime becomes asymptotically flat, which further implies that the Weyl tensor will also vanish. So CKVs provide a deeper insight of the underlying spacetime geometry.

A large number of works on conformal motion have been published by several authors. A class of solutions for anisotropic stars admitting conformal motion have been studied by Rahaman et al. [30]. In a very recent work Rahaman et al. [31] have also described conformal motion in higher-dimensional spacetimes. A charged gravastar admitting conformal motion has been studied by Usmani et al. [32]. Contrary to this work Bhar [33] has studied a higher-dimensional charged gravastar admitting conformal motion, whereas a relativistic star admitting conformal motion has been analyzed by Rahaman et al. [34]. Inspired by this earlier work on conformal motion we are looking for a new class of solutions of anisotropic stars under the framework of general relativity inspired by noncommutative geometry in 4- and higher-dimensional spacetimes.

In the presence of noncommutative geometry there are two different distributions available in the literature: (a) Gaussian and (b) Lorentzian [2]. Though these two mass distributions represent similar quantitative aspects, for the present investigation we are exploiting a particular Lorentzian-type energy density of the static spherically symmetric smeared and particle-like gravitational source in the multi-dimensional general form [1, 2]

$$\begin{aligned} \rho =\frac{M \sqrt{\phi }}{\pi ^{2}(r^{2}+\phi )^{\frac{n+2}{2}}}, \end{aligned}$$

(2)

where $M$ is the total smeared mass of the source, $\phi$ is the noncommutative parameter which corresponds to a minimal width $\sqrt{\phi }$, and $n$ is a positive integer >1. In this approach, generally known as the noncommutative-geometry inspired model, via a minimal length caused by averaging noncommutative coordinate fluctuations one cures the curvature singularity in black holes [21, 35–38]. It has been argued that it is not required to consider the length scale of the coordinate noncommutativity to be the same as the Planck length, as the noncommutativity influences appear on a length scale which may behave as an adjustable parameter corresponding to that pertinent scale [2].

It is interesting to note that Rahaman et al. [30] have found a new class of interior solutions for anisotropic compact stars admitting conformal motion under the $4D$ framework of GR. On the other hand, Rahaman et al. [31] have studied different dimensional fluids, higher as well as lower, inspired by noncommutative geometry with Gaussian distribution of energy density and have shown that at $4D$ only one can get a stable configuration for any spherically symmetric stellar system. However, in the present work we have extended the work of Rahaman et al. [30] to higher dimensions and that of Rahaman et al. [31] to higher dimensions with an energy density in the form of a Lorentzian distribution. In this approach we are able to generalize both above mentioned works to show that compact stars may exist even in higher dimensions.

In this paper, therefore, we use a noncommutative geometry inspired model to combine the microscopic structure of spacetime with the relativistic description of gravity. The plan of the present investigation is as follows: in Sect. 2 we formulate the Einstein field equations for the interior spacetime of the anisotropic star. In Sect. 3 we solve the Einstein field equations by using the density function of Lorentzian distribution type in higher-dimensional spacetime as given by Nozari and Mehdipour [1]. We consider the cases $n=~2,~3,~4$, and $9$, i.e. $4D,~5D,~6D$ and $11D$ spacetimes, in Sect. 4 to examine expressions for the physical parameters, whereas the matching conditions are provided in Sect. 5. Various physical properties are explored in Sect. 6 while studying interesting features of the model and we present them with graphical plots for comparative studies among the results of different dimensional spacetimes. Finally we complete the paper with some concluding remarks in Sect. 7.

2 The interior spacetime and the Einstein field equations

To describe the static spherically symmetric spacetime (in geometrical units $G=1=c$ here and onwards) in higher dimensions the line element can be given in the standard form,

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{e}^{\nu (r)}\mathrm{d}t^{2}+\mathrm{e}^{\lambda (r)}\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega _n^{2}, \end{aligned}$$

(3)

where

$$\begin{aligned} \mathrm{d}\Omega _n^{2}= & {} \mathrm{d}\theta _1^{2}+\sin ^{2}\theta _1\mathrm{d}\theta _2^{2}+ \sin ^{2}\theta _1\sin ^{2}\theta _2\mathrm{d}\theta _3^{2}\nonumber \\&+\cdots +\prod _{j=1}^{n-1}\sin ^{2}\theta _j\mathrm{d}\theta _n^{2}, \end{aligned}$$

(4)

where $\lambda$, $\nu$ are functions of the radial coordinate $r$. Here we have used the notation $D=n+2$, $D$ is the dimension of the spacetime.

The energy–momentum tensor for the matter distribution can be taken in its usual form [39],

$$\begin{aligned} T_{\nu }^{\mu }=(\rho +p_r)u^{\mu }u_{\nu }-p_rg^{\mu }_{\nu }+(p_t-p_r)\eta ^{\mu }\eta _{\nu }, \end{aligned}$$

(5)

with $u^{\mu }u_{\mu }=-\eta ^{\mu }\eta _{\mu }=1$ and $u^{\mu }\eta _{\nu }= 0$. Here the vector $u^{\mu }$ is the fluid $(n+2)$-velocity and $\eta ^{\mu }$ is the unit space-like vector which is orthogonal to $u^{\mu }$, where $\rho$ is the matter density, $p_r$ is the radial pressure in the direction of $\eta ^{\mu }$, and $p_t$ is the transverse pressure in the direction orthogonal to $p_r$. Since the pressure is anisotropic in nature, for our model $p_r \ne p_t$. Here $p_t-p_r = \Delta$ is the measure of anisotropy, as defined earlier.

Now, for a higher-dimensional spacetime ($n \ge 2 )$ the Einstein equations can be written as [22]

$$\begin{aligned}&\mathrm{e}^{-\lambda }\left[ \frac{n\lambda '}{2r}-\frac{n(n-1)}{2r^{2}}\right] +\frac{n(n-1)}{2r^{2}}=8\pi \rho =8\pi T_0^{0},\end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{e}^{-\lambda }\left[ \frac{n(n-1)}{2r^{2}}+\frac{n\nu '}{2r}\right] -\frac{n(n-1)}{2r^{2}}=8\pi p_r=-8\pi T_1^{1},\end{aligned}$$

(7)

$$\begin{aligned}&\frac{1}{2}\mathrm{e}^{-\lambda }\left[ \frac{1}{2}(\nu ')^{2}+\nu ''-\frac{1}{2}\lambda '\nu '+\frac{(n-1)}{r}(\nu '-\lambda ')\right. \nonumber \\&\quad \left. +\frac{(n-1)(n-2)}{r^{2}}\right] \nonumber \\&\quad -\frac{(n-1)(n-2)}{2r^{2}}=8\pi p_t=-8\pi T_2^{2}=-8\pi T_3^{3}, \end{aligned}$$

(8)

where $^\prime$ denotes differentiation with respect to the radial coordinate $r$, i.e. $^{\prime } \equiv \frac{\hbox {d}}{\hbox {d}r}$.

3 The solution under conformal Killing vector

Mathematically, conformal motions or CKVs are motions along which the metric tensor of a spacetime remains invariant up to a scale factor. A conformal vector field can be defined as a global smooth vector field $x$ on a manifold, $\ss$, such that for the metric $g_{ab}$ in any coordinate system on $\ss$ $x_{a;b} = \psi g_{ab} + F_{ab}$, where $\psi : \ss \rightarrow$ real number, is the smooth conformal function of $x$, $F_{ab}$ is the conformal bivector of $x$. This is equivalent to $L_x g_{ik} = \psi g_{ik}$ (as considered in Eq. (1) in the usual form), where $L_x$ signifies the Lie derivative along $x_a$.

To search the natural relation between geometry and matter through the Einstein equations, it is useful to use inheritance symmetry. The well-known inheritance symmetry is the symmetry under CKVs. These provide a deeper insight into the spacetime geometry. The CKVs facilitate the generation of exact solutions to the Einstein field equations. The study of conformal motions in spacetime is physically very important because it can lead to the discovery of conservation laws and one uses them to devise spacetime classification schemes. Einstein’s field equations, being highly non-linear partial differential equations, one can reduce the partial differential equations to ordinary differential equations by use of CKVs. It is still a challenging problem to the theoretical physicists to find the exact nature and characteristics of compact stars and elementary particle-like electrons.

Let us therefore assume that our static spherically symmetry spacetime admits a one parameter group of conformal motion. The CKV, as given in Eq. (1), can be written in a more convenient form:

$$\begin{aligned} L_\xi g_{ik}=\xi _{i;k}+\xi _{k;i}=\psi g_{ik}, \end{aligned}$$

(9)

where both $i$ and $k$ take the values $1,~2,...,~n+2$. Here $\psi$ is an arbitrary function of the radial coordinate $r$ and $\xi$ is the orbit of the group. The metric $g_{ij}$ is conformally mapped onto itself along $\xi _i$.

Let us further assume the orbit of the group to be orthogonal to the velocity vector field of the fluid,

$$\begin{aligned} \xi ^{\mu }u_{\mu }=0. \end{aligned}$$

(10)

As a consequence of the spherical symmetry from Eq. (10) we have

$$\begin{aligned} \xi ^{1}=\xi ^{3}=\cdots =\xi ^{n+1}=0. \end{aligned}$$

Now, the conformal Killing equation for the line element (3) gives the following equations:

$$\begin{aligned}&\xi ^{2}\nu '=\psi ,\end{aligned}$$

(11)

$$\begin{aligned}&\xi ^{n+2}=C_1,\end{aligned}$$

(12)

$$\begin{aligned}&\xi ^{2}=\frac{\psi r}{2},\end{aligned}$$

(13)

$$\begin{aligned}&\xi ^{2}\lambda '+2{\xi ^{2}}^\prime =\psi , \end{aligned}$$

(14)

where $2$ stands for the spatial coordinate $r$, and primes and commas are for the partial derivative with respect to $r$. $C_1$ is a constant.

The above set of equations consequently gives

$$\begin{aligned}&\mathrm{e}^{\nu }=C_2^{2}r^{2},\end{aligned}$$

(15)

$$\begin{aligned}&\mathrm{e}^{\lambda }=\left( \frac{C_3}{\psi }\right) ^{2},\end{aligned}$$

(16)

$$\begin{aligned}&\xi ^{i}=C_1\delta _{n+2}^{i}+\left( \frac{\psi r}{2}\right) \delta _2^{i}, \end{aligned}$$

(17)

where $\delta$ stands for the Kronecker delta and $C_2$, $C_3$ are integration constants.

Using Eqs. (15)–(17) in the Einstein field equations (6)–(8), we get

$$\begin{aligned}&\frac{n(n-1)}{2r^{2}}\left( 1-\frac{\psi ^{2}}{C_3^{2}}\right) -\frac{n\psi \psi '}{rC_3^{2}}=8\pi \rho ,\end{aligned}$$

(18)

$$\begin{aligned}&\frac{n}{2r^{2}}\left[ (n+1)\frac{\psi ^{2}}{C_3^{2}}-(n-1)\right] =8\pi p_r,\end{aligned}$$

(19)

$$\begin{aligned}&\frac{n\psi \psi '}{rC_3^{2}}+n(n-1)\frac{\psi ^{2}}{2r^{2}C_3^{2}}-\frac{(n-1)(n-2)}{2r^{2}}=8\pi p_t.\nonumber \\ \end{aligned}$$

(20)

We thus have three independent Eqs. (18)–(20) with four unknowns $\rho$, $p_r$, $p_t$, $\psi$. So we are free to choose any physically reasonable ansatz for any one of these four unknowns. Hence we choose the density profile $\rho$ in the form given in Eq. (2) in connection to a higher-dimensional static and a spherically symmetric Lorentzian distribution of smeared matter as provided by Nozari and Mehdipour [1]. This density profile will be employed as a key tool in our present study.

Therefore, substituting Eq. (2) into (18) and solving, we obtain

$$\begin{aligned} \psi ^{2}\!=\!C_3^{2}\!-\! \frac{16MC_3^{2}\sqrt{\phi }}{n\pi }\frac{1}{r^{n-1}}\int \frac{r^{n}}{(r^{2}+\phi )^{\frac{n+2}{2}}}\mathrm{d}r+\frac{A}{r^{n-1}},\nonumber \\ \end{aligned}$$

(21)

where $A$ is a constant of integration which is determined by invoking suitable boundary conditions.

Now Eq. (21) gives the expression of the conformal factor $\psi$. Assigning $n=~2,~3,~4$, and $9$, i.e. we have $4D,~5D,~6D$, and $11D$ spacetimes, respectively, if we perform the above integral, then the conformal factor $\psi$ can be obtained for different dimensions, which is necessary to find the other physical parameter, namely $p_r$ and $p_t$ for these dimensions. Here $A,~-\infty <A <\infty$, is a constant of integration that can be found later on from the boundary condition $p_r(R)=0$, $R$ being the radius of the star.

4 Exact solutions of the models in different dimensions

The above set of equations are associated with the dimensional parameter $n$ and hence to get a clear picture of the physical system under different spacetimes we are interested in studying several cases, starting from standard $4D$ to higher $5D$, $6D$, and $11D$ spacetimes, as shown below.

4.1 Four-dimensional spacetime ($n=2$)

The conformal parameter $\psi (r)$ and the metric potential $\mathrm{e}^{\lambda }$ are given as

$$\begin{aligned}&\psi \!=\!\sqrt{C_3^{2}\!-\!\frac{4MC_3^{2}\sqrt{\phi }}{\pi r}\left[ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{r}{\sqrt{\phi }}\right) \!-\!\frac{r}{r^{2}\!+\!\phi } \right] \!+\!\frac{A}{r}},\end{aligned}$$

(22)

$$\begin{aligned}&\mathrm{e}^{-\lambda }\!=\!1\!+\!\frac{A}{C_3^{2}r}\!-\!\frac{4M\sqrt{\phi }}{\pi r}\left[ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{r}{\sqrt{\phi }}\right) \!-\!\frac{r}{r^{2}+\phi }\right] .\nonumber \\ \end{aligned}$$

(23)

The radial and transverse pressures are obtained as

$$\begin{aligned}&p_r=\frac{1}{8\pi r^{2}}\bigg [2+\frac{3A}{C_3^{2}r}-\frac{12M\sqrt{\phi }}{\pi r}\left\{ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{r}{\sqrt{\phi }}\right) \right. \nonumber \\&\qquad \quad \left. -\frac{r}{r^{2}+\phi } \right\} \bigg ],\end{aligned}$$

(24)

$$\begin{aligned}&p_t=\frac{1}{8\pi }\left[ \frac{1}{r^{2}}-\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{2}}\right] . \end{aligned}$$

(25)

To find the above constant of integration we impose the boundary condition $p_r(r=R)=0$, where $R$ is the radius of the fluid sphere as mentioned earlier, which gives

$$\begin{aligned} A\!=\!\frac{4MC_3^{2}\sqrt{\phi }}{\pi }\left\{ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{R}{\sqrt{\phi }}\right) \!-\!\frac{R}{R^{2}\!+\!\phi }\right\} \!-\!\frac{2}{3}C_3^{2}R.\nonumber \\ \end{aligned}$$

(26)

4.2 Five-dimensional spacetime ($n=3$)

In this case the solution set can be obtained as follows:

$$\begin{aligned}&\psi =\sqrt{C_3^{2}+\frac{16MC_3^{3}\sqrt{\phi }}{9\pi r^{2}}\frac{3r^{2}+2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}+\frac{A}{r^{2}}},\end{aligned}$$

(27)

$$\begin{aligned}&\mathrm{e}^{-\lambda }=1+\frac{16M\sqrt{\phi }}{9\pi r^{2}}\frac{3r^{2}+2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}+\frac{A}{C_3^{2}r^{2}},\end{aligned}$$

(28)

$$\begin{aligned}&p_r=\frac{3}{8\pi r^{2}}\left[ 1+\frac{32M\sqrt{\phi }}{9\pi r^{2}}\frac{3r^{2}+2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}+\frac{2A}{C_3^{2}r^{2}}\right] ,\end{aligned}$$

(29)

$$\begin{aligned}&p_t=\frac{1}{8\pi }\left[ \frac{2}{r^{2}}-\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{\frac{5}{2}}}\right] , \end{aligned}$$

(30)

with

$$\begin{aligned} A=-\frac{C_3^{2}R^{2}}{2}\left[ 1+\frac{32M\sqrt{\phi }}{9\pi R^{2}}\frac{3R^{2}+2\phi }{(R^{2}+\phi )^{\frac{3}{2}}}\right] . \end{aligned}$$

(31)

4.3 Six-dimensional spacetime ($n=4$)

Here the solutions are as follows:

$$\begin{aligned} \psi \!=\!\sqrt{C_3^{2}\!-\!\frac{MC_3^{2}\sqrt{\phi }}{2\pi r^{3}}\left[ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) \!-\!\frac{5r^{3}\!+\!3r\phi }{(r^{2}\!+\!\phi )^{2}} \right] \!+\!\frac{A}{r^{3}}},\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned}&\mathrm{e}^{-\lambda } = 1-\frac{M \sqrt{\phi }}{2\pi r^{3}}\left[ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) \right. \nonumber \\&\qquad \qquad \left. -\frac{5r^{3}+3r\phi }{(r^{2}+\phi )^{2}} \right] +\frac{A}{C_3^{2}r^{3}},\end{aligned}$$

(33)

$$\begin{aligned}&p_r = \frac{1}{4 \pi r^{2}}\left[ 2-\frac{5M\sqrt{\phi }}{2\pi r^{3}}\left\{ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) \right. \right. \nonumber \\&\qquad \qquad \left. \left. -\frac{5r^{3}+3r\phi }{(r^{2}+\phi )^{2}} \right\} +\frac{5A}{r^{3}C_3^{2}}\right] ,\end{aligned}$$

(34)

$$\begin{aligned}&p_t = \frac{1}{8\pi }\left[ \frac{3}{r^{2}}-\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{3}}\right] , \end{aligned}$$

(35)

and

$$\begin{aligned} A= & {} \frac{MC_3^{2}\sqrt{\phi }}{2\pi }\left\{ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{R}{\sqrt{\phi }}\right) -\frac{5R^{3}+3r\phi }{(R^{2}+\phi )^{2}} \right\} \nonumber \\&-\frac{2C_3^{2}R^{3}}{5}. \end{aligned}$$

(36)

4.4 Eleven-dimensional spacetime ($n=9$)

For this arbitrarily chosen higher dimension the solutions can be obtained as

$$\begin{aligned}&\psi =\sqrt{C_3^{2}+C_3^{2}\frac{16M\sqrt{\phi }}{2835\pi r^{8}}\frac{315r^{8}+840r^{6}\phi +1008r^{4}\phi ^{2}+576r^{2}\phi ^{3}+128\phi ^{4}}{(r^{2} +\phi )^{\frac{9}{2}}}+\frac{A}{r^{8}}},\end{aligned}$$

(37)

$$\begin{aligned}&\mathrm{e}^{-\lambda }=1+\frac{16M\sqrt{\phi }}{2835\pi r^{8}}\frac{315r^{8}+840r^{6}\phi +1008r^{4}\phi ^{2}+576r^{2}\phi ^{3}+128\phi ^{4}}{(r^{2} +\phi )^{\frac{9}{2}}}+\frac{A}{C_3^{2}r^{8}},\end{aligned}$$

(38)

$$\begin{aligned}&p_r=\frac{9}{8\pi r^{2}}\left[ 1+\frac{16M\sqrt{\phi }}{567\pi r^{8}}\frac{315r^{8}+840r^{6}\phi +1008r^{4}\phi ^{2}+576r^{2}\phi ^{3}+128\phi ^{4}}{(r^{2} +\phi )^{\frac{9}{2}}}+\frac{5A}{C_3^{2}r^{8}}\right] , \end{aligned}$$

(39)

$$\begin{aligned} p_t=\frac{1}{\pi }\left[ \frac{1}{r^{2}}-\frac{M\sqrt{\phi }}{\pi (r^{2}+\phi )^{\frac{11}{2}}}\right] , \end{aligned}$$

(40)

and

$$\begin{aligned} A=-\frac{C_3^{2}}{5}\left[ R^{8}+\frac{16M\sqrt{\phi }}{567\pi }\frac{315R^{8}+840R^{6}\phi +1008R^{4}\phi ^{2} +576R^{2}\phi ^{3}+128\phi ^{4}}{(R^{2} +\phi )^{\frac{9}{2}}}\right] . \end{aligned}$$

(41)

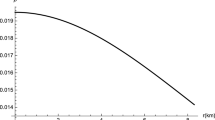
Let us now turn our attention to the physical analysis of the stellar model under consideration, i.e. see whether it is a normal star or something else. To do so, primarily we try to figure out the radius of the stellar configuration. It is to be noted that in Eqs. (29), (34), and (39) the radius of the star $R$ has been mentioned under the boundary condition, $p_r(R) =0$, i.e. we get analytical results in the respective cases. So it seems that we can proceed without further plot descriptions to get $p_r(R) =0$ for all dimensions. However, for the $4D$ case it reveals that the radius of the star is very small with a numerical value of $4.17$ km (Fig. 1). This obviously then indicates that the star is nothing but a compact object (see Table 1 and all references [11, 13–15] for a comparison with the radius of some real compact stars).

Fig. 1

The graphical plot for radial pressure vs. radius which has a definite cut-off at $4.17$ km

Table 1 Values of the model parameter $z_s$ for different strange stars

5 Matching conditions

Now, we match our interior solutions with the exterior vacuum solutions. The generalization of the Schwarzschild solution, as obtained by Tangherlini [40], reads

$$\begin{aligned} \mathrm{d}s ^2 \!=\! - \!\left( 1 \!- \!\frac{\mu _{n}}{ r^{n-1}}\right) \mathrm{d}t^2 \!+ \!\left( 1 \!- \!\frac{\mu _{n}}{ r^{n-1}}\right) ^{-1} \mathrm{d}r^2 + \mathrm{d}\Omega _{n} ^2. \end{aligned}$$

(42)

Here,

$$\begin{aligned} {\Omega }_{ n }=\frac{2 \pi ^{\frac{n+1}{2}}}{\Gamma \left( \frac{n+1}{2}\right) }, \end{aligned}$$

the area of a unit $n$-sphere, and

$$\begin{aligned} \mu _{n}=16\pi GM/n c^2 {\Omega }_{n} \end{aligned}$$

is the constant of integration with $M$, the mass of the black hole with $n=2,~3,~4,~9$.

5.1 Four-dimensional spacetime ($n=2$)

For the $4D$ case, our interior solution should match the exterior Schwarzschild spacetime at the boundary $r=a_4$ given by

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{\mu _2}{r}\right) \mathrm{d}t^{2}+\left( 1-\frac{\mu _2}{r}\right) ^{-1}\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega _{2}. \end{aligned}$$

(43)

Now using the matching conditions at the boundary $r=a_4$, we have

$$\begin{aligned} 1-\frac{\mu _2}{a_4}=C_2^{2}a_4^{2} \end{aligned}$$

(44)

and

$$\begin{aligned} 1-\frac{\mu _2}{a_4}= & {} 1+\frac{A}{C_3^{2}a_4}-\frac{4M\sqrt{\phi }}{\pi a_4}\nonumber \\&\times \left[ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{a_4}{\sqrt{\phi }}\right) -\frac{a_4}{a_4^{2}+\phi }\right] . \end{aligned}$$

(45)

Solving the above two equations, we obtain

$$\begin{aligned}&C_2^{2}=\frac{1}{a_4^{2}}\left( 1-\frac{\mu _2}{a_4}\right) ,\end{aligned}$$

(46)

$$\begin{aligned}&\frac{A}{C_3^{2}}=\frac{4M\sqrt{\phi }}{\pi }\left[ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{a_4}{\sqrt{\phi }}\right) -\frac{a_4}{a_4^{2}+\phi }\right] -\mu _2.\nonumber \\ \end{aligned}$$

(47)

5.2 Five-dimensional spacetime ($n=3$)

For the $5D$ case, our interior solution should match the exterior $5D$ Schwarzschild spacetime at the boundary $r=a_5$, given by

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{\mu _3}{r^{2}}\right) \mathrm{d}t^{2}+\left( 1-\frac{\mu _3}{r^{2}}\right) ^{-1}\mathrm{d}r^{2} +r^{2}\mathrm{d}\Omega _{3}. \end{aligned}$$

(48)

Now using the matching conditions at the boundary $r=a_5$, we have

$$\begin{aligned} 1-\frac{\mu _3}{a_5^{2}}=C_2^{2}a_5^{2} \end{aligned}$$

(49)

and

$$\begin{aligned} 1-\frac{\mu _3}{a_5^{2}}=1+\frac{A}{C_3^{2}a_5^{2}}+\frac{16M\sqrt{\phi }}{9\pi a_5^{2}}\frac{3a_5^{2}+2\phi }{(a_5^{2}+\phi )^{\frac{3}{2}}}. \end{aligned}$$

(50)

Solving the above two equations, we obtain

$$\begin{aligned} C_3^{2}=\frac{1}{a_5^{2}}\left( 1-\frac{\mu _3}{a_5^{2}}\right) \end{aligned}$$

(51)

and

$$\begin{aligned} \frac{A}{C_3^{2}}=-\mu _3-\frac{16M\sqrt{\phi }}{9\pi }\frac{3a_5^{2}+2\phi }{(a_5^{2} +\phi )^{\frac{3}{2}}}. \end{aligned}$$

(52)

5.3 Six-dimensional spacetime ($n=4$)

For the $6D$ case, our interior solution should match the exterior $6D$ Schwarzschild spacetime at the boundary $r=a_6$, given by

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{\mu _4}{r^{3}}\right) \mathrm{d}t^{2}+\left( 1-\frac{\mu _4}{r^{3}}\right) ^{-1}\mathrm{d}r^ {2}+r^{2}\mathrm{d}\Omega _{4}. \end{aligned}$$

(53)

Now using the matching conditions at the boundary $r=a_6$, we have

$$\begin{aligned} 1-\frac{2\mu _4}{a_6^{3}}=C_2^{2}a_6^{2} \end{aligned}$$

(54)

and

$$\begin{aligned} 1-\frac{\mu _4}{a_6^{3}}= & {} 1-\frac{M \sqrt{\phi }}{2\pi a_6^{3}}\left[ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{a_6}{\sqrt{\phi }}\right) \right. \nonumber \\&\left. -\frac{5a_6^{3}+3a_6\phi }{(a_6^{2}+\phi )^{2}} \right] +\frac{A}{C_3^{2}a_6^{3}}. \end{aligned}$$

(55)

Solving the above two equations, we obtain

$$\begin{aligned} C_2^{2}=\frac{1}{a_6^{2}}\left( 1-\frac{\mu _4}{a_6^{3}}\right) \end{aligned}$$

(56)

and

$$\begin{aligned} \frac{A}{C_3^{2}}\!=\!\frac{M \sqrt{\phi }}{2\pi }\left[ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{a_6}{\sqrt{\phi }}\right) \!-\!\frac{5a_6^{3}+3a_6\phi }{(a_6^{2}+\phi )^{2}} \right] -\mu _4.\nonumber \\ \end{aligned}$$

(57)

5.4 Eleven-dimensional spacetime ($n=9$)

For the $11D$ case, our interior solution should match the exterior 11D Schwarzschild spacetime at the boundary $r=a_{11}$, given by

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{\mu _{9}}{r^{8}}\right) \mathrm{d}t^{2}+\left( 1-\frac{\mu _{9}}{r^{8}}\right) ^{-1} \mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega _{9}. \end{aligned}$$

(58)

Now using the matching conditions at the boundary $r=a_{11}$, we have

$$\begin{aligned} 1-\frac{\mu _{9}}{a_{11}^{8}}=C_2^{2}a_{11}^{2} \end{aligned}$$

(59)

and

$$\begin{aligned}&1-\frac{\mu _9}{a_{11}^{8}}= 1+\frac{16M\sqrt{\phi }}{2835\pi a_{11}^{8}}\nonumber \\&\quad \times \frac{315a_{11}^{8}+840a_{11}^{6}\phi +1008a_{11}^{4}\phi ^{2} +576a_{11}^{2}\phi ^{3}+128\phi ^{4}}{(a_{11}^{2} +\phi )^{\frac{9}{2}}}\nonumber \\&\quad +\frac{A}{C_3^{2}a_{11}^{8}}. \end{aligned}$$

(60)

Solving the above two equations, we obtain

$$\begin{aligned} C_2^{2}=\frac{1}{a_{11}^{2}}\left( 1-\frac{\mu _{9}}{a_{11}^{8}}\right) \end{aligned}$$

(61)

and

$$\begin{aligned} \frac{A}{C_3^{2}}\!=\!\frac{M \sqrt{\phi }}{2\pi }\left[ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{a_{11}}{\sqrt{\phi }}\right) \!-\!\frac{5a_{11}^{3}\!+\!3a_{11}\phi }{(a_{11}^{2}+\phi )^{2}} \right] -\mu _{9},\nonumber \\ \end{aligned}$$

(62)

where $a_j (j=4,~5,~6~\mathrm{and}~11)$ are the radii of the fluid spheres in different dimensions.

6 A comparative study of the physical features of the model

Let us now carry out a comparative study of the physical features based on the solutions set obtained in Sect. 4. This can be done in various ways. However, in the present investigation the best method we may adopt for a comparative study, firstly, is in connection to the stability of the models for different dimensions, which may be considered as the most crucial one, and secondly, in connection to other physical parameters viz., density, pressure, pressure anisotropy, pressure gradient, conformal parameter, and metric potential.

6.1 Stability of the stellar configuration

The generalized TOV equation can be written in the form

$$\begin{aligned} -\frac{M_G(r)(\rho +p_r)}{r^{2}}\mathrm{e}^{\frac{\nu -\mu }{2}}-\frac{\mathrm{d}p_r}{\mathrm{d}r}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$

(63)

where $M_G(r)$ is the gravitational mass within the sphere of radius $r$ and is given by

$$\begin{aligned} M_G(r)=\frac{1}{2}{r^{2}}\nu '\mathrm{e}^{\frac{\nu -\lambda }{2}}. \end{aligned}$$

(64)

Substituting (64) into (63), we obtain

$$\begin{aligned} -\frac{\nu '}{2}(\rho +p_r)-\frac{\mathrm{d}p_r}{\mathrm{d}r}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$

(65)

The above TOV equation describes the equilibrium of the stellar configuration under a gravitational force $F_g$, a hydrostatic force $F_h$ and an anisotropic stress $F_a$, so that we can write it in the following form:

$$\begin{aligned} F_g+F_h+F_a=0, \end{aligned}$$

(66)

where

$$\begin{aligned}&F_g=-\frac{\nu '}{2}(\rho +p_r),\nonumber \\&F_h=-\frac{\mathrm{d}p_r}{\mathrm{d}r},\nonumber \\&F_a=\frac{2}{r}(p_t-p_r). \end{aligned}$$

(67)

We have shown the plots of the TOV equations for $4D$, $5D$, $6D$, and $11D$ spacetime in Fig. 2. From the plots it is overall clear that the system is in static equilibrium under three different forces, viz. gravitational, hydrostatic, and anisotropic. For example, in the $4D$ case to attain equilibrium, the hydrostatic force is counter-balanced jointly by gravitational and anisotropic forces. In $5D$ the situation is exactly the same, the only difference being in the radial distances. In $4D$ it is closer to 5 whereas in $5D$ it is closer to 8. This distance factor can also be observed in the higher-dimensional spacetimes, though the balancing features between the three forces are clearly different in the respective cases.

Fig. 2

The three different forces, namely gravitational forces $(F_g)$, hydrostatic forces $(F_h)$, and anisotropic forces $(F_a)$, plotted against $r$ (km) for $4D$ spacetime (top), $5D$ spacetime (upper middle), $6D$ spacetime (lower middle), and $11D$ spacetime (bottom). From the figure the balance status of the forces can be clearly observed for $4D$, $5D$, $6D$, and $11D$ spacetimes

6.2 Energy conditions

Now we check whether all the energy conditions are satisfied or not. For this purpose, we shall consider the following inequalities:

$$\begin{aligned}&\mathrm{(i)~NEC}: \rho +p_r\ge 0,~\rho +p_t\ge 0,\\&\mathrm{(ii)~WEC}: \rho +p_r\ge 0,~\rho \ge 0,~\rho +p_t\ge 0,\\&\mathrm{(iii)~SEC}: \rho +p_r\ge 0,~\rho +p_r+2p_t\ge 0. \end{aligned}$$

Figure 3 indicates that in our model all the energy conditions are satisfied throughout the interior region.

Fig. 3

The energy conditions in the interior plotted against $r$ for $4D$ spacetime (top), $5D$ spacetime (upper middle), $6D$ spacetime (lower middle), and $11D$ spacetime (bottom)

6.3 Anisotropy of the models

We show the possible variation of the radial and transverse pressures in Fig. 4 (top and upper middle of the panel, respectively). Hence the measure of anisotropy $\Delta =(p_t-p_r)$ in the $4$-, $5$-, $6$-, and $11$-dimensional cases are, respectively, given as

$$\begin{aligned} \Delta _4= & {} \frac{1}{8\pi }\Bigg [\frac{12M\sqrt{\phi }}{\pi r^{3}}\left\{ \frac{1}{\sqrt{\phi }}\arctan \left( \frac{r}{\sqrt{\phi }}\right) -\frac{r}{r^{2}+\phi }\right\} \nonumber \\&\left. -\frac{1}{r^{2}} -\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{2}}-\frac{3A}{C_3^{2}r^{3}}\right] ,\end{aligned}$$

(68)

$$\begin{aligned} \\ \Delta _5= & {} \frac{1}{8\pi }\left[ \frac{32M\sqrt{\phi }}{3\pi r^{4}}\left\{ \frac{3r^{2} +2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}\right\} -\frac{1}{r^{2}}\right. \nonumber \\\\&\left. -\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{\frac{5}{2}}}+\frac{6A}{C_3^{2}r^{4}}\right] ,\end{aligned}$$

(69)

$$\begin{aligned} \\ \Delta _6= & {} \frac{1}{8\pi }\left[ \frac{5M\sqrt{\phi }}{\pi r^{5}}\left\{ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{5r^{3}+3r\phi }{(r^{2}+\phi )^{2}} \right\} \right. \nonumber \\\\&\left. -\frac{1}{r^{2}}-\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{3}}-\frac{10A}{r^{5}C_3^{2}}\right] ,\end{aligned}$$

(70)

$$\begin{aligned} \Delta _{11}= & {} \frac{1}{8\pi } \left[ \frac{M\sqrt{\phi }}{4\pi r^{10}}\right. \nonumber \\\\&\times \!\left. \left\{ \!\frac{315r^{8}\!+\!840r^{6}\phi \!+\!1008r^{4}\phi ^{2} \!+\!576r^{2}\phi ^{3}\!+\!128\phi ^{4}}{(r^{2} \!+\!\phi )^{\frac{9}{2}}}\right\} \right. \nonumber \\\\&- \frac{1}{r^{2}}-\frac{8M\sqrt{\phi }}{\pi (r^{2}+\phi )^{\frac{11}{2}}}+\frac{45A}{C_3^{2}r^{10}}\Bigg ]. \end{aligned}$$

(71)

All these are plotted in Fig. 4 (lower middle of the panel). From all the plots we see that $\Delta <0$  i.e., $p_t~<p_r$ and hence the anisotropic force is attractive in nature. A detailed study shows that, firstly, in every case of different dimensions the measure of anisotropy is a decreasing function of $r$. Secondly, from $4D$ onward the measure of anisotropy is increasing gradually and is attaining maximum at $5D$. Surprisingly, it is very high compared to $4D$ and $11D$ spacetimes. This observation therefore shows that the $4D$ configuration represents an almost spherical object; the departure from isotropy is very much smaller than in the higher-dimensional spacetimes.

Fig. 4

Variation of the radial pressure $p_r$ and transverse pressure $p_t$ in the interior of the compact star in $4D, 5D, 6D$, and $11D$ plotted against $r$ (top and upper middle, respectively). The figures show that the profiles are monotonic decreasing functions of $r$. The anisotropic factor $\Delta$ for the $4D, 5D, 6D$, and $11D$ cases are shown against $r$ (lower middle). Pressure gradient vs radius relation is shown in the plot (bottom) for the specified range. In all cases the suffixes in the legends indicate the dimension of the spacetime

Moreover, in all the above cases of various dimensions one may note that the pressure gradient $\frac{\mathrm{d}p_r}{\mathrm{d}r}$ is a decreasing function of $r$ (bottom panel of Fig. 4).

6.4 Compactness and redshift of the star

At the end of the previous section we did a primary test to get a preliminary idea about the structure of the star under consideration and we have seen that the star actually represents a compact object with a radius $4.17$ km. However, for a further test and for confirmation one can perform some specific calculations for the compactness factor [11, 13–15].

To do so we first define the gravitational mass of the system of matter distribution as follows:

$$\begin{aligned} m(r) = \int _0^{ r}~ \left[ \frac{2 \pi ^{\frac{n+1}{2}} }{\Gamma \left( \frac{n+1}{2}\right) }\right] r^n \rho \mathrm{d}r. \end{aligned}$$

(72)

Therefore, the compactness factor and the surface redshift of the star are, respectively, given by

$$\begin{aligned}&u(r)= \frac{m(r) }{r},\end{aligned}$$

(73)

$$\begin{aligned}&z_s= [1-2u]^{-1/2}-1. \end{aligned}$$

(74)

Hence for different dimensions we can calculate the expressions for the above parameters as follows.

${For\,n = 2}:$

$$\begin{aligned}&m(r)=\frac{2M}{\pi }\left[ \mathrm{tan}^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r\sqrt{\phi }}{r^{2}+\phi }\right] ,\end{aligned}$$

(75)

$$\begin{aligned}&u(r)=\frac{2M}{\pi r}\left[ \mathrm{tan}^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r\sqrt{\phi }}{r^{2}+\phi }\right] ,\end{aligned}$$

(76)

$$\begin{aligned}&z_s=\left[ 1-\frac{4M}{\pi r}\left\{ \mathrm{tan}^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r\sqrt{\phi }}{r^{2}+\phi }\right\} \right] ^{-\frac{1}{2}}-1. \end{aligned}$$

(77)

${For\, n=3}:$

$$\begin{aligned}&m(r)=\frac{2M}{3}\left[ 2-\frac{(3r^{2}+2\phi )\sqrt{\phi }}{(r^{2}+\phi )^{\frac{3}{2}}}\right] ,\end{aligned}$$

(78)

$$\begin{aligned}&u(r)=\frac{2M}{3r}\left[ 2-\frac{(3r^{2}+2\phi )\sqrt{\phi }}{(r^{2}+\phi )^{\frac{3}{2}}}\right] ,\end{aligned}$$

(79)

$$\begin{aligned}&z_s=\left[ 1-\frac{4M}{3r}\left\{ 2-\frac{(3r^{2}+2\phi )\sqrt{\phi }}{(r^{2}+\phi )^{\frac{3}{2}}}\right\} \right] ^{-\frac{1}{2}}-1. \end{aligned}$$

(80)

${For\, n=4}:$

$$\begin{aligned}&m(r)=M\left[ \mathrm{tan}^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r\sqrt{\phi }(5r^{2}+3\phi )}{3(r^{2}+\phi )^{2}}\right] ,\end{aligned}$$

(81)

$$\begin{aligned}&u(r)=M\left[ \frac{1}{r}\mathrm{tan}^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{\sqrt{\phi }(5r^{2}+3\phi )}{3(r^{2}+\phi )^{2}}\right] ,\end{aligned}$$

(82)

$$\begin{aligned}&z_s\!=\! \left[ 1\!-\!2M\left\{ \frac{1}{r}\mathrm{tan}^{-1} \left( \frac{r}{\sqrt{\phi }}\right) \!-\!\frac{\sqrt{\phi }(5r^{2}\!+\! 3\phi )}{3(r^{2}\!+\!\phi )^{2}}\right\} \right] ^{-\frac{1}{2}}-1.\nonumber \\ \end{aligned}$$

(83)

${For\, n=9}:$

(84)

(85)

(86)

The nature of the variation of the above expressions for compactness factor and surface redshift of the star can be seen in the Fig. 5 in the top and bottom panel, respectively, for all the values of $n$. It is observed from Fig. 5 (top panel) that the compactness factors for different dimensions are gradually increasing with decreasing $n$ and maximum for $4D$ spacetime. Thus, very interestingly, at the center the star is most dense for $4$-dimension with a very small yet definite core, whereas in the $11D$ case there seems to be no core.

Fig. 5

The compactness factor (top) and surface redshift (bottom) of compact star in $4D$, $5D$, $6D$, $11D$ dimensions plotted against $r$ (km) for the specified range

We note that in connection with the isotropic case and in the absence of a cosmological constant it has been shown for the surface redshift analysis that $z_s \le 2$ [41–43]. On the other hand, Böhmer and Harko [43] argued that for an anisotropic star in the presence of a cosmological constant the surface redshift must obey the general restriction $z_s \le 5$, which is consistent with the bound $z_s \le 5.211$ as obtained by Ivanov [44]. Therefore, for an anisotropic star without cosmological constant the above value $z_s \le 1$ is quite reasonable as can be seen in the $4D$ case (Fig. 5, bottom panel) [11]. In the other cases of higher dimension the surface redshift values are increasing and seem to be within the upper bound [44].

We note that integration of $m(r)$ from $0$ to $R$, where $R$ is the radius of the fluid distribution, gives $M$ (the total mass of the source) i.e.

$$\begin{aligned} M=\int _0^{ R}~ \left[ \frac{2 \pi ^{\frac{n+1}{2}} }{\Gamma \left( \frac{n+1}{2}\right) }\right] r^n \rho \mathrm{d}r. \end{aligned}$$

This equation gives the radius $R$ of the fluid distribution. Thus solutions of the following equations provide the corresponding radius of different dimensional situations.

${For}\,n=2$:

$$\begin{aligned} M=\frac{2M}{\pi }\left[ \mathrm{tan}^{-1}\left( \frac{R}{\sqrt{\phi }}\right) -\frac{R\sqrt{\phi }}{R^{2}+\phi }\right] . \end{aligned}$$

(87)

${For}\,n=3$:

$$\begin{aligned} M=\frac{2M}{3}\left[ 2-\frac{(3R^{2}+2\phi )\sqrt{\phi }}{(R^{2}+\phi )^{\frac{3}{2}}}\right] . \end{aligned}$$

(88)

${For}\,n=4$:

$$\begin{aligned} M=M\left[ \mathrm{tan}^{-1}\left( \frac{R}{\sqrt{\phi }}\right) -\frac{R\sqrt{\phi }(5R^{2}+3\phi )}{3(R^{2}+\phi )^{2}}\right] . \end{aligned}$$

(89)

${For}\,n=9$:

(90)

6.5 Some other physical parameters

In this subsection we have shown the panel of the plots for the conformal parameter $\psi (r)$ (top), the metric potential $\mathrm{e}^{\lambda }$ (middle) and the density $\rho$ (bottom) for $4$ and extra-dimensional spacetimes (Fig. 6). It is observed that for all the physical parameters the features are as usual for $4D$; however, for an extra dimension they take different shapes. Special mention can be made for the density where the central densities are abruptly decreasing as one goes to higher dimensions. Thus, from the plot it becomes clear that the central density is maximum for $4D$, whereas it is minimum for $11D$ spacetime, showing highest compactness of the star for the standard $4$-dimensional case. Note that this same result was observed in Fig. 5 (top panel).

Fig. 6

The conformal factor $\psi (r)$ (top), the metric potential $\mathrm{e}^{\lambda }$ (middle) and matter density (bottom) plotted against $r$ (km) for $4$-, $5$-, $6$-, and $11$-dimensional spacetimes. The suffixes in the top and bottom panel indicate the dimension of the spacetime and for the middle panel $D=n+2$ stands for the dimension of the spacetime

7 Conclusion

In the present paper we have studied thoroughly a set of new interior solutions for anisotropic stars admitting conformal motion in higher-dimensional noncommutative spacetime. Under this spacetime geometry the Einstein field equations are solved by choosing a particular Lorentzian-type density distribution function as proposed by Nozari and Mehdipour [1]. The studies are conducted not only with the standard $4$-dimensional spacetime but also for three special cases with higher dimension: $5D$, $6D$, and $11D$. In general it is noted that the model parameters e.g. the matter-energy density, radial as well as transverse pressures, anisotropy, and other quantities show physical behaviors which are mostly regular throughout the stellar configuration.

Also it is in particular observed that the solutions represent a star with mass $2.27$ $M_{\odot }$ and radius $4.17$ km which falls within the range ($0 < z_s \le 1$) of a compact star [11, 13–15]. However, it has been shown that for a strange star of radius $6.88$ km the surface redshift turns out to be $z_s = 0.5303334$ [11] whereas the maximum surface redshift for the strange star Her X-1 of radius $7.7$ km is $0.022$ [13] and that for the compact star 4U 1820-30 of radius $10$ km turns out to be again $0.022$ [14]. Therefore it seems that our compact star may be a strange quark star (see Table 1).

However, through several mathematical case studies we have put emphasis on the acceptability of the model from a physical point of view for various structural aspects. As a consequence it is observed that, for higher dimensions, i.e. beyond $4D$ spacetime, the solutions exhibit several interesting yet bizarre features. These features seem physically not very unrealistic.

Thus, as a primary stage, the investigation indicates that compact stars may exist even in higher dimensions. But before placing a demand in favor of this highly intriguing issue of compact stars with extra dimensions we need to perform more specific studies and look at the diversity of technical aspects related to higher-dimensional spacetimes of a compact star. Basically, our approach, dependent on a particular energy density distribution of Lorenztian type, which gives existence of compact stars in the higher-dimensional case, may not be the only way to have sufficient evidence in favor of it. We further need to employ other types of density distributions as well. Moreover, one may also think of another than higher-dimensional embedding of GTR and thus opt for alternative theories of gravity to find conclusive proof for higher-dimensional compact stars.

However, in the literature there is some evidence available in favor of extra dimensions in compact stars [45–50].