Search of wormholes in different dimensional non-commutative inspired space-times with Lorentzian distribution

Abstract

In this paper we ask whether the wormhole solutions exist in different dimensional noncommutativity-inspired spacetimes. It is well known that the noncommutativity of the space is an outcome of string theory and it replaced the usual point-like object by a smeared object. Here we have chosen the Lorentzian distribution as the density function in the noncommutativity-inspired spacetime. We have observed that the wormhole solutions exist only in four and five dimensions; however, in higher than five dimensions no wormhole exists. For five dimensional spacetime, we get a wormhole for a restricted region. In the usual four dimensional spacetime, we get a stable wormhole which is asymptotically flat.

1 Introduction

A wormhole is a hypothetical topological feature of the spacetime which connects two distinct spacetimes. Morris and Thorne [1] have shown that the wormhole geometry could be found by solving the Einstein field equation by violating the null energy condition (NEC) which is named as exotic matter. There are a large number of works [2–4] based on the concept of Morris and Thorne.

In recent years, researchers have shown considerable interest on the study of noncommutative spaces. One of the most interesting outcomes of the string theory is that the target spacetime coordinates become noncommuting operators on a D-brane [5, 6]. Now the noncommutatativity of a spacetime can be encoded in the commutator $\left[ x^{\mu }, x^{\nu }\right] =i \theta ^{\mu \nu }$, where $\theta ^{\mu \nu }$ is an anti-symmetric matrix of dimension $(\mathrm{length})^{2}$ which determines the fundamental cell discretization of spacetime. It is similar to the way that the Planck constant $\hbar$ discretizes phase space [7]. In noncommutative space the usual definition of mass density in the form of the Dirac delta function does not hold. So in noncommutative spaces the usual form of the energy density of the static spherically symmetrical smeared and particle-like gravitational source in the form of a Lorentzian distribution is [8]

$$\begin{aligned} \rho =\frac{M\sqrt{\phi }}{\pi ^{2} (r^{2}+\phi )^{\frac{n+2}{2}}}. \end{aligned}$$

Here, the mass $M$ could be the mass of a diffused centralized object such as a wormhole and $\phi$ is the noncommutativity parameter.

Many works inspired by noncommutative geometry are found in the literature. Nozaria and Mehdipoura [8] used a Lorentzian distribution to analyze ‘Parikh–Wilczek Tunneling from Noncommutative Higher Dimensional Black Holes’ [9]. Rahaman et al. have shown that a noncommutative geometrical background is sufficient for the existence of a stable circular orbit and one does not need to consider dark matter for galactic rotation curves. Kuhfittig [10] found that a special class of thin shell wormholes could be possible that are unstable in classical general relativity but are stable in a small region in noncommutative spacetime. By taking a Gaussian distribution as the density function Rahaman et al. [11] have shown that wormhole solutions usually exist in four and in five dimensions only. Banerjee et al. [12] have made a detailed investigation of the thermodynamics, e.g. Hawking temperature, entropy, and the area law for a Schwarzschild black hole in the noncommutative spacetime. Noncommutative wormholes in $f(R)$ gravity with a Lorentzian distribution have been analyzed in [13]. The BTZ black hole inspired by noncommutative geometry has been discussed in [14].

Recently, the extension of general relativity in higher dimensions has become a topic of great interest. The discussion in higher dimensions is essential due to the fact that many theories indicate that extra dimensions exist in our universe. The higher dimensional gravastar has been discussed by Rahaman et al. [15]. Rahaman et al. [16] have investigated whether the usual solar system tests are compatible with higher dimensions. Another study in higher dimensions is the motion of test particles in the gravitational field of a higher dimensional black hole [17].

Inspired by all of this previous work, we are going to analyze whether wormhole solutions exist in four and higher dimensional spacetime in a noncommutativity-inspired geometry where the energy distribution function is taken as a Lorentzian distribution.

The plan of our paper is as follows: in Sect. 2 we formulate the basic Einstein field equations. In Sect. 3, we solve those fields equations in different dimensions, and in Sect. 4 the linearized stability analysis for four dimensional spacetime is worked out. Active mass function and total gravitational energy of four and five dimensional wormhole have been discussed in Sects. 5 and 6 respectively. Some discussions and concluding remarks are presented in the final section.

2 Einstein field equation in higher dimension

To describe the static spherically symmetry spacetime (we have geometrical units $G = 1 =c$ here and onwards) in higher dimensions, we consider the line element in the standard form

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{e}^{\nu (r)}\mathrm{d}t^{2}+\mathrm{e}^{\lambda (r)}\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega _n^{2} \end{aligned}$$

(1)

where

$$\begin{aligned} \mathrm{d}\Omega _n^{2}&= \mathrm{d}\theta _1^{2}+\sin ^{2}\theta _1\mathrm{d}\theta _2^{2}+ \sin ^{2}\theta _1\sin ^{2}\theta _2\mathrm{d}\theta _3^{2}\nonumber \\&+\cdots +\prod _{i=1}^{n-1}\sin ^{2}\theta _i\mathrm{d}\theta _n^{2}. \end{aligned}$$

(2)

The most general form of the energy momentum tensor for the anisotropic matter distribution can be taken as [2]

$$\begin{aligned} T_{\nu }^{\mu }=(\rho +p_r)u^{\mu }u_{\nu }-p_rg^{\mu }_{\nu }+(p_t-p_r)\eta ^{\mu }\eta _{\nu } \end{aligned}$$

(3)

with $u^{\mu }u_{\mu }=-\eta ^{\mu }\eta _{\mu }=1$.

Here $\rho$ is the energy density, and $p_r$ and $p_t$ are, respectively, the radial and transverse pressures of the fluid.

In higher dimensions, the Einstein field equations can be written as [11]

$$\begin{aligned} \mathrm{e}^{-\lambda }\left( \frac{n\lambda '}{2r}-\frac{n(n-1)}{2r^{2}}\right) +\frac{n(n-1)}{2r^{2}}&= 8\pi \rho ,\end{aligned}$$

(4)

$$\begin{aligned} \mathrm{e}^{-\lambda }\left( \frac{n(n-1)}{2r^{2}}+\frac{n\nu '}{2r}\right) -\frac{n(n-1)}{2r^{2}}&= 8\pi p_r, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{1}{2}\mathrm{e}^{-\lambda }\left[ \frac{1}{2}(\nu ')^{2}+\nu ''-\frac{1}{2}\lambda '\nu ' +\frac{(n-1)}{r}(\nu '-\lambda ')\right] \nonumber \\&\quad +\frac{(n-1)(n-2)}{2r^{2}}(\mathrm{e}^{-\lambda }-1)=8\pi p_t. \end{aligned}$$

(6)

Here a prime denotes differentiation with respect to the radial co-ordinate $r$.

In higher dimensions, the density function of a static and spherically symmetric Lorentzian distribution of smeared matter is as follows [8]:

$$\begin{aligned} \rho =\frac{M\sqrt{\phi }}{\pi ^{2}(r^{2}+\phi )^{\frac{n+2}{2}}} \end{aligned}$$

(7)

where $M$ is the smeared mass distribution.

3 Model of the wormhole

Let us assume the constant redshift function for our model, the so-called tidal force solution. Therefore, we have

$$\begin{aligned} \nu =\nu _0 \end{aligned}$$

(8)

where $\nu _0$ is a constant. Using Eq. (8) the Einstein field equations become

$$\begin{aligned}&\frac{nb'}{2r^{2}}+\frac{n(n-2)b}{2r^{3}}=\frac{8\pi M\sqrt{\phi }}{\pi ^{2}(r^{2}+\phi )^{\frac{n+2}{2}}},\end{aligned}$$

(9)

$$\begin{aligned}&8\pi p_r=-\frac{n(n-1)}{2r^{3}}b,\end{aligned}$$

(10)

$$\begin{aligned}&8\pi p_t=\frac{(3-n)(n-1)}{2r^{3}}b-\frac{(n-1)b'}{2r^{2}} \end{aligned}$$

(11)

where $b(r)=r(1-\mathrm{e}^{-\lambda })$ is termed the shape function of the wormhole.

From Eq. (9) we get

$$\begin{aligned} b(r)=\frac{16M\sqrt{\phi }}{n\pi }\frac{1}{r^{n-2}}\int \frac{r^{n}}{(r^{2}+\phi )^{\frac{n+2}{2}}}\mathrm{d}r+\frac{C}{r^{n-2}}. \end{aligned}$$

(12)

Now, the following criteria need to be imposed for the existence of a wormhole solution:

• 1. The redshift function $\nu (r)$ must be finite everywhere (traversability criterion).

• 2. $\frac{b(r)}{r}\rightarrow 0$ as $n \rightarrow \infty$ (asymptotically flat spacetime).

• 3. At the throat $(r_0)$ of the wormhole $b(r_0)=r_0$ and $b'(r_0)<1$ (flaring out condition).

• 4. $b(r)<r$ for $r>r_0$ (regularity of metric coefficient).

3.1 Four dimensional spacetime ($n=2$)

In four dimensional spacetime, the shape function of the wormhole is given by

$$\begin{aligned} b(r)=\frac{4M\sqrt{\phi }}{\pi }\left\{ \frac{1}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r}{r^{2}+\phi } \right\} +C \end{aligned}$$

(13)

where $C$ is an integration constant.

The radial and transverse pressure can be obtained as

$$\begin{aligned} 8\pi p_r&= -\frac{1}{r^{3}}\left[ \frac{4M\sqrt{\phi }}{\pi }\left\{ \frac{1}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) \!-\!\frac{r}{r^{2}\!+\!\phi }\right\} \!+\!C\right] ,\end{aligned}$$

(14)

$$\begin{aligned} 8\pi p_t&= \frac{1}{2r^{3}}\left[ \frac{4M\sqrt{\phi }}{\pi }\left\{ \frac{1}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r}{r^{2}+\phi } \right\} +C \right] \nonumber \\&-\frac{4M\sqrt{\phi }}{\pi }\frac{1}{(r^{2}+\phi )^{2}}. \end{aligned}$$

(15)

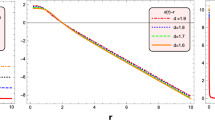
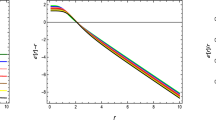
Next, we are going to verify whether the shape function $b(r)$ (see Fig. 1) satisfies all the physical requirements to form a wormhole structure (which is given in Sect. 3). For this purpose we assign some arbitrary values to the parameters (mentioned in the figures). Form Fig. 2, we see that $\frac{b(r)}{r}\rightarrow 0$ as $r\rightarrow \infty$, which verifies that the spacetime is asymptotically flat. The throat $r_0$ of the wormhole occurs where $b(r_0)=r_0$, which is the root of the function $G(r)=b(r)-r$. We have plotted $G(r)$ in Fig. 3. The throat of the wormhole occurs where $G(r)$ cuts the $r$ axis. From this figure, we see that $r_0=0.165$. Figure 3 also indicates that $G(r)<0$ when $r > r_0$, which implies $\frac{b(r)}{r}<1$ when $r > r_0$. One can also notice from Eq. (9) that at the throat of the wormhole $(r_0=0.165)$ $b'(0.165)=0.207 < 1$. Hence the flare-out condition is also satisfied.

Fig. 1

A diagram of the shape function of the wormhole in four dimensions against $r$

Fig. 2

Asymptotically flatness condition in four dimensional spacetime against $r$

Fig. 3

The throat of the wormhole in 4D occurs where $G(r)$ cuts the $r$-axis

According to Morris and Thorne [1] the embedding surface of the wormhole is denoted by the function $z(r)$, which satisfies the following differential equation:

$$\begin{aligned} \frac{\mathrm{d}z}{\mathrm{d}r}=\pm \frac{1}{\sqrt{\frac{r}{b(r)}-1}}. \end{aligned}$$

(16)

In the above equation $\frac{\mathrm{d}z}{\mathrm{d}r}$ diverges at the throat of the wormhole, from which one concludes that the embedding surface is vertical at the throat. Equation (16) gives

$$\begin{aligned} z=\pm \int _{r_0^{+}}^{r}\frac{\mathrm{d}r}{\sqrt{\frac{r}{b(r)}-1}}. \end{aligned}$$

(17)

The proper radial distance of the wormhole is given by

$$\begin{aligned} l(r)=\pm \int _{r_0^{+}}^{r}\frac{\mathrm{d}r}{\sqrt{1-\frac{b(r)}{r}}} \end{aligned}$$

(18)

(here $r_0$ is the throat of the wormhole.) The two integrals mentioned in Eqs. (17) and (18) cannot be done analytically. But we can perform it numerically. The numerical values are obtained by fixing a particular value of the lower limit and by changing the upper limit, as given in Tables 1 and 2, respectively. The embedding diagram $z(r)$ and the radial proper distance $l(r)$ of the 4D wormhole are depicted in Figs. 4 and 5, respectively. Figure 6 represents the full visualization of the 4D wormhole obtained by rotating the embedding curve about the $z$-axis.

Table 1 Values of $z(r)$ for different $r$. $r_0^{+} =0.17$, $\phi =0.001$, $M=0.075$

Table 2 Values of $l(r)$ for different $r$. $r_0^{+} =0.17$, $\phi =0.001$, $M=0.075$

Fig. 4

The embedding diagram of the 4D wormhole against $r$

We can match our interior wormhole spacetime with the Schwarzschild exterior spacetime

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{2m}{r}\right) \mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{1-\frac{2m}{r}}+r^{2}\mathrm{d}\Omega _2^{2} \end{aligned}$$

(19)

where

$$\begin{aligned}\mathrm{d}\Omega _2^{2}=\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}.\end{aligned}$$

Fig. 5

The radial proper length of the 4D wormhole against $r$

Now by using the Darmois–Israel [18, 19] junction condition the surface energy density ($\sigma$) and the surface pressure ($\mathcal {P}$) at the junction surface $r=R$ can be obtained as

$$\begin{aligned} \sigma&= -\,\frac{1}{4\pi R}\left[ \sqrt{1-\frac{2m}{R}\!+\!\dot{R}^{2}}-\sqrt{1\!-\!\frac{b(R)}{R}+\dot{R}^{2}}\right] ,\end{aligned}$$

(20)

$$\begin{aligned} \mathcal {P}&= \frac{1}{8\pi R}\left[ \frac{1-\frac{m}{R}+\dot{R}+R\ddot{R}}{\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}}\right. \nonumber \\&- \left. \frac{1-\frac{b(R)}{R} +\dot{R}^{2}+R\ddot{R}-\frac{\dot{R}^{2}}{2}\frac{b-b'R}{R-b}}{\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}}\right] . \end{aligned}$$

(21)

The mass of the thin shell $(m_\mathrm{s})$ is given by

$$\begin{aligned} m_\mathrm{s}=4\pi R^{2}\sigma . \end{aligned}$$

(22)

Using the expression of $\sigma$ in Eq. (20) (considering the static case) one can obtain the mass of the wormhole as

$$\begin{aligned} m=\frac{b(R)}{2}-\frac{m_\mathrm{s}}{2}\left[ \frac{m_\mathrm{s}}{R}+2\sqrt{1-\frac{b(R)}{R}}\right] . \end{aligned}$$

(23)

This gives the mass of the wormhole in terms of the thin shell mass.

Fig. 6

The full visualization of the 4D wormhole surface is obtained by rotating the embedding curve with respect to the $z$-axis

Let us use the conservation identity given by

$$\begin{aligned} S_{j,i}^{i}=-\left[ \dot{\sigma }+2\frac{\dot{R}}{R}(\mathcal {P} +\sigma )\right] , \end{aligned}$$

which gives the following expression:

$$\begin{aligned} \sigma '=-\frac{2}{R}(\mathcal {P}+\sigma )+\Xi \end{aligned}$$

(24)

where $\Xi$ is given by

$$\begin{aligned} \Xi =-\frac{1}{4\pi R}\frac{b-b'R}{2(R-b)}\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}. \end{aligned}$$

(25)

The above expression $\Xi$ will be used to discuss the stability analysis of the wormhole. From Eq. (22) we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2a}\right) ''=\Upsilon -4\pi \sigma '\eta \end{aligned}$$

where

$$\begin{aligned} \eta =\frac{\mathcal {P}'}{\sigma '} \quad \text {and}\quad \Upsilon =\frac{4\pi }{R}(\sigma +\mathcal {P})+2\pi R\Xi ' \end{aligned}$$

where the parameter $\sqrt{\eta }$ generally denotes the velocity of the sound. So one must have $0<\eta \le 1$.

3.2 Five dimensional spacetime ($n=3$)

In five dimensional spacetime, the shape function of the wormhole is given by

$$\begin{aligned} b(r)=\frac{1}{r}\left\{ -\frac{16M\sqrt{\phi }}{9\pi }\frac{3r^{2}+2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}+C\right\} . \end{aligned}$$

(26)

The radial and transverse pressures can be obtained as

$$\begin{aligned} 8\pi p_r=-\frac{3}{r^{4}}\left\{ -\frac{16M\sqrt{\phi }}{9\pi }\frac{3r^{2} +2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}+C\right\} , \end{aligned}$$

(27)

$$\begin{aligned} 8\pi p_t&= \frac{1}{r^{4}}\left\{ -\frac{16M\sqrt{\phi }}{9\pi }\frac{3r^{2} +2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}+C\right\} \nonumber \\&-\frac{16M\sqrt{\phi }}{3\pi }\frac{1}{(r^{2}+\phi )^{\frac{5}{2}}}. \end{aligned}$$

(28)

Next our aim is to verify whether $b(r)$ (see Fig. 7) satisfies all the physical requirements to form a shape function. From Fig. 8 we see that $\frac{b(r)}{r}\rightarrow 0$ as $n\rightarrow \infty$, so spacetime is asymptotically flat. The throat of the wormhole is the point where $G(r)=b(r)-r$ cuts the $r$ axis. From Fig. 9 we see that $G(r)$ cuts the ‘$r$’ axis at 0.16, so the throat of the wormhole occurs at $r=0.16$ for the 5D spacetime. Consequently, we see that $b'(0.16)=0.89<1$. For $r>r_0$, we see that $b(r)-r <0$, which implies $\frac{b(r)}{r}<1$ for $r>r_0$. The slope of the shape function is still positive up to $r_1 = 0.22$ but soon it becomes negative (see Fig. 10). So we have a valid wormhole solution from the throat up to a certain radius, say, $r_1$ = 0.22, which is a convenient cut-off for the wormhole. This indicates that we get a restricted class of wormholes in five dimensional spacetime. In this case we can match our interior solution to the exterior 5D line element given by

$$\begin{aligned} \mathrm{d}s^{2}&= -\left( 1-\frac{2\mu }{r^2}\right) \mathrm{d}t^{2}+\left( 1-\frac{2\mu }{r^2}\right) ^{-1}\mathrm{d}r^{2}\\&+r^{2}\left( \mathrm{d}\theta _1^{2}+\sin ^{2}\theta _1\mathrm{d}\theta _2^{2}+\sin ^{2}\theta _1\sin ^{2}\theta _2\mathrm{d}\theta _3^{2}\right) \end{aligned}$$

where $\mu$, the mass of the 5D wormhole, is defined by $\mu =\frac{4Gm}{3\pi }$.

Fig. 7

Diagram of the shape function of the wormhole in five dimensions against $r$

Fig. 8

Diagram of the flatness of the wormhole spacetime in five dimensions against $r$

Fig. 9

The throat of the wormhole in 5D case

Fig. 10

The slope is still positive up to $r_1 = 0.22$ but soon becomes negative

To obtain the profile of embedding diagram and radial proper distance in a $\theta _3= \mathrm{constant}$ plane in the 5D wormhole spacetime, we have to find the integral of Eqs. (17) and (18), respectively. But it is not possible to perform it analytically. So we will need the help of numerical integration. The numerical values are obtained by fixing a particular value of the lower limit and by changing the upper limit, which are given in Tables 3 and 4, respectively. The embedding diagram $z(r)$ and the radial proper distance $l(r)$ of the 5D wormhole are depicted in Figs. 12 and 11, respectively. Figure 13 represents the full visualization of the 5D wormhole obtained by rotating the embedding curve about the $z$-axis.

Table 3 Values of $z(r)$ of 5D spacetime for different $r$. $r_0^{+} =0.16$, $\phi =0.001$, $M=0.075$

Table 4 Values of $l(r)$ of 5D spacetime for different $r$. $r_0^{+} =0.165$, $\phi =0.001$, $M=0.075$

Fig. 11

The radial proper distance of the 5D wormhole in $\theta _3=0$ plane

Fig. 12

The embedding diagram of the 5D wormhole in $\theta _3=0$ plane

Fig. 13

The full visualization of the 5D wormhole in $\theta _3=0$ plane

3.3 Six and seven dimensional spacetime ($n=4$) and ($n=5$)

In six dimensional spacetime, the shape function of the wormhole is given by

$$\begin{aligned} b(r)\!=\!\frac{1}{r^{2}}\left[ \frac{M\sqrt{\phi }}{2\pi }\left\{ \frac{3}{\sqrt{\phi }}\tan ^{-1}\left( \frac{r}{\sqrt{\phi }} \right) \!-\!\frac{5r^{3}\!+\!3r\phi }{(r^{2}\!+\!\phi )^{2}}\right\} \!+\!C \right] .\nonumber \\ \end{aligned}$$

(29)

The other parameters are given by

$$\begin{aligned} 8\pi p_r&= \!-\!\frac{6}{r^{5}}\left[ \frac{M\sqrt{\phi }}{2\pi }\left\{ \frac{3}{\sqrt{\phi }}\tan ^{-1} \left( \frac{r}{\sqrt{\phi }} \right) \!-\!\frac{5r^{3}\!+\!3r\phi }{(r^{2}\!+\!\phi )^{2}}\right\} \!+\!C \right] \nonumber \\\end{aligned}$$

(30)

$$\begin{aligned} 8\pi p_t&= \frac{3}{2r^{5}}\left[ \frac{M\sqrt{\phi }}{2\pi }\left\{ \frac{3}{\sqrt{\phi }}\tan ^{-1} \left( \frac{r}{\sqrt{\phi }}\right) \!-\!\frac{5r^{3}\!+\!3r\phi }{(r^{2}\!+\!\phi )^{2}}\right\} \!+\!C \right] \nonumber \\&-\frac{6M\sqrt{\phi }}{\pi }\frac{1}{(r^{2}+\phi )^{3}}. \end{aligned}$$

(31)

Next we want to verify whether $b(r)$ obeys the physical conditions (see Sect. 3) to be a shape function of a wormhole. From Fig. 14 we see that $b(r)$ is a strictly decreasing function of $r$, and the same situation arises in seven dimensional spacetime $(n=5)$. In seven dimensional spacetime the shape function of the wormhole (see Fig. 15) is given by

$$\begin{aligned} b(r)=\frac{1}{r^{3}}\left[ -\frac{16M\sqrt{\phi }}{75\pi }\frac{15r^{4}+20r^{2}\phi +8\phi ^{2}}{(r^{2}+\phi ) ^{\frac{5}{2}}} +C\right] . \end{aligned}$$

(32)

Fig. 14

Diagram of the shape function of the wormhole in six dimensions against $r$

Fig. 15

Diagram of the shape function of the wormhole in seven dimensions against $r$

So it is clear that no wormhole solutions exist for $n>3$ because for $n>3$ the shape function $b(r)$ [see Eq. (12)] contains a factor $\frac{1}{r^{n-2}}$, which is a dominating one, and if we consider $n>3$ the shape function becomes monotonically decreasing. As a result $b(r)$ in a higher dimensional spacetime fails to be a shape function.

3.4 Energy condition

In this subsection, we are going to verify whether our particular model of wormholes (both 4D and 5D) satisfies all the energy conditions, namely the NEC, the weak energy condition, the strong energy condition, stated as follows:

$$\begin{aligned}&\rho \ge 0,\end{aligned}$$

(33)

$$\begin{aligned}&\rho +p_r\ge 0,\end{aligned}$$

(34)

$$\begin{aligned}&\rho +p_t\ge 0,\end{aligned}$$

(35)

$$\begin{aligned}&\rho +p_r+2p_t\ge 0. \end{aligned}$$

(36)

The profiles of the energy conditions for four and five dimensional wormholes are shown in Figs. 16 and 17, respectively. The figures indicate that $\rho +p_r <0$ i.e. the NEC is violated to hold a wormhole open.

Fig. 16

The energy condition in 4D against $r$

Fig. 17

Diagram of energy condition for the 5D wormhole plotted against $r$

4 Linearized stability analysis

In this section, we will focus on the stability of the wormhole in four dimensional spacetime ($n=2$).

Using the expression of Eq. (20) in Eq. (22) and rearranging we get

$$\begin{aligned} \dot{R}^{2}+V(R)=0 \end{aligned}$$

(37)

where $V(R)$ is given by

$$\begin{aligned} V(R)=F(R)-\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}-\left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) ^{2} \end{aligned}$$

where $F(R)=1-\frac{b+2m}{2R}$ (for details of the calculation see the Appendix.)

To discuss the linearized stability analysis let us take a linear perturbation around a static radius $R_0$. Expanding $V(R)$ by a Taylor series around the radius of the static solution $R= R_0$, one can obtain

$$\begin{aligned} V(R)&= V(R_0)+(R-R_0)V'(R_0)+\frac{(R-R_0)^{2}}{2}V''(R_0)\nonumber \\&+O\left[ (R-R_0)^{3}\right] \end{aligned}$$

(38)

where the prime denotes the derivative with respect to $R$. Since we are linearizing around the static radius $R=R_0$ we must have $V(R_0)=0,V'(R_0)=0$. The configuration will be stable if $V(R)$ has a local minimum at $R_0$ i.e. if $V''(R_0)>0$.

Now from the relation $V'(R_0)=0$ we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) '&= \left( \frac{R_0}{m_\mathrm{s}(R_0)}\right) \left[ F'(R_0)-2\left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) \right. \nonumber \\&\qquad \qquad \qquad \times \left. \left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) '\right] , \end{aligned}$$

(39)

$$\begin{aligned} V''(R)&= F''(R)-2\left( \frac{m_\mathrm{s}(R)}{2R}\right) \left( \frac{m_\mathrm{s}(R)}{2R}\right) ''\nonumber \\&\quad -2\left\{ \left( \frac{m_\mathrm{s}(R)}{2R}\right) '\right\} ^{2}\!-\!2\left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) \nonumber \\&\quad \times \left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) ''\!-\!2\left\{ \left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) '\right\} ^{2}\nonumber .\end{aligned}$$

Now the configuration will be stable if $V''(R_0)>0$. i.e. if

$$\begin{aligned} \Omega _0>2\pi R_0 \sigma _0 \left( \frac{m_\mathrm{s}(R)}{2R}\right) ''|_{R=R_0} \end{aligned}$$

(40)

where $\Omega _0$ is given by

$$\begin{aligned} \Omega _0&= \frac{F''(R_0)}{2}-\left\{ \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) '\right\} ^{2} -\left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) \\&\quad \times \left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) ''-\left\{ \left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) '\right\} ^{2}. \end{aligned}$$

Now using the expression of $\left( \frac{m_\mathrm{s}}{2R_0}\right) ''$ in Eq. (40) we get

$$\begin{aligned} \eta (R_0) \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R=R_0}>\frac{1}{2\pi }\left[ \sigma _0 \Xi (R_0) -\frac{\Omega _0}{2\pi R_0}\right] \end{aligned}$$

(41)

(for details of the calculation see the Appendix), which gives

$$\begin{aligned} \eta (R_0)>\Theta (R_0) \left( \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}\right) ^{-1}|_{R=R_0}\quad \text {if } \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R=R_0}>0 \end{aligned}$$

(42)

and

$$\begin{aligned} \eta (R_0)<\Theta (R_0) \left( \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}\right) ^{-1}|_{R=R_0} \quad \text {if } \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R=R_0}<0 \end{aligned}$$

(43)

where $\Theta (R_0)=\frac{1}{2\pi }\left[ \sigma (R_0) \Xi (R_0) -\frac{\Omega _0}{2\pi R_0}\right]$.

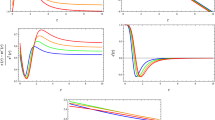
For a wormhole in four dimensional spacetime, we have $\frac{\mathrm{d}\sigma _0^{2}}{\mathrm{d}R_0}<0$ (see Fig. 18). Therefore, we conclude that the stability of the wormhole is given by Eq. (43). Next we are interested to search the region where our 4D wormhole model is stable. To obtain the region we have plotted the graph of $\eta (R_0)=\Theta (R_0) \left( \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}\right) ^{-1}|_{R=R_0}$, which is shown in Fig. 19. The stability region is given by the inequality $\eta (R_0)<\Theta (R_0) \left( \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}\right) ^{-1}|_{R=R_0}$. So the region of stability is given below the curve. Interestingly, we see that $0<\eta \le 1$, which indicates that our wormhole is very stable.

Fig. 18

$\frac{\mathrm{d}\sigma _0^{2}}{\mathrm{d}R_0}$ plotted against $R_0$

Fig. 19

Plot of $\eta (R_0)$

5 Active mass function

We will discuss the active gravitational mass within the region from the throat $r_0$ up to the radius $R$ for two cases, because we have seen earlier that wormholes exist only in four and five dimensional spacetimes. For the 4D case the active gravitational mass can be obtained as

$$\begin{aligned} M_{\mathrm{active}}&= \int _{r_0}^{r}4\pi \rho r^{2}\nonumber \\&= \frac{2M}{\pi }\left[ \tan ^{-1}\left( \frac{r}{\sqrt{\phi }}\right) -\frac{r\sqrt{\phi }}{r^{2}+\phi }\right] _{r_0}^{r}. \end{aligned}$$

(44)

For the 5D case, one can get the active gravitational mass as

$$\begin{aligned} M_{\mathrm{active}}=\int _{r_0}^{r}2\pi ^{2}r^{3}\rho \mathrm{d}r=2M\sqrt{\phi } \left[ -\frac{1}{3}\frac{3r^{2}+2\phi }{(r^{2}+\phi )^{\frac{3}{2}}}\right] _{r_0}^{r}. \end{aligned}$$

(45)

To see the nature of the active gravitational mass $M_{\mathrm{active}}$ of the wormhole, we have drawn Figs. 20 and 21 for four and five dimensional spacetimes, respectively. The positive nature indicates that the models are physically acceptable.

Fig. 20

The variation of $M_{\mathrm{active}}$ for the 4D case against $r$

Fig. 21

The variation of $M_{\mathrm{active}}$ for the 4D case against $r$ in the restricted range

6 Total gravitational energy

Following Lyndell-Bell et al.’s [20] and Nandi et al.’s [21] prescription, we shall try to calculate the total gravitational energy of the wormholes for four and five dimensional spacetimes. For the 4D case we have

$$\begin{aligned} E_g=\frac{1}{2}\int _{r_0}^{r}[1-(g_{rr})^{\frac{1}{2}}]\rho r^{2} \mathrm{d}r +\frac{r_0}{2}. \end{aligned}$$

(46)

For the 5D case we have

$$\begin{aligned} E_g=\frac{\pi }{4}\int _{r_0}^{r}[1-(g_{rr})^{\frac{1}{2}}]\rho r^{3} \mathrm{d}r +\frac{ \pi r_0}{4}, \end{aligned}$$

(47)

where

$$\begin{aligned} g_{rr}=\left( 1-\frac{b(r)}{r}\right) ^{-1}. \end{aligned}$$

Since it not possible to find analytical solutions of these integrals, we solve them numerically assuming the range of the integration from the throat $r_0$ to the embedded radial space of the wormhole geometry (see Tables 5, 6). Figures 22 and 23 show that $E_g > 0$, which indicates that there is repulsion around the throat. This nature of $E_g$ is expected for the construction of a physically valid wormhole.

Table 5 Values of $E_g$ of the 4D wormhole for different $r$. $r_0 =0.165$, $\phi =0.001$, $M=0.075$

Table 6 Values of $E_g$ of the 5D wormhole for different $r$. $r_0 =0.165$, $\phi =0.001$, $M=0.075$

Fig. 22

The variation of $E_g$ for 4D case against $r$

Fig. 23

The variation of $E_g$ for 5D case against $r$ in the restricted range

7 Discussion and concluding remarks

In the present paper, we have obtained a new class of wormhole solutions in the context of a noncommutative geometry background. In this paper we have chosen a Lorentzian distribution function as the density function of the wormhole in noncommutativity-inspired spacetime. We have examined whether wormholes with a Lorentzian distribution exist in different dimensional spacetimes. From the above investigations, we see that the wormholes exist only in four and five dimensional spacetimes. In case of five dimensions, we have observed that a wormhole exists in a very restricted region. From six dimensions and onwards the shape function of the wormhole becomes monotonic decreasing due to the presence of the term $\frac{1}{r^{n-2}}$ in the shape function. So from the above discussion, we can conclude that no wormhole solution exists beyond five dimensional spacetime. In the case of four and five dimensional wormholes, $\rho +p_r<0$, i.e. the NECs are violated. We note that a four dimensional wormhole is large enough, however, one can get a five dimensional wormhole geometry only in a very restricted region. We have matched our interior wormhole solution to the exterior Schwarzschild spacetime in the presence of a thin shell. The linearized stability analysis under a small radial perturbation has also been discussed for a four dimensional wormhole. We have provided the region where the wormhole is stable and with the help of a graphical representation we have proved that $0<\eta \le 1$, i.e. our wormhole is very stable. Finally, we can compare our results with those obtained in Ref. [11]. In both models (ours and the one of Ref. [11]), noncommutativity replaces point-like structures by smeared objects. In Ref. [11], one had used the Gaussian distribution as the density function in the noncommutativity-inspired spacetime, whereas we have used a Lorentzian distribution as the density function in the noncommutativity-inspired spacetime. In both cases, it is shown that wormhole solutions exist only in four and five dimensional spacetimes. However, our study is more complete compared to Ref. [11]. We have studied the stability and calculated the active gravitational mass and the total gravitational energy of the wormhole. Thus, we can comment that this study confirms the result that wormhole solutions exist in noncommutativity-inspired geometry only for four and five dimensional spacetimes.

Appendices

Appendix 1

We have

$$\begin{aligned} m_\mathrm{s}=4\pi R^{2}\sigma ; \end{aligned}$$

using the expression of $\sigma$ we get

$$\begin{aligned}&\mathrm{or}\; \frac{m_\mathrm{s}}{4\pi R^{2}}=\frac{1}{4\pi R}\left[ \sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}.-\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}\right] \\&\quad \mathrm{or}\; \frac{m_\mathrm{s}}{R}=\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}-\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}\\&\quad \mathrm{or} \;\frac{m_\mathrm{s}}{R}-\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}=-\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}. \end{aligned}$$

Squaring both sides we get

$$\begin{aligned}&\left( \frac{m_\mathrm{s}}{R}\right) ^{2}-2\frac{m_\mathrm{s}}{R}\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}=\frac{1}{R}(b-2m)\\&\quad \mathrm{or}\; \frac{m_\mathrm{s}}{R}\left[ \frac{m_\mathrm{s}}{R}-2\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}\right] =\frac{1}{R}(b-2m)\\&\quad \mathrm{or}\; \frac{m_\mathrm{s}}{R}-2\sqrt{1-\frac{b}{R}+\dot{R}^{2}}=\frac{1}{m_\mathrm{s}}(b-2m)\\&\quad \mathrm{or}\; \frac{m_\mathrm{s}}{2R}-\frac{b(R)-2m}{2m_\mathrm{s}}=\sqrt{1-\frac{b(R)}{R}+\dot{R}^{2}}, \end{aligned}$$

and again squaring both sides we get

$$\begin{aligned} \dot{R}^{2}=\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}+\left( \frac{b(R)-2m}{2m_\mathrm{s}}\right) ^{2}+\frac{b+2m}{2R}-1. \end{aligned}$$

Now $\dot{R}^{2}=-V(R)$, which gives

$$\begin{aligned}&V(R)=1-\frac{b+2m}{2R}-\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}-\left( \frac{b-2m}{2m_\mathrm{s}}\right) ^{2}\\&V(R)=F(R)-\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}-\left( \frac{b-2m}{2m_\mathrm{s}}\right) ^{2} \end{aligned}$$

where

$$\begin{aligned} F(R)=1-\frac{b+2m}{2R}. \end{aligned}$$

Appendix 2

We have

$$\begin{aligned}&m_\mathrm{s}=4\pi R^{2}\sigma \\&\mathrm{or}\; \frac{m_\mathrm{s}}{2R}=2\pi R \sigma . \end{aligned}$$

Differentiating both sides with respect to $R$ we get

$$\begin{aligned} \mathrm{or}\; \left( \frac{m_\mathrm{s}}{2R}\right) '&= 2\pi (R \sigma '+\sigma )\\&= 2\pi R\left\{ -\frac{2}{R}(\sigma +\mathcal {P})+\Xi \right\} +2\pi \sigma \\&= -4\pi \mathcal {P}+2\pi R \Xi -2\pi \sigma . \end{aligned}$$

Differentiating both sides with respect to R we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''=-4\pi \mathcal {P}'+2\pi (R \Xi '+\Xi )-2\pi \sigma '. \end{aligned}$$

Using the value of $\sigma '$ we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''&= \!-\!4\pi \mathcal {P}'\!+\!2\pi (R \Xi '+\Xi )\!-\!2\pi \left\{ -\frac{2}{R}(\sigma \!+\!\mathcal {P})\!+\!\Xi \right\} \\&= \frac{4\pi }{R}(\sigma +\mathcal {P})+2\pi R\Xi '-4\pi \eta \sigma '; \end{aligned}$$

therefore,

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''=\Upsilon -4\pi \eta \sigma ' \end{aligned}$$

where

$$\begin{aligned} \Upsilon =\frac{4\pi }{R}(\sigma +\mathcal {P})+2\pi R\Xi '. \end{aligned}$$

Appendix 3

We have

$$\begin{aligned} V''(R)&= F''(R)-2\left( \frac{m_\mathrm{s}(R)}{2R}\right) \left( \frac{m_\mathrm{s}(R)}{2R}\right) ''\\&+2\left\{ \left( \frac{m_\mathrm{s}(R)}{2R}\right) '\right\} ^{2}-2\left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) \\&\times \left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) ''+2\left\{ \left( \frac{2m-b(R)}{2m_\mathrm{s}(R)}\right) '\right\} ^{2}. \end{aligned}$$

Now $V''(R_0)>0$ gives

$$\begin{aligned} \Omega _0>2\pi R_0\sigma _0 \left( \frac{m_\mathrm{s}}{2R_0}\right) '', \end{aligned}$$

where

$$\begin{aligned}&\Omega _0=\frac{F''(R_0)}{2}-2\left\{ \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) '\right\} ^{2}-\left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) \\&\qquad \,\,\times \left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) '' -\left\{ \left( \frac{2m-b(R_0)}{2m_\mathrm{s}(R_0)}\right) '\right\} ^{2}\\&\Omega _0>2\pi R_0\sigma [\Xi (R_0)-4\pi \eta (R_0)\sigma _0']\\&\Omega _0>2\pi R_0\sigma _0\Xi (R_0)-4\pi ^{2}R_0\eta (R_0) \frac{\mathrm{d}\sigma _0^{2}}{\mathrm{d}r_0}\\&\frac{\Omega _0}{2\pi R_0}>\sigma (R_0)\Xi (R_0)-2\pi \eta (R_0)\frac{\mathrm{d}\sigma _0^{2}}{\mathrm{d}r_0}\\&2\pi \eta (R_0)\frac{\mathrm{d}\sigma _0^{2}}{\mathrm{d}r_0}>\sigma _0\Xi (R_0)-\frac{\Omega _0}{2\pi R_0}, \end{aligned}$$

which gives

$$\begin{aligned} \eta (R_0)\frac{\mathrm{d}\sigma _0^{2}}{\mathrm{d}r_0}>\frac{1}{2\pi }\left[ \sigma _0\Xi (R_0)-\frac{\Omega _0}{2\pi R_0}\right] . \end{aligned}$$