1 Introduction

The idea that the spacetime has more than four dimensions and our universe is a brane or domain wall embedded in higher dimensional spacetime [1–6] has been proposed for a long time and discussed extensively. It is believed that the braneworld scenario can supply new insights for solving the gauge hierarchy problem and the cosmological constant problem [7–17].

There are many discussions of branes both in the frames of general relativity and modified gravities. In Refs. [18–23], non-minimal coupling branes in scalar–tensor gravity were discussed and the mass hierarchy problem can be solved in scalar–tensor thin branes model [18]. A brane model in the recently presented EiBI gravity theory was constructed in Ref. [24] and it was found that the four-dimensional Einstein gravity can be recovered on the brane at low energy. Branes in spacetime with torsion were investigated in Refs. [25, 26] and it was shown that in \(f(T)\) gravity that the torsion of spacetime can affect the inner structure of branes [25]. Reference [27] investigated braneworld teleparallel gravity. For brane models in higher-derivative gravity there are also many references; see for examples Refs. [28–38].

In this paper, we are interested in brane solutions in the framework of higher-derivative gravities. As is well known, general relativity is a non-renormalizable theory and it suffers from the singularity problem as well as other problems. In a quantum gravity theory or the low energy effective theory of string theory, higher-order curvature terms would be added to the Einstein–Hilbert action. The principal candidates for such corrections are contracted quadratic products of the Riemann curvature tensor. With this kind of corrections, the most general correction terms has the form of \(\alpha ' R^{2}+\beta ' R_{MN}R^{MN}+\gamma ' R_{MNPQ}R^{MNPQ}\), or \(\alpha R^{2}+\beta R_{MN}R^{MN}+\gamma {\mathcal L}_{\mathrm {GB}}\), where

$$\begin{aligned} {\mathcal L}_{\mathrm {GB}}=R_{MNPQ}R^{MNPQ}-4R_{MN}R^{MN}+R^{2} \end{aligned}$$
(1)

is the Gauss–Bonnet term and it is topological invariant in four dimensions. Gravity theories with this kind of corrections were studied in detail in Ref. [39].

Nevertheless, an action with quadratic curvature terms implies that the field equations contain the fourth derivations of the metric and thus would lead to a massive ghost-like graviton. Recently, it was shown in Ref. [40] that the massive scalar mode can be eliminated and the massive ghost-like graviton becomes massless when the parameters of the quadratic curvature terms satisfy the critical condition. The corresponding theory is called critical gravity. It was generalized to higher dimensions in Ref. [41]. See Refs. [42–46] for work related to critical gravity.

In general, it is very hard to solve analytically the Einstein field equations of a higher-derivative gravity for a system with matter fields. However, for a codimension-1 brane system with the metric \(\mathrm{d}s^2 = {\mathrm {e}}^{2A(y)} \hat{g}_{\mu \nu }\) \( \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } + \mathrm{d}y^{2}\) (\(\hat{g}_{\mu \nu }\) is the maximally symmetric metric) in critical gravity, the Einstein field equations are of second order at the critical point. So it is possible to get analytical solutions in this higher-derivative gravity theory and to give some insight into some interesting questions. In Ref. [47], a flat brane scenario in five-dimensional critical gravity was investigated and some analytical solutions were found for a thin brane with the use of the junction conditions and for a thick brane. It was found that scalar perturbations for all these brane solutions are stable.

However, the flat brane scenario is the simplest case for the study of the brane world. It is well known that there are three types of branes with maximally symmetry: flat, de Sitter, and anti-de Sitter branes. Furthermore, the study of Friedmann–Robertson–Walker (FRW) branes is also interesting. It is expected that the warped brane models in higher-derivative gravities such as critical gravity may provide a new scenario in the study of the AdS/CFT correspondence, cosmologies, and phenomenological model building [29, 48]. In this paper, we generalize the work of Ref. [47] and construct the flat and warped brane solutions in \(n\)-dimensional critical gravity. The organization of this paper is as follows. In Sect. 2, we first derive the Gibbons–Hawking boundary term on the thin brane and give the junction conditions. Then we construct analytic flat and warped brane solutions with the junction conditions and investigate the hierarchy problem in the thin brane scenario. In Sect. 3, thick branes generated by a scalar field are investigated and the conditions of the splitting of the branes are obtained. Finally, our conclusion is given in Sect. 4.

2 Thin brane solutions

First we consider the thin brane models in the frame of \(n\)-dimensional critical gravity. The action is [41]

$$\begin{aligned} S = \frac{1}{2\kappa ^{2}}\int \mathrm{d}^{n}x \sqrt{-g} {\mathcal L}_{\mathrm {G}} + S_{\mathrm {B}}, \end{aligned}$$
(2)

where

$$\begin{aligned} {\mathcal L}_{\mathrm {G}}= R - (n-2)\varLambda _{0}+\alpha R^{2}+ \beta R_{MN}R^{MN} + \gamma {\mathcal L}_{\mathrm {GB}}, \end{aligned}$$
(3)

and \(\kappa \) denotes the \(n\)-dimensional gravitational constant with \(\kappa ^{2}=8\pi /M_{*}^{4}\), where \(M_{*}\) is the \(n\)-dimensional Planck mass scale. The parameters \(\alpha \) and \(\beta \) satisfy the following critical condition [41]:

$$\begin{aligned} {4(n-1)\alpha +n\beta }=0. \end{aligned}$$
(4)

The brane part \(S_{\mathrm {B}}\) of the above action is given by

$$\begin{aligned} S_{\mathrm {B}}=\int \mathrm{d}^{n-1}x\sqrt{-q}(-V_{0}), \end{aligned}$$
(5)

where \(V_0\) is the brane tension and \(q_{\mu \nu }\) is the induced metric on the brane, which is assumed to be located at the origin of the extra dimension \(x^n=y\). The capital letters \(M,N,\ldots =0,1,2,3,\ldots ,n-2,n\) and the Greek letters \(\mu ,\nu ,\ldots =0,1,2,\ldots ,n-2\) denote the indices of the \(n\)-dimensional bulk and \((n-1)\)-dimensional brane, respectively.

The equations of motion (EoMs) derived from the action (2) read

$$\begin{aligned} {\mathcal G}_{MN}+E_{MN}-\frac{\gamma }{2}H_{MN} = \kappa ^{2}T_{MN}, \end{aligned}$$
(6)

where

$$\begin{aligned} {\mathcal G}_{MN}&= R_{MN}-\frac{1}{2} R~ g_{MN} + \frac{1}{2}(n-2) \varLambda _0 g_{MN}, \end{aligned}$$
(7)
$$\begin{aligned} E_{{MN}}&= 2 \alpha R \left( R_{{MN}} -\frac{1}{4}R ~g_{{MN}}\right) \nonumber \\&+ (2\alpha + \beta ) ( g_{{MN}} \square - \nabla _M\nabla _N ) R \nonumber \\&+ 2 \beta R^{{PQ}} \left( R_{{MPNQ}} - \frac{1}{4} R_{{PQ}}~g_{{MN}}\right) \nonumber \\&+\beta \square \left( R_{{MN} }-\frac{1}{2} R~ g_{MN}\right) , \end{aligned}$$
(8)
$$\begin{aligned} H_{MN}&= g_{MN}{\mathcal L}_{\mathrm {GB}} -4 R R_{MN} + 8 R_{MP} R^{P}_{N} \nonumber \\&+ 8 R_{MANB} R^{AB} - 4R_{MABC} R_{N}^{~~ABC}, \end{aligned}$$
(9)
$$\begin{aligned} T_{MN}&= - \frac{2}{\sqrt{-g}} \frac{\delta S_{B}}{\delta g^{MN}}. \end{aligned}$$
(10)

In an \(n\)-dimensional space, we have the following relation:

$$\begin{aligned}&\alpha R^2+\beta R_{MN}R^{MN}+\gamma {\mathcal L}_{\mathrm {GB}} \nonumber \\&\quad = \frac{(n-2)\beta }{4(n-3)}C^2 -\frac{\zeta {\mathcal L}_{\mathrm {GB}} }{4(n-3)} +\frac{4(n-1)\alpha +n\beta }{4(n-1)}R^2, \end{aligned}$$
(11)

where

$$\begin{aligned} \zeta =(n-2)\beta -4(n-3)\gamma , \end{aligned}$$
(12)

and \(C^2:=C^{MNPQ}C_{MNPQ}\) is the square of the \(n\)-dimensional Weyl tensor,

$$\begin{aligned} C_{MNPQ}&= R_{MNPQ}-\frac{2}{n-2}(g_{M[P}R_{Q]N}-g_{N[P}R_{Q]M}) \nonumber \\&+\frac{2}{(n-1)(n-2)}R~g_{M[P}g_{Q]N}. \end{aligned}$$
(13)

Note that, under the critical condition (4), the last term \(R^2\) in the right hand side of Eq. (11) vanishes. So, the Lagrangian density \({\mathcal L}_G\) for the critical gravity can be reexpressed as

$$\begin{aligned} {\mathcal L}_{\mathrm {G}}={\mathcal L}_{\mathrm {EGB}}+\frac{(n-2)\beta }{4(n-3)}C^2, \end{aligned}$$
(14)

where \({\mathcal L}_{\mathrm {EGB}}\) is the Einstein–Gauss–Bonnet (EGB) term:

$$\begin{aligned} {\mathcal L}_{\mathrm {EGB}} = R - (n-2) \varLambda _{0} -\frac{\zeta {\mathcal L}_{\mathrm {GB}}}{4(n-3)}. \end{aligned}$$
(15)

In the following, we first generalize the result of the junction conditions in five dimensions in Ref. [47] to \(n\) dimensions for flat, AdS, and dS thin branes. Then we will use the generalized junction conditions to give the thin brane solutions.

2.1 Junction conditions

Following Ref. [47], we adopt the Gibbons–Hawking method to derive the junction conditions. The basic idea is as follows. The whole spacetime \(M\) is divided into two submanifolds by the thin brane, which is the boundary \(\partial M\) of the two submanifolds. The unit vector normal to the boundary \(\partial M\) is denoted by \(n^Q\) and it is outward pointing. Then the induced metric on the brane is \(q^{MN}=g^{MN}-n^M n^N\). The extrinsic curvature is defined as \(K_{MN}={\mathcal L}_\mathbf{n} q_{MN}/2 \). We denote \([F]_{\pm }:=F(0+)-F(0-)\). In the following, we let \(n^{Q}(0_{+})=n^{Q}:=(0,0,0,0,-1)\) and \(n^{Q}(0_{-}):=(0,0,0,0,+1)\) for the right and left sides, respectively. Due to the \(Z_2\) symmetry of the extra dimension, we only need to calculate the right side. See e.g. Refs. [47, 49, 50] for details.

We will deal with the \(C^2\) term and EGB term, respectively. We first consider a general geometry instead of the special case of branes with \(\mathrm{d}s^2=\mathrm{e}^{2A(y)}\hat{g}_{\mu \nu }(x)\mathrm{d}x^\mu \mathrm{d}x^\nu +\mathrm{d}y^2\). For the \(C^2\) term, we have

$$\begin{aligned}&\delta \int _M \mathrm{d}^{n} x \sqrt{-g} C^2 \supset 4\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \nonumber \\&\quad \Big [(C^{MPNQ}n_Q \delta g_{MN})_{;P} -\left( (C^{MPNQ}n_Q)_{;P}\right. \nonumber \\&\qquad \left. +\,C^{MPNQ}_{~~~~~~;Q}n_P \right) \delta g_{MN}\Big ]. \end{aligned}$$
(16)

Here, the bulk term has been omitted and only the relevant boundary term is given explicitly. In order to have a well-posed variational principle, we introduce an auxiliary field \(\varphi ^{MNPQ}\) and replace \(C^2\) with \(2\varphi ^{MNPQ}C_{MNPQ} -\varphi ^{MNPQ}\varphi _{MNPQ}\). Then from the EoM of the auxiliary field, \(\varphi ^{MNPQ}=C^{MNPQ}\), we can see that \(\varphi ^{MNPQ}\) has the same symmetry as the Weyl tensor and is also totally traceless. With the new field \(\varphi ^{MNPQ}\), Eq. (16) becomes

$$\begin{aligned}&\delta \int _M \mathrm{d}^{n} x \sqrt{-g} C^2 \supset 4\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \nonumber \\&\quad \Big [(\varphi ^{MPNQ}n_Q \delta g_{MN})_{;P}- \left( (\varphi ^{MPNQ}n_Q)_{;P}\right. \nonumber \\&\qquad \left. +\,\varphi ^{MPNQ}_{~~~~~~;Q}n_P \right) \delta g_{MN}\Big ]. \end{aligned}$$
(17)

Then with the identity [47]

$$\begin{aligned} X^M_{;M}&= D_M(q^{M}_N X^N)+ K n_NX^N+{\mathcal L}_{{\mathbf {n}}}(n_NX^N), \end{aligned}$$
(18)

where \(D_M(q^P_N X^N):=q_M^Q q^P_R(q^R_N X^N)_{;Q}\), we can show that

$$\begin{aligned}&\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} (\varphi ^{MPNQ}n_Q \delta g_{MN})_{;P}\nonumber \\&\quad =\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \Big [ \varphi ^{MPNQ}n_Q n_P{\mathcal L}_\mathbf{n} \delta g_{MN} \nonumber \\&\qquad +\Big (K\varphi ^{MPNQ}n_Q n_P +{\mathcal L}_{{\mathbf {n}}}(\varphi ^{MPNQ}n_Q n_P) \Big ) \delta g_{MN} \Big ].\nonumber \\ \end{aligned}$$
(19)

Further, the first term in the above equation can be reduced to

$$\begin{aligned}&\varphi ^{MPNQ}n_Q n_P{\mathcal L}_{{\mathbf {n}}} \delta g_{MN} \nonumber \\&\quad =2\varphi ^{MN}\delta K_{MN} -\varphi ^{MN}K_{MN}n^P n^Q\delta g_{PQ}\nonumber \\&\qquad + 2D_N(\varphi ^{MN}n^P\delta g_{PM}) -2\varphi ^{PM}_{;P}n^N\delta g_{MN}, \end{aligned}$$
(20)

where \(\varphi ^{MN}:=\varphi ^{MPNQ}n_Q n_P\). So the surface term for the \(C^2\) part is

$$\begin{aligned} \delta S_{C^2}&\supset \delta \left( \frac{1}{2\kappa ^2} \frac{(n-2)\beta }{4(n-3)} \int _M \mathrm{d}^{n-1} x \sqrt{-g} {C^2}\right) \nonumber \\&= \frac{(n-2)\beta }{2(n-3)\kappa ^2}\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \Big \{ 2\varphi ^{MN}\delta K_{MN} \nonumber \\&\quad +\Big [{\mathcal L}_\mathbf{n}\varphi ^{MN} + K\varphi ^{MN} - \varphi ^{PQ}K_{PQ}n^M n^N \nonumber \\&\quad - 2\varphi ^{P(M}_{;P}n^{N)} - (\varphi ^{MPNQ}n_Q)_{;P} \nonumber \\&\quad -\varphi ^{MPNQ}_{~~~~~~;Q}n_P \Big ] \delta g_{MN}\Big \}. \end{aligned}$$
(21)

Then with \(2\varphi ^{MN}\delta K_{MN} = 2\varphi ^{MN}\delta (K_{MN}-\frac{1}{n-1}q_{MN}K)+\frac{2}{n-1}K\varphi ^{MN}\delta q_{MN}\), we finally obtain

$$\begin{aligned} \delta S_{C^2}&\supset \frac{(n-2)\beta }{2(n-3)\kappa ^2}\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \Big [ 2\varphi ^{MN}\delta \bar{K}_{MN} \nonumber \\&\qquad +\big (W^{MN}-\varphi ^{PQ}K_{PQ}n^M n^N \big ) \delta g_{MN} \Big ], \end{aligned}$$
(22)

where

$$\begin{aligned} \bar{K}_{MN}&:= K_{MN}-\frac{1}{n-1}q_{MN}K, \end{aligned}$$
(23)
$$\begin{aligned} W^{MN}&:= \frac{n+1}{n-1}K\varphi ^{MN}+{\mathcal L}_\mathbf{n}\varphi ^{MN} -2\varphi ^{P(M}_{;P}n^{N)} \nonumber \\&- (\varphi ^{MPNQ}n_Q)_{;P} -\varphi ^{MPNQ}_{~~~~~~;Q}n_P. \end{aligned}$$
(24)

It can be shown that \(W^{MN}n_M\) \(=\) \(W^{MN}\) \(q_{MN}\) \(=\) \(W^{MN}\) \(g_{MN}\) \(=0\).

Now we can introduce the corresponding Gibbons–Hawking surface term [51] for the \(C^2\) term:

$$\begin{aligned} S_{C^2}^{\mathrm {suf}}=-\frac{(n-2)\beta }{(n-3)\kappa ^2}\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g}~\varphi ^{MN} \bar{K}_{MN}. \end{aligned}$$
(25)

So we have (considering the whole spacetime)

$$\begin{aligned}&\delta (S_{C^2}+S_{C^2}^{\mathrm {suf}})=\frac{(n-2)\beta }{2(n-3)\kappa ^2}\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \nonumber \\&\qquad \times \Big \{-2 \big [\bar{K}_{MN}\big ]_{\pm } {\delta \varphi ^{MN}} - \big [\varphi ^{PQ}K_{PQ}\big ]_\pm n^M n^N\delta g_{MN} \nonumber \\&\qquad +\big [W^{MN}\big ]_\pm \delta g_{MN} \Big \}. \end{aligned}$$
(26)

Next, we come to the EGB term in Eq. (15), for which the Gibbons–Hawking surface term was given in Refs. [52–54]:

$$\begin{aligned} S_{\mathrm {EGB}}^{\mathrm {surf}}&= \frac{1}{2\kappa ^2}\int _{\partial M}\mathrm{d}^{n-1} x \sqrt{-g} \nonumber \\&\times \Big (2K-\frac{\zeta }{(n-3)}(J-2\tilde{G}_{\mu \nu }K^{\mu \nu })\Big ) \end{aligned}$$
(27)

with \(\tilde{G}_{\mu \nu }=\tilde{R}_{\mu \nu }-q_{\mu \nu }\tilde{R}/2\) the Einstein tensor of the induced metric \(q_{\mu \nu }\) and \(J\) the trace of the following tensor:

$$\begin{aligned} J_{MN}&= \frac{1}{3}\Big (2K K_M^P K_{PN}+K^{PQ}K_{PQ}K_{MN} \nonumber \\&-K^2K_{MN}-2K_{MP}K^{PQ}K_{QN}\Big ). \end{aligned}$$
(28)

Then we have

$$\begin{aligned}&\delta (S_{\mathrm {EGB}}+S_{\mathrm {EGB}}^{\mathrm {surf}}) \nonumber \\&\quad =\frac{1}{2\kappa ^2} \delta \int _M \mathrm{d}^{n}x \sqrt{-g} \Big [ R - (n-2) \varLambda _{0} -\frac{\zeta }{4(n-3)}{\mathcal L}_{\mathrm {GB}} \Big ] \nonumber \\&\qquad +\frac{1}{2\kappa ^2} \delta \int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g}\Big (2K\!-\!\frac{\zeta }{(n\!-\!3)}(J\!-\!2\tilde{G}_{\mu \nu }K^{\mu \nu })\Big ) \nonumber \\&\quad \supset \frac{1}{2\kappa ^2}\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} (-E_{\mathrm {EGB}}^{MN})\delta g_{MN}, \end{aligned}$$
(29)

where

$$\begin{aligned} E_{\mathrm {EGB}}^{MN}&:= [K^{MN}]_{\pm }-q^{MN}[K]_{\pm } \nonumber \\&-\frac{\zeta }{2(n-3)} \Big (3[J^{MN}]_{\pm } -q^{MN} [J]_{\pm } \nonumber \\&-2P^{MPNQ}[K_{PQ}]_{\pm }\Big ), \end{aligned}$$
(30)
$$\begin{aligned} P_{MNPQ}&:= \tilde{R}_{MNPQ}-2q_{M[Q}\tilde{R}_{P]N} \nonumber \\&+2q_{N[Q}\tilde{R}_{P]M}+\tilde{R}q_{M[P}q_{Q]N}. \end{aligned}$$
(31)

Thus, from Eqs. (26) and (29), for \(n\)-dimensional critical gravity theory, we finally get

$$\begin{aligned}&\delta \big ( S_{\mathrm {EGB}}+S_{C^2} +S_{\mathrm {EGB}}^{\mathrm {surf}}+S_{C^2}^{\mathrm {suf}} \big ) \nonumber \\&\quad \supset \frac{1}{2\kappa ^2}\int _{\partial M} \mathrm{d}^{n-1} x \sqrt{-g} \Big \{\frac{(n-2)\beta }{(n-3)}\Big (-2 \big [\bar{K}_{MN}\big ]_{\pm } {\delta \varphi ^{MN}} \nonumber \\&\qquad - \big [K_{PQ}\varphi ^{PQ}\big ]_\pm n^M n^N\delta g_{MN} +\big [W^{MN}\big ]_\pm \delta g_{MN} \Big ) \nonumber \\&\qquad - E_{\mathrm {EGB}}^{MN}\delta g_{MN} \Big \}. \end{aligned}$$
(32)

So, the junction conditions are

$$\begin{aligned}&\big [\bar{K}_{MN}\big ]_\pm =0,\end{aligned}$$
(33)
$$\begin{aligned}&\big [K_{PQ}\varphi ^{PQ}\big ]_\pm =\bar{K}_{PQ}[\varphi ^{PQ}]_\pm =0,\end{aligned}$$
(34)
$$\begin{aligned}&\big [E^{MN}_{\mathrm {EGB}}\big ]_\pm -\frac{(n-2)\beta }{n-3}\big [W^{MN}\big ]_\pm =\kappa ^2T_{({\mathrm {brane}})}^{MN}. \end{aligned}$$
(35)

Here \(T_{({\mathrm {brane}})}^{MN}\) denotes the singular part of \(T^{MN}\). To avoid the \(\delta \)-function in the junction conditions, we need the stronger condition \([\varphi ^{MN}]_\pm =0\).

For the special warped geometries of flat, AdS, and dS branes, whose metrics have the form

$$\begin{aligned} \mathrm{d}s^2=\mathrm{e}^{2A(y)}\hat{g}_{\mu \nu }(x)\mathrm{d}x^\mu \mathrm{d}x^\nu +\mathrm{d}y^2, \end{aligned}$$
(36)

the first condition (33) gives no more constraint for brane solutions because \(\bar{K}_{MN}\equiv 0\); and \(C^{MPNQ}\) is continuous and its contribution vanishes. So the above junction conditions for flat, AdS, and dS brane solutions in the critical gravity are simplified as

$$\begin{aligned} \big [E^{MN}_{\mathrm {EGB}}\big ]_\pm =\kappa ^2T_{({\mathrm {brane}})}^{MN}, \end{aligned}$$
(37)

where the nonvanishing components of the brane energy-momentum tensor are \(T_{\mu \nu }^{{\mathrm {brane}}}=-V_0 \hat{g}_{\mu \nu }\). The reduced metric is \(q_{\mu \nu }=\hat{g}_{\mu \nu }(x)\mathrm{e}^{2A(y)}\). With the constraint \(A(0)=0\) and the assumption of the \(Z_2\) symmetry of the extra dimension (\(A(y)=A(-y)\)), we have \(K_{\mu \nu }(0_+)=-K_{\mu \nu }(0_-)=-A'(0_+)\hat{g}_{\mu \nu }\), and hence \([K_{\mu \nu }]_{\pm }-q_{\mu \nu }[K]_{\pm }=2(n-3)A'(0_{+})\hat{g}_{\mu \nu }\).

Next, we mainly consider the branes with maximum symmetry, namely, flat (Minkowski), AdS, and dS branes. With the explicit junction conditions, we will give the thin brane solutions. The flat brane solution in five-dimensional critical gravity has been found in Ref. [47].

2.2 Flat brane

The line element of a flat brane with the most general \((n-1)\)-dimensional Poincaré-invariant is

$$\begin{aligned} \mathrm{d}s^2 = {\mathrm {e}}^{2A(y)} \eta _{\mu \nu } \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } + \mathrm{d}y^{2}, \end{aligned}$$
(38)

where \( {\mathrm {e}}^{2A(y)} \) is the warp factor. Such a compactification is known as a warped compactification. Considering the \( Z_2 \) symmetry of the brane model, we have \( A(y)=A(-y)\). Furthermore, we can set \( {\mathrm {e}}^{2A(0)}=1\) in order to get \(q^{\mu \nu }=\eta ^{\mu \nu }\) on the brane. The bulk energy-momentum tensor reads

$$\begin{aligned} T_{MN}=-V_0 \delta ^{\mu }_{M} \delta ^{\nu }_{N}{\mathrm {e}}^{2A(y)} \eta _{\mu \nu } \delta (y), \end{aligned}$$
(39)

from which the brane energy-momentum tensor is given by

$$\begin{aligned} T_{MN}^{{\mathrm {brane}}}=-V_0 \delta ^{\mu }_{M} \delta ^{\nu }_{N} \eta _{\mu \nu }\quad {\mathrm {or}}\quad T_{\mu \nu }^{{\mathrm {brane}}}=-V_0 \eta _{\mu \nu }. \end{aligned}$$
(40)

For arbitrary \( \alpha \) and \( \beta \), the field equations (6) are fourth-order differential ones. However, at the critical point \(\alpha = - \frac{n}{4(n-1)} \beta \) [41], the bulk field equations turn out to be

$$\begin{aligned}&[2+(n-4)\zeta A'^{2}]A''=0 ,\end{aligned}$$
(41)
$$\begin{aligned}&4 \varLambda _{0} + (n-1) A'^{2} [4 + (n-4) \zeta A'^{2}]=0, \end{aligned}$$
(42)

where \(\zeta \) is given by Eq. (12), and the prime and double prime stand for the first-order and second-order derivations with respect to \(y\), respectively. Throughout this paper we will use the critical condition (4). The junction conditions read

$$\begin{aligned} (n-2)\Big [{A'+\frac{1}{6}(n-4)\zeta A'^3}\Big ]_{\pm } =-\kappa ^{2}V_{0} \end{aligned}$$
(43)

or

$$\begin{aligned} 2(n-2)\Big ({A'(0_{+})+\frac{1}{6}(n-4)\zeta A'^3(0_{+})}\Big ) =-\kappa ^{2}V_{0}, \end{aligned}$$
(44)

due to the \(Z_2\) symmetry of the extra dimension.

The solution for the warp factor \(A(y)\) is

$$\begin{aligned} A(y)&= -k |y|, \end{aligned}$$
(45)

where \(k\) is a positive parameter since we are interested in the exponentially decreasing warp factor, which could solve the hierarchy problem if we consider the two-brane model with an \(S^1/Z_2\) extra dimension [7]. Then, from Eq. (42), the naked cosmological constant is given by

$$\begin{aligned} \varLambda _0 = - (n-1) \left( 1 + \frac{1}{4}(n-4) \zeta k^2 \right) k^2. \end{aligned}$$
(46)

The brane tension is determined by the junction condition (44):

$$\begin{aligned} V_0=\frac{n-2}{3\kappa ^{2}} \left( 6+(n-4)\zeta k^2\right) k. \end{aligned}$$
(47)

It is clear that the result is consistent with the one in general relativity when \(\zeta =0\). The naked cosmological constant and brane tension are, respectively, negative and positive when \(\zeta =0\) (in this paper, we assume that \(n\ge 5\)), and they can be positive, zero, and negative when \(\zeta <0\), depending on the magnitude of \(\zeta \) compared with \(k^{-2}\). If we require that the higher-order terms in (3) are small compared with the \(R\) term, which implies \(\zeta k^2 \ll 1\), then we will have negative \(\varLambda _0\) and positive brane tension for any such \(\zeta \). If we rewrite the Einstein equations (6) as \(G_{MN}=\kappa ^{2}T^{\mathrm {eff}}_{MN}\), namely, and identify \((E_{MN}-\frac{\gamma }{2}H_{MN})/\kappa ^2 + T_{MN}\) as an effective energy-momentum tensor, then we will always get an effective positive brane tension.

The flat thin brane is embedded in an AdS\(_{n}\) spacetime, with the effective cosmological constant \(\varLambda \) given by \(\varLambda = -(n-1)k^2\). Therefore, the higher-order terms only affect the naked cosmological constant and brane tension.

For the case \(n=5\), the result reads

$$\begin{aligned} \varLambda _0&= -(4 + \zeta k^2)k^2, \end{aligned}$$
(48)
$$\begin{aligned} V_{0}&= {\kappa ^{-2}}\left( 6+\zeta k^2\right) k, \end{aligned}$$
(49)

which is the thin brane solution found in Ref. [47].

2.3 AdS brane

The metric describing an AdS brane embedded in an AdS\(_n\) spacetime is assumed to be

$$\begin{aligned} \mathrm{d}s^2&= \mathrm{e}^{2A(y)} \big [{\mathrm {e}}^{2Hx_{n-2}} (-\mathrm{d}t^{2} + \mathrm{d}x_{1}^{2} +\cdots + \mathrm{d}x_{n-3}^{2} )\nonumber \\&+\mathrm{d}x_{n-2}^{2} \big ]+ \mathrm{d}y^{2}. \end{aligned}$$
(50)

The corresponding Einstein equations beyond the thin brane turn out to be

$$\begin{aligned}&({\mathrm {e}}^{2A} A'' \!-\!H^{2})\left[ 2 + (n\!-\!4 )H^{2}\zeta {\mathrm {e}}^{-2A}+(n\!-\!4)\zeta A'^{2} \right] \!=\!0,\nonumber \\ \end{aligned}$$
(51)
$$\begin{aligned}&(n-1) A'^{2} \left[ 2(n-4)H^{2}\zeta + {\mathrm {e}}^{2A}(4+(n-4)\zeta A'^{2}) \right] \nonumber \\&\quad +4(n\!-\!1) H^{2}+ (n\!-\!1)(n-4)H^{4}\zeta {\mathrm {e}}^{-2A}+ 4\varLambda _{0}{\mathrm {e}}^{2A} \!=\!0.\nonumber \\ \end{aligned}$$
(52)

The junction conditions read

$$\begin{aligned} (n-2)\Big [A'+\frac{1}{6}(n-4)\zeta (A'^3+3H^{2}A')\Big ]_{\pm } = -{\kappa ^{2}}V_{0}. \end{aligned}$$
(53)

The solution for Eq. (51) is

$$\begin{aligned} A(y)=\ln \left[ \frac{H}{k} \cosh (k|y| + \sigma ) \right] \end{aligned}$$
(54)

with

$$\begin{aligned} \sigma ={\mathrm {arccosh}}\left( \frac{k}{H}\right) . \end{aligned}$$
(55)

Here, the two parameters should satisfy the relation: \(k>H\). Substituting the solution (54) into the second Eq. (52), we get the naked cosmological constant:

$$\begin{aligned} \varLambda _0 = - (n-1) \left( 1+ \frac{1}{4}(n-4)\zeta k^2 \right) k^2. \end{aligned}$$
(56)

Since \(R_{MN}=\varLambda g_{MN}=-(n-1)k^2 g_{MN}\), the cosmological constant of the AdS\(_{n}\) is \(\varLambda =-(n-1)k^2\). The naked cosmological constant can be positive, zero, and negative, depending on the value of the combine of the parameters \(\beta \) and \(\gamma \) (i.e., \(\zeta =-4\gamma (n-3)+\beta (n-2)\)). The junction conditions (53) give the brane tension:

$$\begin{aligned} ~V_0 = \frac{n-2}{3\kappa ^2} \left[ 6+ (n-4)(k^2+2H^2) \zeta \right] \sqrt{k^2-H^2}, \end{aligned}$$
(57)

which can be positive, negative, or zero.

2.4 dS brane

The metric describing a dS brane has the following form:

$$\begin{aligned} \mathrm{d}s^2 = {\mathrm {e}}^{2A(y)} [\mathrm{d}t^{2}+{\mathrm {e}}^{-2Ht}\delta _{ij} \mathrm{d}x^{i} \mathrm{d}x^{j}]+ \mathrm{d}y^{2}. \end{aligned}$$
(58)

The EoMs at \(y\ne 0\) are

$$\begin{aligned}&({\mathrm {e}}^{2A} A''+H^{2})\left[ 2 \!-\!(n\!-\!4) H^{2}\zeta {\mathrm {e}}^{-2A}+(n\!-\!4)\zeta A'^{2} \right] \!=\!0,\nonumber \\ \end{aligned}$$
(59)
$$\begin{aligned}&(n-1) A'^{2} \left[ -2(n-4)H^{2}\zeta + {\mathrm {e}}^{2A}(4+(n-4)\zeta A'^{2}) \right] \nonumber \\&\quad -4(n\!-\!1) H^{2} + (n\!-\!1)(n-4)H^{4}\zeta {\mathrm {e}}^{-2A}+ 4\varLambda _{0}{\mathrm {e}}^{2A}\!=\!0.\nonumber \\ \end{aligned}$$
(60)

The junction condition is similar to the case of the AdS brane:

$$\begin{aligned} (n-2)\Big [A'+\frac{1}{6}(n-4)\zeta (A'^3-3H^{2}A')\Big ]_{\pm } = -{\kappa ^{2}}V_{0}. \end{aligned}$$
(61)

The solution is

$$\begin{aligned} A(y) = \ln \left[ \frac{H}{k} \sinh (k|y| + \sigma ) \right] , \end{aligned}$$
(62)

where

$$\begin{aligned} \sigma ={\mathrm {arcsinh}}\left( \frac{k}{H}\right) . \end{aligned}$$
(63)

The naked cosmological constant and other parameters are related by

$$\begin{aligned} \varLambda _0 = - (n-1) k^2 \left( 1+ \frac{1}{4}(n-4) k^2 \zeta \right) . \end{aligned}$$
(64)

The junction condition gives the relation between the brane tension and other parameters:

$$\begin{aligned} V_0 = \frac{n-2}{3\kappa ^2}\left[ 6+ (n-4)(k^2-2H^2) \zeta \right] \sqrt{k^2+H^2}. \end{aligned}$$
(65)

Just as the case of the AdS brane, the brane tension here can also be positive, negative, or zero.

For the flat, AdS, and dS thin branes, the metric at \(y\ne 0\) satisfies \( R_{MN}=\varLambda g_{MN}\), where \(\varLambda \) is the \(n\)-dimensional effective cosmological constant. It is because these thin branes are all embedded in AdS\(_{n}\) spacetime. \(\varLambda \) is related to the naked cosmological constant \(\varLambda _{0}\) by

$$\begin{aligned} \varLambda _0 =\varLambda -\frac{n-4}{4(n-1)}\zeta \varLambda ^{2}. \end{aligned}$$
(66)

As discussed in Ref. [41], Eq. (66) has two roots, which correspond to two AdS vacuums. One of the AdS vacuums has negative energy excitations. On the other hand, to render the massive spin-2 mode into massless, we need a second critical condition [41]

$$\begin{aligned} 1+\frac{[-(n-2)^{2}\beta +4(n-3)(n-4)\gamma ]\varLambda }{2(n-1)}=0. \end{aligned}$$
(67)

Under this condition, one obtains the effective cosmological constant \(\varLambda _\mathtt{c }\) of the critical vacuum,

$$\begin{aligned} \varLambda _\mathtt{c }=-\frac{n(n-1)}{2(n-1)(n-2)^{2}\alpha +2n(n-3)(n-4)\gamma }, \end{aligned}$$
(68)

and the corresponding critical naked cosmological constant,

$$\begin{aligned} \varLambda _{0\mathtt c }=-\frac{n^{2}(n-1)\left[ (n-1)(n-2)\alpha +(n-3)(n-4)\gamma \right] }{2(n-1)(n-2)^{2}\alpha +2n(n-3)(n-4)\gamma }.\nonumber \\ \end{aligned}$$
(69)

As shown in Ref. [41], for the critical vacuum, the massive spin-2 mode become massless, and the excitation energy of the massless graviton vanishes; while for the noncritical vacuum, the spectrum still contains both massive and massless modes, and their excitation energies are of opposite signs.

Furthermore, if we require \(\zeta =0\), Eq. (66) renders \(\varLambda _{0}=\varLambda \), and there will be only one AdS vacuum. Equation (3) now is reduced to

$$\begin{aligned} {\mathcal L}_{\mathrm {G}}= R - (n-2) \varLambda _{0}+\frac{(n-2)\beta }{4(n-3)}C^{2} \end{aligned}$$
(70)

with \(\varLambda _{0}=-\frac{n}{8\alpha }\).

2.5 Effective action and mass hierarchy

To derive the effective action of gravity on the brane, we follow the procedure in Ref. [7]. The \(n\)th dimension coordinate ranges from \(-y_b\) to \(y_b\) with the topology of \(S^1/Z_2\), brane I is located at \(y=0\), and brane II at \(y=y_b\). We consider the massless gravitational fluctuations of the background metric (38):

$$\begin{aligned} \mathrm{d}s^2&= {\mathrm {e}}^{2A(y)} \hat{g}_{\mu \nu }(x) \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } + \mathrm{d}y^{2} \nonumber \\&= {\mathrm {e}}^{2A(y)} (\eta _{\mu \nu } + h_{\mu \nu }(x)) \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } + \mathrm{d}y^{2}. \end{aligned}$$
(71)

These massless gravitational fluctuations are the zero modes of the classical solution (38) and \(h_{\mu \nu }(x)\) is the physical graviton of the four-dimensional effective theory. With the help of solution (45), we have

$$\begin{aligned} \sqrt{-g} {\mathcal L}_{\mathrm {G}}&= \sqrt{-g} \big [ R - (n-2) \varLambda _{0} + \alpha R^{2} \nonumber \\&+\beta R_{MN}R^{MN} + \gamma {\mathcal L}_{\mathrm {GB}} \big ] \nonumber \\&= \sqrt{-\hat{g}} \Big [ a {\mathrm {e}}^{-(n-3)k|y|} \hat{R}\nonumber \\&+{\mathrm {e}}^{-(n-5)k|y|} \left( \alpha \hat{R}^{2} + \beta \hat{R}_{\mu \nu }\hat{R}^{\mu \nu } + \gamma \hat{{\mathcal L}}_{\mathrm {GB}} \right) \nonumber \\&+\hbox {function of }A(y), A'(y), \hbox {and }A''(y) \Big ], \end{aligned}$$
(72)

where

$$\begin{aligned} a=1-2k^2 \left[ -\frac{1}{4}(n-2)^2\beta +(n^2-5n+2)\gamma \right] , \end{aligned}$$
(73)

\(M_\mathtt{pl }\) is the \((n-1)\)-dimensional Planck scale on the brane, \(M\) is the \(n\)-dimensional Planck scale satisfying \(2M^{n-2}=\frac{1}{2\kappa ^2}\), and terms like \(\hat{g}\) and \(\hat{R}\) are constructed by \(\hat{g}_{\mu \nu }(x)\). Note that in the action (3) the terms like \(R^2\) and \(R_{MN}R^{MN}\) etc. are considered as higher-order terms compared with the \(R\) term. This is equivalent to \(\alpha R^2\), \(\beta R_{MN}R^{MN}\), and \(\gamma {{\mathcal L}}_{\mathrm {GB}} {\ll } R\), which imply \(\beta k^2,\gamma k^2 {\ll }1\). So we have \(|1-a| \ll 1\). The action of the \(n\)-dimensional gravity is reduced to

$$\begin{aligned} S_{\mathrm {G}}&= 2M^{n-2}\int \mathrm{d}^{n}x \sqrt{-g} {\mathcal L}_{\mathrm {G}} \nonumber \\&\supset 2aM^{n-2}\int _{-y_b}^{y_b} \mathrm{d}y ~{\mathrm {e}}^{-(n-3)k|y|} \int \mathrm{d}^{n-1}x \sqrt{-\hat{g}}\hat{R} \nonumber \\&+ 2M^{n-2}\int _{-y_b}^{y_b} \mathrm{d}y ~{\mathrm {e}}^{-(n-5)k|y|} \nonumber \\&\times \int \mathrm{d}^{n-1}x \sqrt{-\hat{g}}\left( \alpha \hat{R}^{2} + \beta \hat{R}_{\mu \nu }\hat{R}^{\mu \nu } + \gamma \hat{{\mathcal L}}_{\mathrm {GB}} \right) \nonumber \\&\supset S_{\mathrm {eff}}, \end{aligned}$$
(74)

where the \((n-1)\)-dimensional effective action is

$$\begin{aligned}&S_{\mathrm {eff}}= 2 M_\mathtt{pl }^{n-3} \int \mathrm{d}^{n-1}x \sqrt{-\hat{g}} \nonumber \\&\quad \qquad \,\, \times \left[ \hat{R} + b\left( \alpha \hat{R}^{2} + \beta \hat{R}_{\mu \nu }\hat{R}^{\mu \nu } + \gamma \hat{{\mathcal L}}_{\mathrm {GB}} \right) \right] ,\end{aligned}$$
(75)
$$\begin{aligned}&b= \left\{ \begin{array}{ll} \dfrac{(n-3)\left[ 1-{\mathrm {e}}^{-(n-5)ky_b} \right] }{a(n-5)\left[ 1-{\mathrm {e}}^{-(n-3)ky_b} \right] }, &{}\quad {n\ge 6}, \\ \dfrac{(n-3)ky_b}{a\left[ 1-{\mathrm {e}}^{-(n-3)ky_b} \right] }, &{}\quad {n=5}. \end{array} \right. \end{aligned}$$
(76)

Here, the effective Planck scale \(M_\mathtt{pl }\) is related by the fundamental mass \(M\) via

$$\begin{aligned} M_\mathtt{pl }^{n-3}&= \frac{2M^{n-3}}{(n-3)k} a\left[ 1-{\mathrm {e}}^{-(n-3)ky_b} \right] . \end{aligned}$$
(77)

From this, we can see that the relationship between the fundamental scale and the effective one reduces to the case in the RS1 model because \(a \doteq 1\). Hence, the \(n\)-dimensional critical gravity reduces to the \((n-1)\)-dimensional critical gravity on the brane. Substituting the metric (71) into the junction condition (35), we obtain the brane tensions of the two branes:

$$\begin{aligned} V_\mathrm{I}=-V_\mathrm{II}=\frac{n-2}{3\kappa ^{2}} \left( 6+(n-4)\zeta k^2\right) k. \end{aligned}$$
(78)

Let us consider a Higgs field on the brane II with the action (for the case \(n=5\))

$$\begin{aligned} S_H&= \int \mathrm{d}^{4}x \sqrt{-\hat{q}(y_b)} \nonumber \\&\times \left[ -\hat{q}^{\mu \nu }(y_b) D_\mu H^\dagger D_\nu H -\lambda (|H|^2-v_0^2)^2 \right] , \end{aligned}$$
(79)

where \(v_0\) is the vacuum expectation value of the Higgs field. Redefining the field \(\hat{H}={\mathrm {e}}^{-ky_b}H\), we obtain the canonical normalized action of the Higgs field \(\hat{H}\):

$$\begin{aligned} S_H&= \int \mathrm{d}^{4}x \sqrt{-\hat{g}} \nonumber \\&\times \left[ -\hat{g}^{\mu \nu } D_\mu \hat{H}^\dagger D_\nu \hat{H} -\lambda (|\hat{H}|^2-{\mathrm {e}}^{-2ky_b}v_0^2)^2 \right] . \end{aligned}$$
(80)

Therefore, the vacuum expectation value of the Higgs field \(\hat{H}\) would have a redshift due to the influence of the warped extra dimension:

$$\begin{aligned} \hat{v}_0 = {\mathrm {e}}^{-ky_b}v_0, \end{aligned}$$
(81)

which implies that the electro-weak scale has a redshift. On the other hand, the mass of the particles originates from the Yukawa coupling, and the vacuum expectation value of the Higgs field is one of the parameters that determine the mass. Hence, the effective (physical) mass also has a redshift

$$\begin{aligned} m = {\mathrm {e}}^{-ky_b}m_0. \end{aligned}$$
(82)

From the above expression, we see that the redshift of the vacuum expectation value of the Higgs field and the mass of the particles are the same as the RS1 model in Ref. [7]. So, the mass hierarchy problem is also solved in the higher-order braneworld model in the critical gravity.

3 Thick branes generated by a scalar field

In this section we study thick branes generated by a scalar field. The brane part of the action (2) is

$$\begin{aligned} S_{\mathrm {B}}=\int \mathrm{d}^{n}x\sqrt{-g}\left( -\frac{1}{2}g^{MN}\partial _{M}\phi \partial _{N}\phi -V(\phi ) \right) , \end{aligned}$$
(83)

where the scalar field is assumed as \(\phi =\phi (y)\) for flat, AdS, and dS branes considered below.

3.1 Flat brane

The line element of a flat brane generated by a scalar field is also assumed to be (38). The EoMs (6) reduce to the following second-order coupled equations:

$$\begin{aligned}&[2+(n-4)\zeta A'^{2}]A''= -\frac{2\kappa ^{2}}{n-2}\phi '^{2} , \end{aligned}$$
(84)
$$\begin{aligned}&4 \varLambda _{0} + (n-1) A'^{2} [4 + (n-4) \zeta A'^{2}] = \frac{8\kappa ^{2}}{n-2} \Big (\frac{\phi '^{2}}{2}-V\Big ), \nonumber \\ \end{aligned}$$
(85)
$$\begin{aligned}&\phi '' + (n-1)A'\phi ' - V_{\phi } = 0, \end{aligned}$$
(86)

where \(V_{\phi }\equiv \mathrm{d}V/\mathrm{d}\phi \). Note that the above three equations are not independent. To solve these equations, we introduce the superpotential function \(W(\phi )\), which is defined as

$$\begin{aligned} A'=-\frac{\kappa ^{2}}{n-2}W. \end{aligned}$$
(87)

Substituting Eq. (87) into Eqs. (84) and (85), we obtain [47]

$$\begin{aligned} \phi '&= (1+c_{1}W^{2})W_{\phi }, \end{aligned}$$
(88)
$$\begin{aligned} V&= \frac{1}{2}(1+c_{1}W^{2})^{2}W^{2}_{\phi } - c_{2}W^{4} - c_{3}W^{2} -\frac{n-2}{2\kappa ^{2}}\varLambda _{0},\nonumber \\ \end{aligned}$$
(89)

where

$$\begin{aligned} c_{1}&= \frac{(n-4) }{2(n-2)^{2}} \zeta \kappa ^{4}, \nonumber \\ c_{2}&= \frac{ (n-1)(n-4) }{8(n-2)^{3}} \zeta \kappa ^{6} , \\ c_{3}&= \frac{(n-1) }{2(n-2)} \kappa ^{2}. \nonumber \end{aligned}$$
(90)

3.1.1 The case \(\zeta =0\)

For the case \( \zeta = 0 \), we have \(c_1=c_2=0\). In order to support a kink solution for the scalar field, we first use the superpotential \(W = k v_0 \left( \phi -\frac{\phi ^3}{3v_0^2} \right) \), for which the potential is

$$\begin{aligned} V(\phi )\!=\!-\frac{(n-1) k^2\kappa ^2}{18 (n-2) v_0^2} ( \phi ^2 -v_0^2 )^2 \left[ \phi ^2 \!-\!4 v_0^2 \!-\!\frac{9(n-2)}{(n-1) \kappa ^2}\!\right] .\nonumber \\ \end{aligned}$$
(91)

The naked cosmological constant \( \varLambda _0 = -\frac{4 (n-1)k^2 v_0^4 \kappa ^4}{9 (n-2)^2} \) is negative. Substituting the superpotential into Eqs. (87) and (88), we obtain

$$\begin{aligned}&\phi (y) = v_0 \tanh (ky), \end{aligned}$$
(92)
$$\begin{aligned}&{\mathrm {e}}^{2A(y)} = {\mathrm {e}}^{-\frac{v_0^2 \kappa ^2}{3(n-2)}\tanh ^2(k y)} [ \cosh (ky) ]^{ -\frac{4 v_0^2\kappa ^2 }{3(n-2)} }. \end{aligned}$$
(93)

Also we can take another superpotential \( W=\) \(k\phi _0^2 \sin (\phi /\phi _0)\). The solution is

$$\begin{aligned}&V(\phi ) = \frac{1}{2}k^2\phi _0^2 \left( 1 + \frac{n-1}{n-2}\kappa ^2\phi _0^2\right) \cos ^2(\phi /\phi _0),\end{aligned}$$
(94)
$$\begin{aligned}&\phi (y) = 2 \mathrm {sign}(y) \phi _0 ~\arccos \left( \frac{1+{\mathrm {e}}^{-ky}}{\sqrt{2+2{\mathrm {e}}^{-2ky}}} \right) , \end{aligned}$$
(95)
$$\begin{aligned}&{\mathrm {e}}^{2A(y)} = [{\mathrm {sech}}(ky)]^{\frac{2}{n-2}\kappa ^2 \phi _0^2},\end{aligned}$$
(96)
$$\begin{aligned}&\varLambda _0 = -\frac{n-1}{(n-2)^2}k^2\kappa ^4 \phi _0^4 . \end{aligned}$$
(97)

Note that the potential here is the Sine-Gordon potential and the scalar has a single kink-like configuration. The naked cosmological constant \(\varLambda _0\) is also negative.

3.1.2 The case \(\zeta \ne 0\)

In the last subsection we cannot get a physical brane solution for a usual \(\phi ^4\) potential for vanishing \(\zeta \) with the superpotential method. However, for the case \( \zeta \ne 0 \), we can consider the usual \( \phi ^{4} \) potential by setting \( W=a \phi \). The potential turns to

$$\begin{aligned} V&= b ( \phi ^{2} - v_{0}^{2} )^2, \end{aligned}$$
(98)

where

$$\begin{aligned}&b = -\frac{ a^{4}(n\,{-}\,4)\zeta \kappa ^{6} \left[ \,{-}\,4a^{2}\zeta \kappa ^{2}(n\,{-}\,4)+(n\,{-}\,2)(n\,{-}\,1) \right] }{8(n\,{-}\,2)^{4}}, \\&v_{0}^{2} = -\frac{2(n-2)^{2}}{a^{2}(n-4)\zeta \kappa ^{4}} , \end{aligned}$$

and the corresponding cosmological constant is

$$\begin{aligned} \varLambda _{0} = \frac{n-1}{(n-4)\zeta }. \end{aligned}$$
(99)

Here, we consider the case of \(n>4\) and require \(v_0^2>0\) and \(b>0\), these lead to \(\zeta <0\) and \(\varLambda _{0}<0\). The solutions of the scalar field and the warped factor are

$$\begin{aligned}&\phi (y) = v_{0} ~ \mathrm {tanh}(ky), \end{aligned}$$
(100)
$$\begin{aligned}&{\mathrm {e}}^{2A(y)} = \left[ \cosh (ky) \right] ^{ -\frac{ 2\kappa ^{2} v_{0}^{2} }{ n-2 } }, \end{aligned}$$
(101)

where

$$\begin{aligned} k=\sqrt{\frac{-(n-4)\zeta }{2}}\frac{\kappa ^2 a^2}{n-2}. \end{aligned}$$
(102)

If a trigonometric superpotential is used, the scalar field can be a single kink, double kink, or even multi-kink, and there can be various kinds of structure of the brane. The warped factor \(A(y)\) and the scalar field are related with the extra dimension \(y\) by

$$\begin{aligned}&y=\int \frac{1}{\left( 1+c_1 W^2\right) W_{\phi }} \, \mathrm{d}\phi , \end{aligned}$$
(103)
$$\begin{aligned}&A(y)=-\frac{\kappa ^2}{n-2}\int \frac{W}{\left( 1+c_1W^2\right) W_{\phi }} \, \mathrm{d}\phi . \end{aligned}$$
(104)

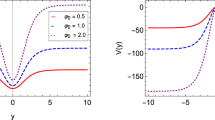
For the case \(W(\phi )=q \phi _0 \sin \frac{\phi }{\phi _0} \), we find that the parameters \(\zeta \) and \(q\) can affect the structure of the brane. To see this, we first plot the scalar potential \(V(\phi )\) in Figs. 1a, b, which show the influence of the parameters \(\zeta \) and \(q\), respectively. We can see that as \(\zeta \) and \(q\) get larger, a fake vacuum of the scalar potential will emerge, which is different from the case in general relativity, i.e. \(\zeta =0\). So we can expect that the scalar field has a double kink solution, which is shown in Figs. 2a and 3a; and the brane is a double brane, which can be seen from the energy density \(\rho (y)=T_{MN}U^M U^N=-{T^{0}}_{0} = \frac{1}{2}\phi '^2+V\) in Figs. 2b and 3b.

The corresponding cosmological constant is

$$\begin{aligned} \varLambda _0=-\frac{(n-1)q^2 \kappa ^4 \phi _0^4 \left[ (n-4)q^2 \zeta \kappa ^4 \phi _0^4+4(n-2)^2\right] }{4 (n-2)^4}.\nonumber \\ \end{aligned}$$
(105)
Fig. 1
figure 1

The shape of the scalar potential \(V(\phi )\) for different values of \(q\) and \(\zeta \). The parameters are set to \(n=5,\phi _0=1\), and \(\kappa =1\)

Full size image
Fig. 2
figure 2

The shape of the scalar field and the energy density for different values of \(\zeta \) for the flat thick brane. The parameters are set as \(q=3,n=5,\phi _0=1,\kappa =1\), and \(\zeta =0\) for the dashed red line, \(\zeta =\zeta _{c1}=\frac{5}{3}\) for the thick blue line, \(\zeta =6\) for the thin black line, and \(\zeta =12\) for the dotdashed green line

Full size image
Fig. 3
figure 3

The shape of the scalar field and the energy density for different values of \(q\) for the flat thick brane. The parameter \(q\) is set to \(q=4\) for the dashed red line, \(q=6\) for the thick blue line, and \(q=8\) for the thin black line. The other parameters are set as \(\zeta =1,n=5,\phi _0=1\), and \(\kappa =1\)

Full size image

The condition that the single brane splits into a double brane is

$$\begin{aligned} \rho ''|_{y=0}>0, \end{aligned}$$
(106)

i.e.,

$$\begin{aligned} \zeta >\zeta _{c1}\equiv \frac{ (n-2) \left[ 2(n-2)+(n-1)\kappa ^2 \phi _0^2 \right] }{2(n-4)\kappa ^4 \phi _0^2 q^2}. \end{aligned}$$
(107)

From Fig. 3b, it can be seen that with the increase of the parameter \(\zeta \), the brane becomes fatter. When \(\zeta \) reaches the critical value \(\zeta _{c1}\), there will be a wide platform around the brane location. When \(\zeta >\zeta _{c1}\), there will be a minimum for the energy density at the center of the brane and two sub-branes appear. Such a brane with inner structure may support resonant KK modes for various bulk matter fields.

3.2 AdS thick brane

Now we consider the AdS thick brane, for which the line element is also assumed as (50) and the EoMs read

$$\begin{aligned}&\left[ (n-4)\zeta H^{2}{\mathrm {e}}^{-2A} + (n-4)\zeta A'^{2} +2 \right] ( A''-H^{2}{\mathrm {e}}^{-2A}) \nonumber \\&\quad = -\frac{2\kappa ^{2}}{n-2}\phi '^{2}, \end{aligned}$$
(108)
$$\begin{aligned}&(n-1) A'^{2}\left[ (n-4)\zeta A'^{2}+2(n-4)H^{2}\zeta {\mathrm {e}}^{-2A}+ 4 \right] \nonumber \\&\qquad +4(n-1)H^{2}{\mathrm {e}}^{-2A} + (n-4)(n-1)\zeta H^{4}{\mathrm {e}}^{-4A} + 4\varLambda _{0} \nonumber \\&\quad =\frac{8\kappa ^{2}}{n-2}\Big (\frac{1}{2}\phi '^{2}-V\Big ), \end{aligned}$$
(109)
$$\begin{aligned}&\phi '' + (n-1)A'\phi '-\frac{\partial V}{\partial \phi } = 0. \end{aligned}$$
(110)

3.2.1 The case \(\zeta =0\)

For the case \(\zeta =0\), we consider the Sine-Gordon potential

$$\begin{aligned} V(\phi ) = -\frac{1}{16} (n-2) \phi _0^2 \, \left[ \mathrm {cos} \left( \frac{4k \phi }{\phi _0} \right) +1 \right] . \end{aligned}$$
(111)

Then we get the following solution:

$$\begin{aligned}&{\mathrm {e}}^{2A(y)} = {\mathrm {cosh}}^2(k y), \end{aligned}$$
(112)
$$\begin{aligned}&\phi (y) = \frac{ \phi _0 }{k} ~ \mathrm {arctan}\left( \mathrm {tanh}\left( \frac{k y}{2}\right) \right) , \end{aligned}$$
(113)

where

$$\begin{aligned} \phi _0&= \frac{2\sqrt{(n-2)(H^2-k^2)}}{ \kappa }. \end{aligned}$$
(114)

The cosmological constant is

$$\begin{aligned} \varLambda _0&= -(n-1)k^2, \end{aligned}$$
(115)

which is negative. Therefore, the AdS thick brane is embedded in an asymptotic AdS spacetime. It is interesting to note that the single kink scalar connects the adjacent locations of the extrema of the scalar potential, and the energy density

$$\begin{aligned} \rho = -\frac{1}{8}(n-2)\phi _0^2 {\mathrm {sech}}^2(ky) \end{aligned}$$
(116)

is negative. This is very different from the case of flat branes.

3.2.2 The case \(\zeta \ne 0\)

For the case \(\zeta <0\), we find a solution for a \(\phi ^4\) model:

$$\begin{aligned} {\mathrm {e}}^{A(y)}&= \sqrt{ -\frac{1}{2} H^{2} \zeta (n-4) } \cosh (ky), \end{aligned}$$
(117)
$$\begin{aligned} \phi (y)&= \mathrm {sign}(y) \phi _{0}(1-{\mathrm {sech}}(ky)), \end{aligned}$$
(118)
$$\begin{aligned} V(\phi )&= b [ (| \phi | - \phi _{0})^{2} - v_{0}^{2} ]^2 - b v_0^4, \end{aligned}$$
(119)

in which

$$\begin{aligned}&b = -\frac{ (n-3)(n-4) \zeta \kappa ^2 k^4}{2 (n-2) \left[ {2+k^2 (n-4) \zeta }\right] ^2}, \end{aligned}$$
(120)
$$\begin{aligned}&\phi _{0} = \frac{1}{k{\kappa }}\left| {2+ (n-4)\zeta k^2} \right| \sqrt{-\frac{(n-2) }{2(n-4) \zeta }}, \end{aligned}$$
(121)
$$\begin{aligned}&v_{0}^2 = \frac{n-2}{n-3} \phi _0^2. \end{aligned}$$
(122)

The energy density \(\rho (y)\) of the system is

$$\begin{aligned} \rho (y)&= \frac{\phi _0^2}{4k^2} [ (k^4-n+2){\mathrm {cosh}}(2ky) \nonumber \\&-k^2-1]{{\mathrm {sech}}}[k y]^4. \end{aligned}$$
(123)

From the above expression of the energy density we can see that the brane tension of the AdS brane is negative, which is different from the cases of flat and dS branes. The solution of the scalar field is a double kink. At the boundaries of the extra dimension, the scalar field \( \phi \rightarrow \pm \phi _0\), which are locations of the extrema of the scalar potential, but not the locations of the minima. This is the reason why the energy density is negative. The shape of the scalar field, the potential, and the energy density are shown in Fig. 4a–c.

Fig. 4
figure 4

The shape of the potential, the scalar field, and the energy density for different values of \(k\) for the AdS thick brane. The parameter \(\zeta \) is set to \(\zeta =-1.0\) for the dashed red line, \(\zeta =-1.5\) for the thick blue line, and \(\zeta =-2.0\) for the thin black line. The other parameters are set as \(n=5,H=1.0,k=0.5\), and \(\kappa =1.0\)

Full size image

The cosmological constant is

$$\begin{aligned} \varLambda _0 =-\frac{1}{4} k^2 (n-1) \left[ (n-4) \zeta k^2+4 \right] . \end{aligned}$$
(124)

For the following warped factor:

$$\begin{aligned} {\mathrm {e}}^{2A(y)}={\mathrm {cosh}}^{-2}(ky), \end{aligned}$$
(125)

the numerical solutions of the scalar field and energy density are shown in Fig. 5a, b for different values of \(\zeta \). From Eq. (108), \(\phi '^2(y)\ge 0\) implies

$$\begin{aligned} \zeta \ge -\frac{2}{(n-4)H^2}, \end{aligned}$$
(126)

which yields

$$\begin{aligned} \rho \le 0,\quad \rho ''|_{y=0}>0. \end{aligned}$$
(127)

Therefore, the brane is a single brane with negative tension. It is interesting to note that, the scalar is a double kink when \(\zeta = -\frac{2}{(n-4)H^2}\). This double-kind structure could contribute to the resonant structure of bulk fermions. The cosmological constant is

$$\begin{aligned} \varLambda _0 =-\frac{1}{4} (n-1) k^2 \left[ (n-4) \zeta k^2+4 \right] . \end{aligned}$$
(128)
Fig. 5
figure 5

The shape of the scalar field and energy density for different values of \(\zeta \) for the AdS thick brane. The parameter \(\zeta \) is set to \(\zeta = -\frac{2}{(n-4)H^2}\) for the dashed red line, \(\zeta =0\) for the thick blue line, and \(\zeta = \frac{2}{(n-4)H^2}\) for the thin black line. The other parameters are set to \(n=5,\kappa =1.0,k=1.0\), and \(H=2.0\)

Full size image

3.3 dS thick brane

In order to simplify the EoMs in the case of dS brane, we introduce the conformal coordinates. The line element is assumed as

$$\begin{aligned} \mathrm{d}s^2 = \mathrm{e}^{2A} [-\mathrm{d}t^{2}+{\mathrm {e}}^{-2Ht}\delta _{ij} \mathrm{d}x^{i} \mathrm{d}x^{j}+ \mathrm{d}z^{2}]. \end{aligned}$$
(129)

Then the EoMs turn out to be

$$\begin{aligned}&\left[ (n-4)\zeta {\mathrm {e}}^{-2A} (A'^{2}-H^{2}) +2 \right] (A''+H^{2}-A'^2) \nonumber \\&\quad = -\frac{2\kappa ^{2}}{n-2}\phi '^{2}, \end{aligned}$$
(130)
$$\begin{aligned}&(n-1)(A'^{2}-H^{2})\left[ (n-4)\zeta {\mathrm {e}}^{-2A}(A'^{2}-H^{2})+4 \right] \nonumber \\&\qquad + 4{\mathrm {e}}^{-2A}\varLambda _0 =\frac{4\kappa ^{2}}{n-2}(\phi '^{2}-2{\mathrm {e}}^{2A}V), \qquad \end{aligned}$$
(131)
$$\begin{aligned}&{\mathrm {e}}^{-2A}\left[ \phi ''+(n-2)A'\phi '\right] -\frac{\partial V}{\partial \phi } = 0, \end{aligned}$$
(132)

where the prime denotes the derivative with respect to \(z\).

3.3.1 The case \(\zeta =0\)

For the case \(\zeta =0\), the EoMs reduce to the ones in general relativity. The solution for \(n=5\) has been given in Ref. [55–57] in general relativity. For arbitrary \(n\), we consider the following potential:

$$\begin{aligned} V(\phi )&= \frac{(n-2)}{2p \kappa ^2 } \left[ (n-2)p+1 \right] H^{2} \cos ^{2(1-p)}\left( \frac{2\phi }{\phi _0}\right) ,\nonumber \\ \end{aligned}$$
(133)

where the parameter \(p\) satisfies \(0<p<1\). The solution of the warped factor and scalar field is

$$\begin{aligned}&{\mathrm {e}}^{2A(z)} = {\mathrm {cosh}}^{-2p}\left( \frac{Hz}{p}\right) , \end{aligned}$$
(134)
$$\begin{aligned}&\phi (z) = \phi _{0} \mathrm {arctan}\left( \mathrm {tanh}\left( \frac{Hz}{2p}\right) \right) , \end{aligned}$$
(135)

with

$$\begin{aligned} \phi _0 = \frac{2}{ \kappa }\sqrt{(n-2)p(1-p)}. \end{aligned}$$
(136)

The corresponding naked cosmological constant is

$$\begin{aligned} \varLambda _0 = 0. \end{aligned}$$
(137)

Since \(R_{MN}(z\rightarrow \infty )\rightarrow 0\), the effective cosmological constant is also zero. So the dS thick brane is embedded in an \(n\)-dimensional Minkowski spacetime. The energy density is given by

$$\begin{aligned} \rho = \frac{3(1+p)H^2}{p\kappa ^2} {\mathrm {sech}}^{2(1-p)}\left( \frac{H}{p}z\right) . \end{aligned}$$
(138)

3.3.2 The case \(\zeta \ne 0\)

For the case \(\zeta \ne 0\), it is hard to find a closed solution. For the following warped factor:

$$\begin{aligned} {\mathrm {e}}^{2A(z)}&= {\mathrm {cosh}}^{-2p}\left( \frac{Hz}{p}\right) , \end{aligned}$$
(139)

the numerical solutions of the scalar field and energy density are shown in Figs. 6 and 7 for different values of \(H\) and \(\zeta \), respectively.

Fig. 6
figure 6

The shape of the scalar field and energy density for different values of \(H\) for the dS thick brane. The parameter \(H\) is set to \(H=0.8\) for the dashed red line, \(H=1.1\) for the thick blue line, and \(H=1.4\) for the thin black line. The other parameters are set to \(n=5,p=0.1,\varLambda _0=0.0,\kappa =1.0\), and \(\zeta =1.0\)

Full size image
Fig. 7
figure 7

The shape of the scalar field and energy density for different values of \(\zeta \) for the dS thick brane. The parameters are set to \(n=5,\varLambda _0=0.0,\kappa =1.0,p=0.1,H=1.0\), and \(\zeta =0\) for the dashed red line, \(\zeta =\zeta _{c2}=1.12195\) for the thick blue line, \(\zeta =1.56\) for the thin black line, and \(\zeta =\frac{2}{(n-4)H^2}=2\) for the dotdashed green line

Full size image

We can see that as \(H\) and \(\zeta \) get larger, the scalar field turns to a double kink (see Figs. 6a, 7a); and the brane splits into two sub-branes, which can be seen from the energy density \(\rho \) in Figs. 6b and 7b. This is different from the case of \(\zeta =0\).

The condition that the single brane splits into a double brane is

$$\begin{aligned} \zeta > \zeta _{c2} \equiv \frac{ 2(n-2)p +4 }{(n-4)\left[ (n-4)p+4 \right] H^2}. \end{aligned}$$
(140)

4 Conclusion

In this paper, we generalized the Minkowski brane models in five-dimensional critical gravity in Ref. [47] to warped ones in \(n\) dimensions. For thin brane models in arbitrary dimensional critical gravity theory, the Gibbons–Hawking surface term and the junction conditions were derived. It was found that for the special case of flat, AdS, and dS thin branes the \(C^2\) term in the action has no contribution to these junction conditions. The solutions for both thin and thick branes were obtained at the critical point \(\alpha =-\frac{n}{4(n-1)}\beta \).

We found that the combination of the parameters \(\beta \) and \(\gamma \) in the action (3), i.e., \(\zeta \equiv \beta (n-2)-4\gamma (n-3)\), has a nontrivial effect on the brane solutions. All the flat, AdS, and dS thin branes are embedded in an AdS\(_{n}\) spacetime, and the effective cosmological constant \(\varLambda \) of the AdS\(_{n}\) spacetime equals the naked one \(\varLambda _0\) only when the combined coefficient \(\zeta =0\). The naked cosmological constant and brane tension can be positive, zero, and negative, depending on the value of \(\zeta \). Following the procedure in Ref. [7], we reduce the \(n\)-dimensional critical gravity to the \((n-1)\)-dimensional critical gravity on the brane, and the mass hierarchy problem was also solved in the higher-order braneworld model in the critical gravity.

For the thick flat branes, when \(\zeta =0\), we got two analytical solutions, both of which describe a single brane generated by a kink-like scalar. When \(\zeta \ne 0\), the analytical and numerical solutions were obtained. It was found that the brane will split into a double brane when one of the parameters \(\zeta \) and \(k\) is larger than its critical value. Such a brane with inner structure may support resonant KK modes for various bulk matter fields. All these flat branes are embedded in an \(n\)-dimensional AdS spacetime.

For the thick AdS branes, the scalar connects the adjacent locations of the extrema of the scalar potential, and the energy density is negative. This is very different from the cases of flat and dS branes. The scalar can have a single or double kink configuration, but the brane has no inner structure. These AdS branes are also embedded in an \(n\)-dimensional AdS spacetime.

For the thick dS branes, when \(\zeta =0\) and the scalar potential is taken as the Sine-Gordon one, the brane has positive energy density but has no inner structure. When \(\zeta \ne 0\), the inner structure of the dS brane will appear when the parameter \(\zeta \) or \(H\) is larger than its critical value. The energy density of the brane system is positive for any \(\zeta \). These dS branes are embedded in an \(n\)-dimensional Minkowski spacetime.

We have investigated the branes with maximally symmetry, where a dS brane can be considered as an \((n-1)\)-dimensional exponentially expanding universe. We can also consider a FRW brane and reconsider the cosmological constant problem and inflation in the frame of brane cosmology [58]. Moreover, we can also consider higher codimension branes, but the equations of motion will be fourth-order differential ones even if the critical condition (4) is satisfied. It will be difficult to solve them analytically.