1 Introduction

Cosmic acceleration is one of the biggest puzzles in modern cosmology [1–17]. There are mainly two approaches to explain this extremely counterintuitive phenomenon: dark energy (DE) [18–88] and modified gravity (MG) [89–98]. For recent reviews, see [99–108].

Cosmological observations are of essential importance to understanding cosmic acceleration, and one of the most important observations is type Ia supernovae (SNe Ia) [109–113]. In 2010, the Supernova Legacy Survey (SNLS) group released their 3 years data, i.e. SNLS3 dataset [114]. Soon after, using this dataset, Conley et al. [115] and Sullivan et al. [116] presented the SN-only cosmological results and the joint cosmological constraints, respectively. Unlike other supernova (SN) group, the SNLS team treated two important quantities, stretch–luminosity parameter \(\alpha \) and color–luminosity parameter \(\beta \) of SNe Ia, as free model parameters.

There are many factors that can lead to systematic uncertainties of SNe Ia. One of the most important factors is the potential SN evolution, i.e. the possibility for the redshift evolution of \(\alpha \) and \(\beta \). The current studies show that \(\alpha \) is consistent with a constant, but the hints for the evolution of \(\beta \) have been found in [117–121]. For example, in [122], using a linear \(\beta (z) = \beta _0 + \beta _1 z\), Mohlabeng and Ralston studied the case of Union2.1 dataset and found that \(\beta \) deviates from a constant at 7\(\sigma \) confidence levels (CL). Wang and Wang [123] found, for the SNLS3 data, \(\beta \) increases significantly with \(z\) at the 6\(\sigma \) CL; moreover, they proved that this conclusion is insensitive to the lightcurve fitter models, or the functional form of \(\beta (z)\) assumed [123]. Therefore, the evolution of \(\beta \) is a common phenomenon for various SN datasets, and should be taken into account seriously.

It is very interesting to study the effects of a time-varying \(\beta \) on parameter estimation. Wang et al. [124] explored this issue by considering the \(\Lambda \)-cold-dark-matter (\(\Lambda \)CDM) model, the \(w\)CDM model, and the Chevallier–Polarski–Linder (CPL) model. Soon after, Wang et al. [125] studied the case of holographic dark energy (HDE) model, which is a physically plausible DE candidate based on the holographic principle. It is found that, for all these DE models, adding a parameter of \(\beta \) can reduce \(\chi ^2_{\min }\) by \(\sim \)36; in addition, considering the evolution of \(\beta \) is helpful in reducing the tension between SN and other cosmological observations. It should be mentioned that, in principle, there is always an important possibility that DE directly interacts with CDM. This factor was not considered in [124, 125]. To do a comprehensive analysis on the effects of a time-varying \(\beta \), it is necessary to extend the corresponding discussions to the case of interacting dark energy (IDE) models.

In this paper, we explore the effects of a time-varying \(\beta \) on the cosmological constraints of the IDE model. Three kinds of interaction terms are taken into account. In addition to the SNLS3 data, we also use the Planck distance prior data [126], the galaxy clustering (GC) data from sloan digital sky survey (SDSS) data release 7 (DR7) [127] and baryon oscillation spectroscopic survey (BOSS) [128], as well as the direct measurement of Hubble constant \(H_0=73.8\pm 2.4 \,\mathrm{km/s/Mpc}\) from the Hubble Space Telescope (HST) observation [17].

We describe our method in Sect. 2, present our results in Sect. 3, and conclude in Sect. 4. In this paper, we assume today’s scale factor \(a_{0}=1\), thus the redshift \(z=a^{-1}-1\). The subscript “0” always indicates the present value of the corresponding quantity, and the natural units are used.

2 Methodology

2.1 Theoretical models

In this paper, we consider a non-flat universe. The Friedmann equation can be written as

$$\begin{aligned} 3M_{\mathrm{pl}}^{2}H^{2}=\rho _{c}+\rho _{de}+\rho _{r}+\rho _{b}+\rho _{k}, \end{aligned}$$
(1)

where \(M_{\mathrm{pl}}\equiv 1/\sqrt{8\pi G}\) is the reduced Planck mass, \(\rho _{c}\), \(\rho _{de}\), \(\rho _{r}\), \(\rho _{b}\) and \(\rho _{k}\) are the energy densities of CDM, DE, radiation, baryon and curvature, respectively. The reduced Hubble parameter \(E(z)\equiv H(z)/H_{0}\) satisfies

$$\begin{aligned} E^{2}&= \Omega _{c0}\frac{\rho _{c}}{\rho _{c0}}+\Omega _{de0}\frac{\rho _{de}}{\rho _{de0}} +\Omega _{r0}\frac{\rho _{r}}{\rho _{r0}}+\Omega _{b0}\frac{\rho _{b}}{\rho _{b0}}\nonumber \\&+\,\Omega _{k0}\frac{\rho _{k}}{\rho _{k0}}, \end{aligned}$$
(2)

where \(\Omega _{c0}\), \(\Omega _{de0}\), \(\Omega _{r0}\), \(\Omega _{b0}\) and \(\Omega _{k0}\) are the present fractional densities of CDM, DE, radiation, baryon and curvature, respectively. Since \(\Omega _{c0}+\Omega _{de0}+\Omega _{r0}+\Omega _{b0}+\Omega _{k0}=1\), we do not treat \(\Omega _{de0}\) as an independent parameter in this paper. In addition, \(\rho _{r}=\rho _{r0}(1+z)^{4}\), \(\rho _{b}=\rho _{b0}(1+z)^{3}\), \(\rho _{k}=\rho _{k0}(1+z)^{2}\), \(\Omega _{r0}=\Omega _{m0} / (1+z_\mathrm{eq})\), where \(\Omega _{m0} = \Omega _{c0}+\Omega _{b0}\) and \(z_\mathrm{eq}=2.5\times 10^4 \Omega _{m0} h^2 (T_\mathrm{cmb}/2.7\,\mathrm{K})^{-4}\) (here we take \(T_\mathrm{cmb}=2.7255\,\mathrm{K}\)).

Considering the interaction between dark sectors, the dynamical evolutions of CDM and DE become

$$\begin{aligned}&\dot{\rho }_c+3H\rho _c=Q, \end{aligned}$$
(3)
$$\begin{aligned}&\dot{\rho }_{de}+3H(\rho _{de}+p_{de})=-Q, \end{aligned}$$
(4)

where the over dot denotes the derivative with respect to the cosmic time \(t\), \(p_{de} = w\rho _{de}\) is the pressure of DE, \(w\) is the equation of state of DE, and \(Q\) is the interaction term, which describes the energy transfer rate between CDM and DE. Notice that \(a=\frac{1}{1+z}\) and \(H=\frac{\dot{a}}{a}\), we have \(\frac{\mathrm{d}}{\mathrm{d}t}=-H(1+z)\frac{\mathrm{d}}{\mathrm{d}z}\). Then Eqs. (3) and (4) can be rewritten as

$$\begin{aligned}&(1+z)\frac{\mathrm{d}\rho _{c}}{\mathrm{d}z}-3\rho _{c}=-Q/H,\end{aligned}$$
(5)
$$\begin{aligned}&(1+z)\frac{\mathrm{d}\rho _{de}}{\mathrm{d}z}-3(1+w)\rho _{\mathrm{d}e}=Q/H. \end{aligned}$$
(6)

The solutions of these two equations depend on the specific forms of \(Q\).

So far, the microscopic origin of interaction between dark sectors is still a big puzzle to us. To study the issue of interaction, one has to write down the possible forms of \(Q\) by hand. In this paper we consider the following four cases:

$$\begin{aligned} Q_{0}&= 0,\end{aligned}$$
(7)
$$\begin{aligned} Q_{1}&= 3\gamma H\rho _{c},\end{aligned}$$
(8)
$$\begin{aligned} Q_{2}&= 3\gamma H\rho _{de},\end{aligned}$$
(9)
$$\begin{aligned} Q_{3}&= 3\gamma H\frac{\rho _{c}\rho _{de}}{\rho _{c}+\rho _{de}}, \end{aligned}$$
(10)

where \(\gamma \) is a dimensionless coupling parameter describing the strength of interaction. Notice that the model with \(Q_{0}\) denotes the case without dark sector interaction; the models with \(Q_{1}\) and \(Q_{2}\) are very popular, and both of them have been widely studied in the literature (see, e.g., [129–153]); the model with \(Q_{3}\) is proposed in [154], and it can solve the early-time superhorizon instability and future unphysical CDM density problems at the same time. For simplicity, hereafter we call them \(w\)CDM model, I\(w\)CDM1 model, I\(w\)CDM2 model, and I\(w\)CDM3 model, respectively.

For the \(w\)CDM model, the reduced Hubble parameter \(E(z)\equiv H(z)/H_{0}\) can be written as

$$\begin{aligned} E(z)&= \big (\Omega _{r0}(1+z)^{4}+(\Omega _{c0}\!+\!\Omega _{b0})(1+z)^{3}\!+\!\Omega _{k0}(1+z)^{2} \nonumber \\&\quad +\Omega _{de0}(1+z)^{3(1+w)}\big )^{1/2}. \end{aligned}$$
(11)

For the I\(w\)CDM1 model, Eq. (5) has a general solution

$$\begin{aligned} \rho _{c}=\rho _{c0}(1+z)^{3(1-\gamma )}. \end{aligned}$$
(12)

Substituting Eq. (12) into Eq. (6) and using the initial condition \(\rho _{de}(z=0)=\rho _{de0}\), we get

$$\begin{aligned} \rho _{de}&= \frac{\gamma \rho _{c0}}{\gamma +w}\bigg ((1+z)^{3(1+w)}-(1+z)^{3(1-\gamma )}\bigg )\nonumber \\&+\,\rho _{de0}(1+z)^{3(1+w)}. \end{aligned}$$
(13)

Then substituting Eqs. (12) and (13) into Eq. (2), we obtain

$$\begin{aligned} E(z)&=\Bigg (\Omega _{r0}(1+z)^{4}+\Omega _{b0}(1+z)^{3}+\Omega _{k0}(1+z)^{2}\nonumber \\&\quad +\Omega _{de0}(1+z)^{3(1+w)}+\Omega _{c0}\big (\frac{\gamma }{w+\gamma }(1+z)^{3(1+w)}\nonumber \\&\quad +\frac{w}{w+\gamma }(1+z)^{3(1-\gamma )}\big )\Bigg )^{1/2}. \end{aligned}$$
(14)

For the I\(w\)CDM2 model, Eq. (6) has a general solution

$$\begin{aligned} \rho _{de}=\rho _{de0}(1+z)^{3(1+w+\gamma )}. \end{aligned}$$
(15)

Substituting Eq. (15) into Eq. (5) and using the initial condition \(\rho _{c}(z=0)=\rho _{c0}\), we get

$$\begin{aligned} \rho _{c}&= \rho _{c0}(1+z)^{3}+\frac{\gamma \rho _{de0}}{w+\gamma }(1+z)^{3}\nonumber \\&-\frac{\gamma \rho _{de0}}{w+\gamma }(1+z)^{3(1+w+\gamma )}. \end{aligned}$$
(16)

Then substituting Eqs. (15) and (16) into Eq. (2), we have

$$\begin{aligned}&E(z)\!=\!\Bigg (\Omega _{r0}(1+z)^{4}\!+\!(\Omega _{c0}\!+\!\Omega _{b0})(1+z)^{3}\!+\!\Omega _{k0}(1+z)^{2}\nonumber \\&\quad +\Omega _{de0}\big (\frac{\gamma }{w+\gamma }(1+z)^{3} + \frac{w}{w+\gamma }(1+z)^{3(1+w+\gamma )} \big )\Bigg )^{1/2}.\nonumber \\ \end{aligned}$$
(17)

For the I\(w\)CDM3 model, the energy densities of CDM and DE satisfy

$$\begin{aligned} \rho _{c}&=\rho _{c0}(1+z)^{3}\nonumber \\&\quad \times \Bigg (\frac{\rho _{c0}}{\rho _{c0}+\rho _{de0}} +\frac{\rho _{de0}}{\rho _{c0}+\rho _{de0}}(1+z)^{3(w+\gamma )}\Bigg )^{-\frac{\gamma }{w+\gamma }},\end{aligned}$$
(18)
$$\begin{aligned} \rho _{de}&=\rho _{de0}(1+z)^{3(1+w+\gamma )}\nonumber \\&\quad \times \Bigg (\frac{\rho _{c0}}{\rho _{c0}+\rho _{de0}} +\frac{\rho _{de0}}{\rho _{c0}+\rho _{de0}}(1+z)^{3(w+\gamma )}\Bigg )^{-\frac{\gamma }{w+\gamma }}. \end{aligned}$$
(19)

Substituting Eqs. (18) and (19) into Eq. (2), we get

$$\begin{aligned} E(z)&=\Bigg (\Omega _{c0}C(z)(1+z)^{3}+\Omega _{de0}C(z)(1+z)^{3(1+w+\gamma )} \nonumber \\&\quad +\Omega _{r0}(1+z)^{4}+\Omega _{b0}(1+z)^{3}+\Omega _{k0}(1+z)^{2}\Bigg )^{1/2}, \end{aligned}$$
(20)

where

$$\begin{aligned} C(z)=\Bigg (\frac{\Omega _{c0}}{\Omega _{c0}+\Omega _{de0}}+\frac{\Omega _{de0}}{\Omega _{c0}+\Omega _{de0}}(1+z)^{3(w+\gamma )}\Bigg )^{-\frac{\gamma }{w+\gamma }}.\nonumber \\ \end{aligned}$$
(21)

Note that in Eqs. (11), (14), (17), (20), and (21), \(\Omega _{de0}\) is not an independent parameter, which is given by \(\Omega _{de0}=1-\Omega _{c0}-\Omega _{b0}-\Omega _{r0}-\Omega _{k0}\).

2.2 Observational data

In this subsection, we introduce how to include the SNLS3 data into the \(\chi ^2\) analysis.

For the SNLS3 sample, the observable is \(m_B\), which is the rest-frame peak B-band magnitude of the SN. By considering three functional forms (linear case, quadratic case, and step function case), Wang and Wang [123] showed that the evolutions of \(\alpha \) and \(\beta \) are insensitive to functional form of \(\alpha \) and \(\beta \) assumed. So in this paper, we just adopt a constant \(\alpha \) and a linear \(\beta (z) = \beta _{0} + \beta _{1} z\). Then the predicted magnitude of an SN becomes

$$\begin{aligned} m_\mathrm{mod}=5 \log _{10}\mathcal{D}_L(z) - \alpha (s-1) +\beta (z) \mathcal{C} + \mathcal{M}, \end{aligned}$$
(22)

where \(s\) and \(\mathcal{C}\) are the stretch measure and the color measure for the SN light curve. Here \(\mathcal{M}\) is a parameter representing some combination of SN absolute magnitude \(M\) and Hubble constant \(H_0\). It must be emphasized that, to include host-galaxy information in the cosmological fits, Conley et al. [115] split the SNLS3 sample based on host-galaxy stellar mass at \(10^{10} M_{\odot }\), and made \(\mathcal{M}\) to be different for the two samples. Therefore, unlike other SN samples, there are two values of \(\mathcal{M}\), \(\mathcal{M}_1\) and \(\mathcal{M}_2\), for the SNLS3 data Moreover, Conley et al. removed \(\mathcal{M}_1\) and \(\mathcal{M}_2\) from cosmology fits by analytically marginalizing over them (for more details, see the appendix C of [115], as well as the the public code which is available at https://tspace.library.utoronto.ca/handle/1807/24512). In this paper, we just follow the recipe of [115]. The luminosity distance \(\mathcal{D}_L(z)\) is defined as

$$\begin{aligned} \mathcal{D}_L(z)\equiv H_0 (1+z_\mathrm{hel}) r(z), \end{aligned}$$
(23)

where \(z\) and \(z_\mathrm{hel}\) are the CMB rest frame and heliocentric redshifts of SN. In addition, the comoving distance \(r(z)\) is given by

$$\begin{aligned} r(z)=H_0^{-1}\, |\Omega _{k0}|^{-1/2} \mathrm{sinn}\big (|\Omega _{k0}|^{1/2}\, \Gamma (z)\big ), \end{aligned}$$
(24)

where \(\Gamma (z)=\int _0^z\frac{dz'}{E(z')}\), and \(\mathrm{sinn}(x)=\sin (x)\), \(x\), \(\sinh (x)\) for \(\Omega _{k0}<0\), \(\Omega _{k0}=0\), and \(\Omega _{k0}>0\), respectively.

For a set of \(N\) SNe with correlated errors, the \(\chi ^2\) function is

$$\begin{aligned} \chi ^2_{SN}=\Delta {\mathbf m}^T \cdot {\mathbf C}^{-1} \cdot \Delta {\mathbf m}, \end{aligned}$$
(25)

where \(\Delta m \equiv m_B-m_\mathrm{mod}\) is a vector with \(N\) components, and \({\mathbf C}\) is the \(N\times N\) covariance matrix of the SN, given by

$$\begin{aligned} {\mathbf C}={\mathbf D}_\mathrm{stat}+{\mathbf C}_\mathrm{stat}+{\mathbf C}_\mathrm{sys}. \end{aligned}$$
(26)

\({\mathbf D}_\mathrm{stat}\) is the diagonal part of the statistical uncertainty, given by [115]

$$\begin{aligned} {\mathbf D}_{\mathrm{stat},ii}&= \sigma ^2_{m_B,i}+\sigma ^2_\mathrm{int} + \sigma ^2_\mathrm{lensing}+ \sigma ^2_{\mathrm{host}\,\mathrm{correction}} \nonumber \\&+ \left[ \frac{5(1+z_i)}{z_i(1+z_i/2)\ln 10}\right] ^2 \sigma ^2_{z,i} \nonumber \\&+\alpha ^2 \sigma ^2_{s,i}+\beta (z_i)^2 \sigma ^2_{\mathcal{C},i} + 2 \alpha C_{m_B s,i} \nonumber \\&- 2 \beta (z_i) C_{m_B \mathcal{C},i} -2\alpha \beta (z_i) C_{s \mathcal{C},i}, \end{aligned}$$
(27)

where \(C_{m_B s,i}\), \(C_{m_B \mathcal{C},i}\), and \(C_{s \mathcal{C},i}\) are the covariances between \(m_B\), \(s\), and \(\mathcal{C}\) for the \(i\)th SN, \(\beta _i=\beta (z_i)\) are the values of \(\beta \) for the \(i\)th SN. Notice that \(\sigma ^2_{z,i}\) includes a peculiar velocity residual of 0.0005 (i.e., 150 km/s) added in quadrature. Following [115], we fix the intrinsic scatter \(\sigma _{\mathrm{int}}\) to ensure that \(\chi ^2/\mathrm{dof}=1\). Varying \(\sigma _{\mathrm{int}}\) could have a significant impact on parameter estimation; see [119, 155] for details.

We define \({\mathbf V} \equiv {\mathbf C}_\mathrm{stat} + {\mathbf C}_\mathrm{sys}\), where \({\mathbf C}_\mathrm{stat}\) and \({\mathbf C}_\mathrm{sys}\) are the statistical and systematic covariance matrices, respectively. After treating \(\beta \) as a function of \(z\), \({\mathbf V}\) is given in the form,

$$\begin{aligned} {\mathbf V}_{ij}&= V_{0,ij}+\alpha ^2 V_{a,ij} + \beta _i\beta _j V_{b,ij} +\alpha V_{0a,ij} +\alpha V_{0a,ji} \nonumber \\&-\beta _j V_{0b,ij}-\beta _i V_{0b,ji} -\alpha \beta _j V_{ab,ij} - \alpha \beta _i V_{ab,ji}.\nonumber \\ \end{aligned}$$
(28)

It must be stressed that, while \(V_0\), \(V_{a}\), \(V_{b}\), and \(V_{0a}\) are the same as the “normal” covariance matrices given by the SNLS data archive, \(V_{0b}\), and \(V_{ab}\) are not the same as the ones given there. This is because the original matrices of SNLS3 are produced by assuming \(\beta \) is constant. We have used the \(V_{0b}\) and \(V_{ab}\) matrices for the “Combined” set that are applicable when varying \(\beta (z)\) (A. Conley, private communication, 2013).

To improve the cosmological constraints, we also use some other cosmological observations, including the Planck distance prior data [126], the GC data extracted from SDSS DR7 [127] and BOSS [128], as well as the direct measurement of Hubble constant \(H_0=73.8\pm 2.4 \,\mathrm{km/s/Mpc}\) from the HST observations [17]. For the details of including Planck and GC data into the \(\chi ^2\) analysis, see [124]. Now the total \(\chi ^2\) function is

$$\begin{aligned} \chi ^2=\chi ^2_{\mathrm{SN}}+\chi ^2_{\mathrm{CMB}}+\chi ^2_{\mathrm{GC}}+\chi ^2_{H_0}. \end{aligned}$$
(29)

In addition, assuming the measurement errors are Gaussian, the likelihood function satisfies

$$\begin{aligned} \mathcal{{L }} \propto \mathrm{e}^{-\chi ^{2}/2}, \quad \mathrm {Likelihood} \equiv \mathcal{{L }}/\mathcal{{L }}_{max} = \mathcal{{L }}/\mathcal{{L }}(\chi ^{2}_{\min }). \end{aligned}$$
(30)

It should be mentioned that in this paper we just use the purely geometric measurements, and do not consider the cosmological perturbations in the DE models. As analyzed in detail in [156], adopting a new framework for calculating the perturbations, the cosmological perturbations will always be stable in all IDE models (for a related discussion concerning the stability, see [154]). Therefore, the use of the Planck distance prior is sufficient for our purpose.

Finally, we perform an MCMC likelihood analysis [157] to obtain \(\mathcal{O}\)(\(10^6\)) samples for each model considered in this paper.

3 Results

3.1 Evolution of \(\beta \)

In this subsection, we explore the evolution of \(\beta \) in the frame of IDE.

In Table 1, we list the fitting results for various constant \(\beta \) and linear \(\beta (z)\) cases, where the SNe+CMB+GC+\(H_0\) data are used. An obvious feature of this table is that varying \(\beta \) can significantly improve the fitting results: for all the models, adding a parameter of \(\beta \) can reduce the best-fit values of \(\chi ^2\) by \(\sim \)34. Based on the Wilk theorem, 34 units of \(\chi ^2\) is equivalent to a Gaussian fluctuation of 5.8\(\sigma \). This means that the result of \(\beta _1=0\) is ruled out at 5.8\(\sigma \) confidence level (CL). As shown in [124, 125], for the cases of various DE models (such as \(\Lambda \)CDM, \(w\)CDM, CPL, and HDE model) without interaction, \(\beta \) deviates from a constant at 6\(\sigma \) CL. Therefore, we further confirm the redshift evolution of \(\beta \) for the SNLS3 data.

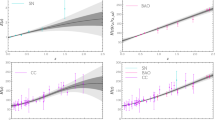
Table 1 Fitting results for various constant \(\beta \) and linear \(\beta (z)\) cases, where the SNe+CMB+GC+\(H_0\) data are used
Full size table

In Fig. 1, using the SNe+CMB+GC+\(H_0\) data, we plot the 1\(\sigma \) confidence constraints of \(\beta (z)\), for the \(w\)CDM model, the I\(w\)CDM1 model, the I\(w\)CDM2 model, and the I\(w\)CDM3 model. For comparison, we also plot the best-fit result of the constant \(\beta \) case for the \(w\)CDM model. From this figure one can see that the 1\(\sigma \) regions of \(\beta (z)\) of all these models are almost overlapping. This shows that the evolution of \(\beta \) is independent of the IDE models. In addition, for all the models, \(\beta (z)\) rapidly increases with \(z\). This result is consistent with the results of [124, 125], showing that the evolution of \(\beta \) is insensitive to dark energy models including those with interaction between dark sectors.

Fig. 1
figure 1

1\(\sigma \) confidence constraints for the evolution of \(\beta (z)\), given by the SNe+CMB+GC+\(H_0\) data, for the \(w\)CDM model, the I\(w\)CDM1 model, the I\(w\)CDM2 model, and the I\(w\)CDM3 model. The solid black lines denote the \(w\)CDM model, the dashed red lines denote the I\(w\)CDM1 model, the dotted blue lines denote the I\(w\)CDM2 model, and the dashed-dotted pink lines denote the I\(w\)CDM3 model. To make a comparison, for the \(w\)CDM model, the best-fit result of the constant \(\beta \) case is also plotted, shown as the horizontal dashed black line

Full size image

It should be pointed out that the evolutionary behaviors of \(\beta (z)\) depends on the SN samples used. Mohlabeng and Ralston [122] found that, for the Union 2.1 SN data, \(\beta (z)\) decreases with \(z\). This is similar to the case of the Pan-STARRS1 SN data [121].

It is interesting to study how different segments of the SNLS3 dataset give rise to different behavior of \(\beta \). To do this, we perform the following test: (1) Per [115], we evenly divide the redshift range \([0, 1]\) into 9 bins and assume that both \(\alpha \) and \(\beta \) are constant within each bin. (2) For each redshift bin, we make a small covariance matrix corresponding to only SNe in that bin. (3) Since we have already proved that the evolution of \(\beta \) is insensitive to dark energy models, per [115], we just adopt a fixed cosmological background (a flat \(\Lambda \)CDM model with \(\Omega _{m0}\) = 0.26) to do this test. (4) We fit \(\alpha \) and \(\beta \) separately for the 9 redshift bins. Based on the best-fit analysis, it is found that \(\beta \) is relatively flat till the seventh bin, and then it rapidly increases along with redshift \(z\). In other words, the rapid increase of \(\beta (z)\) is mainly due to the contributions from high-redshift (\(z>0.7\)) SN samples of the SNLS3 dataset. It should be mentioned that, to keep this paper focused on its main purpose, here we just briefly present the conclusion, instead of describing all the detailed results of the test. To understand why high-redshift SNLS3 samples will yield this kind of evolutionary behavior of \(\beta \), some numerical simulation studies may be needed. We will study this issue in future works.

3.2 Effects of time-varying \(\beta \)

In this subsection, we discuss the effects of varying \(\beta \) on parameter estimation of IDE models.

In Fig. 2, using SNe+CMB+GC+\(H_0\) data, we plot the 1D marginalized probability distributions of \(\Omega _{c0}\), for all the models considered in this paper. We find that varying \(\beta \) yields a larger \(\Omega _{c0}\): for the constant \(\beta \) case, the best-fit results are \(\Omega _{c0}=0.224\), 0.232, 0.226, and 0.225, for the \(w\)CDM, the I\(w\)CDM1, the I\(w\)CDM2, and the I\(w\)CDM3 model, respectively; while for the linear \(\beta (z)\) case, the best-fit results are \(\Omega _{c0}=0.231\), 0.244, 0.238, and 0.244, for the \(w\)CDM, the I\(w\)CDM1, the I\(w\)CDM2, and the I\(w\)CDM3 model, respectively. In addition, as shown in [124, 125], for various DE models without interaction term, a time-varying \(\beta \) also yields a larger fractional matter density \(\Omega _{m0} \equiv \Omega _{c0}+\Omega _{b0}\). Therefore, we can conclude that the effects of varying \(\beta \) on the present fractional matter density are insensitive to the interaction between dark sectors.

Fig. 2
figure 2

The 1D marginalized probability distributions of \(\Omega _{c0}\), given by the SNe+CMB+GC+\(H_0\) data, for the \(w\)CDM model and the three IDE models. Both the results of the constant \(\beta \) (dashed black lines) and the linear \(\beta (z)\) (solid red lines) cases are presented

Full size image

For all the models considered in this paper, the 1D marginalized probability distributions of \(w\) are plotted in Fig. 3. It is found that varying \(\beta \) yields a larger \(w\): for the constant \(\beta \) case, \(w=-1.118^{+0.065}_{-0.071}, -1.105^{+0.075}_{-0.069}, -1.124^{+0.070}_{-0.062}\), and \(-1.116^{+0.059}_{-0.072}\), for the \(w\)CDM model, the I\(w\)CDM1 model, the I\(w\)CDM2 model, and the I\(w\)CDM3 model, respectively; while for the linear \(\beta (z)\) case, \(w=-1.042^{+0.068}_{-0.072}, -1.016^{+0.075}_{-0.063}, -1.052^{+0.070}_{-0.068}\), and \(-1.038^{+0.068}_{-0.080}\), for the \(w\)CDM model, the I\(w\)CDM1 model, the I\(w\)CDM2 model, and the I\(w\)CDM3 model, respectively. In other words, \(w<\) \(-\)1 is preferred at more than 1\(\sigma \) CL for the constant \(\beta \) case, while \(w\) is consistent with \(-1\) at 1\(\sigma \) CL for the linear \(\beta (z)\) case. This means that, compared to the constant \(\beta \) case, the results from the varying \(\beta \) case are in better agreement with a cosmological constant. This conclusion is consistent with the noninteracting cases [124, 125], showing that the effects of varying \(\beta \) on \(w\) are insensitive to the interaction between dark sectors.

Fig. 3
figure 3

The 1D marginalized probability distributions of \(w\), given by the SNe+CMB+GC+\(H_0\) data, for the \(w\)CDM model and the three IDE models. Both the results of the constant \(\beta \) (dashed black lines) and the linear \(\beta (z)\) (solid red lines) cases are presented

Full size image

In Fig. 4, we plot the 1D marginalized probability distributions of \(h\), for all the models considered in this paper. It can be seen that, for the \(w\)CDM model, varying \(\beta \) yields a smaller \(h\); this result is consistent with the noninteracting cases [124, 125]. However, for all the IDE models, the 1D distribution results of \(h\) of the linear \(\beta \) case are almost same with those of the constant \(\beta \) case. In other words, once considering the interaction between dark sectors, varying \(\beta \) will not change the fitting results of \(h\). This result is quite different from the results of Figs. 2 and 3, showing that there is a degeneracy between \(h\) and \(\gamma \).

Fig. 4
figure 4

The 1D marginalized probability distributions of \(h\), given by the SNe+CMB+GC+\(H_0\) data, for the \(w\)CDM model and the three IDE models. Both the results of the constant \(\beta \) (dashed black lines) and the linear \(\beta (z)\) (solid red lines) cases are presented

Full size image

Next, we turn to the constraints on interaction parameter \(\gamma \). In Fig. 5, we plot 1\(\sigma \) and 2\(\sigma \) confidence contours for \(\{\gamma ,h\}\), for all the IDE models. Again, one can see that varying \(\beta \) has no impact on \(h\). To the contrary, varying \(\beta \) yields a smaller \(\gamma \): for the constant \(\beta \) case, the best-fit results are \(\gamma =-0.0028, -0.0105\), and \(-0.0198\), for the I\(w\)CDM1 model, the I\(w\)CDM2 model, and the I\(w\)CDM3 model, respectively; while for the linear \(\beta (z)\) case, the best-fit results are \(\gamma =-0.0053, -0.0322\), and \(-0.0732\), for the I\(w\)CDM1 model, the I\(w\)CDM2 model, and the I\(w\)CDM3 model, respectively. In other words, \(\gamma <0\) is slightly more favored in the linear \(\beta (z)\) case. This means that energy will transfer from dark matter to dark energy. In addition, we find that \(\gamma \) and \(h\) are anti-correlated, showing that there is a degeneracy between \(h\) and \(\gamma \).

Fig. 5
figure 5

The 1\(\sigma \) and 2\(\sigma \) confidence contours for \(\{\gamma ,h\}\), for the three IDE models. Both the results of the constant \(\beta \) (red regions) and the linear \(\beta (z)\) (dark cyan regions) cases are presented

Full size image

In Fig. 6, to make a visual comparison among three interaction forms, we plot the 2\(\sigma \) confidence contours for \(\{\Omega _{c0},\gamma \}\), based on the linear \(\beta (z)\) case, for all the IDE models. From this figure one can see that \(\gamma \) is tightly constrained in the I\(w\)CDM1 model; to the contrary, \(\gamma \) cannot be well constrained in the I\(w\)CDM2 and I\(w\)CDM3 models. This result is consistent with the result of [158], in which only the constant \(\beta \) case was considered.

Fig. 6
figure 6

The 2\(\sigma \) confidence contours for \(\{\Omega _{c0},\gamma \}\), based on the linear \(\beta (z)\) case, for the I\(w\)CDM1 model (solid black line), the I\(w\)CDM2 model (dashed red line), and the I\(w\)CDM3 model (dotted blue line)

Full size image

4 Discussion and summary

In recent years, more and more SNe Ia have been discovered, and the systematic errors of SNe Ia have drawn more and more attentions. One of the most important systematic uncertainties for SNe Ia is the potential SN evolution. The hints for the evolution of \(\beta \) have been found [117–121]. For example, Mohlabeng and Ralston [122] studied the case of Union2.1 and found that \(\beta \) deviates from a constant at 7\(\sigma \) CL. Wang and Wang [123] found that, for the SNLS3 data, \(\beta \) increases significantly with \(z\) at the 6\(\sigma \) CL; moreover, they proved that this conclusion is insensitive to the lightcurve fitter models, or the functional form of \(\beta (z)\) assumed [123].

It is clear that a time-varying \(\beta \) will have significant impact on parameter estimation. Adopting a constant \(\alpha \) and a linear \(\beta (z) = \beta _{0} + \beta _{1} z\), Wang et al. [124] explored this issue by considering the \(\Lambda \)CDM model, the \(w\)CDM model, and the CPL model. Soon after, Wang et al. [125] studied this issue in the frame of HDE model, which is a physically plausible DE candidate based on the holographic principle. It is found that, for all these DE models, \(\beta \) deviates from a constant at 6\(\sigma \) CL; in addition, considering the evolution of \(\beta \) is helpful in reducing the tension between SN and other cosmological observations. It should be pointed out that, in principle, there is always an important possibility that DE directly interacts with CDM. This factor was not considered in [124, 125].

In this paper, we extend the corresponding discussions to the case of IDE model. To perform the cosmology fits, the \(w\)CDM model is adopted. Moreover, three kinds of interaction forms are considered: \(Q_{1}=3\gamma H\rho _{c}\), \(Q_{2}=3\gamma H\rho _{de}\), and \(Q_{3}=3\gamma H\frac{\rho _{c}\rho _{de}}{\rho _{c}+\rho _{de}}\). In addition to the SNLS3 SN data, we also use the Planck distance priors data, the GC data extracted from SDSS DR7 and BOSS, as well as the direct measurement of Hubble constant from the HST observation.

We further confirm the redshift evolution of \(\beta \) for the SNLS3 data: for all the IDE models, adding a parameter of \(\beta \) can reduce \(\chi ^2\) by \(\sim \)34, indicating that \(\beta _1 = 0\) is ruled out at 5.8\(\sigma \) CL. In addition, we find that the 1\(\sigma \) regions of \(\beta (z)\) of all these models are almost overlapping, showing that the evolution of \(\beta \) is insensitive to the interaction between dark sectors. These results further verify the importance of considering the evolution of \(\beta \) in the cosmology fits.

Furthermore, we find that a time-varying \(\beta \) has significant effects on the results of parameter estimation: for all the models considered in this paper, varying \(\beta \) yields a larger \(\Omega _{c0}\) and a larger \(w\); on the other side, varying \(\beta \) yields a smaller \(h\) for the \(w\)CDM model, while varying \(\beta \) has no influence on \(h\) for the three IDE models. Moreover, we find that \(\gamma \) and \(h\) are anti-correlated, showing that there is a degeneracy between \(h\) and \(\gamma \). In addition, we find that \(\gamma \) is tightly constrained in the I\(w\)CDM1 model, but it cannot be well constrained in the I\(w\)CDM2 and I\(w\)CDM3 models.

In all, these results show that the evolution of \(\beta \) is insensitive to the interaction between dark sectors, and they highlight the importance of considering \(\beta \)’s evolution in the cosmology fits.

So far, only the effects of varying \(\beta \) on DE models are considered. It is of great interest to study the effects of varying \(\beta \) on parameter estimation in MG models. In addition, some other factors, such as the evolution of \(\sigma _{\mathrm{int}}\) [155], may also cause the systematic uncertainties of SNe Ia. These issues will be studied in future works.