Is $Y(4008)$ possibly a $1^{--} \psi (3^3S_1)$ state?

Abstract

The strong decays of the radially excited $\psi (3^3S_1)$ state are studied within the $^3P_0$ model. As a believed $\psi (3^3S_1)$, some strong decay widths and relevant ratios of $\psi (4040)$ are calculated in the model. In a similar way, as a possible $\psi (3^3S_1)$, the same strong decay widths and relevant ratios of $Y(4008)$ are presented. Our study indicates that $Y(4008)$ is hard to be identified with a $\psi (3^3S_1)$ charmonium once it is confirmed under the $D^*\bar{D}^*$ threshold, but it is possibly a $\psi (3^3S_1)$ charmonium once it is confirmed above the $D^*\bar{D}^*$ threshold by experiment.

1 Introduction

Since the discovery of $J/\psi$, many charmonium and charmonium like states have been observed [1]. In these states, most of them are confirmed as $c\bar{c}$ charmonium states, some of them do not fit the predicted features of $c\bar{c}$ charmonium. Especially, in the past few years, some neutral “$X,~Y$” and charged “$Z$” resonances which cannot be simply accommodated in the $c\bar{c}$ picture have been observed and explored [1]. How to understand and identify these resonances is a big challenge.

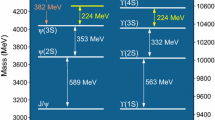
Several years ago, the Belle Collaboration observed a significant enhancement with mass $M=4008\pm 40^{+114}_{-28}$ MeV and width $\varGamma =226\pm 44\pm 87$ MeV when measuring the cross section for $e^+e^-\rightarrow \pi ^+\pi ^-J/\psi$ [2]. From its production, $Y(4008)$ has $J^{PC}=1^{--}$. There is a large uncertainty on the measured mass. $Y(4008)$ was not confirmed by the BaBar Collaboration [3].

Based on some analyses, the $\psi (3^3S_1)$ and $D^* \bar{D}^*$ molecular state possibility of $Y(4008)$ is studied in Ref. [4]. Through the calculated mass with the heavy quark-antiquark potential, $Y(4008)$ is suggested the $\psi (3^3S_1)$ [5]. In a one boson exchange model [6], the study does not support the interpretation of $Y(4008)$ as a $D^*\bar{D}^*$ molecule. In order to identify $Y(4008)$, it is interesting to study its strong decays in detail.

In fact, there is a $\psi (4040)$ which is commonly believed the $J^{PC}=1^{--} \psi (3^3S_1)$ [1, 7, 8]. $\psi (4040)$ has mass and width

$$\begin{aligned} M=4{,}039\pm 1~\mathrm {MeV},\quad \varGamma =80\pm 10~\mathrm {MeV}. \end{aligned}$$

(1)

The measured mass and total width of $\psi (4040)$ is consistent with theoretical predictions [7, 8].

Now the fact is that there are two states $\psi (4040)$ and $Y(4008)$, which are close to the threshold of $D^*\bar{D}^*$. Furthermore, these two states have different total decay widths. Even though the calculation of the strong decay of $\psi (4040)$ within the $^3P_0$ model has been performed in Ref. [7], in order to find the difference and have a comparison, it will be interesting to study the strong decays of $\psi (4040)$ and $Y(4008)$ in the $^3P_0$ model at the same time.

The paper is organized as follows. After the introduction, the $^3P_0$ model is briefly reviewed and possible strong decay channels and decay amplitudes of the $\psi (3^3S_1)$ state are presented in Sect. 2. In Sect. 3, the numerical results in the $^3P_0$ model are obtained. The last section is devoted to a simple discussion and summary.

2 $^3P_0$ model and possible charmonium strong decays of $\psi (4040)$ and $Y(4008)$

Up to now, many strong decay models have been developed to describe the transition of hadrons to open-flavor final states. The $^3P_0$ model [9–15] was first proposed by Micu [9], and further developed by Orsay Group [10–15]. In the model, the created quark-antiquark pair is supposed the vacuum quantum numbers $J^{PC}=0^{++}$. Although the intrinsic mechanism and the relation to the Quantum Chromodynamics are not very clear, the model is widely employed to study the OZI-allowed strong decays of a meson into two other mesons, as well as the two-body strong decays of baryons and other hadrons [17–23].

A meson decay process $A\Rightarrow B+C$ is showed in Fig. 1. In the nonrelativistic limit, the transition operator is written as

$$\begin{aligned} T&= -3\gamma \sum _{m} \langle 1m;1-m|00 \rangle \int \mathrm{d}\mathbf {k}_{3}\mathrm{d}\mathbf {k}_{4}\delta ^{3}( \mathbf {k}_{3}+\mathbf {k}_{4})\nonumber \\&\times y_{1m}\left( \frac{\mathbf {k}_{3}-\mathbf {k}_{4}}{2}\right) \chi _{1, -m}^{34}\varphi ^{34}_{0}\omega ^{34}_{0} b^{\dagger }_{3i}(\mathbf {k}_{3})\mathrm{d}^{\dagger }_{4j}( \mathbf {k}_{4}) \end{aligned}$$

(2)

where $i$ and $j$ denote the color indices for the $q\bar{q}$ pair. The flavor wave function for the $q\bar{q}$ pair is $\varphi ^{34}_{0}=(u\bar{u}+d\bar{d}+s\bar{s})/\sqrt{3}$, and $\omega ^{34}_{0}=\delta _{ij}$ for the flavor and color singlet. $\chi _{1, - m}^{34}$ is the spin triplet. $y_{1m}(\mathbf k )=|\mathbf k |\times Y_{1m}(\Omega )$ is the solid harmonic polynomial corresponding to the p-wave quark pair. The dimensionless constant $\gamma$ indicates the strength of the quark pair creation from the vacuum. Therefore, the helicity amplitude of the process $A\Rightarrow B+C$ reads as

$$\begin{aligned}&\!\!\!\fancyscript{M}^{M_{J_A } M_{J_B } M_{J_C }} \nonumber \\&\!\!\!\quad = \sqrt{8E_A E_B E_C } \gamma \sum _{M_{L_A } ,M_{S_A } ,M_{L_B } ,M_{S_B } ,M_{L_C },M_{S_C } ,m} \nonumber \\&\!\!\!\qquad \times \langle {1m;1 - m}|{00} \rangle \langle {L_A M_{L_A } S_A M_{S_A } }| {J_A M_{J_A } }\rangle \nonumber \\&\!\!\!\qquad \times \langle L_B M_{L_B } S_B M_{S_B }|J_B M_{J_B }\rangle \nonumber \\&\!\!\!\qquad \times \langle L_C M_{L_C } S_C M_{S_C }|J_C M_{J_C }\rangle \langle \varphi _B^{13} \varphi _C^{24}|\varphi _A^{12}\varphi _0^{34}\rangle \nonumber \\&\!\!\!\qquad \times \langle \chi _{S_B M_{S_B }}^{13} \chi _{S_C M_{S_C } }^{24}|\chi _{S_A M_{S_A } }^{12} \chi _{1 - m}^{34}\rangle \nonumber \\&\!\!\!\qquad \times I_{M_{L_B } ,M_{L_C } }^{M_{L_A } ,m} (\mathbf {K}) \end{aligned}$$

(3)

where $E_A=m_A$, $E_B =\sqrt{m_B^2 + \mathbf {K}_\mathbf {B}^2 }$ and $E_C =\sqrt{m_C^2+ \mathbf {K}_\mathbf {C}^2 }$ are the total energy of mesons $A$, $B$ and $C$. $\langle \varphi _B^{13} \varphi _C^{24}|\varphi _A^{12}\varphi _0^{34} \rangle$ and $\langle \chi _{S_B M_{S_B }}^{13} \chi _{S_C M_{S_C } }^{24}|\chi _{S_A M_{S_A } }^{12} \chi _{1 - m}^{34}\rangle$ are the matrix elements of favor wave functions and spin wave functions, respectively. For the flavor matrix element $\langle \varphi _B^{13} \varphi _C^{24}|\varphi _A^{12}\varphi _0^{34} \rangle$, there are several definitions which will give different numbers. In our calculation, the following flavor matrix element

$$\begin{aligned} \langle \varphi _B^{13} \varphi _C^{24}|\varphi _A^{12}\varphi _0^{34} \rangle&= \sum _{I,I^3 } \langle {I_C I_C^3; I_B I^3_B }|{I_A, I_A^3 }\rangle \nonumber \\&\quad \times [(2I_B + 1)(2I_C + 1)(2I_A + 1)]^{1/2} \nonumber \\&\quad \times \left( \begin{array}{ccc} {I_1} &{}\quad {I_3} &{}\quad {I_C}\\ {I_2} &{}\quad {I_4} &{}\quad {I_B}\\ {I_A} &{}\quad {0} &{}\quad {I_A}\\ \end{array} \right) \end{aligned}$$

(4)

is employed, where $I_i~(i=u,d,s,c)$ is the isospin of four quarks. The spin matrix element can be written in terms of Wigner’s $9j$ symbols [16]:

$$\begin{aligned}&\langle {\chi _{S_B M_{S_B } }^{13} \chi _{S_C M_{S_C } }^{24} } |{\chi _{S_A M_{S_A } }^{12} \chi _{1 - m}^{34} } \rangle \nonumber \\&\quad =(-1)^{S_C + 1} [3(2S_B + 1)(2S_C + 1)(2S_A + 1)]^{1/2} \nonumber \\&\qquad \times \sum _{S,M_S } {\langle {S_B M_{S_B } S_C M_{S_C } }|{SM_S }\rangle \langle {SM_S }|{S_A M_{S_A } ;1, - m}\rangle }\nonumber \\&\qquad \times \left( \begin{array}{ccc} {1/2} &{}\quad {1/2} &{}\quad {S_B}\\ {1/2} &{}\quad {1/2} &{}\quad {S_C}\\ {S_A} &{}\quad {1} &{}\quad {S}\\ \end{array} \right) . \end{aligned}$$

(5)

$I_{M_{L_B } ,M_{L_C } }^{M_{L_A } ,m} (\mathbf {K})$ in Eq. (3) is a spatial integral

$$\begin{aligned} I_{M_{L_B } ,M_{L_C } }^{M_{L_A } ,m} (\mathbf {K})&= \int \mathrm{d} \mathbf {k}_1 \mathrm{d} \varvec{k}_2 \mathrm{d} \mathbf {k}_3 \mathrm{d} \varvec{k}_4 \delta ^3 (\mathbf {k}_1 + \varvec{k}_2)\delta ^3 (\mathbf {k}_3+ \varvec{k}_4)\nonumber \\&\quad \times \delta ^3 (\mathbf {k}_B- \varvec{k}_1- \mathbf {k}_3 )\delta ^3 (\mathbf {k}_C- \varvec{k}_2 -\mathbf {k}_4)\nonumber \\&\quad \times \varPsi _{n_B L_B M_{L_B } }^* (\mathbf {k}_1 ,\varvec{k}_3)\varPsi _{n_cL_C M_{L_c}}^* (\mathbf {k}_2 ,\varvec{k}_4)\nonumber \\&\quad \times \varPsi _{n_A L_A M_{LA}} (k_1 ,k_2 )Y _{1m}\left( \frac{\mathbf {k_3}-\varvec{k}_4}{2}\right) \end{aligned}$$

(6)

where $\varPsi _{n_A L_A M_{L_A }}(\mathbf {k_1},\varvec{(}k_2))$ is the SHO wave function

$$\begin{aligned} {\varPsi }_{nLM_L }&= (-1)^n(-i)^LR^{L+3/2} \sqrt{\frac{2n!}{\varGamma (n+L+3/2)}} \nonumber \\&\times \exp \left( {-\frac{R^2k^2}{2}}\right) \nonumber \\&\times L_n^{L+1/2}(R^2k^2)\times Y_{lm}(\mathbf k ). \end{aligned}$$

(7)

In this equation, $R$ is a simple harmonic oscillator (SHO) wave function parameter, $Y_{lm}(\mathbf k )$ is a spherical harmonic function, and $L_n^{L+1/2}(R^2k^2)$ denotes a associated Laguerre polynomial.

Fig. 1

The decay process of $A\Rightarrow B+C$ in the $^3P_0$ model [24]

Using the Jacob–Wick formula [25, 26], the helicity amplitude can be transformed into the partial wave amplitude:

$$\begin{aligned} \fancyscript{M}^{JL} (A \!\rightarrow \! BC) \!&= \! \frac{{\sqrt{2L \!+\! 1} }}{{2J_A \!+\! 1}}\sum _{M_{J_B } ,M_{J_C } } \langle {L0JM_{J_A } } |{J_A M_{J_A } }\rangle \nonumber \\&\quad \times \langle {J_B M_{J_B } J_C M_{J_C } } | {JM_{J_A } } \rangle {{\fancyscript{M}}}^{M_{J_A } M_{J_B } M_{J_C } }\nonumber \\ \end{aligned}$$

(8)

where $\mathbf {J}=\varvec{J_B}+\mathbf {J}_\mathbf {C}$, $\mathbf {J}_\mathbf {A}=\mathbf {J}_\mathbf {B}+\mathbf {J}_\mathbf {C}+\mathbf {L}$, $M_{J_A}=M_{J_B}+M_{J_C}$. The decay width is thus obtained as

$$\begin{aligned} \varGamma = \pi ^2 \frac{|\mathbf {K}|}{m_A^2}\sum _{JL} |{\fancyscript{M}^{JL}}|^2 \end{aligned}$$

(9)

where $|\mathbf {K}|$ is the momentum of the daughter meson in the initial meson A’s center mass frame

$$\begin{aligned} |\mathbf {K}|= \frac{{\sqrt{[m_A^2 - (m_B - m_C )^2 ][m_A^2 - (m_B + m_C )^2 ]} }}{{2m_A }}. \end{aligned}$$

(10)

With these formula in hand, we proceed with the study of the strong decays of $\psi (4040)$ and $Y(4008)$. $\psi (4040)$ and $Y(4008)$ have the same quantum number $J^{PC}=1^{--}$. Once they are assigned as the $1^{--}$ $\psi (3^3S_1)$ state, all possible open-charm strong decay modes allowed by the OZI rule above the $D^*\bar{D}^*$ threshold are given in Table 1. Accordingly, the decay amplitudes and the detailed decay channels are presented, where the explicit expression of the spatial integral $I_{00}$ is

$$\begin{aligned} I_{00}\!&= \!\frac{\exp (\frac{k^2\alpha ^2}{2\delta }\!+\!k^2\xi ) k}{2\sqrt{5}\pi ^{\frac{5}{4}}\delta ^{\frac{13}{2}}R_A^{-\frac{11}{2}}R_B^{-\frac{3}{2}}R_C^{-\frac{3}{2}}} \times [4 k^4\alpha ^4 (-\alpha \!+\!\delta )\!+\!20\delta ^2 \nonumber \\&\times \, (-7\alpha +3\delta )+8k^2\alpha ^2\delta (-7\alpha +5\delta )+20\delta ^2(k^2\alpha ^2\nonumber \\&\ \times \, (\alpha -\delta )\!+\!(5\alpha -3\delta )\delta )R_A^{-2}\!+\!15\delta ^4(-\alpha +\delta )R_A^{-4}].\nonumber \\ \end{aligned}$$

(11)

In this equation, $\delta =R_A^2+R_B^2+R_C^2$, $\mu _1=\frac{m_1}{m_1+m_3}$, $\mu _2=\frac{m_2}{m_2+m_4}$, $\alpha =R_B^2\mu _1+R_C^2\mu _2$, $\xi =-\frac{1}{2}(R_B^2\mu _1^2+R_C^2\mu _2^2)$.

Table 1 The allowed open-charm strong decays of $1^{--}$ $\psi ({3^{3}S_{1}})$ for $\psi (4040)$ and $Y(4008)$, where $\varepsilon =\gamma \sqrt{8E_AE_BE_C}$

3 Numerical results

In order to get the numerical results within the $^3P_0$ model, several parameters are chosen as follows. The masses of constituent quarks are taken as $m_u=m_d=0.33~\mathrm {GeV}$, $m_s=0.55~\mathrm {GeV}$ and $m_c=1.6~\mathrm {GeV}$ [23]. The masses of relevant charmed mesons [1] are listed in Table 2, where $(\pm )$ indicates the charged mesons and (0) indicates the charge neutral mesons.

Table 2 The relevant mass and $R$ values of charmed mesons used in our calculation

There are other two important parameters in the $^3P_0$ model, the strength of quark pair creation $\gamma$ and the $R$ value in the SHO wave function. For a color saturation, a color matrix element as a constant can be absorbed into the dimensionless constant $\gamma$. Accordingly, the overlap of the flavor wave function will be different. For our calculation of the flavor matrix element, $\gamma$ is chosen with $\gamma =8.42$ [23]. $\gamma =8.42$ is chosen similarly as that in Refs. [27–30] with a factor $\sqrt{96\pi }$ larger than that in Refs. [7, 23] for a different definition of the flavor matrix element. The $R$ value in the SHO wave function can be obtained from the Schrodinger equation within the potential model [31]. In general, there are two ways to choose $R$: a constant around $2$ $\mathrm {GeV}^{-1}$ [7, 19, 32] and an effective varying value [23, 29]. In this paper, an effective $R$ is chosen. The $R$ of the final states are from Ref. [23], and the suitable $R$ of the initial state (refers to $R_A$ in this paper) is fixed by the total decay width of $\psi (4040)$ and $Y(4008)$, respectively. Of course, our numerical results depend on $R_A$. To learn this dependence, the variation of our results with $R_A$ are also presented.

3.1 $\psi$(4040)

As a commonly believed $\psi (3^3S_1)$, the variation of the decay width of $\psi (4040)$ for different modes with $R_A$ is shown in Fig. 2a. The variation of the total decay width of $\psi (4040)$ with $R_A$ is presented in Fig. 2b. From PDG [1], three horizontal lines in the figure are drawn to indicate the lower, central and upper values of the total width of $\psi (4040)$ ($\varGamma =0.08\pm 0.01$ GeV). $R_A$ is therefore fixed by the three lines at the region $2.96\rightarrow 3.29$ GeV$^{-1}$ with the central value $3.13$ GeV$^{-1}$. The fixed $R_A$ is larger than that in Ref. [7]. At $R_A=3.13$ GeV$^{-1}$, the widths of all possible open-flavor strong decay channels are calculated and given in Table 3. As a comparison, the results in Ref. [7] are also listed. Obviously, the dominant decays of $\psi (4040)$ are $D\bar{D}$ , $D^*\bar{D}/D\bar{D}^*$ and $D^*\bar{D}^*$ channels.

Table 3 Open-flavor strong decays of $\psi (4040)$ at universal $R_A=3.13$ GeV$^{-1}$ (in MeV)

Fig. 2

a Possible partial strong decay widths of $\psi (4040)$ versus $R_A$; b The total strong decay width of $\psi (4040)$ versus $R_A$

Unlike the decay widths, the ratios of the decay widths are less sensitive to the uncertainties of the $^3P_0$ model. Therefore, some relevant ratios are calculated and presented in Table 4. The experimental data are those from PDG [1].

Table 4 Relevant ratios of $\psi (4040)$ at $R_A=3.13$ GeV$^{-1}$

Our results for $\frac{\varGamma (D\bar{D})}{\varGamma (D^*\bar{D}+c.c.)}$ and $\frac{\varGamma (D^*(2010)^+D^-)}{\varGamma (D^*(2007)^0\bar{D}^0+c.c.)}$ are in accord with experiments. Our results for $\frac{\varGamma (D^*(2007)^0\bar{D}^*(2007)^0)}{\varGamma (D^*(2007)^0\bar{D}^0+c.c.)}$ and $\frac{\varGamma (D^0\bar{D}^0)}{\varGamma (D^*(2007)\bar{D}^0+c.c.)}$ are largely different with the experimental results (measured in 1977 [1, 33]). Our result of $BR(\psi (4040)\Rightarrow D\bar{D})$ is $13.9^{+5.2}_{-6.0}\,\%$, which is smaller than the BABAR data $(31.2\pm 5.3)\,\%$ [34]. In Ref. [35], the obtained $BR(\psi (4040) \Rightarrow D\bar{D})=(25.3\pm 4.5)\,\%$. In our results, $\frac{\varGamma (D\bar{D})}{\varGamma (D^*\bar{D}+c.c.)}$ and $\frac{\varGamma (D^0\bar{D}^0)}{\varGamma (D^*(2007)\bar{D}^0+c.c.)}$ have poles around $R_A=2.6$ GeV$^{-1}$ as pointed out in Refs. [19, 36, 37].

3.2 $Y(4008)$

As indicated in the first section, $Y(4008)$ as a possible $\psi (3^3S_1)$ is close to the $D^*\bar{D}^*$ threshold while has a large mass uncertainty. Therefore, more decay channels may open when $Y(4008)$ has a larger mass. To learn the dependence of the total width of $Y(4008)$ on $R_A$, two figures corresponding to the central and upper mass are drawn in Fig. 3, respectively, where the horizontal lines indicate the experimental result. In Fig. 3a, the predicted total decay width doesn’t meet the data from Belle. In Fig. 3b, the predicted total decay width meets the data from Belle. That is to say, when $Y(4008)$ has the central or lower mass, the $D^*\overline{D}^*$ channel does not open. Therefore, $Y(4008)$ can hardly have a large total decay width as the Belle observed. However, when $Y(4008)$ has the upper mass, the $D^*\overline{D}^*$ channel opens, and it may have such large total decay width.

Fig. 3

Total decay widths of $Y(4008)$ versus $R_A$ for: a the central mass 4,008 MeV; b the upper mass 4,162 MeV

Following a similar fitting procedure as $\psi (4040)$, $R$ is fixed at $R_A=2.27$ GeV$^{-1}$ by the total decay width $\varGamma =226$ MeV. The fixed $R_A$ is smaller than the $R_A=3.13$ GeV$^{-1}$ fixed by $\psi (4040)$. In Fig. 3b, the plot is not flat at the left side of $R_A=2.6$ GeV$^{-1}$, which means that the total decay width depends heavily on the $R_A$ in this region. To deduce the dependence, relevant ratios instead of the partial decay widths of $Y(4008)$ are computed and presented in Table 5 at $R_A=2.27$ GeV$^{-1}$.

Table 5 Relevant ratios of $Y(4008)$ with upper mass

Taking into account the fact that there is a large uncertainty on the total decay width of $Y(4008)$, $Y(4008)$ may have a total decay width around 120 MeV, which may implies a larger fixed $R_A$. Therefore, we computed the relevant ratios of $Y(4008)$ at $R_A=3.13$ GeV$^{-1}$ as an example. The results are presented in Table 6. Obviously, the numerical results depends heavily on the $R_A$. Unfortunately, there is no such relevant experimental data at present, and the suitable $R_A$ is not easy to be fixed. These predictions wait for a check by forthcoming experiments.

Table 6 Relevant ratios of $Y(4008)$ with upper mass

The decay width depends also on the mass of the initial meson A, the dependence of the total width of $Y(4008)$ on $m_A$ at $R_A=2.27$ GeV$^{-1}$ is drawn in Fig. 4.

Fig. 4

Total decay widths of $Y(4008)$ versus $m_A$ at $R_A=2.27$ for: a $Y(4008)$ with the central mass does not open the $D^*\overline{D}^*$ channel; b $Y(4008)$ with the upper mass does open the $D^*\overline{D}^*$ channel

4 Summary and discussion

In this work, the strong decay of the $1^{--}$ $\psi (3^3S_1)$ resonance is studied in the $^3P_0$ model. As a commonly believed $\psi (3^3S_1)$, the dominant strong decay of $\psi (4040)$ are $D\bar{D}$, $D^*\bar{D}/D\bar{D}^*$ and $D\bar{D}^*$ channels. Accordingly, the decay widths of these channels are calculated. Based on these decay widths, some relevant ratios are obtained. Our results for $\frac{\varGamma (D\bar{D})}{\varGamma (D^*\bar{D}+c.c.)}$ and $\frac{\varGamma (D^*(2010)^+D^-)}{\varGamma (D^*(2007)^0\bar{D}^0+c.c.)}$ are in accord with experiments. Our results for $\frac{\varGamma (D^*(2007)^0\bar{D}^*(2007)^0)}{\varGamma (D^*(2007)^0\bar{D}^0+c.c.)}$ and $\frac{\varGamma (D^0\bar{D}^0)}{\varGamma (D^*(2007)\bar{D}^0+c.c.)}$ are largely different with the experimental results which were measured in 1977 [33]. Of course, the uncertainties related to the $^3P_0$ model are not studied in this paper, which may bring in some uncertainties.

$Y(4008)$ are close to the threshold of $D^*\bar{D}^*$ and has a large mass uncertainty. For this reason, the strong decays of $Y(4008)$ with different mass are studied. Under the threshold of $D^*\bar{D}^*$, it is hard to understand the wide decay width of $Y(4008)$ if $Y(4008)$ is assumed as the $\psi (3^3S_1)$. However, above the threshold of $D^*\bar{D}^*$, $Y(4008)$ is possibly the $\psi (3^3S_1)$. In this case, more information is required to distinguished $\psi (4040)$ from $Y(4008)$ both in theory and in experiment.

To have a clear picture of the charmonium spectroscopy, the observed $X,~Y$ and $Z$ have to be understood and identified. Unfortunately, people has not a comprehensive understanding of these resonances. Besides, $Y(4008)$ was observed only by the Belle Collaboration, and only the total decay width was given. More experiments are required to confirm its existence or not. Especially, the mass uncertainty of $Y(4008)$ has to be deduced if it is confirmed in forthcoming experiment. Only when more decay channels and their branching fractions ratios have been measured, can we understand $Y(4008)$ and $\psi (4040)$. As a cross-check, the detailed estimates of the decay widths and relevant ratios are required in other models.