CMB anomalies from an inflationary model in string theory

Abstract

Recent Planck measurements show some CMB anomalies on large angular scales, which confirms the early observations by WMAP. We show that an inflationary model, in which before the slow-roll inflation the Universe is in a superinflationary phase, can generate a large-scale cutoff in the primordial power spectrum, which may account for not only the power suppression on large angular scales, but also a large dipole power asymmetry in the CMB. We discuss an implementation of our model in string theory.

1 Introduction

Recently, the Planck collaboration has reported a hemispherical power asymmetry in the CMB [1], which conformed the result of WMAP, but it has better precision. Such asymmetry has also been found by estimating the power spectrum in the two hemispheres by using the quadratic maximum likelihood [2]. In addition, the Planck collaboration has also reported a power deficit in the low-$l$ CMB power spectrum at $l\lesssim 40$ [1] with the statistical significance $2.5\sim 3\sigma$, which is not concordant with the Planck best-fit model, although the data points are still consistent well with the cosmic variance.

The Planck data have larger statistical significance than the WMAP data, which makes it difficult to attribute the anomalies to the foregrounds, e.g. [3, 4]. Thus it seems that these anomalies should have an underlying and common physical origin, which deserves to be considered seriously.

The CMB power asymmetry might be modeled as a dipole modulation of the power [5, 6], see also [7], which results from a superhorizon perturbation crossing the observable Universe [8, 9]. This modulation can be explained in light of the spatial change of the spectrum of primordial curvature perturbation $\mathcal{R}$,

$$\begin{aligned} \mathcal{P}^{1/2}_\mathcal{R}(k,\mathbf {x})=\left( 1+ A(k){\hat{\mathbf {p}}\cdot \mathbf {x}\over x_\mathrm{ls}}\right) \mathcal{P}^{1/2}_{\mathcal{R}}(k), \end{aligned}$$

(1)

where $\hat{\mathbf {p}}$ is the unit vector of the dipole modulation direction, $x_\mathrm{ls}$ is the distance to the last scattering surface, $\mathcal{P}_{\mathcal{R}}(k)$ is the power spectrum with index $n_\mathcal{R}(k)$, and $A(k)$ is the amplitude of modulation, which is [9, 10]

$$\begin{aligned} A(k)&= {|\nabla \mathcal{P}^{1/2}_{\mathcal{R}}(k,\mathbf {x})|\over \mathcal{P}^{1/2}_{\mathcal{R}}}\,x_\mathrm{ls}\nonumber \\&= \left( 1-\epsilon \right) \left[ {n_\mathcal{R}(k)-1\over 2}\right] k_\mathrm{L} x_\mathrm{ls}\mathcal{P}^{1/2}_{\mathcal{R},\mathrm{L}}, \end{aligned}$$

(2)

where $\mathcal{P}_{\mathcal{R},\mathrm{L}}$ is the amplitude of the power spectrum of the modulating mode $k_\mathrm{L}$, and $\epsilon =-{\dot{H}}/H^2$. We have $(k_L x_\mathrm{ls})\mathcal{P}^{1/2}_{\mathcal{R},\mathrm{L}}\lesssim 0.1$ [8, 9, 11, 12].

In single field inflationary scenario, the spectrum $n_{\mathrm{inf}}-1\sim 0.04$ is almost scale invariant. Thus on large angular scales the amplitude of the modulation is too small to fit the observation [8, 9]. In addition, the almost scale invariance of the inflationary spectrum also fails to explain the power deficit on large angular scales.

However, it could be observed that a large amplitude of the modulation consistent with the observations actually requires the breaking of the scale invariance of power spectrum on large angular scales, while simultaneously such a breaking also helps to explain the power suppression on corresponding scales, e.g. [10]. In this angle of view, the anomalies on large angular scales may be a hint of the pre-inflationary physics, which might be relevant with the initial singularity, e.g. [13–16].

Here, we will show that an inflationary model, in which before the slow-roll inflation the Universe is in a superinflationary phase, can generate a large-scale cutoff in the primordial power spectrum, which may account for not only the power suppression on large angular scales, but also a large dipole power asymmetry in the CMB.

It is generally thought that the pre-inflationary physics ought to be controlled by a fundamental theory, e.g. string theory. How to embed the inflationary scenario into string theory has been a significant issue, which has been studied intensively; see Reference [17]. Thus it is intriguing and might be naturally expected that a stringy mechanism of inflation could give rise to the CMB anomalies on large angular scales, e.g. [4, 18] with a string landscape, and also [19, 20] with a fast-roll phase in fiber inflation [21]. For how to involve the degrees of freedom of the standard model; see e.g. Reference [22, 23]. We will discuss an implementation of our model in string theory, based on References [24, 25].

2 The modulating mode from a superinflationary phase

We first will calculate the primordial perturbation generated in such an inflationary model, and identify the corresponding modulating mode from a superinflationary phase.

The equation of the curvature perturbation $\mathcal R$ in momentum space is

$$\begin{aligned} u_k^{\prime \prime } +\left( c^2_s k^2-{z^{\prime \prime }\over z}\right) u_k = 0, \end{aligned}$$

(3)

after $u_k \equiv z\mathcal{R}_k$ is defined, where $'$ is for the derivative with respect to the conformal time $\eta =\int \mathrm{d}t/a$, $z\equiv {a\sqrt{2M_P^2\epsilon }/ c_s}$. We have $c_s^2=1$ for a canonical scalar field.

The Universe initially is in a superinflationary phase with $\epsilon _{\mathrm{Pre-inf}}\sim -\mathcal{O}(1)$; hereafter, it will get into an inflationary phase with $\epsilon _\mathrm{inf}\ll 1$. We will neglect the matching details for simplicity. Thus in conformal time, after adopting an instantaneous matching, we have

$$\begin{aligned} a&\simeq {a_0\over \sqrt{1-2\mathcal{H}_0\eta }}, \,\,\,\mathrm{for}\,\,\mathrm{the }\,\,\mathrm{superinflation} \nonumber \\&{a_0\over 1-\mathcal{H}_0\eta }, \,\,\, \mathrm{for} \,\,\mathrm{the }\,\,\mathrm{inflation}, \end{aligned}$$

(4)

where $\eta <0$ in the superinflationary phase and $\eta >0$ in the inflationary phase, respectively, and $a=a_0$ for $\eta =0$ is set, $\mathcal{H}_0$ is the comoving Hubble length at matching time $\eta =0$, which sets the inflationary energy scale by $H_\mathrm{inf}=\mathcal{H}_0/a_0$. Here, $\epsilon _{\mathrm{Pre-inf}}=-1$ is applied. In principle, another value with $|\epsilon _{\mathrm{Pre-inf}}| \gtrsim 1$ may also be used, which, however, hardly would alter the result qualitatively. The evolution of the superinflationary phase with arbitrary $\epsilon <0$ and the primordial perturbation generated have been studied earlier in Reference [26]. The case with $\epsilon \ll -1$ corresponds to the slow expansion scenario of the primordial universe, which has been proposed earlier in Reference [27] and investigated in detail in Reference [28–30].

When $k^2\gg {z^{\prime \prime }\over z}$, the perturbation is deep inside its horizon, we have $u_k\sim {1\over \sqrt{2k}} e^{-ik\eta }$. In the superinflationary phase,

$$\begin{aligned} {z^{\prime \prime }\over z}\simeq {3\mathcal{H}_0^2\over (1-2\mathcal{H}_0 \eta )^2}. \end{aligned}$$

(5)

When $k^2\ll {z^{\prime \prime }\over z}$, the solution of Eq. (3) is

$$\begin{aligned} {u_k}=\sqrt{\pi (1-2\mathcal{H}_0\eta )\over 8\mathcal{H}_0}H_1^{(1)}\left( -k\eta +{k\over 2\mathcal{H}_0}\right) , \end{aligned}$$

(6)

where $H_1^{(1)}$ is the first-order Hankel function of the first kind.

In the inflationary phase,

$$\begin{aligned} {z^{\prime \prime }\over z} \simeq {2\mathcal{H}_0^2 \over (1-\mathcal{H}_0\eta )^2}. \end{aligned}$$

(7)

When $k^2\ll {z^{\prime \prime }\over z}$, i.e. $-k\eta +{k/\mathcal{H}_0}\ll 1$, the solution of Eq. (3) is

$$\begin{aligned}&{u_k} = \sqrt{-k\eta }\,\sqrt{1 -{1\over \mathcal{H}_0\eta }}\nonumber \\&\quad \times \left( C_1 H_{3/2}^{(1)}\left( -k\eta +{k\over \mathcal{H}_0}\right) +C_2 H_{3/2}^{(2)}\left( -k\eta +{k\over \mathcal{H}_0}\right) \right) ,\nonumber \\ \end{aligned}$$

(8)

where $H_{3/2}^{(1)}$ is the 3/2th-order Hankel function of the first kind, $H_{3/2}^{(2)}$ is the 3/2th-order Hankel function of the second kind, $C_1$, $C_2$ $\sim 1/\sqrt{\mathcal{H}_0}$ are only dependent on $k$.

We require that all physical quantities continuously pass through the matching surface. The continuity of the curvature perturbation gives

$$\begin{aligned} C_1&= { \frac{i\pi e^{-ik/\mathcal{H}_0}}{16 \sqrt{\mathcal{H}_0}}\left( 1-\frac{\mathcal{H}_0}{k}i\right) } \left[ H^{(1)}_0\left( \frac{k}{2\mathcal{H}_0 }\right) -H^{(1)}_2\left( \frac{k}{2\mathcal{H}_0}\right) \right] \nonumber \\&- \frac{\pi e^{-ik/\mathcal{H}_0}}{8\sqrt{\mathcal{H}_0}}\left( 1-\frac{2\mathcal{H}_0^2}{k^2}-\frac{2\mathcal{H}_0}{k}i\right) H^{(1)}_1\left( \frac{k}{2\mathcal{H}_0}\right) ,\end{aligned}$$

(9)

$$\begin{aligned} C_2&= { -\frac{i\pi e^{ik/\mathcal{H}_0}}{16\sqrt{\mathcal{H}_0}}\left( 1+\frac{\mathcal{H}_0}{k}i\right) } \left[ H^{(1)}_0\left( \frac{k}{2\mathcal{H}_0 }\right) -H^{(1)}_2\left( \frac{k}{2\mathcal{H}_0}\right) \right] \nonumber \\&- \frac{\pi e^{ik/\mathcal{H}_0}}{8\sqrt{\mathcal{H}_0}}\left( 1-\frac{2\mathcal{H}_0^2}{k^2}+\frac{2\mathcal{H}_0}{k}i\right) H^{(1)}_1\left( \frac{k}{2\mathcal{H}_0}\right) , \end{aligned}$$

(10)

where $H_0^{(1)}$ is the zeroth-order Hankel function of the first kind and $H_2^{(1)}$ is the second-order Hankel function of the first kind.

Thus the power spectrum of $\mathcal R$ is

$$\begin{aligned} \mathcal{P}_\mathcal{R} = {k^3\over 2\pi ^2}\left| {u_k\over z}\right| ^2=\mathcal{P}_\mathcal{R}^\mathrm{inf} {2\over \pi }k\left| C_1 -C_2\right| ^2, \end{aligned}$$

(11)

where $\mathcal{P}_\mathcal{R}^\mathrm{inf} = {H_\mathrm{inf}^2\over 4 \pi ^2 M_P^2 \epsilon _\mathrm{inf}}$ is that of the standard slow-roll inflation, which may has a slight red spectrum consistent with the observation, and $C_1$ and $C_2$ are determined by Eqs. (9) and (10), respectively. The spectrum index of $\mathcal R$ is $n_\mathcal{R}= n_\mathrm{inf}+{d\ln {(k|C_1 -C_2|^2)}\over d\ln k}$.

In Reference [31], the perturbation from a superinflationary phase was also calculated. However, it is assumed that before the superinflationary phase a nonsingular bounce appears, which is not required here.

Here, $\mathcal{H}_0$ is the comoving Hubble length at matching surface $\eta =0$. The modulating mode corresponds to that on large scales $k\ll \mathcal{H}_0$, which is generated during the superinflationary evolution.

We may expand the Hankel functions in terms of $k\ll \mathcal{H}_0$ and have

$$\begin{aligned} \mathcal{P}_\mathcal{R}^{k < \mathcal{H}_0} \simeq \mathcal{P}_\mathcal{R}^\mathrm{inf}\frac{2k}{\pi \mathcal{H}_0}\left( 1+\frac{k^2}{12\mathcal{H}^2_0}\ln \frac{k}{\mathcal{H}_0}\right) ^2 \sim {k\over \mathcal{H}_0}. \end{aligned}$$

(12)

The details of the calculations are given in the appendix. Thus the spectrum is strongly blue tilt.

Meanwhile, at intermediate and small angular scales, i.e. $k \gg \mathcal{H}_0$, we have

$$\begin{aligned} \mathcal{P}_\mathcal{R}^{k> \mathcal{H}_0}\simeq \mathcal{P}_\mathcal{R}^\mathrm{inf}\left( 1-\frac{{3\mathcal{H}_0}}{{8k}}\sin \left( \frac{2k}{\mathcal{H}_0}\right) \right) . \end{aligned}$$

(13)

Thus the spectrum is almost scale invariant but modulated with a small oscillation, which is the standard result of slow-roll inflationary evolution. We plot $\mathcal{P}_\mathcal{R}$ in Eq. (11) in Fig. 1, which is consistent with our analytical result. Here, it is just the superinflationary evolution that brings the modulating mode with $1-\epsilon _{\mathrm{Pre-inf}}\gtrsim 1$ and $n_\mathcal{R}-1\gtrsim 1$ on large angular scales.

Fig. 1

Best-fit primordial power spectrum of curvature perturbations for the pure power law (dashed) and our model (solid) using Planck+WP data

In Reference [10], a slightly similar spectrum has been found for a bouncing inflation model, in which before the slow-roll inflation the Universe is in a contracting phase; see Reference [13, 14] for an earlier study.

3 The CMB angular power spectrum with Planck

We will show the fit of our model to the CMB TT spectrum, and also the corresponding signals in the TE and EE power spectra.

The slow-roll inflationary spectrum $\mathcal{P}_\mathcal{R}^\mathrm{inf}$ in Eq. (11) may be parameterized as a power law with $\mathcal{P}_\mathcal{R}^\mathrm{inf}\!=\!A_\mathrm{inf}(k/k_0)^{n_\mathrm{inf}-1}$, where $A_\mathrm{inf}$ is the amplitude of perturbation; see [32] for possible features in the primordial power spectrum and [33–35] for the general shape reconstructed from the CMB data. We follow Reference [1] and choose the pivot scale to be $k_0=0.05\, \mathrm{Mpc}^{-1}$, roughly in the middle of the logarithmic range of scales probed by Planck.

We assume that the late-time cosmology is the standard flat $\Lambda$CDM model described by four free cosmological parameters: $\Omega _bh^2$, $\Omega _ch^2$, $\Theta _s$ and $\tau$. Here $h$ is the dimensionless Hubble parameter such that $H_0 = 100$ h km s$^{-1}$ Mpc$^{-1}$ (noting that here $H_0$ is not related with the cutoff scale $\mathcal{H}_0$), $\Omega _b h^2$ and $\Omega _ch^2$ are the physical baryon and dark matter densities relative to the critical density at the present day, respectively, $\Theta _s$ is the ratio of the sound horizon to the angular diameter distance at the photon decoupling, and $\tau$ is the Thomson scattering optical depth due to reionization.

We modify the numerical Boltzmann code CAMB [36] to calculate the lensed TT, TE, EE power spectra and two-point correlation function, and show the results in Fig. 2. The blue dashed curves show the pure power law while the black solid curves show our model (11) with the best-fit value of $\ln (\mathcal{H}_0/\mathrm{Mpc}^{-1})=-7.47$. We see that the TT, TE, and EE spectra for our model are suppressed in the range $l<6$, compared to the pure power law. Since the corresponding signals are induced in the TE and EE spectra, the ongoing Planck polarization data are expected to improve the constraints on the model parameter $\mathcal{H}_0$. As shown in [37], the polarization data can be used to test the parity asymmetry of the CMB pattern. Note that there is a small bump around $l\sim 10$ in the TT spectrum due to oscillations of the primordial power spectrum at large scales. The predicted two-point correlation function at $\theta > 50^\circ$ fits the Planck data much better than the pure power-law spectrum [38, 39].

Fig. 2

Best-fit TT (upper left), TE (lower left), EE (lower right) power spectra, and two-point correlation function (upper right) for the pure power law (dashed) and our model (solid) using Planck+WP data. The red points show the Planck data with 1$\sigma$ errors

We use the Planck CMB temperature likelihood [1] supplemented by the WMAP large-scale polarization likelihood [40] (Planck+WP). The Planck temperature likelihood consists of the high-$l$ TT data ($50 \le l \le 2{,}500$) and the low-$l$ TT data ($2 \le l \le 49$). Because of contributions to the multi-frequency spectra from unresolved radio point sources, cosmic infrared background, Sunyaev–Zeldovich effects, and calibration and beam uncertainties, the Planck high-$l$ likelihood includes 14 nuisance parameters, which should be marginalized in the analysis. As discussed in [1], the large-scale E-mode polarization data is important for constraining reionization. Hence we also use the 9-year WMAP large-scale polarization likelihood including the TE, EE, and BB spectra in the range $2\le l \le 23$.

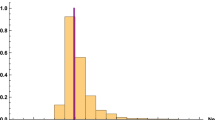
We use the Markov Chain Monte Carlo sampler as implemented in the CosmoMC package [41] to construct the posterior parameter probabilities. Since the Planck high-$l$ likelihood includes many nuisance parameters which are fast parameters, a new sampling method for decorrelating fast and slow parameters is adopted in our analysis to efficiently scan the parameter space [42]. We impose a flat prior on the logarithm of $\mathcal{H}_0$ in the range [$-12,-4$]. For the other cosmological parameters, prior ranges are chosen to be much larger than the posterior. For the Planck+WP likelihood we find the best-fit value of $\ln (\mathcal{H}_0/\mathrm{Mpc}^{-1})\!=\!-7.47$ with $-2\ln \mathcal{L}_\mathrm{max}\!=\!9{,}803.0$. This means that our model can improve the fit to the data with $-2\Delta \ln \mathcal{L}_\mathrm{max}=-4.8$ with respect to the standard power-law model. However, a two-parameter exponential-form cutoff of the primordial power spectrum improves the fit only with $-2\Delta \ln \mathcal{L}_\mathrm{max}=-2.9$ reported in [43]. The reason is that the small bump in the temperature spectrum induced by oscillation of primordial power spectrum improves the fit to the data. Figure 3 shows the marginalized posterior distributions for $\mathcal{H}_0$ from the Planck+WP data, which illustrates the asymmetric shape of the likelihood functions.

Fig. 3

Marginalized posterior distributions for $\mathcal{H}_0$ from the Planck+WP data

Here, since $n_\mathcal{R}-1\simeq 1$ on large angular scales and $n_\mathcal{R}-1\simeq 0$ on small angular scales, the running $d n_\mathcal{R}/d\ln k$ of $n_\mathcal{R}$ is negligible on corresponding scales. The strongly blue-tilt spectrum on large angular scales implies a large-scale cutoff in the primordial power spectrum. However, due to the integrated Sachs–Wolfe effect, the CMB TT angular power spectrum does not show a sharp cutoff on corresponding scales; see the upper-left panel in Fig. 2.

The strongly blue tilt on large angular scales will bring about a large dipole power asymmetry on corresponding scale. In light of Eq. (2), since $n_\mathcal{R}-1\simeq 1$ and $\epsilon _{\mathrm{Pre-inf}}\simeq -1$, we have $A(k)<0.1$ for $(k_L x_\mathrm{ls})\mathcal{P}^{1/2}_{\mathcal{R},\mathrm{L}}\lesssim 0.1$, which may explain the hemispherical power asymmetry in the CMB, reported by the Planck collaboration. While since on small angular scales $n_\mathcal{R}-1\simeq -0.04$, which is that in the slow-roll inflationary phase, we have $A(k)<0.001$, which may be consistent with the constraint from the SDSS sample of quasars [44] and also [45]. Thus our scenario accounts not only for the power suppression on large angular scales, but also for a large dipole power asymmetry in the CMB.

Recently, some explanations appeared which attempted to provide a mechanism to the anomalies, [9, 11, 12, 18, 46–51] and also [52]. However, most of them involved only the dipole power asymmetry in CMB, not the lack of power on large angular scales. By contrast, our model not only generates the power asymmetry but also a suppression of power on large angular scales; see also [10] for a bouncing inflationary model.

The power suppression on large angular scales has also been implemented in fiber inflation [19–21], and also [15, 16] for brane SUSY breaking models [53–55], and [56, 57] for the punctuated inflation. However, how to explain the dipole power asymmetry in the CMB was not illustrated in these studies.

4 An implementation in string theory

How to embed such an inflationary model into string theory is interesting. We will discuss an implementation of our model in string theory. In warped compactifications with the brane/flux annihilation [58], the effective potential controlling the relevant evolution may potentially support a cosmological inflation [24, 25]. However, we find that there may be a superinflationary phase before the slow-roll inflation.

In a ten dimensional CY manifold with a warped KS throat, the metric of the warped throat is

$$\begin{aligned} \mathrm{d}s^2= {1\over \sqrt{f(r)}}\mathrm{d}s^2_{(4)}+\sqrt{f(r)}(\mathrm{d}r^2+r^2 \mathrm{d}s_{(5)}^2) \end{aligned}$$

(14)

for $r<r_*$, where $r$ is the proper distance to the tip of the throat, $\mathrm{d}s^2_{(5)}$ is the angular part of the internal metric, and $f(r)$ is the warp factor, which has a minimal value at $r_0$ and is determined by $\beta \equiv {r_0\over R}\sim e^{-{2\pi \mathcal{K}\over 3g_s \mathcal{M}}}$, in which $R^4 ={27\pi \over 4} g_s N\alpha ^{\prime 2}$, $N$ equals the product of the fluxes $\mathcal{M}$ and $\mathcal{K}$ for the RR and NSNS three-forms, respectively, $g_s$ is the string coupling and $\alpha ^\prime$ is set by the string scale. When $r>r_*$, this metric can be glued to the metric of the bulk of the compact space, which is usually taken to be a CY manifold. When $r_0< r <r_{*}$, $f(r)$ is approximately $f(r)= ({R\over r})^4$.

We follow Reference [58]. When $p(\ll \mathcal{M})$ $\overline{ D3 }$-branes sit at the tip of KS throat, the system is a nonsupersymmetric NS5-brane “giant graviton” configuration, in which the NS5-brane warps a $S^2$ in $S^3$, and carries $p$ unites flux, which induces the $\overline{ D3 }$-charge. $S^2$ is inclined to expand as a spherical shell in $S^3$, which may be parameterized by an angle $0 \leqslant \psi \leqslant \pi$, in which $\psi =0$ corresponds to the north pole of $S^3$ and $\psi =\pi$ is the south pole. The angular position may be regarded as a scalar in the world volume action, which describes the motion of the NS5-brane across the $S^3$. The effective potential controlling the relevant evolution is

$$\begin{aligned} V_\mathrm{eff}(\psi )= \mathcal{M}\beta ^4 T_3\left( \sqrt{{b_0^2 \sin ^4{\psi }\over \pi ^2}+{\tilde{V}}^2(\psi )}+{\tilde{V}}(\psi )\right) \end{aligned}$$

(15)

with $b_0\simeq 0.9$, where ${\tilde{V}}(\psi ) ={p\over \mathcal{M}}-{\psi -{\sin {(2\psi )}\over 2}\over \pi }$ and $T_3$ is the $\overline{ D3 }$-brane tension. This potential is plotted in Fig. 4 with respect to $\psi$.

In the regime with $p/\mathcal{M} < 0.08$, the metastable bound state forms, which corresponds to a static NS5-brane wrapping a $S^2$ in $S^3$.

This metastable bound state corresponds to $\psi = 0$ and $V_\mathrm{eff}(0)=2p\beta ^4 T_3$; see Fig. 4. The true minimum is at $\psi = \pi$, in which the potential energy is $0$.

In the regime $p/\mathcal{M} \gtrsim 0.08$, this metastable state disappears, which implies that the nonsupersymmetric configuration of $p$ $\overline{ D3 }$-branes becomes classically unstable and will relax to a supersymmetric minimum by a classical rolling of $\psi$ along its potential. This classical rolling may lead to a slow-roll inflation, which has been studied in detail in Reference [25]. When $\psi =\pi$, in which the potential energy is $0$, the inflation will end. The result of this evolution is $\mathcal{M}-p$ D3-branes instead of the original $p$ $\overline{ D3 }$-branes appearing at the tip of the throat, while the three-form flux $\mathcal{K}$ is changed to $\mathcal{K}-1$, i.e. we have brane/flux annihilation [58].

During the period before the slow-roll inflation, in which $p/\mathcal{M} < 0.08$, the Hubble expansion of the Universe is given by

$$\begin{aligned} H^2= {2p\beta ^4 T_3 \over 3}, \end{aligned}$$

(16)

where $8\pi /M_P^2= 1$. When $\overline{ D3 }$-branes are pulled into the throat continuously, the metastable minimum will increase [59], see Fig. 4, which implies that $H$ will increase rapidly during this period.

Thus the parameter $\epsilon$ is

$$\begin{aligned} \epsilon _{\mathrm{Pre-inf}} =-{{\dot{H}}\over H^2}\sim -\left( {{\dot{p}}\over 2Hp}\right) . \end{aligned}$$

(17)

Thus in units of $\Delta t= 1/H$, we approximately have $|\epsilon _{\mathrm{Pre-inf}}| \sim {\Delta p\over 2p}$, where $\Delta p$ is the change of $p$ in unit of $1/H$.

We assume ${\Delta p\over 2p}\gtrsim 1$, which may be consistent with $\mathcal{M}\sim 10^4$ and $p_{I}\sim \mathcal{O}(1)$, where $p_{I}$ is the initial number of $\overline{ D3 }$-branes at the tip of the KS throat. Here, all the moduli is assumed to be fixed, and the interaction between $\overline{ D3 }$-branes has been also neglected for simplicity.

Fig. 4

The figure of the potential Eq. (15). When $\overline{ D3 }$-branes are pulled into the throat continuously, the metastable minimum will rise inch by inch

Thus in this model the Universe initially is in a superinflationary phase with $\epsilon _{\mathrm{Pre-inf}}\sim -\mathcal{O}(1)$, during which the number of $\overline{ D3 }$-branes at the tip of throat will increase rapidly. After a sufficient number of $\overline{ D3 }$-branes enter into the throat, which makes $p$ reaching its critical value, $\psi$ will slowly roll down to its real minimum at $\psi = \pi$, during which the Universe is in a slow-roll inflationary phase. Thus as has been argued, it is just the stringy physics before the slow-roll inflation that results in a large-scale cutoff in the primordial power spectrum.

We conclude that a stringy model of inflation in which initially the Universe is in a superinflationary phase can generate a large-scale cutoff in the primordial power spectrum, which may account for not only the power suppression on large angular scales, but also a large dipole power asymmetry in the CMB. In the meantime this model also predicts distinct signals in TE and EE power spectra, which may be falsified by the observation of CMB polarization.

Appendix

We rewrite $C_1-C_2$ as, with Eqs. (9) and (10),

$$\begin{aligned}&C_1-C_2 = \frac{\pi }{8i{\sqrt{\mathcal {H}}_{0}}}\left( H^{(1)}_0\left( \frac{{\tilde{k}}}{2}\right) -H^{(1)}_2\left( \frac{{\tilde{k}}}{2}\right) \right) \left( \frac{\sin {\tilde{k}}}{{\tilde{k}}}-\cos {\tilde{k}}\right) \nonumber \\&\quad - \frac{\pi }{4i{\sqrt{{\mathcal {H}}}_{0}}}H^{(1)}_1\left( \frac{{\tilde{k}}}{2}\right) \left( \sin {\tilde{k}}-\frac{2\sin {\tilde{k}}}{{\tilde{k}}^2}+\frac{2\cos {\tilde{k}}}{{\tilde{k}}}\right) , \end{aligned}$$

(18)

where ${\tilde{k}}=k/\mathcal{H}_0$ is defined for simplicity. When ${\tilde{k}}\ll 1$,

$$\begin{aligned}&H^{(1)}_0\left( \frac{{\tilde{k}}}{2}\right) \simeq -i\frac{2}{\pi }\ln \frac{4}{{\tilde{k}}},\end{aligned}$$

(19)

$$\begin{aligned}&H^{(1)}_1\left( \frac{{\tilde{k}}}{2}\right) \simeq -i\frac{4}{{\tilde{k}}\pi },\end{aligned}$$

(20)

$$\begin{aligned}&H^{(1)}_2\left( \frac{{\tilde{k}}}{2}\right) \simeq -i\frac{16}{{\tilde{k}}^2\pi }. \end{aligned}$$

(21)

Thus $C_1-C_2$ is approximately

$$\begin{aligned} C_1-C_2&\simeq \frac{1}{\sqrt{\mathcal {H}}_{0}} \left( -\frac{1}{4}\ln \frac{4}{{\tilde{k}}}+\frac{2}{{\tilde{k}}^2}\right) \left( \frac{\sin {\tilde{k}}}{{\tilde{k}}}- \cos {\tilde{k}}\right) \nonumber \\&+ \frac{1}{\sqrt{{\mathcal {H}}}_{0} {\tilde{k}}}\left( \sin {\tilde{k}}-2\frac{\sin {\tilde{k}}}{{\tilde{k}}^2}+2\frac{\cos {\tilde{k}}}{{\tilde{k}}}\right) \nonumber \\&\simeq \frac{1}{\sqrt{\mathcal {H}}_{0}}\left( 1+\frac{{\tilde{k}}^2}{12}\ln {\tilde{k}}\right) . \end{aligned}$$

(22)

Thus Eq. (12) is obtained.