New physics in $B_{d,s}$–${\bar{B}}_{d,s}$ mixings and $B_{d,s}\rightarrow \mu ^+\mu ^-$ decays

Abstract

A new way of probing new physics in the $B$ meson system is provided. We define double ratios for the observables of $B_{d,s}$–${\bar{B}}_{d,s}$ mixings and $B_{d,s}\rightarrow \mu ^+\mu ^-$ decays, and find simple relations between the observables. By using the relations we predict the yet-to-be-measured branching ratio of $B_d\rightarrow \mu ^+\mu ^-$ to be (0.809–1.03)$\times 10^{-10}$, up to the new physics models.

1 Introduction

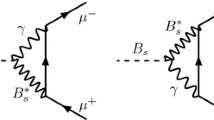
The recent discovery of a Higgs boson at the large hadron collider (LHC) opened a new era of high energy physics. It may take time to confirm whether the new particle is really the Higgs boson of the standard model (SM), but it looks more and more like the SM Higgs. The discovery of the Higgs boson would mean a completion of the SM. On the other hand, we have many reasons to believe that there must be new physics (NP) beyond the SM. Unfortunately, the LHC up to now has not reported any clues of NP. But it is too early to say that there is no NP at all. $B_{d,s}$ mesons are good test beds for NP. Especially, $B_{d,s}$–${\bar{B}}_{d,s}$ mixings and $B_{d,s}\rightarrow \mu ^+\mu ^-$ decays are loop-induced phenomena in the SM and very sensitive to NP effects. The current status of the experiments is well compatible with the SM predictions. For example, the LHCb and the CMS collaboration reported [1, 2]

$$\begin{aligned}&\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)=(2.9^{+1.1}_{-1.0})\times 10^{-9},~\nonumber \\&\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)<7.4\times 10^{-10}~(\mathrm{LHCb}), \end{aligned}$$

(1)

$$\begin{aligned}&\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)=(3.0^{+1.0}_{-0.9})\times 10^{-9},\nonumber \\&\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)<1.1\times 10^{-9}~(\mathrm{CMS}). \end{aligned}$$

(2)

The measured value is slightly smaller than the previous LHCb measurements [3]:

$$\begin{aligned}&\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)=(3.2^{+1.5}_{-1.2})\times 10^{-9},\nonumber \\&\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)<9.4\times 10^{-10}. \end{aligned}$$

(3)

For comparison: the SM predictions are [4, 5]

$$\begin{aligned}&\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)=(3.25\pm 0.17)\times 10^{-9},\end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)=(1.07\pm 0.10)\times 10^{-10}. \end{aligned}$$

(5)

But there is still some room for NP, as discussed in [4, 6, 7]. In this paper, we provide a very simple and quick way to probe NP in $B_{d,s}$–${\bar{B}}_{d,s}$ mixings and $B_{d,s}\rightarrow \mu ^+\mu ^-$ decays. The idea is that a double ratio for one observable between different flavors extracts the relevant couplings for NP, and they are directly related to the other observable. Schematically, for a physical observable $\mathcal{O}_i^a$ with flavor $a$,

$$\begin{aligned} R_i^{ab}\equiv \frac{\mathcal{O}_{i,\mathrm{exp}}^a/\mathcal{O}_{i,\mathrm{SM}}^a-1}{\mathcal{O}_{i,\mathrm{exp}}^b/\mathcal{O}_{i,\mathrm{SM}}^b-1} \simeq f_i\left( \frac{c^a}{c^b}\right) , \end{aligned}$$

(6)

where the $c^a$ are the new couplings and $f_i$ is some function of $c^a/c^b$. For another observable $\mathcal{O}_j$ we can define a similar quantity, $R_j^{ab}$, which would behave $\simeq f_j(c^a/c^b)$. Consequently, $R_i^{ab}$ and $R_j^{ab}$ are related through the functions $f_i$ and $f_j$, and the relations are remarkably simplified when the new couplings belong to the category of the minimal flavor violation (MFV). In this way, we can establish simple relations between the observables of $B_{d,s}$–${\bar{B}}_{d,s}$ mixings and $B_{d,s}\rightarrow \mu ^+\mu ^-$ decays. The relations are very useful because $R_i^{ab}$ and $R_j^{ab}$ are directly connected, and the relations are different for various NP models. For example, we can predict $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)$ from other known observables such as $\Delta M$ of $B_{d,s}$–${\bar{B}}_{d,s}$ mixings, without knowing the values of the new couplings. Or if we measure the branching ratio $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)$, we can find from the double ratio relations which NP is realized in $B$ physics. In this paper we specifically consider flavor changing scalar (un)particles and vector boson ($Z'$) scenarios. Actually it is already known that $\Delta M_q$ and $\mathrm{Br}(B_q\rightarrow \mu ^+\mu ^-)$ can be related to each other [8–10]. In our approach, the $R_i^{ab}$ are directly proportional to the NP effects, so the resulting relations are solely those of NP. The relations might be different for various models, which makes it easier to see which kind of NP is realized.

The NP couplings adopted in this analysis are summarized as follows [4, 11]:

$$\begin{aligned} \mathcal{L}_{Z'}&= [ \Delta _L^{sb}(Z')({\bar{s}}\gamma _\mu P_Lb)+\Delta _R^{sb}(Z')({\bar{s}}\gamma _\mu P_Rb)\nonumber \\&+\,\Delta _L^{\ell \ell }(Z')({\bar{\ell }}\gamma _\mu P_L\ell )+\Delta _R^{\ell \ell }(Z')({\bar{\ell }}\gamma _\mu P_R\ell )]Z'^\mu ,\end{aligned}$$

(7)

$$\begin{aligned} \mathcal{L}_H&= [\Delta _L^{sb}(H)({\bar{s}}P_Lb)\!+\!\Delta _R^{sb}(H)({\bar{s}}P_Rb) \!+\!\Delta _L^{\ell \ell }(H)({\bar{\ell }}P_L\ell )\nonumber \\&+\,\Delta _R^{\ell \ell }(H)({\bar{\ell }}P_R\ell )]H,\end{aligned}$$

(8)

$$\begin{aligned} \mathcal{L}_\mathcal{U}&= \frac{c_{\mathcal{U}L}^{bs}}{\Lambda _\mathcal{U}^{d_\mathcal{U}}}{\bar{s}}\gamma _\mu (1\!-\!\gamma _5)b~\partial ^\mu \mathcal{O}_\mathcal{U}\!+\!\frac{c_{\mathcal{U}L}^\ell }{\Lambda _\mathcal{U}^{d_\mathcal{U}}}\bar{\ell }\gamma _\mu (1\!-\!\gamma _5)\ell ~\partial ^\mu \mathcal{O}_\mathcal{U},\nonumber \\ \end{aligned}$$

(9)

where $P_{L,R}=(1\mp \gamma _5)/2$. In $\mathcal{L}_\mathcal{U}$ one can also include the right-handed couplings, but here (and in [11]) only the minimal extension of the SM is considered for simplicity.

First consider the $B_{d,s}$–${\bar{B}}_{d,s}$ mixing. The mixing effect is parametrized as the following quantity:

$$\begin{aligned} \Delta M_q=\frac{G_F^2}{6\pi ^2}M_W^2m_{B_q}|V_{tb}^*V_{tq}|^2F_{B_q}^2\eta _B|S(B_q)|, \end{aligned}$$

(10)

where

$$\begin{aligned} S(B_q)=S_0(x_t)+\Delta S(B_q)\equiv |S(B_q)|e^{i\theta _S^{B_q}}, \end{aligned}$$

(11)

and $x_t=m_t^2/m_W^2$. Here the loop function

$$\begin{aligned} S_0(x_t)=\frac{4x_t-11x_t^2+x_t^3}{4(1-x_t)^2}-\frac{3x_t^2\log x_t}{2(1-x_t)^3}, \end{aligned}$$

(12)

and

$$\begin{aligned} \Delta S(B_q)&= [\Delta S(B_q)]_{V(S){ LL }}+[\Delta S(B_q)]_{V(S){ RR }}\nonumber \\&+\,[\Delta S(B_q)]_{V(S){ LR }}, \end{aligned}$$

(13)

where the subscript $V(S)$ stands for $Z'(H)$ contributions. Explicitly [6, 7],

$$\begin{aligned} {[S(B_q)]}_{{ VLL }}&= \left[ \frac{\Delta _L^{bq}(Z')}{V_{tb}^{*} V_{tq}}\right] ^2\frac{4{\tilde{r}}}{M_{Z'}^2g_\mathrm{SM}^2},\end{aligned}$$

(14)

$$\begin{aligned} {[S(B_q)]}_{{ VRR }}&= \left[ \frac{\Delta _R^{bq}(Z')}{V_{tb}^{*} V_{tq}}\right] ^2\frac{4{\tilde{r}}}{M_{Z'}^2g_\mathrm{SM}^2}, \end{aligned}$$

(15)

$$\begin{aligned} {[S(B_q)]}_{{ VLR }}&= \frac{\Delta _L^{bq}(Z')\Delta _R^{bq}(Z')}{T(B_q)M_{Z'}^2}\nonumber \\&\quad \times \,[ C_1^{ VLR }(\mu _{Z'}) \langle Q_1^{ VLR }(\mu _{Z'},B_q)\rangle \nonumber \\&\quad +\,C_2^{ VLR }(\mu _{Z'})\langle Q_2^{ VLR }(\mu _{Z'},B_q)\rangle ], \end{aligned}$$

(16)

where

$$\begin{aligned} gSM&\equiv \frac{4G_F}{\sqrt{2}}\frac{\alpha }{2\pi \sin ^2\theta _W},\end{aligned}$$

(17)

$$\begin{aligned} T(B_q)&\equiv \frac{G_F^2}{12\pi ^2}F_{B_q}^2{\hat{B}}_{B_q}m_{B_q}M_W^2(V_{tb}^*V_{tq})^2\eta _B, \end{aligned}$$

(18)

and ${\tilde{r}}=0.985$ for $M_{Z'}=1$ TeV. For the scalar field,

$$\begin{aligned} {[\Delta S(B_q)]}_{SLL}&= -\frac{[\Delta _L^{bq}(H)]^2}{T(B_q)2M_H^2}\nonumber \\&\quad \times \,[C_1^{SLL}(\mu _H)\langle Q_1^{SLL}(\mu _H, B_q)\rangle \nonumber \\&\quad +\,C_2^{SLL}(\mu _H)\langle Q_2^{SLL}(\mu _H, B_q)\rangle ], \end{aligned}$$

(19)

$$\begin{aligned} {[\Delta S(B_q)]}_{SRR}=[\Delta S(B_q)]_{SLL}(L\rightarrow R), \end{aligned}$$

(20)

$$\begin{aligned} {[\Delta S(B_q)]}_{SLR}&= -\frac{\Delta _L^{bq}(H)\Delta _R^{bq}(H)}{T(B_q)M_H^2}\nonumber \\&\quad \,\times [C_1^{SLR}(\mu _H)\langle Q_1^{SLR}(\mu _H, B_q)\rangle \nonumber \\&\quad +\,C_2^{SLR}(\mu _H)\langle Q_2^{SLR}(\mu _H, B_q)\rangle ]. \end{aligned}$$

(21)

The expectation values of the operators $Q_i^a$ are

$$\begin{aligned} \langle Q_i^a(\mu _M, B_q)\rangle \equiv \frac{1}{3}m_{B_q}F_{B_q}^2 P_i^a(\mu _M, B_q). \end{aligned}$$

(22)

For the case of $\Delta _R^{bq}=0$,

$$\begin{aligned} \frac{\Delta M_q(Z')}{\Delta M_q^\mathrm{SM}}&= \left| 1+\frac{[S(B_q)]_{VLL}}{S_0(x_t)}\right| \nonumber \\&\simeq 1+\,\frac{1}{S_0(x_t)}\mathrm{Re}\left[ \frac{\Delta _L^{bq}(Z')}{V_{tb}^*V_{tq}}\right] ^2 \frac{4{\tilde{r}}}{M_{Z'}^2g_\mathrm{SM}^2}, \end{aligned}$$

(23)

up to the leading order of $\Delta _L^{bq}$. Now we define a double ratio $R_{\Delta M}^{Z'}$ as

$$\begin{aligned} R_{\Delta M}^{Z'}\equiv \frac{\Delta M_s(Z')/\Delta M_s^\mathrm{SM}-1}{\Delta M_d(Z')/\Delta M_d^\mathrm{SM}-1} =\frac{\mathrm{Re}\left[ \Delta _L^{bs}(Z')/V_{ts}\right] ^2}{\mathrm{Re}\left[ \Delta _L^{bd}(Z')/V_{td}\right] ^2}, \end{aligned}$$

(24)

where the result of Eq. (23) is applied. Similarly, for the scalar contribution (with $\Delta _R^{bq}=0$),

$$\begin{aligned} R_{\Delta M}^H\!\equiv \! \frac{\Delta M_s(H)/\Delta M_s^\mathrm{SM}-1}{\Delta M_d(H)/\Delta M_d^\mathrm{SM}-1} =\frac{{\hat{B}}_{B_d}}{{\hat{B}}_{B_s}} \frac{\mathrm{Re}\left[ \Delta _L^{bs}(H)/V_{ts}\right] ^2}{\mathrm{Re}\left[ \Delta _L^{bd}(H)/V_{td}\right] ^2}. \end{aligned}$$

(25)

We assumed here that the light-quark dependence on $P_i^a(\mu _H,B_q)$ is negligible [12], and thus $P_i^a(\mu _H,B_d)\simeq P_i^a(\mu _H,B_s)$. In the scalar unparticle scenario [11],

$$\begin{aligned} \frac{\Delta M_q^\mathcal{U}}{\Delta M_q^\mathrm{SM}}-1&\equiv |\Delta _\mathcal{U}|-1 =\mathrm{Re}[(c_{\mathcal{U}L}^{bq})^2 f_\mathcal{U}^q\cot {d_\mathcal{U}}\pi ] \nonumber \\&\quad +\,\mathrm{Im}[(c_{\mathcal{U}L}^{bq})^2 f_\mathcal{U}^q]+\mathcal{O}(c_{\mathcal{U}L}^4). \end{aligned}$$

(26)

Here

$$\begin{aligned} f_\mathcal{U}^q= \frac{5}{24 M_{12}^\mathrm{SM}} A_{d_\mathcal{U}}\left( \frac{F_{B_q}^2}{m_{B_q}}\right) \left( \frac{m_{B_q}^2}{\Lambda _\mathcal{U}}\right) ^{d_\mathcal{U}}, \end{aligned}$$

(27)

where $M_{12}^\mathrm{SM}$ is the SM contribution and

$$\begin{aligned} A_{d_\mathcal{U}}\equiv \frac{16\pi ^{5/2}}{(2\pi )^{2{d_\mathcal{U}}}}\frac{\Gamma ({d_\mathcal{U}}+1/2)}{\Gamma ({d_\mathcal{U}}-1)\Gamma (2{d_\mathcal{U}})}, \end{aligned}$$

(28)

with ${d_\mathcal{U}}$ being the scaling dimension of the scalar unparticle operator. The double ratio for the scalar unparticle is

$$\begin{aligned} R_{\Delta M}^\mathcal{U}\!&\equiv \frac{\Delta M_s^\mathcal{U}/\Delta M_s^\mathrm{SM}-1}{\Delta M_d^\mathcal{U}/\Delta M_d^\mathrm{SM}-1}\nonumber \\&\simeq \left( \frac{{\hat{B}}_{B_d}}{{\hat{B}}_{B_s}}\right) \left( \frac{m_{B_s}^2}{m_{B_d}^2}\right) ^{{d_\mathcal{U}}-1} \frac{\mathrm{Re}({\tilde{c}}_{\mathcal{U}L}^{bs})^2\cot {d_\mathcal{U}}\pi \!+\!\mathrm{Im}({\tilde{c}}_{\mathcal{U}L}^{bs})^2}{\mathrm{Re}({\tilde{c}}_{\mathcal{U}L}^{bd})^2\cot {d_\mathcal{U}}\pi \!+\!\mathrm{Im}({\tilde{c}}_{\mathcal{U}L}^{bd})^2},\nonumber \\ \end{aligned}$$

(29)

where we put $c_{\mathcal{U}L}^{bq}\equiv {\tilde{c}}_{\mathcal{U}L}^{bq}\cdot V_{tb}^*V_{tq}$. For real ${\tilde{c}}_{\mathcal{U}L}^{bq}$, one has

$$\begin{aligned} R_{\Delta M}^\mathcal{U}= \left( \frac{{\hat{B}}_{B_d}}{{\hat{B}}_{B_s}}\right) \left( \frac{m_{B_s}^2}{m_{B_d}^2}\right) ^{{d_\mathcal{U}}-1} \left( \frac{{\tilde{c}}_\mathcal{U}^{bs}}{{\tilde{c}}_{\mathcal{U}L}^{bd}}\right) ^2. \end{aligned}$$

(30)

If ${\tilde{c}}_{\mathcal{U}L}^{bq}$ is purely imaginary, one gets a similar result.

Now we move to $B_{d,s}\rightarrow \mu ^+\mu ^-$ decays. The relevant effective Hamiltonian is given by

$$\begin{aligned} \mathcal{H}_\mathrm{eff} =-\frac{G_F\alpha }{\sqrt{2}\pi }\left[ V_{ts}^*V_{tb}\sum _i^{10,S,P}(C_i\mathcal{O}_i+C_i'\mathcal{O}_i')+\mathrm{h.c.}\right] , \end{aligned}$$

(31)

where the operators $\mathcal{O}_i$ are

$$\begin{aligned} \mathcal{O}_{10}\!&= \!({\bar{s}}\gamma _\mu P_L b)({\bar{\ell }}\gamma ^\mu \gamma _5\ell ),\quad \mathcal{O}_{10}'=({\bar{s}}\gamma _\mu P_R b)({\bar{\ell }}\gamma ^\mu \gamma _5\ell ),\nonumber \\\end{aligned}$$

(32)

$$\begin{aligned} \mathcal{O}_S&= m_b({\bar{s}}P_R b)({\bar{\ell }}\ell ),\quad \mathcal{O}_S'=m_b({\bar{s}}P_L b)({\bar{\ell }}\ell ),\end{aligned}$$

(33)

$$\begin{aligned} \mathcal{O}_P&= m_b({\bar{s}}P_R b)({\bar{\ell }}\gamma _5\ell ),\quad \mathcal{O}_P'=m_b({\bar{s}}P_L b)({\bar{\ell }}\gamma _5\ell ).\nonumber \\ \end{aligned}$$

(34)

For $B_s$ decay it is convenient to define [13, 14]

$$\begin{aligned} {\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)\equiv \frac{1}{r(y_s)}\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{th}, \end{aligned}$$

(35)

where

$$\begin{aligned}&r(y_s)\equiv \frac{1-y_s^2}{1+y_s\mathcal{A}_{\Delta \Gamma }},\end{aligned}$$

(36)

$$\begin{aligned}&y_s \equiv \tau _{B_s}\frac{\Delta \Gamma _s}{2}=0.088\pm 0.014, \end{aligned}$$

(37)

and we have the asymmetric parameter

$$\begin{aligned} \mathcal{A}_{\Delta \Gamma }\equiv \frac{R_H-R_L}{R_H+R_L}, \end{aligned}$$

(38)

where $R_{H(L)}\exp [-\Gamma ^{(s)}_{H(L)}t]$ is the decay rate of the heavy (light) mass eigenstate. Here $\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{th}$ is a theoretical prediction, while ${\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)$ would be directly compared with the experimental results. In general,

$$\begin{aligned} \frac{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)}{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{SM}} =\frac{1+y_s\mathcal{A}_{\Delta \Gamma }}{1+y_s}(|P|^2+|S|^2), \end{aligned}$$

(39)

where

$$\begin{aligned} P&\equiv \frac{C_{10}-C_{10}'}{C_{10}^\mathrm{SM}} +\frac{m_{B_s}^2}{2m_\mu }\frac{m_b}{m_b+m_s}\frac{C_P-C_P'}{C_{10}^\mathrm{SM}} \equiv |P|e^{i\varphi _P},\nonumber \\\end{aligned}$$

(40)

$$\begin{aligned} S&\equiv \sqrt{1-\frac{4m_\mu ^2}{m_{B_s}^2}}~\frac{m_{B_s}^2}{2m_\mu }\frac{m_b}{m_b+m_s}\frac{C_S-C_S'}{C_{10}^\mathrm{SM}} \equiv |S|e^{i\varphi _S}. \end{aligned}$$

(41)

The standard model contribution is

$$\begin{aligned} C_{10}^\mathrm{SM}=-\frac{1}{\sin ^2\theta _W}\eta _Y Y_0(x_t), \end{aligned}$$

(42)

with $\eta _Y=1.012$ and

$$\begin{aligned} Y_0(x_t) =\frac{x_t}{8}\left[ \frac{x_t-4}{x_t-1}+\frac{3x_t\log x_t}{(x_t-1)^2}\right] . \end{aligned}$$

(43)

For the $Z'$ model,

$$\begin{aligned} \sin ^2\theta _W C_{10}(Z')\!&= \! -\eta _Y Y_0(x_t)\!\!-\!\frac{1}{g_\mathrm{SM}^2}\frac{1}{M_{Z'}^2} \frac{\Delta _L^{sb}(Z')\Delta _A^{\mu \mu }(Z')}{V_{ts}^*V_{tb}},\nonumber \\\end{aligned}$$

(44)

$$\begin{aligned} \sin ^2\theta _W C_{10}'(Z')&= -\frac{1}{g_\mathrm{SM}^2}\frac{1}{M_{Z'}^2} \frac{\Delta _R^{sb}(Z')\Delta _A^{\mu \mu }(Z')}{V_{ts}^*V_{tb}}, \end{aligned}$$

(45)

while the other coefficients are vanishing. Using $\Delta _{L,R}^{sb}(Z')=\Delta _{L,R}^{bs}(Z')^*$, one has

$$\begin{aligned}&\frac{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)}{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\simeq \frac{y_s}{1+y_s}[\cos (2\theta _Y^{B_s}+\theta _S^{B_s})-1]\nonumber \\&\quad +\frac{1}{1+y_s}\frac{1}{\eta _Y Y_0(x_t)}\frac{1}{M_{Z'}^2g_\mathrm{SM}^2}2\mathrm{Re}\left[ \frac{(\Delta _L^{bs*}-\Delta _R^{bs*})\Delta _A^{\mu \mu }}{V_{ts}^*V_{tb}}\right] ,\nonumber \\ \end{aligned}$$

(46)

and

$$\begin{aligned}&\frac{{\overline{\mathrm{Br}}}(B_d\rightarrow \mu ^+\mu ^-)}{{\overline{\mathrm{Br}}}(B_d\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}\nonumber \\&\quad -1\simeq \frac{1}{\eta _Y Y_0(x_t)}\frac{1}{M_{Z'}^2g_\mathrm{SM}^2} 2\mathrm{Re}\left[ \frac{(\Delta _L^{bd*}-\Delta _R^{bd*})\Delta _A^{\mu \mu }}{V_{td}^*V_{tb}}\right] ,\nonumber \\ \end{aligned}$$

(47)

up to $\mathcal{O}(y_s\Delta _{L,R}\Delta _A)$. For $\Delta _R=0$ and $\Delta _L^{bq}={\tilde{\Delta }}_L^{bq} V_{tq}$ where ${\tilde{\Delta }}_L^{bq}$ is real, the double ratio

$$\begin{aligned} R_{\mu \mu }^{Z'}&\equiv \left[ \frac{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_{Z'}}{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\right] \bigg /\nonumber \\&\left[ \frac{\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_{Z'}}{\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\right] \end{aligned}$$

(48)

remarkably reduces to

$$\begin{aligned} R_{\mu \mu }^{Z'}=\frac{1}{1+y_s}\left( \frac{{\tilde{\Delta }}_L^{bs}}{{\tilde{\Delta }}_L^{bd}}\right) . \end{aligned}$$

(49)

In this case we have the ratio $R_{\Delta M}^{Z'}=({\tilde{\Delta }}_L^{bs}/{\tilde{\Delta }}_L^{bd})^2$, and thus one arrives at the very simple relation

$$\begin{aligned} R_{\mu \mu }^{Z'}(1+y_s)=\sqrt{R_{\Delta M}^{Z'}}. \end{aligned}$$

(50)

For neutral scalar $H$, the coefficients are

$$\begin{aligned} C_{10}(H)&= C_{10}^\mathrm{SM},\end{aligned}$$

(51)

$$\begin{aligned} C_S(H)&= \frac{1}{m_b\sin ^2\theta _W}\frac{1}{g_\mathrm{SM}^2}\frac{1}{M_H^2} \frac{\Delta _R^{sb}(H)\Delta _S^{\mu \mu }(H)}{V_{ts}^*V_{tb}},\end{aligned}$$

(52)

$$\begin{aligned} C_S'(H)&= \frac{1}{m_b\sin ^2\theta _W}\frac{1}{g_\mathrm{SM}^2}\frac{1}{M_H^2} \frac{\Delta _L^{sb}(H)\Delta _S^{\mu \mu }(H)}{V_{ts}^*V_{tb}},\end{aligned}$$

(53)

$$\begin{aligned} C_P(H)&= \frac{1}{m_b\sin ^2\theta _W}\frac{1}{g_\mathrm{SM}^2}\frac{1}{M_H^2} \frac{\Delta _R^{sb}(H)\Delta _P^{\mu \mu }(H)}{V_{ts}^*V_{tb}},\end{aligned}$$

(54)

$$\begin{aligned} C_P'(H)&= \frac{1}{m_b\sin ^2\theta _W}\frac{1}{g_\mathrm{SM}^2}\frac{1}{M_H^2} \frac{\Delta _L^{sb}(H)\Delta _P^{\mu \mu }(H)}{V_{ts}^*V_{tb}}. \end{aligned}$$

(55)

One can define a double ratio $R_{\mu \mu }^H$ similar to Eq. (48). For simplicity we assume that $\Delta _R=0$ and $\Delta _L^{bq}={\tilde{\Delta }}_L^{bq} V_{tq}$ with real ${\tilde{\Delta }}_L^{bq}$. Note that in this case

$$\begin{aligned} R_{\Delta M}^H=\frac{{\hat{B}}_{B_d}}{{\hat{B}}_{B_s}} \left( \frac{{\tilde{\Delta }}_L^{bs}}{{\tilde{\Delta }}_L^{bd}}\right) ^2. \end{aligned}$$

(56)

For the case of $\Delta _S^{\mu \mu }(H)=0$, the double ratio reduces to

$$\begin{aligned} R_{\mu \mu }^H&\equiv \left[ \frac{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_H}{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\right] \bigg / \nonumber \\&\left[ \frac{\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_H}{\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\right] \nonumber \\&= \frac{1}{1+y_s}\left( \frac{m_{B_s}^2}{m_{B_d}^2}\frac{m_b+m_d}{m_b+m_s}\right) ^2 \left( \frac{{\hat{B}}_{B_s}}{{\hat{B}}_{B_d}}\right) R_{\Delta M}^H. \end{aligned}$$

(57)

On the other hand if $\Delta _P^{\mu \mu }=0$,

$$\begin{aligned} R_{\mu \mu }^H&= \left( \frac{1-2y_s}{1+y_s}\right) \left( \frac{1-4m_\mu ^2/m_{B_s}^2}{1-4m_\mu ^2/m_{B_d}^2}\right) \nonumber \\&\times \left( \frac{m_{B_s}^2}{m_{B_d}^2}\frac{m_b+m_d}{m_b+m_s}\right) ^2 \left( \frac{{\hat{B}}_{B_s}}{{\hat{B}}_{B_d}}\right) R_{\Delta M}^H. \end{aligned}$$

(58)

For scalar unparticles [15],

$$\begin{aligned} P&= 1-\frac{\sin ^2\theta _W}{\eta _Y Y_0(x_t)}\frac{\sqrt{2}\pi A_{d_\mathcal{U}}}{\alpha G_F m_{B_s}^2} \left( \frac{m_{B_s}}{\Lambda _\mathcal{U}}\right) ^{2{d_\mathcal{U}}}\nonumber \\&\times \left( \frac{m_b}{m_b+m_s}\right) \left( \frac{c_{\mathcal{U}L}^{bs}c_{\mathcal{U}L}^\ell }{V_{tb}^*V_{ts}}\right) ^* (\cot {d_\mathcal{U}}\pi +i),\end{aligned}$$

(59)

$$\begin{aligned} S&= 0, \end{aligned}$$

(60)

and thus $\mathcal{A}_{\Delta \Gamma }=\cos (2\varphi _P-\phi _s^\mathcal{U})$. Here $\phi _s^\mathcal{U}$ is the phase of $\Delta _\mathcal{U}$ in Eq. (26). For real ${\tilde{c}}_{\mathcal{U}L}^{bq}, c_{\mathcal{U}L}^\ell$, $\cos (2\varphi _P-\phi _s^\mathcal{U})\simeq 1$ up to $\mathcal{O}(c_{\mathcal{U}L})^4$, and the double ratio is

$$\begin{aligned} R_{\mu \mu }^\mathcal{U}&\equiv \left[ \frac{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathcal{U}}{{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\right] \Bigg /\nonumber \\&\left[ \frac{\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_\mathcal{U}}{\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_\mathrm{SM}}-1\right] \nonumber \\&= \frac{1}{1+y_s}\left( \frac{m_{B_s}}{m_{B_d}}\right) ^{2{d_\mathcal{U}}-2} \left( \frac{m_b+m_d}{m_b+m_s}\right) \left( \frac{{\tilde{c}}_{\mathcal{U}L}^{bs}}{{\tilde{c}}_{\mathcal{U}L}^{bd}}\right) \nonumber \\&= \frac{1}{1+y_s}\left( \frac{m_{B_s}}{m_{B_d}}\right) ^{{d_\mathcal{U}}-1} \left( \frac{m_b+m_d}{m_b+m_s}\right) \sqrt{\frac{{\hat{B}}_{B_s}}{{\hat{B}}_{B_d}}} \sqrt{R_{\Delta M}^\mathcal{U}},\nonumber \\ \end{aligned}$$

(61)

where the result of Eq. (30) is used. Our results are summarized as follows:

$$\begin{aligned} R_{\mu \mu }^{Z'}(1+y_s)&= \sqrt{R_{\Delta M}^{Z'}}, \end{aligned}$$

(62)

$$\begin{aligned} R_{\mu \mu }^H(1+y_s)&= \left( \frac{m_{B_s}^2}{m_{B_d}^2}\frac{m_b+m_d}{m_b+m_s}\right) ^2\nonumber \\&\times \left( \frac{{\hat{B}}_{B_s}}{{\hat{B}}_{B_d}}\right) R_{\Delta M}^H~(\mathrm{if}~\Delta _S^{\mu \mu }=0), \end{aligned}$$

(63)

$$\begin{aligned} R_{\mu \mu }^H(1+y_s)&= \left( 1-2y_s\right) \left( \frac{1-\frac{4m_\mu ^2}{m_{B_s}^2}}{1-\frac{4m_\mu ^2}{m_{B_d}^2}}\right) \left( \frac{m_{B_s}^2}{m_{B_d}^2}\frac{m_b+m_d}{m_b+m_s}\right) ^2\nonumber \\&\times \left( \frac{{\hat{B}}_{B_s}}{{\hat{B}}_{B_d}}\right) R_{\Delta M}^H~(\mathrm{if}~\Delta _P^{\mu \mu }=0), \end{aligned}$$

(64)

$$\begin{aligned} R_{\mu \mu }^\mathcal{U}(1+y_s)&= \left( \frac{m_{B_s}}{m_{B_d}}\right) ^{{d_\mathcal{U}}-1} \left( \frac{m_b+m_d}{m_b+m_s}\right) \sqrt{\frac{{\hat{B}}_{B_s}}{{\hat{B}}_{B_d}}} \sqrt{R_{\Delta M}^\mathcal{U}}.\nonumber \\ \end{aligned}$$

(65)

The reason why $R_{\mu \mu }^H\sim R_{\Delta M}^H$ is that in $R_{\mu \mu }^H$, $\mathrm{Br}/\mathrm{Br}_\mathrm{SM}-1$ is non-vanishing only at $\mathcal{O}(c^2)$, due to the fact that $\Delta _P^{\mu \mu }$ is purely imaginary [4].

Numerically, Eqs. (62)–(65) are

$$\begin{aligned}&R_{\mu \mu }^{Z'}=0.919\times \sqrt{R_{\Delta M}^{Z'}}=0.775,\end{aligned}$$

(66)

$$\begin{aligned}&R_{\mu \mu }^{H,\Delta _S=0}=0.993\times R_{\Delta M}^H=0.707,\end{aligned}$$

(67)

$$\begin{aligned}&R_{\mu \mu }^{H,\Delta _P=0}=0.818\times R_{\Delta M}^H=0.583,\end{aligned}$$

(68)

$$\begin{aligned}&R_{\mu \mu }^\mathcal{U}=(1.02)^{{d_\mathcal{U}}-1}\times 0.925\sqrt{R_{\Delta M}^\mathcal{U}}=0.780\times (1.02)^{{d_\mathcal{U}}-1},\nonumber \\ \end{aligned}$$

(69)

where $R_{\Delta M}=0.712$ is used. The above results can be used to predict the yet-to-be-measured branching ratio, $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)$. Table 1 shows the predicted values of $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)$.

Table 1 Predictions for $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)$ for various $\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)$ measurements. For unparticles, the branching ratio is given at a reference point ${d_\mathcal{U}}=1.5$

Note that the values of Table 1 are all far below the current upper bound, $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)<7.4\times 10^{-10}$ by the LHCb [1] and $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)<1.1\times 10^{-9}$ by the CMS [2], and slightly smaller than the SM prediction, $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)_\mathrm{SM}=1.05\times 10^{-10}$. This is because ${\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)<{\overline{\mathrm{Br}}}(B_s\rightarrow \mu ^+\mu ^-)_\mathrm{SM}=(3.56\pm 0.18)\times 10^{-9}$ [4] and $R_{\Delta M}=0.712>0$. Note also that the predictions are made without knowing any numerical details of the new couplings, except that they are small enough to neglect higher orders. In this way, by measuring $\mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)$ we can easily figure out which kind of NP is realized in $B$ systems.

In conclusion, we derived new relations between $B_{d,s}$ observables. The relations are valid only when NP exists in $B_{d,s}$ systems, which is a very plausible assumption. The relations are different in specific models. In this analysis we only consider flavor changing scalar (un)particles and vector bosons. For other models one can define similar double ratios as given in this work. The double ratios become very simple when there are only left- (or right-) handed couplings, and the couplings are MFV-like. If this were not the case, then our simple relations would not hold any more. In other words, if we confirm that the simplified double ratio relations really hold, then we may conclude that NP is realized in a minimal way.

One point to be mentioned is that our double ratio becomes meaningless if there were no NP at all. In this case both numerator and denominator are vanishing and one cannot take a ratio. Thus the double ratio is not adequate to check whether there is any NP or not, but to see which kind of NP is involved once the observables turn out to be quite different from the SM predictions. The current status of NP searches in the case of the $B$ meson is not so pessimistic. According to [16], the relative size of NP in $\Delta M_{d,s}$ ($=h_{d,s}$) is currently $\lesssim$0.2–0.3, and would be $\lesssim$0.1 in the near future (“Stage I” where the LHCb will end). As for $B_d\rightarrow \mu ^+\mu ^-$, the current upper bound is almost an order of magnitude larger than the SM prediction. It is predicted in [17] that at $2\sigma$, $0.3\times 10^{-10}\lesssim \mathrm{Br}(B_d\rightarrow \mu ^+\mu ^-)\lesssim 1.8\times 10^{-10}$. If the measured branching ratio does not lie within this window, it would be a clear indication of NP. It is also found in [17] that although the measured value of $\mathrm{Br}(B_s\rightarrow \mu ^+\mu ^-)$ provides constraints on NP, there are still sizable regions allowed for $C_S$–$C_S'$ and $C_P$–$C_P'$ parameter space.

Besides the current status of NP searches, we need NP for various reasons (dark matter for example). Although there have been no smoking-gun signals for NP up to now, we believe that the SM is not (and should not be) the full story of particle physics. In this context the double ratio analysis might be very promising with the coming flavor precision era, and it can also be applied to $K$ meson systems.