Transversity in exclusive vector-meson leptoproduction

Abstract

The role of transversity or helicity-flip generalized parton distributions (GPDs) in leptoproduction of vector mesons is investigated within the framework of the handbag approach. The transversity GPDs in combination with twist-3 meson wave functions occur in the amplitudes for transitions from a transversely polarized virtual photon to a longitudinal polarized vector meson. The importance of the transversity GPDs can be examined in some of the spin density matrix elements and in transverse target spin asymmetries. Using suitable parametrizations of both helicity-flip and -non-flip GPDs, which are essentially taken from our previous papers, we estimate these observables and compare the results with available data.

1 Introduction

While, in the framework of the handbag approach, the roles of the helicity-non-flip GPDs, $H, E, \widetilde{H}$ and $\widetilde{E}$, in deeply virtual Compton scattering and in exclusive meson leptoproduction have intensively been studied during the last 15 years, the applications of the transversity or helicity-flip GPDs are rare. Only a few publications on this issue can be found in the literature, e.g. [1–10]. This is in sharp contrast to the situation of transversity in semi-inclusive reactions where a rich literature exists, see for instance the review articles [11, 12]. The reason for this fact is that, for the quark transversity GPDs, the emitted and reabsorbed partons have opposite helicities. Since the interactions of light quarks with gluons or photons conserve helicity, the initial parton helicity flip can only be compensated by higher-twist meson wave functions. Therefore, the contribution from the quark transversity GPDs are small in most cases and are difficult to separate from those of the helicity non-flip GPDs. For the gluon transversity GPDs the situation is different but it seems that their contributions are even smaller.

Leptoproduction of pseudoscalar mesons is an exception. On the one hand, the contributions from $\widetilde{H}$ and $\widetilde{E}$ are rather small in this case. On the other hand, those from the transversity GPDs are comparably large since their contributions are enhanced by the chiral condensate which appears in the wave function for a (ground state) pseudoscalar meson [9]. This fact entails the dominance of the amplitudes for the transitions from a transversely polarized virtual photon to the pseudoscalar meson, $\gamma ^*_T\rightarrow P$. The asymptotically leading amplitudes for the transitions from a longitudinally polarized photon, $\gamma ^*_L\rightarrow P$, are much smaller according to the estimates made in [9, 10]. The only substantial contributions to these amplitudes are the meson-pole terms as, for instance, the pion pole in $\pi ^+$ leptoproduction.¹

Here, in this work, we are going to investigate the role of the transversity GPDs in vector-meson leptoproduction. We will utilize the parametrizations of the helicity-non-flip GPDs advocated for in [13] as well as those of the valence-quark transversity GPDs used in our study of leptoproduction of pseudoscalar mesons [9, 10]. In addition we will allow for sea-quark contributions from these GPDs, which, as it turns out, play only a minor role. With regard to the prominent role of the transversity GPDs in pion leptoproduction [9, 10] it seems legitimate to examine the size of their contributions to vector-meson leptoproduction without carrying out a systematic analysis of all possible corrections to a given order of accuracy. As in [9, 10] we will not perform detailed fits to experimental data. In so far the results we will present below are to be understood as estimates. A more exact determination of the transversity GPDs is to be left for future investigations. Prerequisite to such an analysis are data on, say, the $\pi ^0$ cross section at reasonably large photon virtuality, $Q^2$, and large c.m.s. energy, $W$. Such data may come from the COMPASS experiment or the upgraded Jefferson Lab.

The plan of the paper is the following: In the next section we will outline the handbag approach, referring to our previous work [9, 10, 13, 14] and giving only details for the treatment of the contributions from the transversity GPDs. In this section we will also discuss the calculation of the subprocess amplitude for quark helicity flip and present the parametrizations of the GPDs. In Sect. 3 we will present our results for those observables of vector-meson leptoproduction which are sensitive to the transversity GPDs. The paper is closed with a summary.

2 The handbag approach

We consider the process $\gamma ^*(q,\mu )\, p(p,\nu )\rightarrow V(q^\prime ,\mu ')$ $p(p^\prime ,\nu ')$ in the generalized Bjorken-regime of large $Q^2$ and large $W$ but fixed Bjorken-$x$, $x_\mathrm{Bj}$. The symbols in the brackets denote the momenta and the helicities of the particles. The square of the momentum transfer, $\Delta =p^\prime -p$, is assumed to be much smaller than $Q^2$ ($t=\Delta ^2$). We also restrict ourselves to small values of $x_\mathrm{Bj}$, i.e. to values of the skewness,

$$\begin{aligned} \xi \,=\,\frac{(p-p^\prime )^+}{(p+p^\prime )^+}\simeq \frac{x_\mathrm{Bj}}{2-x_\mathrm{Bj}}\,(1+m_V^2/Q^2), \end{aligned}$$

(1)

smaller than about 0.1 ($m_V$ denotes the mass of the vector meson $V$). We stress that throughout the paper we neglect terms which are suppressed as $\sqrt{-t}/Q$ or stronger. We will work in a photon–proton center-of-mass system where the proton momenta are defined as $p=\bar{p}-\Delta /2$ and $p^\prime =\bar{p}+\Delta /2$. The average proton momentum is $\bar{p}=(p+p^\prime )/2$ and we choose its three-momentum part to point along the 3-axis.

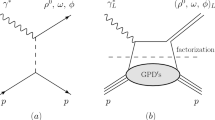
As described in detail in [13, 14] a helicity amplitude ${\mathcal {M}}_{\mu \nu ',\mu \nu }$ is assumed to factorize in a hard subprocess amplitude $H_{\mu \lambda ,\mu \lambda }$ (where $\lambda$ is the helicity of the internal partons, quarks or gluons) and a soft proton matrix element, parametrized in terms of GPDs, see Fig. 1. Since the partons which are emitted and reabsorbed from the proton collinearly to its initial and final state momentum, have the same helicity in this subprocess amplitude the GPDs $H$ and $E$ appear in the convolution. There are, however, also small, nearly negligible contributions from $\widetilde{H}$ and $\widetilde{E}$ to the $\mu =\pm 1$ amplitudes.

Fig. 1

A typical graph for meson leptoproduction. The helicity labels refer to the amplitude ${\mathcal {M}}_{0-,++}$ and to the subprocess $\gamma ^*q\rightarrow (q\bar{q})q$

The subprocess amplitudes are calculated within the modified perturbative approach [15] in which quark transverse degrees of freedom in the subprocess as well as Sudakov suppressions are taken into account. This entails the necessity to use a light-cone wave function for the meson instead of a distribution amplitude. In the limit of $Q^2, W \rightarrow \infty$ the subprocess amplitudes for transitions from a longitudinally polarized photon to a likewise polarized vector meson, $\gamma ^*_L\rightarrow V_L$, can be shown to turn into the collinear result, i.e. the familiar asymptotic factorization formula emerges for the amplitude ${\mathcal {M}}_{0\nu ',0\nu }$. The factorization of ${\mathcal {M}}_{0\nu ',0\nu }$ has rigorously been proven to hold in the limit of $Q^2, W \rightarrow \infty$ [16, 17]. The infrared singularities known to occur in the subprocess amplitudes for transversely polarized photons and mesons $H^V_{\pm \lambda ,\pm \lambda }$ in collinear approximation, are regularized by the quark transverse momentum, $\mathbf{k}_{\perp }$, in the modified perturbative approach. (Note that explicit helicities are labeled by their signs or by zero.) The $\gamma ^*_T\rightarrow V_T$ amplitudes are therefore suppressed by $\sqrt{\langle k^2_\perp \rangle }/Q$ with respect to those for $\gamma ^*_L\rightarrow V_L$ transitions.² For further details of the handbag approach we refer to [13, 14].

The role of the transversity GPDs [1, 19] $H_T$, $\bar{E}_T=2\widetilde{H}_T+E_T$, $\ldots$ in exclusive leptoproduction of pseudoscalar mesons has been investigated in [9, 10]. Since for these GPDs the emitted and reabsorbed partons have opposite helicities they only contribute to the amplitudes for transversely polarized photons to the order of accuracy we are working. As discussed in [9, 10] the contributions from the transversity GPDs seem to be dominant in most of the pseudoscalar channels. For instance, the transverse cross section for $\pi ^0$ production is estimated in [10] to be about 10 times larger than the longitudinal cross section which seems to be in agreement with experiment [20, 21].

Here, in this work we are going to explore the role of the transversity GPDs in vector-meson leptoproduction. In full analogy to the case of pseudoscalar mesons the quark transversity GPDs contribute to the amplitudes ${\mathcal {M}}^V_{0\nu ',\pm \nu }$ for $\gamma ^*_T\rightarrow V_L$ transitions:

$$\begin{aligned} {\mathcal {M}}^V_{0+,++}&= \frac{e_0}{2}\,\frac{\sqrt{-t^\prime }}{2m} \sum _a e_a{\mathcal {C}}_V^a \int \mathrm{d}x \sum _\lambda \left[ 2\lambda H^V_{0\lambda ,+-\lambda }\right. \nonumber \\&\times \,\left. (\bar{E}_T^a-\xi \widetilde{E}_T^a) + H^V_{0\lambda ,+-\lambda }\,(\widetilde{E}_T^a-\xi E_T^a)\right] ,\nonumber \\ {\mathcal {M}}^V_{0+,-+}&= -\frac{e_0}{2}\,\frac{\sqrt{-t^\prime }}{2m} \sum _a e_a{\mathcal {C}}_V^a \int \mathrm{d}x \sum _\lambda \left[ 2\lambda H^V_{0\lambda ,+-\lambda }\right. \nonumber \\&\times \,\left. (\bar{E}_T^a-\xi \widetilde{E}_T^a) - H^V_{0\lambda ,+-\lambda }\,(\widetilde{E}_T^a-\xi E_T^a)\right] ,\nonumber \\ {\mathcal {M}}_{0-,++}&= e_0\sqrt{1-\xi ^2}\,\sum _a e_a{\mathcal {C}}_V^a \nonumber \\&\times \,\int \mathrm{d}x \left[ H^V_{0-++}\left( H_T+\frac{\xi }{1-\xi ^2}(\widetilde{E}_T^a-\xi E_T^a)\right) \right. \nonumber \\&+\,\left. \frac{t^\prime }{2m^2}\,\sum _\lambda \lambda H^V_{0\lambda ,+-\lambda }\,\widetilde{H}_T^a\right] ,\nonumber \\ {\mathcal {M}}^V_{0-,-+}&= e_0\sqrt{1-\xi ^2}\, \sum _a e_a{\mathcal {C}}_V^a \nonumber \\&\times \int \mathrm{d}x \left[ H^V_{0--+}\left( H_T^a+\frac{\xi }{1-\xi ^2}(\widetilde{E}_T^a-\xi E_T^a)\right. \right. \nonumber \\&-\, \left. \left. \frac{t^\prime }{2m^2}\,\sum _\lambda \lambda H^V_{0\lambda ,+-\lambda }\right) \,\widetilde{H}_T^a\right] . \end{aligned}$$

(2)

As independent amplitudes we choose those with $\nu =1/2$. The amplitudes with $\nu =-1/2$ are related to the other ones by parity conservation:³

$$\begin{aligned} {\mathcal {M}}^V_{-\mu '-\nu ',-\mu -\nu }\,=\, (-1)^{\mu -\nu -\mu '+\nu '}{\mathcal {M}}^V_{\mu '\nu ',\mu \nu }. \end{aligned}$$

(3)

Since we neglect contributions which are suppressed at least by $\sqrt{-t}/Q$, only helicity-non-flip subprocess amplitudes can appear in the convolutions (2). For quark helicity-flip the only subprocess amplitude of this type is $H^V_{0-,++} ({=}H^V_{0+,--})$ and, hence, only the $\gamma ^*_T\rightarrow V_L$ transitions are fed by the transversity GPDs to the order of accuracy we are working. The expressions (2) can easily be derived with the help of the proton–quark matrix elements given in [19]. In (2) $m$ is the proton mass, $a$ denotes the quark flavor and $e_a$ the quark charges in units of the positron charge, $e_0$. For unflavored mesons the non-zero flavor weight factors, ${\mathcal {C}}_V^a$, read

$$\begin{aligned} {\mathcal {C}}^u_{\rho ^0}\,=\,-{\mathcal {C}}^d_{\rho ^0}\,=\,{\mathcal {C}}^u_{\omega }\,=\,{\mathcal {C}}^d_{\omega }\,=\,1/\sqrt{2}, \qquad {\mathcal {C}}^s_\phi \,=\,1. \end{aligned}$$

(4)

For the flavored mesons, $\rho ^+$ and $K^{*0}$, the $p\rightarrow n$ and $p\rightarrow \Sigma ^+$ transition GPDs appear. As a consequence of isospin symmetry or SU(3) flavor symmetry the transition GPDs can be related to the corresponding proton GPDs [22]⁴

$$\begin{aligned} K^{\rho ^+} \,=\, K^u - K^d, \qquad K^{K^{*0}}\,=\, -K^d+K^s, \end{aligned}$$

(5)

where K is some GPD. For these mesons there are no flavor weight factors and the charges have to be absorbed into the subprocess amplitudes. Finally, $t'=t-t_0$ where

$$\begin{aligned} t_0\,=\,-4m^2\frac{\xi ^2}{1-\xi ^2} \end{aligned}$$

(6)

is the minimal value of $-t$ allowed in the process in question. Since we only consider small values of the skewness $-t_0$ is very small and the difference between $t'$ and $t$ is tiny.

An interesting property of the helicity amplitudes can be inferred from (2). With the help of parity conservation one sees that part of the amplitudes (2) behave like those for the exchange of a particle with either natural ($N$) or unnatural parity ($U$)

$$\begin{aligned} \begin{aligned} {\mathcal {M}}^{V N}_{-\mu '\nu ',-\mu \nu }&= (-1)^{\mu '-\mu } {\mathcal {M}}^{V N}_{\mu '\nu ',\mu \nu },\\ {\mathcal {M}}^{V U}_{-\mu '\nu ',-\mu \nu }&= - (-1)^{\mu '-\mu } {\mathcal {M}}^{V U}_{\mu '\nu ',\mu \nu }. \end{aligned} \end{aligned}$$

(7)

Thus, the combinations $\bar{E}_T-\xi \widetilde{E}$ and $\widetilde{H}_T$ behave like natural parity exchange while $\widetilde{E}_T-\xi E_T$ behaves like unnatural parity. Remarkably, the proton helicity-flip amplitudes in (2) cannot be splitted in natural and unnatural parity contributions completely. Such a behavior of the amplitude ${\mathcal {M}}_{0-,++}$ is known to hold for photoproduction of pions since the late-1960s [23] and was the reason for the introduction of Regge cuts. According to [9] the GPDs $H$ ($\widetilde{H}$) and $E$ ($\widetilde{E}$) also behave like (un)natural parity exchange. The $\gamma ^*_T\rightarrow V_T$ amplitudes can therefore be written as

$$\begin{aligned} {\mathcal {M}}^V_{+\pm ,++}\,=\,{\mathcal {M}}^{VN}_{+\pm ,++}+{\mathcal {M}}^{VU}_{+\pm ,++}. \end{aligned}$$

(8)

Other $\gamma ^*_T\rightarrow V_T$ amplitudes are related to these amplitudes either by the symmetry (7) or by parity invariance. The amplitude ${\mathcal {M}}^{VU}_{+-,++}$ is fed by the $\xi \tilde{E}$ [14]. Since we are interested in small skewness and since it is no reason known why $\tilde{E}$ could be larger than the other GPDs we neglect it. Also the contribution from the pion pole (contained in $\tilde{E}$) to the observables of interest in this paper is negligible small, even for the case of $\omega$ production where it is three times larger than for $\rho ^0$ production.

With regard to the fact that the GPD $\widetilde{E}_T$ is antisymmetric in $\xi$: $\widetilde{E}_T(\xi )=-\widetilde{E}_T(-\xi )$, we neglect $\widetilde{E}_T$ and $E_T$ in (2) for small skewness. Moreover, we also neglect the amplitude $H^V_{0-,-+}$ in (2) since it proportional to $t{/}Q^2$ due to angular momentum conservation in contrast to the helicity-non-flip amplitude $H^V_{0-,++}$, which is not forced to vanish for forward scattering by this conservation law. Finally, we disregard the GPD $\widetilde{H}_T$ in (2) by the admittedly weak argument that its contribution is proportional to $t/(4m^2)$. Taking all these simplifications into account the amplitudes given in (2) reduce to

$$\begin{aligned} {\mathcal {M}}^V_{0-,++}&= e_0 \sum _a e_a {\mathcal {C}}_V^a\nonumber \\&\times \int \mathrm{d}x H^V_{0-,++}(x,\xi ,Q^2,t=0)H^a_T(x,\xi ,t),\nonumber \\ {\mathcal {M}}^V_{0+,\pm +}&= \mp e_0\frac{\sqrt{-t^\prime }}{4m} \sum _a e_a {\mathcal {C}}_V^a\nonumber \\&\times \int \mathrm{d}x H^V_{0-,++}(x,\xi ,Q^2,t=0) \bar{E}^a_T(x,\xi ,t),\nonumber \\ {\mathcal {M}}^V_{0-,-+}&= 0. \end{aligned}$$

(9)

Although the transversity GPDs are leading twist, the amplitudes given in (2) and (9) are of twist-3 nature. Quark and antiquark forming the valence Fock state of the longitudinally polarized vector meson have the same helicity in $H^V_{0-,++}$, see Fig. 1. This necessitates the use of twist-3 meson wave functions which will be discussed in Sect. 2.1.

We repeat that (9) only refers to the quark transversity GPDs. The contributions from their gluonic partners require the non-flip subprocess amplitude $H^V_{--,++}$, i.e. the amplitude with gluon as well as photon–meson helicity flip (all helicities are either plus or minus 1). The convolutions of $H^V_{--,++}$ and the gluonic transversity GPDs determine the $\gamma ^*_T\rightarrow V_{-T}$ amplitudes ${\mathcal {M}}^V_{\mp \nu ',\pm \nu }$. As is well-known from the SDMEs for $\rho ^0$ and $\phi$ production (e.g. $r^1_{11}$) measured for instance by HERMES [24] and H1 [25], these amplitudes are very small, compatible with zero within errors and usually neglected in analyses of vector-meson leptoproduction.⁵ We will do so here as well. Small $\gamma ^*_T\rightarrow V_{-T}$ amplitudes are consistent with the assumption of small gluonic transversity GPDs. This assumption is not in conflict with rather large quark transversity GPDs since the quark and gluon transversity GPDs evolve independently with the scale [1, 26]. The amplitudes for $\gamma ^*_L\rightarrow V_T$ transitions will be neglected too. They are experimentally small [24, 25] and strongly suppressed in the handbag approach.

2.1 Calculation of the twist-3 subprocess amplitude

We begin with the discussion of the light-cone wave function for the valence Fock component of a helicity-zero vector meson that moves along the 3-direction and for which quark and antiquark have the same helicity, see Fig. 1. Obviously, this configuration requires one unit of orbital angular momentum projection $l_3$. Such a light-cone wave function has been given in [27] recently

$$\begin{aligned}&|V;q',\mu '=0,|l_3|=1 \rangle \nonumber \\&\quad = \frac{1}{\sqrt{2}} \int \frac{\mathrm{d}\tau \mathrm{d}^2\mathbf{k}_{\perp }}{16\pi ^3} \Psi ^{(2)}_V(\tau ,k^2_\perp ) \frac{1}{m_V\sqrt{\tau \bar{\tau }}} \nonumber \\&\qquad \times \,\left[ k^-_{\perp }b^\dagger _+(\tau ,\mathbf{k}_{\perp }){d}^\dagger _+(\bar{\tau },-\mathbf{k}_{\perp }) \right. \nonumber \\&\qquad -\,\left. k^+_{\perp } b^\dagger _-(\tau ,\mathbf{k}_{\perp }) {d}^\dagger _-(\bar{\tau },-\mathbf{k}_{\perp })\right] \mid 0\rangle , \end{aligned}$$

(10)

Color and flavor factors are omitted for convenience. The quark fields, $b^\dagger$ and $d^\dagger$, depend on the momentum fractions $\tau$ and $\bar{\tau }\equiv 1-\tau$ of the meson’s momentum, $q'$, and on the quark transverse momentum, $\mathbf{k}_{\perp }$. The combinations of its one- and two-components

$$\begin{aligned} k^{\pm }_\perp \,=\, k^1_\perp \pm i k^2_\perp \end{aligned}$$

(11)

represent one unit of $l_3$. Acting on the perturbative vacuum the quark fields create quark and antiquark momentum eigenstates

$$\begin{aligned} \begin{aligned}&\mid q' (\tau , \mathbf{k}_{\perp }); \lambda \rangle = b^\dagger _{q\lambda }(\tau , \mathbf{k}_{\perp })\mid 0\rangle ,\\&\mid \bar{q}' (\bar{\tau }, -\mathbf{k}_{\perp }); \lambda \rangle = d^\dagger _{q\lambda }(\bar{\tau }, -\mathbf{k}_{\perp })\mid 0\rangle . \end{aligned} \end{aligned}$$

(12)

It has been shown in [27] that the wave function (10) has the correct behavior under the parity operation for a helicity-zero $\rho$ meson. In contrast to [27] we divide by the meson mass in order to have a scalar wave function $\Psi ^{(2)}$ of the same dimension as the wave function $\Psi ^{(1)}$ appearing in the expression for the usual $l_3=0$ Fock component of the vector meson

$$\begin{aligned}&|V;q^\prime ,\mu '=0,l_z=0 \rangle = \frac{1}{\sqrt{2}} \int \frac{\mathrm{d}\tau \mathrm{d}^2\mathbf{k}_{\perp }}{16\pi ^3} \Psi ^{(1)}_V(\tau ,k^2_\perp )\frac{1}{\sqrt{\tau \bar{\tau }}}\nonumber \\&\quad \times \left[ b^\dagger _+(\tau ,\mathbf{k}_{\perp }){d}^\dagger _{-}(\bar{\tau },-\mathbf{k}_{\perp })\!+\! b^\dagger _-(\tau ,\mathbf{k}_{\perp }){d}^\dagger _+(\bar{\tau },-\mathbf{k}_{\perp })\right] \,\mid 0\rangle . \nonumber \\ \end{aligned}$$

(13)

The states (10) and (13) respect covariant particle state normalization. Hence, the probabilities of the $\mid l_3\mid \, =1$ and $0$ Fock components are given by

$$\begin{aligned} \begin{aligned}&\int \frac{\mathrm{d}\tau \mathrm{d}^2\mathbf{k}_{\perp }}{16\pi ^3} \frac{k^2_\perp }{m_V^2} \mid \Psi _V^{(2)}(\tau ,k^2_\perp )\mid ^2\, = P_{\mid l_3\mid =1},\\&\int \frac{\mathrm{d}\tau \mathrm{d}^2\mathbf{k}_{\perp }}{16\pi ^3} \mid \Psi _V^{(1)}(\tau ,k^2_\perp )\mid ^2\, = P_{l_3=0}, \end{aligned} \end{aligned}$$

(14)

with $P_{\mid l_3\mid \, =\, 1}+P_{l_3\, =\, 0}\le 1$. The spin part of (10) is equivalent to the following expression:

(15)

for an incoming vector meson. The four-vector $k$ is defined as

$$\begin{aligned} k\,=\,[0,0,\mathbf{k}_{\perp }], \end{aligned}$$

(16)

in light-cone coordinates. This spin wave function can be transformed to the frame we are working by a transverse boost. The equivalence of (15) and the spin part of (10) can readily be derived. Representing the parton states in (10) by Dirac spinors in the rest frame, one sees

(17)

A boost of this expression to the frame where the meson moves rapidly along the 3-axis leads to

(18)

with the quark and antiquark momenta being defined as

$$\begin{aligned}&p_1 =\left[ \tau q'{}^{+},\frac{\tau ^2m_V^2+k^2_\perp }{2\tau q^{'+}},\mathbf{k}_{\perp }\right] ,\nonumber \\&p_2=\left[ \bar{\tau } q'{}^{+},\frac{\bar{\tau }^2m_V^2+k^2_\perp }{2\bar{\tau } q^{'+}},-\mathbf{k}_{\perp }\right] . \end{aligned}$$

(19)

The quark and antiquark masses are taken as $m_1=\tau m_V$ and $m_2=\bar{\tau } m_V$. This guarantees that $q'=p_1+p_2$ up to corrections of order $k^2_\perp$. From (18) one easily derives (15).

By counting the numbers of $\gamma$ matrices in the Feynman expression for this amplitude (including the two from the proton matrix element for parton helicity flip) one sees that only the first and the third term of the spin wave function (15) contribute to the parton helicity-flip amplitude. The first term, , leads to a contribution of order $t/Q^2$ and is consequently neglected. Hence, the subprocess amplitude $H^V_{0-,++}$ is generated by the third term. Performing the LO calculation of $H^V_{0-,++}$ from that term and the set of Feynman graphs of which an example is shown in Fig. 1, we obtain

$$\begin{aligned}&H^{V}_{0-,++}=32\pi \frac{m_V\xi }{Q^2} \frac{C_F}{\sqrt{N_c}} \int \mathrm{d}\tau \int \frac{\mathrm{d}k^2_\perp }{16\pi ^2} \frac{k^2_\perp }{2\tau \bar{\tau }m_V^2} \Psi _V^{(2)}(\tau ,k^2_\perp ) \nonumber \\&\qquad \quad \times \, \alpha _\mathrm{s}(\mu _\mathrm{r}) \left( \frac{1}{x-\xi +i\epsilon }\frac{1}{\bar{\tau }(x-\xi )-2\xi k^2_\perp /Q^2+i\epsilon }\right. \nonumber \\&\qquad \quad \left. +\, \frac{1}{x+\xi -i\epsilon }\frac{1}{\tau (x+\xi )+2\xi k^2_\perp /Q^2-i\epsilon }\right) . \end{aligned}$$

(20)

The number of colors is denoted by $N_c$, $C_F=4/3$ and $\mu _\mathrm{R}$ is an appropriate renormalization scale (see below). Equation (20) holds for unflavored vector mesons. As we already mentioned for flavored mesons built up by a quark $q_a$ and an antiquark $\bar{q}_b$, the corresponding quark charges $e_a$ and $e_b$ multiply the first and second term of (20), respectively. Following [15] we only retain $k_\perp ^2$ in the denominators of the parton propagators. There the parton transverse momentum plays a decisive role since it competes with the terms $\propto \tau (\bar{\tau })Q^2$, which become small in the end-point regions where either $\tau$ or $\bar{\tau }$ tends to zero. We stress that, to the order of accuracy we are working, the amplitude (20) respects gauge invariance.

The distribution amplitude associated with the third term of the wave function (15), reads

$$\begin{aligned} \int \frac{\mathrm{d}k^2_\perp }{16\pi ^2}\frac{k^2_\perp }{2\tau \bar{\tau }m^2_V}\Psi ^{(2)}_V(\tau ,k^2_\perp )\,=\, \frac{f^T_V}{2\sqrt{2N_c}} h_{\Vert V}^{(s)}(\tau ). \end{aligned}$$

(21)

According to [28], the twist-3 chiral-odd distribution amplitude $h_{\Vert }^{(s)}$ is defined by the meson-vacuum matrix element⁶

$$\begin{aligned} \langle 0| \bar{q}(z)q(-z)|V;q^\prime ,\mu '=0\rangle \end{aligned}$$

(22)

(a path-ordered gauge factor along the straight line connecting the points $z$ and $-z$ is understood). This distribution amplitude comes along with the tensor decay constant $f_V^T$ of the vector meson. The latter depends on the factorization scale $\mu _\mathrm{F}$ to be specified below

$$\begin{aligned} f^T_V(\mu _\mathrm{F})\,=\,f^T_V(\mu _0)\left( \frac{\alpha _\mathrm{s}(\mu _\mathrm{F})}{\alpha _\mathrm{s}(\mu _0)}\right) ^{4/27}\!. \end{aligned}$$

(23)

For the tensor decay constant we use the QCD sum rule estimate give in [29]. According to this work it amounts to about 0.8 times the usual decay constant of a longitudinally polarized $l_3=0$ vector meson at the scale $\mu _0=1\,~\mathrm{GeV}$. As a consequence of the nature of the wave function $\Psi _V^{(2)}$ the subprocess amplitude $H^V_{0-,++}$ is of twist-3 accuracy and is parametrically suppressed by $m_V/Q$ as compared to the leading-twist amplitudes $H^V_{0+,0+}$. Our results for the $\gamma _T^*\rightarrow V_L$ amplitudes are therefore consistent with the statements made in [4, 5] that the transversity GPDs do not contribute to vector-meson leptoproduction at leading-twist accuracy.

In principle, there is also a contribution to $H_{0-,++}$ from the $q\bar{q}g$ Fock component of the vector meson. The corresponding wave function and distribution amplitude is twist-4 and is interrelated to the wave function $\Psi _V^{(2)}$ by the equation of motion [28]. The inclusion of the three-particle Fock component in the analysis will only change the strength of the $\gamma ^*_T\rightarrow V_L$ amplitudes somewhat. Since the present knowledge of the $q\bar{q}g$ wave function is rather limited, we ignore this contribution in consistency with our analysis of pion production [9, 10]. The neglect of the three-particle wave function implies that the distribution amplitude $h_\Vert ^{(s)}$ takes the asymptotic form $6\tau \bar{\tau }$. The role of the three-particle contribution is explored in general higher-twist scenarios in [30].

In the modified perturbative approach we are using, the amplitude (20) is Fourier transformed from the $\mathbf{k}_{\perp }$-space to the canonically conjugated impact parameter space $\mathbf{b}$, for details see [13]. The obtained $\mathbf{b}$-space expression is multiplied with the Sudakov factor, $\exp {[-S(\tau ,\mathbf{b},Q^2)]}$, representing gluon radiation calculated to next-to-leading-log accuracy using resummation techniques and having recourse to the renormalization group [15]. The impact parameter $\mathbf{b}$, which is the quark–antiquark separation, acts as an infrared cut-off. Radiative gluons with wave lengths between the infrared cut-off and a lower limit (related to the hard scale $Q^2$) yield suppression; softer gluons are part of the meson wave function, while harder ones are an explicit part of the subprocess amplitude. Consequently, the factorization scale is given by the quark–antiquark separation $\mu _\mathrm{F}=1/b$. The renormalization scale, $\mu _\mathrm{R}$, is taken to be the largest mass scale appearing in the subprocess amplitude, i.e. $\mu _\mathrm{R}=\mathrm{max}(\tau Q,\bar{\tau }Q,1/b)$. For $\Lambda _\mathrm{QCD}$ a value of $220\,~\mathrm{MeV}$ is used in the Sudakov factor and in the evaluation of $\alpha _\mathrm{s}$ from the one-loop expression.

2.2 Parametrization of the GPDs

In order to evaluate the convolutions in (9) and the analogous ones for the other amplitudes we need the GPDs. We adopt for them the parametrizations proposed in our previous work [9, 10, 13]. The GPDs are constructed from the zero-skewness GPDs with the help of the double distribution ansatz [31]

$$\begin{aligned}&K^i(x,\xi ,t)\nonumber \\&\quad \!=\!\int _{-1}^1 \mathrm{d}\rho \, \int _{-1+\mid \rho \mid }^{1-\mid \rho \mid }\mathrm{d}\eta \delta (\rho +\xi \eta -x) K^i(\rho ,\xi \!=\!0,t) w_i(\rho ,\eta ),\nonumber \\ \end{aligned}$$

(24)

where $K$ is a GPD and $i$ stands for gluon, sea or valence quarks. A possible $D$ term [32] is neglected. For the weight function $w$ that generates the skewness dependence we use [33]

$$\begin{aligned} w_i(\rho ,\eta )\,=\,\frac{\Gamma (2n_i+2)}{2^{2n_i+1}\Gamma ^2(n_i+1)}\, \frac{[(1-\mid \rho \mid )^2-\eta ^2]^{n_i}}{(1-\mid \rho \mid )^{2n_i+1}}. \end{aligned}$$

(25)

For the parameter $n_i$ a value of 2 is taken for the gluon and sea-quark helicity-non-flip GPDs and 1 in all other cases. The zero-skewness GPDs are parametrized as

$$\begin{aligned} K^i(\rho ,\xi =0,t)\,=\,k^i(\rho )\exp {[t p_{ki}(\rho )]}, \end{aligned}$$

(26)

where $k^i$ is the forward ($t=0$) limit of the zero-skewness GPD which for $H$, $\widetilde{H}$ and $H_T$ are the unpolarized, polarized and transversity PDFs, respectively. For the other GPDs the forward limits are parametrized like the PDFs

$$\begin{aligned} k^i(\rho )\,=\,N_{ki}\rho ^{-\alpha _{ki}}(1-\rho )^{\beta _{ki}}. \end{aligned}$$

(27)

The profile function $p_{ki}$ in (26) is parametrized in a Regge-like manner

$$\begin{aligned} p_{ki}(\rho )\,=\,-\alpha ^\prime _{ki}\ln {(\rho )} + b_{ki}, \end{aligned}$$

(28)

where $\alpha ^\prime _{ki}$ represents the slope of a Regge trajectory and $b_{ki}$ parametrizes the $t$ dependence of its residue.

The best determined GPD is $H$, since it controls the cross sections for leptoproduction of flavor-neutral vector mesons. The values of the parameters which specify $H$, are obtained from fits to the cross section data at small skewness and can be found in [13]. The GPDs $\widetilde{H}$ and $\widetilde{E}$ play no role in the observables we are going to discuss below. The GPD $E$ for the valence quarks, on the other hand, is of importance for some of the observables of interest. The values of its parameters are given in [13, 34]. This parametrization of $E$ for valence quarks at zero skewness is in agreement with the findings of an analysis of the nucleon form factors in terms of GPDs [35]. According to this analysis the second moments of $E$ for $u$ and $d$ valence quarks at $t=0$ have about the same magnitude but opposite sign. Due to a sum rule for the second moments of $E$ at $\xi =t=0$ [36, 37] the respective moments for the gluon and sea quarks cancel each other to a large extent. Since, for our parametrization, the zero-skewness GPDs have no nodes except at the end points $x=0$ and $1$, this cancellation approximately happens for other moments too. It even approximately occurs for the convolutions with the subprocess amplitudes. For this reason we do not consider $E$ for gluons and sea quarks in this work. In passing we note that the set of helicity-non-flip GPDs proposed in [13, 34] has been examined in a calculation of DVCS to leading-twist accuracy and leading-order of perturbative QCD [38]. The results are found to be in satisfactory agreement with all small-skewness data. Recently the form-factor analysis from 2004 [35] has been updated [39]. All the new data on the nucleon form factors are taken into account in the update as well as more recent parton distributions [40]. The zero-skewness valence-quark GPDs $H$ and $E$ obtained in this analysis do not differ much from those proposed in the 2004 analysis at low $-t$. We checked that the use of these new valence-quark GPDs do not alter our results perceptibly.

The only available small-skewness data which provide clear evidence for strong contributions from transversely polarized virtual photons and therefore information on the transversity GPDs, are the $\pi ^+$ electroproduction cross section [41] and the asymmetries measured with a transversely polarized target [42]. However, the $\pi ^+$ data provide only information on the combination $H_T^u-H_T^d$. The forward limit of $H_T$ is the transversity distribution, $\delta (x)$, which has been determined by Anselmino et al. [43] in an analysis of the data on the azimuthal asymmetry in semi-inclusive deep inelastic lepton–nucleon scattering and in inclusive two-hadron production in electron–positron annihilation. The moments of the transversity distributions proposed in [43], i.e. the lowest moments of $H_T$ at $t'=0$, are about 40 $\%$ smaller than a lattice QCD result [44], they are also substantially smaller than model results (cf. [43] and references therein). Also the analysis of $\pi ^0$ leptoproduction performed in [10], suggest larger moments of $H_T$. In order to surmount this difficulty we leave unchanged the parametrization of the transversity distributions given in [10, 43] but adjust their normalizations to the lattice QCD moments of [44]. The other transversity GPD, $\bar{E}_T$, is only constrained by lattice QCD results [45], its contribution to $\pi ^+$ production is very small. The values of the parameters for the valence-quark GPDs $H_T$ and $\bar{E}_T$ proposed in [10], are quoted in Table 1. Given the uncertainties of the present lattice QCD results [46] we consider these parametrizations as rough estimates which only allow exploratory studies of transversity effects in exclusive meson leptoproduction. In other words, we only achieve estimates of various observables. For this reason we do not attempt an error assessment of our results; this is beyond feasibility at present. Evolution of the transversity GPDs is not taken into account; all pertinent experimental data cover only a very limited range of $Q^2$.

The last item we have to specify are the sea-quark transversity GPDs. A flavor symmetric sea is assumed with the parameters quoted in Table 1. These parameters are adjusted to the data discussed below.

The $l_3=0$ wave functions for the vector mesons are specified in [13, 34]. Basically they are simple Gaussians in $\mathbf{k}_{\perp }$. This type of wave function is also used for the scalar $\mid l_3\mid \,=1$ wave function

$$\begin{aligned} \Psi ^{(2)}_V(\tau ,k^2_\perp )\!=\! 16\pi ^2\sqrt{2N_c}f_V^Tm^2_Va_{VT}^4 \exp {[-a_{VT}^2k^2_\perp /(\tau \bar{\tau })]}. \nonumber \\ \end{aligned}$$

(29)

Its associated distribution amplitude is just the asymptotic form for mesons

$$\begin{aligned} h_{\Vert V}^{(s)}=6\tau \bar{\tau }. \end{aligned}$$

(30)

In principle, this is the leading term of a Gegenbauer series [28]. We, however, disregard all higher Gegenbauer terms except of the $C_1^{3/2}$-term for the $K^{*0}$ meson for which we take a value of 0.1 for its coefficient. As discussed in [47] the higher Gegenbauer terms are strongly suppressed in the modified perturbative approach.

The wave function (29) leads to the probability of the $\mid l_3\mid =1$ Fock component

$$\begin{aligned} P_{\mid l_3\mid =1}\,=\,\frac{4}{15}\, \pi N_c (f_V^Tm_Va^2_{VT})^2 \end{aligned}$$

(31)

and the r.m.s. $k_\perp$ is

$$\begin{aligned} \langle k^2_\perp \rangle \,=\, \frac{3}{14}\,a_{VT}^{-2}. \end{aligned}$$

(32)

With $a_{\rho T}\simeq 1\,~\mathrm{GeV}$ and $f_\rho ^T=167\,~\mathrm{MeV}$ (see [13]) one finds the plausible values $P_{\mid l_3\mid =1}=0.13$ and $\langle k^2_\perp \rangle ^{1/2}=0.46\,~\mathrm{GeV}$.

3 Results

3.1 Spin-density matrix elements

The $\gamma ^*_T\rightarrow V_L$ amplitudes can be probed by some of the SDMEs. Using the simplifications discussed in Sect. 2, one finds for the relevant SDMEs [48]

$$\begin{aligned}&r_{00}^1(V) \sigma _0^V= -\mid {\mathcal {M}}_{0+++}^V\mid ^2, \nonumber \\&r_{00}^5(V) \sigma _0^V \!=\! \sqrt{2}\,\mathrm{Re}[{\mathcal {M}}_{0+++}^{V*} {\mathcal {M}}_{0+0+}^V \!+\! \frac{1}{2}{\mathcal {M}}_{0-++}^{V*} {\mathcal {M}}_{0-0+}^V], \nonumber \\&\mathrm{Re}\,r^{04}_{10}(V)\sigma _0^V = -\mathrm{Re}\, r^{1}_{10}(V)\sigma _0^V \,=\,\mathrm{Im}\,r^2_{10}(V)\sigma _0^V \nonumber \\&\quad = \frac{1}{2}\,\mathrm{Re}[{\mathcal {M}}_{0+++}^{V*} {\mathcal {M}}_{++++}^{VN}+ \frac{1}{2} {\mathcal {M}}_{0-++}^{V*} {\mathcal {M}}_{+-++}^{VN}], \end{aligned}$$

(33)

where

$$\begin{aligned} \sigma _0^V&= \mid {\mathcal {M}}_{++,+ +}^V\mid ^2 + \mid {\mathcal {M}}_{+-,+ +}^V\mid ^2+ \mid {\mathcal {M}}_{0+,+ +}^V\mid ^2\nonumber \\&+ \frac{1}{2}\mid {\mathcal {M}}_{0-,+ +}^V\mid ^2+ \varepsilon [\mid {\mathcal {M}}_{0+,0 +}^V\mid ^2+ \mid {\mathcal {M}}_{0-,0 +}^V\mid ^2]. \nonumber \\ \end{aligned}$$

(34)

The ratio of the longitudinal and transverse photon flux is denoted by $\varepsilon$. Up to a phase space factor, $\sigma _0^V$ is the unseparated cross section $d\sigma = d\sigma _T +\varepsilon d\sigma _L$. The contribution from the $\gamma ^*_T\rightarrow V_L$ amplitudes to the transverse cross section for $\rho ^0$ production is negligibly small, it amounts to only 2–3 $\%$.

A particularly interesting SDME is $r^1_{00}$. It measures the absolute value of the amplitude ${\mathcal {M}}_{0+++}$, which is fed by the GPD $\bar{E}_T$ in the combination $e_u\bar{E}_T^u-e_d\bar{E}_T^d$ for $\rho ^0$ production, see (4) and (9). Since $\bar{E}_T^u$ and $\bar{E}_T^d$ have the same sign and almost the same strength, this amplitude is rather large. The signs of these GPDs are fixed by the lattice QCD results [45]. In fact, for the tensor anomalous magnetic moment of the nucleon which represents the lowest moment of $\bar{E}_T$ at $t=0$, $\kappa _T^u\simeq \kappa _T^d > 0$ is found in [45]. Models support this result [49, 50].

The SDME $r^5_{00}$ is more complicated. It measures the real part of a combination of two interference terms; in terms of GPDs

$$\begin{aligned} r^5_{00} \sim \mathrm{Re} \left[ \langle \bar{E}_T\rangle ^*_{LT}\langle H\rangle _{LL}+\frac{1}{2}\langle H_T\rangle ^*_{LT}\langle E\rangle _{LL}\right] \end{aligned}$$

(35)

where $\langle K\rangle _{XY}$ denotes the convolution of the GPD $K$ with the subprocess amplitude for a $\gamma ^*_Y\rightarrow V_X$ transition ($X, Y$ label longitudinal or transverse polarization). I.e. $r^5_{00}$ is related to interference terms of amplitudes fed by transversity GPDs with leading $\gamma ^*_L\rightarrow V_L$ amplitudes. The first term in (35) dominates by far since $\langle H \rangle _{LL}$ is much larger than $\langle E \rangle _{LL}$ while both transversity contributions are of roughly the same strength. Thus, $r^5_{00}$ essentially probes $\bar{E}_T$, too. As is to be seen from Fig. 2 we achieve fair agreement between the HERMES data on $\rho ^0$ production [24] and our handbag results for $r^1_{00}$ and $r^5_{00}$. A point worth mentioning is that $r_{00}^5\propto \sqrt{-t'}$ and $r_{00}^1\propto t'$ for $t'\rightarrow 0$ as a consequence of angular momentum conservation.

Fig. 2

Left Handbag results for the SDMEs $r^5_{00}$ (solid line) and $r^1_{00}$ (dashed line) for $\rho ^0$ production. Data taken from HERMES [24]. Right Predictions for $r^5_{00}$ and $r^1_{00}$ at $W=8.1\,~\mathrm{GeV}$ (solid and dashed line, respectively) and $W=3\,~\mathrm{GeV}$ (dash-dotted lines)

Also for the SDMEs $\mathrm{Re}\,r^1_{00}$, $\mathrm{Re}\, r^{04}_{10}$ and $\mathrm{Im}\, r^2_{10}$ we find good agreement with the data on $\rho ^0$ production, see Fig. 3 for the latter two SDMEs. Within the handbag approach the three SDMEs are equal (up to a sign) and probe a similar combination of interference terms as $r_{00}^5$. The difference is that for these SDMEs $H$ and $E$ are convoluted with the subprocess amplitude for $\gamma ^*_T\rightarrow V_T$ transitions. For these SDMEs the $\bar{E}_T$ term is also dominant. The contribution from $\bar{E}_T$ for the sea quarks is less than 5 $\%$ for all SDMEs, and the valence quarks dominate.

Fig. 3

The SDMEs $\mathrm{Re}\, r^{04}_{10}$ and $\mathrm{Im}\, r^2_{10}$. Data taken from HERMES [24]. The solid lines represent our results

These results are an addendum to our previous study of SDMEs [13]. In summary we achieve a fair description of all SDMEs within the handbag approach now. An exception is the relative phase between the amplitudes for $\gamma ^*_T\rightarrow \rho ^0_T$ and $\gamma ^*_L\rightarrow \rho ^0_L$ transitions which is too small in the handbag approach as compared to experiment [24]. It would be of interest to probe the transversity contributions to the SDMEs also at other energies. As an example we show in Fig. 2 $r_{00}^5$ and $r_{00}^1$ at the COMPASS energy of $8.1\,~\mathrm{GeV}$ and at $3\,~\mathrm{GeV}$, which is typical of the upgraded JLab.

3.2 Transversely polarized target asymmetries

There are the following non-zero modulations of the transverse target spin asymmetry $A_{UT}$:

$$\begin{aligned}&A_{UT}^{\sin (\phi -\phi _s)}(V) \sigma _0^V\nonumber \\&\quad =-2\, \mathrm{Im}\Big [\varepsilon {\mathcal {M}}_{0-,0+}^{V*}{\mathcal {M}}_{0+,0+}^V +{\mathcal {M}}_{+-,++}^{VN*} {\mathcal {M}}_{++,++}^{VN}\nonumber \\&\qquad +\, \frac{1}{2}\,{\mathcal {M}}_{0-,++}^{V*} {\mathcal {M}}_{0+,++}^V\Big ],\nonumber \\&A_{UT}^{\sin (\phi _s)}(V) \sigma _0^V\nonumber \\&\quad = \sqrt{\varepsilon (1+\varepsilon )}\, \mathrm{Im}\left[ {\mathcal {M}}_{0+++}^{V*} {\mathcal {M}}_{0-0+}^V-{\mathcal {M}}_{0-++}^{V*} {\mathcal {M}}_{0+0+}^V\right] , \nonumber \\&A_{UT}^{\sin (\phi +\phi _s)}(V) \sigma _0^V =\varepsilon \, \mathrm{Im} \left[ {\mathcal {M}}_{0-,++}^{V*}{\mathcal {M}}_{0+,++}^V \right] ,\nonumber \\&A_{UT}^{\sin (2\phi -\phi _s)}(V) \sigma _0^V =-\sqrt{\varepsilon (1+\varepsilon )}\, \mathrm{Im}\left[ {\mathcal {M}}_{0+,++}^{V*} {\mathcal {M}}_{0-,0+}^V\right] ,\nonumber \\ \end{aligned}$$

(36)

which can easily be derived from the expressions given in [51].⁷ Here, $\phi$ is the azimuthal angle between the lepton and the hadron plane and $\phi _s$ specifies the orientation of the target spin vector with respect to the lepton plane. It is to be stressed that the COMPASS collaboration [52], which has measured these modulations recently, took out the $\varepsilon$-dependent prefactors $\sqrt{\varepsilon (1\pm \varepsilon )}$ and $\varepsilon$ (for the $\sin (\phi + \phi _s)$ modulation) in their definition of the asymmetries ($\varepsilon \simeq 0.8$ for HERMES and ${\simeq }0.96$ for COMPASS kinematics).

The $\sin (\phi -\phi _s)$ modulation of $A_{UT}$ has been measured by the HERMES [53] and COMPASS collaborations [54] for $\rho ^0$ leptoproduction. In [34] this asymmetry has already been investigated by us and shown to be in reasonable agreement with experiment. However, the transversity GPDs were not taken into account in this analysis. The present analysis reveals that their contribution to the $\sin (\phi -\phi _s)$ modulation is small, the $\langle E\rangle ^*_{LL}\langle H\rangle _{LL}$ and $\langle E\rangle ^*_{TT}\langle H\rangle _{TT}$ interference terms are dominant.⁸ This is obvious from the $\sin {(\phi +\phi _s)}$ modulation shown in Fig. 4, which is related to just the same interference term, $\langle \bar{E}_T\rangle _{LT}^*\langle H_T\rangle _{LT}$, as the contributions from the $\gamma ^*_T\rightarrow V_L$ transitions to the $\sin (\phi -\phi _s)$ modulation. A small, almost zero $\sin (\phi +\phi _s)$ modulation is in agreement with experiment [52] within errors. Hence, the results presented in [34] essentially remain valid. For completeness we show these results here again, see Fig. 5. The $\sin (2\phi - \phi _s)$ modulation which is also shown in Fig. 4, is very small in agreement with experiment [52]. It is related to the $\langle \bar{E}_T\rangle ^*_{LT} \langle E\rangle _{LL}$ interference term. The $\sin (3\phi -\phi _s)$ modulation is strictly zero in our approach since it is related to interference terms with the neglected ${\mathcal {M}}^V_{0-,-+}$ and $\gamma ^*_T\rightarrow V_{-T}$ amplitudes. At large values of $-t^\prime$ this is not in good agreement with the COMPASS data [52], the deviations amount to a bit more than one standard deviation.

Fig. 4

The $\sin {(\phi + \phi _s)}$ and $\sin {(2\phi -\phi _s)}$ modulations of $A_{UT}$ for $\rho ^0$ leptoproduction divided by $\varepsilon$ and $\sqrt{\varepsilon (1+\varepsilon )}$, respectively. The results from the handbag approach are represented by solid lines. Data are taken from COMPASS [52]

Fig. 5

The $\sin {(\phi -\phi _s)}$ modulation of $A_{UT}(\rho ^0)$ for HERMES (left) and COMPASS (right) kinematics. The results of our calculations, shown as solid lines, are compared to the data from [53, 54]

The $\sin (\phi _s)$ modulation is related to interference terms between transversity GPDs and $H, E$ like the SDME $r^5_{00}$, but with interchanged $H$ and $E$ contributions,

$$\begin{aligned} A_{UT}^{\sin (\phi _s)} \sim \mathrm{Im} [\langle \bar{E}_T\rangle ^*_{LT}\langle E\rangle _{LL}-\langle H_T\rangle ^*_{LT} \langle H\rangle _{LL}]. \end{aligned}$$

(37)

The first term makes up the $\sin (2\phi -\phi _s)$ modulation and we already know that it is very small, see Fig. 4. The second term in (37) is larger since, as we already mentioned, $\langle H\rangle _{LL}$ is much larger than $\langle E\rangle _{LL}$. This term is an interference term of two helicity-non-flip amplitudes and is therefore not forced to vanish for forward scattering by angular momentum conservation in contrast to the first term which behaves $\propto t'$ for $t'\rightarrow 0$. The results for the $\sin (\phi _s)$ modulation are shown in Fig. 6. For COMPASS kinematics it is negative and amounts to about 0.02 in absolute value. This is in reasonable agreement with experiment, given that our results are only estimates and do not represent detailed fits to the data. For HERMES kinematics the $\sin (\phi _s)$ modulation is very small while, at $W=3\,~\mathrm{GeV}$, we find for it larger values and a zero at $t'\simeq -0.12~\mathrm{GeV}^2$.

Fig. 6

As Fig. 5 but for the $\sin (\phi _s)$ modulation. For COMPASS kinematics (right) the factor $\sqrt{\varepsilon (1+\varepsilon )}$ is taken out. Data are taken from [52]. Left Predictions at $W=5\,~\mathrm{GeV}$ (solid line) and $3\,~\mathrm{GeV}$ (dash-dotted line)

For a transversely polarized target and a longitudinally polarized beam various modulations of the asymmetry $A_{LT}$ can be measured. In terms of helicity amplitudes the non-zero modulations read

$$\begin{aligned}&A_{LT}^{\cos {\phi _s}}(V)\sigma _0^V = \sqrt{\varepsilon (1-\varepsilon )}\, \mathrm{Re}\left[ {\mathcal {M}}^{V*}_{0+,++}{\mathcal {M}}_{0-,0+}^V\right. \nonumber \\&\quad \left. - {\mathcal {M}}^{V*}_{0-,++}{\mathcal {M}}_{0+,0+}^V\right] , \nonumber \\&A_{LT}^{\cos {(\phi -\phi _s)}}(V)\sigma _0^V = \sqrt{1-\varepsilon ^2}\, \mathrm{Re}\left[ {\mathcal {M}}^{V*}_{0-,++} {\mathcal {M}}_{0+,++}^V\right. \nonumber \\&\qquad \left. -2 {\mathcal {M}}^{VN*}_{+-.++}{\mathcal {M}}^{VU}_{++,++}\right] \nonumber \\&A_{LT}^{\cos {(2\phi -\phi _s)}}(V)\sigma _0^V = -\sqrt{\varepsilon (1-\varepsilon )}\, \mathrm{Re}\left[ {\mathcal {M}}^{V*}_{0+,++} M_{0-,0+}^V\right] .\nonumber \\ \end{aligned}$$

(38)

Leaving aside the $\varepsilon$-dependent prefactors in (38) the modulations $\cos (\phi _s)$ and $\cos {(2\phi -\phi _s)}$ of $A_{LT}$ are related to the same combinations of helicity amplitudes as the corresponding modulations of $A_{UT}$ except that the imaginary parts are to be substituted by the real parts. The $\cos (\phi -\phi _s)$ modulation contains the real part of the $\langle \bar{E}_T\rangle _{LT}^*\langle H_T\rangle _{LT}$ interference term as in $A_{UT}^{\sin {(\phi \,-\,\phi _s)}}$ and a $\langle E\rangle ^*_{TT}\langle \widetilde{H}\rangle _{TT}$ term. The imaginary part of the $\langle \bar{E}_T\rangle _{LT}^*\langle H_T\rangle _{LT}$ interference term also controls the $\sin (\phi +\phi _s)$ modulation of $A_{UT}$. In our handbag approach the $\cos (\phi -\phi _s)$ and $\cos {(2\phi -\phi _s)}$ modulations are very small as are the $\sin (\phi +\phi _s)$ and $\sin (2\phi -\phi _s)$ ones. The $\cos (\phi _s)$ modulation is similar in sign and size to $A_{UT}^{\sin (\phi _s)}$. These results are in agreement with the COMPASS data [52] within, however, huge experimental errors. Two examples of the $A_{LT}$ modulations are shown in Fig. 7. In contrast to the SDMEs discussed in Sect. 3.1, for which the contributions from $\bar{E}_T$ are dominant, the only substantial contribution from the transversity GPDs to the asymmetries $A_{UT}$ and $A_{LT}$ is that from $H_T$. The $\cos (\phi _s)$ modulation is rather strongly influenced by $H_T^s$. Without it this modulation would be positive in conflict with experiment.

Fig. 7

The $\cos {(\phi -\phi _s)}$ (left) and $\cos (\phi _s)$ (right) modulation of the asymmetry $A_{LT}$ for $\rho ^0$ leptoproduction. The prefactors $\sqrt{1-\varepsilon ^2}$ and $\sqrt{\varepsilon (1+\varepsilon )}$ in (38) are taken out. The handbag results are displayed as solid lines. Data are taken from [52]

The COMPASS collaboration [52] has also measured the $Q^2$ and the $x_\mathrm{Bj}$ dependence of the asymmetries $A_{UT}$ and $A_{LT}$ for $\rho ^0$ leptoproduction. In Fig. 8 we confront the $Q^2$ dependence of these data with our results. Again agreement is to be seen within experimental errors. Results of similar quality are obtained for the $x_\mathrm{Bj}$ dependence. The calculated asymmetries are often very small and hardly to distinguish from zero in the plots.

Fig. 8

The $\sin (\phi _s)$ (left) and $\cos (\phi _s)$ (right) modulations for $\rho ^0$ leptoproduction versus $Q^2$ at COMPASS kinematics. The prefactors $\sqrt{\varepsilon (1\pm \varepsilon )}$ are taken out. The handbag results are shown as solid lines. Data are taken from [52]

3.3 Predictions for other vector mesons

Estimates of the unseparated cross sections for $\omega$, $\rho ^+$ and $K^{*0}$ leptoproduction without the $\gamma ^*_T\rightarrow V_L$ transitions have been given in [34]. For the case of the $\omega$ the new contributions increase the cross section a little, about 2–3 $\%$ as is the case for the $\rho ^0$ channel. On the other hand, for $\rho ^+$ and $K^{*0}$ production the cross sections increase by about 20–30 $\%$ as compared to the estimates presented in [34] (the quoted values are for COMPASS kinematics). Worth to mention is that the $\omega$ cross section is about an order of magnitude smaller than the $\rho ^0$ one. Due to the absence of the contributions from $H$ for gluons the $\rho ^+$ and $K^{*0}$ cross sections are even suppressed by about a factor of 100.

Since the $u$ and $d$ valence-quark GPDs of $\bar{E}_T$ have the same sign and roughly the same strength (see Table 1) a partial cancellation of contributions occurs for both $\omega$ and $\rho ^+$ production as a consequence of the flavor composition of these mesons, see (4) and (5). The resulting rather small contribution from $\bar{E}_T$ is, however, compensated to some extent by smaller cross sections. These properties result in substantially different SDMEs. As examples we show $r_{00}^1$ and $r_{00}^5$ in Fig. 9 for typical COMPASS kinematics. As is to be seen from this figure both SDMEs, $r_{00}^1$ (in absolute value) and $r_{00}^5$, are slightly larger for the $\omega$ channel than for the $\rho ^0$ one. For the case of the $\rho ^+$ the SDMEs are noticeably larger. Even strikingly larger SDMEs are found for the $K^{*0}$ channel. This is so because only $\bar{E}_T^{d_v}$ contributes and the cross section is very small. We note in passing that the HERMES collaboration [55] has shown preliminary data on the SDME for $\omega$ production at the DIS 2013 ($W=5\,~\mathrm{GeV}$, $Q^2=2\,~\mathrm{GeV}^2$). For the SDMEs under control of the transversity GPDs we find fair agreement between these data and the results from our handbag approach.

Table 1 Parameters for the transversity GPDs at a scale of $2\,~\mathrm{GeV}$

Fig. 9

Predictions for the SDME $r_{00}^1$ (left) and $r_{00}^5$ (right) for $\omega$ (solid), $\rho ^0$ (dash-dotted), $\rho ^+$ (dotted) and $K^{*0}$ (dashed line) leptoproduction at COMPASS kinematics

Since $H_T$ for $u$ and $d$ valence quarks have opposite signs (see Table 1) a partial cancellation of the two contributions takes place for the $\rho ^0$ channel while they add for $\omega$ and $\rho ^+$ production. Moreover, the absence of the contribution from $H$ for gluon leads to very different relative phases between $\langle H_T\rangle _{LT}$ and $\langle H\rangle _{LL}$ for $\rho ^+$ and $K^{*0}$ production. Thus, larger modulations of $A_{UT}$ and $A_{LT}$ are to be expected in particular for the $\rho ^+$ and $K^{*0}$ channels than for $\rho ^0$ production. Indeed for the $\sin (\phi _s)$ and $\cos (\phi _s)$ modulations displayed in Fig. 10, this pattern is clearly seen.

Fig. 10

Predictions for $A_{UT}^{\sin (\phi _s)}$ (left) and $A_{LT}^{\cos (\phi _s)}$ (right) for $\omega$ (solid line), $\rho ^+$ (dotted line) and $K^{*0}$ (dashed line) leptoproduction at a typical COMPASS kinematics. The prefactors $\sqrt{\varepsilon (1\pm \varepsilon )}$ are taken out. The handbag results are shown as solid lines. Data are taken from [52]

Predictions for $A_{UT}^{\sin (\phi -\phi _s)}$ for $\omega , K^{*0}$ and $\rho ^+$ leptoproduction are already given in [34]. With regard to the fact that the contributions from the $\gamma ^*_T\rightarrow V_L$ amplitudes play only a minor role for this modulation, the results presented in [34] remain unchanged practically. The $\sin (\phi -\phi _s)$ modulation is much larger for $\omega$, $\rho ^+$ and $K^{*0}$ channels than for $\rho ^0$ production. The largest asymmetry $A_{UT}^{\sin (\phi -\phi _s)}$ is found for $\rho ^+$ production. It also exhibits a very different $t'$-dependence and opposite sign than for the other vector meson channels. This is a consequence of the large helicity-flip amplitude ${\mathcal {M}}_{0-,0+}$, which is related to the GPD $E$. The amplitude ${\mathcal {M}}_{0+,0+}$ is not much larger than the flip amplitude for this channel since the gluon GPD does not contribute and because of the cancellation in the flavor combination of $u$ and $d$ valence quarks for $H$ while, for $E$, the two contributions add. For further details of this asymmetry it is referred to [34]. For $\phi$ leptoproduction all modulations of $A_{UT}$ and $A_{LT}$ as well as the SDMEs given in (33) are very small since the strange transversity GPDs $H_T$ and $\bar{E}_T$ are small. On the other hand, experimental data on these observables may allow for a better determination of these GPDs.

3.4 Longitudinal polarization

More asymmetries can be measured with a longitudinally polarized beam and/or target. Though there is no data on such asymmetries available as yet except of a few data points for exclusive $\rho ^0$ production on the proton [56, 57] and the deuteron [58] with, however, very large errors, we will discuss them briefly here. Using the simplifications discussed is Sect. 2 (see (9)) and ignoring again the difference between the directions of the virtual photon and the incoming lepton, we find the following non-zero observables:

$$\begin{aligned}&A_{LU}^{\sin (\phi )}(V)\sigma _o^V =-\sqrt{\varepsilon (1-\varepsilon )}\nonumber \\&\quad \times \mathrm{Im}\left[ 2{\mathcal {M}}_{0+,++}^{V*}{\mathcal {M}}_{0+,0+}^V + {\mathcal {M}}_{0-,++}^{V*}{\mathcal {M}}_{0-,0+}^V\right] , \nonumber \\&A_{UL}^{\sin (\phi )}(V)\sigma _o^V=-\sqrt{\varepsilon (1+\varepsilon )}\, \mathrm{Im}\left[ {\mathcal {M}}_{0-,++}^{V*}{\mathcal {M}}_{0-,0+}^V\right] , \nonumber \\&A_{LL}^{\cos (0\phi )}(V)\sigma _0^V=\sqrt{1-\varepsilon ^2}\nonumber \\&\quad \times \left\{ 2\mathrm{Re}[{\mathcal {M}}_{++,++}^{VN*}{\mathcal {M}}_{++,++}^{VU}] + \frac{1}{2} |{\mathcal {M}}_{0-,++}^V|^2 \right\} ,\nonumber \\&A_{LL}^{\cos (\phi )}(V)\sigma _0^V=-\sqrt{\varepsilon (1-\varepsilon )}\,\mathrm{Re}\left[ {\mathcal {M}}_{0-,++}^{V*}{\mathcal {M}}_{0-,0+}^V\right] .\nonumber \\ \end{aligned}$$

(39)

The asymmetry $A_{LU}$ measures the imaginary part of the same interference term as the SDME $r_{00}^5$. Thus, we expect an $A_{LU}$, divided by $\sqrt{2\varepsilon (1-\varepsilon )}$, slightly smaller than $r_{00}^5$. As we discussed in Sect. 3.1 the term ${\mathcal {M}}^*_{0-,++}{\mathcal {M}}_{0-,0+}$ being related to the GPDs $H_T$ and $\tilde{E}$, is very small with the consequence of small $A_{UL}$ and $A_{LL}^{\cos (\phi )}$ at least for $\rho ^0$ and $\omega$ production. The asymmetry $A_{LL}^{\cos (0\phi )}$ receives a contribution from the $\gamma ^*_T\rightarrow V_T$ amplitudes, i.e. from the interference term of $\langle H\rangle _{TT}$ and $\langle \widetilde{H}\rangle _{TT}$. There is also a contribution to it from the transversity GPD $H_T$ which was not taken into account in our previous work [13, 14] where we already analyzed $A_{LL}$ for $\rho ^0$ production. Since in our approach $|{\mathcal {M}}_{0-,++}|<|{\mathcal {M}}_{0+,++}|$ the additional term is smaller than $-r^1_{00}/2$. With regard to our results on the SDME $r_{00}^1$ displayed in Figs. 2 and 9, and those on the interference of the $\gamma _T^*\rightarrow V_T$ amplitudes presented in [13] we find a small asymmetry $A_{LL}^{\cos (0\phi )}$ for $\rho ^0$ and $\omega$ production at COMPASS kinematics. However, a revision of the parametrization of $\widetilde{H}$ given in [13] seems to be advisable.

4 Summary

The role of transversity GPDs in vector-meson leptoproduction is investigated. It is argued that these GPDs control the $\gamma ^*_T\rightarrow V_L$ transition amplitudes and constitute a twist-3 effect consisting of leading-twist GPDs in combination with twist-3 meson wave functions. As compared to the asymptotically leading $\gamma ^*_L\rightarrow V_L$ amplitudes the $\gamma ^*_T\rightarrow V_L$ ones are suppressed by $m_V/Q$. In contrast to pion leptoproduction the $\gamma ^*_T\rightarrow V_L$ amplitudes do not affect the unpolarized cross sections considerably; they only influence markedly some of the SDMEs and asymmetries measured with a transversely polarized target. In most cases they contribute via interferences with amplitudes under control of the helicity-non-flip GPDs. For the estimates made in this work the parametrizations of the GPDs are taken from our previous work [10, 13]. The only new pieces introduced here are the sea-quark transversity GPDs. From this set of GPDs we evaluate various SDMEs and modulations of the asymmetries $A_{UT}$ and $A_{LT}$ and compare the results to HERMES [24, 53] and COMPASS data [52, 54]. In general fair agreement with experiment is obtained.

We stress that we do not attempt detailed fits of the transversity GPDs to the data on SDMEs and asymmetries. A precise calculation, including an error assessment, of the transversity effects in leptoproduction of vector mesons is beyond feasibility at present. There are many uncertainties like the parameterization of the transversity GPDs or the exact treatment of the twist-3 contribution (e.g. the neglect of possible three-particle configurations of the meson state). Also higher-order perturbative corrections other than those included in the Sudakov factor and, implicitly, in the experimental electromagnetic form factor of the pion appearing in the pion-pole contribution to $\pi ^+$ leptoproduction, are ignored. According to [59] the NLO corrections to the leading-twist contribution are rather large for the cross sections for $Q^2\mathop {<}\limits _{\sim }10\,~\mathrm{GeV}^2$. Further uncertainties occur for $K^{*0}$ production. In contrast to the case of the $\rho ^+$ where the $p\rightarrow n$ transition GPDs are related to the diagonal proton ones by isospin symmetry, the proton—$\Sigma ^+$ transition GPDs are connected to the proton GPDs by SU(3) flavor symmetry which is less accurate than isospin symmetry. The assumption of a flavor symmetric sea for all GPDs is also stronger for $K^*$ than for $\rho$ mesons. With regard to all these uncertainties we consider our investigation of leptoproduction of vector mesons as an estimate of the pertinent observables. The trends and magnitudes of the SDME and asymmetries are likely correct but probably not the details. Despite these uncertainties our estimates of transversity effects in $\rho ^0$ production for which data is available, work surprisingly well. Data on other vector-meson channels are highly welcome; they will provide further checks of the transversity effects we are advocating. Such data may be provided by COMPASS and by the upgraded Jlab in future. We are aware that such measurements are a challenge for experimenters. We have shown only a few examples of SDMEs and asymmetries for $\omega$, $\rho ^+$ and $K^{*0}$ leptoproduction but we have results for all observables discussed in this paper. Tables of these results can be obtained from the authors on request.