1 Introduction

There is an increasing interest in the construction of a high energy electron–positron collider [1–3]. The primary goal of this new facility will be to carry out precision measurements of electroweak physics, including the Higgs boson properties. An important byproduct of this program will be the study of high energy photon–photon collisions [4] and the continuation, at energies one order of magnitude higher, of the measurements performed at CERN-LEP, almost 15 years ago. Photon–photon collisions are a very clean laboratory for the theory of strong interactions—quantum chromodynamics (QCD)—where we can test details of the QCD dynamics at high energies, such as the evolution both in virtuality (\(Q^2\)) and in energy (1 / x) (for a review see, e.g. Ref. [5]). It has motivated the development of a large number of phenomenological studies in the last two decades [6–38]. In particular, several authors have discussed the possibility of use the scattering of two off-shell photons at high energy in \(e^+\,e^-\) colliders as a probe of the parton saturation effects in the QCD dynamics, which are predicted to be present in the high energy regime [39–43]. Although the experimental results on several inclusive and diffractive observables measured in ep scattering at HERA and hadron–hadron collisions at RHIC and LHC suggest that these effects are already observed in the energy regime probed by current colliders, these observations still need further confirmation.

The state-of-art framework to treat QCD at high energies is the color glass condensate (CGC) formalism [44–52], which predicts the saturation of the growth of parton distributions, with the evolution with the energy being described by an infinite hierarchy of coupled equations for the correlators of Wilson lines—the Balitsky-JIMWLK hierarchy (for recent reviews see [39–43]). In the mean field approximation, this set of equations can be approximated by the Balitsky–Kovchegov (BK) equation [53–55]. As emphasized in Ref. [23], in general, the applications of the CGC formalism to scattering problems require an asymmetric frame, in which the projectile has a simple structure and the evolution occurs in the target wave function, as it is the case in deep inelastic scattering. Therefore the extension of the BK equation to the calculation of the \(\gamma \gamma \) scattering cross section is not a trivial task. In Ref. [23] we have discussed this generalization in order to use the solution of the BK equation as input of our calculations of the total \(\gamma ^* \gamma ^*\) cross sections and photon structure functions, which were compared with the LEP data. In particular, in Ref. [23] we have improved the treatment of the dipole–dipole cross section, which is the main ingredient of the description of the \(\gamma \gamma \) interactions in the dipole picture. Differently from previous phenomenological studies, which disregarded the impact parameter dependence, we have proposed an educated guess for this dependence and demonstrated that the LEP data can be described in this approach. The high energy behavior of the observables predicted in Ref. [23] is largely different from those obtained in previous studies. This conclusion motivates us to review the analysis of other observables which could be measured at the ILC. One promising observable is double vector meson production in \(\gamma \gamma \) collisions, which has attracted the attention of several theoretical groups in the last years, with the cross section being estimated in different theoretical frameworks [24–38], as, for instance, the solution of the BFKL equation and impact factors at leading and next-to-leading orders. In this paper we will estimate the total \(\gamma (Q_1^2) + \gamma (Q_2^2) \rightarrow V_1 + V_2\) cross sections for \(V_i = \rho \), \(\phi \), \(J/\psi \), and \(\varUpsilon \) considering the improved treatment of the dipole–dipole cross section and the energy and virtuality dependencies of the total cross sections will be analyzed in detail. Our analysis is strongly motivated by the fact that our knowledge about vector meson wave functions has improved considerably over the last years with the progress of phenomenological studies of vector meson production at HERA. As a consequence the main ingredients of our calculations are constrained by LEP and HERA data and hence our predictions for the ILC energies have only one free parameter—the slope parameter \(B_{V_1V_2}\)—which determines the t-dependence of the cross sections. The magnitude of this parameter for different combinations of vector mesons is still an open issue that deserves more detailed studies.

This paper is organized as follows. In the next section we present a brief review of the formalism, discussing in more detail the vector meson wave functions and the dipole–dipole cross section, which are the main inputs of our calculations. In Sect. 3 we present our predictions for the production of different combinations of vector mesons. In particular, the dependencies of the cross sections on the energy and photon virtualities are analyzed in detail. Finally, in Sect. 4 we present our summary.

2 Double vector meson production

2.1 The cross section

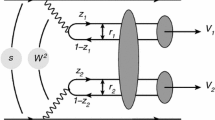
Let us review the main formulas of vector meson production in the color dipole picture (for more details see, e.g. Ref. [34]). The relevant scattering process is \(\gamma ^* \gamma ^* \rightarrow V_1 \, V_2\), where \(V_i\) stands for both light and heavy vector mesons. At high energies, this scattering can be seen as a succession in time of three factorizable subprocesses (see Fig. 1): (i) the photons fluctuate into quark–antiquark pairs (the dipoles), (ii) these color dipoles interact and, (iii) the pairs convert into the vector meson final states. Using as kinematic variables the \(\gamma ^* \gamma ^*\) c.m.s. energy squared \(s=W^2=(p+q)^2\), where p and q are the photon momenta, the photon virtualities squared given by \(Q_1^2=-q^2\) and \(Q_2^2 = -p^2\), and t, the squared momentum transfer, the total cross section for double vector meson production is given by

$$\begin{aligned} \sigma \, (\gamma \gamma \rightarrow V_1 \, V_2)= & {} \int \hbox {d}t \, \frac{\hbox {d}\sigma (\gamma \gamma \rightarrow V_1 \, V_2)}{\hbox {d}t}\, \nonumber \\= & {} \frac{1}{B_{V_1 \,V_2}} \left. \frac{\hbox {d}\sigma (\gamma \gamma \rightarrow V_1 \, V_2)}{\hbox {d}t}\,\right| _{t_{\min }=0}\nonumber \\= & {} \frac{[{\mathcal I}m \, {\mathcal A}(s,\,t=0)]^2}{16\pi \,B_{V_1 \,V_2}} \;, \end{aligned}$$
(1)

where we have approximated the t-dependence of the differential cross section by an exponential with \(B_{V_1 \, V_2}\) being the slope parameter. The imaginary part of the amplitude at zero momentum transfer \({\mathcal A}(s,\,t=0)\) reads

$$\begin{aligned}&{\mathcal I}m \, {\mathcal A}\, (\gamma ^* \gamma ^* \rightarrow V_1 \, V_2) \nonumber \\&\quad = \sum _{h, \bar{h}} \sum _{n, \bar{n}} \int \hbox {d}z_1\, \hbox {d}^2\varvec{r}_1 \,\varPsi ^\gamma _{h, \bar{h}}(z_1,\,\varvec{r}_1,\,Q_1^2)\times \, \varPsi ^{V_1*}_{h, \bar{h}}(z_1,\,\varvec{r}_1)\nonumber \\&\qquad \times \int \hbox {d}z_2\, \hbox {d}^2\varvec{r}_2\times \varPsi ^\gamma _{n, \bar{n}}(z_2,\,\varvec{r}_2,\,Q_2^2)\,\, \varPsi ^{V_2 *}_{n, \bar{n}}(z_2,\,\varvec{r}_2)\,\nonumber \\&\qquad \times \, \sigma _{d d}(\varvec{r}_1, \varvec{r}_2,Y), \end{aligned}$$
(2)

where \(\varPsi ^{\gamma }\) and \(\varPsi ^{V_i}\) are the light-cone wave functions of the photon and vector meson, respectively. The quark and antiquark helicities are labeled by h, \(\bar{h}\), n, and \(\bar{n}\) and reference to the meson and photon helicities are implicitly understood. The variable \(\varvec{r}_1\) defines the relative transverse separation of the pair (dipole) and \(z_1\) \((1-z_1)\) is the longitudinal momentum fraction of the quark (antiquark). Similar definitions are valid for \(\varvec{r}_2\) and \(z_2\). The variable Y is the rapidity and it will be defined later. The basic blocks are the photon wave function, \(\varPsi ^{\gamma }\), the meson wave function, \(\varPsi _{T,\,L}^{V}\), and the dipole–dipole cross section, \(\sigma _\mathrm{dd}\).

Fig. 1
figure 1

Double vector meson production in \(\gamma ^* \gamma ^*\) interactions at high energies in the color dipole picture

Full size image

2.2 Wave functions

In the dipole formalism, the light-cone wave functions \(\varPsi _{h,\bar{h}}(z,\,\varvec{r})\) in the mixed representation \((\varvec{r},z)\) are obtained through two dimensional Fourier transform of the momentum space light-cone wave functions \(\varPsi _{h,\bar{h}}(z,\,\varvec{k})\) [56]. This subject has been intensely discussed in several references (see e.g. Refs. [57–61]). In what follows we present, for completeness, some of the main formulas. The normalized light-cone wave functions for longitudinally (L) and transversely (T) polarized photons are given by

$$\begin{aligned} \varPsi ^{L}_{h,\bar{h}}(z,\,\varvec{r})= & {} \sqrt{\frac{N_{c}}{4\pi }}\,\delta _{h,-\bar{h}}\,e\,e_{f}\,2 z(1-z)\, Q \frac{K_{0}(\varepsilon r)}{2\pi }, \end{aligned}$$
(3)
$$\begin{aligned}&\varPsi ^{T(\gamma =\pm )}_{h,\bar{h}}(z,\,\varvec{r})\nonumber \\&\quad = \pm \sqrt{\frac{N_{c}}{2\pi }} \,e\,e_{f} [i e^{ \pm i\theta _{r}} (z \delta _{h\pm ,\bar{h}\mp } -(1-z) \delta _{h\mp ,\bar{h}\pm }) \partial _{r}\nonumber \\&\qquad + \, m_{f} \,\delta _{h\pm ,\bar{h}\pm }]\frac{K_{0}(\varepsilon r)}{2\pi }, \end{aligned}$$
(4)

where \(\varepsilon ^{2} = z(1-z)Q^{2} + m_{f}^{2}\). The quark mass \(m_f\) plays the role of a regulator when the photoproduction regime is reached. The electric charge of the quark of flavor f is given by \(e\,e_f\).

Table 1 Parameters of the “Gauss-LC” vector meson wave functions
Full size table

One simple way to model the vector meson wave function is to assume, following Refs. [57, 59–61], that the vector meson is a quark–antiquark state and that the spin and polarization structure is the same as in the photon case. The transversely polarized vector meson wave function is then given by

$$\begin{aligned}&\varPsi ^V_{h\bar{h},\lambda =\pm 1}(r,z)\nonumber \\&\quad =s\pm \sqrt{2N_c}\, \frac{1}{z(1-z)} \, \{ \mathrm {i}e^{\pm \mathrm {i}\theta _r}[ z\delta _{h,\pm }\delta _{\bar{h},\mp }\nonumber \\&\qquad -\, (1-z)\delta _{h,\mp }\delta _{\bar{h},\pm }] \partial _r+ m_f \delta _{h,\pm }\delta _{\bar{h},\pm }\}\, \phi _T(r,z). \end{aligned}$$
(5)

and the longitudinally polarized wave function is given by

$$\begin{aligned}&\varPsi ^V_{h\bar{h},\lambda =0}(r,z) \nonumber \\&\quad = \sqrt{N_c}\, \delta _{h,-\bar{h}} \, \left[ M_V\,+ \, \delta \, \frac{m_f^2 - \nabla _r^2}{M_Vz(1-z)}\, \right] \, \phi _L(r,z), \end{aligned}$$
(6)

where \(\nabla _r^2 \equiv (1/r)\partial _r + \partial _r^2\) and \(M_V\) is the meson mass. The overlaps between the photon and the vector meson wave functions read then

$$\begin{aligned} (\varPsi _V^*\varPsi )_{T}= & {} \hat{e}_f e\, \frac{N_c}{\pi z(1-z)} \, \left\{ m_f^2 K_0(\epsilon r)\phi _T(r,z)\right. \nonumber \\&\left. - \left[ z^2+(1-z)^2\right] \epsilon K_1(\epsilon r) \partial _r \phi _T(r,z)\right\} , \end{aligned}$$
(7)
$$\begin{aligned} (\varPsi _V^*\varPsi )_{L}= & {} \, \hat{e}_f e \, \frac{N_c}{\pi }\, 2Qz(1-z)\,K_0(\epsilon r)\nonumber \\&\times \left[ M_V\phi _L(r,z)+ \delta \,\frac{m_f^2 - \nabla _r^2}{M_Vz(1-z)} \phi _L(r,z)\right] ,\qquad \end{aligned}$$
(8)

where the effective charge \(\hat{e}_f=1/3\), 2 / 3, 1 / 3, or \(1/\sqrt{2}\), for \(\varUpsilon \), \(J/\psi \), \(\varPhi \), or \(\rho \) mesons, respectively. The assumption that the quantum numbers of the meson are saturated by the quark–antiquark pair and that the possible contributions of gluon or sea-quark states to the wave function may be neglected, allows the normalization of the vector meson wave functions to unity. The normalization conditions for the scalar parts of the wave functions are then

$$\begin{aligned} 1&= \frac{N_c}{2\pi }\int _0^1\!\frac{\hbox {d}z}{z^2(1-z)^2}\int \! \hbox {d}^2\mathbf {r}\nonumber \\&\quad \times \, \left\{ m_f^2\phi _T^2+\left[ z^2+(1-z)^2\right] \left( \partial _r\phi _T\right) ^2\right\} ,\end{aligned}$$
(9)
$$\begin{aligned} 1&= \frac{N_c}{2\pi } \int _0^1\! \hbox {d}z\, \int \! \hbox {d}^2\mathbf {r}\; \left[ M_V\phi _L+ \delta \, \frac{m_f^2-\nabla _r^2}{M_V z(1-z)}\,\phi _L\right] ^2. \end{aligned}$$
(10)

Another important constraint on the vector meson wave functions is obtained from the decay width. It is commonly assumed that the decay width can be described in a factorized way: the perturbative matrix element \(q \bar{q} \rightarrow \gamma ^* \rightarrow l^+ l^-\) factorizes out from the details of the wave function, which contributes only through its properties at the origin. The decay widths are then given by

$$\begin{aligned} f_{V,T}&= \hat{e}_f\, \frac{N_c}{2\pi M_V} \int _0^1\!\frac{\hbox {d}z}{z^2(1-z)^2}\nonumber \\&\quad \times \left\{ m_f^2-\left[ z^2+(1-z)^2\right] \nabla _r^2\right\} \phi _T(r,z)|_{r=0},\end{aligned}$$
(11)
$$\begin{aligned} f_{V,L}&= \hat{e}_f\, \frac{N_c}{\pi } \int _0^1\! \hbox {d}z\, \left[ M_V +\delta \, \frac{m_f^2-\nabla _r^2}{M_Vz(1-z)}\right] \phi _L(r,z)|_{r=0}. \end{aligned}$$
(12)

The coupling of the meson to the electromagnetic current, \(f_V\), is obtained from the measured electronic decay width by

$$\begin{aligned} \varGamma _{V\rightarrow e^+e^-} = \frac{4\pi \alpha _\mathrm{em}^2f_V^2}{3M_V}. \end{aligned}$$
(13)

We need now to specify the scalar parts of the wave functions, \(\phi _{T,L}(r,z)\). Dosch, Gousset, Kulzinger and Pirner (DGKP) [57] made the assumption that the longitudinal momentum fraction z fluctuates independently of the transverse quark momentum \(\mathbf {k}\), where \(\mathbf {k}\) is the Fourier conjugate variable to the dipole vector \(\mathbf {r}\). In the DGKP model one chooses \(\delta =0\) in Eqs. (6), (8), (10), and (12). The DGKP model was further simplified by Kowalski and Teaney [60, 61], who assumed that the z dependence of the wave function for the longitudinally polarized meson is given by the short-distance limit of \(z(1-z)\). For the transversely polarized meson they set \(\phi _T(r,z) \propto [z(1-z)]^2\) in order to suppress the contribution from the end-points (\(z\rightarrow 0,1\)). This leads to the “Gauss-LC” [60, 61] wave functions given by

$$\begin{aligned} \phi _{T}(r,z)&= N_{T} [z(1-z)]^2\exp (-r^2/2R_{T}^2),\end{aligned}$$
(14)
$$\begin{aligned} \phi _{L}(r,z)&= N_{L} z(1-z)\exp (-r^2/2R_{L}^2). \end{aligned}$$
(15)

The values of the constants \(N_{T,L}\) and \(R_{T,L}\) in Eqs. (14) and (15), determined by requiring the correct normalization and by the condition \(f_V=f_{V,T}=f_{V,L}\), are given in Table 1. It is important to emphasize that this model allows to describe the HERA data and the recent LHC data for the exclusive vector meson photoproduction in hadron–hadron collisions (see, e.g. Refs. [62–64]).

Fig. 2
figure 2

Energy dependence of the product \(B_{V_1V_2} \, \sigma [\gamma ^*(Q_1^2)\gamma ^*(Q_2^2) \rightarrow V_1V_2]\) assuming \(V_1 = V_2\) (\(V_i = \rho , \phi , J/\varPsi , \varUpsilon \)) and considering \(Q_1^2 = Q_2^2 = 0\)

Full size image

2.3 The dipole–dipole scattering cross section

At lowest order, the dipole–dipole interaction can be described by the two-gluon exchange between the dipoles, with the resulting cross section being energy independent (see, e.g. Ref. [65]). Taking into account the leading corrections associated to terms \(\propto \log (1/x)\), as described by the BFKL equation, implies a power-law energy behavior for the cross section, which violates the unitarity at high energies. These unitarity corrections were addressed in Ref. [66], considering the color dipole picture and independent multiple scatterings between the dipoles, and in Refs. [67, 68] considering the Color Glass Condensate formalism. In the eikonal approximation the dipole–dipole cross section can be expressed as follows:

$$\begin{aligned} \sigma ^\mathrm{dd} (\varvec{r}_1,\varvec{r}_2,Y) = 2 \int \hbox {d}^2\varvec{b}\,{\mathcal {N}}(\varvec{r}_1,\varvec{r}_2,\varvec{b},Y) \end{aligned}$$
(16)

where \({\mathcal {N}}(\varvec{r}_1,\varvec{r}_2,\varvec{b},Y)\) is the scattering amplitude for the two dipoles with transverse sizes \(\varvec{r}_1\) and \(\varvec{r}_2\), relative impact parameter \(\varvec{b}\) and rapidity separation Y. How to write \({\mathcal {N}}\) for the interaction of two dipoles of similar sizes is still an open question (see, e.g. Ref. [69]). In a first approximation, it is useful to express \({\mathcal {N}}\) in terms of the solution of the BK equation (obtained disregarding the \(\varvec{b}\) dependence), which has been derived considering an asymmetric frame where the projectile has a simple structure and the evolution occurs in the target wave function. A shortcoming of this approach, used in a previous analysis of double vector meson production, is that although the unitarity of the S-matrix (\({\mathcal {N}} \le 1\)) is respected by the solution of the BK equation, the associated dipole–dipole cross section can still rise indefinitely with the energy, even after the black disk limit (\({\mathcal {N}} = 1\)) has been reached at central impact parameters, due to the non-locality of the evolution. In Ref. [23] we have proposed a more elaborated model for the impact parameter dependence in order to obtain more realistic predictions for the dipole–dipole cross section. Basically, we assumed that only the range \(b < R\), where \(R =\) Max\((r_1,r_2)\), contributes to the dipole–dipole cross section, i.e., we assumed that \({\mathcal {N}}\) is negligibly small when the dipoles have no overlap with each other (\(b>R\)). Therefore the dipole–dipole cross section can be expressed as follows [23]:

$$\begin{aligned} \sigma ^\mathrm{dd} (\varvec{r}_1,\varvec{r}_2,Y) = 2 \, {{N}}(\varvec{r},Y) \int _0^R \hbox {d}^2\varvec{b}= 2 \pi R^2 {{N}}(\varvec{r},Y),\qquad \end{aligned}$$
(17)

where \({{N}}(\varvec{r},Y)\) is the dipole scattering amplitude. The explicit form of \(\sigma ^\mathrm{dd}\) reads

$$\begin{aligned} \sigma ^\mathrm{dd} (\varvec{r}_1,\varvec{r}_2,Y)= & {} 2 \pi r_1^2 N(r_2,Y_2) \, \Theta (r_1 - r_2)\nonumber \\&+\, 2 \pi r_2^2 N(r_1,Y_1) \, \Theta (r_2 - r_1), \end{aligned}$$
(18)

where \(Y_i = \ln (1/x_i)\) and

$$\begin{aligned} x_i = \frac{Q_i^2 + 4 m_f^2}{W^2 + Q_i^2}. \end{aligned}$$
(19)

Following Ref. [23] this model for \(\sigma _\mathrm{dd}\) will be called Model 2. As input for this model we will use two forward dipole scattering amplitudes. The first one is the solution of the BK equation obtained in Ref. [70], which we call rcBK. The second one is the phenomenological model of the forward dipole scattering N(r, Y) proposed in Ref. [71] and updated in [72], which was constructed so as to reproduce two limits of the LO BK equation analytically under control: the solution of the BFKL equation for small dipole sizes, \(r\ll 1{/}Q_s(x)\), and the Levin–Tuchin law for larger ones, \(r\gg 1{/}Q_s(x)\). In the updated version of this parametrization [72], the free parameters were obtained by fitting the new H1 and ZEUS data. In this parametrization the forward dipole scattering amplitude is given by

$$\begin{aligned} {{N}}(\varvec{r},Y) = \left\{ \begin{array}{ll} {\mathcal N}_0\, \left( \frac{r\, Q_s}{2}\right) ^{2\left( \gamma _s + \frac{\ln (2/r Q_s)}{\kappa \,\lambda \,Y}\right) }, &{} \quad \text{ for } r Q_s(x) \le 2,\\ 1 - \exp ^{-a\,\ln ^2\,(b\,r\, Q_s)}, &{} \quad \text{ for } r Q_s(x) > 2, \end{array} \right. \nonumber \\ \end{aligned}$$
(20)

where a and b are determined by continuity conditions at \(\varvec{r}Q_s(x)=2\), \(\gamma _s= 0.6194\), \(\kappa = 9.9\), \(\lambda =0.2545\), \(Q_0^2 = 1.0\) GeV\(^2\), \(x_{0}=0.2131\times 10^{-4}\), and \({\mathcal N}_0=0.7\). Hereafter, we shall call the model above IIM-S. The first line from Eq. (20) describes the linear regime whereas the second one includes saturation effects. One of the main motivations to use this model in our analysis is that it allows one to estimate the magnitude of the saturation effects, by the comparison between the predictions of the full model with those obtained considering only the linear term. As demonstrated in Ref. [23], using this model we can describe the LEP data for the total \(\gamma \gamma \) cross sections and photon structure functions.

Finally, for the sake of comparison with a previous analysis, in what follows we also will present the predictions obtained using the phenomenological model for the dipole–dipole cross section proposed in [22], which disregards the impact parameter dependence and, consequently, presents the shortcoming discussed above. The inclusion of these predictions in our analysis allows us to estimate the theoretical uncertainty present in ILC predictions, as well as to make comparisons with existing results in the literature. The dipole–dipole cross section proposed in Ref. [22] is the following:

$$\begin{aligned} \sigma ^\mathrm{dd}_{a,b}(r_1,r_2,Y) = \sigma _0^{a,b}\,{{N}}(\varvec{r}_1,\varvec{r}_2,Y) \end{aligned}$$
(21)

with \(\sigma _0^{a,b} = (2/3) \sigma _0\), where \(\sigma _0\) is a free parameter in the saturation model considered, fixed by fitting the DIS HERA data. In the above equation \({{N}}(\varvec{r}_1,\varvec{r}_2,Y) = {{N}}(\varvec{r}_\mathrm{\small eff},Y=\ln (1/\bar{x}_{ab}))\), where

$$\begin{aligned} r^2_\mathrm{\small eff}\; = \;{r_1^2r_2^2\over r_1^2+r_2^2}\,\,\, \text{ and }\,\,\, \bar{x}_{ab} \; = \;{Q_1^2 + Q_2^2 +4m_a^2+4m_b^2\over W^2+Q_1^2+Q_2^2}.\nonumber \\ \end{aligned}$$
(22)

Keeping the notation introduced in [23], this model will be called Model 1. As input for the calculations, we will use the same two dipole amplitudes: rcBK and IIM-S.

3 Results

In what follows, as in Ref. [23], we will denote the predictions obtained using the dipole–dipole cross section given by Eq. (21) by model 1 and those using Eq. (18) as input by model 2. Moreover, we will consider the rcBK and IIM-S models for the scattering amplitude \({{N}}(\varvec{r},Y) \). The parameters of our calculations are the same used in Ref. [23] and this implies that our model gives a good description of the LEP data. As the value of the slope \(B_{V_1V_2}\) for the different combinations of vector mesons in the final state is still poorly known, we will, in almost all cases, present our predictions for the product \(B_{V_1V_2} \, \sigma (\gamma ^*\gamma ^* \rightarrow V_1V_2)\), which can be estimated without free parameters, since all parameters are constrained by the LEP and HERA data.

Fig. 3
figure 3

Energy dependence of the product \(B_{V_1V_2} \, \sigma [\gamma ^*(Q_1^2)\gamma ^*(Q_2^2) \rightarrow V_1V_2]\) assuming \(V_1 \ne V_2\) (\(V_1 V_2 = \rho J/\varPsi , \phi J/\varPsi , J/\varPsi \varUpsilon , \rho \varUpsilon \)) and considering \(Q_1^2 = Q_2^2 = 0\)

Full size image

In Fig. 2 we present our predictions for the energy dependence of the product \(B_{V_1V_2} \, \sigma (\gamma ^*\gamma ^* \rightarrow V_1V_2)\) assuming \(V_1 = V_2\) (\(V_i = \rho , \phi , J/\varPsi , \varUpsilon \)) and considering \(Q_1^2 = Q_2^2 = 0\). In this case only the transverse photon polarizations contribute to the total cross sections. It is important to emphasize that the color dipole picture allows us to treat simultaneously double \(\rho \) production by real photons, which is a typical soft process, and double \(\varUpsilon \) production, which is the ideal laboratory to study the basic example of a hard process at high energies: the onium–onium scattering. Moreover, it allows us to study the transition between these two regimes, where we expect to see nonlinear (saturation) effects in the QCD dynamics. In our calculations we consider the two different models for the dipole–dipole cross section as well as the two models for the forward dipole scattering amplitude. We can observe that the main distinction is associated to the choice of the dipole–dipole cross sections. The predictions obtained using model 2 are always smaller than those from model 1. Consequently, assuming that model 2 is more adequate to describe the dipole–dipole interaction, we see that the previous estimates of the double vector production have overestimated the magnitude of the total cross sections. This behavior was expected from our previous results for the total \(\gamma ^*\gamma ^*\) cross section [23]. We also see that the difference between the predictions increases with the quark masses, going from a factor 4, in the \(\rho \rho \) case, to almost two orders of magnitude in the case of \(\varUpsilon \varUpsilon \) production. This suggests that the experimental analysis of double vector production at ILC can, in principle, constrain the model for the dipole–dipole interaction. Moreover, in the case of model 1, the IIM-S and rcBK predictions are almost identical for all combinations of vector mesons in the final state. In model 2 the IIM-S predictions are smaller than the rcBK ones for light vector meson production and larger for heavy vector meson production. Such behavior is directly associated to the distinct transition between small and large dipoles predicted by these two models for the forward dipole scattering amplitude (see Fig. 2 in Ref. [23]). As expected, we find that our predictions are strongly dependent on the quark mass, with the cross sections being smaller for the production of heavier vector mesons. Similar conclusions are obtained in the analysis shown in Fig. 3, where we present our predictions for the energy dependence of the product \(B_{V_1V_2} \, \sigma [\gamma ^*(Q_1^2)\gamma ^*(Q_2^2) \rightarrow V_1V_2]\) assuming \(V_1 \ne V_2\) (\(V_1 V_2 = \rho J/\varPsi , \phi J/\varPsi , J/\varPsi \varUpsilon , \rho \varUpsilon \)) and considering \(Q_1^2 = Q_2^2 = 0\).

Fig. 4
figure 4

Dependence on the photon virtualities \(Q_1^2 = Q_2^2 = Q^2\) of the product \(B_{V_1V_2} \, \sigma [\gamma ^*(Q_1^2)\gamma ^*(Q_2^2) \rightarrow V_1V_2]\) assuming \(V_1 = V_2\) (\(V_i = \rho , \phi , J/\varPsi , \varUpsilon \)) for a fixed center-of-mass energy (\(W = 500\) GeV)

Full size image
Fig. 5
figure 5

Dependence on the photon virtualities \(Q_1^2 = Q_2^2 = Q^2\) of the product \(B_{V_1V_2} \, \sigma [\gamma ^*(Q_1^2)\gamma ^*(Q_2^2) \rightarrow V_1V_2]\) assuming \(V_1 \ne V_2\) (\(V_1 V_2 = \rho J/\varPsi , \phi J/\varPsi , J/\varPsi \varUpsilon , \rho \varUpsilon \)) for a fixed center-of-mass energy (\(W = 500\) GeV).

Full size image
Fig. 6
figure 6

Energy dependence of the normalized cross sections (see text) for different final states and different values of \(Q_1^2 = Q_2^2 = Q^2\). a \( Q^2 = 0\) and b \( Q^2 = 20\) GeV\(^2\)

Full size image

In Fig. 4 we present our predictions for the dependence on the photon virtualities \(Q_1^2 = Q_2^2 = Q^2\) of the product \(B_{V_1V_2} \, \sigma [\gamma ^*(Q_1^2)\gamma ^*(Q_2^2) \rightarrow V_1V_2]\) for different combinations of vector mesons in the final state and fixed center-of-mass energy (\(W = 500\) GeV). In this case we take into account the contributions of the transverse and longitudinal photon polarizations, i.e.:

$$\begin{aligned}&\sigma [\gamma ^*(Q_1^2) \gamma ^*(Q_2^2) \rightarrow V_1V_2] \nonumber \\&\quad = \sigma [\gamma _L^*(Q_1^2) \gamma _L^*(Q_2^2) \rightarrow V_1V_2] \nonumber \\&\qquad +\sigma [\gamma _L^*(Q_1^2) \gamma _T^*(Q_2^2) \rightarrow V_1V_2]\nonumber \\&\qquad +\, \sigma [\gamma _T^*(Q_1^2)\gamma _L^*(Q_2^2) \rightarrow V_1V_2] \nonumber \\&\qquad +\, \sigma [\gamma _T^*(Q_1^2)\gamma _T^*(Q_2^2) \rightarrow V_1V_2]. \end{aligned}$$
(23)

For \(Q^2 \ne 0\) we have two hard scales present in the process: the mass of the quarks (vector mesons) and the photon virtualities. For the double light vector meson (\(\rho \rho , \phi \phi \)) production, the dominant scale is the photon virtuality. In this case our predictions strongly decrease with \(Q^2\). On the other hand, for the double \(\varUpsilon \) production, our predictions are almost \(Q^2\)-independent in the range considered, since the dominant scale that defines the size of the two interacting dipoles is the bottom quark mass. In contrast, for the double \(J/\varPsi \) production, the characteristic dipole sizes are determined at small \(Q^2\) by the charm quark mass and at medium \(Q^2\) by the photon virtualities. Consequently, we observe a mild \(Q^2\) dependence in the corresponding predictions. Moreover, we observe that the difference between model 1 and model 2 predictions increases at larger \(Q^2\) and for heavier vector mesons. In Fig. 5 we present our predictions for the production of two different vector mesons, which are similar to those observed in the production of identical vector mesons. Basically, the \(Q^2\) dependence is reduced for larger values of the sum of the masses of the vector mesons in the final state.

In order to illustrate how the energy behavior depends on the masses of the final state mesons, on the photon virtualities \(Q_1^2 = Q_2^2 = Q^2\) and on the choice of the model for the dipole–dipole cross section, in Fig. 6 we present our predictions for the normalized cross sections. The different cross sections were all normalized to the unity at \(W = 100\) GeV to better exhibit the different trends. For \(Q^2 = 0\) we observe a clear transition between the soft and hard regimes, with the growth with the energy being faster for heavier mesons in the final state. Moreover, we find that model 2 predicts a smaller slope than model 1. For \(Q^2 = 20\) GeV\(^2\), a similar behavior is observed, but in this case already for the \(\rho \rho \) production we see a steep rise of the cross section with the energy, which is directly associated to the presence of the hard scale \(Q^2\).

Fig. 7
figure 7

Energy dependence of the \(\gamma \gamma \rightarrow V_1 V_2\) cross section for different final states considering \(Q_1^2 = Q_2^2 = 0\)

Full size image

In certain cases, where the slope parameters are phenomenologically known, it is possible to make definite predictions. In Fig. 7 we show the cross sections calculated with models 1 and 2 as a function of the energy W with the proper slope coefficients, taken from [34]: \(B_{\rho \rho } = 10\) GeV\(^{-2}\), \(B_{\rho \psi } = 5\) GeV\(^{-2}\), and \(B_{\psi \psi } = 0.44\) GeV\(^{-2}\). Our predictions with model 1 are similar to those obtained in [34], with small differences mainly associated to the different forward dipole scattering amplitude and to the treatment of the vector meson wave functions. In contrast, with model 2, we predict that at \(W = 1\) TeV the cross sections are \(\sigma ( \gamma \gamma \rightarrow \rho \rho ) \approx 15\) nb, \(\sigma ( \gamma \gamma \rightarrow \rho J/\varPsi ) \approx 1.2\) nb and \(\sigma ( \gamma \gamma \rightarrow J/\varPsi J/\varPsi ) \approx 0.25\) nb, which are a factor \(\approx 4\) smaller than previous estimates in the literature [27, 28] obtained using the color dipole picture. In our calculation we have been using a formalism in which the real part of the amplitude is neglected. This might not be a good approximation for heavy mesons. Nevertheless, since one of our primary goals in this work is to investigate the predictions of our dipole–dipole scattering model, we keep using this approximation to compare our numbers with those obtained in [27, 28], where the same approximation was made.

A similar analysis can be performed for the interaction of virtual photons. In this case we can compare our predictions with those obtained in Refs. [31–33] for the double \(\rho \) production. In [31–33] the \(\gamma ^* \gamma ^* \rightarrow \rho \rho \) cross section was obtained using the \(k_T\)-factorization formalism, with the scattering amplitude being given in terms of the convolution between the impact factors, BFKL kernel and the corresponding leading twist distribution amplitude, which describes the hadronization into the final state \(\rho \) mesons. The authors have considered the BFKL evolution in the leading logarithm (LL) approximation as well as the renormalization group improved BFKL kernel, which gives good agreement with the next-to-leading logarithm (NLL) evolution derived in Refs. [35, 36]. In comparison with [31–33], our results are a factor \(\approx 10^3\) smaller than the LL BFKL predictions and similar to the NLL BFKL one.

Fig. 8
figure 8

Comparison between the linear and full IIM-S predictions for the energy behavior of the \(\gamma \gamma \rightarrow \rho \rho \) cross section

Full size image

Although saturation effects of QCD dynamics are expected to take over at higher energies, this change of dynamics can manifest itself with different strength for different observables. For this reason, when working with the dipole approach, which is naturally prepared to incorporate nonlinear corrections, it is always interesting to quantify the importance of the saturation effects. In Fig. 8 we show our results for the energy dependence of the \( \gamma \gamma \rightarrow \rho \rho \) cross section, where we compare the full IIM-S model predictions with those obtained considering the linear regime of this model [first line in Eq. (20)]. We see that the high energy behavior of the cross section is strongly modified by saturation effects. This conclusion was already obtained in [34] and we see that it remains valid even after updating the dipole cross sections and model for the dipole–dipole interaction.

A final comment is in order. Recently, in Refs. [73, 74], the dipole representation of vector meson electroproduction was studied beyond the standard twist-2 level. The authors of these references have considered the description of hard exclusive processes beyond the leading twist approximation derived in Refs. [75, 76] and demonstrated that the helicity amplitudes, expressed in the impact parameter space and computed in the collinear factorization scheme, factorize into the dipole cross section and the wave functions of the virtual photon combined with the first moments of the \(\rho \) meson wave functions parametrized by the distribution amplitudes. In Ref. [74] the predictions of this approach were compared with the HERA ep data and a good description was obtained for \(Q^2 \ge 5\) GeV\(^2\). The extension of this approach to \(\gamma ^* \gamma ^*\) interactions and the comparison of its predictions with those obtained in this paper is an important issue to be addressed in the future.

4 Summary

The scattering of two off-shell photons at high energy in \(e^+\,e^-\) colliders is an interesting process to look for parton saturation efffects. In these two-photon reactions, the photon virtualities can be made large enough to ensure the applicability of perturbative methods or can be varied in order to test the transition between the soft and hard regimes of the QCD dynamics. In recent years, a series of studies have discussed in detail the treatment of the total cross section and the exclusive production of different final states in \(\gamma \gamma \) interactions considering very distinct theoretical approaches. One great motivation for these works is the possibility that in a near future \(\gamma \gamma \) interactions may be investigated at the International Linear Collider (ILC). In particular, in Ref. [23] we presented a detailed analysis of the \(\gamma \gamma \) cross section at high energies using the color dipole picture and taking into account saturation effects, which are expected to be visible at high energies. In this paper we extended our approach to double vector meson production, improving the previous analysis in three important aspects: (i) the theoretical treatment of the dipole–dipole cross section; (ii) the forward scattering amplitude, considering the solution of the running coupling BK equation (which is the state-of-art of the CGC formalism); and (iii) the treatment of the vector meson wave functions. Considering that all parameters of our approach have been fixed by fitting HERA and LEP data, our predictions for double vector meson production at ILC are parameter free, except for the only unknown parameter: the slope parameter \(B_{V_1 V_2}\), which deserves a more detailed analysis. Our main conclusion is that the improvement of the theoretical framework for double vector meson production in \(\gamma \gamma \) interactions resulted in a reduction of the previously estimated cross sections at ILC energies. However, our results indicate that the experimental analysis at ILC is feasible and may be useful to constrain the QCD dynamics at high energies. As a final remark we would like to say that understanding vector meson production in \(\gamma \gamma \) collisions is very important not only for the phenomenology of future electron–positron colliders but also for exclusive double vector meson production in hadron–hadron collisions, which have been studied at the LHC and that could be further studied in future hadronic colliders.