Abstract
A combination of the inclusive diffractive cross section measurements made by the H1 and ZEUS Collaborations at HERA is presented. The analysis uses samples of diffractive deep inelastic ep scattering data at a centre-of-mass energy \(\sqrt{s}=318~\mathrm{GeV}\) where leading protons are detected by dedicated spectrometers. Correlations of systematic uncertainties are taken into account, resulting in an improved precision of the cross section measurement which reaches 6 % for the most precise points. The combined data cover the range 2.5<Q 2<200 GeV2 in photon virtuality, \(0.00035 < \mbox{$x_{\mathbb{P}}$}< 0.09\) in proton fractional momentum loss, 0.09<|t|<0.55 GeV2 in squared four-momentum transfer at the proton vertex and 0.0018<β<0.816 in \(\beta=x/\mbox{$x_{\mathbb{P}}$}\), where x is the Bjorken scaling variable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Diffractive collisions in deep inelastic electron-proton scattering (DIS), ep→eXp, where the proton in the final state carries most of the beam momentum and X represents all other final state particles, have been studied extensively at the HERA collider. They can be viewed as resulting from processes in which a photon exchanged between the electron and the proton probes a colour-singlet combination of partons with vacuum quantum numbers emitted by the proton. The negative four-momentum squared of the virtual photon, Q 2, supplies a hard scale, which allows the application of perturbative quantum chromodynamics (QCD). Diffractive reactions in DIS are a tool to investigate low-momentum partons in the proton, notably through the study of diffractive parton distribution functions (DPDFs), determined by a QCD analysis of the data.
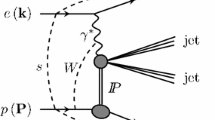
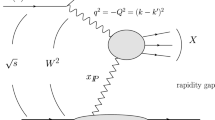
In diffractive ep scattering the virtual photon dissociates at a photon-proton centre-of-mass energy W and squared four-momentum transfer t at the proton vertex (Fig. 1), producing a hadronic system X with mass M X . The fractional longitudinal momentum loss of the proton is denoted as \(\mbox{$x_{\mathbb{P}}$}\), while the fraction of this momentum taking part in the interaction with the photon is denoted as β. These variables are related to Bjorken x by \(x=\beta\, \mbox{$x_{\mathbb{P}}$}\). The variable β is related to M X , t and Q 2 by \(\beta =Q^{2}/(Q^{2}+M_{X}^{2}-t)\). The variable \(\mbox{$x_{\mathbb{P}}$}\) is given by \(\mbox{$x_{\mathbb{P}}$}=(Q^{2}+M_{X}^{2}-t)/(Q^{2}+W^{2}-m_{p}^{2})\), where m p is the proton mass. The variables W, Q 2 and the fractional energy loss y of the electron in the proton rest frame are related by W 2≃sy−Q 2, where s is the square of the ep centre-of-mass energy.
Similarly to inclusive DIS, diffractive cross section measurements are conventionally expressed in terms of the reduced diffractive cross section, \(\sigma_{r}^{D(4)}\), which is related to the measured ep cross section by

The reduced cross section \(\sigma_{r}^{D(3)}(\beta,Q^{2},\mbox{$x_{\mathbb{P}}$})\) is obtained byintegrating \(\sigma_{r}^{D(4)}(\beta,Q^{2},\mbox{$x_{\mathbb{P}}$},t)\) over t. The diffractive reduced cross section is related to the diffractive structure functions by:

Experimentally, diffractive ep scattering is characterised by the presence of a leading proton in the final state and by a depletion of hadronic activity in the pseudo-rapidityFootnote 1 distribution of particles (large rapidity gap, LRG) in the forward (proton) direction. Both of these signatures have been exploited in various analyses by H1 and ZEUS to select diffractive samples either by tagging the outgoing proton in dedicated proton spectrometers [1–4] or by requiring the presence of a large rapidity gap [4–6]. The two methods differ partially in the accessible kinematic ranges (lower x ℙ reach for the LRG data) and substantially in their dominant sources of systematic uncertainties. In LRG-based measurements, the largest uncertainty arises from proton dissociative events, ep→eXN, in which the proton dissociates into a low mass state N. Low \(\mbox{$x_{\mathbb{P}}$}\) samples selected by the proton spectrometers have little or no proton dissociation contribution, but their precision is limited statistically by the small acceptances and systematically by large uncertainties in the proton tagging efficiency, which strongly depends on the proton-beam optics. The results from both methods are found to be consistent [1, 2, 4, 6, 7].
Combining measurements can provide more precise and kinematically extended data than the individual measurements. In this paper, a combination of the H1 [1, 2] and the ZEUS [3, 4] proton spectrometer results is presented. The combination is performed using the weighted averaging method introduced in [8] and extended in [9, 10]. The correlated systematic uncertainties and global normalisations are constrained in the fit such that one consistent data set is obtained. Since H1 and ZEUS have employed different experimental techniques, using different detectors and methods of kinematic reconstruction, the combination leads to significantly reduced uncertainties. The kinematic range of the combined data is: 2.5≤Q 2≤200 GeV2, 0.0018≤β≤0.816, 0.00035≤x ℙ≤0.09 and 0.09<|t|<0.55 GeV2. The latter range restricts the analysis to the t values directly accessible by both the H1 and ZEUS proton spectrometers.
2 Combination of the H1 and ZEUS measurements
2.1 Data samples
The H1 [11–13] and ZEUS [14] detectors were general purpose instruments which consisted of tracking systems surrounded by electromagnetic and hadronic calorimeters and muon detectors, ensuring close to 4π coverage about the ep interaction point. Both detectors were equipped with proton spectrometers; the Leading Proton Spectrometer (LPS) for ZEUS, the Forward Proton Spectrometer (FPS) and the Very Forward Proton Spectrometer (VFPS) for H1. The LPS and FPS spectrometers were located between 60 and 90 m away from the main detectors in the forward (proton beam) direction. The VFPS spectrometer was located around 220 m away from the main H1 detector in the forward direction.
The combination is based on the cross sections measured with the H1 FPS [1, 2] and the ZEUS LPS [3, 4]. The bulk of the data [1, 2, 4] was taken at electron and proton beam energies of E e ≃27.5 GeV and E p =920 GeV, respectively, corresponding to an ep centre-of-mass energy of \(\sqrt{s} = 318~\mathrm{GeV}\). The earlier ZEUS LPS data [3] collected at E p =820 GeV are corrected to a common \(\sqrt{s} = 318~\mathrm{GeV}\) by using the extrapolation procedure described in Sect. 2.1.2. The three-fold differential reduced cross sections, \(\sigma _{r}^{D(3)}\)(β, Q 2, \(\mbox{$x_{\mathbb{P}}$}\)), are combined. For the original measurements, the main H1 and ZEUS detectors are used to reconstruct Q 2,W and x, whereas M X , β, \(\mbox{$x_{\mathbb{P}}$}\) and t are derived from the proton spectrometer measurements or from combined information of the proton spectrometers and the main detectors. In Table 1 the data sets used for the combination are listed together with their kinematic ranges and integrated luminosities.
2.1.1 Restricted t range
In the individual analyses [1–4] the reduced cross sections are directly measured for ranges of the squared four-momentum transfer t visible to the proton spectrometers (see Table 1) and extrapolated to the rangeFootnote 2 |t min|<|t|<1 GeV2 (denoted in the following as ‘the full t range’), assuming an exponential t dependence of the diffractive cross section and using the exponential slope measured from the data. Due to the uncertainties of the slope parameters measured by H1 [1, 2] and ZEUS [3, 4], this extrapolation introduces an additional uncertainty in the normalisation of the cross section. To reduce this source of systematic uncertainty, the H1 and ZEUS cross sections are combined in the restricted t range 0.09<|t|<0.55 GeV2 covered by the proton spectrometer acceptances of both detectors for the bulk of the data. The correction factors from the visible t range of the ‘FPS HERA I’ and ‘LPS 1’ data samples to the restricted t range are evaluated by using the t dependencies as a function of x ℙ measured for each sample. The correction factors for the most precise ‘FPS HERA II’ data are applied in bins of β,Q 2 and x ℙ. For the ‘LPS 2’ sample the restricted range coincides with the visible range. Because of the uncertainty on the exponential slope parameter, such factors introduce uncertainties of 2.2 %, 1.1 % and 5 % on the ‘FPS HERA II’, ‘FPS HERA I’ and ‘LPS 1’ data, respectively, which are included in the normalisation uncertainty on each sample. The total normalisation uncertainties of the data samples are listed in Table 2. In the restricted t range, these uncertainties are in general smaller and the average normalisations are in better agreement than in the full t range; the ratio of the ‘FPS HERA II’ to the ‘LPS 2’ data averaged over the measured data points, which is 0.85±0.01 (stat)±0.03 (sys) \({}^{+0.09}_{-0.12}\) (norm) in the full t range [2], becomes 0.91±0.01 (stat)±0.03 (sys)±0.08 (norm) in the restricted t range. Within the uncertainties, the ratio does not show any significant β, Q 2 or \(\mbox{$x_{\mathbb{P}}$}\) dependence.
2.1.2 Extrapolation to a common (Q 2, \(\mbox{$x_{\mathbb{P}}$}\), β) grid
The original binning schemes of the \(\sigma_{r}^{D(3)}\) measurements are very different for H1 and ZEUS. In the H1 case the measurements are extracted at fixed β, whereas for ZEUS the cross section is measured at fixed M X ; also the Q 2 and \(\mbox{$x_{\mathbb{P}}$}\) central values differ. Therefore, prior to the combination, the H1 and ZEUS data are transformed to a common grid of (β,Q 2,x ℙ) points. The grid points are based on the original binning scheme of the ‘FPS HERA II’ data. The (\(Q^{2}, \mbox{$x_{\mathbb{P}}$}\)) grid points at the lowest Q 2 value of 2.5 GeV2 and at the lowest and highest x ℙ values, which are beyond the ‘FPS HERA II’ data grid, are taken from the ‘LPS 2’ measurement.
The transformation of a measurement from the original ith point (\(\beta_{i}, Q^{2}_{i}, \mbox{$x_{\mathbb{P}}$}_{i}\)) to the nearest grid point (\(\beta_{\mathrm{grid}}, Q^{2}_{\mathrm{grid}},\allowbreak \mbox{$x_{\mathbb{P}}$}_{\mathrm{grid}}\)) is performed by multiplying the measured cross section by the ratio \(\sigma _{r}^{D(3)}(\beta_{\mathrm{grid}}, Q^{2}_{\mathrm{grid}}, \mbox{$x_{\mathbb{P}}$}_{\mathrm{grid}})/ \sigma _{r}^{D(3)}(\beta_{i}, Q^{2}_{i},\allowbreak \mbox{$x_{\mathbb{P}}$}_{i})\) calculated with the Next-to-Leading-Order (NLO) DPDF ‘ZEUS SJ’ parameterisation [15]. Most of the corrections are smaller than 10 %, while a few points undergo corrections up to ∼30 %. The procedure is checked by using the NLO DPDF ‘H1 Fit B’ parameterisation [5]. The resulting difference is treated as a procedural uncertainty on the combined cross section, as discussed in Sect. 2.3.2.
The cross sections from all the data sets are shown in Fig. 2 after correcting to 0.09<|t|<0.55 GeV2 and transforming to the common grid.
Reduced diffractive cross section \(x_{\mathbb {P}} \, \sigma _{r}^{D(3)}(\beta,Q^{2},x_{\mathbb {P}})\) for 0.09<|t|<0.55 GeV2 as a function of Q 2 for different values of β and \(\mbox{$x_{\mathbb{P}}$}\). The H1 ‘FPS HERA II’ [2], H1 ‘FPS HERA I’ [1], ZEUS ‘LPS 2’ [4] and ZEUS ‘LPS 1’ [3] data are presented. The inner error bars indicate the statistical uncertainties, while the outer error bars show the statistical and systematic uncertainties added in quadrature. Normalisation uncertainties are not included in the error bars of the individual measurements
2.2 Combination method
The combination is based on the χ 2 minimisation method described in [8] and used for previous combined HERA results [10]. The averaging procedure is based on the assumption that at a given kinematic point the H1 and ZEUS experiments are measuring the same cross section. The correlated systematic uncertainties are floated coherently. The procedure allows a model independent check of the data consistency and leads to a significant reduction of the correlated uncertainties.
For an individual data set, the χ 2 function is defined as:

Here μ i is the measured cross section value at a point i (β i , \(Q^{2}_{i}\), \(\mbox{$x_{\mathbb{P}}$}_{i}\)), and \(\gamma^{i}_{j}\), δ i,stat and δ i,uncor are the relative correlated systematic, relative statistical and relative uncorrelated systematic uncertainties, respectively. The vector m of quantities m i expresses the values of the combined cross section for each point i and the vector b of quantities b j expresses the shifts of the correlated systematic uncertainty sources, j, in units of the standard deviation. The relative uncertainties \(\gamma^{i}_{j}\) and δ i,uncor are multiplied by the combined cross section m i in order to take into account the fact that the correlated and uncorrelated systematic uncertainties are to a good approximation proportional to the central values (multiplicative uncertainties). On the other hand, the statistical uncertainties scale with the square root of the expected number of events, which is determined by the expected cross section, corrected for the biases due to the correlated systematic uncertainties. This is taken into account by the \(\delta^{2}_{i,\mathrm{stat}} \mu^{i} ( m^{i} - \sum_{j} \gamma^{i}_{j} m^{i} b_{j} )\) term.
If several analyses provide measurements at the same (β, Q 2, \(\mbox{$x_{\mathbb{P}}$}\)) values, a \(\chi^{2}_{\mathrm{tot}}\) is built [9] from the sum of the \(\chi^{2}_{\exp}\) of each data set, assuming the individual data sets to be statistically uncorrelated. The \(\chi ^{2}_{\mathrm{tot}}\) is minimised with respect to the m i and b j from each data set with an iterative procedure. The ratio \(\chi^{2}_{\min} / n_{\mathrm{dof}}\) is a measure of the consistency of the data sets. The number of degrees of freedom, n dof, is calculated as the difference between the total number of measurements and the number of averaged points. The uncertainties of the combined cross sections are evaluated from the \(\chi^{2}_{\min}+1\) criteria [8–10]. For some of the (β,Q 2,x ℙ) points there is only one measurement; however, because of the systematic uncertainty correlations such measurements may be shifted with respect to the original values, and the uncertainties may be reduced.
2.3 Uncertainties
2.3.1 Experimental systematic uncertainties and their correlations
The input cross sections are published with their statistical and systematic uncertainties. The statistical uncertainties correspond to δ i,stat in Eq. (3). The systematic uncertainties are classified as point-to-point correlated or point-to-point uncorrelated, corresponding to \(\gamma^{i}_{j}\) and δ i,uncor respectively, according to the information provided in the corresponding publications, as follows:
-
For the two older analyses, ‘FPS HERA I’ and ‘LPS 1’, only the total systematic uncertainties are given [1, 3], with no information on the single contributions and point-to-point correlations. For these two samples only the normalisation uncertainties (Table 2) are considered among the correlated systematics, while the remaining uncertainties are treated as uncorrelated.
-
For the sample ‘FPS HERA II’ all the systematic sources discussed in [2] are treated as point-to-point correlated. The hadronic energy scale uncertainty is taken as correlated separately for \(\mbox{$x_{\mathbb{P}}$}< 0.012\) and \(\mbox{$x_{\mathbb{P}}$}> 0.012\). This is to account for the different sensitivity to this systematic source for the two \(\mbox{$x_{\mathbb{P}}$}\) regions, where different methods are used to reconstruct the variable β, which are typically sensitive to different regions of the H1 central calorimeter. For x ℙ<0.012, where the mass M X of the hadronic final state is used to reconstruct β, the effect on the cross section due to the hadronic energy scale uncertainty is 4 % on average and reaches 6.7 %. For x ℙ>0.012, where β is reconstructed with the leading proton energy measured by the FPS, the cross section shows almost no sensitivity to the hadronic energy scale.
-
In the ‘LPS 2’ case, the total systematic uncertainties quoted in [4] are decomposed in correlated and uncorrelated following the prescriptions in [15]. They are symmetrised by taking the average of the positive and negative uncertainties.
In the H1 ‘FPS HERA II’ analysis, the systematic effects related to the leading proton measurement are considered as correlated and derived from the variation of the acceptance in the x ℙ and t bins when shifting the FPS energy scale and transverse momentum within the estimated uncertainties [2]. In the ZEUS ‘LPS 2’ case, the systematic uncertainty related to the leading proton measurement is dominated by the incomplete knowledge of the beam optics, of the position of the beamline aperture limitations and of the intrinsic transverse-momentum spread of the proton beam at the interaction point. The beam optics contribution is largely independent of the kinematic variables and therefore is taken as a normalisation uncertainty [4]. The other contributions are quantified by varying the cut on the distance of closest approach of the reconstructed proton track to the beampipe, and the value of the intrinsic transverse-momentum spread assumed in the simulation. They are treated as uncorrelated uncertainties.
All the H1 systematic uncertainties are treated as independent of the ZEUS uncertainties, and vice versa. Possible effects due to correlations between the two experiments are taken into account in the procedural uncertainties, discussed in Sect. 2.3.2. In total, 23 independent sources of correlated systematic uncertainties are considered, including the global normalisation for each sample. The full list is given in Table 3.
2.3.2 Procedural uncertainties
The following uncertainties on the combined cross sections due to the combination procedure are studied:
-
The χ 2 function given by Eq. (3) treats all systematic uncertainties as multiplicative, i.e. proportional to the expected central values. While this generally holds for the normalisation uncertainties, it may not be the case for the other uncertainties. To study the sensitivity of the average result to this issue, an alternative averaging is performed. Only the normalisation uncertainty and those related to the t reconstruction (the uncertainties on the ‘FPS HERA II’ proton p x , p y reconstruction and on the ‘FPS HERA II’ and ‘LPS 2’ t reweighting) which, for the reasons explained in Sect. 2.1.1, can affect the normalisation, are taken as multiplicative, while all other uncertainties are treated as additive. The difference between this average and the nominal result is of the order of 1 % on average and 6.4 % at most.
-
The H1 and ZEUS experiments use similar methods for detector calibration, apply similar reweighting to the Monte Carlo models used for the acceptance corrections and employ similar Monte Carlo models for QED radiative corrections, for the hadronic final state simulation and for background subtraction. Such similarities may lead to correlations between the measurements of the two experiments. Three systematic source are identified as the most likely to be correlated between the two experiments. These are the electromagnetic energy scale and the reweighting of the simulation in \(\mbox{$x_{\mathbb{P}}$}\) and t. Averages are formed for each of the 23 possible assumptions on the presence of correlations of these systematic uncertainties between the experiments and are compared with the nominal average for which all sources are assumed to be uncorrelated. The maximum difference between the nominal and the alternative averages is taken as an uncertainty. It is 1.4 % on average and 6.6 % at most, with no particular dependence on the kinematics.
-
The bias introduced by transforming the data to the common grid (see Sect. 2.1.2) is studied by using correction factors obtained from the NLO DPDF ‘H1 Fit B’ [5] parameterisation. For a few bins this changes the result by up to 8 %, but the average effect is 1.2 %.
-
The averaging procedure shifts the H1 hadronic energy scale at \(\mbox{$x_{\mathbb{P}}$}< 0.012\) by substantially more than 1σ of the nominal value (see Sect. 3). To study the sensitivity of the average result to the treatment of the uncertainty on the H1 hadronic energy scale, an alternative averaging is performed for which this uncertainty is considered as point-to-point uncorrelated. The difference between the alternative and nominal results is 0.9 % on average and reaches 8.7 % at low x ℙ.
For each combined data point the difference between the average obtained by considering each of the procedural effects and the nominal average is calculated and summed in quadrature. The effect of the procedural uncertainties is 2.9 % on average and 9.3 % at most.
3 Results
In the minimisation procedure, 352 data points are combined to 191 cross section measurements. The data show good consistency, with \(\chi^{2}_{\min} / n_{\mathrm{dof}} = 133 / 161\). The distributions of pulls [10], shown in Fig. 3 for each data set, exhibit no significant tensions. For data with no correlated systematic uncertainties pulls are expected to follow Gaussian distributions with zero mean and unit width. Correlated systematic uncertainties lead to narrowed pull distributions.
The effects of the combination on the correlated systematic uncertainties are summarised in Table 3 in terms of shifts in units of the original uncertainty and of values of the final uncertainties as percentages of the originals. The combined cross section values are given in Table 4 together with statistical, uncorrelated systematic, correlated systematic, experimental, procedural and total uncertainties. The experimental uncertainty is obtained as the quadratic sum of the statistical, uncorrelated systematic and correlated systematic uncertainties. The total uncertainty is defined as the quadratic sum of the experimental and procedural uncertainties. The full information about correlations can be found elsewhere.Footnote 3 As the global normalisations of the input data sets are fitted as correlated systematic uncertainties, the normalisation uncertainty on the combined data is included in the correlated systematic uncertainty given in Table 4.
Most of the 23 correlated systematic uncertainties shift by less than 0.5 σ of the nominal value in the averaging procedure. None of them shifts by substantially more than 1σ, with the exception of the hadronic energy scale for \(\mbox{$x_{\mathbb{P}}$}<0.012\) for the ‘FPS HERA II’ sample. Detailed studies show that there is a tension between the H1 ‘FPS HERA II’ and ZEUS ‘LPS 2’ data at low \(\mbox{$x_{\mathbb{P}}$}\); the average ratio of the H1 to ZEUS cross sections is above 1.0 for β>0.1 and below 0.9 for β<0.1. The H1 cross section uncertainty is positively correlated with the hadronic energy scale for β>0.1 and anti-correlated for β<0.1. As a result, the combination shifts the H1 cross sections for \(\mbox{$x_{\mathbb{P}}$}<0.012\) in the direction opposite to the cross section uncertainty due to the H1 hadronic energy scale. Conversely the combined statistical and uncorrelated uncertainty on the ZEUS data is much larger than the ZEUS hadronic energy scale uncertainty; consequently the fit is less sensitive to the ZEUS hadronic energy scale.
The influence of several correlated systematic uncertainties is reduced significantly for the combined result. Specifically, the uncertainty on the FPS proton energy measurement and the normalisation uncertainties on the ‘FPS HERA I’ and ‘LPS 1’ samples are reduced by more than a factor of 2. The H1 hadronic energy scale uncertainty for the low \(\mbox{$x_{\mathbb{P}}$}\)-range (\(\mbox{$x_{\mathbb{P}}$}<0.012\)) and the ZEUS hadronic energy scale uncertainty are reduced to around 55 % of those for the individual data sets. Since H1 and ZEUS use different reconstruction methods, similar systematic sources influence the measured cross section differently. Therefore, requiring the cross sections to be consistent at all (β, Q 2, \(\mbox{$x_{\mathbb{P}}$}\)) points constrains the systematic uncertainties efficiently. Due to this cross calibration effect, the combined measurement shows an average improvement of the experimental uncertainty of about 27 % with respect to the most precise single data set, ‘FPS HERA II’, though the latter data set contains five times more events than the second largest data set, ‘LPS 2’. The correlated part of the experimental uncertainty is reduced from about 69 % in [2] to 49 % in the combined measurement. The statistical, experimental and procedural uncertainties on the combined data are on average 11 %, 13.8 % and 2.9 %, respectively. The total uncertainty on the cross section is 14.3 % on average and is 6 % for the most precise points. The normalisation uncertainty, which contributes to the correlated systematic uncertainty on the combined data, is on average 4 %. The combined result extends the kinematic coverage with respect to the H1 and ZEUS measurements taken separately and the resulting cross section covers the region 2.5≤Q 2≤200 GeV2, 0.0018≤β≤0.816 and 0.00035≤x ℙ≤0.09, for 0.09<|t|<0.55 GeV2. Figure 4 shows the HERA combined cross section as a function of Q 2 at x ℙ=0.05, for different values of β, compared with the individual measurements used for the combination. The reduction of the total uncertainty of the HERA measurement compared to the input cross sections is visible. The derivative of the reduced cross section as a function of log(Q 2) decreases with β, a feature characteristic of the scaling violations in diffractive DIS, which are now measured precisely from proton-tagged as well as LRG data. Figures 5 and 6 show the HERA combined diffractive reduced cross sections as a function of Q 2 and \(\mbox{$x_{\mathbb{P}}$}\), respectively.
Reduced diffractive cross section \(x_{\mathbb {P}} \, \sigma _{r}^{D(3)}(\beta,Q^{2},x_{\mathbb {P}})\) for 0.09<|t|<0.55 GeV2 as a function of Q 2 for different values of β at \(\mbox{$x_{\mathbb{P}}$}= 0.05\). The HERA combined data are compared to the H1 and ZEUS data inputs to the averaging procedure. The error bars indicate the statistical and systematic uncertainties added in quadrature for the input measurements and the statistical, systematic and procedural uncertainties added in quadrature for the combined points. Normalisation uncertainties are not included in the error bars of the individual measurements, whereas they are included in the error bars of the combined points
HERA combined reduced diffractive cross section \(x_{\mathbb {P}} \, \sigma_{r}^{D(3)}(\beta,Q^{2},x_{\mathbb {P}})\) for 0.09<|t|<0.55 GeV2 as a function of Q 2 for different values of β and \(\mbox{$x_{\mathbb{P}}$}\). The error bars indicate the statistical, systematic and procedural uncertainties added in quadrature. The normalisation uncertainty is included
HERA combined reduced diffractive cross section \(x_{\mathbb {P}} \, \sigma_{r}^{D(3)}(\beta,Q^{2},x_{\mathbb {P}})\) for 0.09<|t|<0.55 GeV2 as a function of \(\mbox{$x_{\mathbb{P}}$}\) for different values of β and Q 2. The error bars indicate the statistical, systematic and procedural uncertainties added in quadrature. The normalisation uncertainty is included
At low \(\mbox{$x_{\mathbb{P}}$}\lesssim0.01\), where the proton spectrometer data are free from proton dissociation contributions, the combined data provide the most precise determination of the absolute normalisation of the diffractive cross section.
4 Conclusions
The reduced diffractive cross sections, \(\sigma_{r}^{D(3)}(ep \to eXp)\), measured by the H1 and ZEUS Collaborations by using proton spectrometers to detect the leading protons are combined. The input data from the two experiments are consistent with a \(\chi^{2}_{\min} / n_{\mathrm{dof}} = 133 / 161\). The combination of the measurements results in more precise and kinematically extended diffractive DIS data in the t-range 0.09<|t|<0.55 GeV2. The total uncertainty on the cross section measurement is 6 % for the most precise points. The combined data provide the most precise determination of the absolute normalisation of the ep→eXp cross section.
Notes
The pseudo-rapidity is defined as η=−lntanθ/2 where the polar angle θ is measured with respect to the proton beam direction.
The smallest kinematically accessible value of |t| is denoted as |t min|.
The combined data together with the full correlation information are provided at the URL. http://www.desy.de/h1zeus
References
A. Aktas et al. (H1 Collaboration), Eur. Phys. J. C 48, 749 (2006)
A. Aktas et al. (H1 Collaboration), Eur. Phys. J. C 71, 1578 (2011)
S. Chekanov et al. (ZEUS Collaboration), Eur. Phys. J. C 38, 43 (2004)
S. Chekanov et al. (ZEUS Collaboration), Nucl. Phys. B 816, 1 (2009)
A. Aktas et al. (H1 Collaboration), Eur. Phys. J. C 48, 715 (2006)
F.D. Aaron et al. (H1 Collaboration), Eur. Phys. J. C 72, 2074 (2012)
P. Newman, M. Ruspa, arXiv:0903.2957
A. Glazov, AIP Conf. Proc. 792, 237 (2005)
F.D. Aaron et al. (H1 Collaboration), Eur. Phys. J. C 63, 625 (2009)
F.D. Aaron et al. (H1 and ZEUS Collaborations), J. High Energy Phys. 1001, 109 (2010)
I. Abt et al. (H1 Collaboration), Nucl. Instrum. Methods Phys. Res. A 386, 310 (1997)
I. Abt et al. (H1 Collaboration), Nucl. Instrum. Methods Phys. Res. A 386, 348 (1997)
R.D. Appuhn et al. (H1 SPACAL Group), Nucl. Instrum. Methods Phys. Res. A 386, 397 (1997)
U. Holm (ed.) (ZEUS Collaboration), The ZEUS detector. Status Report (unpublished), DESY, 1993. Available on http://www-zeus.desy.de/bluebook/bluebook.html
S. Chekanov et al. (ZEUS Collaboration), Nucl. Phys. B 831, 1 (2010)
Acknowledgements
We are grateful to the HERA machine group whose outstanding efforts have made these experiments possible. We appreciate the contributions to the construction and maintenance of the H1 and ZEUS detectors of many people who are not listed as authors. We thank our funding agencies for financial support, the DESY technical staff for continuous assistance and the DESY directorate for their support and for the hospitality they extended to the non-DESY members of the collaborations.
Author information
Authors and Affiliations
Consortia
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
The H1 and ZEUS Collaborations., Aaron, F.D., Abramowicz, H. et al. Combined inclusive diffractive cross sections measured with forward proton spectrometers in deep inelastic ep scattering at HERA. Eur. Phys. J. C 72, 2175 (2012). https://doi.org/10.1140/epjc/s10052-012-2175-y
Received:
Revised:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-012-2175-y