Production of exclusive dijets in diffractive deep inelastic scattering at HERA

Abstract

Production of exclusive dijets in diffractive deep inelastic $e^\pm p$ scattering has been measured with the ZEUS detector at HERA using an integrated luminosity of 372 pb$^{-1}$. The measurement was performed for $\gamma ^{*}$–p centre-of-mass energies in the range $90< W < {250}\,{\mathrm{GeV}}$ and for photon virtualities $Q^2 > {25}\,{\mathrm{GeV}^{2}}$. Energy flows around the jet axis are presented. The cross section is presented as a function of $\beta$ and $\phi$, where $\beta =x/x_\mathrm{I\!P}$, x is the Bjorken variable and $x_\mathrm{I\!P}$ is the proton fractional longitudinal momentum loss. The angle $\phi$ is defined by the $\gamma ^{*}$–dijet plane and the $\gamma ^{*}$–$e^\pm$ plane in the rest frame of the diffractive final state. The $\phi$ cross section is measured in bins of $\beta$. The results are compared to predictions from models based on different assumptions about the nature of the diffractive exchange.

1 Introduction

The first evidence for exclusive dijet production at high-energy hadron colliders was provided by the CDF experiment at the Fermilab Tevatron $p\bar{p}$ collider [1] and had an important impact on theoretical calculations of exclusive Higgs boson production at the Large Hadron Collider. This paper describes the first measurement of exclusive dijet production in high energy electron¹–proton scattering. A quantitative understanding of the production of exclusive dijets in lepton–hadron scattering can improve the understanding of more complicated processes like the exclusive production of dijets in hadron–hadron scattering [2] or in lepton–ion scattering at a future eRHIC accelerator [3].

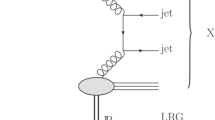
A schematic view of the diffractive production of exclusive dijets, $e + p \rightarrow e+ \mathrm {jet}1 + \mathrm {jet}2 + p$, is shown in Fig. 1. In this picture, electron–proton deep inelastic scattering (DIS) is described in terms of an interaction between the virtual photon, $\gamma ^{*}$, and the proton, which is mediated by the exchange of a colourless object called the Pomeron ($\mathrm{I\!P}$). This process in the $\gamma ^{*}$–$\mathrm{I\!P}$ centre-of-mass frame is presented in Fig. 2, where the lepton and jet planes are marked. The lepton plane is defined by the incoming and scattered electron momenta. The jet plane is defined by the jet momenta, which are always back-to-back, and the virtual photon momentum. The angle between these planes is labelled $\phi$. The jet polar angle is defined with respect to the virtual photon momentum and called $\theta$.

Fig. 1

Schematic view of the diffractive production of exclusive dijets in electron–proton DIS

Fig. 2

Definition of planes and angles in the $\gamma ^{*}$–$\mathrm{I\!P}$ centre-of-mass system. The lepton plane is defined by the $\gamma ^{*}$ and e momenta. The jet plane is defined by the $\gamma ^{*}$ and dijet directions. The angle $\phi$ is the angle between these two planes. The jet polar angle, $\theta$, is the angle between the directions of the jets and $\gamma ^{*}$

The production of exclusive dijets in DIS is sensitive to the nature of the object exchanged between the virtual photon and the proton. Calculations of the single-differential cross section of dijet production as a function of $\phi$ in $k_t$-factorisation [4] and collinear factorisation [5] have shown that, when the quark and antiquark jets are indistinguishable, the cross section is proportional to $1 + A(p_{T,\mathrm{jet}}) \cos 2\phi$, where $p_{T,\mathrm{jet}}$ is the jet transverse momentum. It was pointed out for the first time by Bartels et al. [4, 6] that the parameter A is positive if the quark–antiquark pair is produced via the interaction of a single gluon with the virtual photon and negative if a system of two gluons takes part in the interaction. The absolute value of the A parameter is expected to increase as the transverse momentum of the jet increases.

The production of exclusive dijets is also sensitive to the gluon distribution in the proton and is a promising reaction to probe the off-diagonal (generalised [7]) gluon distribution. The off-diagonal calculations predict a larger cross section compared to calculations based on conventional gluon distributions. In this context, the exclusive production of dijets is a complementary process to the exclusive production of vector mesons which has been extensively studied at HERA[8–16].

This paper describes the measurement of differential cross sections as a function of $\beta$ and in bins of $\beta$ as a function of $\phi$. The former quantity is defined as $\beta =x/x_\mathrm{I\!P}$, where x is the Bjorken variable and $x_\mathrm{I\!P}$ is the fractional loss of proton longitudinal momentum. The results of this analysis are compared to predictions from the Two-Gluon-Exchange model [6, 17] and the Resolved-Pomeron model of Ingelman and Schlein [18].

2 Experimental set-up

A detailed description of the ZEUS detector can be found elsewhere [19]. A brief outline of the components that are most relevant for this analysis is given below.

In the kinematic range of the analysis, charged particles were tracked in the central tracking detector (CTD) [20–22] and the microvertex detector (MVD) [23]. These components operated in a magnetic field of 1.43 T provided by a thin superconducting solenoid. The CTD consisted of 72 cylindrical drift-chamber layers, organised in nine superlayers covering the polar-angle² region $15^{\circ }<\theta < 164^{\circ }$. The MVD silicon tracker consisted of a barrel (BMVD) and a forward (FMVD) section. The BMVD contained three layers and provided polar-angle coverage for tracks from $30^{\circ }$ to $150^{\circ }$. The four-layer FMVD extended the polar-angle coverage in the forward region to $7^{\circ }$. After alignment, the single-hit resolution of the MVD was 24 $\upmu \mathrm{m}$. The transverse distance of closest approach (DCA) of tracks to the nominal vertex in X–Y was measured to have a resolution, averaged over the azimuthal angle, of $(46 \oplus 122 / p_{T}) \upmu \mathrm{m}$, with $p_{T}$ in $\mathrm{GeV}$. For CTD–MVD tracks that pass through all nine CTD superlayers, the momentum resolution was $\sigma (p_{T})/p_{T} = 0.0029 p_{T} \oplus 0.0081 \oplus 0.0012/p_{T}$, with $p_{T}$ in $\mathrm{GeV}$.

The high-resolution uranium–scintillator calorimeter (CAL) [24–27] consisted of three parts: the forward (FCAL), the barrel (BCAL) and the rear (RCAL) calorimeters. Each part was subdivided transversely into towers and longitudinally into one electromagnetic section (EMC) and either one (in RCAL) or two (in BCAL and FCAL) hadronic sections (HAC). The smallest subdivision of the calorimeter was called a cell. The CAL energy resolutions, as measured under test-beam conditions, were $\sigma (E)/E=0.18/\sqrt{E}$ for electrons and $\sigma (E)/E=0.35/\sqrt{E}$ for hadrons, with E in $\mathrm{GeV}$.

The position of electrons scattered at small angles to the electron beam direction was determined with the help of RHES [28], which consisted of a layer of approximately 10, 000 $(2.96\times 3.32\,\mathrm{cm^2})$ silicon-pad detectors inserted in the RCAL at a depth of 3.3 radiation lengths.

The luminosity was measured using the Bethe–Heitler reaction $ep\,\rightarrow \, e\gamma p$ by a luminosity detector which consisted of independent lead–scintillator calorimeter [29–31] and magnetic spectrometer [32] systems. The fractional systematic uncertainty on the measured luminosity was 2 % [33].

3 Monte Carlo simulation

Samples of Monte Carlo (MC) events were generated to determine the response of the detector to jets of hadrons and the correction factors necessary to obtain the hadron-level jet cross sections. The hadron level is defined in terms of hadrons with lifetime $\ge$ 10 ps. The generated events were passed through the GEANT 3.21-based [34] ZEUS detector- and trigger-simulation programs [19]. They were reconstructed and analysed by the same program chain used for real data.

In this analysis, the model SATRAP [35, 36] as implemented in the RAPGAP [37] program was used to generate diffractive events. SATRAP is a colour-dipole model [38] which includes saturation effects. It describes DIS as a fluctuation of the virtual photon into a quark–antiquark dipole which scatters off the proton. The CTEQ5D [39] parameterisation was used to describe the proton structure. Hadronisation was simulated with the JETSET 7.4 [40, 41] program which is based on the Lund string model [42]. Radiative corrections for initial- and final-state electromagnetic radiation were taken into account with the HERACLES 4.6.6 [43–45] program. The diffractive MC was weighted in order to describe the measured distributions (see Sect. 5).

The proton-dissociation process was modelled using the EPSOFT [46, 47] generator. The production of dijets is not implemented in EPSOFT. Therefore dijets with proton dissociation were simulated with SATRAP, where the intact proton was replaced with a dissociated proton. Such a solution is based on the factorisation hypothesis which assumes that the interaction at the lepton and at the proton vertex factorises. The factorisation hypothesis has been verified for diffractive processes in ep collisions at HERA [48–51].

To estimate the non-diffractive DIS background, a sample of events was generated using HERACLES 4.6.6 [43–45] with DJANGOH 1.6 [52] interfaced to the hadronisation process. The QCD cascade was simulated using the colour-dipole model (CDM) [53–55] as implemented in ARIADNE 4.08 [56, 57].

To estimate the background of diffractive dijet photoproduction, a sample of events was generated using the PYTHIA 6.2 [58] program with the CTEQ4L [59] parton density function of the proton. The hadronisation process was simulated with JETSET 7.4.

For the model predictions, events were generated using RAPGAP where both the Resolved-Pomeron model and the Two-Gluon-Exchange model are implemented. The hadronisation was simulated with ARIADNE. The generated events do not include proton dissociation.

In this analysis, the number of diffractive MC events was normalised to the number of events observed in the data after all selection cuts and after subtraction of background from photoproduction and non-diffractive DIS. The numbers of background events were estimated based on generator cross sections.

4 Event selection and reconstruction

This analysis is based on data collected with the ZEUS detector at the HERA collider during the 2003–2007 data-taking period, when electrons or positrons of $27.5\,{\mathrm{GeV}}$ were collided with protons of $920\,{\mathrm{GeV}}$ at a centre-of-mass energy of $\sqrt{s}=318\,{\mathrm{GeV}}$. The data sample corresponds to an integrated luminosity of 372 pb$^{-1}$.

A three-level trigger system was used to select events online [19, 60]. At the first level, only coarse calorimeter and tracking information were available. Events consistent with diffractive DIS were selected using criteria based on the energy and transverse energy measured in the CAL. At the second level, charged-particle tracks were reconstructed online by the ZEUS global tracking trigger [61, 62], which combined information from the CTD and MVD. These online tracks were used to reconstruct the interaction vertex and to reject non-ep background. At the third level, neutral current DIS events were accepted on the basis of the identification of a scattered electron candidate using localised energy depositions in the CAL.

The scattered electron was identified using a neural-network algorithm [63]. The reconstruction of the scattered electron variables was based on the information from the CAL. The energy of electrons hitting the RCAL was corrected for the presence of dead material using the rear presampler detector [64]. Energy-flow objects (EFOs [65, 66]) were used to combine the information from the CAL and the CTD.

4.1 DIS selection

A clean sample of DIS events with a well-reconstructed electron was selected by the following criteria:

• the electron candidate was reconstructed with calorimeter information and was required to have energy reconstructed with double-angle method [67], $E_e^\prime > 10\,{\mathrm{GeV}}$ and, if reconstructed in the CTD acceptance region, also an associated track;

• the reconstructed position of the electron candidate in the CAL was required to be outside the regions of CAL in which the scattered electron might have crossed a substantial amount of inactive material or regions with poor acceptance;

• the vertex position along the beam axis was required to be in the range $|Z_{\mathrm{vtx}}| < 30\,\mathrm{cm}$;

• $E_{\mathrm {had}}/E_{\mathrm {tot}} > 0.06$, where $E_{\mathrm {had}}$ is the energy deposited in the hadronic part of the CAL and $E_{\mathrm {tot}}$ is the total energy in the CAL; this cut removes purely electromagnetic events;

• $45< (E - P_Z) < 70\,{\mathrm{GeV}}$, where E is the total energy, $E = \sum _i{E_i}$, $P_{Z} = \sum _i{p_{Z,i}}$ and $p_{Z,i} = E_i \cos \theta _{i}$, where the sums run over all EFOs including the electron; this cut removes events with large initial-state radiation and further reduces the background from photoproduction.

Events were accepted if $Q^2 > 25\,{\mathrm{GeV}^{2}}$ and $90< W < 250\,{\mathrm{GeV}}$. In this analysis, the photon virtuality, $Q^2$, and the total energy in the virtual-photon–proton system, W, were reconstructed using the double-angle method which was found to be more precise than other reconstruction methods in the kinematic region of this measurement [68]. The inelasticity, y, which was reconstructed with the electron method was limited to the range $0.1< y < 0.64$. The limits come from the selection criteria applied to other variables reconstructed with the double-angle method. The use of two methods to reconstruct DIS kinematic quantities, increases the purity if the sample.

4.2 Diffractive selection

Diffractive events are characterised by a small momentum exchange at the proton vertex and by the presence of a large rapidity gap (LRG) between the proton beam direction and the hadronic final state. Diffractive DIS events were selected by the following additional criteria:

• $x_\mathrm{I\!P} < 0.01$, where $x_\mathrm{I\!P}$ is the fraction of the proton momentum carried by the diffractive exchange, calculated according to the formula $x_\mathrm{I\!P} = \left( Q^2 + M_X^2 \right) / \left( Q^2+W^2 \right)$, in which $M_X$ denotes the invariant mass of the hadronic state recoiling against the leading proton and was reconstructed from the EFOs excluding the scattered electron candidate; this cut reduces the non-diffractive background;

• $\eta _\mathrm{max} < 2$, where $\eta _\mathrm{max}$ is defined as the pseudorapidity of the most forward EFO, with an energy greater than $E_{\mathrm {EFO}}= 400\,\mathrm{MeV}$; this cut ensures the presence of a LRG in the event;

• $M_X > 5\,{\mathrm{GeV}}$; this cut removes events with resonant particle production and ensures that there is enough energy in the system to create two jets with high transverse momenta.

The origin of exclusive dijet events in diffraction is not unique. The most natural contribution comes from exclusive production of quark–antiquark pairs, but other contributions, in particular from quark–antiquark–gluon, are not excluded. It is predicted [17] that the ratio of $q\overline{q}$ to $q\overline{q}g$ production changes significantly with the parameter $\beta$ (or $M_X$) in contrast to other kinematic variables. To get insight into the origin of exclusive diffractive dijet events, the data were analysed as a function of $\beta$, calculated according to $\beta = Q^2/\left( Q^2 + M_X^2 \right)$.

4.3 Jet selection

The $k_T$-cluster algorithm known as the Durham jet algorithm [69, 70], as implemented in the FastJet package [71], was used for jet reconstruction. Exclusive jets are of interest in this analysis, so the algorithm was used in “exclusive mode” i.e. each object representing a particle or a group of particles had to be finally associated to a jet. The algorithm is defined in the following way: first all objects were boosted to the $\gamma ^{*}$–$\mathrm{I\!P}$ rest frame. Then, the relative distance of each pair of objects, $k_{T\,ij}^2$, was calculated as

$$\begin{aligned} k_{T\,ij}^2 = 2\, \mathrm{min}(E_i^2,E_j^2)(1-\cos \theta _{ij}), \end{aligned}$$

where $\theta _{ij}$ is the angle between objects i and j and $E_i$ and $E_j$ are the energies of the objects i and j. The minimum $k_{T\,ij}^2$ was found and if

$$\begin{aligned} y_{ij}= \frac{k_{T\,ij}^2}{M_X^2} < y_{\mathrm{cut}} \end{aligned}$$

objects i and j were merged. The merging of the 4-vectors was done using the recombination “E-scheme”, with simple 4-vector addition, which is the only Lorentz invariant scheme [72]. It causes the cluster objects to acquire mass and the total invariant mass, $M_X$, coincides with the invariant mass of the jet system. The clustering procedure was repeated until all $y_{ij}$ values exceeded a given threshold, $y_{\mathrm{cut}}$, and all the remaining objects were then labelled as jets. Applied in the centre-of-mass rest frame, this algorithm produces at least two jets in every event. The same jet-search procedure was applied to the final-state hadrons for simulated events.

Figure 3 shows the measured fractions for 2, 3 and 4 jets in the event as a function of the jet resolution parameter, $y_{\mathrm{cut}}$ [69], in the region $0.01< y_{\mathrm{cut}}<0.25$. The rate of dijet reconstruction varies from 70 % at $y_{\mathrm{cut}}=0.1$ to 90 % at $y_{\mathrm{cut}}=0.2$. The measured jet fractions were compared to jet fractions predicted by SATRAP after reweighting of kinematic variables as described in Sect. 5. SATRAP provides a good description of the measurement. Jets were reconstructed with a resolution parameter fixed to $y_{\mathrm{cut}} = 0.15$. Events with exactly two reconstructed jets were selected.

Fig. 3

The probability of finding two, three and four jets in the final state as a function of the $y_{\rm cut}$ parameter (see text). Data are shown as full dots. Statistical errors are smaller than the dot size. Predictions of SATRAP are shown as histograms. The distributions are not corrected for detector effects

Finally, a lower limit of the jet transverse momenta in the centre-of-mass frame was required, $p_{T,\mathrm{jet}}> 2\,{\mathrm{GeV}}$. This value was chosen as a compromise between having a value of $p_{T,\mathrm{jet}}$ large enough so that perturbative calculations are still valid and on the other hand small enough so that a good statistical accuracy can be still obtained.

5 Comparison between data and Monte Carlo

Data and Monte Carlo predictions for several kinematic and jet variables were compared at the detector level. The MC event distributions which had been generated with SATRAP were reweighted in a multidimensional space with respect to: inelasticity y, jet pseudorapidity $\eta _\mathrm{jet}$, $p_{T,\mathrm{jet}}, M_X, Q^2, \beta$ and $x_\mathrm{I\!P}$. In addition, the prediction of $q \bar{q}$ production from Bartels et al. [6] was used for reweighting in $\phi$.

The background originating from diffractive dijet photoproduction and non-diffractive dijet production was estimated from Monte Carlo simulations as described in Sect. 3. The background from beam-gas interactions and cosmic-ray events was investigated using data taken with empty proton-beam bunches and estimated to be negligible.

For each of the distributions presented in this section, all selection criteria discussed above were applied except the cut on the shown quantity. The estimated background, normalised to the luminosity of this analysis, is also shown.

Figure 4 shows the variables characterising the DIS events, $Q^2$, $E_e^\prime$, y, W, $E-P_Z$ and $Z_{\mathrm{vtx}}$, while Fig. 5 shows the variables characterising the diffractive events, $x_\mathrm{I\!P}$, $M_\mathrm{X}$, $\beta$ and $\eta _\mathrm{max}$. Besides exclusive events, the data contains proton dissociation, $e + p \rightarrow e + \mathrm{jet}{}1 + \mathrm{jet}{2} + Y$, for which the particles stemming from the process of dissociation disappear undetected in the proton beam hole. Except for $\eta _{\mathrm{max}}$, the events with proton dissociation are expected to yield the same shape of the distributions as the exclusive dijet events, changing only the normalisation (according to the factorisation hypothesis, see Sect. 3), and are not shown separately. These events were not treated as a background. The experimental distributions were compared to the sum of the background distributions and the SATRAP MC. The background was normalised to the luminosity and the SATRAP MC to the number of events remaining in the data after background subtraction. The $\eta _{\mathrm{max}}$ distribution (Fig. 5d) shows the distribution of events with proton dissociation which was determined separately as described in Sect. 6. In Fig. 5d, the $\eta _{\mathrm{max}}$ distribution is compared to the normalised sum of three contributions including that of events with proton dissociation. All data distributions, except for y and $\eta _\mathrm{max}$, are reasonably well described by the MC predictions. Most of the difference between data and MC in the y distribution is outside the analysed region ($y > 0.64$). The incorrect y description at the cut value was taken into account in the systematic uncertainty which was determined by varying the cut. The shift in the $\eta _{\mathrm{max}}$ distribution is accounted for in the systematic uncertainty of the proton dissociation background (see Sect. 6).

Fig. 4

Comparison between data (dots) and the sum (line) of the SATRAP MC and background contributions (shaded), where events with a dissociated proton are not treated as background, for kinematic variables: a exchanged photon virtuality, $Q^2$, b scattered electron energy, $E_{e}^\prime$, c inelasticity, y, d invariant mass of the $\gamma ^{*}$–p system, W, e the quantity $E-P_Z$ and f the Z-coordinate of the interaction vertex. The error bars represent statistical errors (generally not visible). The background was normalised to the luminosity and the SATRAP MC to the number of events remaining in the data after background subtraction. All selection cuts are applied except for the cut on the variable shown in each plot

Fig. 5

Comparison between data (dots) and the sum (line) of the SATRAP MC and background contributions (dark histogram), where events with a dissociated proton were not treated as background, for the kinematic variables of the diffractive process: a fraction loss in the longitudinal momentum of the proton, $x_\mathrm{I\!P}$, b the invariant mass of the diffractive system, $M_\mathrm{X}$, c the Bjorken-like variable, $\beta$, and d the pseudorapidity of the most forward EFO, $\eta _\mathrm{max}$. In d, the component from events with a dissociated proton is also shown (light histogram). Other details as for Fig. 4

In Fig. 6, jet properties in the $\gamma ^{*}$–$\mathrm{I\!P}$ centre-of-mass system are presented: the distributions of the jet angles $\theta$ and $\phi$, the number of EFOs clustered into the jets and the jet transverse momentum $p_{T,\mathrm{jet}}$. All distributions are reasonably well described by the sum of SATRAP events and the background distribution. The difference between data and MC for values of $\phi$ close to 0 is not expected to affect the result of unfolding in this quantity (see Sect. 7).

Fig. 6

Comparison between data and MC for variables characterising the jet properties in the $\gamma ^{*}$–$\mathrm{I\!P}$ rest frame: a the azimuthal angle, $\phi$, b the polar angle, $\theta$, c the number of EFOs clustered into a jet and d the jet transverse momentum, $p_{T,\mathrm{jet}}$. Other details as for Fig. 4

Jets reconstructed in the $\gamma ^{*}$–$\mathrm{I\!P}$ rest frame were transformed back to the laboratory (LAB) system. In Fig. 7 the distributions of the jet pseudorapidity and the jet transverse energy are shown in the laboratory system separately for higher- and lower-energy jets. They are well described by the predicted shape.

Fig. 7

Comparison between data and MC for variables characterising the properties of the higher and the lower energy jets in the LAB frame: a and b the jet pseudorapidity, c and d the jet transverse energy. Other details as for Fig. 4

The jet algorithm used allows the association of the individual hadrons with a unique jet on an event-by-event basis. To study the topology of the jets, the energy flow of particles around the jet axes was considered in both the centre-of-mass system and the laboratory system. In this study, $\Delta \eta$ and $\Delta \varphi$ denote the differences between the jet axis and, respectively, the pseudorapidity and the azimuthal angle of the EFOs in the event. In Fig. 8 the energy flows around the axis of the reference jet, that is the jet with positive Z-component of the momentum, are shown in the $\gamma ^{*}$–$\mathrm{I\!P}$ centre-of-mass system. The corresponding distributions in the laboratory system are presented in Fig. 9. It is observed that energy flows around the reference jet axis are well reproduced by the SATRAP MC. As expected, the jets are produced back-to-back in the $\gamma ^{*}$–$\mathrm{I\!P}$ centre-of-mass system, and are quite broad. However, in the laboratory system, most of their energy is concentrated within a cone of radius approximately equal to one unit in the $\eta$–$\varphi$ plane with distance defined as $r = \sqrt{\Delta \eta ^2 + \Delta \varphi ^2}$.

Fig. 8

The energy flow in the $\gamma ^{*}$–$\mathrm{I\!P}$ rest frame around the jet axis, averaged over all selected dijet events, is shown as a function of distances in azimuthal angle and pseudorapidity ($\Delta \varphi$ and $\Delta \eta$). In both cases, the energy flow is integrated over the full available range of the other variable. Data for both jets are shown as full dots. Statistical uncertainties are smaller than point markers. The energy flow of EFOs belonging to the reference jet only are shown as full squares, where the reference jet was chosen as the jet with positive $p_Z$ momentum. Predictions of the SATRAP MC are shown as histograms

Fig. 9

The energy flow in the laboratory frame, around the jet axis, averaged over all selected dijet events, is shown as a function of distances in azimuthal angle and pseudorapidity ($\Delta \varphi$ and $\Delta \eta$). In both cases, the energy flow is integrated over the full available range of the other variable. Data for both jets are shown as full dots. Statistical uncertainties are smaller than point markers. The energy flow of EFOs belonging to the reference jet only are shown as full squares, where the reference jet was chosen as the jet with positive $p_Z$ momentum. Predictions of the SATRAP MC are shown as histograms

The quality of the description of the data by the MC gives confidence in the use of the MC for unfolding differential cross sections to the hadron level (see Sect. 7).

6 Estimate of dijet production with proton dissociation

The contribution of events with a detected dissociated proton system is highly suppressed due to the nominal selection cuts applied to the data, i.e. by requiring exactly two jets, $x_{\mathrm{I\!P}}<0.01$ and $\eta _{\mathrm{max}}<2$, and has been considered to be negligible. However, the contribution of proton-dissociative events, where the proton-dissociative system escapes undetected, is not negligible. It was estimated using EPSOFT, after further tuning of the distribution of the mass of the dissociated proton system, $M_Y$. The simulation shows that due to the acceptance of the calorimeter, determined by the detector geometry, a dissociated proton system of mass smaller than about 6 ${\mathrm{GeV}}$ stays undetected.

In order to estimate the amount of dissociated proton events, a sample enriched in such events was selected as follows. Kinematic variables and jets were reconstructed from the EFOs in the range $\eta <2$. All selection cuts described in Sect. 4, except the $\eta _{\mathrm{max}}$ cut, were then applied. In order to suppress non-diffractive contributions to the dijet sample, events with EFOs in the range $2< \eta <3.5$ were rejected. The remaining sample of events with EFOs in the range $\eta >3.5$ consisted almost entirely of diffractive dijets with a detected dissociated proton system. From the comparison of the energy sum of all EFOs with $\eta > 3.5$ between data and simulated events, the following parameterisation of the $M_Y$ distribution was extracted:

$$\begin{aligned} \frac{ \mathrm{d}\sigma _{\gamma p\rightarrow \mathrm{jet}_1 \mathrm{jet}_2 Y}}{\mathrm{d}M_Y^2} \propto {\frac{1}{M_Y^{1.4}}}. \end{aligned}$$

The fraction of simulated events with proton dissociation was determined by a fit to the distribution of $\eta _{\mathrm{max}}$ shown in Fig. 5d.

The systematic uncertainty of this fraction was estimated in the following steps:

• the shape of the $M_Y$ distribution was varied by changing the exponent by $\pm 0.6$, because in this way the $\chi ^2$ of the comparison between data and EPSOFT simulation was raised by 1;

• the fit of the fraction was repeated taking into account a shift of $\eta _{\mathrm{max}}$ by $+0.1$ according to the observed shift between data and simulated events.

Both uncertainties were added in quadrature.

The fraction of events with $\eta _{\mathrm{max}}<2$ associated to the proton-dissociative system, which escaped undetected in the beam hole, was estimated to be $f_{\mathrm{pdiss}}= 45 \pm 4~\%\, \mathrm{(stat.)} \pm 15~\% \,\mathrm{(syst.)}$. No evidence was found that $f_{\mathrm{pdiss}}$ depends on $\phi$ or $\beta$. Therefore, in the following sections, the selected data sample was scaled by a constant factor correcting for proton-dissociative events.

7 Unfolding of the hadron-level cross section

An unfolding method was used to obtain hadron-level differential cross sections for production of dijets, reconstructed with jet-resolution parameter $y_{\mathrm{cut}}=0.15$, as a function of $\beta$ and $\phi$ in the following kinematic region:

• $Q^2> 25\,{\mathrm{GeV}^{2}}$;

• $90< W < 250\,{\mathrm{GeV}}$;

• $x_\mathrm{I\!P} < 0.01$;

• $M_X > 5\,{\mathrm{GeV}}$;

• $N_{\mathrm{jets}}=2$;

• $p_{T,\mathrm{jet}}> 2\,{\mathrm{GeV}}$.

The unfolding was performed by calculating a detector response matrix, which represents a linear transformation of the hadron-level two-dimensional distribution of $\phi$–$p_{T,\mathrm{jet}}$ or $\beta$–$p_{T,\mathrm{jet}}$ to a detector-level distribution. The response matrix was based on the weighted SATRAP MC simulation. It includes effects of limited detector and trigger efficiencies, finite detector resolutions, migrations from outside the phase space and distortions due to QED radiation. The unfolding procedure was based on the regularised inversion of the response matrix using singular value decomposition (SVD) as implemented in the TSVDUnfold package [73]. The implementation was prepared for one-dimensional problems and the studied two-dimensional distributions were transformed into one-dimensional distributions [68]. The regularisation parameter was determined according to the procedure suggested by the authors of the unfolding package.

The used unfolding method takes into account the imperfect hadron level MC simulation and corrects for it.

8 Systematic uncertainties

The systematic uncertainties of the cross sections were estimated by calculating the difference between results obtained with standard and varied settings for each bin of the unfolded distribution, except for the uncertainty on $f_{\mathrm{pdiss}}$, which was assumed to give a common normalisation uncertainty in all the bins.

The sources of systematic uncertainty were divided into two types. Those originating from detector simulation were investigated by introducing changes only to MC samples at the detector level, while the data samples were not altered. The following checks were performed:

• the energy scale of the calorimeter objects associated with the jet with the highest transverse momentum in the laboratory frame was varied by $\pm 5~\%$; the corresponding systematic uncertainty is in the range of $+2~\%,-8~\%$;

• the jet transverse momentum resolution was varied by $\pm 1~\%$, because in this way the $\chi ^2$ of the comparison of data to MC in the distribution of the jet transverse momentum was raised by 1.

Systematic effects originating from event-selection cuts were investigated by varying the criteria used to select events for both data and simulated events in the following ways:

• $Q^2>25 \pm 1.7\,{\mathrm{GeV}^{2}}$;

• $90 \pm 7.4\,{\mathrm{GeV}}< W < 250 \pm 8.4\,{\mathrm{GeV}}$;

• $0.1 \pm 0.04< y < 0.64 \pm 0.03$;

• $\mid Z_{\mathrm{vtx}} \mid < 30 \pm 5\,\mathrm{cm}$;

• $x_\mathrm{I\!P} < 0.01 \pm 0.001$;

• $\eta _{\mathrm{max}}< 2 \pm 0.2$;

• $M_X > 5 \pm 0.8\,{\mathrm{GeV}}$;

• $E_{\mathrm{EFO}} > 0.4 \pm 0.1\,{\mathrm{GeV}}$.

The uncertainty related to the $M_X$-cut variation is in the range of $\pm 5~\%$. The total uncertainty related to the event-selection cuts excluding the $M_X$ cut is smaller than $\pm 6~\%$. Uncertainties originating from the most significant sources are presented in Fig. 10.

Fig. 10

The most significant sources of systematic uncertainties for $\mathrm{d}\sigma /\mathrm{d}\beta$ and $\mathrm{d}\sigma /\mathrm{d}\phi$ in five $\beta$ ranges. Total systematic uncertainties and total uncertainties (systematic and statistical added in quadrature) are shown as shaded and dark-shaded bands

Positive and negative uncertainties were separately added in quadrature. The corresponding total systematic uncertainty is also shown in Fig. 10. The normalisation uncertainty of the cross section related to the luminosity (see Sect. 2) as well as to $f_{\mathrm{pdiss}}$ is not shown on the following figures but is included as a separate column in the tables of cross sections. The total uncertainties of the measured cross sections are dominated by the systematic component.

9 Cross sections

Cross sections were measured at the hadron level in the kinematic range described in Sect. 7. Backgrounds from diffractive photoproduction and non-diffractive dijet production were subtracted.

In order to calculate the cross sections for exclusive dijet production, the measured cross sections were scaled by a factor of $(1-f_{\mathrm{pdiss}})=0.55$ according to the estimate of the proton-dissociative background described in Sect. 6.

The values of the cross-sections $\mathrm{d}\sigma /\mathrm{d}\beta$ and $\mathrm{d}\sigma /\mathrm{d}\phi$ in five bins of $\beta$ are given in Tables 1 and 2 and shown in Fig. 11. The statistical uncertainties presented in the figures correspond to the diagonal elements of the covariance matrices, which are available in electronic format [74]. The $\mathrm{d}\sigma /\mathrm{d}\beta$ distribution is, due to the kinematics, restricted to the range $0.04<\beta < 0.92$. The $\mathrm{d}\sigma /\mathrm{d}\phi$ distribution is shown in five bins of $\beta$ in the range $0.04<\beta <0.7$. The cut at 0.7 excludes a region with a low number of events.

Table 1 Differential cross-section $\mathrm{d}\sigma /\mathrm{d}\beta$ in the kinematic range: $Q^2> 25\,{\mathrm{GeV}^{2}}$, $90< W < 250\,{\mathrm{GeV}}$, $x_\mathrm{I\!P} < 0.01$, $M_X > 5\,{\mathrm{GeV}}$ and $p_{T,\mathrm{jet}}> 2\,{\mathrm{GeV}}$. The statistical uncertainties are given by the diagonal part of the covariance matrix. Systematic uncertainties are explained in the text. The contribution from proton dissociation was subtracted. The uncertainty of the subtraction determines the uncertainty of the normalisation also given in the table

Table 2 Differential cross-section $\mathrm{d}\sigma /\mathrm{d}\phi$ in the kinematic range: $Q^2> 25\,{\mathrm{GeV}^{2}}$, $90< W < 250\,{\mathrm{GeV}}$, $x_\mathrm{I\!P} < 0.01$, $M_X > 5\,{\mathrm{GeV}}$ and $p_{T,\mathrm{jet}}> 2\,{\mathrm{GeV}}$. Statistical uncertainties are given by the diagonal elements of the covariance matrix. Systematic uncertainties are explained in the text. The contribution from proton dissociation was subtracted. The uncertainty of the subtraction determines the uncertainty of the normalisation given in the table

Fig. 11

Differential cross sections for exclusive dijet production: $\mathrm{d}\sigma /\mathrm{d}\beta$ (in log scale) and $\mathrm{d}\sigma /\mathrm{d}\phi$ (in linear scale) in five bins of $\beta$. Contributions from proton-dissociative dijet production were subtracted. The full line represents the fitted function proportional to $1+ A \cos 2\phi$. Statistical and systematic uncertainties were included in the fit. The total error bars show statistical and systematic uncertainties added in quadrature. The statistical uncertainties were taken from the diagonal elements of the covariance matrix. The systematic uncertainties do not include the uncertainty of the subtraction of the proton-dissociative contribution. This normalisation uncertainty is shown as a grey band only in the $\mathrm{d}\sigma /\mathrm{d}\beta$ distribution

The $\phi$ distributions show a significant feature: when going from small to large values of $\beta$, the shape varies and the slope of the angular distribution changes sign. The variation of the shape was quantified by fitting a function to the $\phi$ distributions including the full statistical covariance matrix and the systematic uncertainties, the latter by using the profile method [75]. The fitted function is predicted by theoretical calculations (see Sect. 1) to be proportional to ($1+A \cos 2\phi$). The data are well described by the fitted function. The resulting values of A are shown in Table 3 and Fig. 12. The parameter A decreases with increasing $\beta$ and changes sign around $\beta =0.4$.

Table 3 Results of the fit to the cross-section $\mathrm{d}\sigma /\mathrm{d}\phi$ in bins of $\beta$. The fitted function is proportional to $(1+A \cos 2\phi )$. The uncertainty includes both statistical and systematical contributions (see text)

Fig. 12

The shape parameter A as a function of $\beta$ resulting from the fits to $\mathrm{d}\sigma /\mathrm{d}\phi$ with a function proportional to $1+A \cos 2\phi$. The statistical and systematic uncertainties were included in the fit

10 Comparison with model predictions

The differential cross sections were compared to MC predictions for the Resolved-Pomeron model and the Two-Gluon-Exchange model. In the Resolved-Pomeron model [18], the diffractive scattering is factorised into a Pomeron flux from the proton and the hard interaction between the virtual photon and a constituent parton of the Pomeron. An example of such a process is shown in Fig. 13, where a $q \bar{q}$ pair is produced by a boson–gluon fusion (BGF) process associated with the emission of a Pomeron remnant. This model requires the proton diffractive gluon density as an input for the calculation of the cross section. The predictions considered in this article are based on the parameterisation of the diffractive gluon density obtained from fits (H1 2006 fits A and B) to H1 inclusive diffractive data [51]. The shape of the $\phi$ distribution is essentially identical in all models based on the BGF process, including both the Resolved-Pomeron and the Soft Colour Interactions (SCI) model [76].

Fig. 13

Diagram of diffractive boson–gluon fusion in the Resolved-Pomeron model

In the Two-Gluon-Exchange model [4–6, 17], the diffractive production of a $q \bar{q}$ pair is due to the exchange of a two-gluon colour-singlet state. The process is schematically shown in Fig. 14. The $q \bar{q}$ pair hadronises into a dijet final state. For large diffractive masses, i.e. at low values of $\beta$, the cross section for the production of a $q \bar{q}$ pair with an extra gluon is larger than that of the $q \bar{q}$ production. The diagram of this process is shown in Fig. 15. The $q\bar{q}g$ final state also contributes to the dijet event sample if two of the partons are not resolved by the jet algorithm (see Sect. 4.3).

Fig. 14

Example diagram of $q\bar{q}$ production in the Two-Gluon-Exchange model

Fig. 15

Example diagram of $q\bar{q}g$ production in the Two-Gluon-Exchange model

The $q\bar{q}$ pair production was calculated to second order in QCD, using the running strong-interaction coupling constant $\alpha _s(\mu )$ with the scale $\mu =p_{T}\sqrt{1+Q^2/M_X^2}$ [4, 6], where $p_{T}$ denotes the transverse momentum of the quarks in the $\gamma ^{*}$–$\mathrm{I\!P}$ rest frame with respect to the virtual photon momentum and $M_X$ is the invariant mass of the diffractive system. The prediction was calculated with a cut on the transverse momentum of the quarks, $p_T > 1\,{\mathrm{GeV}}$. The cross section is proportional to the square of the gluon density of the proton, $g(x_\mathrm{I\!P},\mu ^2)$

$$\begin{aligned} d\sigma \propto \left[ \frac{\alpha _s(\mu )}{p_{T}^2}x_\mathrm{I\!P}g(x_\mathrm{I\!P},\mu ^2) \right] ^2. \end{aligned}$$

The cross section for the $q\bar{q}g$ final state was calculated taking into account that it is proportional to the square of the gluon density of the proton, $g(x_\mathrm{I\!P},\hat{k}_T^2)$, at a scale $\hat{k}_T^2$, which effectively involves the transverse momenta of all three partons. For the calculation of the cross section, a fixed value of $\alpha _s=0.25$ [17] and the GRV [77] parameterisation of the gluon density were used and the same cut was applied on the transverse momentum of all partons: $p_{T,\mathrm {parton}} > p_{T,\mathrm{cut}}$ with the value adjusted to the data (see Sect. 10.1). In contrast to $q\bar{q}$ production, the exclusive dijet cross section calculated for the $q\bar{q}g$ final state is sensitive to the parton-level cut $p_{T,\mathrm{cut}}$. This is a consequence of the fact that two of the partons form a single jet.

10.1 Contribution of the $\varvec{q \bar{q}}$ dijet component in the prediction of the Two-Gluon-Exchange model

In the Two-Gluon-Exchange model, the $\phi$ distribution predicted for $q \bar{q}$ and $q\bar{q} g$ have different shapes. This allows the ratio $R_{q \bar{q}} = \sigma (q \bar{q})/\sigma (q \bar{q} + q \bar{q} g)$ to be determined by studying the measured $\phi$ distributions. The results are shown in Fig. 16. The ratio was measured only in the region of $\beta \in (0.3, 0.7)$ since elsewhere the uncertainty estimation is unreliable due to the measured value being too close to 0 or 1. The ratio $R_{q \bar{q}}$ predicted by the model depends on the parton transverse-momentum cut applied. The $p_{T,\mathrm{cut}}$ value of $\sqrt{2}\,{\mathrm{GeV}}$ used in the original calculation [17] significantly underestimates the ratio. A scan of the parton transverse-momentum cut showed that the measured ratio can be well described throughout the considered range with $p_{T,\mathrm{cut}}= 1.75\,{\mathrm{GeV}}$. Both this value of $p_{T,\mathrm{cut}}$ and the original value were used for calculating the Two-Gluon-Exchange model predictions.

Fig. 16

The $R_{q \bar{q}} = \sigma (q\bar{q})/(\sigma (q\bar{q})+\sigma (q\bar{q}g))$, determined in a fit of the predicted shapes to the measured $\phi$ distributions given in Fig. 11. The fit takes into account the full covariance matrix. The predicted ratio is shown for two choices of $p_{T,\mathrm{cut}}$: for the $\sqrt{2}\,{\mathrm{GeV}}$ used for the published calculations [17] and for $1.75\,{\mathrm{GeV}}$, determined in a fit

10.2 Differential cross-section $\varvec{\mathrm{d}\sigma /\mathrm{d}\beta }$

The cross-section $\mathrm{d}\sigma /\mathrm{d}\beta$ is shown in Fig. 17 together with the predictions from both models. The prediction of the Resolved-Pomeron model decreases with increasing $\beta$ faster than the measured cross section, for both fit A and fit B. The difference between data and prediction is less pronounced for fit A than for fit B, which is consistent with the observation that the ratio of gluon densities increases with increasing $\beta$ [51]. Predictions and data differ by a factor of two for small values of $\beta$ and about ten for large values.

Fig. 17

Differential cross sections as in Fig. 11 in comparison to model predictions $\mathrm{d}\sigma /\mathrm{d}\beta$ (in log scale) and $\mathrm{d}\sigma /\mathrm{d}\phi$ in bins of $\beta$ (in linear scale). Contributions from proton-dissociative dijet production were subtracted. The systematic uncertainties do not include the uncertainty due to the subtraction. The Two-Gluon-Exchange model is presented with $p_{T,\mathrm{cut}}= 1.75\,{\mathrm{GeV}^{2}}$. The bands on theoretical expectations represent statistical uncertainties only

The Two-Gluon-Exchange model prediction, which includes $q \bar{q}$ and $q \bar{q} g$, describes the shape of the measured $\beta$ distribution reasonably well. The predicted integrated cross section is $\sigma = 38\,\mathrm{pb}$, while the measured cross section is $\sigma = 72\,\mathrm{pb}$ with a normalisation uncertainty originating from the proton-dissociation background of $u(f_{\mathrm{pdiss}}) / (1 - f_{\mathrm{pdiss}})= 27~\%$, where $u(f_{\mathrm{pdiss}})$ is the uncertainty in the fraction of events with a dissociated proton. Although the difference between the predicted and measured cross section is not significant, it could indicate that the NLO corrections are large or the cross-section enhancement arising from the evolution of the off-diagonal gluon distribution is significant [7]. The prediction based on $q\bar{q}$ production alone fails to describe the shape of the distribution at low values of $\beta$ but is almost sufficient to describe it at large $\beta$, where the $q \bar{q} g$ component is less important.

10.3 Differential cross-section $\varvec{\mathrm{d}\sigma /\mathrm{d}\phi }$

The cross-sections $\mathrm{d}\sigma /\mathrm{d}\phi$ are shown in Fig. 17 in five different $\beta$ ranges together with the predictions of both models. The comparison of the shapes has been quantified by calculating the slope parameter A. The results are shown in Fig. 18. The Resolved-Pomeron model predicts an almost constant, positive value of A in the whole $\beta$ range. The Two-Gluon-Exchange model ($q \bar{q} + q \bar{q} g$) predicts a value of A which varies from positive to negative. In contrast to the Resolved-Pomeron model, the Two-Gluon-Exchange model agrees quantitatively with the data in the range $0.3< \beta < 0.7$. The prediction based on $q \bar{q}$ production alone describes the shape of the distributions at large $\beta$, where the $q \bar{q} g$ component is less important.

Fig. 18

The shape parameter A as a function of $\beta$ in comparison to the values of A obtained from distributions predicted by the Resolved-Pomeron model and the Two-Gluon-Exchange model. The bands on BGF Fit B and two-gluon $p_{T,\mathrm{cut}}= 1.75\,{\mathrm{GeV}}$ represent statistical uncertainties

11 Summary

The first measurement of diffractive production of exclusive dijets in deep inelastic scattering, $\gamma ^{*} + p \rightarrow \mathrm{jet}{}1 + \mathrm{jet}{}2 + p$, was presented. The differential cross-sections $\mathrm{d}\sigma /\mathrm{d}\beta$ and $\mathrm{d}\sigma /\mathrm{d}\phi$ in bins of $\beta$ were measured in the kinematic range: $Q^2 > 25\,{\mathrm{GeV}^{2}}$, $90< W < 250\,{\mathrm{GeV}}$, $M_X > 5\,{\mathrm{GeV}}$, $x_\mathrm{I\!P} < 0.01$ and $p_{T,\mathrm{jet}}> 2\,{\mathrm{GeV}}$ using an integrated luminosity of $372\,{\mathrm{pb}^{-1}}$.

The measured absolute cross sections are larger than those predicted by both the Resolved-Pomeron and the Two-Gluon-Exchange models. The difference between the data and the Resolved-Pomeron model at $\beta > 0.4$ is significant. The Two-Gluon-Exchange model predictions agree with the data within the experimental uncertainty and are themselves subject to possible large theoretical uncertainties. The shape of the $\phi$ distributions was parameterised with the function $1 + A \cos 2\phi$, as motivated by theory. The Two-Gluon-Exchange model predicts reasonably well the measured value of A as a function of $\beta$, whereas the Resolved-Pomeron model exhibits a different trend.