Search for charged Higgs bosons in e⁺e⁻ collisions at $\sqrt{s}=189\mbox{--}209\ \mbox{GeV}$

Abstract

A search is made for charged Higgs bosons predicted by Two-Higgs-Doublet extensions of the Standard Model (2HDM) using electron-positron collision data collected by the OPAL experiment at $\sqrt{s}=189\mbox{--}209\ \mbox{GeV}$, corresponding to an integrated luminosity of approximately 600 pb⁻¹. Charged Higgs bosons are assumed to be pair-produced and to decay into $\mathrm{q} \bar{\mathrm{q}}$, τν _τ or AW^±. No signal is observed. Model-independent limits on the charged Higgs-boson production cross section are derived by combining these results with previous searches at lower energies. Under the assumption $\mathrm{BR} (\mathrm{H}^{\pm} \to \tau\nu_{\tau}) + \mathrm{BR} (\mathrm{H}^{\pm} \to \mathrm{q} \bar{\mathrm{q}}) = 1$, motivated by general 2HDM type II models, excluded areas on the $[m_{\mathrm{H}^{\pm}} , \mathrm{BR} (\mathrm {H}^{\pm} \to \tau\nu_{\tau})]$ plane are presented and charged Higgs bosons are excluded up to a mass of 76.3 GeV at 95 % confidence level, independent of the branching ratio BR(H^±→τν _τ ). A scan of the 2HDM type I model parameter space is performed and limits on the Higgs-boson masses $m_{\mathrm{H}^{\pm}}$ and m _A are presented for different choices of tanβ.

Introduction

In the Standard Model (SM) [1–3], the electroweak symmetry is broken via the Higgs mechanism [4–6] generating the masses of elementary particles. This requires the introduction of a complex scalar Higgs-field doublet and implies the existence of a single neutral scalar particle, the Higgs boson. While the SM accurately describes the interactions between elementary particles, it leaves several fundamental questions unanswered. Therefore, it is of great interest to study extended models.

The minimal extension of the SM Higgs sector required, for example, by supersymmetric models contains two Higgs-field doublets [7] resulting in five Higgs bosons: two charged (H^±) and three neutral. If CP-conservation is assumed, the three neutral Higgs bosons are CP-eigenstates: h and H are CP-even and A is CP-odd. Two-Higgs-Doublet Models (2HDMs) are classified according to the Higgs-fermion coupling structure. In type I models (2HDM(I)) [8, 9], all quarks and leptons couple to the same Higgs doublet, while in type II models (2HDM(II)) [10], down-type fermions couple to the first Higgs doublet, and up-type fermions to the second.

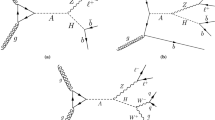
Charged Higgs bosons are expected to be pair-produced in the process e⁺e⁻→ H⁺H⁻ at LEP, the reaction e⁺e⁻→H^±W^∓ having a much lower cross section [11]. In 2HDMs, the tree-level cross section [12] for pair production is completely determined by the charged Higgs-boson mass and known SM parameters.

The H^± branching ratios are model-dependent. In most of the 2HDM(II) parameter space, charged Higgs bosons decay into the heaviest kinematically allowed fermions, namely τν _τ and quark pairs.¹ The situation changes in 2HDM(I), where the decay H^±→AW^± can become dominant if the ratio of the vacuum expectation values of the two Higgs-field doublets is such that tanβ⪆1 and the A boson is sufficiently light [13, 14].

In this paper we search for charged Higgs bosons decaying into $\mathrm {q}\bar {\mathrm {q}}$, τν _τ and AW^± using the data collected by the OPAL Collaboration in 1998–2000. The results are interpreted within general 2HDM(II) assuming $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}+ \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$})$}= 1$ for the branching ratios and in 2HDM(I) taking into account decays of charged Higgs bosons via AW^±, as well. Our result is not confined to $\mathrm{q} \bar{\mathrm{q}}=\{\mathrm{c}\bar{\mathrm{s}}, \bar {\mathrm{c}}\mathrm{s}\}$ although that is the dominant hadronic decay channel in most of the parameter space.

The previously published OPAL lower limit on the charged Higgs-boson mass, under the assumption of $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}+ \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$})$}= 1$, is $m_{\mathrm{H}^{\pm}}>59.5\ \mbox{GeV}$ at 95 % confidence level (CL) using data collected at $\sqrt{s}\leq183\ \mbox{GeV}$ [15, 16]. Lower bounds of 74.4–79.3 GeV have been reported by the other LEP collaborations [17–19] based on the full LEP2 data set. The DELPHI Collaboration also performed a search for H^±→AW^± decay and constrained the charged Higgs-boson mass in 2HDM(I) [18] to be $m_{\mathrm{H}^{\pm}}\geq76.7\ \mbox{GeV}$ at 95 %CL.

Experimental considerations

The OPAL detector is described in [20–23]. The events are reconstructed from charged-particle tracks and energy deposits (clusters) in the electromagnetic and hadron calorimeters. The tracks and clusters must pass a set of quality requirements similar to those used in previous OPAL Higgs-boson searches [24]. In calculating the total visible energies and momenta of events and individual jets, corrections are applied to prevent double-counting of energy in the case of tracks and associated clusters [24].

The data analyzed in this paper were collected in 1998–2000 at center-of-mass energies of 189–209 GeV as given in Table 1. Due to different requirements on the operational state of the OPAL subdetectors, the integrated luminosity of about 600 pb⁻¹ differs slightly among search channels.

Table 1 Data-taking year, center-of-mass energy bins, luminosity-weighted average center-of-mass energies, the energies of signal and background Monte Carlo simulations, and integrated luminosities of the data. The data correspond to total integrated luminosities of 623.9 pb⁻¹ for the two-tau, 615.1 pb⁻¹ for the two-jet plus tau and the four-jet channels and 603.1 pb⁻¹ for the H^±→AW^± selections

In this paper the following final states are sought:

• $\mathrm{H}^{+}\mathrm{H}^{-}\to\tau^{+}\nu_{\tau}\tau^{-}\bar{\nu}_{\tau}$ (two-tau final state, 2τ),

• $\mathrm{H}^{+}\mathrm{H}^{-}\to\mathrm{q}\bar{\mathrm{q}}\tau\nu_{\tau}$ (two-jet plus tau final state, 2j+τ),

• $\mathrm{H}^{+}\mathrm{H}^{-}\to\mathrm{q}\bar{\mathrm{q}}\mathrm{q}\bar{\mathrm{q}}$ (four-jet final state, 4j),

• $\mathrm{H}^{+}\mathrm{H}^{-}\to \mathrm{AW}^{+*} \mathrm{AW}^{-*}\to \mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}\mathrm{b} \bar{\mathrm{b}} \mathrm{q}\bar{\mathrm{q}}$ (eight-jet final state, 8j),

• $\mathrm{H}^{+}\mathrm{H}^{-}\to \mathrm{AW}^{+*} \mathrm{AW}^{-*}\to \mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}} \mathrm{b} \bar{\mathrm{b}}\ell\nu_{\ell}$ (six-jet plus lepton final state, 6j+ℓ),

• $\mathrm{H}^{+}\mathrm{H}^{-}\to \mathrm{AW}^{\pm*}\tau\nu_{\tau}\to\mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}} \tau\nu_{\tau}$ (four-jet plus tau final state, 4j+τ).

The signal detection efficiencies and accepted background cross sections are estimated using a variety of Monte Carlo samples. The HZHA generator [25] is used to simulate H⁺H⁻ production at fixed values of the charged Higgs-boson mass in steps of 1–5 GeV from the kinematic limit down to 50 GeV for fermionic decays and 40 GeV for bosonic decays.

The background processes are simulated primarily by the following event generators: PYTHIA [26, 27] and KK2F [28, 29] ($Z/\gamma^{*}\to \mathrm{q}\bar{\mathrm{q}} (\gamma)$), grc4f [30, 31] (four-fermion processes, 4f), BHWIDE [32] and TEEGG [33] (e⁺e⁻(γ)), KORALZ [34] and KK2F (μ ⁺ μ ⁻(γ) and τ ⁺ τ ⁻(γ)), PHOJET [35, 36], HERWIG [37], Vermaseren [38] (hadronic and leptonic two-photon processes).

The generated partons, both for the signal and the SM Monte Carlo simulations, are hadronized using JETSET [26, 27], with parameters described in [39]. For systematic studies, cluster fragmentation implemented in HERWIG for the process $Z/\gamma^{*}\to \mathrm{q}\bar{\mathrm{q}} (\gamma)$ is used. The predictions of 4f processes are cross-checked using EXCALIBUR [40], KoralW [41] and KandY [42].

The obtained Monte Carlo samples are processed through a full simulation of the OPAL detector [43]. The event selection is described below.

Search for four-fermion final states

In most of the parameter space of 2HDM(II) and with a sufficiently heavy A boson in 2HDM(I), the fermionic decays of the charged Higgs boson dominate and lead to four-fermion final states. The most important decay mode is typically H^±→τν _τ , with the hadronic mode $\mathrm{H}^{\pm}\to\mathrm{q}\bar{\mathrm{q}}$ reaching about 40 % branching ratio at maximum.

The search for the fully leptonic final state $\mathrm{H}^{+}\mathrm{H}^{-}\to \tau^{+}\nu_{\tau}\tau^{-}{\bar{\nu}}_{\tau}$ is described in [44]. The searches for the $\mathrm{H}^{+}\mathrm{H}^{-} \to \mathrm{q}\bar{\mathrm{q}}\tau\nu_{\tau}$ and the $\mathrm{H}^{+}\mathrm{H}^{-}\to\mathrm{q}\bar{\mathrm{q}}\mathrm{q}\bar{\mathrm{q}}$ events are optimized using Monte Carlo simulation of $\mathrm{H}^{+}\to\mathrm{c} \bar{\mathrm{s}}$ decays. The sensitivities to other quark flavors are similar and the possible differences are taken into account as systematic uncertainties. Therefore, our results are valid for any hadronic decay of the charged Higgs boson.

Four-fermion final states originating from H⁺H⁻ production would have very similar kinematic properties to W⁺W⁻ production, which therefore constitutes an irreducible background to our searches, especially when $m_{\mathrm{H}^{\pm}}$ is close to $m_{\mathrm {W}^{\pm }}$. To suppress this difficult SM background, a mass-dependent likelihood selection (similar to the technique described in [45]) is introduced. For each charged Higgs-boson mass tested (m _test), a specific analysis optimized for a reference mass (m _ref) close to the hypothesized value is used.

We have chosen a set of reference charged Higgs-boson masses at which signal samples are generated. Around these reference points, mass regions (labeled by m _ref) are defined with the borders centered between the neighboring points. For each individual mass region, at each center-of-mass energy, we create a separate likelihood selection. The definition of the likelihood function is based on a set of histograms of channel specific observables, given in [16]. The signal histograms are built using events generated at m _ref. The background histograms are composed of the SM processes and are identical for all mass regions.

When testing the hypothesis of a signal with mass m _test, the background and data rate and discriminant (i.e. the reconstructed Higgs-boson mass) distribution depend on the mass region to which m _test belongs. The signal quantities depend on the value of m _test itself and are determined as follows. The signal rate and discriminant distribution are computed, with the likelihood selection optimized for m _ref, for three simulated signal samples with masses m _low, m _ref and m _high. Here, m _low and m _high are the closest mass points to m _ref at which signal Monte Carlo samples are generated, with m _low<m _ref<m _high. The signal rate and discriminant distribution for m _test are then calculated by linear interpolation from the quantities for m _low and m _ref if m _test<m _ref, or for m _ref and m _high if m _test>m _ref.

When building the likelihood function three event classes are considered: signal, four-fermion background (including two-photon processes) and two-fermion background. The likelihood output gives the probability that a given event belongs to the signal rather than to one of the two background sources.

The two-jet plus tau final state

The analysis closely follows our published one at $\sqrt{s}=183\ \mbox{GeV}$ [16]. It proceeds in two steps. First, events consistent with the final state topology of an isolated tau lepton, a pair of hadronic jets and sizable missing energy are preselected and are then processed by a likelihood selection. The sensitivity of the likelihood selection is improved by building mass-dependent discriminant functions as explained above.

Events are selected if their likelihood output (${\mathcal{L}}$) is greater than a cut value chosen to maximize the sensitivity of the selection at each simulated charged Higgs-boson mass (m _ref). Apart from the neighborhood of the W⁺W⁻ peak, the optimal cut does not depend significantly on the simulated mass and is chosen to be ${\mathcal{L}} > 0.85$. Around the W⁺W⁻ peak, it is gradually reduced to 0.6.

The number of selected events per year is given in Table 2 for a test mass of $m_{\mathrm{H}^{\pm}}=75\ \mbox{GeV}$. In total, 331 events are selected in the data sample with 316.9±3.2 (stat.) ±38.4 (syst.) events expected from SM processes. The sources of systematic uncertainties are discussed below. Four-fermion processes account for more than 99 % of the SM background and result in a large peak in the reconstructed mass centered at the W^± mass (with a second peak at the Z mass for test masses of $m_{\mathrm{H}^{\pm}}>85\ \mbox{GeV}$). The signal detection efficiencies for the various LEP energies are between 25 % and 53 % for any charged Higgs-boson mass.

Table 2 Observed data and expected SM background events for each year for the 2j+τ and 4j final states. The uncertainty on the background prediction due to the limited number of simulated events is given

The likelihood output and reconstructed di-jet mass distributions for simulated Higgs-boson masses of 60 GeV and 75 GeV are presented in Figs. 1(a)–(d). The reconstructed Higgs-boson mass resolution is 2.0–2.5 GeV [16]. Figure 2(a) gives the mass dependence of the expected number of background and signal events and compares them to the observed number of events at each test mass.

Fig. 1

Likelihood output and reconstructed di-jet mass distributions for the (a)–(d) 2j+τ and (e)–(h) 4j channels. The distributions are summed up for all center-of-mass energies and correspond to 60 GeV and 75 GeV simulated charged Higgs-boson masses. All Monte Carlo distributions are normalized to the integrated luminosity of the data. When plotting the likelihood output, the signal expectation is scaled up by a factor of 10 for better visibility. A hadronic branching ratio of 0.5 is assumed for the 2j+τ signal, and 1.0 for the 4j signal. The reconstructed mass distributions are shown after the likelihood selection

Fig. 2

The number of observed data, expected background and signal events for the (a) 2j+τ and (b) 4j channels. The numbers are summed up for all center-of-mass energies and shown as a function of the reference charged Higgs-boson mass. A hadronic branching ratio of 0.5 is assumed for the 2j+τ signal, and 1.0 for the 4j signal. Each bin corresponds to a different likelihood selection optimized for the mass at which the dot is centered. Since the same background simulations are used to form the reference histograms and the same data enter the selection, the neighboring points are strongly correlated

The systematic uncertainties are estimated for several choices of the charged Higgs-boson mass from 50 GeV to 90 GeV at center-of-mass energies of $\sqrt{s}=189\ \mbox{GeV}$, 200 GeV and 206 GeV to cover the full LEP2 range. The following sources of uncertainties are considered: limited number of generated Monte Carlo events, statistical and systematic uncertainty on the luminosity measurement, modeling of kinematic variables in the preselection and in the likelihood selection, tau lepton identification, dependence of the signal detection efficiency on final-state quark flavor, signal selection efficiency interpolation between generated Monte Carlo points, background hadronization model, and four-fermion background model. The contributions from the different sources are summarized in Table 3.

Table 3 Relative systematic uncertainties on the expected background and signal rates for the 2j+τ and 4j final states. The numbers are given in % and depend on the center-of-mass energy and the reference charged Higgs-boson mass. N.A. stands for not applicable, N. for negligible

In the limit calculation, the efficiency and background estimates of the 2j+τ channel are reduced by 0.8–1.7 % (depending on the center-of-mass energy) in order to account for accidental vetoes due to accelerator-related backgrounds in the forward detectors.

The four-jet final state

The event selection follows our published analysis at $\sqrt{s}=183\ \mbox{GeV}$ [16]: first, well-separated four-jet events with large visible energy are preselected; then a set of variables is combined using a likelihood technique. To improve the discriminating power of the likelihood selection, a new reference variable is introduced: the logarithm of the matrix element probability for W⁺W⁻ production averaged over all possible jet-parton assignments computed by EXCALIBUR [40]. Moreover, we introduce mass-dependent likelihood functions as explained above. As the optimal cut value on the likelihood output is not that sensitive to the charged Higgs-boson mass in this search channel, we use the condition ${\mathcal{L}} > 0.45$ at all center-of-mass energies and for all test masses.

There is a good agreement between the observed data and the SM Monte Carlo expectations at all stages of the selection. The number of selected events per year is given in Table 2 for a test mass of $m_{\mathrm{H}^{\pm}}=75\ \mbox{GeV}$. In total, 1100 events are selected in the data, while 1117.8±5.9 (stat.) ±74.4 (syst.) events are expected from SM processes. The four-fermion processes account for about 90 % of the expected background and result in a large peak centered at the W^± mass and a smaller one at the Z boson mass. The signal detection efficiencies are between 41 % and 59 % for any test mass and center-of-mass energy.

Typical likelihood output and reconstructed di-jet mass distributions of the selected events together with the SM background expectation and signal shapes for simulated charged Higgs-boson masses of 60 GeV and 75 GeV are plotted in Figs. 1(e)–(h). The Higgs-boson mass can be reconstructed with a resolution of 1–1.5 GeV [16]. Figure 2(b) shows the mass dependence of the expected number of background and signal events and compares them to the observed number of events at each test mass. Systematic uncertainties are estimated in the same manner as for the 2j+τ search and are given in Table 3.

Search for AW^+∗AW^−∗ events

In a large part of the 2HDM(I) parameter space, the branching ratio of H^±→AW^± dominates. The possible decay modes of the A boson and the W^± lead to many possible H⁺H⁻→AW^+∗AW^−∗ event topologies. Above m _A≈12 GeV, the A boson decays predominantly into a $\mathrm {b} \bar {\mathrm {b}}$ pair, and thus its detection is based on b-flavor identification. Two possibilities, covering 90 % of the decays of two W^±, are considered: quark pairs from both W^± bosons or a quark pair from one and a leptonic final state from the other. The event topologies are therefore “eight jets” or “six jets and a lepton with missing energy”, with four jets containing b-flavor in both cases.

The background comes from several Standard Model processes. ZZ and W⁺W⁻ production can result in multi-jet events. While ZZ events can contain true b-flavored jets, W⁺W⁻ events are selected as candidates when c-flavored jets fake b-jets. Radiative QCD corrections to $\mathrm{e}^{+}\mathrm{e}^{-}\to\mathrm{q}\bar{\mathrm{q}}$ also give a significant contribution to the expected background.

Due to the complexity of the eight-parton final state, it is more efficient to use general event properties and variables designed specifically to discriminate against the main background than a full reconstruction of the event. As a consequence, no attempt is made to reconstruct the charged Higgs-boson mass.

The analysis proceeds in two steps. First a preselection is applied to select b-tagged multi-jet events compatible with the signal hypothesis. Then a likelihood selection (with three event classes: signal, four-fermion background and two-fermion background) is applied.

The preselection of multi-jet events uses the same variables as the search for the hadronic final state in [16] with optimized cut positions. However, it introduces a very powerful new criterion, especially against the W⁺W⁻ background, on a combined b-tagging variable (${{\mathcal{B}}_{\mathrm{evt}}}$) requiring the consistency of the event with the presence of b-quark jets.

The neural network method used for b-tagging in the OPAL SM Higgs-boson search [24] is used to calculate on a jet-by-jet basis the discriminating variables $f^{i}_{\mathrm{c/b}}$ and $f^{i}_{\mathrm{uds/b}}$. These are constructed for each jet i as the ratios of probabilities for the jet to be c- or uds-like versus the probability to be b-like. The inputs to the neural network include information about the presence of secondary vertices in a jet, the jet shape, and the presence of leptons with large transverse momentum. The Monte Carlo description of the neural network output was checked with LEP1 data with a jet energy of about 46 GeV. The main background in this search at LEP2 comes from four-fermion processes, in which the mean jet energy is about 50 GeV, very close to the LEP1 jet energy; therefore, an adequate modeling of the background is expected with the events reconstructed as four jets.

The AW^+∗AW^−∗ signal topology depends on the Higgs-boson masses. At m _A≈12 GeV or $\mbox {$m_{\mathrm{A}}$}\approx m_{\mathrm{H}^{\pm}}$, the available energy in the A or W^± system is too low to form two clean, collimated jets. At high $m_{\mathrm{H}^{\pm}}$, the boost of the A and W^± bosons is small in the laboratory frame and the original eight partons cannot be identified. At low $m_{\mathrm{H}^{\pm}}$, the A and W^± bosons might have a boost, but it is still not possible to resolve correctly the two partons from their decay. From these considerations, one can conclude that it is not useful to require eight (or even six) jets in the event, as these jets will not correspond to the original partons. Consequently, to get the best possible modeling of the background, four jets are reconstructed with the Durham jet-finding algorithm [46–49] before the b-tagger is run.

The flavor-discriminating variables are combined for the four reconstructed jets by

$$ \mbox {${{\mathcal{B}}_{\mathrm{evt}}}$}= \frac{1}{1+\alpha\cdot\prod_i f^i_\mathrm{c/b} + \beta \cdot\prod_i f^i_\mathrm{uds/b}}. $$

(1)

The index i runs over the reconstructed jets (i=1,…,4) and the parameters α and β are numerical coefficients whose optimal values depend on the flavor composition of the signal and background final states. However, since the expected sensitivity of the search is only slightly dependent on the values of α and β, they are fixed at α=0.1 and β=0.7. Events are retained if $\mbox {${{\mathcal{B}}_{\mathrm{evt}}}$}>0.4$.

The preselections of the two event topologies (8j and 6j+ℓ) are very similar. However, in the 6j+ℓ channel, no kinematic fit is made to the $\mathrm{W}^{+}\mathrm{W}^{-}\to\mathrm{q}\bar{\mathrm{q}}\mathrm{q}\bar{\mathrm{q}}$ hypothesis and, therefore, no cuts are made on the fit probabilities. No charged lepton identification is applied; instead the search is based on indirect detection of the associated neutrino by measuring the missing energy.

After the preselection the observed data show an excess over the predicted Monte Carlo background. This can partly be explained by the apparent difference between the gluon splitting rate into cc̅ and bb̅ pairs in the data and in the background Monte Carlo simulation. The measured rates at $\sqrt{s}=91\ \mbox{GeV}$ are $g_{\mathrm{c}\bar{\mathrm{c}}} = 3.2 \pm0.21 \pm0.38\ \%$ [50] and $g_{\mathrm{b}\bar{\mathrm{b}}} = 0.307 \pm0.053 \pm0.097\ \%$ [51] from the LEP1 OPAL data. The gluon splitting rates in our Monte Carlo simulation are extracted from $\mathrm{e}^{+}\mathrm{e}^{-}\to\mathrm{ZZ}\to\ell^{+} \ell^{-}\mathrm{q}\bar{\mathrm{q}}$ events, where the $\mathrm{Z}\to \mathrm{q}\bar{\mathrm{q}}$ decays have similar kinematic properties to the ones in the LEP1 measurement. Note that $\mathrm{e}^{+}\mathrm{e}^{-}\to\mathrm{ZZ}\to \mathrm{q}\bar{\mathrm{q}}\mathrm{q}\bar{\mathrm{q}}$ events can not be used as the two $\mathrm {q}\bar {\mathrm {q}}$ pairs interact strongly with each other. The rates are found to be $g_{\mathrm{c}\bar{\mathrm{c}}}^{\mathrm{MC}} = 1.33 \pm0.06\ \%$ and $g_{\mathrm{b}\bar{\mathrm{b}}}^{\mathrm{MC}} = 0.116 \pm0.0167\ \%$, averaged over all center-of-mass energies. This mismodeling can be compensated by reweighting the SM Monte Carlo events with gluon splitting to heavy quarks and at the same time deweighting the non-split events to keep the total numbers of W⁺W⁻, ZZ and two-fermion background events fixed at generator level. The reweighting factor is 2.41 for $g\to \mathrm{c}\bar{\mathrm{c}}$ and 2.65 for $\mathrm{g}\to \mathrm{b}\bar{\mathrm{b}}$. The same reweighting factors are used for W⁺W⁻, ZZ and two-fermion events with gluon splitting at all LEP2 energies, noting that all background samples were hadronized with the same settings and assuming that the $\sqrt{s}$ dependence of the gluon splitting of a fragmenting two-fermion system is correctly modeled by the Monte Carlo generator. It is known that the generator reproduces the energy dependence predicted by QCD in the order α _s with resummed leading-log and next-to-leading log terms [52]. This correction results in a background enhancement factor of 1.08 to 1.1 after the preselection, depending on the search channel and the center-of-mass energy, but it does not affect the shape of the background distributions.

The numbers of preselected events after the reweighting are given in columns 2 and 3 of Table 4. At this stage of the analysis the 8j and 6j+ℓ data samples are highly overlapping. The observed rates still show an excess over the background predictions, adding up to about 1.6 standard deviations in both samples. Although this difference is statistically not significant, it can be shown that the Monte Carlo prediction has minor imperfections. For the 8j case, the distributions of three variables used in the analysis, namely y ₃₄, y ₅₆ and $\mathcal{B}_{\mathrm{evt}}$, are plotted in the right part of Fig. 3. As can be seen, the variable y ₅₆ is most powerful to reject the background. Both the y ₃₄ and the y ₅₆ distributions are slightly shifted towards the position of a hypothetical Higgs signal and the $\mathcal{B}_{\mathrm{evt}}$ distribution shows an excess over the predicted background at intermediate $\mathcal{B}_{\mathrm{evt}}$ values, but the excess events are not distributed according to the expectation for a Higgs signal. The shifts are visible with better statistical significance in the left part of Fig. 3. It shows the same variables for a background enriched data sample, where the preselection cuts on y ₃₄ and $\mathcal{B}_{\mathrm{evt}}$ are dropped, except for the study of the y ₅₆ variable where we keep the cut on y ₃₄ to select multi-jet events. The resulting samples are completely dominated by background, the contribution of a Higgs signal being at most 0.5 %. Since heavy quark production in the Monte Carlo generator is already corrected, the origin of the discrepancies is likely a slight mismodeling of the topology of multi-jet events, especially if they contain heavy quarks. No further correction is applied to the estimated background. Excess events passing the final selection, even if they do not look signal-like, are thus counted with a certain weight as signal events in the statistical analysis, to be discussed later.

Fig. 3

Most important selection variables: (a)–(b) log₁₀ y ₃₄, (c)–(d) log₁₀ y ₅₆ and (e)–(f) ${{\mathcal{B}}_{\mathrm{evt}}}$ in the 8j channel at $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$. The distributions are shown (left) in a background-enriched data sample (see text for explanation) and (right) after the full preselection. To form the signal histograms, the Monte Carlo distributions are averaged for all simulated $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ mass combinations in the mass range of interest. The Monte Carlo reweighting to the measured gluon splitting rates is included. The expectations from SM processes are normalized to the data luminosity. The preselection cuts on y ₃₄ and ${{\mathcal{B}}_{\mathrm{evt}}}$ are indicated by vertical lines

Table 4 Observed data and expected SM background events for each year in the AW^+∗AW^−∗ searches. The 8j and 6j+ℓ event samples after the preselection step (3rd and 4th columns) are highly overlapping. After the likelihood selection, the overlapping events are removed from the 8j and 6j+ℓ samples and form a separate search channel (last three columns). The uncertainty on the background prediction due to the limited number of simulated events is given. The Monte Carlo reweighting to the measured gluon splitting rates is included

As a final selection, likelihood functions are built to identify signal events. The reference distributions depend on the LEP energy, but they are constructed to be independent of the considered $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ combination. To this end, we form the signal reference distributions by averaging all simulated H⁺H⁻ samples in the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ mass range of interest.

Since the selections at $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$ are aimed at charged Higgs-boson masses around the expected sensitivity reach of about 80–90 GeV, all masses up to the kinematic limit are included. On the other hand, at $\sqrt{s}=189\ \mbox{GeV}$ only charged Higgs-boson masses up to 50 GeV are included since the selections at this energy are optimized to reach down to as low as a charged Higgs-boson mass of 40 GeV where the LEP1 exclusion limit lies. The input variables for the 8j final state are: the Durham jet-resolution parameters² log₁₀ y ₃₄ and log₁₀ y ₅₆, the oblateness [53] event shape variable, the opening angle of the widest jet defined by the size of the cone containing 68 % of the total jet energy, the cosine of the W production angle multiplied with the W charge (calculated from the jet charges [54]) for the $\mathrm{e}^{+}\mathrm{e}^{-} \rightarrow \mathrm{W}^{+}\mathrm{W}^{-} \rightarrow \mathrm{q} \bar{\mathrm{q}} \mathrm{q}\bar{\mathrm{q}}$ interpretation, and the b-tagging variable ${{\mathcal{B}}_{\mathrm{evt}}}$. At $\sqrt{s}=189\ \mbox{GeV}$, log₁₀ y ₂₃, log₁₀ y ₄₅, log₁₀ y ₆₇, and the maximum jet energy are also used. Moreover, the sphericity [55] event shape variable has more discriminating power and thus replaces oblateness. Although the y _ij variables are somewhat correlated, they contain additional information: their differences reflect the kinematics of the initial partons.

The input variables for the 6j+ℓ selection are: log₁₀ y ₃₄, log₁₀ y ₅₆, the oblateness, the missing energy of the event, and ${{\mathcal{B}}_{\mathrm{evt}}}$. At $\sqrt{s}=189\ \mbox{GeV}$, log₁₀ y ₂₃, the maximum jet energy and the sphericity are also included.

Events are selected if they pass a lower cut on the likelihood output. The likelihood distributions are shown in Fig. 4. The positions of the likelihood cuts are indicated by vertical lines. The discrepancies observed in Fig. 3 in background-enriched samples, propagate into the likelihood distributions. Since the excess events in Fig. 3 are shifted relative to the background expectation, but do not agree with the Higgs distribution, they give likelihood values between the mean background and signal values in Fig. 4. With large statistical errors, the effect can be seen at intermediate likelihood values. Some of the excess events pass the final likelihood cut.

Fig. 4

Likelihood output distributions for the (a)–(b) 8j and (c)–(d) 6j+ℓ channels at $\sqrt{s}=189\ \mbox{GeV}$ and 192–209 GeV. To form the signal histograms, the Monte Carlo distributions are averaged for all simulated $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ mass combinations in the mass range of interest. The Monte Carlo reweighting to the measured gluon splitting rates is included. The expectations from SM processes are normalized to the data luminosity. The lower cuts on the likelihood output are indicated by vertical lines

To assure that every event is counted only once in the final analysis, the overlapping 8j and 6j+ℓ event samples, as obtained after the final likelihood cut are redistributed into three event classes: (i) events exclusively classified as 8j candidates, (ii) events exclusively classified as 6j+ℓ candidates and (iii) events accepted by both selections. If an event falls into class (iii), the larger likelihood output of the two selections is kept for further processing. The final results using the above classification are quoted in Table 4. After all selection cuts, an excess of events appears in the 1999 data sample. The excess (1.9σ) is not statistically significant and it is consistent with the results of the other years. This modified channel definition not only removes the overlap but also increases the efficiency for detecting signal events by considering the cross-channel efficiencies (e.g. the efficiency to select $\mathrm{H}^{+}\mathrm{H}^{-}\to \mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}\mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}$ signal by the exclusive 6j+ℓ selection can be as high as 18 %, though it is typically only a few %). The efficiencies are determined independently for all simulated $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ combinations and interpolated to arbitrary $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ by two-dimensional spline interpolation. The behavior of the selection efficiencies depends strongly on the targeted charged Higgs-boson mass range and also varies with the mass difference $\Delta m=m_{\mathrm{H}^{\pm }}-m_{\mathrm{A}}$. In most cases the overlap channel has the highest efficiency. At $\sqrt {s}=189\ \mbox{GeV}$ and $m_{\mathrm{H}^{\pm}}=45\ \mbox{GeV}$, it reaches 32 % for the $\mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}\mathrm{b} \bar{\mathrm{b}}\ell\nu_{\ell}$ and 44 % for the $\mathrm{H}^{+}\mathrm{H}^{-}\to \mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}\mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}$ signal. At $\sqrt{s}=206\ \mbox{GeV}$ and $m_{\mathrm{H}^{\pm}}=90\ \mbox{GeV}$, the overlap efficiency can be as high as 62 % for the $\mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}\mathrm{b} \bar{\mathrm{b}}\ell\nu_{\ell}$ and 71 % for the $\mathrm{H}^{+}\mathrm{H}^{-}\to \mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}\mathrm{b} \bar{\mathrm{b}}\mathrm{q}\bar{\mathrm{q}}$ signal. The exclusive 6j+ℓ selection has efficiencies typically below 20–30 %, while the exclusive 8j selection below 10–15 %. Table 5 gives the selection efficiencies at selected $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ points.

Table 5 Signal selection efficiencies in percent for the H^±→AW^± final states in the different search channels at $\sqrt{s}=189\ \mbox{and}\ 206\ \mbox{GeV}$ at representative $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ points

The composition of the background depends on the targeted Higgs-boson mass region. In the low-mass selection ($\sqrt{s}=189\ \mbox{GeV}$) that is optimized for $m_{\mathrm{H}^{\pm}}=40\mbox{--}50\ \mbox{GeV}$, the Higgs bosons are boosted and therefore the final state is two-jet-like with the largest background contribution coming from two-fermion processes: they account for 52 % in the exclusive 8j, 80 % in the exclusive 6j+ℓ and 76 % in the overlap channel. On the other hand, in the high-mass analysis ($\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$) the four-fermion fraction is dominant: 69 % in the 8j, 56 % in the 6j+ℓ and 70 % in the overlap channel.

Systematic errors arise from uncertainties in the preselection and from mismodeling of the likelihood function. The variables y ₃₄ and ${{\mathcal{B}}_{\mathrm{evt}}}$ appear both in the preselection cuts and in the likelihood definition. The total background rate is known to be underestimated after the preselection step. The computation of upper limits on the production cross section, with this background rate subtracted, results in conservative limits, assuming the modeling of the other preselection variables and the signal and background likelihoods to be correct. Therefore, no systematic uncertainty is assigned to the percentage of events passing the y ₃₄ and ${{\mathcal{B}}_{\mathrm{evt}}}$ preselection cuts. The systematic errors related to preselection variables other than y ₃₄ and ${{\mathcal{B}}_{\mathrm{evt}}}$, evaluated from background enriched data samples, are taken into account.

As already mentioned, the discrepancies shown in Fig. 3 have an impact on the likelihood function. Event-by-event correction routines for the variables y ₃₄ and ${{\mathcal{B}}_{\mathrm{evt}}}$ were developed to describe the observed shapes, keeping the normalization above the preselection cuts fixed. The systematic errors were estimated by computing the likelihood for all MC events with the modified values of y ₃₄ and ${{\mathcal{B}}_{\mathrm{evt}}}$ and counting the accepted MC events. The systematic errors related to all other reference variables were estimated in the same manner.

Systematic uncertainties also arise due to the gluon splitting correction. The experimental uncertainty on the gluon splitting rate translates into uncertainties on the total background rates. Moreover, there is an uncertainty due to the Monte Carlo statistics of the $\mathrm{g}\to \mathrm{c}\bar{\mathrm{c}}$ and bb̅ events.

Finally, uncertainties due to the limited number of simulated signal and background events are included. The different contributions are summarized in Table 6. Uncertainties below the 1 % level are neglected.

Table 6 Relative systematic uncertainties in percent for the AW^+∗AW^−∗ searches. Where two values are given separated by a “/”, the first belongs to the 189 GeV selection and the second to the 192–209 GeV selections. For the signal, the uncertainties due to the limited Monte Carlo statistics are calculated by binomial statistics for a sample size of 500 events and they also depend, via the selection efficiency, on the assumed Higgs-boson masses. N.A. stands for not applicable. The multiplicative gluon splitting correction factors, used to obtain the background-rate estimates as explained in the text, are given in the last line

Search for AW^± τν _τ events

In some parts of the 2HDM(I) parameter space, both the fermionic H^±→τν _τ and the bosonic H^±→AW^± decay modes contribute. To cover this transition region at small $m_{\mathrm{H}^{\pm}}-m_{\mathrm{A}}$ mass differences, a search for the final state H⁺H⁻→AW^± τν _τ is performed. The transition region is wide for small tanβ and narrow for large tanβ; therefore, this analysis is more relevant for lower values of tanβ.

Only the hadronic decays of W^± and the decay $\mathrm{A}\to \mathrm{b} \bar{\mathrm{b}}$ are considered. Thus the events contain a tau lepton, four jets (two of which are b-flavored) and missing energy. Separating the signal from the W⁺W⁻ background becomes difficult close to $m_{\mathrm{H}^{\pm}}=m_{\mathrm{W}^{\pm}}$.

The preselection is designed to identify hadronic events containing a tau lepton plus significant missing energy and transverse momentum from the undetected neutrino. In most cases it is not practical to reconstruct the four jets originating from the AW^± system. Instead, to suppress the main background from semi-leptonic W⁺W⁻ events, we remove the decay products of the tau candidate and force the remaining hadronic system into two jets by the Durham algorithm. The requirements are then based on the preselection of Sect. 3.1 with additional preselection cuts on the effective center-of-mass energy, log₁₀ y ₁₂ and log₁₀ y ₂₃ of the hadronic system, and the charge-signed W^± production angle.

The likelihood selection uses seven variables: the momentum of the tau candidate, the cosine of the angle between the tau momentum and the nearest jet, log₁₀ y ₁₂ of the hadronic system, the cosine of the angle between the two hadronic jets, the charge-signed cosine of the W^± production angle, the invariant mass of the hadronic system, and the b-tagging variable ${{\mathcal{B}}_{\mathrm{evt}}}$. Here, ${{\mathcal{B}}_{\mathrm{evt}}}$ is defined using the two jets of the hadronic system using Eq. (1) of Sect. 4, with i=1,2 and α=β=1. To form the signal reference distributions, all simulated H⁺H⁻ samples in the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ mass range of interest are summed up. Since the search at $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$ targets intermediate charged Higgs-boson masses (60–80 GeV), all masses up to the kinematic limit are included. At $\sqrt{s}=189\ \mbox{GeV}$, only charged Higgs-boson masses up to 50 GeV are included since the selection is optimized for low charged Higgs-boson masses (40–50 GeV).

The likelihood output distributions are shown in Fig. 5. There is an overall agreement between data and background distributions, apart from a small discrepancy at 189 GeV. Events are selected if their likelihood output is larger than 0.9. In total, 15 data events survive the selection at $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$, to be compared with 14.8±0.6 (stat.) ±1.9 (syst.) events expected from background sources. At $\sqrt{s}=189\ \mbox{GeV}$, where the selection is optimized for low Higgs-boson masses, 13 data events are selected with 6.1±0.5 (stat.) ±1.3 (syst.) events expected. The contribution of four-fermion events, predominantly from semi-leptonic W⁺W⁻ production, amounts to 67 % at $\sqrt{s}=189\ \mbox{GeV}$ and to 90 % at $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$.

Fig. 5

Likelihood output distribution for the 4j+τ channel at (a) $\sqrt{s}=189\ \mbox{GeV}$ and (b) $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$. To form the signal histograms, the Monte Carlo distributions are averaged for all simulated $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ mass combinations in the mass range of interest. The expectations from SM processes are normalized to the data luminosity. The lower cuts on the likelihood output are indicated by vertical line

At $\sqrt{s}=192\mbox{--}209\ \mbox{GeV}$, the signal selection efficiency starts at about 5 % at $m_{\mathrm{H}^{\pm}}=40\ \mbox{GeV}$, reaches its maximum of about 40 % (depending on the mass difference $\Delta m=m_{\mathrm{H}^{\pm}}-m_{\mathrm{A}}$) at $m_{\mathrm{H}^{\pm}}=60\ \mbox{GeV}$, then decreases to 12 % at $m_{\mathrm{H}^{\pm}}=90\ \mbox{GeV}$. In the low-mass selection at $\sqrt{s}=189\ \mbox{GeV}$, the efficiency depends strongly on the mass difference: at $m_{\mathrm{H}^{\pm}}=40\ \mbox{GeV}$, it is 27 % for Δm=2.5 GeV and 60 % for Δm=10 GeV. The selection efficiency approaches its maximum at $m_{\mathrm{H}^{\pm}}=50\ \mbox{GeV}$ (73 % for Δm=15 GeV) and then drops to zero at $m_{\mathrm{H}^{\pm}}=80\ \mbox{GeV}$. Table 5 gives selection efficiencies at representative $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ points.

The systematic uncertainties due to the modeling of selection variables are evaluated with the method developed for the AW^+∗AW^−∗ channels and summarized in Table 7.

Table 7 Systematic uncertainties in percent for the 4j+τ channel. Where two values are given separated by a “/”, the first one belongs to the 189 GeV selection and the second to the 192–209 GeV selections. For the signal, the uncertainties due to the limited Monte Carlo statistics are calculated by binomial statistics for a sample size of 500 events and they also depend, via the selection efficiency, on the assumed Higgs-boson masses

Interpretation

None of the searches has revealed a signal-like excess over the SM expectation. The results presented here and those published previously [16, 44] by the OPAL Collaboration are combined using the method of [56] to study the compatibility of the observed events with “background-only” and “signal plus background” hypotheses and to derive limits on charged Higgs-boson production. The statistical analysis is based on weighted event counting, with the weights computed from physical observables, also called discriminating variables of the candidate events (see Table 8). Systematic uncertainties with correlations are taken into account in the confidence level (p-value) calculations. To improve the sensitivity of the analysis, they are also incorporated into the weight definition [56].³

Table 8 Discriminating variables entering the statistical analysis for each search topology. Previously published results are also included

The results are interpreted in two different scenarios: in the traditional, supersymmetry-favored 2HDM(II) (assuming that there are no new additional light particles other than the Higgs bosons) and in the 2HDM(I) where under certain conditions fermionic couplings are suppressed.

First, we calculate 1−CL _b , the confidence [56] under the background-only hypothesis, and then proceed to calculate limits on the charged Higgs-boson production cross section in the signal + background hypothesis. These results are used to provide exclusions in the model parameter space, and in particular, on the charged Higgs-boson mass.

2HDM type II

First a general 2HDM(II) is considered, where $\mathrm{BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $} \mbox {${\tau \nu _{\tau }}$}) + \mathrm{BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$}) = 1$. This model was thoroughly studied at LEP. It is realized in supersymmetric extensions of the SM if no new additional light particles other than the Higgs bosons are present. As our previously published mass limit in such a model is $m_{\mathrm{H}^{\pm}}>59.5\ \mbox{GeV}$ [16], only charged Higgs-boson masses above 50 GeV are tested. Cross-section limits for lower masses can be found in [15]. In this model, the results of the 2τ, 2j+τ and 4j searches enter the statistical combination.

The confidence 1−CL _b is plotted for each channel separately in Fig. 6(a) and combined in Fig. 6(b). Note that 1−CL _b <0.5 translates to negative values of sigma (as indicated by the dual y-axis scales in Fig. 6(a)) and indicates an excess of events. No deviation reaches the 2σ level.

Fig. 6

The observed confidence levels for the background interpretation of the data, 1−CL _b , (a) for the three different final states as a function of the charged Higgs-boson mass, and (b) for the combined result in 2HDM(II) assuming $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}+ \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$})$}= 1$ on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}]$ plane. The significance values corresponding to the different shadings are shown by the bar at the right

The results are used to set upper bounds on the charged Higgs-boson pair production cross section relative to the 2HDM prediction as calculated by HZHA. The limits obtained are shown for each channel separately in Figs. 7(a)–(c) and combined in Fig. 7(d). The combined results are shown by “isolines” along which $\sigma_{95}( \mbox {$\mathrm {H}^{+}$}\mbox {$\mathrm {H}^{-}$})/\sigma_{\mathrm{2HDM}}$, the ratio of the limit on the production cross section and the 2HDM cross-section prediction, is equal to the number indicated next to the curves.

Fig. 7

Observed and expected 95 % CL upper limits on the H⁺H⁻ production cross section times the relevant H^± decay branching ratios relative to the theoretical prediction for the (a) τν _τ τν _τ   (b) $\mathrm{q}\bar{\mathrm{q}}\tau\nu_{\tau}$ and (c) $\mathrm{q}\bar{\mathrm{q}}\mathrm{q}\bar{\mathrm{q}}$ channels. The horizontal lines indicate the maximum possible branching ratios for a given channel. In (b), $\mathrm{BR}_{\mathrm{qq}\tau\nu} = 2\cdot \mathrm{BR}(\mathrm{H}^{\pm}\to\tau\nu_{\tau}) \cdot\mathrm{BR}(\mathrm{H}^{\pm}\to\mathrm{q} \bar{\mathrm{q}})$. (d) Upper limits on the production cross section relative to the 2HDM prediction on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}]$ plane in 2HDM(II) assuming $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}+ \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$})$}= 1$. The plotted curves are isolines along which the observed limit is equal to the number indicated

Excluded areas on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}]$ plane are presented for each channel separately in Fig. 8(a) and combined in Fig. 8(b). The expected mass limit from simulated background experiments, assuming no signal, is also shown. For the combined results, the 90 % and 99 % CL contours are also given. Charged Higgs bosons are excluded up to a mass of 76.3 GeV at 95 % CL, independent of $\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$. Lower mass limits for different values of $\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$ are presented in Table 9.

Fig. 8

Observed and expected excluded areas at 95 % CL on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}]$ plane (a) for each search channel separately and (b) combined in 2HDM(II) assuming $\mathrm{BR}(\mathrm{H}^{\pm}\to \tau\nu_{\tau})+ \mathrm{BR}(\mathrm{H}^{\pm}\to \mathrm{q}\bar{\mathrm{q}})= 1$. For the combined result, the 90 % and 99 % CL observed limits are also shown. See Table 9 for numerical values of the combined limit

Table 9 Observed and expected lower limits at 95 % CL on the mass of the charged Higgs boson in 2HDM(II) assuming $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}+ \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$})$}= 1$. For the results independent of the branching ratio (last line), the $\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$value at which the limit is set, is given in parenthesis

2HDM type I

We present here for the first time an interpretation of the OPAL charged Higgs-boson searches in an alternative theoretical scenario, a 2HDM(I). The novel feature of this model with respect to the more frequently studied 2HDM(II) is that the fermionic decays of the charged Higgs boson can be suppressed. If the A boson is light, the H^±→AW^± decay may play a crucial role.

The charged Higgs-boson sector in these models is described by three parameters: $m_{\mathrm{H}^{\pm}}$, m _A and tanβ. To test this scenario, the Higgs-boson decay branching ratios H^±→τν _τ , $\mathrm {c} \bar {\mathrm {s}}$, $\mathrm {c} \bar {\mathrm {b}}$, AW^± and $\mathrm{A}\to\mathrm{b} \bar{\mathrm{b}}$ are calculated by the program of Akeroyd et al. [13, 14], and the model parameters are scanned in the range: $40\ \mbox{GeV} \leq m_{\mathrm{H}^{\pm}} \leq94\ \mbox{GeV}$, $12\ \mbox{GeV} \leq \mbox {$m_{\mathrm{A}}$}< m_{\mathrm{H}^{\pm}}$, $0\leq \mbox {$\tan \beta $}\leq 100$. Charged Higgs-boson pair production is excluded below 40 GeV by the measurement of the Z boson width [57]. As the A boson detection is based on the identification of b-quark jets, no limits are derived for m _A<2m _b.

Both the fermionic (2τ, 2j+τ and 4j) and the bosonic (4j+τ, 6j+ℓ and 8j) final states play an important role and therefore their results have to be combined. There is, however, a significant overlap between the events selected by the $\mathrm{H}^{+}\mathrm{H}^{-}\to\mathrm{q}\bar{\mathrm{q}}\mathrm{q}\bar{\mathrm{q}}$ and H⁺H⁻→AW^+∗AW^−∗ selections, and the events selected by the $\mathrm{H}^{+}\mathrm{H}^{-}\to\mathrm{q}\bar{\mathrm{q}}\tau\nu_{\tau}$ and H⁺H⁻→AW^± τν _τ selections. Therefore, an automatic procedure is implemented to switch off the less sensitive of the overlapping channels, based on the calculation of the expected limit assuming no signal. In general the fermionic channels are used close to the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ diagonal and for low tanβ, and the searches for H^±→AW^± are crucial for low values of m _A and high values of tanβ.

The confidence 1−CL _b is calculated for the combination of the 8j and 6j+ℓ searches and for the 4j+τ search, without requiring the 2HDM(I) branching ratios (model independent scan), and for tanβ dependent combinations of all channels, including the fermionic ones, taking the 2HDM(I) cross section predictions into account (model dependent scan).

The result for the 8j and 6j+ℓ combination is calculated assuming SM branching ratios [58] for the W^± decay and is shown in Fig. 9(a). Close to the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ diagonal, the eight- or six-jet structure of a H^±→AW^± signal becomes less pronounced and the final state turns out four-jet-like with a few soft extra particles. As the selection variables for the signal and the background become similar, the likelihood cut removes more signal events, resulting in a drop in efficiency and extrapolations towards the $m_{\mathrm{H}^{\pm }}=m_{\mathrm{A}}$ limit are unreliable. Morever, within the 2HDM(I), the branching ratio for the bosonic Higgs decay vanishes at $m_{\mathrm{H}^{\pm }}=m_{\mathrm{A}}$. Results for $\mbox {$m_{\mathrm{A}}$}> m_{\mathrm{H}^{\pm}}-3\ \mbox{GeV}$ are thus not included in Fig. 9(a). In this mass region, the branching ratios for both H⁺H⁻→8j and H⁺H⁻→6j+ℓ are always less than 10⁻⁴. The largest deviation from background expectation, 1−CL _b =0.029, corresponding to 1.9σ is reached at $m_{\mathrm{H}^{\pm}}=70\ \mbox{GeV}$ and m _A=64 GeV. Another local minimum at $m_{\mathrm{H}^{\pm}}=60\ \mbox{GeV}$ and m _A=12 GeV, not visible in Fig. 9(a), has 1−CL _b =0.052. However, the mean background shift on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane amounts only to 1.1σ.

Fig. 9

The confidence 1−CL _b on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane (a) for H⁺H⁻→AW^+∗AW^−∗ combining the results of the 6j+ℓ and 8j searches, and (b) for H⁺H⁻→AW^± τν _τ from the 4j+τ search. The combined results in 2HDM(I) for (c) tanβ=10 and (d) tanβ=100 are also shown. The significance values corresponding to the different shadings are shown by the bars at the right

The 1−CL _b values for the 4j+τ channel is shown in Fig. 9(b). Mass combinations with $\mbox {$m_{\mathrm{A}}$}> m_{\mathrm{H}^{\pm}} -2.5\ \mbox{GeV}$ are not included. In this mass region, the 2HDM(I) prediction for the H⁺H⁻→ 4j+τ branching ratio is less than 0.005. The largest deviation 1−CL _b =0.013 corresponding to 2.2σ appears for low charged Higgs-boson masses ($m_{\mathrm{H}^{\pm}}=40\ \mbox{GeV}$, m _A=21 GeV), reflecting the excess of events in the $\sqrt{s}=189\ \mbox{GeV}$ search. The mean background shift for this channel is 0.8σ.

When all channels are combined within the 2HDM(I), the confidence levels shown in Figs. 9(c)–(d) are obtained. Close to the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ diagonal, the results are determined by the analysis of the fermionic channels. The 2HDM(I) predicts BR(H^±→τν _τ )≈0.65 for the branching ratio, depending only weakly on $m_{\mathrm{H}^{\pm}}$. The upper parts of Figs. 9(c)–(d) correspond thus to an almost horizontal cut in Fig. 6(b) at BR(H^±→τν _τ )=0.65. The lower parts of Figs. 9(c)–(d) are essentially weighted combinations of the results in Figs. 9(a)–(b), depending on tanβ and the masses involved. However, it has to be noted that also the decays $\mathrm{H}^{+}\mathrm{H}^{-}\to\tau^{+}\nu_{\tau}\tau^{-}{\bar{\nu}}_{\tau}$ are included and that the event weights in the statistical analysis are somewhat different for the model independent scans in Figs. 9(a)–(b) and the model dependent scans in Figs. 9(c)–(d). In general, excesses in Figs. 9(a)–(b) add up to excesses less than 2σ in the combination. A few regions with a significance above 2σ are present. For tanβ=10, the largest excess 1−CL _b =0.014, corresponding to 2.2σ, is found at $m_{\mathrm{H}^{\pm}}=55\ \mbox{GeV}$ and m _A=34 GeV (just before switching from the bosonic to the fermionic channels). This excess corresponds to a signal rate of 28.5 % of the 2HDM(I) expectation. Noting that the event weights depend on the hypothetical signal rate, structures in the 1−CL _b distribution as a function of $\Delta m = m_{\mathrm{H}^{\pm}} - m_{\mathrm{A}}$ are due to the similar increase of the signal cross-section with Δm for different $m_{\mathrm{H}^{\pm}}$ values. The rise of the cross-section is steeper for larger tanβ, therefore the low 1−CL _b region shrinks from Fig. 9(c) to Fig. 9(d).

In the limit of small m _A and large values of tanβ, the Higgs decay into the τν _τ channel is suppressed. The structures of the 1−CL _b bands close to m _A=12 GeV in Figs. 9(a) and 9(d) are therefore very similar.

As mentioned previously, the H^±→AW^± decay becomes dominant if the A boson is sufficiently light. The smaller tanβ is, the smaller m _A should be. This is clearly seen from the structure of the result in Figs. 9(c)–(d): for tanβ=10, the bosonic decay becomes dominant at $m_{\mathrm{A}} \lessapprox m_{\mathrm{H}^{\pm}}-18\ \mbox{GeV}$, while for tanβ=100, it dominates already at $m_{\mathrm{A}} \lessapprox m_{\mathrm{H}^{\pm}}- 6\ \mbox{GeV}$.

The model-independent limits on the charged Higgs-boson production cross section relative to the 2HDM prediction are presented in Fig. 10(a) for the H⁺H⁻→AW^+∗AW^−∗ and in Fig. 10(b) for H⁺H⁻→AW^± τν _τ searches, with the only assumption that W^± decays with SM branching ratios. The exclusion line for 40 % of the total production cross section in Fig. 10(a) forms an island around $m_{\mathrm{H}^{\pm}}=60\ \mbox{GeV}$ and m _A=12 GeV, corresponding to the minimum of 1−CL _b at this point.

Fig. 10

The 95 % CL upper limits on the production cross section times relevant H^± and A boson decay branching ratios relative to the 2HDM prediction on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane for the process (a) H⁺H⁻→AW^+∗AW^−∗ and (b) H⁺H⁻→AW^± τν _τ . The plotted curves are isolines along which the observed limit is equal to the number indicated. The expected limits are given for (a) $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {AW}^{\pm* }$})$}^{2} \cdot \mbox {$\mathrm {BR}(A\mbox {$\rightarrow $}\mbox {$\mathrm {b} \bar {\mathrm {b}}$})$}^{2} = 1$ and (b) $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}\cdot \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {AW}^{\pm* }$})$}\cdot \mbox {$\mathrm {BR}(A\mbox {$\rightarrow $}\mbox {$\mathrm {b} \bar {\mathrm {b}}$})$}= 0.25$ corresponding to the maximal value in 2HDM(I). Please note that the plotted quantity on (b) is scaled by 4 to take into account this maximal branching fraction

The results combining all channels using 2HDM(I) branching ratios are shown in Fig. 11 for different choices of tanβ. For 0≤tanβ≤0.1, the excluded mass region is independent of m _A, since the AW^± final state does not contribute. The Higgs mass limit is identical to the 2HDM(II) limit at BR(H^±→τν _τ )=0.65. This limit is also reached at the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ diagonal for any value of tanβ. For intermediate and large values of tanβ, the boundary lines of the excluded mass regions have two local $m_{\mathrm{H}^{\pm}}$ minima. The first minimum at m _A=12 GeV is due to the excess of events in the AW^+∗AW^−∗ searches. The second minimum is at a region extending parallel to the $(\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$})$ diagonal (see the full and dotted black curves corresponding to a cross-section ratio of 1.0). This reflects the loss of sensitivity in the AW^+∗AW^−∗ searches for mass combinations without a pronounced 8j or 6j+ℓ structure and is also due to the channel switching procedure implemented to avoid the use of overlapping events as explained above.

Fig. 11

The 95 % CL upper limits on the production cross section in 2HDM(I) relative to the theoretical prediction on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane for different choices of tanβ: (a) 0.1, (b) 1.0, (c) 10.0 and (d) 100.0. The plotted curves are isolines along which the observed limit is equal to the number indicated

To further study the behavior of the unexcluded regions, 90 %, 95 % and 99 % CL excluded areas are shown in Fig. 12 for different choices of tanβ. The island at $m_{\mathrm{H}^{\pm}}=60\ \mbox {GeV}$ can not be excluded at the 99 % CL.

Fig. 12

Excluded areas at 90 %, 95 % and 99 % CL on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane in 2HDM(I) for different choices of tanβ: (a) 0.1, (b) 1.0, (c) 10.0 and (d) 100.0

Due to the excess of events in the H⁺H⁻→AW^+∗AW^−∗ searches in the year 1999 data, the observed limit is lower than the expectation in all regions where the H^±→AW^± decay dominates. Our final results are presented, for all tanβ, in Fig. 13, and the limits on charged Higgs-boson mass are summarized in Table 10. Since an excess is present in both the 8j and 6j+ℓ combination and the 4j+τ channel, and the relative weighting of these channels depends on tanβ, the size of the mentioned island is tanβ dependent. The absolute lower limit on the charged Higgs boson mass for 95 % CL is set by tanβ=3.5, as indicated in Fig. 13. It amounts to 56.8 GeV for $0\leq \mbox {$\tan \beta $}\leq100$ and $12\ \mbox{GeV} \leq \mbox {$m_{\mathrm{A}}$}\leq m_{\mathrm {H}^{\pm}}$, to be compared with an expectation of 71.1 GeV. The unexcluded island is no longer present at 90 % CL where the observed mass limit improves to 66.0 GeV.

Fig. 13

Excluded areas in 2HDM(I) on the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane independent of tanβ at 95 % CL. The weakest overall mass limit is defined by the tanβ=3.5 exclusion, which is also shown

Table 10 Lower mass limits for the charged Higgs boson in 2HDM(I). For the tanβ≤100 results, the tanβ value at which the limit is set is indicated in parenthesis. For any tanβ value, an extrapolation of the exclusion limits to $m_{\mathrm{H}^{\pm}}=\mbox {$m_{\mathrm{A}}$}$ gives the result quoted in Table 9 for BR(H^±→τν _τ )=0.65

For m _A>15 GeV, the tanβ-independent lower limit on the charged Higgs-boson mass at 95 % CL is 65.0 GeV with 71.3 GeV expected. The limit is found in the transition region where the bosonic and fermionic channels have comparable sensitivities. The 6 GeV difference is due to the excess observed in the H⁺H⁻→AW^+∗AW^−∗ search.

Summary

A search is performed for the pair production of charged Higgs bosons in electron-positron collisions at LEP2, considering the decays H^±→τν _τ , $\mathrm {q}\bar {\mathrm {q}}$ and AW^±. No signal is observed. The results are interpreted in the framework of Two-Higgs-Doublet Models.

In 2HDM(II), required by the minimal supersymmetric extension of the SM, charged Higgs bosons are excluded up to a mass of 76.3 GeV (with an expected limit of 75.6 GeV) when $\mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$}+ \mbox {$\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {$\mathrm {q}\bar {\mathrm {q}}$})$}= 1$ is assumed. $\mathrm {BR}(\mbox {$\mathrm {H}^{\pm }$}\mbox {$\rightarrow $}\mbox {${\tau \nu _{\tau }}$})$-dependent limits are given in Fig. 8 and Table 9.

In 2HDM(I), where fermionic decays can be suppressed and H^±→AW^± can become dominant, a tanβ-independent lower mass limit of 56.8 GeV is observed for m _A>12 GeV (with an expected limit of 71.1 GeV) due to an excess observed at $\sqrt{s}=192\mbox{--}202\ \mbox{GeV}$ in the H⁺H⁻→AW^+∗AW^−∗ search, discussed in Sect. 4. For m _A>15 GeV, the observed limit improves to $m_{\mathrm{H}^{\pm }} >65.0\ \mbox{GeV}$ (with an expected limit of 71.3 GeV). Figure 13 shows the excluded areas in the $[\mbox {$m_{\mathrm {H}^{\pm }}$}, \mbox {$m_{\mathrm{A}}$}]$ plane and Table 10 reports selected numerical results.