1 Introduction

Due to its high computational power and efficient information processing, the human brain has attracted a lot of interest in the field of hardware-based artificial neural networks. However, great interest also lies in the study of much simpler neuronal networks, because unveiling core principles of neural information processing and fundamental, functional subcircuits is much easier in smaller networks. A popular choice for this purpose is the neuronal network of the nematode Caenorhabditis elegans (C. elegans), since it consists of only 302 neurons and its connectome is fully described. Of these 302 neurons, 282 neurons belong to the somatic system and 279 neurons are especially considered when studying its locomotion [1]. See appendix A for a list of the considered neurons and their type. This locomotion is associated with a sinusoidal-like wave motion of the worm. It is generated by 95 muscles, which are divided into dorsal left (DL), dorsal right (DR), ventral left (VL), and ventral right (VR) muscles [2]. A sketch of C. elegans is shown in Fig. 1. Locomotion can be triggered by various touch sensors but is also linked to, e.g., the chemosensory system [3].

C. elegans as a model organism is not only relevant to biology, but also to technology and electrical circuits. For instance, it enables the derivation of locomotion-generating circuits for robotic applications [4]. Studying C. elegans and its neuronal network can also improve the control of robotics in the simultaneous presence of different stimuli, locomotion in C. elegans is generated while multiple types of sensory information are processed. Moreover, C. elegans also allows for studying the principles behind an information processing that is far more efficient than that of today’s computers. Energy efficiency has for instance been studied with respect to the sparsity of a neuronal network [5, 6]. Moreover, an energy homeostasis principle shaping the neuronal dynamics has been proposed in [7] by considering a balance between energy supply, energy costs, and availability of energy. Concerning C. elegans, energy-efficiency of a subset of its neuronal network coupled only via gap junctions has been investigated in [8].

Fig. 1
figure 1

Illustration of the sinusoidal body shape during locomotion, with x denoting the muscle index per group (ventral left, ventral right, dorsal left, dorsal right)

Full size image

In this work, our aim is to investigate the power consumption of the individual building blocks of C. elegans’ neuronal network, i.e. synapses, gap junctions, and ion channels of neurons during locomotion behavior. To our utmost knowledge, such an analysis has not been considered for C. elegans. Based on this analysis, we can provide insights into a functional neuronal network topology design of C. elegans with respect to energy efficiency principles. This allows us to deduce potential design principles that can aid in designing more energy-efficient hardware-based neuronal networks. For this purpose, we model the neuronal network of C. elegans by an electrical circuit and derive a run-time efficient circuit simulation algorithm. Existing circuit realizations of C. elegans are for instance based on an FPGA emulation for leaky-integrate-and-fire models as neurons of C. elegans as part of the Si elegans project [9, 10]. Moreover, a memristive circuit has recently been proposed for the locomotory neuronal network [4]. In contrast to these approaches, we design an ideal, bio-inspired electrical circuit based on analog circuit elements that accounts for the 279 somatic neurons and 95 body wall muscles. This offers several advantages. First, due to its analog nature, the circuit can potentially be used to extract electrical subcircuits that mimic functional, neuronal subnetworks of C. elegans for, e.g., specific motor control or sensory information processing tasks. Second, including the body wall muscles allows us to link the mimicked neuronal activity to locomotion behavior. Third, considering the 279 somatic neurons instead of only a subset, such as the locomotory circuit, enables us to take the influence of other neurons on the generation of locomotion into account. This way, we can derive network design principles for the entire somatic network with respect to a specific behavior, namely forward locomotion. To this end, we derive circuit models for neurons and for muscles and verify the resulting full system via wave digital simulations [11]. This framework has, for instance, been applied to simulate single neurons [12, 13] and small neuronal networks [14], and provides a flexible, potentially real-time capable algorithm.

The rest of this paper is organized as follows: In Sects. 2 and 3, circuit models for the neurons and muscles are derived. Section 4 discusses the circuit realization of the interconnections between neurons as well as between neurons and muscles. Simulation results for the locomotion behavior as well as an analysis of the corresponding energy consumption are presented in Sect. 5. Finally, conclusions are given in Sect. 6.

2 Neuron model

A detailed biology-based modeling of C. elegans’ neuronal network is a very challenging task for two major reasons. First, as of now, electrophysiological recordings are not available for most neurons. Second, standard spiking neuron models have very limited applicability to the neurons of C. elegans. This is because the neurons of C. elegans were for long believed to not fire action potentials at all, but rather to be isopotential [15]. This is related to the fact that no sodium channels have been found in neurons of C. elegans, hinting that neuronal activity might be driven by voltage-gated calcium channels instead [15, 16]. Up to now, action potentials have been found in the sensory neuron AWA [16, 17] and in enteric motor neurons [18]. For these reasons, we use a generic modeling approach for the neurons by classifying them into three functional types: (i) sensory neurons that receive sensory signals via receptors, (ii) motor neurons that innervate and control muscles, and (iii) interneurons that relay signals between sensory and motor neurons, see Fig. 2.

Fig. 2
figure 2

Differentiation of sensory neurons, motor neurons, and interneurons

Full size image

Here, neurons of the same type show the same behavior. The classification is based on [19], where a list of all neurons and their types can be found. Note that some neurons play multiple roles, e.g., there can be sensory-motor neurons. Since we consider a strict classification, we treat potential sensory inter and inter motor neurons as purely interneurons. Moreover, we consider all sensory neurons that are also motor neurons to be purely motor neurons. In total, this leads to 104 motor neurons, 96 interneurons, and 79 sensory neurons, cf. A.

Let us now define the activity patterns of the three classes as follows: (i) Interneurons most likely show isopotential behavior [15, 20, 21], which we assume for all interneurons in our modeling approach. (ii) Motor neurons related to the locomotion show oscillatory behavior [22], but no action potentials have been found [18]. However, at least in the neuron RMD, plateau potentials have been found [15, 20]. We assume this behavior for all motor neurons. (iii) Action potentials have been found for the sensory neuron AWA, which is why we model all sensory neurons to generate action potentials. As a generic neuron model, we make use of the Morris–Lecar model, since it offers several advantages. First, it is a biologically reasonable model that is computationally simpler than, e.g., Hodgkin-Huxley models. Second, it naturally comes with a calcium instead of a sodium channel, which is more precise when accounting for C. elegans neurons. Third, the Morris–Lecar modeling framework is a conductance-based model and is thus directly interpretable as an electrical circuit. The circuit representation also allows us to directly calculate power flows, which we require for the investigation of energy consumption. The Morris–Lecar model is based on the electrochemical processes observed from an electrically excitable cell membrane visualized in Fig. 3.

Fig. 3
figure 3

Electrochemical processes taking place at a cell membrane, e.g., of neurons, which is currently in its resting state. j and \(u_\textrm{n}\) denote the input current and membrane potential, respectively

Full size image

Non-voltage-dependent ion transport mechanisms are summarized as leakage channels, while calcium and potassium channels only let their specific ions pass through if the membrane potential measured between the inside and the outside is large enough. These voltage levels are met when ions due to an input current enter the region of the channels. This current can stem from various sources such as synaptic transmission, electrical coupling via channels called gap junctions, or in the case of sensory neurons from sensory receptors. This behavior is mathematically described by the following set of differential equations [23, 24]:

$$\begin{aligned} C_\textrm{n}\dot{u}_\textrm{n}&=j_\textrm{n} + j_\textrm{t} - i_\textrm{K} - i_\textrm{Ca} - i_\textrm{L}\end{aligned}$$
(1a)
$$\begin{aligned} i_\textrm{Ca}&= g_\textrm{Ca}(u_\textrm{n})\left[ u_\textrm{n}-E_\textrm{Ca}\right] \end{aligned}$$
(1b)
$$\begin{aligned} i_\textrm{K}&= W_\textrm{K}\left[ u_\textrm{n}-E_\textrm{K}\right] \,,\quad W_\textrm{K}(z) = z G_\textrm{K}\end{aligned}$$
(1c)
$$\begin{aligned} i_\textrm{L}&= G_\textrm{L}\left[ u_\textrm{n}-E_\textrm{L}\right] \end{aligned}$$
(1d)
$$\begin{aligned} g_\textrm{Ca}(u_\textrm{n})&= \frac{G_\textrm{Ca}}{2}\left[ 1+ \textrm{tanh}\left( \frac{u_\textrm{n}-U_{\textrm{Ca},1}}{U_{\textrm{Ca},2}}\right) \right] \end{aligned}$$
(1e)
$$\begin{aligned} \dot{z}&= \left[ z_{\infty }(u_\textrm{n}) -z \right] F\textrm{cosh}\left( \frac{u_\textrm{n}-U_{\textrm{K},1}}{2U_{\textrm{K},2}}\right) \end{aligned}$$
(1f)
$$\begin{aligned} z_{\infty }(u_\textrm{n})&= \frac{1}{2}\left[ 1+ \textrm{tanh}\left( \frac{u_\textrm{n}-U_{\textrm{K},1}}{U_{\textrm{K},2}}\right) \right] \,. \end{aligned}$$
(1g)

Here, the membrane potential \(u_\textrm{n}\) and the fraction of open potassium channels z are the dynamical variables. \(C_\textrm{n}\) is the membrane capacitance, \(j_\textrm{n}\) is the input current due to synapses and gap junctions, and \(j_\textrm{t}\) is the input current due to a sensed touch. Furthermore, \(i_\textrm{K}\), \(i_\textrm{Ca}\), and \(i_\textrm{L}\) denote the potassium current, calcium current, and leakage current, respectively. \(G_\textrm{L}\) and \(E_\textrm{L}\) are the conductance of the leakage channel and its resting potential, respectively. \(g_\textrm{Ca}(u_\textrm{n}), G_\textrm{Ca}, U_{\textrm{Ca},1},\) and \(U_{\textrm{Ca},2}\) are the conductance of the calcium channel, its maximum conductance, the threshold voltage, and the edge steepness for the opening of the channel, respectively. \(W_\textrm{K}\) denotes the memductance of the potassium channel, cf. [24], \(G_\textrm{K}\) is its maximum conductance and \(z_\infty \) describes the fraction of open channels when the membrane potential is equal to its resting potential. F is the opening rate of the potassium channel, \(U_{\textrm{K},1}\) is the corresponding threshold voltage, and \(U_{\textrm{K},2}\) refers to the corresponding edge steepness. Note that the potassium channel has originally been considered as a nonlinear conductance, but has later been identified to be a memristor [24]. We adopt this understanding for this work. The corresponding circuit is shown in Fig. 4.

Fig. 4
figure 4

Morris–Lear circuit corresponding to Eqs. (1)

Full size image

In the following, we briefly discuss the specific modeling of sensory, inter, and motor neurons. As the action potentials observed for the neuron AWA are in the order of milliseconds [16], we use a scaled version of the parameters presented in [12] for the sensory neurons. For the interneurons, we strongly decrease the maximum conductance value \(G_\textrm{K}\) such that no action potentials arise. Considering the motor neurons, we design the parameters such that action potentials with long-lasting phases of positive membrane potential are present. The duration of these action potentials is congruent with those of enteric motor neurons, which have been reported to be in the order of seconds [18]. The parameters used throughout this paper are listed in Table 1. They are roughly in the same order of magnitude as parameters for biophysically detailed modeling of specific neurons of C. elegans [25].

Fig. 5
figure 5

Membrane potentials of sensory, inter, and motor neurons. The gray shaded areas highlight the time for which a constant current stimulus j is applied

Full size image
Table 1 Neuron and muscle circuit parameters
Full size table

Exemplary membrane potential behavior for all three types is shown in Fig. 5, where each neuron is stimulated by a current pulse lasting for \(1.7\,\textrm{s}\). As can be seen, sensory neurons generate short action potentials with a high frequency, while motor neurons generate an action potential that lasts approximately \(1\,\textrm{s}\). Lastly, the membrane potential of interneurons rapidly increases to a positive voltage, but they do not generate spikes and remain at this voltage until the current stimulus is turned off. This behavior is approximately comparable to that of an RC circuit.

So far, the circuit model for the neurons only allows for observing membrane potentials and ion currents. Membrane potentials are typically considered as the output signal of neurons, but cannot always be measured because electrophysiological recordings can be difficult to conduct. Instead, fluorescence traces of neurons are recorded via calcium imaging. To take this second type of output signal into account, we extend our circuit to model fluorescence traces as well. Note that for the artificially generated fluorescence traces to be comparable to real measurements, stimuli perceived by the recorded worm have to be known. This is not the case for existing recordings of freely moving animals reported in, e.g., [26,27,28]. For this reason, we focus on forward locomotion induced by a gentle touch, for which the sensory input is known to be primarily perceived by the neurons PLML and PLMR (cf. A).

We model the generation of fluorescence values based on calculating the calcium concentration changes occurring due to the neuronal activity. The dynamics of the calcium concentration \(\eta _\textrm{Ca}\) can be described by

$$\begin{aligned} \dot{\eta }_\textrm{Ca} = \alpha \left[ i_\textrm{Ca} - i_\textrm{Ca,rest}\right] -\frac{1}{\tau }\left[ \eta _\textrm{Ca} - \eta _\textrm{Ca,rest}\right] \,, \end{aligned}$$
(2)

see [13], with the resting concentration \(\eta _\textrm{rest}\), the calcium current \(i_\textrm{Ca}\) as well as its resting value \(i_\textrm{Ca,rest}\), and the decay time \(\tau \). Moreover, \(\alpha \) is a factor for converting current into concentration change, which we choose to be \(\alpha = 10^3 \frac{\textrm{mol}}{\mathrm {m^3C}}\).

Following [13], Eq. (2) can be realized by an equivalent RC circuit governed by

$$\begin{aligned} \dot{u}_\eta&= \frac{1}{C_\eta }i_\textrm{Ca} - \frac{1}{R_\eta C_\eta }\left[ u_\eta - U_{\eta ,\textrm{rest}}\right] \,,\end{aligned}$$
(3a)
$$\begin{aligned} U_{\eta ,\textrm{rest}}&= k \left[ \tau \alpha i_\textrm{Ca,rest} + \eta _\textrm{Ca,rest}\right] \,,\end{aligned}$$
(3b)
$$\begin{aligned} C_\eta&= \frac{1}{k\alpha }\,,\quad R_\eta = k \tau \alpha \,,\quad k = 1\, \frac{\mathrm {Vm^3}}{\textrm{mol}}\,. \end{aligned}$$
(3c)

Here, \(u_\eta \) is a voltage representing the calcium concentration, \(U_{\eta ,\textrm{rest}}\) is a constant voltage, \(C_\eta \) is a capacitance, \(R_\eta \) is a resistance, and k is a normalization constant.

Fig. 6
figure 6

RC circuit for calculating the calcium concentration

Full size image

Note that since the Morris–Lecar circuit already provides calcium current, we can directly extend this circuit with the RC circuit by interconnecting them via a current follower. The RC circuit is shown in Fig. 6, where the current follower is represented as a controlled current source.

Given the calcium concentrations, we can now calculate fluorescence values. In general, calcium concentration can be inferred from fluorescence via

$$\begin{aligned} \Delta \eta _\textrm{Ca}&= K_\textrm{D}\frac{F_\textrm{max}}{F_0}\frac{\left[ 1- D_F^{-1}\right] \Delta F/F_0}{\left[ \frac{\Delta F_\textrm{max}}{F_0}-\frac{\Delta F}{F_0}\right] \frac{\Delta F_\textrm{max}}{F_0}},\end{aligned}$$
(4a)
$$\begin{aligned} \Delta \eta _\textrm{Ca}&= \eta _\textrm{Ca} - \eta _\textrm{Ca,rest}\,, \quad \Delta F = F-F_0\,,\end{aligned}$$
(4b)
$$\begin{aligned} \frac{\Delta F_\textrm{max}}{F_0}&= \frac{1-D_F^{-1}}{D_F^{-1} + \bar{\eta }_\textrm{Ca}/K_\textrm{D}}\,,\end{aligned}$$
(4c)
$$\begin{aligned} \Delta F_\textrm{max}&= F_\textrm{max}-F_0\,, \end{aligned}$$
(4d)

see [29, 30]. F is the fluorescence, \(K_\textrm{D}\) is the dissociation constant, \(D_\textrm{F}\) is the dynamic range of the fluorescence, \(F_\textrm{max}\) is the maximum fluorescence value, and \(F_0\) is the baseline value of the fluorescence. \(\Delta F\) and \(\Delta F_\textrm{max}\) are the fluorescence and maximum fluorescence without the baseline value, and \(\Delta F/F_0\) is the normalized fluorescence change. By solving for \(\Delta F/F_0\), we obtain

$$\begin{aligned} \Delta F/F_0&= \frac{\Delta \eta _\textrm{Ca}\left[ 1 - D_F^{-1}\right] }{\eta _\textrm{Ca}\left[ D_F^{-1} + \eta _\textrm{Ca,rest}/K_\textrm{D}\right] }\,, \end{aligned}$$
(5)

which can be seen as a post-processing of the calcium concentration provided by the RC circuit. Note that for this work, we assume the usage of the calcium indicator GCaMP6s, which is a popular choice for calcium imaging. Due to this, we choose \(D_F = 63.2\), \(K_\textrm{D} = 144\,\textrm{nM}\), and \(\tau = 0.79\,\textrm{s}\) based on [31]. Moreover, we assume a resting calcium concentration of \(\eta _\textrm{Ca,rest} = 50\,\textrm{nM}\) which is a typical value for the neurons [25].

3 Muscle model

In this section, we derive an electrical circuit for the muscular behavior of C. elegans’ locomotion. Existing modeling approaches for the muscular behavior focus on the muscle activation as well as on the mechanical interconnection of the muscles, see [32,33,34]. Since this work investigates the energy consumption of the neuronal information processing during forward locomotion, the muscle model mainly serves to verify that locomotion is generated. As such, a detailed biomechanical model is not required. Instead, we focus on a simple muscle activity model. Here, we take the muscle activity as a direct representation of the behavior. Based on [1, 32], the muscle activity can be described by the leaky integrator

$$\begin{aligned} \dot{m}&= \frac{1}{\tau _m}\left[ 1 - m + f(u_\textrm{n})\right] \,, \end{aligned}$$
(6)

where m is the dimensionless muscle activity that physically captures the muscular calcium concentration [35]. \(\tau _m=100\,\textrm{ms}\) accounts for the muscle response time [1], and \(f(u_\textrm{n})\) is a function that accounts for synaptic inputs. Since this is a first-order differential equation, the muscle activity can be modeled by an equivalent RC circuit governed by

$$\begin{aligned} C_m\dot{u}_m&= I_m + j_m(u_\textrm{n}) - G_0u_m\,,\end{aligned}$$
(7)
$$\begin{aligned} C_m&= \tau _m G_0\,,\quad I_m = I_0\,, \end{aligned}$$
(8)

with the capacitance \(C_m\), the voltage \(u_m\) representing the muscle activity, a constant current \(I_m\), the input currents due to synapses \(j_m(u_\textrm{n})\), a normalization conductance \(G_0\) and a normalization current \(I_0\). The resulting muscle circuit hence consists of an ideal current source, a capacitance, and a conductance, and is illustrated in Fig. 7.

Fig. 7
figure 7

RC-Circuit modeling the activity of a single muscle

Full size image

4 Interconnection network

In this section, we discuss the interconnection network of neuron and muscle circuits to model the generation of forward locomotion. While a distinct locomotory circuit is known, we use the full connectome for the interconnection network. The latter can be described via adjacency matrices, which we have taken from [1]. Making use of the full connectome allows us to not only investigate the energy consumption of the locomotory circuit but also to compare it to the energy consumption of the complete network. The locomotory circuit primarily responsible for the forward locomotion of C. elegans is depicted in Fig. 8.

Fig. 8
figure 8

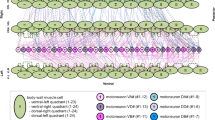
Neuronal subcircuit for forward locomotion, with sensory neurons, interneurons, and motor neurons in orange, blue, and red, respectively. Neuron names are composed of abbreviations for the anatomical positions and the subgroup of neurons, i.e., posterior lateral microtubule (PLM), posterior ventral process C (PVC), anterior ventral process B (AVB), dorsal B-type motor neuron (DB), dorsal D-type motor neuron (DD), ventral B-type motor neuron (VB), and ventral D-type motor neuron (VD) [19]. An excerpt of the corresponding interconnection network is depicted at the bottom, with additional letters for the neuron names indicating whether neurons are located on the left or right side of the worm’s body. The complete interconnection network is shown in [1]

Full size image

It consists of the sensory neurons PLM responsible for sensing a gentle touch, interneurons PVC and AVB, as well as motor neurons. The latter are divided into the first layer motor neurons VB and DB, acting excitatory on the muscles, and the second layer motor neurons VD and DD, inhibiting muscle activity. Note that some neurons are associated with the ventral or dorsal side of the worm, which is indicated by the letters V and D, respectively.

In this work, we model connections between neurons as either gap junctions or synapses, and interconnections between neurons and muscles only as synapses. We neglect muscle-to-muscle interconnections, as this coupling is typically considered to be weak in comparison to the synaptic ones [1]. In the following, let us first consider the neuronal interconnections. In the electrical circuit of the \(\mu \)-th neuron described by equations (1) and (4), these interconnections are accounted for via the current \(j_{\textrm{n},\mu }\)

$$\begin{aligned} j_{\textrm{n},\mu }&= j_{\textrm{g},\mu } + j_{\textrm{s},\mu } \,, \quad \mu =1,\ldots ,N\end{aligned}$$
(9a)
$$\begin{aligned} j_{\textrm{g},\mu }&= G_\textrm{el} \sum _{k=1}^{N} \left[ u_{\textrm{n},k} - u_{\textrm{n},\mu }\right] a_{\mu k}^{\textrm{el}}\,, \end{aligned}$$
(9b)

where N is the total amount of neurons. \(j_{\textrm{g},\mu }\) is the input current caused by gap junctions, \(j_{\textrm{s},\mu }\) is the synaptic current, \(G_\textrm{el}\) is the associated coupling strength, and \(a_{\mu k}^{\textrm{el}}\) is the \(\mu k\)-th element of the weighted adjacency matrix \(\textbf{A}_\textrm{el}\) that describes the gap-junction-based connections from neuron k to neuron \(\mu \). In our electrical circuit, for each positive entry in the adjacency matrix \(\textbf{A}_\textrm{el}\), we interconnect the corresponding neuron circuits with a constant series resistor. Note that the absolute resistance values differ for the individual gap junctions because there can be multiple gap junctions between a pair of neurons. This is reflected in the weight of the adjacency matrix.

The synaptic current \(j_{\textrm{s},\mu }\) is composed of the Glu current \(j_{\textrm{n},\mu }^{\textrm{Glu}}\), the ACh current \(j_{\textrm{n},\mu }^{\textrm{Glu}}\), and the GABA current \(j_{\textrm{n},\mu }^{\textrm{Glu}}\), which yields

$$\begin{aligned} j_{\textrm{s},\mu }&= j_{\textrm{n},\mu }^{\textrm{Glu}} + j_{\textrm{n},\mu }^{\textrm{ACh}} + j_{\textrm{n},\mu }^{\textrm{GABA}}\end{aligned}$$
(10a)
$$\begin{aligned} j_{\textrm{n},\mu }^{\textrm{Glu}}&= \sum _{k=1}^{N} S(u_{\textrm{n},k})G_\textrm{Glu}\,a_{\textrm{n},\mu k}^{\textrm{Glu}} \left[ u_{\textrm{n},\mu }-E_\textrm{exc}\right] \,,\end{aligned}$$
(10b)
$$\begin{aligned} j_{\textrm{n},\mu }^{\textrm{ACh}}&= \sum _{k=1}^{N} S(u_{\textrm{n},k})G_\textrm{ACh}\,a_{\textrm{n},\mu k}^{\textrm{ACh}} \left[ u_{\textrm{n},\mu }-E_\textrm{exc}\right] \,,\end{aligned}$$
(10c)
$$\begin{aligned} j_{\textrm{n},\mu }^{\textrm{GABA}}&= \sum _{k=1}^{N} S(u_{\textrm{n},k})G_\textrm{GABA}\,a_{\textrm{n},\mu k}^{\textrm{GABA}} \left[ u_{\textrm{n},\mu }-E_\textrm{inh}\right] ,\end{aligned}$$
(10d)
$$\begin{aligned} S(u_{\textrm{n},k})&= \left[ 1 + e^{-\left[ u_{\textrm{n},k}-U_\textrm{s1}\right] / U_\textrm{s2}}\right] ^{-1}\,. \end{aligned}$$
(10e)

Here, \(G_\textrm{Glu}, G_\textrm{ACh}\), and \(G_\textrm{GABA}\) are the coupling strengths for the neurotransmitters Glu, ACh, and GABA, respectively, \(E_\textrm{exc}\) denotes the resting potential for an excitatory synapse, and \(E_\textrm{inh}\) is the resting potential for an inhibitory synapse. \(a_{\textrm{n},\mu k}^{\textrm{Glu}}, a_{\textrm{n},\mu k}^{\textrm{ACh}}\), and \(a_{\textrm{n},\mu k}^{\textrm{GABA}}\) are the \(\mu k\)-th elements of the adjacency matrices \(\textbf{A}_\textrm{n}^\textrm{Glu}, \textbf{A}_\textrm{n}^\textrm{ACh}\), and \(\textbf{A}_\textrm{n}^\textrm{GABA}\), respectively, which describe the connections between neurons due to the corresponding type of neurotransmitter. Finally, \(S(u_\textrm{n})\) is the synaptic activation function, with the threshold voltage \(U_\textrm{s1}\) and a voltage determining the slope \(U_\textrm{s2}\).

Individual synapses are typically represented by nonlinear resistive voltage sources, see Fig. 9a. Here, the nonlinear resistor can be realized by a voltage-controlled switch in series to a constant resistor \(G_\textrm{syn}\), where the switch accounts for the synaptic activation function and can be realized by, e.g., transistors, cf. [36] for a comparable transistor-based approach. This is illustrated in Fig. 9b. \(G_\textrm{syn}\) depends on the type of neurotransmitter and is a multiple of either \(G_\textrm{Glu}, G_\textrm{ACh}\), or \(G_\textrm{GABA}\). The exact factor depends on the weight of the specific adjacency matrix entry. For our circuit simulation, we treat the synapses as voltage-controlled current sources shown in Fig. 9c, allowing for a generic circuit simulation.

Fig. 9
figure 9

Circuit models for neuronal synapses. a Equivalent circuit of neuronal synapses typically found in literature. b Equivalent circuit of neuronal synapses realized with a voltage-controlled switch. c Circuit representation of neuronal synapses as arbitrary voltage-controlled current sources

Full size image

Similar to the synapses between neurons, we model the neuromusculuar synaptic currents via

$$\begin{aligned} j_{m,\mu } = \sum _{k=1}^{M} u_{\textrm{n},k} \left[ G_\textrm{ACh}\,a_{m,\mu k}^{\textrm{ACh}} + G_\textrm{GABA}\,a_{m,\mu k}^{\textrm{GABA}}\right] \,, \end{aligned}$$
(11)

where \(j_{m,\mu }\) is the synaptic input current of the \(\mu \)-th muscle, with \(\mu = 1,\ldots ,M\) and the total number of muscle cells M. \(a_{m,\mu k}^{\textrm{ACh}}\) and \(a_{m,\mu k}^{\textrm{GABA}}\) are the \(\mu k\)-th elements of the adjacency matrices \(\textbf{A}_m^\textrm{ACh}\) and \(\textbf{A}_m^\textrm{GABA}\), respectively, which denote the synaptic couplings from neurons to muscles based on ACh and GABA transmitters, respectively.

Since the muscle model is not biologically accurate, it does not include synaptic ion channels as it is the case for the neuronal synapses. Instead, the muscular synaptic current is directly calculated as the product of the neuronal membrane potential \(u_\textrm{n}\) and the coupling strength of the synapse-specific neurotransmitter. From a circuit-theoretical point of view, this results in a voltage-to-current converter and can be represented by a voltage-controlled current source as well, see Fig. 10.

Fig. 10
figure 10

Voltage-controlled current source as a circuit model for synapses between neurons and muscles

Full size image

5 Simulating locomotion and analysis of power consumption

Let us now discuss the simulation of the combined circuit model. Taking all interconnections into account leads to a highly complex circuit diagram that requires great effort to simulate it via circuit simulation techniques like SPICE. To reduce this complexity, we consider vector-valued neuron and muscle models by virtually stacking, e.g., N Morris–Lecar circuits on top of each other to model N neurons. This approach results in the complete circuit model illustrated in Fig. 11 and is composed of vector-valued subcircuits for neurons, calcium concentration calculation, muscles, and interconnection elements introduced in the previous sections. The vector-valued nature of the complete circuit is advantageous for our simulation approach based on the wave digital concept [11]. In particular, a vector-valued representation makes the complete circuit model generic, as in this case more neurons and muscles only scale the dimensions of the corresponding subcircuits. As such, it enables an improved run-time efficiency of the simulation approach. Details about the wave digital concept are provided in the following.

Fig. 11
figure 11

Complete circuit model for mimicking the locomotory behavior of C. elegans. Note that the individual circuits are vector-valued variants of the Morris–Lecar circuit in Fig. 4, the calcium concentration circuit in Fig. 6, the muscle circuit in Fig. 7, the neuronal synapses in Fig. 9c, and the neuromuscular synapses in Fig. 10

Full size image

5.1 Wave digital algorithm

We obtain simulation results using a wave digital algorithm implemented in MATLAB. Compared to other simulation techniques such as SPICE or ODE solvers, this provides us with a run-time efficient, real-time capable algorithm that has a direct correspondence with the reference circuit. In particular, the algorithm can be derived from the equivalent electrical circuit by first decomposing the circuit into its ports and then translating the ports as well as the interconnection structure using the bijective transformation

$$\begin{aligned} a&= u+Ri\,,&b&= u-Ri\,,&R&>0\,, \end{aligned}$$
(12)

see [11]. Here, a, b, and R are the incident wave, the reflected wave, and the port resistance, respectively. To translate the complete circuit of Fig. 11, we consider the subcircuits individually and start with the Morris–Lecar circuit. A corresponding scalar wave digital has been derived in [12, 13] and its extension to vector-valued models is achieved when applying the bijective transformation to vectors of voltages and currents instead of scalar ones. This has for instance been used in [14] to couple Morris–Lecar circuit networks of arbitrary size. It is based on a general adaptor that represents arbitrary Kirchhoff interconnections, see [37, 38]. This adaptor takes the incidence matrix of the interconnection structure as topology information and connects the Morris–Lecar circuits with the chosen coupling element. This is directly applicable to the interconnection network via gap junctions presented in this work, with the vector-valued resistor \(\varvec{G}_\textrm{el} = G_\textrm{el}\varvec{A}_\textrm{el}\) as coupling element. To connect this resistor to the vector-valued Morris–Lecar circuit, the adjacency matrix \(\varvec{A}_\textrm{el}\) is translated into a corresponding incidence matrix that is used for the general adaptor. The wave digital equivalent of the resistor then corresponds to

$$\begin{aligned} \varvec{b} = \textbf{0}\,, \end{aligned}$$
(13)

given that its port resistance matrix is chosen to \(\varvec{R}=\textbf{1}/G_\textrm{el}\), where \(\textbf{1}\) is the unity matrix. The interconnection network for the neuronal synapses consists of the vector-valued controlled current source \(\varvec{j}_\textrm{s}(\varvec{u}_\textrm{n})\) that is translated by applying the bijective transformation. Its wave digital equivalent is

$$\begin{aligned} \varvec{a} = \varvec{b} + 2\varvec{R}\varvec{j}_\textrm{s}(\varvec{u}_\textrm{n}) \end{aligned}$$
(14)

and is interconnected to the Morris–Lecar circuit via a parallel adaptor - the wave digital equivalent of a parallel connection, see [11] for more details.

A wave digital model of a scalar calcium concentration circuit has been presented in [13] and can also be extended to a vector-valued variant by considering vectors of voltages and currents for the wave digital translation. The translation of the muscle circuit works similarly, since both the muscle circuit and the calcium concentration circuit are essentially RC circuits. The muscle circuits’ interconnection structure is given by the controlled current source \(\varvec{j}_m(\varvec{u}_\textrm{n})\) whose translation is identical to equation (14). This current source is again connected to the muscle circuit via a parallel adaptor.

To implement the wave digital equivalents of the individual subcircuits as a wave digital algorithm, the nonlinearities contained in the subcircuits have to be specially considered. This is because these nonlinearities give rise to implicit relationships between the incident and reflected wave of a port, known as delay-free loops. It is in general advisable to prevent as many loops as possible from arising, since typical solution approaches via iterative approaches [39,40,41] pose an increased computational effort. Delay-free loops can be prevented via reflection-free ports of the parallel adaptors [11], but also via source transformation of the nonlinearities contained in the Morris–Lecar model, see [12]. We deploy fixed-point iterations based on [39] for the remaining delay-free loops.

5.2 Neuronal and muscular activity

As an input signal, we apply a constant current of \(100\,\textrm{pA}\) to the circuits modeling the neurons PLML and PLMR. This reflects a continuously sensed gentle touch that should trigger forward locomotion. The utilized parameters are given in Tables. 1 and 2. Here, the ratio of the coupling strengths is taken from [1]. In the following, we first discuss the simulation results for the membrane potentials and fluorescence traces to verify that forward locomotion is indeed generated. Afterwards, we study energy consumption rates of the neuronal network occurring during this locomotion.

Table 2 Parameters for the coupling structure
Full size table

Results for the membrane potentials of all 279 neurons are depicted in the top panel of Fig. 12 and relative fluorescence traces can be seen in the center panel of Fig. 12. Motor neurons can be identified by their slowly oscillating activity pattern, see e.g. neurons labeled with 239–279. Interneurons exhibit a more or less constant membrane potential, see e.g. neurons labeled with 11–23. Activity of sensory neurons is given by fast oscillations, but is barely visible because there are no larger groups of active sensory neurons. Evaluating which neurons are active in particular, it turns out that almost all motor neurons, approximately 2/3 of all interneurons, and only 3 sensory neurons show activity. The latter are in particular the neurons PLML,PLMR, and ALM. Even though ALM is part of the backward locomotory circuit, this might be reasonable, as hints have been found that neurons of the mechanosensory system influence each other [42].

Fig. 12
figure 12

Neuronal and muscular activity. Top: Membrane potentials of all 279 neurons. Center: Relative fluorescence traces of all 279 neurons. Bottom: Muscle activity of all 95 muscles. White lines are used to highlight the four different groups of muscles

Full size image

Taking a look at the muscle activity illustrated in the bottom panel of Fig. 12, we observe that after a transient phase of 10 s, activity within each muscle group is propagating approximately diagonally from low indices to high indices. Note that the transient phase is due to the neuron and muscle circuits being initialized near their resting states. The diagonally propagating activity is especially observable for the dorsal left (DL) and dorsal right (DR) muscles, and to a lesser extend also from the ventral left (VL) and ventral right (VR) muscles. In light of the fact that the muscles of these groups are arranged from head to tail with increasing index, these results suggest that locomotion is indeed generated.

5.3 Power consumption

Finally, we investigate the power consumption of the neuronal ion channels, neuronal synapses and gap junctions present in the neuronal network of C. elegans. Based on [43, 44], the rate of energy consumption for the ion channels \(p_\textrm{ion}\) and gap junctions \(p_\textrm{gap}\), equivalent to power, can be calculated via

$$\begin{aligned} p_\textrm{ion}&= \sum _{\mu =1}^{N}-i_{\textrm{Ca},\mu }\left[ u_{\textrm{n,}\mu }-E_{\textrm{Ca},\mu }\right] \end{aligned}$$
(15a)
$$\begin{aligned}&\quad -i_{\textrm{K},\mu }\left[ u_{\textrm{n},\mu }-E_{\textrm{K},\mu }\right] -i_{\textrm{L},\mu }\left[ u_{\textrm{n},\mu }-E_{\textrm{L},\mu }\right] \nonumber \\ p_\textrm{gap}&= \textbf{u}_\textrm{n}\mathbf {\Lambda }_\textrm{el}\textbf{u}_\textrm{n}^T,\, \textbf{u}_\textrm{n} = \begin{bmatrix} u_{\textrm{n},1}&...&u_{\textrm{n},N} \end{bmatrix}^T, \end{aligned}$$
(15b)

where \(\mathbf {\Lambda }_\textrm{el}\) is a Laplacian matrix describing the connections via gap junctions. Following this approach, the energy consumption rate for the synapses is given by

$$\begin{aligned} p_\textrm{syn}&= \sum _{\mu =1}^{N} -j_{\textrm{n},\mu }^{\mathrm {\textrm{ACh}}}\left[ u_{\textrm{n},\mu } - E_\textrm{exc}\right] \nonumber \\&\quad - j_{\textrm{n},\mu }^{\textrm{Glu}}\left[ u_{\textrm{n,}\mu } - E_\textrm{exc}\right] - j_{\textrm{n},\mu }^{\textrm{GABA}}\left[ u_{\textrm{n},\mu } - E_\textrm{inh}\right] \,. \end{aligned}$$
(15c)

Calculating these energy consumption rates for the neuronal network of C. elegans during locomotion (cf. Figure 12), yields the results shown in Fig. 13. Comparing Fig. 13a, d, we find that the ion channels have by far the highest energy consumption rate. Gap junctions and synapses, on the other hand, account for only a small fraction of the consumed energy. From an energy-efficiency point of view, it seems advantageous to have small numbers of neurons but a large number of interconnections. This is supported by the fact that C. elegans possesses merely 300 neurons, but several thousand connections via gap junctions or synapses. Moreover, this suggests that neurons with a high degree of connectivity, such as interneurons, are especially important for an energy-efficient information processing.

Fig. 13
figure 13

Energy consumption rates. a Rates for the ion channels of all neurons, and b average rates for ion channels of a single, active neuron. c Comparison of average rates with respect to the number of active sensory, motor, and interneurons. d Rates for all gap junctions and synapses, and e rates for all synapses of a specific neurotransmitter type. f Average rates for a single synaptic or gap junctions connection vs the total number of connections present for the type of connection (i.e. ACh-synapse, GABA-synapse, Glu-synapse, gap junction)

Full size image

Observing Fig. 13a, we see that the motor neurons show the highest energy consumption rate, followed by the inter and the sensory neurons. This is directly related to the fact that during locomotion, almost all motor neurons of the entire neuronal network are active, but only 2/3 of the interneurons and only three of the sensory neurons. Considering the average energy consumption rates of single, active neurons depicted in Fig. 13b shows that a motor neuron consumes the least amount of energy. A sensory neuron has the highest average energy consumption rate, although the rate fluctuates strongly due to the fast oscillating behavior of the sensory neurons. The average consumption rate of interneurons is only slightly lower than the one of a sensory neuron, but higher than that of a motor neuron by a factor of 1.6. This can be explained by the isopotential behavior of the interneurons. This type of behavior implies that the neurons are constantly in a state that is not their resting state and hence constantly consume energy. Figure 13c presents the average energy consumption rates of individual sensory, inter, and motor neurons. The rates are ordered by how many neurons of each type are active during locomotion. The figure shows that the more energetically expensive a neuron type is, the less frequently it occurs. This supports the idea that the neuronal network is designed with respect to energy-efficiency.

From Fig. 13d, we can see that the energy consumption rate of the gap junctions is lower than that of the synapses by a factor of five. As there are 1028 gap junctions and 2005 synapses [1], the average energy consumption rate of a single gap junction and a single synapse is \(0.3\,\textrm{pW}\) and \(0.82\,\textrm{pW}\), respectively. Hence, gap junctions consume less energy than synapses. This makes sense because gap junctions are represented by constant resistors in series to the neuron circuits and lead to synchronization effects. Synchronization of the neuronal membrane potentials in turn leads to extremely small voltage differences across the gap junction resistors, and as such, the dissipated powers are also very low.

Let us now take a look at the energy consumption rates of the different synapse types shown in Fig. 13e. It turns out that the sum of all ACh-sensitive synapses consumes the most energy, followed by Glu-sensitive synapses and GABA-sensitive synapses. Average consumption rates for single synapses with respect to how often their neurotransmitter type occurs are depicted in Fig. 13f. This shows that a single GABA-sensitive synapse consumes by far the most energy, followed by ACh-sensitive and Glu-sensitive synapses. Even in comparison to the single synapse types, gap junctions are still energetically cheaper. However, we can also see that energetically more expensive connections do not necessarily occur less frequently. In particular, even though ACh-sensitive synapses occur the most, they are energetically more expensive than, e.g., Glu-sensitive synapses. This indicates that a low energy-consumption is not the only design criterion for the neuronal network and that there probably is a balance, e.g., between ensuring functionality and keeping energy costs as low as possible.

6 Conclusion

In this work, we have designed an ideal electrical circuit modeling the somatic neuronal network and muscle system of C. elegans. For the neurons, we have used Morris–Lecar circuits in combination with RC circuits to calculate the membrane potential and a relative fluorescence of each neuron. The muscle circuits are based on a leaky integrator model, which translates into an RC circuit as well.

Simulation results of the complete circuit structure have shown that when applying an input current representing a gentle touch of the worm, a locomotion behavior can indeed be observed from the muscle activities. Results for the membrane potentials of the neurons have shown that despite simulating a forward locomotion, more than half of the entire neuronal network and almost all motor neurons are active instead of only the neurons typically associated with forward locomotion. It is very likely that this is due to the overall interconnection structure of the neurons, since experiments have been reported where, e.g., different neurons of the mechanosensory system influence each other.

In the second step, we have investigated the energy consumption rates occurring during the simulated locomotion. This has revealed that by far the most energy is consumed by the ion channels of the neurons and only a small fraction is consumed by gap junctions and synapses. Hence, a low number of neurons in contrast to a high number of interconnections is energetically favorable. This highlights the importance of strongly interconnected neurons such as interneurons. We have also considered the average energy consumption rates of the different neuron types with respect to the occurrences of the neuron types. This has shown that the more energy is consumed, the less likely a neuron type occurs in the neuronal network used for generating locomotion. Concerning the neuronal interconnections, our results have shown that gap junctions consume less energy than synapses and that from the synapses, GABA-sensitive ones are the energetically most expensive ones. Average energy consumption rates for the connection types with respect to their respective occurrences have mostly also shown the tendency that energetically expensive connections occur less frequently, with the exception of ACh-synapses. These occur the most frequently but are not the energetically cheapest connection type. As a design criterion for neuronal networks, there probably is some kind of balance between functionality and energy costs.

Table 3 Neurons with number 0–122 and their types
Full size table

As a simulation technique, we have used a wave digital algorithm that is run-time efficient and potentially real-time capable and thus especially useful for simulating larger neuronal networks. Moreover, the algorithm retains the port-wise structure of the electrical circuit due to its direct correspondence with the circuit. This allows for plasticity studies of the C. elegans connectome that can be adjusted during the run-time of the simulation.