Bifurcation analysis of strongly nonlinear injection locked spin torque oscillators

Abstract

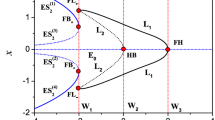
We investigate analytically and numerically the dynamics of an injection locked in-plane uniform spin torque oscillator for several forcing configurations at large driving amplitudes. For the analysis, the spin wave amplitude equation is used to reduce the dynamics to a general auto oscillator equation in which the forcing is a complex valued function $\mathcal {F}(p,\psi ) \propto \epsilon _1(p)cos(\psi )+i \epsilon _2(p)sin(\psi )$. Assuming that the oscillator is strongly non-isochronous and/or forced by a power forcing ( $|\nu \epsilon _1 / \epsilon _2|\gg 1$), we show that the parameters $\epsilon _{1,2}(p)$ govern the main bifurcation features of the Arnold tongue diagram: (i) the locking range asymmetry is mainly controlled by the derivative $d\epsilon _1/dp$, (ii) the loss of stability when the frequency mismatch between the generator and the oscillator increases occurs for a power threshold depending on $\epsilon _{1,2}(p)$ and (iii) the frequency hysteretic range is related to the transient regime at zero mismatch frequency. Then, the model is compared with the macrospin simulation for driving amplitudes as large as $10^0-10^3 A/m$ for the magnetic field and $10^{10}-10^{12} A/m^2$ for the current density. As predicted by the model, the forcing configuration (nature of the driving signal, applied stimuli direction, harmonic orders) affects substantially the oscillator dynamic. However, some discrepancies are observed. In particular, the prediction of the frequency and power locking range boundaries may be misestimated if the hysteretic boundaries are of same magnitude order. Moreover, the misestimation can be of two different types according to the bifurcation type. These effects are a further manifestation of the complexity of the dynamics in non-isochronous auto-oscillators.

Graphical Abstract

Appendices

Conversion to $m_x$, $m_y$, $m_z$ Coordinates

The Hamiltonian spin wave formalism consists in transforming the dynamic of the oscillator from the real space variable $\textbf{m}(t) =(m_x,m_y,m_z)$ to complex valued variables a(t), b(t) and $c(t)=\sqrt{p}e^{i\phi (t)}$ with the oscillation power p and the free running phase $\phi (t)$. The relation between c(t) and the complex variable d(t) used in this report is given by: $d(t)=c(t)exp(-(i \omega _gt)/n)$.

The trajectory orbit $p=cst$ in c variable can be expressed in the real space by:

$$\begin{aligned} m_x =&\, 1+2p( \frac{\mathcal {B}}{\mathcal {A}} cos(2\phi )-1) \end{aligned}$$

(A.1a)

$$\begin{aligned} m_y =&\, cos(\phi ) \sqrt{2p(1-p+ \frac{\mathcal {B}}{\mathcal {A}} p cos(2\phi ))} \nonumber \\&\left( \sqrt{1+\mathcal {G}( \frac{\mathcal {B}}{\mathcal {A}} )}- Sign( \frac{\mathcal {B}}{\mathcal {A}} )\sqrt{1+\mathcal {G}( \frac{\mathcal {B}}{\mathcal {A}} )}\right) \end{aligned}$$

(A.1b)

$$\begin{aligned} m_z =&\, -sin(\phi ) \sqrt{2p(1-p+ \frac{\mathcal {B}}{\mathcal {A}} p cos(2\phi ))} \nonumber \\&\left( \sqrt{1+\mathcal {G}( \frac{\mathcal {B}}{\mathcal {A}} )}+ Sign( \frac{\mathcal {B}}{\mathcal {A}} )\sqrt{1+\mathcal {G}( \frac{\mathcal {B}}{\mathcal {A}} )}\right) \end{aligned}$$

(A.1c)

With the function $\mathcal {G}(x)=\sqrt{1-x^2}$, the ellipticity parameter $-1 \le \mathcal {B}/\mathcal {A}\le 1$ and $0 \le \phi < 2\pi$. Some orbits are illustrated in Fig. A1.

Fig. 12

Theoretical orbits represented in the real space oriented along the $\textbf{u}_x$ axis for different ellipticities $\mathcal {B}/\mathcal {A}$ and oscillation power p. a $\mathcal {B}/\mathcal {A}=0$, b $\mathcal {B}/\mathcal {A}=-2/3$ and c $\mathcal {B}/\mathcal {A}\approx -0.91$ (studied IP-STNO). The power $p_{opp} = 1/(1+|\mathcal {B}/\mathcal {A}|)$ delimits the in-plane precession mode from the out of plane precession mode

Stability Analysis and Hopf Bifurcation

The dynamical system Eq. 3 is resumed:

$$\begin{aligned}&\dot{p}=-2Z(p)+2p \epsilon _1(p) a_g cos{\psi } \end{aligned}$$

(B.2a)

$$\begin{aligned}&\dot{\psi } = n \omega (p) - \omega _g+ n\epsilon _2(p) a_g sin(\psi ) \end{aligned}$$

(B.2b)

To simplify the calculations, we have set $\theta =0$ and define $Z(p)=p\Gamma (p)$.

On the first hand, the stationary states of Eq. B.2 must verify the equilibrium conditions $\dot{p}=0$ and $\dot{\psi }=0$, which rewrite:

$$\begin{aligned}&cos(\psi )=\frac{Z(p)}{p a_g \epsilon _1(p)} \end{aligned}$$

(B.3a)

$$\begin{aligned}&sin(\psi ) = \frac{-n \omega (p)+\omega _g}{n a_g \epsilon _2(p)} \end{aligned}$$

(B.3b)

On the other hand, the Jacobian matrix J of Eq. B.2 evaluated at the stationary point $(p,\psi )$ is:

$$\begin{aligned} J(p,\psi ) = \begin{bmatrix} -2 Z^{(1)} + 2a_g(\epsilon _1+p \epsilon _1^{(1)})cos(\psi ) &{} -2 p a_g \epsilon _1sin(\psi ) \\ nN + n a_g \epsilon _2^{(1)}sin(\psi ) &{} n a_g \epsilon _2cos(\psi ) \end{bmatrix}\nonumber \\ \end{aligned}$$

(B.4)

Now, we focus on the quantity $Tr(J(p,\psi ))$:

$$\begin{aligned} Tr(J)=-2Z^{(1)} + 2 a_g(\epsilon _1+p \epsilon _1^{(1)}) cos(\psi ) \nonumber \\ + n a_g \epsilon _2cos(\psi ) \end{aligned}$$

(B.5)

Removing $\psi$ with Eq. B.3a leads to:

$$\begin{aligned} Tr(J) = \frac{Z}{p} \left( -2\frac{Z^{(1)}p}{Z}+\frac{2(\epsilon _1+p\epsilon _1^{(1)})}{\epsilon _1}+\frac{n \epsilon _2}{\epsilon _1} \right) \end{aligned}$$

(B.6)

Note the useful relation:

$$\begin{aligned} \frac{Z^{(1)}(p)p}{Z(p)} = 1+\frac{p}{\Delta p} \end{aligned}$$

(B.7)

with $\Delta p=p-p_0$ and $p_0$ the free running power.

Inserted Eq. B.7 in Eq. B.6 gives:

$$\begin{aligned} Tr(J)=\frac{2Z}{p\Delta p} \left( -p+\frac{p\Delta p \epsilon _1^{(1)}}{\epsilon _1} + \frac{\Delta p n \epsilon _2}{2\epsilon _1} \right) \end{aligned}$$

(B.8)

The threshold power $p_{h}$ is defined by $Tr(J(p_{h}))=0$ so that we obtain Eq. 9:

$$\begin{aligned}{} & {} p_h ( p_h - p_0 ) \frac{\epsilon _1^{(1)}(p_h)}{\epsilon _1(p_h)} + (p_h-p_0) \frac{n \epsilon _2(p_h)}{2 \epsilon _1(p_h)} \nonumber \\{} & {} \quad - p_h =0 \end{aligned}$$

(B.9)

Transient regime

The Jacobian matrix $J(p,\psi )$ Eq. 8 or Eq. B.4 with $\epsilon _2= 0$ is evaluated at zero detuning ($\delta =0$, $p=p_0$, $\psi =\pi /2$):

$$\begin{aligned} J(p,\psi ) = \begin{bmatrix} -2 \Gamma _p&{} -2 p a_g \epsilon _1\\ nN &{} 0 \end{bmatrix} \end{aligned}$$

(C.10)

The eigenvalues of the matrix are given by:

$$\begin{aligned} \lambda _{\pm } = -\Gamma _p\left( 1\pm \sqrt{1-\frac{2\Delta \Omega _S}{\Gamma _p}} \right) \end{aligned}$$

(C.11)

The transient regime becomes oscillatory for the condition $\Delta \Omega _S>\Gamma _p/2$ with the complex eigenvalues:

$$\begin{aligned} \lambda _{\pm } = -\Gamma _p\left( 1\pm i \sqrt{\frac{2\Delta \Omega _S}{\Gamma _p}-1} \right) \end{aligned}$$

(C.12)

We denote $|\lambda |=|\lambda _{\pm }|$ the frequency of the transient oscillation in absence of damping:

$$\begin{aligned} |\lambda | = \sqrt{2\Gamma _p\Delta \Omega _S} \end{aligned}$$

(C.13)

If the transient regime is oscillatory, one can define the frequency of the pseudo-oscillation in presence of damping [41, 42]:

$$\begin{aligned} \Omega = \sqrt{2\Gamma _p\Delta \Omega _S-\Gamma _p^2} \end{aligned}$$

(C.14)

There is also the resonant frequency of the system $\omega _{roll-off}$, which can be measured from the phase noise diagram of the oscillator [40]. Resuming the expression of the phase noise Eq.5 in Ref. [40], $\omega _{roll-off}$ is obtained by maximizing the denominator:

$$\begin{aligned} \omega _{roll-off} = \sqrt{2\Gamma _p\Delta \Omega _S-2\Gamma _p^2} \end{aligned}$$

(C.15)

In our case, the oscillator is strongly non isochronous and the damping $\Gamma _p$ is weak compared to $\Delta \Omega _S$, so that the three frequencies become equivalent:

$$\begin{aligned} |\lambda | \approx \Omega \approx \omega _{roll-off} \end{aligned}$$

(C.16)