Critical phenomena in complex networks: from scale-free to random networks

Abstract

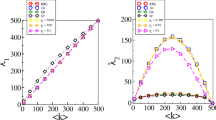
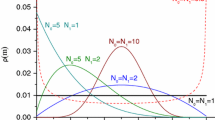
Within the conventional statistical physics framework, we study critical phenomena in configuration network models with hidden variables controlling links between pairs of nodes. We obtain analytical expressions for the average node degree, the expected number of edges in the graph, and the Landau and Helmholtz free energies. We demonstrate that the network’s temperature controls the average node degree in the whole network. We also show that phase transition in an asymptotically sparse network leads to fundamental structural changes in the network topology. Below the critical temperature, the graph is completely disconnected; above the critical temperature, the graph becomes connected, and a giant component appears. Increasing temperature changes the degree distribution from power-degree for lower temperatures to a Poisson-like distribution for high temperatures. Our findings suggest that temperature might be an inalienable property of real networks.

Graphical abstract

Appendices

A Generalized configuration model: $\mu < \varepsilon _0$

In this section, we will discuss a general configuration model with exponential distribution of the density of states, assuming that the chemical potential and energy are limited by a maximum value of $\varepsilon _0$ so that $\mu \le \varepsilon _0$ and $0 \le \varepsilon _i \le \varepsilon _0$. By imposing the standard normalization condition, $\int _0^{\varepsilon _0 }\rho (\varepsilon ) \textrm{d} \varepsilon =1$, we obtain

$$\begin{aligned} \rho _g(\varepsilon ) = \,&\frac{\alpha \beta e^{\alpha \beta (\varepsilon - \varepsilon _0/2)}}{2\sinh (a\beta \varepsilon _0/2)}, \quad \textrm{Type} \, A \end{aligned}$$

(91)

$$\begin{aligned} \rho _d(\varepsilon ) = \,&\frac{\alpha \beta e^{-a \beta (\varepsilon - \varepsilon _0/2)}}{2\sinh (a\beta \varepsilon _0/2)}, \quad \textrm{Type} \, B \end{aligned}$$

(92)

where $\alpha = \beta _c (\gamma -1)/\beta$, and $\beta _c =1/T_c$ is a constant with dimension of inverse temperature. The computation of the expected vertex degree ${\bar{k}} (\varepsilon )$, expected number of links L, and the Landau free energy $\Omega$ yields

• Type A

  $$\begin{aligned}&{\bar{k}}_g(\varepsilon ) = \frac{N-1}{2\sinh (\alpha \beta \varepsilon _0/2)} \Big ( e^{\alpha \beta \varepsilon _0/2 } \nonumber \\&\qquad \times {}_{2}F_{1} \big (1, \alpha ; 1+\alpha ;-e^{ \beta (\varepsilon + \varepsilon _0- \mu )} \big ) \nonumber \\&\qquad - e^{-\alpha \beta \varepsilon _0 /2}{}_{2}F_{1} \big (1, \alpha ; 1+\alpha ;- e^{ \beta (\varepsilon -\mu )} \big ) \Big ) , \end{aligned}$$

  (93)
  $$\begin{aligned}&L_g= \frac{N(N-1) }{8\sinh ^2(\alpha \beta \varepsilon _0/2)} \Big ( e^{\alpha \beta \varepsilon _0 } \nonumber \\&\qquad \times {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ \beta (2 \varepsilon _0 - \mu )} \big ) \nonumber \\&\qquad - 2 {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ \beta (\varepsilon _0 - \mu )}\big ) \nonumber \\&\qquad + e^{ -\alpha \beta \varepsilon _0} {}_{3}F_{2}\big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ -\beta \mu } \big )\Big ), \end{aligned}$$

  (94)
  $$\begin{aligned}&\Omega _g= -\frac{1}{a \beta }L_g - \frac{N(N-1) }{8 \beta \sinh ^2(\alpha \beta \varepsilon _0/2)} \Big ( e^{\alpha \beta \varepsilon _0} \nonumber \\ {}&\qquad \times \ln \big (1 + e^{\beta (\mu - 2\varepsilon _0)} \big ) \nonumber \\&\qquad -2\ln \big (1 + e^{\beta (\mu - \varepsilon _0)} \big ) +e^{-\alpha \beta \varepsilon _0} \ln \big (1 + e^{\beta \mu } \big )\nonumber \\&\qquad + e^{\alpha \beta \varepsilon _0} \Phi (-e^{\beta (2\varepsilon _0-\mu )},1,\alpha ) \big ) \nonumber \\&\qquad -2 \Phi (-e^{\beta (\varepsilon _0-\mu )},1,\alpha ) \big ) + e^{-\alpha \beta \varepsilon _0}\Phi (-e^{-\beta \mu },1,\alpha ) \Big ) , \end{aligned}$$

  (95)

• Type B

  $$\begin{aligned}&{\bar{k}}_d (\varepsilon )= \frac{(N-1) \alpha e^{\beta (\mu - \varepsilon ) } e^{\alpha \beta \varepsilon _0/2 } }{2(1 +\alpha )\sinh (\alpha \beta \varepsilon _0/2)} \nonumber \\&\qquad \times \Big ({}_{2}F_{1} \big (1, 1+\alpha ; 2+\alpha ;-e^{ \beta (\mu -\varepsilon )} \big )\nonumber \\&\qquad - e^{-(1+\alpha )\beta \varepsilon _0 }{}_{2}F_{1} \big (1, 1+\alpha ; 2 +\alpha ;- e^{ \beta ( \mu - \varepsilon - \varepsilon _0 )} \big ) \Big ) , \end{aligned}$$

  (96)
  $$\begin{aligned}&L_d = \frac{N(N-1)\alpha ^2 e^{\beta ( \mu - \varepsilon _0 )}}{8(1+\alpha )^2\sinh ^2(\alpha \beta \varepsilon _0/2)} \Big (e^{(1+\alpha ) \beta \varepsilon _0} \nonumber \\&\qquad \times {}_{3}F_{2} \big (1, 1+\alpha ,1+\alpha ; 2+\alpha , 2+\alpha ;- e^{ \beta \mu } \big ) \nonumber \\&\qquad + e^{-(1+\alpha ) \beta \varepsilon _0}{}_{3}F_{2} \big (1, 1+\alpha ,1+\alpha ;\nonumber \\&\qquad 2+\alpha , 2+\alpha ;- e^{\beta (\mu - 2\varepsilon _0 )}\big ) \nonumber \\&\qquad - 2 {}_{3}F_{2} \big (1,1+ \alpha ,1+ \alpha ; 2+\alpha , 2+\alpha ;- e^{\beta (\mu - \varepsilon _0 )} \big ) \Big ). \end{aligned}$$

  (97)
  $$\begin{aligned}&\Omega _d= \frac{1}{\alpha \beta }L_d - \frac{N(N-1) }{8 \beta \sinh ^2(\alpha \beta \varepsilon _0/2)} \nonumber \\ {}&\qquad \times \Big ( e^{-\alpha \beta \varepsilon _0} \ln \big (1 + e^{\beta (\mu - 2\varepsilon _0)} \big )\nonumber \\&\qquad -2\ln \big (1 + e^{\beta (\mu - \varepsilon _0)} \big ) \nonumber \\&\qquad +e^{\alpha \beta \varepsilon _0} \ln \big (1 + e^{\beta \mu } \big ) + e^{-\alpha \beta \varepsilon _0} \Phi (-e^{\beta (2\varepsilon _0-\mu )},1,-\alpha \big ) \nonumber \\&\qquad -2 \Phi \big (-e^{\beta (\varepsilon _0-\mu )},1,-\alpha \big ) \nonumber \\&\qquad + e^{\alpha \beta \varepsilon _0}\Phi \big (-e^{-\beta \mu },1,-\alpha \big ) \Big ) , \end{aligned}$$

  (98)

where ${}_{p}F_{q}(a_1, \dots , a_p; b_1, \dots , b_q; z)$ is the generalized hypergeometric function, and $\Phi (z,a,b)$ denotes the Lerch transcendent [40, 41].

B Deduction of the constant $\nu$

This section examines the chemical potential $\mu = T_c\ln (\nu /\kappa )$ to determine the constant $\nu$. To proceed, we use the relation $L = \langle k \rangle N/2$ for the Type A graph (see Eq. (27))

$$\begin{aligned}&L= \frac{N(N-1) }{8\sinh ^2(\alpha \beta \mu /2)} \Big ( e^{\alpha \beta \mu } {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ \beta \mu } \big ) \nonumber \\&\qquad - 2 {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- 1\big ) \nonumber \\&\qquad + e^{ -\alpha \beta \mu } {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ -\beta \mu } \big )\Big ). \end{aligned}$$

(99)

Hereafter, we omit the subindices g/d in all calculations. After substitution of $\langle k \rangle =(N-1)\nu e^{- \beta _c\mu }$, we obtain

$$\begin{aligned}&\nu = \frac{e^{ \beta _c\mu }}{4\sinh ^2(\alpha \beta \mu /2)} \Big ( e^{\alpha \beta \mu } {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ \beta \mu } \big ) \nonumber \\&\qquad - 2 {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- 1\big ) \nonumber \\&\qquad + e^{ -\alpha \beta \mu } {}_{3}F_{2} \big (1, \alpha , \alpha ; 1+\alpha , 1+\alpha ;- e^{ -\beta \mu } \big )\Big ). \end{aligned}$$

(100)

We make use of the asymptotic properties of the generalized hypergeometric functions [40, 41, 43] to get

$$\begin{aligned} \nu = \bigg (\frac{\gamma -1}{\gamma -2}\bigg )^2 e^{(\beta _c - \beta )\mu }+ {{\mathcal {O}}} (e^{-(\gamma -2 )\beta _c \mu } ). \end{aligned}$$

(101)

As seen, the asymptotic series converges when $\gamma > 2$. Still supposing $\gamma > 2$ and, in addition, assuming that $\mu (T) \rightarrow \infty$ when $T \rightarrow T_c+$, we obtain

$$\begin{aligned} \nu = \bigg (\frac{\gamma -1}{\gamma -2}\bigg )^2. \end{aligned}$$

(102)

For high temperatures, $T \gg T_c$, similar consideration yields

$$\begin{aligned} \nu e^{-\beta _c \mu } = - \alpha ^2 \beta '(\alpha ) + {{\mathcal {O}}} (1 -e^{-\beta \mu } ). \end{aligned}$$

(103)

Substituting $\alpha = \beta _c (\gamma -1)/\beta$ and taking the limit of $T \rightarrow \infty$, we get

$$\begin{aligned} \mu \rightarrow \mu _0 = \ln \bigg (\frac{2(\gamma -1)^2}{(\gamma -2)^2} \bigg )\quad \textrm{and } \quad \kappa \rightarrow \frac{1}{2}. \end{aligned}$$

(104)

C Generating function

Following Ref. [28], we define a generating function as

$$\begin{aligned} G_0(z) = \sum _k z^k P(k) , \end{aligned}$$

(105)

where P(k) is the degree distribution (the probability that any given vertex has degree k). Further, all calculations will be confined to the region $0\le z\le 1$.

Having the generating function, one can easily calculate the degree distribution and its moments:

(106)

(107)

In particular, this yields

$$\begin{aligned} \langle k \rangle =G'_0(1), \,\, \langle k^2 \rangle = G''_0(1) + G'_0(1). \end{aligned}$$

(108)

Further, it is convenient to introduce the abbreviation for derivatives of the generating function:

$$\begin{aligned} z_n =\frac{\textrm{d}^n}{\textrm{d}z^n}G_0(z)\Big {|}_{z=1}. \end{aligned}$$

(109)

Then, using Eq. (107), we obtain $\langle k \rangle = z_1$, $\langle k^2 \rangle = z_2 + z_1$, etc.

We are now ready to analyze the topological properties of the network. First, we are interested in the degree distribution, P(k) . To proceed, we employ the generating functions approach presented in Appendix C. To compute $G_0(z)$, we use the generating function formalism for networks with hidden variables developed in Ref. [47]. Following Ref. [47], one can write the degree distribution as

$$\begin{aligned} P(k) = \int g(k \mid \varepsilon )\rho (\varepsilon ) \textrm{d}\varepsilon , \end{aligned}$$

(110)

where $g(k \mid \varepsilon )$ denotes the propagator, with the normalization condition $\sum _k g(k \mid \varepsilon ) =1$. Substituting P(k) in Eq. (105), we obtain

$$\begin{aligned} G_0(z) = \int \textrm{d}\varepsilon \rho (\varepsilon )\sum _k z^k g(k \mid \varepsilon ). \end{aligned}$$

(111)

As shown in Ref. [47],

$$\begin{aligned} \ln \sum _k z^k g(k \mid \varepsilon )= N\int \textrm{d}\varepsilon ^{\prime }\rho (\varepsilon ^{\prime }) \ln \big (1-(1-z) p(\varepsilon , \varepsilon ^{\prime })\big ). \end{aligned}$$

(112)

Using this result in Eq. (111), we obtain

(113)

Employing (113) and the results of Ref. [47], one can write the generating function as

(114)

where ${\bar{k}} (\varepsilon ) = N \int p(\varepsilon , \varepsilon ' ) \rho (\varepsilon ' ) \textrm{d} \varepsilon '$ is the expected degree of the node with the hidden variable $\varepsilon$.