A method to detect quantum coherent transport in memristive devices

Abstract

While the size of functional elements in memristors becomes of the orders of nano-meters or even smaller, the quantum effects in their dynamics can significantly influence their transport properties, consistent with recent experimental observations of conductance quantisation in memristors. This requires the development of experimentally accessible signatures of quantum behaviour in memristive systems, such as a superposition of quantum states with different memristances. Here we discuss one such protocol. Our simulations show that periodic projective measurements induce additional spectral components in the response of quantum memristor to a harmonic input signal. Moreover, the response demonstrates a resonant behaviour when the frequency of the projective measurements commensurates with the frequency of the input. We demonstrate that observation of such harmonic mixing can be used as experimental evidence of quantum effects in memristors.

Graphic abstract

1 Introduction

Memristors were first proposed back in 1971 [1] as a logically necessary complement to the fundamental lumped circuit elements (resistors, capacitors, and inductors). These elements parameterise the relations between the dynamical variables of the circuit: current I, charge q, voltage V and magnetic flux through a closed contour (or, equivalently, the integral over time of the voltage on a circuit element) $\varphi$. Memristors were the “missing link”; its appearance restores the symmetry in the set of fundamental circuit elements including resistor, capacitor and inductor by coupling charge and magnetic flux. The term (a portmanteau of “memory” and “resistor”) reflects that a memristor can be considered a resistor, the resistance of which depends on the cumulative q or $\varphi$ [2]. Later, a more general terminology was introduced, such as ”memristive devices”, where the resistance is assumed to be a function of some internal variable, which changes depending on the voltage and current across the memristive element. [3] In the following we use the term ”memristor” for both Chua memristors and more general ”memristive systems”.

It is well known that reactive circuit elements have their fully quantum analogues (see, e.g., [4]) and can be realised via qubit-based structures, which demonstrate quantum superpositions of states with different inductances (capacitances). For lossy circuit elements, such behaviour may seem impossible due to the inevitable dissipation, detrimental to quantum coherence. Nevertheless, such a conclusion would be hasty. Here we state that full quantum analogues also exist for active circuit elements, i.e., resistors and memristors. In particular, these elements (quantum resistors and memristors) can be put in a quantum superposition of states with different resistances or memristances. This seemingly paradoxical possibility is provided by the fact that in a number of mesoscopic structures (such as point contacts) the momentum and energy relaxation is controlled by separate mechanisms with different temporal and spatial characteristics. The standard example of this is given by the Landauer–Büttiker expression of electric conductance between two bulk reservoirs connected through a quantum scatterer in terms of the latter’s scattering matrix [5], in the simplest case given by $G=\frac{e^2}{h} |\mathcal{T} |^2$ ($\mathcal T$ being the transmission amplitude).

While the conductance is determined by the elastic, quantum coherent scattering of electrons, the relaxation towards the equilibrium distribution takes place deep in the bulk of the reservoirs spatially separated from the scatterer. This produces two different time scales, for momentum and energy relaxation of the electrons. Only the latter necessarily destroys quantum coherence. Therefore, a quantum scatterer in a superposition of states with different scattering matrices can be legitimately considered a quantum resistor. Similar considerations will hold for an abstract quantum memristor.

The upper limit on the lifetime of such a superposition, $\tau =1/\Gamma$, can be obtained from the result by Averin and Sukhorukov [6], who showed that electrons passing between two thermal baths through a qubit-controlled point contact realise a continuous weak readout of qubit’s quantum state with the rate $\Gamma =\frac{eV}{h} \ln |\mathcal{T}_0 \mathcal{T}_1^* + \mathcal{R}_0 \mathcal{R}_1^*|$ where V is the voltage across the contact, and $\mathcal{T}_{0,1}$, $\mathcal{R}_{0,1}$ are the transmission and reflection coefficients when the qubit is in the state 0 or 1, respectively. This result can be considered a quantum elaboration of the Landauer–Büttiker formalism [5], since the reversible scattering process, which determines the resistance, and irreversible processes of electron equilibration are separated both spatially and temporally. In this paper we consider the case when the weak readout rate $\Gamma$ is low, and the collapse of the quantum state of the system can be enforced by strong projective measurements of the state of the system (which is equivalent to measuring the voltage across it) repeated at intervals significantly shorter than $\tau$.

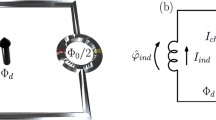
We analyse the nonlinear effects arising from repeated measurements of the memristor. The proposed system is essentially a Schrödinger’s cat, with the memristive electrical circuit controlled by quantum switch. Specific physical implementations of this qubit-controlled memristive device, which will be referred below as a quantum memristor, will be considered elsewhere. For now, we note that it can be formally represented by two classical memristors in parallel and a quantum switch sending electron pulse through either of them (Fig. 1). We look at the effects of regular measurement on spectral properties of the output of a proposed device. We use the simplest mathematical model of quantum memristor to better understand its expected behaviour under the influence of noise. We consider a noise process described via a gaussian function with a large standard deviation, to ensure that our methodology is robust enough to detect the signatures of transport in realistically unideal cases, suitable for practical implementation.

Fig. 1

Schematics of our simulated system. A superposition of states of a quantum scatterer, S, imposes a superposition of memristances

2 Classical memristors

First, consider the general case of a classical current-driven memristance M at a time t. The memristance depends on the state variables x, where M and x are described by the following: [2]

$$\begin{aligned}&V = M(x,I,t) I \end{aligned}$$

(1)

$$\begin{aligned}&\frac{dx}{dt}= f(x,I,t) \end{aligned}$$

(2)

Here, in an agreement with what was stated above, the voltage V is treated as the response of the memristor to the controlling current I(t). The function M(x, I, t), without the loss of generality, can be represented as $M(x,I,t)=M_0 + M_1(x,I,t)$. Then implies that for a piece-wise smooth $M_1$, one should expect a linear response to a weak enough sinusoidal input signal $I(t)=I_0\sin (\omega _s t)$:

$$\begin{aligned} V_C = I_0 M_1(x,t) \sin (\omega _st)+I_0 M_0 \sin (\omega _st) \end{aligned}$$

(3)

The methods detailed in this report can be utilised for other peaks in the spectra, but their amplitudes may not be as significant, leading them to be more sensitive to noise. This method would also be appropriate for an equivalent resistive system.

3 Quantum model

We are not concerned here with a specific realisation of a quantum memristor (Fig. 1), though one can speculate that it can be achieved by introducing a quantum scatterer into a Van der Waals heterostructure [7] or a singularly charged pair of quantum dots, where electrons in each state get transported to different memristive filaments. The superposition of memristive states that arises in such a system is due to a superposition in position, akin to Young’s double slit experiment. Measuring the state of the qubit (as clarified in the following section) gives an eigenvalue j=0,1, corresponding to the qubit states $|0\rangle$, $|1\rangle$, corresponding to transport through memristor ’0’ or ’1’. Even though most of our simulation are done for quantum switch described by pure states, our approach can be easily extended to the case when the switch is described by the density matrix $\rho$ parametrised by the component of the Bloch vector (X, Y, Z) (see, e.g., in [8]).

Between measurements, the quantum switch evolves according either to the Schrödinger equation for its wave function, or, in the presence of dephasing and relaxation, to the master equation for its density matrix. Either will determine the probability of switching ($P_{sw}$) at each measurement. We describe state switching through pulse functions $\Pi _j(t)$. If the $k^{th}$ measurement projects onto the state j, then during the proceeding time interval (between times [$t_{mk}$,$t_{mk+1}$]), we had $\Pi _j=1$ and $\Pi _{1-j}=0$. This acts as an on/off switch for each state, illustrated in Fig. 2. $V_{Cj}$ is the voltage response we would expect from the classical memristor in state j, with no switching. This equation is how we generate $V_Q$ from our projective measurements:

$$\begin{aligned} V_Q(t)=\sum _{j=0}^1 \Pi _j(t) V_{Cj}(t) \end{aligned}$$

(4)

Fig. 2

Square wave switching functions $\Pi _j$ for periodic measurements. a Is an example $\Pi _0$, with a 100% switching probability, $P_{sw}=1$. The arrows demonstrate the period of the square wave, $2\pi /\omega _m$. b is an example with a lower $P_{sw}=0.4$

Pulse widths in $\Pi _j$ are characterised by the statistics of measurement events and $P_{sw}$. $P_{sw}$ acts as a mediator between the classical and quantum cases. The $P_{sw}=0$ case corresponds to a classical system of electron transport through only one of the memristive filaments (no superpositions of electron position). $P_{sw}$ depends on the state at the measurement times.

We utilise a pseudospin Hamiltonian for the purposes of this report (Eq. (5)) where the tunnelling amplitude, $\Delta$, and the bias, $\epsilon$, had been chosen to give a high switching probability:

$$\begin{aligned} H_0=-\frac{1}{2}(\Delta \sigma _x+\epsilon \sigma _z) \end{aligned}$$

(5)

For a pure quantum switch, we have the evolution of the wave function $|\psi \rangle =a_0|0\rangle +a_1|1\rangle$ described by the Schrödinger equation

$$\begin{aligned} \frac{d}{dt}|\psi \rangle =\frac{1}{i\hbar }H_0|\psi \rangle \end{aligned}$$

(6)

resulting in the set of equations:

$$\begin{aligned} i\hbar \frac{da_0}{dt}= & {} -\frac{\epsilon }{2}a_0-\frac{\Delta }{2}a_1 \end{aligned}$$

(7)

$$\begin{aligned} i\hbar \frac{da_1}{dt}= & {} -\frac{\Delta }{2}a_0+\frac{\Delta }{2}a_1 \end{aligned}$$

(8)

The evolution of the Bloch vector is defined by the master equation:

$$\begin{aligned} \frac{dX}{dt}= & {} \Delta Y-\Gamma _{\varphi }X \end{aligned}$$

(9)

$$\begin{aligned} \frac{dY}{dt}= & {} -\Delta X+\epsilon Z-\Gamma _{\varphi }Y\end{aligned}$$

(10)

$$\begin{aligned} \frac{dZ}{dt}= & {} -\epsilon Y-\Gamma _{T}(Z-Z_T) \end{aligned}$$

(11)

with $\Gamma _{\varphi }$ and $\Gamma _{T}$ being dephasing and relaxation rates, while $Z_T=\tanh (\Delta /2k_BT)$ with the Boltzmann constant $k_B$ and temperature T. The probability for the system to switch to $|0\rangle$ state is $P_0=a_0a^*_0$ for unitary and $P_0=(1+Z)/2$ for non-unitary evolution, while the probability of switching to state $|1\rangle$ is respectively $P_1=a_1a^*_1$ or $P_1=(1-Z)/2$. For Figs. 4 and 5b we consider a pure quantum switch. In Fig. 5 we include a case with decoherence, a non-pure switch.

We also consider examples where there is some uncertainty in the measurement frequency to model realistically imperfect measurement protocols. This uncertainty is normally distributed around the average measurement frequency $\omega _m$, by a variance of $\sigma _\omega ^2$.

The spectrum of the output signal VQ(t) defined by Eq. (4), ${\tilde{V}}_Q(\omega )$, can be calculated as the convolution of ${\tilde{\Pi }}_j(\omega )$ and ${\tilde{V}}_{Cj}(\omega )$:

$$\begin{aligned} {\tilde{V}}_Q(\omega )&= \sum _{j=0}^1 {\tilde{\Pi }}_j(\omega ) * {\tilde{V}}_{Cj}(\omega ). \end{aligned}$$

(12)

To determine ${\tilde{\Pi }}_j(\omega )$, we use our ideal model for $\Pi _j(t)$, a periodic square wave of frequency $\omega _m/2\pi$ (halved since 4 measurements are needed for a full wave form, see Fig. 2a). For this figure, we assume a 100% switching probability, a suitable approximation, since we selected a Hamiltonian to give a high switching probability (at our measurement frequency).

The most significant peaks in ${\tilde{\Pi }}_j(\omega )$ are at odd multiples of $\omega _m/2\pi$. To find ${\tilde{\Pi }}_j(\omega )$, we first found the Fourier coefficients for $\Pi _j(t)$, before using this to calculate the one-sided Fourier transform. We let $\overline{\psi _j}$ be the time-average of $\Pi _j$ (for a high switching rate, this will be $\approx$0.5).

Using our general form for each memristive site (Eq. (3)), we see two terms in the Fourier transform ${\tilde{V}}_{Cj}$. We are only interested in the primary peak in this work, so we let the Fourier transform of the first term ($I_0M_1\sin (\omega _st))$ be ${\tilde{V}}'_{j}$, we are not interested in the specifics of these peaks in the spectra. We also assume that the time-average of $V_{Cj}$ is negligible.

$$\begin{aligned} {\tilde{\Pi }}_j(\omega )&\approx \overline{\psi _j}\delta (\omega ) + i \sqrt{\frac{\pi \omega _m}{2}}\sum _{n=0}^N \frac{\delta (\omega -\frac{(2n+1)\omega _{m}}{2})}{\omega } \end{aligned}$$

(13)

$$\begin{aligned} {\tilde{V}}_{Cj}(\omega )&= {\tilde{V}}_j' +i M_{0j}I_0 \delta (\omega -\omega _s) \end{aligned}$$

(14)

By solving Eq. (12) at the primary peak, we get

$$\begin{aligned} \begin{aligned}&{\tilde{V}}_Q(\omega _s)\approx \sum _{j=0}^1 M_{0j}I_0 \biggl ( i\overline{\psi _j} \\ {}&\quad - ... \sqrt{\frac{\pi \omega _m}{2 \omega _s^2}} \sum _{n=0}^N \delta (\omega _s- \frac{(2n+1)\omega _m}{4\pi })\biggr ) \end{aligned}\nonumber \\ \end{aligned}$$

(15)

From this, we expect resonant peaks in ${\tilde{V}}_Q(\omega _s)$ when $\omega _s=\frac{(2n+1)\omega _m}{4\pi }$. This frequency mixing is characteristic of the application of projective measurements, we do not expect to observe this in the classical case.

Fig. 3

Schematic diagram demonstrating the measurement process. The qubit is collapsed at a time $t_m$, and the voltage is measured within the interval $t_m<t<t_m+\tau$

4 Measurement

In our model, the memristance of the system is controlled by the quantum bit, as is schematically shown in Fig. 3, and the observed memristance is determined by the qubit’s quantum state at the exact moment of measurement, $t_m$, before which it undergoes a free unitary evolution. This description is literally true if the projective measurement of the qubit state is performed first, and the voltage across the structure is measured once it is established, within $\tau$ after that. This is a possible approach, since the fast qubit readout is a well-established experimental procedure [9].

A straightforward measurement of the voltage across the system will also effectively read out the state of the qubit, but the moment of the measurement will be determined within the interval $\tau ^\prime <\tau$ necessary for establishing the memristance of the system in the presence of a voltmeter. In either case, the requirement $t_m \ll \tau$ must be satisfied, which is the same requirement for the applicability of our model.

5 Simulations

We use powers of two for many variables, since having $2^k$ data points is most efficient for calculations using the fast Fourier transform. We find appropriate convergence with a step size of $dt=2^{-16}/\omega _m$, where $\omega _m$ is the measurement frequency. (Or, in the cases with noise, $\omega _m$ is the average of the gaussians which determine the measurement frequencies.)

We simulate frequency sweeps to look for evidence of the signal mixing described in Eq. 15. To look for periodicity, we collect data up to the $10^{th}$ harmonic of $\omega _m$, 0$< \omega _s < 10\omega _m$. $2^9$ consecutive measurement events are analysed for each $\omega _s$.

Fig. 4

Emergence of spikes in the spectra as the probability of switching ($P_{sw}$) increases for $\omega _s$=100Hz, characteristic of the signal mixing we aim to observe. When $P_{sw}=0$, there is no (relevant) real part to the spectrum. For low switching probabilities, the real part mimics the imaginary part, with a reduced amplitude. We see the emergence of the characteristic peaks/troughs at mid-range probabilities. At high $P_{sw}$ we see all resonances, the ’odd’ set (i.e., odd n in $\omega /\omega _s=n/4$) having a higher amplitude than the even set

Fig. 5

Real component of the primary peak as $\omega _s$ is varied. We see the signatures of the measurement process as predicted, peaks in the spectra at the key frequencies of $\omega _s=\frac{2n+1}{4\pi }\omega _m$. These are in addition to the peak at the square wave frequency, $\omega _s=\omega _m/2\pi$. 5a shows the clear differences between the classical and quantum cases. We simulated cases with pure and mixed quantum switches, i.e., the mixed switch exhibits some thermalisation. This lead to a reduction in the significance of the key peaks, but their position is still evident, especially compared to the simulated pure case. 5b demonstrates this method can be used in noisy systems, we still see peaks at many of the characteristic frequencies when there is a 10% standard deviation in the measurement frequency. We use $\Delta =3450$ and $\epsilon =5$ for our Hamiltonian parameters. These values ensured a high probability of switching across the trials conducted

We initiate quantum state of the switch as $a_0=1,\ a_1=0$ (that is $|\psi \rangle =|0\rangle$) for pure system and $Z=1$ for the mixed system. Next, using the 4$^{th}$ order Runge–Kutta method, we numerically integrate Eqs. (8) for the simulations of the pure state and (11) for the mixed state, until the first measurements at $t_m=2\pi /\omega _m$. We then estimate the probability of the system collapsing to the ground state $P_0$ or the excited state $P_1$, using this to simulate the collapse of the wave function by comparing these values to a generated random number between 0 and 1. The ground state has parameters $a_0=1, \ a_1=0$ for the pure case and $Z=1, X=0, Y=0$ for the mixed case; the excited state has $a_0=0, \ a_1=1$ for the pure case and $Z=0, X=1, Y=1$ for the mixed case. This then identifies the initial condition for the switch at the beginning of the next time interval $2\pi /\omega _m<t<4\pi /\omega _m$. Continuing this process, we define all switching events of the system. The memristors comprising each coherent state of the Schrödinger’s cat evolve according to the following (classical) equations:

$$\begin{aligned} I&=I_0 \sin (\omega _s t) \end{aligned}$$

(16)

$$\begin{aligned} q&=\frac{I_0}{\omega _s}(1-\cos (\omega _s t))\end{aligned}$$

(17)

$$\begin{aligned} V_{Cj}&=I \bigl ( M_{1j}(x,t)+M_{0j}\bigr ) \end{aligned}$$

(18)

6 Results

First, we look for the emergence of signal mixing in ${\tilde{V}}_Q(\omega )$ as $P_{sw}$ increases. This demonstrates that $P_{sw}$ is a mediator between the quantum and classical cases. In Fig. 4, we see characteristic signal mixing of $\omega _m$ and $\omega _s$ for mid and high values of $P_{sw}$. [10] The $P_{sw}=98\%$ data set is of a very high switching probability, the switching function being close to that in Fig. 2a. We do not illustrate the $P_{sw}=0$ example since there is no real component to the spectra we are interested in.

Figure 5a demonstrates how the real amplitude of the primary peak varies with $\omega _s$ in three cases, the classical (i.e., no state switching), the mixed (i.e., non-unitary evolution guided by the master equation, with low $\Gamma$) and the pure (with unitary quantum evolution). As expected from Eq. 15, we see peaks in the unitary case at odd multiples of $\omega _m/4\pi$, this is in clear contrast to the classical case, with no such signal mixing. The mixed (or non-unitary) case is intermediate between the pure and classical cases.

For the mixed state, we set $Z_T=0.1$, and use a low value for $\Gamma , \ \Gamma =1/100\omega _m$. This, essentially, gave a slight preferential collapse towards the $|1\rangle$ state at each measurement time, compared to the pure case. The effect is enough to reduce the significance of the relevant peaks in the sweep (i.e., the peak-trough height) but we still see a fair amount of evidence for the signal mixing in Fig. 5a. Not all peaks are as clear compared to the pure case, but there is periodicity evident.

The average probability of switching $P_{sw}$ across the pure trial was 98.7±0.9%, for the mixed it was slightly lower at 90.4±0.9%. $P_{sw}$ was high enough in both cases for our model $\Pi _j$ function to be a suitable approximation. As such, we can confidently conclude that the presence of resonance at the predicted points is indicative of the application of regular projective measurements.

Finally, we looked at cases with varying statistics of measurement events, to test the robustness of this methodology. We simulate trials where the standard deviations in $\omega _m$ is 5% and 10%. In other words, the measurement frequencies are normally distributed around $\omega _m$ by 0.05$\omega _m$ and 0.1$\omega _m$. $P_{sw}$ varies across the 5% trials as $P_{sw}=0.889\pm 0.014$, and across the 10% trials as $P_{sw}=0.810\pm 0.017$.

Figure 5b demonstrates the differences in peak heights and widths as expected. The higher $\sigma _\omega$, the larger the deviation from the idealised case, especially at high frequencies. In the 5% trial, the first 7 peaks in the data set have similar positions to the $\sigma _\omega =0$ trial. In the 10% trial, we see analogues for the first four peaks. In both cases, we clearly see the effects of signal mixing near the predicted frequencies.

7 Conclusions

We have simulated the voltage response of a simple model quantum memristor and demonstrated the features serving as signatures of its quantum behaviour. We look for characteristic signal mixing of our two frequencies of consideration, the measurement and source frequencies, to demonstrate the effects of the quantum measurement process on the system.

We have demonstrated how the probability of switching of the qubit-controlled memristive Schrödinger’s cat affects the ’amount’ of quantumness we see in the voltage spectra. The higher the probability of switching, the more obvious the frequency mixing in an individual spectrum.

We also conducted frequency sweeps, varying the source frequency and looking for resonance in the primary spectral peak (Fig. 5a). This alternate method to find evidence of the frequency mixing would be particularly useful in noisy systems, where the signal in an individual spectrum may be shrouded. And indeed we see indications for quantum behaviour in the spectral patterns for noisy and mixed systems. We find strong evidence of frequency mixing even in the case where the measurement frequency varies by 10%. This method is stable enough that the characteristic resonance patterns are still evident across all trials we have conducted. This is particularly important since noise is a crucial part in the operation of some memristive systems, as well as mesoscopic superconducting systems. The full importance of noise in such systems is out of our scope, but for relevant reading, see, for example, Refs. [11,12,13,14].