1 Introduction

The understanding of complex networks has greatly improved over recent decades, and researchers have made tremendous achievements in both theory and application. However, these remarkable efforts do not mean that we have a sufficient understanding of complex networks, because the framework of a complex network is partly systematic and partly chaotic [1], and becomes increasingly intricate with the acceleration of internet development. Recently, the focus of network science has been shifting from discovering macroscopic statistic regularity [2,3,4] to decomposing microscopic structural organization [5, 6] and further revealing the explicit roles played by such microscopic elements as nodes [7] and edges [8].

Indeed, nodes play different roles not only in structures but also in the function of complex systems, and understanding how nodes affect each other is critical for further research. It is important to identify vital nodes functionally and topologically [9], which helps us to control epidemic outbreaks [10, 11] and rumors [12], reduce and eliminate the damage from cyber attacks [13,14,15,16], prevent catastrophic outages in power grids [17] and the internet, maintain traffic and telecommunication networks [18], target receptor proteins and key genes for molecular biological drugs [19], and predict successful persons or groups based on collaborative networks [20, 21].

However, a perfect method for identifying vital nodes has not yet been found, as it is never a trivial task, and the directions in identification methods and even various criteria have been inconsistent. In the first place, there are two main branches for identifying vital nodes [22], one based on the neighborhood and the other based on the path. In reality, different methods fit different situations, which means that for vital node identification, a universal method is theoretically and practically unavailable. Moreover, the criteria in this task are diverse for the same reason. In some scenarios where we need to protect populations from an epidemic, a susceptible-infected-susceptible (SIS) model, susceptible-infected-recovered (SIR) model [23], or susceptible-infected-recovered-infected) model [24] perform well. And in other scenarios where we have to maintain a network and minimize loss when it is not possible to implement protection for all nodes, node removal is more suitable. Last but not least, sometimes identifying a group of coupled vital nodes is more useful than identifying a series of single nodes; topologically, it means the vital element could be a motif or a community in the identification process. However, identification of vital motifs or vital communities will be explored in future research; this paper will focus on nodes.

As mentioned above, methods for vital node identification can be divided into two branches, methods based on neighborhood and methods based on path, and these methods can also be classified according to the topological structure: chain, star, or cycle [25]. Researchers have pieced together an increasingly clear picture of the function and interaction of disparate structures in a variety of dynamical processes, including the roles of different motifs in biological networks, the transmission of information and behaviors, and the self-sustaining process of star structures in an epidemic. Aside from chain and star structures, cycles are a ubiquitous part of networks and play an unalterable role in storage, synchronizability, and controllability of network function. A cycle is a measurement of similitude between a target network and tree network, which means the model network cannot reproduce cycles as well as the real network [26]. The methods proposed in this paper, a supra-cycle number and supra-cycle ratio, are based on a cycle structure, where the former index describes the importance of the node in a global scale, while the latter index describes the same in a local scale. A cycle ratio is designed like a clustering coefficient and edge multiplicity [7]; the three methods focus on the local proportion of a certain structure in a network.

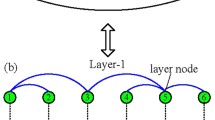
Methods of identifying vital nodes were originally designed for single-layer networks, but in reality, individuals have multiple relationships, and it is biased to describe a complex system as a single-layer network. A multiplex network is a pragmatic framework in which multiple relationships of individuals are represented in different layers (same relations are represented in a single layer). There are same nodes in each layer, and inter-layer connection only exists between the same nodes represented in a different layer. The framework of a multiplex network is shown in Fig. 1. A multiplex network is a special multilayer network. On the one hand, it retains some characteristics of a single-layer network, in that every layer in a multiplex network can be considered a single-layer network because there are same nodes in each layer, and inter-layer connections are special; on the other hand, inter-layer connections do exist, which is the hallmark of a multilayer network.

Considering the special nature of a multiplex network, the symbolically basic element we focus on can be different. Zhao et al. [27, 28] divide the nodes of a multiplex network into two categories: a multiplex node (MN, a collection of the same node in different layers) and a layer node (LN, the replica of a MN in each layer). Researchers have made much progress based on the MN. Halu et al. [29] define Multiplex PageRank by drawing on biased random walks. Solé-Ribalta et al. [30] redefine the betweenness centrality and proposed an algorithm to compute it in an efficient way. Solá et al. [31] extend the concept of eigenvector centrality to a multiplex network. But by contrast, the LN has received less attention. Zhao et al. [32] extend several indexes or algorithms from single-layer networks to multiplex networks and find explosive immunization is always best for the identification of vital LNs by performing them on different kinds of multiplex model networks.

In this paper, we focus on cycle number and cycle ratio [33], which were newly proposed indexes for vital node identification, and extend them to multiplex networks. We compare the evaluation results to other indexes through robustness, synchronization, and immunization, and we make a further conclusion from two viewpoints (MN and LN), which reveals the applicability of our method.

This paper is organized as follow. Initially, we mathematically define the problem we are focused upon and introduce several indexes and our indexes in the Methods section. Then we present the main idea of our algorithm and the time complexity in the experiments section, and we analyze the experimental results. Finally, we make a conclusion based on a theoretical perspective and the experimental results in the Conclusion section.

2 Problem definition

A multiplex network is a combination of several single-layer networks which contain the same nodes (or replicas of the same nodes) and a different intra-layer connection. A multiplex network is a framework to perfectly describe the multiple relationships between individuals in real-world complex systems including social networks, transportation networks, biological networks, etc.

Fig. 1
figure 1

Illustrations of MNs and LNs in a multiplex network. a, b Different relationships between four users on TikTok and Facebook. c, d Aviation and railway relationships between four cities. e, f Physical and functional relationships between four gene fragments

Full size image

Figure 1 gives three illustrations of a multiplex framework. We take Fig. 1a, b as an example. Users are connected on different social apps. Every user is an MN when the user is embedded in the framework as a node. Users interact on TikTok via blue links and on Facebook via green links (as shown in the left panel). When different users are connected with a kind of link in the same layer and there are same the individuals in different layers, the individuals are LNs in each layer (as shown in the right panel). As a result, MNs represent individuals, and LNs represent accounts of social apps, and there is same explanation for Fig. 1c–f. Different cities are connected by aviation via a blue link in Fig. 1c and by railway via a green link in Fig. 1d, where MNs represent cities, and LNs represent stations; different gene fragments are physically connected via a blue link in Fig. 1e and functionally connected via a green link in Fig. 1f, where MNs represent gene fragments, and LNs represent the specific role the gene fragments play.

Per the definitions of MN and LN we show above, the difference between MNs and LNs is whether the basic element is a coupled node or a single node. Mathematically, multiplex network G with N nodes and M layers can be described as follows:

$$\begin{aligned} D_\mu&= \overbrace{ \{ G_\alpha , G_\beta , \cdots \} }^{M} \end{aligned}$$
(1)

Research based on MNs help us understand the individuals that have multiple interactions in a complex system, and research based on LNs helps us focus on every single role played by individuals, and benefits us when focusing on a multilayer network with different nodes in each layer. Thus, the task of vital node identification in multiplex networks can be defined as follows.

Problem definition: Propose an index or algorithm to rank MNs/LNs, such that we can find a set of MNs/LNs to better protect or minimize the damage in specific tasks.

3 Methods

Many methods of identifying vital nodes are designed for single-layer networks, and researchers put effort into reframing them for multiplex networks. In this section, we introduce several methods and compare them with our methods through percolation, synchronization, and immunization.

3.1 Methods based on a star structure

3.1.1 Degree centrality

Degree centrality is the easiest way to achieve identification, and it has been well performed in all sorts of networks. When it comes to a multiplex network with M layers and N nodes in each layer, the degree centrality of an LN \(v_\alpha \) in layer \(\alpha \), denoted as \({\text {DCL}}(i^\alpha )\), is shown as follows:

$$\begin{aligned} {\text {DC}}(i^\alpha )&= \sum _{i^\alpha , j^\alpha \in V^\alpha } a_{i^\alpha j^\alpha } \end{aligned}$$
(2)

where \(a_{i^\alpha j^\alpha }\) is the element of the adjacency matrix for layer \(\alpha \) in row i column j, and \(a_{i^\alpha j^\alpha }\) equals 1 if \(v_i^\alpha \) and \(v_j^\alpha \) are connected and 0 otherwise; \(V^\alpha \) is the set of nodes in layer \(\alpha \).

Similarly, the degree centrality of an MN \(v_i\), denoted as \({\text {DCM}}(i)\), is shown as follows:

$$\begin{aligned} {\text {DC}}(i^\alpha )&= \sum _{m \in L}^{M} \sum _{i^m , j^m \in V^m} a_{i^m j^m} \end{aligned}$$
(3)

where L is the set of layers. Mathematically, the degree centrality of an MN couples the degree centrality of LNs.

3.1.2 K-core decomposition

K-core decomposition is a process to obtain important nodes, which decomposes graph step by step. According to degree centrality, nodes with higher degree are more important than the others, which means these vital nodes are in the inner layer. The steps are as follows: in the first stage of removal, nodes with degree one are removed at first, then if other nodes with degree one appear because of the removal, the network is repeatedly processed until there is no node with degree one. Thus, all the removed nodes are considered to have the same importance in this method, and these removed nodes form the 1-core. The next stage of removal is conducted for the nodes with degree two. Repeat the removal stage by stage until the network is completely decomposed.

The k-core decomposition is applied in each single layer of the multiplex network [34], which means for LNs, the coreness (k-core value) of nodes is still a number, but for MNs, the k-core value of nodes is a label consisting of several number; for example, a node with k-core value \((a_\alpha ,b_\beta )\) means the coreness is a in layer \(\alpha \), and the coreness is b in layer \(\beta \)). For the sake of obtaining a united standard, we sum up the coreness of the LN as the coreness of the MN.

3.1.3 ClusterRank

Unlike the degree and k-core decomposition, for the ClusterRank [35], researchers not only consider the number of nearest neighbors but also take into account the interaction among them. ClusterRank was originally designed for a directed network, but it can also be applied to an undirected network. In a multiplex network with M layers and N nodes in each layer, the ClusterRank value of LN \(v_i^\alpha \) in layer \(\alpha \) can be redefined as follows:

$$\begin{aligned} {\text {DR}}(i^\alpha )&= f(c_{i^\alpha })\sum _{j^\alpha \in \Gamma _{i_\alpha }}(k_\textrm{out}+1) \end{aligned}$$
(4)

where \(f(c_{i^\alpha })\) is a function of the clustering coefficient \(c_{i^\alpha }\) of \(v_i^\alpha \), \(k_out\) is the out degree of \(v_i^\alpha \), and \(\Gamma _{i_\alpha }\) is the set of nearest neighbors of \(v_i^\alpha \).

Similarly, the ClusterRank value of the MN \(v_i\) can be redefined as follows:

$$\begin{aligned} {\text {DR}}(i)&= \sum _{m \in L}^{M} f(c_{i^m})\sum _{j^m \in \Gamma _{i_m}}(k_\textrm{out}+1) \end{aligned}$$
(5)

where L is the set of layers in the multiplex network.

3.1.4 Semi-local centrality

Semi-local centrality [36] makes a good balance between the neighbor and path. These vital methods of node identification based on neighbors have the advantage of simplicity, but the topological structure is never taken into consideration. These methods based on the path effectively process the topological structure, but they are not suitable for large-scale networks because of great complexity. Essentially, semi-local centrality takes into account the direct neighbors of nodes, including first-order and second-order neighbors, and the first-order and second-order neighbors of these direct neighbors. In semi-local centrality, researchers partly introduce the characteristics of the path and keep the simplicity at the same time. In a multiplex network with M layers and N nodes in each layer, the semi-local centrality of LN \(v_i^\alpha \) in layer \(\alpha \) can be redefined as follows:

$$\begin{aligned} \textrm{SCL}(i^\alpha )&= \sum _{j^\alpha \in \Gamma (i^\alpha )} \sum _{k^\alpha \in \Gamma (j^\alpha )}N(k^\alpha ) \end{aligned}$$
(6)

where \(\Gamma (i^\alpha )\) is the set of first-order neighbors of LN \(v_i^\alpha \), \(\Gamma (j^\alpha )\) is the set of first-order neighbors of LN \(v_j^\alpha \), and \(N(k^\alpha )\) is the amount of neighbors which \(v_i^\alpha \) can reach in a 2-hop.

When it comes to an MN, we take the inter-layer structure into consideration, and the semi-local centrality of the MN is redefined as follows:

$$\begin{aligned} \textrm{SCL}(i^\alpha )&= \sum _{m,n \in L}^{M} \sum _{j^m \in \Gamma (i^m)} \sum _{k^\alpha \in \Gamma (j^m) \cup \Gamma (i^m)}N(k) \end{aligned}$$
(7)

Topologically, this definition couples the intra-layer and the inter-layer neighbors which LNs can reach in a 4-hop.

3.2 Methods based on a chain structure

3.2.1 Betweenness centrality

Betweenness centrality in a single-layer network is defined as the proportion of shortest paths that pass through a given node. Nodes with high betweenness centrality usually act as hub, and thus a bridge which connects subgraphs is constructed when several such nodes are connected (a bridge may also consist of one hub node), and the network is probably cut into pieces when such nodes are removed. In a multiplex network with M layers and N nodes in each layer, because paths can be inter-layer or intra-layer, the betweenness centrality of LN \(v_i^\alpha \) is redefined as follows:

$$\begin{aligned} \textrm{BC}(i^\alpha )&= \sum _{s^m \in V^m, t^n \in V^n, i^\alpha \in V^\alpha }\frac{\sigma (s^m,t^n \mid i^\alpha )}{\sigma (s^m,t^n)} \end{aligned}$$
(8)

where \(V^m\), \(V^n\), \(V^\alpha \) is the set of nodes in layer m, n, \(\alpha \), \(\sigma (s^m,t^n)\) is the number of shortest paths from LN \(v_s^m\) in layer m to LN \(v_t^n\) in layer n, and \(\sigma (s^m,t^n\Vert i^\alpha )\) is the number of shortest paths that pass through the given LN \(v_i^\alpha \) in \(\sigma (s^m,t^n)\). Specifically, if \(v_i^\alpha \in \{v_s^m, v_t^n\}\), \(\sigma (s^m,t^n\Vert i^\alpha )=0\).

Similarly, the betweenness centrality of MN \(v_i\) is redefined as follows:

$$\begin{aligned} \textrm{BC}(i)&= \sum _{m,n,r \in L}^{M} \sum _{s^m \in V^m, t^n \in V^n, i^r \in V^r}\frac{\sigma (s^m,t^n\mid i^r)}{\sigma (s^m,t^n)} \end{aligned}$$
(9)

where L is the set of layers in the multiplex network.

3.2.2 Closeness centrality

Closeness centrality eliminates the disturbance by summarizing the distance from the target node to all other nodes while evaluating the importance of nodes. When it comes to a multiplex network with M layers and N nodes in each layer, the closeness centrality of LN \(v_i^\alpha \) is redefined as follows:

$$\begin{aligned} \textrm{CC}(i^\alpha )&= \frac{N-1}{\sum _{i^\alpha \in V^\alpha , j^m \in V^m}d(j^m, i^\alpha )} \end{aligned}$$
(10)

where \(v^m\), \(v^\alpha \) is the set of nodes in layer m, \(\alpha \), and \(d(j^m,i^\alpha )\) is the distance from LN \(j^m\) in layer m to LN \(i^\alpha \) in layer \(\alpha \).

Similarly, the closeness centrality of MN \(v_i\) is redefined as follows:

$$\begin{aligned} \textrm{CC}(i)&= \sum _{n,m \in L}^{M} \frac{N-1}{\sum _{i^n \in V^n, j^m \in V^m}d(j^m, i^n)} \end{aligned}$$
(11)

where L is the set of layers in the multiplex network.

3.3 Methods based on a cycle structure

3.3.1 Supra-cycle number

A cycle is a path which contains three or more nodes; the nodes are connected end to end, and the size of cycle is the number of nodes it contains. Once a cycle does not contain a smaller cycle inside, it is the basic cycle, and the smallest basic cycle is the smallest one in the basic cycle of a given node. For a node \(v_i\), the length of the smallest basic cycle is the girth of \(v_i\) when the cycle contains the node. As shown in Fig. 2, we can obtain the incidence matrix by enumerating all the smallest basic cycles in the network, and the cycle number matrix from the incidence matrix (algebraically, the cycle number matrix equals the incidence matrix multiplied by the inverse of the incidence matrix, and topologically, the cycle number matrix is the distribution of the smallest basic cycle where the element in row i, column j equals the number of smallest basic cycle containing node \(v_i\) and node \(v_j\)).

When the network shifts from a single-layer network to a multiplex network, the cycle is not only intra-layer but also inter-layer; thus, we set a weight for the inter-layer cycle because network dynamics and behaviors change when inter-layer interactions happen. Also, the situation changes when the basic elements shift from LNs to MNs. We set the quotient between the maximum in the spectrum of inter-layer networks and the maximum in the spectrum of intra-layer networks as the weight of inter-layer edges [37], and this process is shown in Fig. 3.

3.3.2 Supra-cycle ratio

The cycle ratio of node \(v_i\) in a single-layer network with n nodes is defined as follows based on the cycle number:

$$\begin{aligned} \textrm{CR}(i)&= {\left\{ \begin{array}{ll} 0, &{} c_{ij}=0 \\ \sum _{j=1}^{n} \frac{c_{ij}}{c_{jj}}, &{} \textrm{otherwise} \\ \end{array}\right. } \end{aligned}$$
(12)

where \(c_{ij}\) is the element of the cycle number matrix in row i column j. The process of calculation is shown in Fig. 2.

When the ratio index is based on the supra-cycle number rather than the cycle number, the index becomes a supra-cycle ratio, and the process is shown in Fig. 3.

Fig. 2
figure 2

Cycle number and cycle ratio in a single-layer network. a An example of a single-layer network with ten nodes. b Cycle number matrix of the network example, and how the cycle ratio is obtained from the cycle number matrix

Full size image

When the cycle ratio is applied in a multiplex network, the results of the supra-cycle ratio change with supra-cycle number, but the process from cycle number to cycle ratio, which is shown in Fig. 3, does not change (Table 1).

Table 1 Enumerating the smallest basic cycles, the cycle number (CN) and the cycle ratio (CR) of a network example are calculated
Full size table
Fig. 3
figure 3

The supra-cycle number and supra-cycle ratio in a multiplex network. a An example of a multiplex network with two layers (layer \(\alpha \) and layer \(\beta \)). b The “unweighted” supra-cycle number and supra-cycle ratio calculation in the network example. c The weighted supra-cycle number and supra-cycle ratio for a multiplex network, where \(D_{\alpha \beta }\) is the weight of the inter-layer edge, which is 0.4 in this case

Full size image

If we treat the inter-layer edge the same as the intra-layer edge, the process of cycle number and cycle ratio calculation in the single-layer network can be performed without changing the supra-cycle number. The unweighted supra-cycle number and supra-cycle ratio are not performed well enough because the inter-layer edge usually plays different roles in the multiplex network, and the difference between the inter-layer edge and intra-layer edge does not influence the index. We reset the importance of the inter-layer cycle that is adaptive for a multiplex network structure (Table 2).

Table 2 Enumerating the smallest basic cycles, the supra-cycle number and the supra-cycle ratio of the network example are calculated. We denote node \(v_i\) in layer \(\alpha \) as i, and node \(v_i\) in layer \(\beta \) as \(i'\). The wSCN is the weighted supra-cycle number, and the wSCR is the weighted supra-cycle ratio
Full size table

We designed an algorithm to calculate the supra-cycle number and supra-cycle ratio. Firstly, we cut off all nodes with coreness one because a coreness greater than one is a necessary condition for a cycle structure. Secondly, we enumerate all the smallest basic cycles. Each search for the smallest basic cycle can be regarded as the shortest path problem, and the complexity of the shortest path problem is \(o(N+E)\) in a network with N nodes and M edges. Finally, we get the supra-cycle number and supra-cycle ratio. The multiplex network has E edges, M layers, and N nodes in each layer. The complexity of our algorithm is \(o(N(N+E))\), and in a real network, the complexity is \(o(N'(N'+E'))\), where \(N'\ll N\), \(E'\ll E\). A real network is usually sparse, and an amount of nodes are removed from the original network initially; thus, the network we actually process is \(N'\) nodes and \(E'\) edges, which is much smaller than the original network).

3.3.3 Minimum flux criterion

The weight setting of an inter-layer edge is usually put into use on layers pair by pair, and it is not only for precision of weights but also for complexity, because the complexity of spectrum calculation increases exponentially when a network grows. But an inter-layer cycle structure is not limited to two layers; when an inter-layer cycle stretches across more than two layers, we introduce the minimum flux criterion to evaluate the significance.

The minimum flux criterion is stated as follows: the importance of the inter-layer cycle structure equals the minimum weight of the inter-layer edges it contains. One of the characteristics of a path is its flux depends on the minimum flux along the whole path, which works like a bottleneck, and the cycle structure can be regarded as a specific path structure with directional or bidirectional infinite continuity.

3.3.4 Graph mapping simplification

This algorithm will not perform well when a multiplex network explosively grows. Specifically, we can map all layers into a single layer, which is shown as Fig. 4. This mapping process will cause distortion (in Fig. 4, inter-layer cycle {3, 5, 3\(^{\prime }\), 5\(^{\prime }\)} disappear after mapping), but in comparison with the simplification in complexity, the distortion is acceptable.

Fig. 4
figure 4

a The original structure of a multiplex network. b The structure of a multiplex network after mapping

Full size image

3.3.5 Hybrid indexes based on Bayesian inference

Although we introduce an inter-layer cycle structure to identify vital nodes in the framework of a multiplex network, and make adjustment to the nonequivalent importance between inter-layer edges and intra-layer edges, the reliability of the adjustment is not quantified. For a convincing and precise theoretical method, we introduce Bayesian inference to make a choice between the unweighted indexes and the weighted indexes.

To describe the reliability of an index, we set up a random event set \(\Omega \) at first, where \(\Omega = \{\Theta _1, \Theta _2, \Theta _3\}\), \(P(\Theta _1)+P(\Theta _2)+P(\Theta _3)=1\), event \(\Theta _1\) represents the index is highly reliable, event \(\Theta _2\) represents the index is unreliable, and event \(\Theta _3\) represents the reliability of index is uncertain. Taking the cycle number of node \(v_i\) as an example and denoting it as CN(i), the basic probability assignment [38] can be defined as follows:

$$\begin{aligned} P_i(\Theta _1)&= \frac{|\textrm{CN}(i)-\textrm{CN}_{\min }|}{\textrm{CN}_{\max }-\textrm{CN}_{\min }+\alpha } \end{aligned}$$
(13)
$$\begin{aligned} P_i(\Theta _2)&= \frac{|\textrm{CN}(i)-\textrm{CN}_{\max }|}{\textrm{CN}_{\max }-\textrm{CN}_{\min }+\alpha } \end{aligned}$$
(14)

where \(CN_{\max }=\max \{\textrm{CN}(1),\textrm{CN}(2),\ldots ,\textrm{CN}(n) \}\), \(\textrm{CN}_{\min }=\min \{\textrm{CN}(1), \textrm{CN}(2),\ldots ,\textrm{CN}(n) \}\), and \(\alpha \) is a user-defined parameter, \(\alpha \in [0,1]\). For the sake of simplicity, the \(\alpha \) equals 1 in this paper. There are two states \(\Theta _1\) and \(\Theta _2\) in \(\Theta _3\), and the ratio \(\beta = \frac{P(\Theta _1 \Theta _3)}{\Theta _3}\) is designed to describe preference for the reliability, \(\beta \in [0,1]\). The ratio \(\beta \) is also a user-defined parameter, and it usually equals 0.5. The reliability can be easily rewritten as \(P(\Theta _1)+\beta P(\Theta _3)\).

The disadvantage for the reliability mentioned above is obvious; the parameters \(\alpha \) and \(\beta \) contain too much subjective decision. Thus, we use Bayesian inference to make a better decision. Firstly, the indexes should be normalized within 0 and 1. Then we set a probability evaluation function as follows:

$$\begin{aligned} P(\Theta _1 \mid \lnot \Theta '_1)&= \frac{P(\Theta _1)\prod _{i=2,3}P(\Theta '_1 \mid \Theta )}{P(\Theta '_1)} \end{aligned}$$
(15)

where \(\Theta \) and \(\Theta '\) represent two different indexes. We choose an index as the reliable index of the node when the probability of the index is higher than another. We denote the index from the unweighted cycle number and weighted cycle number by probability as a hybrid supra-cycle number, and we get a hybrid supra-cycle ratio in the same way. The hybrid supra-cycle number and hybrid supra-cycle ratio of the example graph in Fig. 3 can be recalculated, and the ranks similar to the weighted supra-cycle number and weighted supra-cycle ratio come out, which is shown in Table 3.

Table 3 Recalculation of the indexes, the hybrid supra-cycle number, and the hybrid supra-cycle ratio of a network example. wSCN is the weighted supra-cycle number, wSCR is the weighted supra-cycle ratio, HSCN is the hybrid supra-cycle number, and HSCR is the hybrid supra-cycle ratio
Full size table

For the sake of rigor, we will compare the hybrid supra-cycle number, the hybrid supra-cycle ratio, and some other methods in the Experiments section.

Table 4 The essential information of the test multiplex network
Full size table

4 Experiments

In this section, we test and compare the indexes mentioned above by their performance on robustness, synchronization, and transmission dynamics. All the experiments for evaluation apply in four real multiplex networks: multiplex social networks of a sample of physicians in the United States [39], a multiplex air transportation network of the European Union [40], a multiplex genetic and protein interaction network of Caenorhabditis elegans [41, 42], and a multiplex co-authorship network of the arXiv free scientific repository [43]. The essential information of each network is shown in Table 4.

4.1 Robustness analysis

Robustness and stability are always the core issue in network study. In the identification of vital nodes, reinforcing the protection for these vital nodes we select will help us to maintain the network, which can enhance its robustness and stability. Node removal attack [44] is a common method to evaluate the rank of vital nodes, where we assume a network is under attack by removal of nodes, and the removal always takes place on the most important node of the rank in each iteration; and the size of the largest giant connected component (GCC) in the left part of the network represents the performance of our vital node identification method.

The difference between removal of MNs and LNs is obvious: when removal happens to a node, all replicas of the node will be removed from the network if we do research on the MN, and only the node itself will be removed if we do research on the LN. Experiments on four multiplex networks are shown in Figs. 5, 6, 7, and 8.

Fig. 5
figure 5

The GCC size of a multiplex network after a q fraction of LNs is removed. We compare indexes about cycle structure here in these subgraphs. a CKM–physicians–innovation multiplex network. b EU air transportation multiplex network. c C. elegans multiplex GPI network. d ArXiv Netscience multiplex

Full size image
Fig. 6
figure 6

The GCC size of a multiplex network after a q fraction of LNs is removed. We compare best performing indexes in Fig. 5 with several other indexes. a CKM–physicians–innovation multiplex network. b EU air transportation multiplex network. c C. elegans multiplex GPI network. d ArXiv Netscience multiplex

Full size image

In Figs. 5 and 6, we compare indexes, including the unweighted supra-cycle ratio (SCR), unweighted supra-cycle number (SCN), hybrid supra-cycle ratio (HCR), hybrid supra-cycle number (HCN), degree centrality (D), semi-local centrality (S), ClusterRank (Clu), k-core index (Co), betweenness centrality (B), and closeness centrality (Clo).

In Fig. 5, it is obvious that HCN and HCR do not perform as well as SCN and SCR when the network is not huge enough (Fig. 5a), and the situation changes when the network grows (Fig. 5b–d). By the way, degree centrality and betweenness centrality have good performance as well, for which there are two reasons. On one hand, nodes with a high degree work as hubs and nodes with betweenness centrality working as bridges in the network; GCCs are vulnerable on removal of these nodes. On the other hand, node removal attack does not reflect the difference between inter-layer interaction and intra-layer interaction.

In a multiplex network with M layers and N nodes in each layer, robustness [45] of the network is defined as follows:

$$\begin{aligned} R&= \frac{1}{N} \sum _{i}^{N}g(i) \end{aligned}$$
(16)

where the relative size g(i) is the number of nodes in the largest giant connected component after removing i nodes, and the normalization factor 1/N makes sure the robustness of different networks can be compared. Obviously, a smaller R means a quicker collapse, thus better performance. The result is shown in Table 5.

Table 5 Robustness of four multiplex networks by the indexes mentioned above on LN removal
Full size table

When it comes to MNs, we can get several other indexes by mapping all the layers of the network into a single-layer network. In Fig. 7, SCRM, HCRM, SCNM, and HCNM are SCR, HCR, SCN, and HCN, respectively, in the mapping network.

Fig. 7
figure 7

The GCC size of a multiplex network after a q fraction of LNs is removed. We compare indexes about cycle structure here in these subgraphs. a CKM–physicians–innovation multiplex network. b EU air transportation multiplex network. c C. elegans multiplex GPI network. d ArXiv Netscience multiplex

Full size image

We select the best performing index in Fig. 7 and compare it with other indexes in Fig. 8. The results reveal that the hybrid indexes based on cycle structure have better performance, and the indexes in the mapping network have advantages both in performance and complexity.

Fig. 8
figure 8

The GCC size of a multiplex network after a q fraction of LNs is removed. We compare indexes about cycle structure with other indexes in these subgraphs. a CKM–physicians–innovation multiplex network. b EU air transportation multiplex network. c C. elegans multiplex GPI network. d ArXiv Netscience multiplex

Full size image

There are multiple reasons for the better performance of HCNM and HCRM; the removal of MNs diminishes the influence of the inter-layer edge on GCC, and apparently the weight setting more or less fixes distortion caused by mapping. We quantify the robustness of networks on MN removals, which is shown in Table 6.

Table 6 Robustness of four multiplex networks by the indexes mentioned above on MN removal
Full size table

4.2 Pinning control

We evaluate the validity of the indexes in synchronization by pinning these selected top nodes of rank [46]. Generally, the interacting dynamics of a network with N nodes is shown as follows:

$$\begin{aligned} \dot{x_i}&= f(x_i)+\sigma \sum _{j=1}^{N}l_{ij}\Gamma (x_{ij})+U_i(x_1,\ldots ,x_n) \qquad \end{aligned}$$
(17)

where the \(x_i \in \mathbb {R}\) is the state of node i, the coupled strength is denoted as positive constant \(\sigma \), \(l_{ij}\) is the elements of a Laplacian matrix of the network, the inner coupled matrix \(\Gamma \) is positive semi-definite, and \(U_i\) is the controller of node i. The goal of pinning control is driving the system from an initial state to a target state in finite time by pinning some nodes. Similar to the robustness test, all the nodes are ranked in descending order by the indexes; then the nodes are successively pinned, which starts from the top rank. The synchronization can be measured by the smallest nonzero eigenvalue of the principal submatrix [46, 47], and the higher synchronization is correlated with the higher value. We denote it as \(\mu (L_{-Q})\), where Q is the number of pinned nodes, and \(L_{-Q}\) is the principal submatrix after deleting Q nodes. Inspired by the evaluation equation of robustness, the analogous evaluation equation for synchronization is proposed by researchers:

$$\begin{aligned} P&= \frac{1}{Q_{\max }}+ \sum _{Q=1}^{Q_{\max }}\mu (L_{(-Q)}) \end{aligned}$$
(18)

where \(Q_{\max }\) is the maximum of pinned nodes. In simulations, we set the maximum equal to 10% nodes. The result of pinning LNs by different indexes is presented in Table 6. We highlight the top two indexes in each network, and the result shows that indexes based on a cycle structure have good performance on synchronization but not the best all the time (Tables 7, 8).

Table 7 Synchronization of four multiplex networks by the indexes mentioned above on pinning LNs
Full size table
Table 8 Synchronization of four multiplex networks by the indexes mentioned above on pinning MNs
Full size table

4.3 Transmission dynamics

The SIR model is a classical method for network transmission dynamic research, and it can also be used for evaluation of vital nodes identification. Researchers developed the SIR model to simulate the pandemic. Every individual can be in one of three states: susceptible (S), infected (I), recovered (R). Individuals in the S state are regarded as healthy ones and easy to be infected. Individuals in the I state are able to infect healthy ones and can also probably transfer into state R (simulating recovery). Individuals will not be infected or infect others again once transferring into state R. Recently, scholars did abundant research on the SIR model in a disease–information coupled multiplex network [48], which revealed the inhibition effect of information on disease spread. When those vital nodes we select are set as initially infected individuals (seed nodes), the speed and breadth of transmission reflects the importance of seed nodes, which is deemed as the performance of the vital node identification method.

In this paper, epidemic spread is not limited in every single layer; nodes in the I state can infect others in different layers. Unlike the single-layer network, when transmission happens in the same layer, nodes in the I state infect others with a probability \(\beta _1\), and with probability \(\beta _2\) when transmission happens in different layers. Nodes in the I state recover at recovery rate \(\gamma \). For LNs, inter-layer transmission is easy to define: transmission between a node and its replica is inter-layer. But for MNs, the node is infected in every layer once any one of its replicas is infected, and in this circumstance, inter-layer transmission should be defined in another way: a transmission process is inter-layer if an MN gets infected in a layer and infects others in different layers. Figure 9 provides a diagram of inter-layer transmission for LNs and MNs.

Fig. 9
figure 9

Inter-layer transmission in a multiplex network consisting of two layers and five nodes in each layer. The nodes in the S state are blue, the nodes in the I state are red, and the orange arrow is the transmission process. a Inter-layer transmission for LNs: node \(v_1^\alpha \) infects \(v_1^\beta \). b Inter-layer transmission for MNs: node \(v_1\) gets infected in layer \(\alpha \) and infects node \(v_4\) in layer \(\beta \)

Full size image
Fig. 10
figure 10

When the LN is the subject of study, comparison between SCN and HCN is in subgraph (a–d), and comparison between SCR and HCR is in subgraph (e–h). Subgraphs (a) and (e) are simulations in the CKM–physicians–innovation multiplex network. Subgraphs (b) and (f) are simulations in the EU air transportation multiplex network. Subgraphs (c) and (g) are simulations in the C. elegans multiplex GPI network. Subgraphs (d) and (h) are simulations in the ArXiv Netscience multiplex

Full size image
Fig. 11
figure 11

Comparison among several sets of LNs from different indexes. a CKM–physicians–innovation multiplex network. b EU air transportation multiplex network. c C. elegans multiplex GPI network. d ArXiv Netscience multiplex

Full size image
Fig. 12
figure 12

When MN is the subject of study, comparison between SCN, HCN, SCNM, and HCNM is in subgraph (a–d), and comparison between SCR, HCR, SCRM, and HCRM is in subgraph (e–h). Subgraphs (a) and (e) are simulations in a CKM–physicians–innovation multiplex network. Subgraphs (b) and (f) are simulations in an EU air transportation multiplex network. Subgraphs (c) and (g) are simulations in a C. elegans multiplex GPI network. Subgraphs (d) and (h) are simulations in an ArXiv Netscience multiplex

Full size image
Fig. 13
figure 13

Comparison among several sets of MNs from different indexes. a CKM–physicians–innovation multiplex network. b EU air transportation multiplex network. c C. elegans multiplex GPI network. d ArXiv Netscience multiplex

Full size image

The dynamic equations of the SIR model in a multiplex network are shown as follows:

$$\begin{aligned} \frac{{\text {d}}(s)}{{\text {d}}t}&= -\beta _1s(t)i(t)-\beta _2s(t)i(t) \end{aligned}$$
(19)
$$\begin{aligned} \frac{{\text {d}}i(s)}{{\text {d}}t}&= \beta _1s(t)i(t)+\beta _2s(t)i(t)-\gamma i(t) \end{aligned}$$
(20)
$$\begin{aligned} \frac{{\text {d}}y(t)}{{\text {d}}t}&= \gamma i(t) \end{aligned}$$
(21)

where t is the time (iteration steps), and S, i(t), and \(\gamma (t)\) are the number of nodes in states S, I, and R. When the intra-layer infection rate \(\beta _1\) equals 0.01, the inter-layer infection rate \(\beta _2\) equals 0.005, and the recovery rate \(\gamma \) equals 0.05. We select the top 1% nodes as seed nodes and simulate the whole process of the transmission 50 times, then compare the average of variable proportion of nodes in state I under different vital node identification methods, which is shown in Figs. 10, 11, 12, and 13.

When an LN is the basic element in our research, we make comparison between SCN and HCN, and SCR and HCR in multiplex networks we used above. The results show that HCN and HCR have better performance most of time, and the advantages of HCN and HCR are not clear when the network is way too small. The transmission of LNs shows some similar characteristics to transmission in a single-layer network, because the transmission of LNs can be regarded as transmission in a single-layer network with two infection rates. Because of the similitude, HCN and HCR do not show overwhelming advantages, and if we take simplicity into consideration, indexes based on an unweighted cycle structure show less but similar practicability in the transmission task.

We make comparison among HCN, HCR, and some other indexes in four multiplex networks. Although HCN and HCR do not have more superb performance than SCN and SCR all the time, situations with other indexes are much better, where HCR is the best for both speed and breadth of transmission in three cases [subgraph (b), subgraph (c), and subgraph (d)] and the second best once [subgraph (a)]; HCN just has less performance than HCR and betweenness centrality in two cases [subgraph (b) and subgraph (d)]. There is an exception that betweenness centrality is also one of the best methods for the transmission task, but betweenness centrality has tremendous disadvantages for complexity, which is a disaster when a network grows. And comparing with betweenness centrality, our algorithm of HCN and HCR has remarkable success for complexity in a huge sparse network.

When we work on MNs, the performance of HCN and HCR gets better. In Fig. 12, we make a comparison with CNs and CRs. The data prove that HCN and HCR have advantages for both speed and breadth. But the interesting thing is that HCN and HCR not only perform well; HCNM and HCRM also have advantages for both speed and breadth, and sometimes they are even better than HCN and HCR (Fig. 12b, f). This phenomenon suggests that HCNM and HCRM have good performance in transmission tasks as well, and when the algorithm is applied to a very huge multiplex network, especially a very dense multiplex network, mapping the network into a single layer can achieve good compromise between complexity and performance.

The reason why the transmission process performs well based on HCNM and HCRM is very clear. Although an inter-layer transmission is redefined on MNs, it is not real layer-to-layer transmission because this inter-layer transmission requires continuity in the process or step. Real inter-layer transmission is a topological process, but the principle of transmission for an MN is once a node gets infected, all replicas get infected; thus, it is impossible to redefine inter-layer transmission topologically. With the limit of the principle, the effect of inter-layer edges is ignored for a multiplex network.

The disadvantage of transmission for an MN causes similar performance between HCN and HCNM, and HCR and HCRM, but it does not mean the inter-layer cycle structure and the weight setting are worthless. The limit of the transmission principle for the MN does not change the fact that the transmission process still works on inter-layer cycle structures, and these inter-layer cycle structures are not as important as the intra-layer cycle structures, which makes sure that the hybrid indexes based on cycle structure are an effective way to deal with transmission tasks.

5 Conclusion

In this paper, we introduce the cycle number and cycle ratio at first and develop them into a multiplex network. We integrate the nonequivalent importance between inter-layer edges and intra-layer edges and the reliability of the nonequivalence by Bayesian inference, then propose two indexes, the hybrid supra-cycle number and hybrid supra-cycle ratio, to identify two different types of vital nodes (LNs and MNs), and evaluate their performance with several different indexes in three aspects: robustness, synchronization, and transmission dynamics. In most cases, the two indexes have good performance, and we draw the following conclusions based on these experimental results: (i) Comparing with hybrid supra-cycle number, the hybrid supra-cycle ratio has better performance on a local scale; (ii) Our index is more suitable for study on MNs than LNs; and (iii) Mapping a multilayer network into a single-layer network is a time-saving and space-saving preprocessing step, especially for research on MNs in very huge multiplex networks.

We end this paper by presenting several open issues. Firstly, we work a lot on the LN because there is more than one kind of multilayer network, and we try to develop the cycle structure into a general multilayer network which may contain different nodes in different layers, and the MN will not exist; but the hybrid supra-cycle number and hybrid supra-cycle ratio on the LN do not work as well as on the MN, which means more reasonable, more effective, and more practical methods are needed. Moreover, although we preprocess the multiplex network by removing nodes in which the k-core number is equal or less than 1, the complexity of our algorithm on a huge but sparse network greatly decreases, which causes uncertainty in vital node identification. Besides, the order of cycle is not involved in the framework. Similar to the high-order cluster coefficient, we try to frame and analyze the order of cycle on network function and dynamics, and quantify these effects and interactive behaviors. Last but not least, our work focuses on topology, and the properties of nodes are not, but should be, involved for a better understanding of complex networks. We hope these missing parts are fulfilled in the future.