Cooper approach to pair formation in a tight-binding model of La-based cuprate superconductors

Abstract

We study numerically, in the framework of the Cooper approach from 1956, mechanisms of pair formation in a model of La-based cuprate superconductors with longer-ranged hopping parameters reported in the literature at different values of center of mass momentum. An efficient numerical method allows to study lattices with more than a million sites. We consider the cases of attractive Hubbard and d-wave type interactions and a repulsive Coulomb interaction. The approach based on a frozen Fermi sea leads to a complex structure of accessible relative momentum states which is very sensitive to the total pair momentum of static or mobile pairs. It is found that interactions with attraction of approximately half of an electronvolt give a satisfactory agreement with experimentally reported results for the critical superconducting temperature and its dependence on hole doping. Ground states exhibit d-wave symmetries for both attractive Hubbard and d-wave interactions which is essentially due to the particular Fermi surface structure and not entirely to an eventual d-wave symmetry of the interaction. We also find pair states created by Coulomb repulsion at excited energies above the Fermi energy and determine the different mechanisms of their formation. In particular, we identify such pairs in a region of negative mass at rather modest excitation energies which is due to a particular band structure.

Graphic Abstract

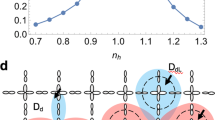
In the frame of Cooper approach, the pair formation is studied numerically in La-based cuprate superconductors. The approach based on a frozen Fermi sea leads to a complex Fermi surface structure for static and mobile pairs. The attractive interactions (Hubbard or d-wave) of about 0.5 eV give a satisfactory agreement with experimental results for the critical superconducting temperature and its dependence on hole doping (shown in Figure by dashed and color curves for experiment and numerics). There are also pairs created by Coulomb repulsion at excited energies.

Appendix

1.1 Numerical Cooper pair method

Let us consider the mathematical eigenvalue problem of a Hamiltonian matrix of the form:

$$\begin{aligned} H_{k,k'}=\delta _{k,k'}\varepsilon _k-\frac{|U|}{N_2}\,g_k\,g_{k'}, \end{aligned}$$

(8)

with diagonal unperturbed energies $\varepsilon _k\ge 0$ and an “interaction” or “coupling” matrix of rank one. For the considerations in this appendix, both $\varepsilon _k (\ge 0)$ and $g_k$ may be rather arbitrary, but for the physical applications in this work $\varepsilon _k$ represents the excitation energy of two particles (holes) of the form:

$$\begin{aligned} \varepsilon _k=\pm \left[ E_{1p}\left( \frac{{\vec {p}}_+}{2}-\varDelta {\vec {p}}\right) +E_{1p}\left( \frac{{\vec {p}}_+}{2}+\varDelta {\vec {p}}\right) -2E_{\text {F}} \right] \end{aligned}$$

(9)

with k corresponding to $\varDelta {\vec {p}}$, “$+$” (“−”) for particle (hole) excitations, ${\vec {p}}_+$ being the conserved total momentum of the particle (hole) pair and only the values of k (or $\varDelta {\vec {p}}$) are allowed such that $E_{1p}({\vec {p}}_+/2\pm \varDelta {\vec {p}})-E_{\text {F}}>0$ for both particles (or $<0$ for both holes). The number $N_2$ corresponds to the dimension of the full unrestricted sector of ${\vec {p}}_+$ with all values of $\varDelta {\vec {p}}$. For later use, we note the dimension of the restricted sector (with allowed values of $\varDelta {\vec {p}}$) as $N_2'$ (being a given fraction of $N_2$).

The case $g_k=1$ corresponds to an attractive Hubbard interaction of interaction strength U and $g_k=g_{\varDelta {\vec {p}}}=[\cos (\varDelta p_x)-\cos (\varDelta p_y)]/2$ corresponds to an effective d-wave pairing attractive interaction used in typical mean field approaches (see for example [11]). For $g_k=1$, ${\vec {p}}_+=0$ and a simpler energy band this model was already considered by Cooper in 1956 [13]. His technical trick to compute the ground state energy (or gap) can be generalized to the more general model here and also be exploited for an efficient numerical method.

Let $\psi _k$ be the k-component of an eigenvector of (8) of energy E. It satisfies obviously the equation :

$$\begin{aligned} (E-\varepsilon _k)\psi _k=-\frac{|U|}{N_2}\,g_k\,S\quad ,\quad S=\sum _{k'} g_{k'}\psi _{k'}\ . \end{aligned}$$

(10)

There are two possibilities: either $S=0$ or $S\ne 0$. The case $S=0$ is possible if certain $\varepsilon _k$ values are degenerate, e.g., due to symmetries (there are always 1 to 3 symmetries in our applications for the HTC model, depending on the value of ${\vec {p}}_+$; see [15] for details) and corresponds to anti-symmetric wave functions with respect to those symmetries. Also if $g_k=0$ for certain k-values, we may have $S=0$. For $S=0$, we have obviously $E=\varepsilon _k$ for some k (with degenerate $\varepsilon _k$ or $g_k$=0) and $\psi _{k'}\ne 0$ (or $=0$) if $\varepsilon _{k'}=\varepsilon _{k}$ ($\varepsilon _{k'}\ne \varepsilon _{k},$ respectively) and such states are not affected by the interaction. For $S\ne 0$ (corresponding to totally symmetric states with respect to symmetries), we can insert

$$\begin{aligned} \psi _k=-\frac{|U|}{N_2}\,\frac{g_k\,S}{E-\varepsilon _k} \end{aligned}$$

(11)

into the sum of S and thus obtain an implicit equation for the energy E:

$$\begin{aligned} 1=-\frac{|U|}{N_2}\sum _k \frac{g_k^2}{E-\varepsilon _k}\ . \end{aligned}$$

(12)

Due to the attractive interaction, there is always exactly one (ground state) solution $E=E_{\textrm{min}}$ with $E_{\textrm{min}}<\varepsilon _{\textrm{min}},$ where $\varepsilon _{\textrm{min}}$ is the minimal value of $\varepsilon _k$ (with $g_k\ne 0$ !).

The implicit equation (12) allows for an efficient numerical method to compute the first energy $E_{\textrm{min}}$ (and potentially also other eigenvalues) by standard algorithms to numerically determine function zeros. Once the energy is known, the eigenstate itself is obtained from (11) with S being determined from the normalization. We have implemented this method and verified that it produces identical results to exact full numerical diagonalization (up to numerical precision).

From (12), one can also obtain the limits of $E_{\textrm{min}}$ for very small interaction (retaining in the sum only the $\varepsilon _{\textrm{min}}$-terms) and very large interaction (replacing in the sum all $\varepsilon _k\rightarrow \varepsilon _{\textrm{min}}$) :

$$\begin{aligned} E_{\textrm{min}}&\approx \varepsilon _{\textrm{min}}-\frac{d_{\textrm{min}}|U|}{N_2}&\text{ if }\quad \frac{|U|}{N_2}&\ll \delta _\varepsilon \sim \frac{\varepsilon _{\textrm{max}}}{N_2'}\ , \end{aligned}$$

(13)

$$\begin{aligned} E_{\textrm{min}}&\approx \varepsilon _{\textrm{min}}-\frac{N_2'|U|}{N_2}&\text{ if }\quad \frac{|U|}{N_2}&\gg \varepsilon _{\textrm{max}}\ . \end{aligned}$$

(14)

In (13), $\delta _\varepsilon$ represents the typical spacing of $\varepsilon _k$-levels (close to $\varepsilon _{\textrm{min}}$) and $d_{\textrm{min}}$ is the degeneracy of the level $\varepsilon _{\textrm{min}}$ for the Hubbard case or the sum of $g_k^2$ over the $\varepsilon _{\textrm{min}}$ levels for the d-wave interaction case. Furthermore, $N_2'$ is the number of $\varepsilon _k$-levels (dimension of the ${\vec {p}}_+$-sector of pair excitations).

Following Cooper [13], and for the simple Hubbard interaction case with $g_k=1$, one can also try a continuous limit if $N_2'\gg 1$:

$$\begin{aligned} 1=-\frac{|U|}{N_2}\int _{0}^{\varepsilon _{\textrm{max}}} \rho _2(\varepsilon ) \frac{1}{E_{\textrm{min}}-\varepsilon }\,d\varepsilon , \end{aligned}$$

(15)

where $\rho _2(\varepsilon )$ is the two-particle (two-hole) excitation density of states in the given ${\vec {p}}_+$-sector and normalized by $N_2'=\int _0^{\varepsilon _{\textrm{max}}} \rho _2(\varepsilon )\,d\varepsilon$. For simplicity, we have also replaced $\varepsilon _{\textrm{min}}\rightarrow 0$ by applying a uniform shift to all values of $\varepsilon _k\rightarrow \varepsilon _k-\varepsilon _{\textrm{min}}$ (actually in the limit $N_2'\rightarrow \infty$ we have anyway $\varepsilon _{\textrm{min}}\rightarrow 0$). We also assume that the ratio $N_2'/N_2$ remains finite in the limit $N_2'\rightarrow \infty$ (constant fraction of allowed states in the given ${\vec {p}}_+$-sector; see non-white zones in Figs. 2, 5 and 10).

For the case of a constant density of the states $\rho _2(\varepsilon )=N_2'/\varepsilon _{\textrm{max}},$ one obtains from (15) the expression

$$\begin{aligned} E_{\textrm{min}}=-\varepsilon _{\textrm{max}}\,\left[ \exp \left( \frac{\varepsilon _{\textrm{max}} N_2}{|U|N_2'}\right) -1\right] ^{-1}\ , \end{aligned}$$

(16)

which is very similar to the well-known result of Cooper [13] (only with different notations/parameters). One can note that in the limit of very strong interaction this expression reproduces (14) plus a constant correction being “$+\varepsilon _{\textrm{max}}/2$” (reduction of $|E_{\textrm{min}}|$), which has to be added to (14). On the other hand, for finite $N_2'$, (16) is not valid in the regime where the very small interaction limit (13) applies.

However, for the HTC lattice, at filling factors close to the separatrix point, e.g., $n=0.74$, and for ${\vec {p}}_+=0,$ the density of states is strongly enhanced for small energies due to the effect of the close van Hove singularity (separatrix) as can be seen in the right panel of Fig. S1 of SupMat. To model this behavior, we try the fit-ansatz :

$$\begin{aligned} \rho _2(\varepsilon )=\frac{N_2'}{\varepsilon _{\textrm{max}}\log (1+\alpha )}\, \frac{\alpha }{1+\alpha (\varepsilon /\varepsilon _{\textrm{max}})}, \end{aligned}$$

(17)

where $\alpha$ is a fit parameter reproducing the constant DOS if $\alpha =0$ or providing a strongly enhanced DOS close to small energies if $\alpha \gg 1$ and a power law decay $\rho _2(\varepsilon )\sim 1/\varepsilon$ for larger energies. (Also negative values of $\alpha$ are potentially possible.) This form does not correspond exactly to the van Hove singularity but it is convenient for the subsequent analytical evaluation of (15), and in any case, we want to model the case close but still different from the van Hove singularity where the DOS at $\varepsilon =0$ is still finite. The right panel of Fig. S4 of SupMat shows that this ansatz produces an integrated DOS, which fits very well the exact integrated DOS at $n=0.74$, particles for the sector ${\vec {p}}_+=0$. For $n=0.3$ the fit is of less quality but still provides an improvement.

Using (15) and (17), we obtain:

$$\begin{aligned} E_{\textrm{min}}=-\varepsilon _{\textrm{max}} f^{-1}\left( \frac{\varepsilon _{\textrm{max}} N_2}{|U|N_2'}\right) \end{aligned}$$

(18)

where $f^{-1}(\ldots )$ is the inverse function of:

$$\begin{aligned} f(x)=\frac{\alpha }{1-x\alpha } \left( \frac{\log (x^{-1}+1)}{\log (1+\alpha )}-1\right) \ . \end{aligned}$$

(19)

(Here x represents the ratio $-E_{\textrm{min}}/\varepsilon _{\textrm{max}}$). In the limit $\alpha \rightarrow 0$ we recover from (18) the original Cooper type result (16).

The result (18) is shown as blue curves in Fig. 3 and for $n=0.74$, with the fit value $\alpha =6.589$, the blue curve coincides very well with the numerical data points except for a very small shift, while the green curve based on the assumption of a constant DOS (i.e., $\alpha =0$) provides much smaller gap values. For $n=0.3,$ the situation is different. Here for modest values |U|,  the green curve fits better the numerical data points. This is because in this case, the uniform DOS (or linear integrated DOS) fits better the initial (integrated) DOS at small energies as can be seen in the left panel of Fig. S4 of SupMat where the green line is closer to the red data points for $\varepsilon <0.15\,\varepsilon _{\textrm{max}}$ than the blue curve corresponding to the ansatz (17). However, for larger values of $|U|\approx 8$ (not visible in Fig. 3), the blue curve is closer to the numerical data points since here the full range of energies $\varepsilon \in [0,\varepsilon _{\textrm{max}}]$ is important.

It is also possible to simplify (18) in the limit of very strong interaction, corresponding to $x\gg 1$ in (19), which gives:

$$\begin{aligned} E_{\textrm{min}}=-\left[ \frac{|U|N_2'}{N_2}-A_\alpha \varepsilon _{\textrm{max}}\right] \ ,\ A_\alpha =\frac{1}{\log (1+\alpha )}-\frac{1}{\alpha }, \end{aligned}$$

(20)

which is in agreement with the limit behavior of (16), since $\lim _{\alpha \rightarrow 0} A_\alpha =1/2$. For larger values of $\alpha ,$ the coefficient $A_\alpha$ decreases with respect to this value, e.g., $A_\alpha =0.3416$ for $\alpha =6.589$. Even though, mathematically, the constant term with $A_\alpha$ provides “only a small” correction to the first term $\sim |U|$, the fact that this coefficient decreases from 0.5 (at $\alpha =0$) to 0.3416 (at $\alpha =6.589$) has a considerable impact on the quite significant difference between the blue and green curves in Fig. 3 also for intermediate interaction values. For very large values of |U| these curves are actually parallel with a constant shift due to different values of this coefficient. Furthermore, the third term in the large |U|-expansion of $E_{\textrm{min}}$ would only provide an additional correction of the form $\sim |U|^{-1}$ in (20).

1.2 Local $g_k$-density of states

The density of states $\rho (E)$ for both lattices has a logarithmic van Hove singularity visible in Fig. S1 of SupMat, which is due to the vanishing value of $\vec \nabla E_{1p}({\vec {k}}_s)=0$ at the separatrix points ${\vec {k}}_s=(0,\pm \pi )$ or ${\vec {k}}_s=(\pm \pi ,0)$. Classically, $\rho (E)\,{\text {d}}E$ can be obtained from the (relative) area in ${\vec {k}}$-space between the two Fermi curves at energies E and $E+dE$. As can be seen in Fig. 1, this area is significantly enhanced in the region close to a separatrix point. To see this point more clearly, it is interesting to consider the angle-resolved area between Fermi curves at energies E and $E+dE$ and also angles $\varphi$ and $\varphi +{\text {d}}\varphi ,$ where $\varphi$ is the phase angle of the momentum vector ${\vec {k}}=k_E(\varphi ){\vec {e}}(\varphi )$ in which ${\vec {e}}(\varphi )=(\cos \varphi ,\,\sin \varphi )$ and $k_E(\varphi )$ is determined such that at given energy E and angle $\varphi ,$ we have $E=E_{1p}[k_E\,{\vec {e}}(\varphi )]$. This area (divided over $(2\pi )^2 {\text {d}}E\,{\text {d}}\varphi$) defines the local angle density of states $\rho _\varphi (\varphi ,E),$ which can be formally computed from the integral :

$$\begin{aligned} \rho _{\varphi }(\varphi ,E)= & {} \frac{1}{\pi ^2} \int _0^\pi {\text {d}}k_x \int _0^\pi {\text {d}}k_x \delta [E-E_{1p}({\vec {k}})]\nonumber \\{} & {} \times \delta [\varphi -\arctan (k_y/k_x)], \end{aligned}$$

(21)

$$\begin{aligned}= & {} \frac{k_E(\varphi )}{\pi ^2 |{\vec {e}}(\varphi )\cdot \vec \nabla E_{1p}[k_E(\varphi ){\vec {e}}(\varphi )]|}\, \end{aligned}$$

(22)

In (21), we limit ourselves to the first quadrant with $0\le \varphi \le \pi /2$ such that the normalization prefactor is $1/\pi ^2$. The expression (22) is obtained by computing the integral in polar coordinates for ${\vec {k}}$ and it is valid for angles $\varphi$ such that the equation $E=E_{1p}[k_E\,{\vec {e}}(\varphi )]$ has a solution for $k_E$. If this equation does not have a solution, we simply have $\rho _{\varphi }(\varphi ,E)=0$. For example, for energies above the separatrix energy $E_s=E_{1p}(0,\pi ),$ the local angle–density of states is limited to values $\varphi \le \varphi _{\textrm{max}}<\pi /2$. Close to $\varphi _{\textrm{max}}$ and for energies close to $E_s$ this density is not singular, but has a strong peak value $\sim 1/(\pi /2-\varphi _{\textrm{max}})^2$ (the exponent 2 is due to a combination of small gradient and small scalar product in the denominator, since the gradient and ${\vec {e}}(\varphi )$ are nearly orthogonal). For energies below $E_s,$ there is a minimal angle $\varphi _{\textrm{min}}>0$ with $\varphi \ge \varphi _{\textrm{min}}$ and a density peak $\sim 1/\varphi _{\textrm{min}}^2$.

In this work, we prefer however to use the quantity $g_k=(\cos k_x-\cos k_y )/2$ instead of $\varphi$ with values $g_k\approx 1$ (or $-1$) if $\varphi \approx \pi /2$ ($\varphi \approx 0$) and $g_k=0$ if $\varphi =\pi /4$. This quantity allows also to characterize a position on a Fermi surface at given energy (in the first quadrant). Its local $g_k$-density of states is obtained by a similar expression as (21):

$$\begin{aligned} \rho _{\textrm{g}}(g,E)=\frac{1}{\pi ^2}\int _0^\pi {\text {d}}k_x \int _0^\pi {\text {d}}k_x \delta [E-E_{1p}({\vec {k}})]\, \delta (g-g_k) \end{aligned}$$

(23)

and satisfies the relation:

$$\begin{aligned} \rho _{\textrm{g}}(g_k,E)=\rho _{\varphi }(\varphi ,E) \left( \frac{{\text {d}}g_k}{{\text {d}}\varphi }\right) ^{-1}\ . \end{aligned}$$

(24)

We have used this relation together with (22) (and a numerical evaluation of ${\text {d}}g_k/{\text {d}}\varphi$ by finite differences for a sufficiently dense set of data points) to compute numerically the $g_k$-density with results shown in Fig. S5 of SupMat and also in Fig. 4.

For energies E close to $E_s$ and values $1-g_k\ll 1$, we can apply to $E_{1p}({\vec {k}})$ and $g_k$ a quadratic expansion for ${\vec {k}}$ close to the separatrix point ${\vec {k}}_s=(0,\pi )$ resulting in :

$$\begin{aligned} E_{1p}({\vec {k}})=E_{1p}({\vec {k}}_s)+\frac{1}{2}\left[ a_x\,k_x^2-a_y(\pi -k_y)^2\right] \end{aligned}$$

(25)

with $a_x=a_y=2$ ($a_x=2.084$, $a_y=0.452$) for the NN lattice (HTC lattice) and

$$\begin{aligned} g_k=1-\frac{1}{4}\left[ k_x^2+(\pi -k_y)^2\right] . \end{aligned}$$

(26)

Inserting (25) and (26) in (23), one obtains the following analytical result:

$$\begin{aligned} \rho _{\textrm{g}}(g_k,E)=\frac{C_1}{ \sqrt{(g_{\textrm{max}}-g_k)(g_{\textrm{max}}-g_k+C_2(1-g_{\textrm{max}}))}} \end{aligned}$$

(27)

with constants $C_1=1/(2\pi ^2\sqrt{a_x a_y})$ and $C_2=1+a_x/a_y$ ($C_2=1+a_y/a_x$) if $\varDelta E=E-E_s\ge 0$ ($\varDelta E=E-E_s\le 0$), i.e., if the Fermi curve is above (below) the separatrix curve. Furthermore, $g_{\textrm{max}}$ is the maximal possible value of g given by : $g_{\textrm{max}}=1-\varDelta E/(2a_x)$ [$g_{\textrm{max}}=1+\varDelta E/(2a_y)=1-|\varDelta E|(2a_y)$] if $\varDelta E\ge 0$ ($\varDelta E\le 0$). We also note that (27) is valid for $g_k>0,$ because we have chosen the expansion around the separatrix point ${\vec {k}}_s=(0,\pi )$. Using that $\rho _{\textrm{g}}(g_k,E)=\rho _{\textrm{g}}(-g_k,E)$ due to the $x-y$ exchange symmetry, it is sufficient to replace in (27) $g_k\rightarrow |g_k|$ to obtain a more general expression for other separatrix points where $g_k$ is close to $-1$.

For the separatrix case $\varDelta E=0$ with $g_{\textrm{max}}=1,$ the expression (27) simplifies to the simple power law

$$\begin{aligned} \rho _{\textrm{g}}(g_k,E)=\frac{C_1}{1-g_k}\, \end{aligned}$$

(28)

This power law is also valid for the general case close to but outside the separatrix curve in the range of $g_k$ values sufficiently far away from the singularity at $g_{\textrm{max}}$, i.e., $1-g_{\textrm{max}}\ll g_{\textrm{max}}-g_k\ll 1$. For values very close to the singularity $g_{\textrm{max}}-g_k\ll 1-g_{\textrm{max}},$ the expression (27) becomes a power law with exponent $-1/2$. All these points are very nicely confirmed in Fig. S5 of SupMat.

Actually, the analytical expression (27) based on the separatrix approximation is highly accurate (provided one uses for $g_{\textrm{max}}$ the precise values for a given energy and not the approximate linear expressions in $|\varDelta E|$ given above) even for filling factors not very close to the separatrix values and even in the interval $0\le g_k\le 0.8--0.9,$ it is still rather close to the precise distribution obtained numerically.

Furthermore, from (23), we immediately see that

$$\begin{aligned} \int _{-g_{\textrm{max}}}^{g_{\textrm{max}}} \rho _{\textrm{g}}(g_k,E)\,{\text {d}}E= 2\int _{0}^{g_{\textrm{max}}} \rho _{\textrm{g}}(g_k,E)\,{\text {d}}E =\rho (E), \end{aligned}$$

(29)

where $\rho (E)$ is the total density of states given by an expression similar to (23), but without the delta-function factor $\delta (g-g_k)$. For $1-g_{\textrm{max}}\ll 1$, we find that this integral behaves as $\log (1-g_{\textrm{max}})\sim \log |\varDelta E|=\log |E-E_s|$ (simply using (28) with a cutoff at $|g|<g_{\textrm{max}}$), thus confirming the logarithmic nature of the van Hove singularity in the density of states.