Coulomb electron pairing in a tight-binding model of La-based cuprate superconductors

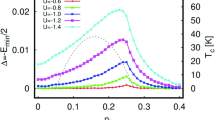
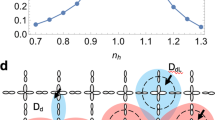
Abstract

We study the properties of two electrons with Coulomb interactions in a tight-binding model of La-based cuprate superconductors. This tight-binding model is characterized by long-ranged hopping obtained previously by advanced quantum chemistry computations. We show analytically and numerically that the Coulomb repulsion leads to a formation of compact pairs propagating through the whole system. The mechanism of pair formation is related to the emergence of an effective narrow energy band for Coulomb electron pairs with conserved total pair energy and momentum. The dependence of the pair formation probability on an effective filling factor is obtained with a maximum around a filling factor of 20 (or 80) percent. The comparison with the case of the nearest neighbor tight-binding model shows that the long-ranged hopping provides an increase of the phase space volume with high pair formation probability. We conjecture that the Coulomb electron pairs discussed here may play a role in high temperature superconductivity.

Graphic abstract

Appendix

In this appendix we present the derivation of the block Hamiltonian (11) and a more detailed discussion about its discrete symmetries. In order to simplify the notations, we will use here the full set $\mathcal{A}'=\mathcal{A}\cup (-\mathcal{A})$ of neighbor vectors (in the full and not only half plane) for the summation over the vectors $\mathbf{a}$ which allows to reduce the number of terms in the following expressions. The TIP Hamiltonian (5) can then be written in a more explicit form as:

$$\begin{aligned} H= & {} -\sum _{\mathbf{r}_1,\mathbf{r}_2}\sum _{\mathbf{a}\in \mathcal{A}'} t_\mathbf{a}\bigl (| \mathbf{r}_1,\mathbf{r}_2 \rangle \langle \mathbf{r}_1+\mathbf{a},\mathbf{r}_2 | +| \mathbf{r}_1,\mathbf{r}_2 \rangle \langle \mathbf{r}_1,\mathbf{r}_2-\mathbf{a} |\bigr )\nonumber \\&+\sum _{\mathbf{r}_1,\mathbf{r}_2}{\bar{U}}(\mathbf{r}_2-\mathbf{r}_1)| \mathbf{r}_1,\mathbf{r}_2 \rangle \langle \mathbf{r}_1,\mathbf{r}_2 | \end{aligned}$$

(13)

where for convenience we have written “$\mathbf{r}_2-\mathbf{a}$” instead of “$\mathbf{r}_2+\mathbf{a}$” (in the second term of the first line) since for $\mathbf{a}\in \mathcal{A}'$ also $-\mathbf{a}\in \mathcal{A}'$. Furthermore, the terms with shifts of $\mathbf{a}$ in the left side have been absorbed by the increased set $\mathcal{A}'$ (with respect to $\mathcal{A}$ used in (1)) combined with a subsequent shift of the summation index $\mathbf{r}_1$ or $\mathbf{r}_2$ and exploiting the periodic boundary conditions.

Applying (13) to a block basis state (10) we find that:

$$\begin{aligned} H| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle= & {} -\frac{1}{N}\sum _{\mathbf{r}_1}\sum _{\mathbf{a}\in \mathcal{A}'} t_\mathbf{a}\Bigl (| \mathbf{r}_1-\mathbf{a},\mathbf{r}_1+{\varDelta \mathbf{r}} \rangle \,\nonumber \\&\times e^{i\mathbf{p}_+\cdot (\mathbf{r}_1+{\varDelta \mathbf{r}}/2)}\nonumber \\&+| \mathbf{r}_1,\mathbf{r}_1+{\varDelta \mathbf{r}}+\mathbf{a} \rangle \,e^{i\mathbf{p}_+\cdot (\mathbf{r}_1+{\varDelta \mathbf{r}}/2)}\Bigr )\nonumber \\&+{\bar{U}}({\varDelta \mathbf{r}})| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle . \end{aligned}$$

(14)

Using the shift $\mathbf{r}_1\rightarrow \mathbf{r}_1+\mathbf{a}$ in the $\mathbf{r}_1$-sum of the first line of this expression we obtain:

$$\begin{aligned} H| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle= & {} -\frac{1}{N}\sum _{\mathbf{r}_1}\sum _{\mathbf{a}\in \mathcal{A}'} t_\mathbf{a}\Bigl (| \mathbf{r}_1,\mathbf{r}_1+{\varDelta \mathbf{r}}+\mathbf{a} \rangle \,\nonumber \\&\times e^{i\mathbf{p}_+\cdot (\mathbf{r}_1+\mathbf{a}+{\varDelta \mathbf{r}}/2)}\nonumber \\&+| \mathbf{r}_1,\mathbf{r}_1+{\varDelta \mathbf{r}}+\mathbf{a} \rangle \,e^{i\mathbf{p}_+\cdot (\mathbf{r}_1+{\varDelta \mathbf{r}}/2)}\Bigr )\nonumber \\&+{\bar{U}}({\varDelta \mathbf{r}})| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle \end{aligned}$$

(15)

which can be rewritten as:

$$\begin{aligned} H| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle= & {} -\frac{1}{N}\sum _{\mathbf{r}_1}\sum _{\mathbf{a}\in \mathcal{A}'} t_\mathbf{a}\,| \mathbf{r}_1,\mathbf{r}_1+{\varDelta \mathbf{r}}+\mathbf{a} \rangle \nonumber \\&\quad \times \,e^{i\mathbf{p}_+\cdot [\mathbf{r}_1+({\varDelta \mathbf{r}}+\mathbf{a})/2]} \underbrace{\left( e^{i\mathbf{p}_+\cdot \mathbf{a}/2}+e^{-i\mathbf{p}_+\cdot \mathbf{a}/2}\right) }_ {2\cos (\mathbf{p}_+\cdot \mathbf{a}/2)}\nonumber \\&+{\bar{U}}({\varDelta \mathbf{r}})| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle \nonumber \\= & {} -2\sum _{\mathbf{a}\in \mathcal{A}'}t_\mathbf{a}\,\cos (\mathbf{p}_+\cdot \mathbf{a}/2)\, | \mathbf{p}_+,{\varDelta \mathbf{r}}+\mathbf{a} \rangle \nonumber \\&+{\bar{U}}({\varDelta \mathbf{r}})| \mathbf{p}_+,{\varDelta \mathbf{r}} \rangle \ . \end{aligned}$$

(16)

The last expression provides exactly the effective block Hamiltonian (11) if we replace the sum over $\mathbf{a}\in \mathcal{A}'$ by a sum over $\mathbf{a}\in \mathcal{A}$ with two contributions “$+\mathbf{a}$” and “$-\mathbf{a}$” and applying for the latter contribution a subsequent shift ${\varDelta \mathbf{r}}\rightarrow {\varDelta \mathbf{r}}+\mathbf{a}$ in the ${\varDelta \mathbf{r}}$ sum. However, there is one additional complication if ${\varDelta \mathbf{r}}+\mathbf{a}=(\varDelta x+a_x,\varDelta y+a_y)$ in (16) leaves the initial square of $\varDelta x,\varDelta y\in \{0,\ldots N-1\}$. Then we have to add (subtract) N to (from) $\varDelta x+a_x$ and/or $\varDelta y+a_y$ which provides according to (10) the factor $e^{\pm ip_{+x}N/2}=e^{\pm i\pi l_{+x}}=(-1)^{l_{+x}}$ (for $\varDelta x$ and similarly for $\varDelta y$) resulting in either periodic or anti-periodic boundary conditions in x- (y-)direction depending on the parity of the integer index $l_{+x}$ ($l_{+y}$).

We close this appendix with a short discussion about the discrete reflection symmetries of the block Hamiltonian (11) and the possibility to reduce its effective matrix size $N^2$ due to such symmetries. For the NN-model, as already discussed in detail in [12], there are at least two symmetries with respect to $\varDelta x\rightarrow N-\varDelta x$ (reflection at the $\varDelta y$-axis) or $\varDelta y\rightarrow N-\varDelta y$ (reflection at the $\varDelta x$-axis) and in case if $p_{+x}=p_{+y}$ there is a third symmetry with respect to $\varDelta x\leftrightarrow \varDelta y$ (reflection at the $\varDelta x$-$\varDelta y$ diagonal) which allows for an effective matrix size of roughly either $N^2/4$ or $N^2/8$ (if $p_{+x}=p_{+y}$).

However, for a more general lattice, such as the HTC-model, or more generally in presence of at least one neighbor vector $\mathbf{a}=(a_x,a_y)$ with both $a_x\ne 0$ and $a_y\ne 0$ (e.g. $\mathbf{a}=(1,1)$) the number of symmetries is reduced. For the most generic case with $p_{+x}\ne p_{+y}$, $p_{+x}\ne 0$ and $p_{+y}\ne 0$ there is only one symmetry corresponding to particle exchange with two simultaneous transformations $\varDelta x\rightarrow N-\varDelta x$ and $\varDelta y\rightarrow N-\varDelta y$ which allows for a reduction of the effective matrix size to $\approx N^2/2$. In this case the factors $\cos (\mathbf{p}_+\cdot \mathbf{a}/2)=\cos [(p_{+x}a_x+p_{+y}a_y)/2]$ appearing in the effective hopping amplitudes are not modified because the replacement $\mathbf{a}\rightarrow -\mathbf{a}$ due the symmetry transformation only changes the global sign inside the cosine argument. However, this is no longer true if we apply for example the transformation $\varDelta x\rightarrow N-\varDelta x$ without modifying $\varDelta y$ which is equivalent to the replacement of $(a_x,a_y)\rightarrow (-a_x,a_y)$ of the neighbor vectors. Therefore a single reflection at the $\varDelta y$ (or $\varDelta x$) axis modifies the hopping amplitude (if both $a_x\ne 0$, $a_y\ne 0$ and also both $p_{+x}\ne 0$, $p_{+y}\ne 0$) and (11) is (in general) not invariant with respect to such transformations. However, if either $p_{+x}=0$ or $p_{+y}=0$ the effective hopping amplitudes are not modified with respect to these two individual reflections and we have two symmetries with an effective matrix size of $\approx N^2/4$. Also if $p_{+x}=p_{+y}\ne 0$ we have two symmetries (particle exchange and reflection at the $\varDelta x$-$\varDelta y$ diagonal) leading also to an effective matrix size of $\approx N^2/4$. Finally, for the special case $p_{+x}=p_{+y}=0$, we have even three symmetries (as in the NN-Model for $p_{+x}=p_{+y}$) with effective matrix size of $\approx N^2/8$.