Abstract
We develop a joint formalism and numerical framework for analyzing the superconducting instability of metals from a weak coupling perspective. This encompasses the Kohn–Luttinger formulation of weak coupling renormalization group for superconductivity as well as the random phase approximation imposed on the diagrammatic expansion of the two-particle Green’s function. The central quantity to resolve is the effective interaction in the Cooper channel, for which we develop an optimized numerical framework. Our code is capable of treating generic multi-orbital models in two as well as three spatial dimensions and, in particular, arbitrary avenues of spin-orbit coupling.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Correlated metals can be the parent state for unconventional superconductivity [1]. Opposed to doped Mott insulators such as the famous copper oxide superconductors [2, 3] where a strong coupling perspective appears unavoidable at low doping, condensed matter research in the past decades has witnessed a plethora of superconducting materials where the parent state is metallic and yet the pairing mechanism is likely to be mediated by electrons rather than phonons. As an indication for its nevertheless correlated character, the metallic state often experiences itinerant magnetism, a pronounced profile of dynamic spin fluctuations, or even charge-type species of seeding particle hole fluctuations. Their impact on pairing, within a leading approximation, is included in the random phase approximation (RPA) treatment of the superconducting instability in the particle–particle channel of the two-particle Green’s function [4,5,6]. There, the RPA reduces to a geometric series summation of the particle–hole bubble, which in principle tracks all types of particle–hole fluctuations that can result in an instability of the metallic state to superconducting pairing. While the assignment of a rigorous convergence radius to the RPA approximation is an open problem, it is apparent that the error should increase with the electronic coupling strength, since most higher order diagrammatic contributions are neglected in the RPA. Nevertheless, the RPA remains a useful tool for a qualitative analysis of superconductivity at intermediate coupling. It rests on the hypothesis that the particle–hole bubble is the central source of pairing and its resummation to arbitrary orders yields a valid description even beyond the limit of perturbative coupling strengths. Further refinements from a metallic parent state can be accomplished by functional renormalization group (FRG) where leading vertex corrections are retained and all two-particle channels are treated on equal footing [7, 8].
From a somewhat complementary perspective, Kohn and Luttinger [1] analyzed the emergence of Fermi surface instabilities in the infinitesimal coupling limit. Decades later, this was the basis for a related more systematic treatment for superconducting instabilities by Raghu, Scalapino, and Kivelson [9,10,11,12,13,14]. The resulting ansatz is henceforth labelled weak coupling renormalization group (wcRG). Its central motif is to retain analytical control over the expansion in the particle–particle channel and thus obtain a rigorous formulation of unconventional pairing in the limit of vanishing coupling. The wcRG and RPA approach hence incorporate a different teleological background even though they still exhibit strong formal similarities. In particular, with respect to numerical performance, everything condenses into the efficient computation of the particle–hole bubble as the central building block for the effective particle–particle interaction in the Cooper channel.
In this article, we develop a joint formalism and numerical framework for the analysis of unconventional superconductivity in correlated metals from the perspective of RPA and wcRG. We show that the generalized susceptibility enables a unified numerical formulation of the RPA and wcRG methods and propose a generalization for the exact treatment of generic long range interactions in both approaches. Including arbitrary types of spin orbit coupling into general multi orbital models can cause problems due to the residual gauge degree of freedom in the choice of eigenstates. This problem and its implications on the exploitation of symmetries is spelled out explicitly and resolved for the two particle Cooper vertex. We present a sophisticated Fermi surface discretization scheme as well as a controlled approximation for the integration of the particle–hole bubble and show that our approach allows for the numerically efficient reproduction of various literature results within the same numerical framework. The model systems we choose for this purpose include the single orbital Hubbard model on the square lattice and the honeycomb Hubbard model, and also consider spin orbit coupling, long-range Coulomb interactions, and hoppings from long-range hybridization. To approach three spatial dimensions, we investigate the transition from a layered square lattice to a simple cubic and body centered cubic lattice.
2 Methods and mathematical formalism
In this section we begin by outlining the class of model Hamiltonians considered in our method description. This is followed by a general formulation of the wcRG in Sect. 2.2. Here we focus on an approach centering around the calculation of the generalized susceptibility \(\chi \) and introduce a strictly more general object \(\aleph \) that may be used to implement long range interactions efficiently. Section 2.3 shows that the same object can be used to calculate the susceptibility in the RPA approximation. This equalizes the scaling of numerical cost in both methods.
2.1 Generalized Hubbard model
The formalism developed in this article concerns a generalized Hubbard type model with combined orbital and sublattice degrees of freedom denoted \(w_i\) occupied by spinful electrons. The kinetic part of such a model can be generically represented by a tight-binding type Hamiltonian
where \(a_i = (w_i,s_i)\) is a fused spin, orbital and sublattice index, \(c^{\dag }_i\) denotes the creation operator of an electron with indices \(a_i\) on a lattice site \(\mathbf {r}_i\) and \(t\) describes the amplitude and phase of a translation invariant hopping process between states \(c^{\dag }_i{|{0}\rangle }\) and \(c^{\dag }_j{|{0}\rangle }\).
Such a model is readily simplified by utilizing its translation invariance with a Fourier transformation
and subsequently solved by numerical diagonalization of the matrix
The solution is described by (possibly degenerate) band energies \(\epsilon _{\alpha _i}(\mathbf {k})\) (eigenvalues) and a complete set of orthonormal eigenvectors \(v_{a_i \alpha _i}(\mathbf {k})\) of the matrix, encoding the orbital-spin structure of the energy eigenstates. For multi site models it is important to note that we use the Fourier transform to momentum space in “proper” gauge as defined in Ref. [15]. In short this amounts to a transformation which acts as if all orbital positions lie in the center of the Brillouin zone, ensuring the momentum space Hamiltonian’s periodicity under reciprocal lattice vectors. This allows the definition of all other operations without explicit specialization of the Brillouin zone (BZ) in which to evaluate as they are equivalent.
A crucial observation to make at this point is the fact that the \(v_{a_i \alpha _i}(\mathbf {k})\) are only defined up to gauge transformations i.e., \(\text {e}^{\text {i}\varphi _{\alpha _i}(\mathbf {k})}v_{a_i \alpha _i}(\mathbf {k})\) are equally valid solutions to the eigenvalue problem given by Eq. (3). Additional care must be taken in the case of degenerate bands where not only the phase but also the basis in the space of degenerate states is undefined by the eigenvalue problem. While the second issue is easily circumvented by analytical separation of the spin degree of freedom in the case of non spin orbit coupled systems, the first is ubiquitous for models requiring a numerical solution of Eq. (3). This ambiguity in the choice of eigenstates poses difficulties in the analysis of Hubbard type models due to the gauge-dependence of the bare interaction in band space as we will elaborate now.
The most general interaction we consider in this article is given by the quartic Hamiltonian
where we define \(\hat{\mathbf {r}}_i = \mathbf {r}_i - \mathbf {r}_0\) to compactify notation and emphasize translational invariance. The sums run over \(\{x_i\}=x_0, x_1, x_2, x_3\). Employing the same Fourier transform as before we find
by introducing the definition
A subsequent transformation into band space seems natural and would result in
From the prior discussion about the gauge freedom in the eigenvectors \(v_{a_i \alpha _i}\) it is clear that this expression is manifestly gauge variant, making it a useful analytical device but not a computationally advantageous quantity. One can trivially avoid this issue by considering the interaction in orbital space only. This, however is not common practice in the wcRG and functional renormalization group (fRG) literature, where calculations in band space are standard. Unfortunately performing calculations in orbital space lead to limitations of the applicability and performance of the established Fermi surface patch formulation of the fRG. The reason is that a restriction of the interaction to the Fermi surface is most useful if the interaction is also decidedly constrained to one band at the Fermi surface, resulting in a reduction of the vertex function by a factor of \(N_{\text {orb}}^4\) [8, 16]. Contrarily, our formulation of the weak coupling renormalization group (wcRG) via the generalized susceptibility allows for gauge invariant calculations in band space.
Having established the representation of models to be analyzed for unconventional superconducting instabilities we are going to discuss two approaches to the problem in the following. We first propose a gauge invariant formulation of the wcRG method that is based on a further generalization of the generalized susceptibility tensor known from the RPA. In a second step we will discuss how this allows a direct analytical connection and results in the natural numerical equivalence between the wcRG and the RPA.
2.2 Weak coupling renormalization group (wcRG)
The central assumption in the weak coupling renormalization group (wcRG) approach to unconventional superconductivity is the proposition of perturbative coupling strength. This allows a twofold simplification of the problem: Firstly we can employ the arguments thoroughly explored in Refs. [1, 9], which deduce that a generic Fermi liquid subject to repulsive interactions has a superconducting and only a superconducting instability under the assumption of interactions much smaller than the bandwidth. This allows restricting the investigations to divergences of couplings in the Cooper channel. Secondly we can calculate perturbative corrections to the bare interactions using second order perturbation theory i.e., one-loop diagrams and neglect all diagrams of higher order. While this approach as well as the possibility for unconventional pairing has been first pointed out by Kohn and Luttinger [1] it was later refined via the language of the perturbative renormalization group [17, 18] and subsequently reformulated for computational convenience and applications to lattice models [9]. Expanding on this work we will now present a generalized formulation of the method applicable to generic tight-binding Hamiltonians described by Eq. (1).
The kinetic energy scale of such a model is given by it’s bandwidth \(W\) i.e., the energy difference between the states with highest and lowest energy possible in the system. Including interactions into the problem can now be done perturbatively in powers of \(U/W \ll 1\) where \(U\) is the largest interaction added and acts as a reference scale for all other interactions \({U_i \,\mathop {<}\limits _{\propto }\, U}\). This procedure is appropriate for the investigation of thermodynamic quantities even at temperature \(T=0\) if an artificial cutoff \(\Omega _0\) is introduced into the problem [9]. As long as this scale is chosen larger than the most divergent terms in the perturbative expansion e.g. the Cooper logarithms in the problem we are allowed to neglect many-body effects on the renormalization of the bare interaction. If we further restrict the cutoff to be significantly smaller then the relevant interaction energy scale for the non-singular i.e., magnetic and charge channels we can neglect it for the calculation of particle–hole fluctuations [10]. In the following \(\rho \) denotes the density of states at the Fermi level. In summary the cutoff \(\Omega _0\) is restricted to a parameter range
such that an effective interaction including the renormalization effects of modes with energies larger than \(\Omega _0\) can be calculated via perturbation theory in \(U/W\). Due to our lower bound for \(\Omega _0\) we are also guaranteed that the resulting interaction will still be small enough for the application of one loop renormalization group equations to the new theory.
Formally we start by formulating our fermionic many body problem in terms of a generating functional for vertex functions written out as a Grassman path integral with the quadratic part of the action given by \(H_0\). We then integrate out all modes with energies larger than \(\Omega _0\) using perturbation theory up to second order in \(U/W\). The resulting theory is now composed of modes restricted to a small annulus of size \(\Omega _0\) around the Fermi energy \(\epsilon (\mathbf {k}_F)\) that interact via a weak renormalized interaction \(U^\text {eff}\) such that one can easily apply the standard Fermi-liquid RG procedure by Shankar and Polchinksi to it [17, 18]. It has been shown by explicit calculations up to fourth order in perturbation theory that this two-step procedure removes any dependence of system properties on the intermediate and artificial cutoff \(\Omega _0\) [9]. The authors also clarified that the central property to be calculated is the effective interaction in the Cooper channel \(U^\text {eff}_{\{\alpha _i\}}(\mathbf {k}_F, \mathbf {q}_F) \) up to one loop where the cutoff \(\Omega _0\) can be neglected in the particle–hole diagrams. From the setup of our calculation it is also clear that we may restrict this calculation to momenta \(\mathbf {k}_F, \mathbf {q}_F\) from the Fermi surface since these are the only relevant degrees of freedom in the second step of the renormalization. We thus adapt our notation to reflect this constraint to the Cooper channel:
In the notation of this review, this effective interaction on the Fermi level may be written as
where \(\mathbf {k}_F\) and \(\mathbf {q}_F\) are restricted to lie on the Fermi surface and we are only interested in band indices \(\alpha _i\) corresponding to zero energy modes at these momenta. The second order correction is given by the sum of the particle–particle (\(\text {PP}\)), direct particle–hole (\(\text {PH}\)) and crossed particle–hole (\(\text {cPH}\)) diagrams
Sticking to band space notation as in related works [9, 19] the different contributions are calculated via the following integrals:
where
are given by momentum conservation. The dependencies on \((\mathbf {k}_F, \mathbf {q}_F)\) on the left side of the equation have been suppressed for notational convenience. In the second step, the fermionic RG treatment of the vertex, couplings at \(\omega _i\ne 0\) will turn out to be irrelevant in an RG sense, which allows a restriction to the static case without any further approximation [17]. With this in mind we drop all frequency labels already at this point to simplify the notation of the subsequent formulas.
In restricting our focus to the zero energy sector of the effective interaction Matsubara summation was used to solve the frequency integration analytically. The propagator pairs reduce to the well known fractions
and
with the Fermi Dirac distribution
and a temperature parameter \(T\) that may be set to zero for the weak coupling approach but is kept explicit to illustrate the generality of the derivation. Note that the particle–particle diagram is explicitly regularized by restricting its integration to modes \(\mathbf {l}\) satisfying \(|\epsilon _{\beta _l}(\pm \mathbf {l})|>\Omega _0\) while no such restriction is needed in the particle–hole diagrams due to the prior assumptions on \(\Omega _0\). However, the removal of the regulator introduces divergences in \(L^{\text {PH}}\) when \(\mathbf{l}= \mathbf{m}\) on degenerate bands, that restrict the BZ integration to the respective zero energy states. We explicitly calculate these occurrences via a line integral along the FS using
where \(v_{F_{\beta _\mathbf{l}}}(\mathbf{l})\) denotes the Fermi velocity on band \(\beta _\mathbf{l}\). The calculation of the particle–particle diagram in Eq. (12) on the other hand would indeed require a careful implementation of the cutoff since its divergence is of physical origin. Fortunately, closer inspection of the formula results in the insight that the vanishing total momentum of Cooper pairs disallows the emergence of new momentum dependencies \(\mathbf {k}_F\) or \(\mathbf {q}_F\). Combining this perception, namely that the particle–particle diagram will always be limited to the momentum dependence of the bare interaction, with the fact that the diagram scales with \(U^2\) compared to \(U\) for the bare interaction, allows us to neglect it completely in the limit of vanishing \(U\) [9, 10].
As hinted at in Sect. 2.1 the formulation of the diagrams in band space is useful for the analysis of models with a closed analytical solution for \(H_0\) but disadvantageous for models where \(H_0\) can only be solved by numerical matrix diagonalization. To formulate everything in terms of gauge invariant and thereby numerically preferable quantities we explicitly insert the orbital band transformation matrices from Eq. (7) into the expression for the direct particle–hole bubble above
and notice that the expression in the last line is indeed gauge invariant. If we were able to remove the interaction terms in orbital space from the \(\mathbf {l}\) integration, the object to calculate would equal the generalized susceptibility known from random phase approximation calculations
Clearly this is possible for the case of local interactions where \(U_{\{a_i\}}(\{\mathbf {k}_i\})\) is momentum independent but we can go beyond local interactions by rewriting the momentum dependence of the bare interaction. Let us first introduce the integrand of this generalized susceptibility as
for notational convenience.
Inspired by the channel decomposition of singular mode [20] and truncated unity fRG [21] we explicitly write our bare interaction in the direct particle–hole diagram representation of these approaches
where the \(f_i(\mathbf {k})\) are a set of envelope functions adapted to the specifics of the input interaction. In the subsequent we will refer to them as form factors. In Appendix A we show that such a reformulation is generically possible for reasonable translationally invariant interactions involving a finite number of bonds and that the number of form factors is bounded by the number of sites involved in the interaction with a reference site.
Plugging Eq. (23) into our expression for the direct particle–hole diagram yields
This approves the replacement of Eq. (22) by an even more generalized susceptibility
where we chose the Hebrew letter \(\aleph \) (Aleph) due to its similarity with the letter \(\chi \). Repeating the same calculation for the crossed particle–hole channel reduces to the same integral i.e., the knowledge of \(\aleph \) for all points \(\mathbf {k}_F\) and \(\mathbf {q}_F\) on the discretized Fermi surface is sufficient for the calculation of both the PH and cPH diagrams without further integration.
The decomposition Eq. (23) may seem peculiar at a first glance, since absorbing the whole momentum dependence in the newly defined \(\aleph \) may reduce the number of required form factors. Yet we are willing to accept the additional numerical effort in the generalized susceptibility calculation to obtain a quantity, which will turn out to be ideally suited as the starting point for a resummation in the RPA approximation (cf. Sect. 2.3). In fact the proposed form factor decomposition is equivalent to the procedure utilized to incorporate long range Coulomb interactions in FLEX implementations [22]. Here however, we only imposed translational invariance on the interaction.
While we have now established a gauge invariant formulation for the numerically expensive momentum integration, the gauge of the effective interaction in band space is not yet fixed. We tackle this problem by enforcing the calculation of the pair interaction between time reversal partner states. This is possible and trivial for generic models as the time reversal operator does not affect the real space, i.e. orbital or sublattice degrees of freedom and can always be represented by
where \(\sigma _y\) acts in spin space, \({\mathcal {K}}\) represents complex conjugation and the orbital sublattice structure is trivial. Instead of analyzing an interaction between states created by operators \(c^{\dag }_{\mathbf {k} \alpha } c^{\dag }_{-\mathbf {k} \beta }\) we rephrase the problem to an interaction between states created by
and define the quantity
This object has the key advantage that it eliminates possible gauge differences between states at \(\mathbf {k}\) and \(-\mathbf {k}\) arising from numerics by using the state at \(\mathbf {k}\) to define the state at \(-\mathbf {k}\) in a natural way.
Since we inspect pairing exclusively in the Cooper channel, the paired states may carry different pseudo-spins but belong to the same band. To ensure invariance under any \(U(1)\) gauge transformation also for systems with degenerate bands we only consider one pseudo-spin orientation \(v_{a\omega \uparrow }\) and construct the state with \(\sigma = \downarrow \) by manual orthogonalization. Thus both pseudo-spin states feature the same phase and Eq. (28) remains \(U(1)\) invariant. However, the choice of the pseudo-spin basis is not fixed by this procedure leaving a residual degree of freedom. A completely gauge invariant formulation of the effective vertex with time reversal partners therefore requires a consistent pseudo-spin base along the FS. For band degeneracies originating from spin rotational invariance this is naturally given and does not have to be enforced. The same holds for systems akin to the spin orbit coupled \({\hbox {Sr}_{2}}{\hbox {RuO}_{4}}\), where rearranging the orbital spin basis properly renders the Hamiltonian block diagonal [23]. For generic systems an unambiguous pseudo-spin basis can be achieved by adiabatically switching on the spin orbit interaction implying a smooth and traceable evolution of the natural spin basis to a pseudo-spin basis as suggested in Ref. [16].
Putting both the gauge invariance of the \(\aleph \) object and the time reversal partner states together we summarize the formulas for the particle–hole diagrams contributing to the effective interaction in the Cooper channel
and
The significance of this rewriting is condensed into the fact that the \(\aleph \) object only contains information about the kinetic model chosen and the set of form factors used. In other words calculating it once allows a detailed scan of the interaction parameter phase diagram without the necessity to calculate additional integrals over the BZ. By using a basis of time reversal partner states for the calculation we simplify the problem of symmetry reduction explored in Sect. 3.3.1 significantly and fix the \(U(1)\) gauge of the effective interaction completely.
Having calculated the effective interaction in the Cooper channel at an intermediate scale \(\Omega _0\) the wcRG procedure continues with the second renormalization step: the analytical RG flow into the superconducting instability. This is done according to standard one-loop Fermi liquid RG since the action generated by the first step is of the exact form required for the input of these approaches: (1) all states in the theory are confined to a small annulus of width \(\Omega _0\) around the Fermi surface such that we can linearise the dispersion for the RG and (2) the effective interaction between the states is still small enough to allow for the application of a one-loop expansion of the RG equations. Phase space arguments for this RG flow indicate that most interactions are marginal i.e., do not renormalize under the flow from \(\Omega _0\) to low energy (smaller cutoffs) [17, 18]. These couplings are called Fermi liquid parameters and are neglected in the wcRG approach. Among these one can also locate all finite transfer momentum instabilities, which are ruled out by the same line of reasoning: The accessible phase space tends to zero when approaching the Fermi level in the absence of perfect FS nesting. Since this requires fine tuning it is neglected within the wcRG [9]. Similar arguments render the frequency dependence of the electronic response irrelevant in the RG flow, which we consequently neglected already in Eq. (17). The interactions in the Cooper channel on the other hand renormalize significantly upon further reduction of the cutoff and their flow can be calculated by the one loop RG equations arising from the particle–particle diagram to be
where the indices i, j, k run over all degrees of freedom for Cooper pairs on the Fermi surface and where the integration measure is absorbed into the definition of
Here \(\text {d}A_{F\alpha }(\mathbf {k}_F)\) and \(v_{F\alpha }(\mathbf {k}_F)\) denote the Fermi surface area and Fermi velocity associated to each discretized point \(\mathbf {k}_F\) on the Fermi surface, \(\alpha \) only runs over the bands at zero energy for these points. \(\rho _\alpha \) and \(A_{F\alpha }\) meanwhile denote the total density of states and total Fermi surface area contributed by a specific band \(\alpha \). The mean of the Fermi velocity on a band is defined via an inverse average
over all Fermi surface momenta on this band. Solving the flow Eq. (31) can now be done trivially via matrix diagonalization of
and realizing that all eigenvalues renormalize independently due to the fact that the set of eigenvectors is orthonormal i.e.,
Clearly the smallest (i.e., most negative) eigenvalue indicates the strongest superconducting instability of the system while all positive eigenvalues renormalize to zero under this flow equation. We will call the smallest eigenvalue \(\lambda _0\) and refer to it as the leading eigenvalue in the following. From the definition of \(g\) we can see that it is a dimensionless matrix scaling with \(U^2\rho W\). Since its eigenvalues \(\lambda \) will scale identically they are not independent of the chosen ratio \(U/W\), making them a non ideal quantity to analyze in the limit of vanishing interactions. We therefore display \(|\lambda |\) or \(V_{\text {eff}} = |\lambda |/\rho \) in units of \(t / U^2\) for all numerical results in Sect. 4. A link between \(|\lambda |\) and an estimate for the superconducting transition temperature is given [9] to be
which is only defined up to a multiplicative constant of order 1. In conventional BCS theory the prefactor of the exponential is given by the typical energy scale of the phonons, the Debye frequency, which allows for a quantitative estimate of the critical temperature of phonon based superconductors [24]. Contrarily, Eq. (36) only provides informations about the scaling behavior of \(T_c\) with the coupling constant, as the wcRG procedure is lacking an overall scale. This is based on the fact, that an explicit calculation of the crossover regime between Fermi liquid and superconducting behaviour in the RG flow is explicitly avoided via the separation of scales in Eq. (8). Consequently no quantitative estimate of the physical energy scale and therefore the proportionality factor can be given [9]. The eigenvector \(\phi _{j0}\) corresponding to \(\lambda _0\) encodes the information about the spin momentum structure of the leading superconducting instability gap function on the Fermi surface
which may be subsequently analyzed in terms of lattice harmonics, orbital texture or singlet/triplet character. However the central information extracted in our analysis is the more fundamental symmetry character of the gap function: Upon inspection of the eigenvalue problem Eq. (34) its relation to the linearised superconducting gap equation
becomes clear and group theory dictates that all solutions \(\Delta _{\alpha _0\alpha _1}(\mathbf {k}_F)\) must transform under irreducible representations (irreps) of the effective interaction’s symmetry group [8]. Since different irreps can’t mix under the effective interaction the information about the symmetry of the superconducting order parameter is expected to be significantly more robust to changes in model parameters or the computational approach for large gaps in the eigenvalue spectrum of Eq. (34), making the distance \(\lambda _1-\lambda _0\) a valuable measure for the robustness of this result.
In summary our formulation paves the way towards a generic and numerically efficient implementation of the wcRG for a wide class of models discussed in Sect. 2.1. The key ingredients necessary for such an implementation are the discretization of the Fermi surface and an efficient solver for the integral in Eq. (25). Our approach to these problems as well as a reduction of the computational effort via the use of symmetries is discussed in Sect. 3 and a variety of benchmark results are shown in Sect. 4.
2.3 Random phase approximation (RPA)
From the notational setup of the wcRG method a striking parallel to the random phase approximation (RPA) becomes apparent: the generalized susceptibility is the central calculational device. We will abstain from repeating the theoretical background of the RPA here and instead point the reader to references on the RPA and fluctuation exchange approaches to the unconventional superconductivity problem [25,26,27,28,29]. Instead the following section of the article focuses on the conceptual discrepancy between wcRG and RPA, explains the notational benefits of using \(\aleph \) for the inclusion of long range interactions in the latter, and shows computational equivalence between the two methods.
As stated in Sect. 2.2 the expansion of the Cooper pair scattering vertex up to second order in the bare interaction Eq. (10) is justified by an appropriate choice of interaction scales. Yet this restriction also exists in the second step of the RG procedure, where all modes above zero energy are integrated out to yield a low energy effective theory at the Fermi level. This is only possible if no finite scale \(\Omega _\text {PT}\) in the system remains, that restricts the renormalization of the bare interaction by higher order effects to energies larger than \(\Omega _\text {PT}\) [9]. Examples of such a physical scale are finite interactions (see Eq. (8)) or temperature. Therefore, the diagonalization of Eq. (32) as the solution of the effective theory on the FS is only the true ground state of the system at \(T = 0\) and infinitesimal couplings. In this limit the wcRG offers an unbiased and exact solution to the generic correlated electron problem.
The RPA on the other hand abandons this aim in order to relax the constraint of infinitesimal interactions, which allows higher order terms to enter in the expansion of the Cooper vertex Eq. (10). By assuming the spin and charge fluctuations of the unrenormalized electronic system drive phase transitions in the Fermi liquid, a small set of resummable diagrams is extracted from all possible extensions of the bare vertex [25, 27]. Because we are interested only in attractive interactions in the Cooper channel it is sufficient to perform the RPA resummation for the particle–hole bubble. The remaining contributions of the one-loop expansion \(U^\text {PH}\) and \(U^\text {cPH}\) give rise to longitudinal and exchange (transverse) fluctuations [30] respectively. This permits expressing \(U_\text {eff}\) in the fluctuation exchange approximation.
In the case of SU(2) invariant systems the resummation for the spin and charge sector can be carried out independently allowing a decomposition of both the interaction tensor \(U^\text {bare}\) and the susceptibility into respective channels. This removes the spin indices from the resummation. For spin orbit coupled systems this is not possible as the bare propagator is non-diagonal in spin components. Instead we must summarize both channels in a joint resummation by explicitly keeping the spin index in \(U^\text {bare}\) and the generalized susceptibility [31]. In order to simplify the resulting equations we first rewrite these tensor functions of the transfer momentum \(\mathbf {q}\) into matrices where each matrix index \({\mathcal {A}}_i\) is comprised of a form factor index \(g\) and a pair of spin orbital indices \(a_i\), representing one particle–hole pair
In this notation the dressed \(\aleph \) can be written as an infinite series of particle–hole bubbles
where all repeated \({\mathcal {B}}_i\) indices are summed over. Note that the alternating sign originates from the varying definition of the generalized susceptibility Eq. (25) compared to common RPA convention Eq. (22) [28]. This can be simplified to a recursive expression
which is commonly solved by a resummation of the geometric series
Inserting the result back into Eqs. (29) and (30) yields the effective interaction in the fluctuation exchange approximation , which corresponds to evaluating the particle–particle ladder diagrams in an analogous resummation procedure [32]. Possible particle hole instabilities are already indicated by a divergence of the newly defined particle–hole susceptibility in Eq. (42), which also provides the ordering vector \(\mathbf{q}\) of the condensate. If no such divergence is found, we know the systems instability to be superconducting and proceed analogously to Sect. 2.2, i.e. apply the linearised gap equation Eq. (38).
Similar to the wcRG approach we restrict our analysis to the static sector of the susceptibility. While it was shown in Ref. [17], that this is exact in the limit of infinitesimal coupling, the employed phase space arguments can not be transferred to the finite coupling regime. Keeping the loop frequency in Eq. (17) would amount to an additional term in the denominator of the integrand. We can therefore deduce, that the dominant contribution will be the static one already at the bare level. As the RPA is only able to perform channel resummations independently, the differences between the individual contributions will accumulate such that the dominant channel is heavily enhanced in comparison to subleading ones. Keeping the backbone of the diagrams in the RPA series should therefore capture the main features of the particle–hole fluctuations. Good qualitative agreement between dressed susceptibilities from static RPA calculations and self consistent FLEX treatments, which take into account self energy effects, has indeed been found in the literature [33]. We therefore rely on the static approximation to avoid increasing the complexity of the susceptibility integral by another dimension in favor of applicability to realistic 3D multiband materials with complicated FS topology, spin orbit coupling and long range interactions.
In the presented scheme we do not calculate the RPA susceptibilities explicitly. Nevertheless a connection to standard RPA can be obtained for momentum independent - i.e., onsite - interactions. In this case the employed formfactor basis collapses to \(f_0(\mathbf{k}) = 1\) and Eq. (25) just depicts the bare susceptibility
Inserting this in the above reveals the well known expression for the RPA susceptibility tensor [31]
For general long range interactions the presented approach exceeds the established formulas for long range RPA susceptibilities, which focus on the treatment of density density interactions in spin rotational invariant systems [22, 34].
2.4 Summary
In conclusion we remark on similarities and differences between the two approaches: Firstly the matrix operations performed here are dwarfed by the cost of the integrations necessary to calculate the \(\aleph \) object itself i.e., the RPA and wcRG are almost identical in computational cost, even for the case of an exact treatment of the long range interactions.
Secondly, the finite interaction scales in RPA offers opportunities for significant performance benefits. As discussed previously the wcRG scheme aims at zero temperature results. However, the fundamental origin for pairing in repulsive systems now poses a serious computational challenge: the sharpness of the Fermi level at \(T = 0\) yields equally sharp features of the integrand Eq. (17), that require prudent calculation of the \(\aleph \) object. It would be therefore desirable to perform the crucial integral at finite temperature where the smoothing of the Fermi distribution simplifies the convergence. Unfortunately the effective interaction and the thereof derived superconducting order parameters are heavily dependent on temperature in wcRG as the sole scale present at low energy. This prohibits an approximation of the true ground state of the system by finite temperature calculations.
In RPA the bare interaction sets out a reference energy. Consequently one can restrict the temperature to be small compared to the interaction and still mimic the system at \(T = 0\). This reduces the effort needed for the particle–hole integral in Eq. (17) significantly compared to the wcRG scheme. The physical explanation is that finite interactions extend the possible pairing channel to all states in a shell of width U around the Fermi level. Then a dilution of the Fermi surface in this energy range does not noticeably decrease the nesting. Combined with the new formulation of the generalized susceptibility this renders extensive long range studies as presented in Ref. [35,36,37] accessible for complex spin orbit coupled three dimensional materials.
Finally we stress that the parallels between the two presented methods exceed the formal level and reside on physical grounds. In either method the bare interaction is screened and modified by the response of the electron gas, leading to Cooper pair formation. In the wcRG the small coupling allows us to truncate the calculation of this effect to one loop perturbation theory i.e. we can calculate the particle–hole susceptibility of the unperturbed system. Contrarily the RPA allows for a phase coherent accumulation of particle–hole fluctuations with fixed transfer momentum \(\mathbf{q}\) in each order of Eq. (40). The susceptibility is therefore evaluated in a Fermi liquid with low energy collective excitations [25].
However, one can reobtain the wcRG results from RPA in the \(U \rightarrow 0\) limit while keeping terms up to order \(U^2\) in the Cooper channel interaction, under which Eq. (42) reveals \(\aleph ^{\text {RPA}} \rightarrow \aleph \). Studies based on a Kohn–Luttinger type of pairing mechanism (such as wcRG) are therefore only a limiting case of RPA studies. While the derivation of the effective interaction coincides for \(U \rightarrow 0\), the central merit of the wcRG treatment is the subsequent and transparent propagation from \(U^\text {eff}\) to the linearised gap equation in Eq. (38) in an asymptotically exact manner. This rigour in the infinitesimal coupling limit is unique to the wcRG approach and requires the careful analysis presented in Ref. [9].
We want to conclude with some remarks on the physical validity of the obtained results. The irreducible representation deduced in either method is expected to accurately represent the symmetries of the superconducting gap. The eigenvalue separation provides a meaningful way to determine the competition between different superconducting instabilities in a given system. The precise values \(\lambda \) on the other hand are numerically difficult to converge and do not reflect physical transition temperatures [9]. Under these considerations several seemingly crude approximations employed during the evaluation of the RPA are put into perspective. Indeed both methods provide reasonable qualitative estimates on the pairing tendencies when compared to more sophisticated and thereby numerically more expensive frameworks [33, 38].
3 Numerical implementation
To nevertheless increase the performance of the wcRG for complicated systems in the absence of temperature regularizations we introduce several ideas for reducing the computational cost of the calculation in this section. We also compare our approach to other methods presented in the literature and demonstrate numerical equivalence with a variety of literature results in the following Sect. 4.
3.1 Caching of the kinetic Hamiltonian
The computationally most expensive part of the calculation is the integration of the propagator pair in the first BZ and its transformation into orbital space Eq. (25). To reduce the complexity of this operation we calculate the energies and orbital band transformation matrices for every momentum required before starting the integration - caching them. This prevents recalculations of the diagonalized form of the kinetic Hamiltonian otherwise required as each momentum will need to be accessed twice for each pair of FS momenta \(\mathbf{k}_F, \mathbf{q}_F\) at \(\mathbf{l}_i\) and \(\mathbf{m}_j = \mathbf{l}_j - \mathbf{k}_F + \mathbf{q}_F\) guaranteed at one \(\mathbf{l}_j \in \) BZ. This reduction becomes especially significant if the system under consideration is described by many bands or long-range orbital dependencies, raising the cost of each diagonalization. In order to cache for all momenta required during the integration, we must know their position prior to the start of the evaluation. This discourages the use of an adaptive integration scheme which would iteratively refine the mesh. Instead we span an equispaced grid within the space of the first BZ and obtain a fixed set of momenta. Even without this choice adaptive integrators are unsuitable for our uses as the sharp features along the FS will inhibit their convergence. There has been an attempt to remedy this by custom adaptive integrators [39] but our scheme reaches equivalent resolution compared to the last iteration of these custom integrators and is thus more accurate. While the loss of adaptive integrators may seem like a downside at first, in their absence the integration is reduced to fixed-size tensor contraction. As this is a common problem in the evaluation of neural networks we can use highly optimized libraries, in our case TensorFlow [40] for the evaluations.
We do however require an approximation that is not present in adaptive schemes: As seen above the caching is needed for the integration mesh’s momentum \(\mathbf{l}\) but also on \(\mathbf{m}= \mathbf{l}- \mathbf{k}_F + \mathbf{q}_F\). To ensure that \(\mathbf{m}\) is a cached momentum point we need to ensure all summands are elements of the grid. We achieve this by constraining the patched Fermi surface points - their exact construction is described in Sect. 3.2 - to the closest available point of the integration grid as shown in Fig. 2. While this may seem like a crude approximation at first, it should be noted that the quality improves linearly in the resolution of the integration grid as shown in Fig. 1. For a sufficiently dense (converged) grid of momentum points the approximation is insignificant.
Analysis of the program performance. a Change of maximal relative difference in \(\aleph \) with grid size. We iteratively increase the number of momenta (\(N_x^2\)) in the equispaced grid spanning the first BZ while approximating the FS points onto grid points as discussed in Sect. 3.1. To gauge the quality of this approximation we determine the average relative difference in the resulting \(\aleph \) when compared to the exact calculation where we refrain from constraining the FS points to the grid. The relative difference we evaluate is defined as \(\delta _\aleph = \sum |\aleph - \aleph _\mathrm {ref} |/ \sum |\aleph _\mathrm {ref} |\) where the maximum and sum are taken with respect to all possible index combinations. As expected the quality of the approximation is low when using few integration points but improves drastically at high resolutions of the integration mesh. The data was calculated employing a two band model for LaNiO\(_3\) as discussed in Ref. [38] with the 32 FS momenta shown in Fig. 2. We want to stress, that due to the utilized error metric \(\delta _\aleph \) decreases as the number of FS points increases. Hence negligible deviations can be expected for the parameter sets used in Sect. 4. In subfigure b we analyze the development of the execution time with the number of threads used in the calculation. We notice two effects: Firstly the drop in speedup beyond 16 threads can be attributed to the advent of Intel Hyper-Threading at thread-counts higher than the number of physical cores. This seems to disrupt the sequentiality of the calculations. Secondly we see deviations from the ideal speedup even at smaller thread counts. We attribute this to the single-threaded overhead of the calculations in the caching
Fermi surface patching schemes. a shows a set of momentum space points (set at equal angular distances for each pocket) along the FS as well as an equispaced grid of points spanning the BZ the area of which is marked in gray. The inset b shows the mapping of the FS points to the closest grid points. It should be noted that this approximation looks rather crude here but improves significantly when using resolutions far exceeding the \(20\times 20\) points used here. The second inset d shows the workings of the marching cube algorithm for one exemplary square. For each cube (square in 2D) we find the edges crossed by the FS (green line) by finding adjacent corners with opposing signs. Along these lines we interpolate the corner weights to find the (approximate) intersection of the FS with the cube. The dashed line then defines one surface element, the sum of which over all cubes makes up the FS. We search along the orthogonal to the center of this surface element for the intersection with the FS, defining this to be the FS point. The area of the associated marching cube triangle (line in 2D) is then used as the size of FS patch for this point. The middle figure c displays the resulting patching from a marching cube calculation. The issues are apparent when observing the inner pocket which is only sparingly patched while less interesting sections of the outer band have multiple points in close proximity. Raising the density to properly represent the inner pocket also introduces more points along the outer pocket. The final figure e is an example of the three dimensional patchings which can now be produced. We patched the same system as in Fig. 2 (i) of [14] but note that instead of 3000 to 4000 patch points only require around 1000 while maintaining resolution of the important features
3.2 Patching
Since the evaluation of the particle–hole bubble remains expensive despite the aforementioned efforts, a key avenue of optimization is a reduction of the number of integrals to be calculated. This number scales quadratically with the number of Fermi surface points in the discretization of the RG equations Eq. (32). In the following we will address the previously neglected issue of obtaining a valid set of points (patches) to represent the FS. We name this process the patching of the FS. Let us first define the requirements imposed on the set of momenta:
-
Each momentum \(\mathbf{k}_F\) is close to the FS: \( \exists \, \alpha : \epsilon _{\alpha }(\mathbf{k}_F) \approx 0\).
-
The set is dense enough to properly represent all FS features.
-
They are reducible to the irreducible wedge of the BZ, the full set can be recovered via symmetry operations.
-
We know the Fermi velocity \(v_F(\mathbf{k}_F)\) at and Fermi surface element \(\hbox {d}A_F(\mathbf{k}_F)\) associated with each point
-
Fewest possible momenta in set while maintaining all of the above.
It is apparent that even the “best” solution for the patching will remain a balancing act between sufficient resolution and reasonable computation times. In the following we present an approach to obtain such an optimized set of points in systems with arbitrary FS topology, which allows a fine tuning of the patching properties to adapt it for the system under study. Special considerations for the establishing of symmetry reducibility are discussed in Sect. 3.3.1.
NN Hubbard model on a square lattice. a wcRG findings for \(t^\prime = 0\) The particle–hole symmetry of the system at \(t^\prime = 0\) allows for calculations constrained to the \(n < 1\) region. At fillings \(n < 0.2\) the leading instabilities are very small and not distinguishable in the numerical error bars. Contrarily close to half filling the nesting of the FS is known to heavily favor the B\(_1\) representation [9]. Consequently we focus on the interesting regions in phase space, where we employed \(N_{\mathbf{k}_F} = 80\) and \(N_\mathbf {l} = (800 \times 800)\). b RPA results for \(t^\prime = 0\) Based on the bare susceptibility responsible for the data in a the RPA resummation with an onsite interaction of \(U = 2 t\) reveals a change in the ordering of instabilities. Whereas the triplet state is suppressed via the enhanced antiferromagnetic spin fluctuations, the extended s-wave solution A\(_1\) represents the leading superconducting order around \(n = 0.5\). Our findings coincide with the results of Ref. [54] (\(t^\prime = 0\) line in Fig. 3). The shaded region around half filling signals the onset of a spin-density wave due to a diverging RPA spin susceptibility as expected from the perfect \((\pi ,\pi )\) nesting of the FS at these fillings. c wcRG calculation for \(t^\prime = -0.3t\) The van-Hove filling is indicated. Unlike the other systems studied in this section, the long range hoppings up the second nearest neighbour break particle– hole symmetry. The scan in electronic filling was performed with \(N_{\mathbf{k}_F} = 160\) and \(N_\mathbf {l} = (800 \times 800)\)
3.2.1 Marching cubes
The starting point for the creation of our Fermi surface patches is the marching cubes algorithm [41]. It spans a grid of equispaced cubes within the BZ and evaluates the non-interacting Hamiltonian for each vertex (corner) in the grid. For each cube we discern edges intersecting the FS by connecting adjacent vertices with opposing signs of the energy. Having thus determined the approximate geometric shape of the FS (from the finite number of possibilities) we approximate the shape within the cube using triangles whose vertices are determined by finding approximate roots of the energy along the edge. For ease of presentation we show the two-dimensional equivalent of this algorithm in Fig. 2.
Building upon the triangles obtained from the marching cubes algorithm we determine their centers c. While these are sufficiently close to the FS to be used as a valid patching, we can increase accuracy by finding the intersect of the line perpendicular on the triangle through c with the FS. The set of all these points within the BZ is a valid patching. We assume the area covered by a point in the patching to be equal to the area of the corresponding marching cubes triangle. This approximation improves as the number of marching cube squares increases (and the FS curvature between points decreases). Note that this method is highly dependent upon the density and position of the initial cubes relative to the Fermi surface features. While a high density of cubes will yield the proper features of the FS, it will also result in a high number of patches. Meanwhile, a low number of initial cubes can be inapt in the description of features as shown in Fig. 2. We can however use the marching cubes algorithm with a high number of cubes as a starting point and subsequently reduce the set to the needed points. A method for such a procedure will be discussed in the next section.
3.2.2 CGAL
Since the patching of an isoplane in three dimensions is a problem not restricted to physics we were certain to find preexisting solutions to many obstacles. The Computer Graphics Algorithms Library (CGAL) [42] is a most promising toolkit of algorithms offering much of the required functionality. It would have been possible to instantiate the entire patching scheme using the thereby provided three dimensional surface mesh generation [43], but due to the random placement of initial sample points for the Delaunay triangulation, the algorithm tends to miss pockets not centered around the Gamma point in systems with complicated FS topologies. To provide a more reliable algorithm we build upon the existing implementation of marching cubes to obtain a consistent set of triangular faces. The current workflow for the creation of a mesh combines the effectiveness of marching cubes at high precision with the capabilities of CGAL to reduce the complexity [44] and obtain a sufficient set of smoothly placed triangles using the isotropic remesh algorithm [45].
To ensure an accurate mapping of the FS for the obtained surface mesh, we start with an overly dense mesh of marching cubes. The subsequent reduction by CGAL simplification routines to a target number of triangles retains a truthful representation of the initial FS throughout the simplification via two cost driven error estimates. While this leads to a varying number of FS patches for the discretization of Eq. (32) when performing phase scans as presented in Sect. 4, the relevant results (symmetry characters of the leading instability, eigenvalue separation, absolute pairing scale) are converged using the density of the initial marching cubes grid.
Having obtained a set of triangles from CGAL we employ the center and orthogonal relocation scheme described at the end of the previous section to obtain the final set of FS points. This workflow is illustrated in Algorithm 1. While it may appear overly complicated we manage to suppress the randomness inherent in the initialization of pure CGAL meshes while returning an optimally spaced grid of points all close to the FS. The remaining challenge lies in the reduction of these FS points to the set of points not equivalent under symmetry operations, and will be discussed in the next section.

3.3 Symmetries
The large number of points required for a detailed mapping of the FS along with the extra dimension of the integration grid renders three dimensional calculations numerically challenging even for simple models. While the latter impediment cannot be diminished without a reduction in integration accuracy, we present a way to address the former by exploiting the symmetries of the effective vertex. We subsequently investigate interdependent entries for an effective vertex as defined in Eq. (10) and their relations of type
with some transformation matrix M in order to identify a minimal set of vertex entries, that have to be calculated. All remaining elements are then determined through the relation above.
3.3.1 Reduction of the numerical effort
As outlined in Sect. 2.2, the quantity \(\aleph \) encapsulates the momentum space integration of the particle–hole bubble and the effective two particle vertex is calculated from it via contraction with the bare interaction tensors (see Eqs. (29, 30). While the interactions effect the spin, orbital, sublattice and momentum indices, \(\mathbf {k}_F\) and \(\mathbf {q}_F\) are directly propagated to \(U^\text {eff}\). Since the symmetries of \(\aleph \) are much more obfuscated and not directly accessible, we stick to the symmetries of the effective vertex and transfer the reduction in momentum space to \(\aleph \), i.e., we only calculate \(\aleph \) at pairs \((\mathbf {k}_F,\,\mathbf {q}_F)\) that have been identified as the minimum set of independent momenta, but to its full extent in spin, orbital and sublattice space. With this preparation at hand Eqs. (29) and (30) give the full effective vertex at these momenta. Yet we need the precise transformation behaviour given by Eq. (45) to construct the remaining \(U^\text {eff}(\mathbf {k}_F,\mathbf {q}_F)\). As Eq. (11) involves both \(U^\text {PH}\) and \(U^\text {cPH}\), i.e., simultaneously \(\aleph (\mathbf {k}_F,\mathbf {q}_F)\) and \(\aleph (\mathbf {k}_F,-\mathbf {q}_F)\), we have to ensure that the calculation of either none or both momentum pairs is omitted during symmetrization.
Spin rotational invariant systems however are an exceptional case. Since this symmetry applies to the generalized susceptibility, \(\aleph \) can be evaluated in only one non vanishing spin channel. The full spin structure can then be restored before contraction with the form factors. The remaining issue is determining relations like Eq. (45) in order to reveal the interdependent momentum sets.
3.3.2 Symmetries of the effective vertex
Taking aside spin rotation invariance, the set of promising vertex symmetries for reducing the computational effort can be classified into two parts: Firstly, the effective vertex features fermionic antisymmetry under particle exchange
and hermiticity
where we used \(U^\text {eff}(\mathbf {k}_F, \mathbf {q}_F) = U^\text {eff}(\mathbf {k}_F,-\mathbf {k}_F,\mathbf {q}_F,-\mathbf {q}_F)\). Both relations already provide the desired shape of Eq. (45). Secondly, the two particle vertex has well-defined transformation properties under symmetry operations which leave the underlying crystal structure invariant. These operations are contained in the point group \({\mathcal {G}}\) of the crystal.
In a first step we expound the transformation behaviour of the general two particle interaction in orbital space Eq. (6) and return to a band space representation of \(U^\text {eff}\) in a second step. This way we hope to explain the effort undertaken by us as well as the difference in required information for different symmetrization approaches. We subsequently denote a symmetry operation by \(g \in {\mathcal {G}}\) with unitary representations in momentum (\({\mathcal {P}}(g)\)) and combined spin, orbital and sublattice space (\({\mathcal {D}}_\mathbf {k}(g)\)). The gauge freedom of the employed Bloch basis renders the representations \(\mathbf {k}\) dependent in general.
The creation and annihilation operators transform under g as
We can now obtain the transformation behavior of the interaction of Eq. (6) as
Comparing the coefficients of the fermionic operators reveals
which maps the interaction tensor at a given momentum set to its symmetry related partner. Knowledge of the representation matrices therefore facilitates a reduction in the number of momentum sets requiring integration. It shrinks by a factor of \(\left|{\mathcal {G}}\right|\), the order of the point group.
The \({\mathcal {P}}(g)\) are given by elements of the SO(3), that can be inspected for example on the Bilbao Crystallographic Server [46]. From these the corresponding elements of the SU(2) can be deduced as spin space representations of \({\mathcal {G}}\). As we consider charge conserving systems only, the extended group elements can be neglected and there is a one to one correspondence between elements of SO(3) and SU(2). In orbital and sublattice space the transformation matrices are constructed to reflect the physical behavior under elements of the point group. The required information is either ascribed to the analytical Hamiltonian of the inspected toy model or obtained from the Wannier data for ab-initio calculations and therefore highly dependent on the system at hand.
The manifestly gauge independent formulation of the effective interaction presented in Sect. 2.2 allows for a less cumbersome incorporation of symmetries in band space. Let us demand a proper definition of pseudo-spin as discussed ibid, i.e. different bands do not hybridize. A consistent labeling of the bands along the FS renders the representations of \({\mathcal {G}}\) in band space one dimensional, i.e.
where we used, that the point group elements are unitary [47]. One dimensional representations are therefore simply expressed by complex band and momentum dependent phases \(\phi _\alpha (\mathbf {k})\). In conjunction with the transformation behaviour of the operators in orbital space Eq. (48) the fermionic operators in band space transform like
under point group operations. For the time reversal partners in Eq. (28) this results in the trivial transformation law
as the complex phases cancel for pairing in the same band. We want to stress that there is no need of commuting the point group operator with \({\hat{T}}\) to act on the fermionic operators. This is due to our construction enforcing the time reversed partner for each \(\mathbf {k}\) separately, such that both creation operators in the above must equal at any \(\mathbf {k}\).
With these operators the Hamilton operator of the effective interaction Eq. (10) is conveniently expressed as
Apparently the cooper pair scattering vertex in band space is invariant under all point group transformations \(U^\text {eff}_{\{\alpha _i\}}(\mathbf {k}_F,\mathbf {q}_F) = U^\text {eff}_{\{\alpha _i\}}({\mathcal {P}}(g)\mathbf {k}_F,{\mathcal {P}}(g)\mathbf {q}_F)\) , which renders the relation Eq. (45) trivial. This offers a striking advantage:
Utilizing an arbitrary gauge does not require knowledge of the point group representations \({\mathcal {D}}_\mathbf {k}(g)\), which are employed in the transformation law in orbital space and the construction of a suitable gauge in previous band space approaches [16]. The reduction of numerical effort via symmetry considerations is therefore facilitated remarkably. Finally we want to remark, that Eq. (54) may not be valid for bands with accidental degeneracies at distinct points in the BZ. At such points the representations of \({\mathcal {G}}\) turn out to be multi-dimensional and a mixing of degenerate bands is possible. Ref. [47] denotes these as awkward bands and covers the issue by introducing a natural basis set for the Bloch states. However, the construction of this specific gauge again involves the representations in orbital space, which we intended to avoid. This is achieved by approaching the problem from a different angle: since \(\mathbf {k}_F\) and \(\mathbf {q}_F\) are restricted to the set of discretized FS points we avoid awkward points by our the symmetrization scheme for the FS patching presented in the following section.
3.3.3 Symmetrization of the FS patching
In order to benefit from Eq. (54), the momenta connected by \({\mathcal {P}}(g)\) must both be part of the employed FS discretization. The patching procedure reviewed in Sect. 3.2 does not yield this property and we therefore have to enforce it via the following procedure.
As the BZ carries the symmetry of the underlying real space Bravais lattice, there exists an irreducible subset of crystal momenta. The whole BZ is then obtained as the star of this subset, which we call the irreducible wedge of the BZ in the following. To identify this wedge we place an initial point \(\mathbf {k}_0\) at an arbitrary position in the BZ, that is not on a high symmetry line, and obtain all symmetry equivalent points \(\mathbf {k}_i = {\mathcal {P}}(g_i) \mathbf {k}_0\) by applying the SO(3) representations of the point group elements \({\mathcal {P}}(g_i)\). In analogy to the determination of a Wigner-Seitz cell we calculate the perpendicular bisectors on the connecting lines between \(\mathbf {k}_0\) and all \(\mathbf {k}_i\) (lines in 2D, planes in 3D). The irreducible wedge is then given by the set of all momenta, which lie on the same side of all bisectors as \(\mathbf {k}_0\).
When truncating a patching as obtained by the algorithm described in Sect. 3.2 to the irreducible wedge, special care must be taken to correctly transfer the associated areas of the triangles. We therefore operate not on the patch points but on the triangulated FS mesh and employ an iterative scheme: If all corners of a triangle are located on the right (wrong) side of a bisector, we keep (drop) the triangle. If the bisector intersects the triangle, we cut the triangle along the intersection and keep the part located on the right side. After iterating over all bisectors, we remain with a surface mesh of the FS inside the wedge.
Since the edges of the cut triangles lie on the boundaries of the wedge, there are no associated FS points (as defined by the centers of the triangles) on these boundaries that coincide with the high symmetry lines/planes in the BZ. As these are the main contributor of occasional degeneracies this method protects the validity of Eq. (54) for the entire FS patching.
The repetitive cutting leads to an increased density of small triangles at the boundary of the wedge. To obtain a high quality mesh, our experience suggests truncation of the FS mesh to the irreducible wedge prior to the application of CGAL’s utilities as described in Sect. 3.2.2. The symmetric patching of the entire BZ is then constructed from the patching in the irreducible wedge via the point group operations \({\mathcal {P}}(g_i)\).
3.4 Performance
The calculation of the \(\aleph \) as defined in Eq. (25), the most expensive part of wcRG or RPA, is trivially parallel in the FS momenta \(\mathbf{k}_F, \mathbf{q}_F\). We can exploit this to parallelize their calculation using Pythons MPI implementation MPI4py [48,49,50,51], distributing the load locally as well as across multiple compute nodes. The speedup of local parallelization can be seen in Fig. 1 with calculations performed on a local cluster using Intel Xeon E5-2630. As the trivial parallelization requires no communication between computation nodes we expect the scaling for multi-node calculations to be similar to the single-node case. Note that the overhead of the kinetic Hamiltonian caching is substantial and prevents ideal speedups as this part of the calculation is currently running single threaded. We can furthermore see that Intel’s Hyper-Threading has a negative effect on runtime. Once we exceed the number of 16 physical cores we observe a decrease in speedup. We attribute this effect to the inhibition of sequential calculations when using multiple threads per core and note that this measurement was performed while constraining the TensorFlow backend to run single-threaded, despite the hope that its threading capabilities might make better use of Hyper-Threading. To reach optimal runtimes we combine the parallelization offered by TensorFlow with our custom parallelization. For the reader to be able to gauge the runtime of the calculation we offer the following measurement: Each phase diagram shown in Fig. 9 needed a run time of \(\approx 11.8\,\text {h}\) on a single node of the SuperMUC-NG cluster featuring a 48 core Intel Skylake Xeon Platinum 8174 processor and \(96\,\text {Gb}\) of memory.
While using parallelization can reduce the time required for the calculation we want to address the second constraint imposed on the calculations: Memory. The caching as explained in Sect. 3.1 yields objects of size \(\propto N_b (N_b + 1) N_{\mathbf{k}}\). This however is dwarfed by the size of the full generalized susceptibility \(\aleph ^{gh}_{\{b_i\}}(\mathbf{k}_F, \mathbf{q}_F)\) which would be an object of size \( N_o^4 \times N_{\mathbf{k}_F}^2 \times N_{ff}^2\) where \(N_{\mathbf{k}_F}\) is the number of FS patches, \(N_o\) is the combined number of orbitals and sublattices and \(N_{ff}\) the number of form factors considered in the expansion given by Eq. (23). The size of these objects inhibits their allocation in memory as a singular object and we therefore implement a method to calculate and save subsets of data iteratively. We once again use the intrinsic parallelism of the calculation to obtain \(\aleph \) for a fixed number of FS momenta at once and save this batch to disc before starting the next calculation. This circumvents the memory constraints otherwise imposed and allows the calculation of all required system sizes. As the calculation of the g-matrices are parallel in the same momenta \(\mathbf{k}_F\) and \(\mathbf{q}_F\), trivially seen in Eq. (32), we never require the entire \(\aleph \) for their evaluation. Note that although \(\aleph \) may exceed memory limitations the \(g_{ij}\) matrix is significantly smaller due to the constraining of all band indices to the states at zero energy at each \(\mathbf {k}_F\). Further simplification is achieved by the contraction of the form factor indices with the interaction tensors.
4 Applications
Having established a general framework for the wcRG method, we will now validate it by providing a comparison between our results and the literature for a wide variety of model systems. Particular focus is placed on to the single orbital Hubbard model as the paradigmatic benchmark case. We extend the basic model of nearest neighbour hopping \(t\) and onsite repulsion \(U\) with a variety of tuning parameters, namely next nearest neighbour hopping terms \(t'\) and density-density interaction terms \(U'\), as well as a non centrosymmetric Rashba spin orbit coupling \(\alpha _R\) and an out of plane hybridization \(t_z\). In order to illustrate the capabilities of our framework and symmetrization for more intricate lattice geometries, we calculate filling dependent ground state phase diagrams for the honeycomb lattice in two and the body centered cubic (bcc) lattice in three dimensions. Clearly any combination of these complications is in principle possible without the need for further refinement of the methodology [32, 52, 53] and the authors are planning separate publications exploring the application of this framework to ab-initio electronic structure models.
For the purpose of this article however, the various extensions of the Hubbard model provide the perfect testbed for the optimization of the numerical methods in terms of efficiency and comparison to previous publications. To provide the reader with all information necessary to benchmark their own implementations we provide the number of points used for the discretization of the Fermi surface \(N_{\mathbf {k}_F}\) as well as the number of points on the employed integration grid \(N_\mathbf {l}=(x\times y\times z)\) for all results. If not indicated otherwise all results were obtained at zero temperature.
The Hamiltonian for all subsequently analyzed models is a version of Eq. (1) with explicit dependencies on the variety of tuning parameters including long-range coupling and Rashba spin orbit coupling and is given by
The interacting Hamiltonian used is of the form
We allow nearest \(t_{\langle i,j\rangle } = t\) and next nearest neighbor hybridization \(t_{\langle \langle i,j\rangle \rangle } = t'\), where unless explicitly negated we constrain the hoppings to reside within the xy-plane. The strength of the Rashba-coupling is determined by \(\alpha _R\) while U is the onsite Hubbard interaction. Note that U is approximately zero in all wcRG studies, which was modelled by setting \(U = 10^{-2} t\) and presenting eigenvalues relative to \(U^{2}\) throughout the following. Using this base model we are able to tune into different regimes:
-
\(\alpha > 0\): Rashba Hubbard model
-
\(t'> 0\): Extended Hubbard model
-
\(U^\prime >0\): Hubbard model with long range interactions
-
\(t_z> 0\): Hubbard model with out of plane hopping
4.1 The Hubbard model: a benchmark case
For the simplest benchmark system we restrict the calculations to a square lattice and set all parameters but t and U equal zero. We calculate the filling dependent phase diagram of this particle–hole symmetric model for the electron doped side only and present our results in Fig. 3a. Not only do we reproduce the initial results by Raghu et al., [9] but also find the small region of spin triplet pairing in the \(E\) irreducible representation at \(n\approx 0.5\) uncovered in [39]. Our quantitative deviation from the results in [9] by a overall factor has been resolved in private communication with the authors.
Using the generalized susceptibilities obtained from these calculations we perform RPA calculations for the same system at \(U=2t\) without any additional numerical cost and present our findings in Fig. 3b. As expected this does not affect the symmetry of the order parameter in regions of large separation between the eigenvalues of \(g\) but introduces qualitative changes at \(n\approx 0.5\). In agreement with the results from [54] an extended s-wave \(A_1\) state is favoured in this transition region between the common nearest neighbour \(B_1\) / \(d_{x^2-y^2}\)-wave state around half filling and the next nearest neighbour \(B_2\) / \(d_{xy}\)-wave state for \(0.25<n<0.45\).
4.2 The \(t-t'\) Hubbard model
The next step of sophistication is the inclusion of finite next nearest neighbour hybridizations \(t'=-0.3t\) into the kinetic theory. This breaks the particle–hole symmetry of the model and we present data for the complete range \(0.2<n<1.8\). Since the van-Hove singularity is shifted from half filling we indicate it by a line at \(n_\text {vH}\approx 0.75\) and notice the suppression of the effective interaction also seen in the [9, 39] which we also match in other areas of the phase diagram. The suppression of \(V_\text {eff}\) as well as the enhancement of spin triplet superconductivity close to \(n_\text {vH}\) is analytically expected [9]. Again we do not show the data for extremely small or large fillings as it is neither conclusive nor significant due to extremely small effective interaction scales.
4.3 The long range Hubbard model
The long range Hubbard model was first analysed via the wcRG in [10] and later explored for a wider range of parameters in [39]. Unfortunately these publications do not agree on the presence of an \(A_1\) extended s-wave regime in the phase diagram making it impossible to reach exact qualitative agreement with both works. However we reproduce the common trends of both a suppression of the \(B_1\) order as well as the enhancement of the \(A_2\) irrep commonly called \(g\)-wave due to its eight line nodes as shown in Fig. 4. Since the \(B_1\) instability can be understood by nearest-neighbour Cooper pairing in real space it is clear that it will be heavily disfavoured by sizable nearest neighbour repulsive interactions.
wcRG phase diagram of the Hubbard model with long-range interactions. For the Hubbard model on a square lattice with NN hoppings as defined in Eq. (56) the leading superconducting instability was calculated while varying both electronic filling n and nearest neighbour repulsion \(U^\prime \). The letter is given as a dimensionless quantity containing the bandwidth W and the onsite repulsion U. The phase diagram was calculated with \(N_{\mathbf{k}_F} = 160\) and \(N_\mathbf {l}= (800 \times 800)\). The \(U^\prime = 0\) line coincides with Fig. 3a
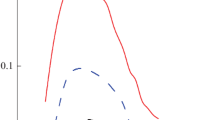
wcRG calculation for NN Hubbard model on the Honeycomb lattice. Only the most prominent symmetry characters are shown. The vertical line signals the position of the van-Hove singularity. Above \(n = 0.9\) the \(E_2\) representation remains leading and reaches a maximum coupling strength of \(\approx 0.09\) around half filling. The calculations were performed with \(N_{\mathbf{k}_F} = 120\) and \(N_\mathbf {l} = (1200 \times 1200)\)
wcRG calculations for the Rashba Hubbard model on the square lattice. We show the leading representations for the Rashba Hubbard model on a square lattice with \(t^\prime = -\,0.3t\). Clearly the impact of the spin orbit term does not manage to break the systems tendency towards \(d\)-wave pairing close to half filling. The spin split Fermi surface enforces an even momentum space structure of the gap function due to fermionic anticommutation. This is reflected by the transition from the \(E\) representation at \(\alpha _R=0\) to an extended \(s\)-wave state in the \(A_1\) irrep at \(n\approx =0.5\). The phase diagram was calculated with \(N_{\mathbf{k}_F} = 120\) and \(N_\mathbf {l} = ( 640 \times 640)\)
4.4 The hexagonal Hubbard model
The Hubbard model on the honeycomb lattice with \(C_{6v}\) symmetry has been intensively studied using a variety of numerical and analytical techniques, making it a perfect benchmark system for the wcRG method for a system with non-trivial sublattice structure. Particular excitement was created by the prediction of the systems tendency towards chiral \(d\)-wave superconductivity when tuned to its van Hove singularity [55,56,57]. Figure 5 clearly shows that we confirm these results within the weak coupling approximation, thereby confirming the calculations of [39] on the same system as a refinement of first results presented in [9]. While this result is interesting for the case of infinitesimal coupling and in the vicinity of \(n_{\text {vH}}\), we want to stress that any competition between superconductivity and magnetism is neglected in the wcRG approach, making it inapplicable at \(n_{\text {vH}}\) due to the perfect nesting of the Fermi surface at this filling.
4.5 The Rashba Hubbard model
Introducing a second band into the one orbital Hubbard model can not only be achieved by the introduction of a sublattice degree of freedom but also by lifting the spin degeneracy of the model via a Rashba type spin orbit coupling term [58]. Previous studies of this system have relied on an analytical solution of the corresponding tight-binding Hamiltonian given in Eq. (55) in order to circumvent the gauge problem posed by numerical matrix diagonalization [19, 31]. We successfully reproduce the wcRG results presented in [19] without relying on analytical eigenstates, but by employing the gauge-fixing introduced in Sect. 2.2. Our resulting phase diagram for \(t'/t=-0.3\) is shown representatively in Fig. 6, while the complete data is summarized in Fig. 9 of the appendix. Since the Rashba term is not centrosymmetric, it lifts the spin degeneracy between the bands at all points in the Brillouin zone with the exception of time reversal invariant momenta and thereby making our gauge choice unique. In addition to reproducing results at \(t'=0.0\) and \(t'=-0.3t\) we provide extensive phase diagram scans in \(\alpha _R\) and filling \(n\) for \(t'/t\in [0.0,-0.1,-0.2,-0.3]\) in Appendix B. We demonstrate the splitting of the superconducting dome at \(\alpha _R=t'=0.0\) and \(n=1\) into two separate domes following the new van Hove singularities established by the two spin orbit separated Fermi surface sheets (compare Fig. 7a–c). We observe an overall suppression of the superconducting pairing strength \(V_\mathrm{eff}\) with larger values of \(t'\) as expected due to the reduction of the systems nesting. While enhancing the spin orbit coupling results in a similar effect for \(t'=0.0\) it does not reduce \(V_\mathrm{eff}\) further for larger values of \(t'\). The perceived enhancement of \(V_\mathrm{eff}\) at e.g. \(t'/t = -0.3\), \(\alpha _R=0.5\) and \(n=0.65\) is attributed to the almost perfect coincidence with the van Hove filling at this parameter. This feature is not captured with the same accuracy for generic parameter combinations due to the chosen sampling.
Based on the calculations for these phase diagrams we were also able to reproduce results from a RPA study of the Rashba Hubbard model [31]. Instead of presenting the leading superconducting instabilities we show identical results for the RPA susceptibility in two separate sectors for three distinct parameter values in Fig. 7. We highlight that reproducing these results was significantly less expensive numerically, since the finite temperature of \(T=0.01t\) and interaction strength of \(U = 0.4 t\) allowed a reduction of the integration grid for the generalized susceptibility to \(N_\mathbf {l}=(100\times 100)\) compared to \(N_\mathbf {l}=(640\times 640)\) for the presented wcRG calculations.
RPA study of the Rashba Hubbard model on the square lattice. We calculated the static (i.e. zero frequency) RPA susceptibilities for the Rashba Hubbard model on a square lattice with \(t^\prime = -\,0.3 t\) and \(\alpha _\text {R} = 0.5 t\) at \(T = 0.01 t\) and \(U = 0.4 t\) and fillings \(n =0.5, 0.83, 0.95\) from left to right column. While a–c visualises the Fermi Surface topology d–f depicts the longitudinal \(\chi _\text {long} = \chi _{\uparrow \uparrow \uparrow \uparrow } - \chi _{\uparrow \downarrow \downarrow \uparrow }\) and g–h the transversal RPA susceptibilities \(\chi _\text {trans} = \chi _{\uparrow \downarrow \uparrow \downarrow }\) in the BZ. As the finite temperature smoothes the integrand in Eq. (25) a sparse grid in comparison to the previous wcRG calculations satisfies a convergent integration. \(N_\mathbf {l}= 100 \times 100\) was sufficient to reproduce the findings of Ref. [31]
4.6 The three dimensional Hubbard model
A common thread in the numerical evaluation of all previously considered models is the comparatively small number of discrete Fermi surface momenta \(N_{\mathbf {k}_F}\) compared to previous studies disclosing this information [9, 39]. We attribute this to the careful placement of the points according to the criteria established in Sect. 3.2 combined with the “correct” treatment of the scattering between Cooper pairs with equal or opposite defining momenta \(\mathbf {k}_F=\pm \mathbf {q}_F\). Since the numerical cost of the method scales quadratically in \(N_{\mathbf{k}_F}\), this enables significantly more cost effective analysis of three dimensional systems in particular.
wcRG analysis of three dimensional systems. a Body centered cubic lattice. The bcc model is most conveniently obtained from Eq. (55) in the limit \(t = t_z\) and \(\alpha _\text{ R } = 0\). The isotropic hoppings introduces many symmetry constraints on the effective vertex due to the underlying O\(\text {h}\) point group. The crossovers of the leading instabilities found in [9] are precisely reproduced. Yet the T\(_\text {1g}\) is much less prominent at low fillings. As for the square lattice Hubbard model the coupling strength increases significantly when approaching van Hove filling at \(n = 1\) as the nesting of the FS is restored. The calculation was performed with \(N_{\mathbf{k}_F} \approx 1500\) and \(N_\mathbf {l} = (200 \times 200 \times 200)\). b Superconducting gap function at \(n=0.5\) We depict one of the two degenerate eigenvectors contained in the leading E\(_\text{ g }\) instability at \(n=0.5\), which is related to the superconducting gap via Eq. (37). For visualization we choose a larger set of FS points \(N_{\mathbf{k}_F} \approx 2000\) than usual or necessary. Light regions on the FS corresponds to nodes in the gap function. c Anisotropic 3D Hubbard model at \(\mu = -3 t\) Unlike the previous phase scans, the coupling strengths still carry a dimension for better comparison with Fig. 4 in Ref. [14]. When increases the out-of-plane hopping \(t_z\) in the Hamiltonian Eq. (55) the filling increases accordingly, as the system exploits the additional dimension to further delocalise the electrons and lowers its energy level. For \(t_\bot = 0\), the electrons can not exploit this additional degree of freedom and the model returns to the square lattice case of Fig. 3a, where \(\mu = -3 t\) corresponds to a filling of \(n = 0.17\). This causes all irreducible representations not present in C\(_\text {4v}\) to vanish. The van-Hove singularities occur on the vertical lines. We choose \(N_{\mathbf {k}_F} \approx 1000\) and \(N_\mathbf {l}= (200 \times 200 \times 100)\)
4.6.1 Body centered cubic lattice
The symmetry reduction proposed in Sect. 3.3.1 reaches its full potential in three dimensional highly symmetric systems when the order of the point group becomes large. The body centered cubic lattice (bcc) is an ideal representative of this. As with the other cubic Bravais lattices the underlying point group is the O\(_\text {h}\) with 48 reducible representations in real space. The obtained leading instabilities in Fig. 8a match previous results in Ref. [9]. Specifically we note that the transitions between order parameters occur at equal fillings, while the effective pairing strength does not show unphysical increases at small fillings, where the FS shrinks to a sphere and poor nesting occurs. On the contrary the coupling near half filling is heavily enhanced by nesting effects similar to the two dimensional systems inspected in Fig. 3a.
We classify the superconducting order in terms of its irreducible representations, which contain an infinite number of higher harmonics. Yet each angular momentum channel increases the number of line nodes of the superconducting gap, which lowers possible energy gain available due to Cooper pair formation. The system therefore tends to favour low order harmonics meaning pairing of sites as near as permitted by the bare repulsive interaction. We exemplify the structure of the obtained gap functions in Fig. 8b for a filling of \(n = 0.5\), which clearly corresponds to the \(d\)-wave \(3z^2-r^2\) harmonic, without significant contributions from higher angular momentum channels. This may signify a proper convergence of the superconducting order in three dimensions even though the integration grids used are much coarser than in two dimensional calculations. In this case we utilized \(N_\mathbf {l} = (200 \times 200 \times 200)\) and \(N_{\mathbf{k}_F} \approx 1500\) Fermi surface points.
4.6.2 Out of plane hybridization of the square lattice model
The lenience in resolutions allowed in our calculation scheme is highlighted by the data presented in Fig. 8c. The anisotropc hopping restricts the symmetry of the system to the D\(_\text {4h}\) subgroup which is of lower order than O\(_\text{ h }\). This raises the computational cost. We therefore reduced the integration grid to \(N_\mathbf {l} = (200 \times 200 \times 100)\) and obtain comparable calculation times. Nonetheless our calculations for out-of-plane hybridization in the three dimensional Hubbard model reproduce the results presented in Ref. [14] with as few as \(N_{\mathbf {k}_F}\approx 1000\) (compared to \(3000<n_\mathbf {k}<4000\) in the reference). Clearly this is not a general solution to the problem of the required three dimensional integration for the evaluation of \(\aleph \) all three dimensional models. We have however shown our patching scheme and symmetry reductions to significantly reduce the number of required calculations. Our findings suggest that the number of FS points can be heavily reduced in comparison to former literature and one can entirely concentrate on improving the convergence of each integration.
5 Conclusion and outlook
In the pursuit of an efficient and reliable framework for the analysis of unconventional superconducting instabilities of correlated metals we have identified the particle–hole bubble as the critical numerically accessible quantity. We provide formulations of both the wcRG and the RPA in terms of this object, formally introduced as the generalized susceptibility \(\chi \) for local and its generalization \(\aleph \) for non-local interactions. By virtue of appropriate optimizations and an elaborate scheme for the discretization of Fermi surfaces in two and three spacial dimensions, we achieve a significant reduction in numerical cost.
This has been further aided by the introduction of a controlled approximation scheme for the required BZ integrations, which will prove to be especially advantageous for the analysis of electronic structures obtained from ab-initio calculations. In addition we have presented a derivation of the implications of point group symmetries for the two particle vertex in the Cooper channel. Combined, using these advances in the methodology of weak coupling approximations we have shown excellent benchmark agreement with previous results in literature at in general higher numerical precision or lower computational cost.
Our work paves the way towards an efficient and reliable numerical toolbox, equipped for the ab-inito analysis of unconventional superconducting instabilities in real materials. Such a framework may start by traditional density functional theory calculations, downfolding of the model to a tight-binding Hamiltonian via Wannierization and analyzing the resulting model within the wcRG or RPA for its propensity towards Fermi surface instabilities.Footnote 1
wcRG calculations for the Rashba Hubbard model on the square lattice. The leading representations (left column) and \(V_\text {eff}\)(right column) are determined for the Rashba Hubbard model on a square lattice with \(t^\prime = 0 \) in a and b, \(t^\prime = -\,0.1 t\) in c and d, \(t^\prime = -\,0.2 t\) in e and f, \(t^\prime = -\,0.3 t\) in g and h. The color coding of the irreducible representations is indicated in figure \(\mathbf {g}\), while the color map for the right column, where yellow (black) denotes a large (small) pairing strength, is normalized differently for each plot
Data availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The datasets displayed in Sect. 4 are available from M.D. on reasonable request. The code base will be made open source by the authors in the near future.]
Notes
HORUS software project, ERC-CoG-2021-HORUS-Thomale-101045071 (submitted).
References
W. Kohn, J.M. Luttinger, New mechanism for superconductivity. Phys. Rev. Lett. 15(12), 524–526 (1965). https://doi.org/10.1103/PhysRevLett.15.524
J.G. Bednorz, K.A. Müller, Possible highTc superconductivity in the Ba-La-Cu-O system. Zeitschr. Phys. B Condens. Matter 64(2), 189–193 (1986). https://doi.org/10.1007/BF01303701
P.A. Lee, N. Nagaosa, X.-G. Wen, Doping a Mott insulator: physics of hightemperature superconductivity. Rev. Modern Phys. 78(1), 17–85 (2006). https://doi.org/10.1103/RevModPhys.78.17
P.W. Anderson, Random-phase approximation in the theory of superconductivity. Phys. Rev. 112(6), 1900–1916 (1958). https://doi.org/10.1103/PhysRev.112.1900
D.J. Scalapino, E. Loh, J.E. Hirsch, \(d\) wave pairing near a spin-density-wave instability. Phys. Rev. B 34(11), 8190–8192 (1986). https://doi.org/10.1103/PhysRevB.34.8190
S. Graser et al., Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides’’. N. J. Phys. 11(2), 025016 (2009). https://doi.org/10.1088/1367-2630/11/2/025016
W. Metzner et al., Functional renormalization group approach to correlated fermion systems. Rev. Modern Phys. 84(1), 299–352 (2012). https://doi.org/10.1103/RevModPhys.84.299
C. Platt, W. Hanke, R. Thomale, Functional renormalization group for multi-orbital Fermi surface instabilities. Adv. Phys. 624(6), 453–562 (2013). https://doi.org/10.1080/00018732.2013.862020
S. Raghu, S.A. Kivelson, D.J. Scalapino, Superconductivity in the repulsive Hubbard model: an asymptotically exact weak-coupling solution. Phys. Rev. B 81(22), 224505 (2010). https://doi.org/10.1103/PhysRevB.81.224505
S. Raghu et al., Effects of longer-range interactions on unconventional superconductivity. Phys. Rev. B 85(2), 024516 (2012). https://doi.org/10.1103/PhysRevB.85.024516
M.L. Kiesel, R. Thomale, Sublattice interference in the kagome Hubbard model. Phys. Rev. B 86(12), 121105 (2012). https://doi.org/10.1103/PhysRevB.86.121105
W. Cho et al., Band structure effects on the superconductivity in Hubbard models. Phys. Rev. B 88(6), 064505 (2013). https://doi.org/10.1103/PhysRevB.88.064505
R. Nandkishore, R. Thomale, A.V. Chubukov, Superconductivity from weak repulsion in hexagonal lattice systems. Phys. Rev. B 89(14), 144501 (2014). https://doi.org/10.1103/PhysRevB.89.144501
H.S. Røising et al., Weak-coupling superconductivity in an anisotropic three-dimensional repulsive Hubbard model. Phys. Rev. B 98(22), 224515 (2018). https://doi.org/10.1103/PhysRevB.98.224515
J. Beyer, J.B. Hauck, L. Klebl, Reference results for the momentum space functional renormalization group. Eur. Phys. J. B 95, 65 (2022). https://doi.org/10.1140/epjb/s10051-022-00323-y
M. Fink, Unconventional and topological superconductivity in correlated non-centrosymmetric systems with spin-orbit coupling. doctoralthesis. Universität Würzburg (2019)
R. Shankar, Renormalization-group approach to interacting fermions. Rev. Mod. Phys. 66(1), 129–192 (1994). https://doi.org/10.1103/RevModPhys.66.129
J. Polchinski, Effective field theory and the fermi surface (1999), arXiv:hep-th/9210046. Accessed 14 Jun 2020
S. Wolf, S. Rachel, Spin-orbit coupled superconductivity: Rashba-Hubbard model on the square lattice. Phys. Rev. B 102(17), 174512 (2020). https://doi.org/10.1103/PhysRevB.102.174512
W.-S. Wang et al., Functional renormalization group and variational Monte Carlo studies of the electronic instabilities in graphene near \(\frac{1}{4}\) doping. Phys. Rev. B 85(3), 035414 (2012). https://doi.org/10.1103/PhysRevB.85.035414
J. Lichtenstein, Functional renormalization group studies on competing orders in the square lattice. Veröffentlicht auf dem Publikationsserver der RWTH Aachen University; Dissertation, RWTH Aachen University, (2018). Dissertation. Aachen: RWTH Aachen University, (2018), 1 Online–Ressource (104 Seiten): Illustrationen, Diagramme.https://doi.org/10.18154/RWTH-2018-225781. https://publications.rwth-aachen.de/record/728603
G. Esirgen, N.E. Bickers, Fluctuation exchange theory for general lattice Hamiltonians. Phys. Rev. B 55(4), 2122–2143 (1997). https://doi.org/10.1103/PhysRevB.55.2122
A.T. Rømer et al., Knight shift and leading superconducting instability from spin fluctuations in \({\text{ Sr}_{2}}{\text{ RuO}_{4}}\). Phys. Rev. Lett. 123(24), 247001 (2019). https://doi.org/10.1103/PhysRevLett.123.247001
J. Bardeen, L.N. Cooper, J.R. Schrieffer, Theory of superconductivity. Phys. Rev. 108(5), 1175–1204 (1957). https://doi.org/10.1103/PhysRev.108.1175
N.F. Berk, J.R. Schrieffer, Effect of ferromagnetic spin correlations on superconductivity. Phys. Rev. Lett. 17(8), 433–435 (1966). https://doi.org/10.1103/PhysRevLett.17.433
N.E. Bickers, D.J. Scalapino, S.R. White, Conserving approximations for strongly correlated electron systems: Bethe-Salpeter equation and dynamics for the two-dimensional hubbard model. Phys. Rev. Lett. 62(8), 961–964 (1989). https://doi.org/10.1103/PhysRevLett.62.961
D.J. Scalapino, E. Loh, J.E. Hirsch, d-wave pairing near a spin-density-wave instability. Phys. Rev. B 34(11), 8190–8192 (1986). https://doi.org/10.1103/PhysRevB.34.8190
S. Graser et al., Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. N. J. Phys. 11(2), 025016 (2009). https://doi.org/10.1088/1367-2630/11/2/025016
N.E. Bickers, S.R. White, Conserving approximations for strongly uctuating electron systems. II. Numerical results and parquet extension. Phys. Rev. B 43(10), 8044–8064 (1991). https://doi.org/10.1103/PhysRevB.43.8044
A.T. Rømer et al., Pairing in the two-dimensional Hubbard model from weak to strong coupling. Phys. Rev. Res. 2(1), 013108 (2020). https://doi.org/10.1103/PhysRevResearch.2.013108
A. Greco, A.P. Schnyder, Mechanism for unconventional superconductivity in the hole-Doped Rashba-Hubbard Model. Phys. Rev. Lett. 120(17), 177002 (2018). https://doi.org/10.1103/PhysRevLett.120.177002
X. Wu et al., Robust \({{\rm d}}_{x^{2}}-{y^{2}}\) -wave superconductivity of infinite-layer nickelates. Phys. Rev. B 101(6), 060504 (2020). https://doi.org/10.1103/PhysRevB.101.060504
K. Björnson et al., Orbital-dependent selfenergy effects and consequences for the superconducting gap structure in multiorbital correlated electron systems. Phys. Rev. B 103(2), 024508 (2021). https://doi.org/10.1103/PhysRevB.103.024508
X. Wu et al., Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A = K; Rb; Cs). Phys. Rev. Lett. 127(17), 177001, 177001 (2021). https://doi.org/10.1103/PhysRevLett.127.177001
G. Esirgen, H.-B. Schüttler, N.E. Bickers, d-Wave pairing in the presence of long- range Coulomb interactions. Phys. Rev. Lett. 82(6), 1217–1220 (1999). https://doi.org/10.1103/PhysRevLett.82.1217
S. Onari et al., Superconductivity from long-range interaction: a crossover between the electron gas and the lattice model. Phys. Rev. B 73(1), 014526 (2006). https://doi.org/10.1103/PhysRevB.73.014526
L.-Y. Xiao et al., Possible singlet and triplet superconductivity on honeycomb lattice. EPL (Europhysics) 115(2), 27008 (2016).https://doi.org/10.1209/0295-5075/115/27008
M. Klett et al., From high Tc to low Tc: multiorbital effects in transition metal oxides. Phys. Rev. B 104(10), L100502 (2021). https://doi.org/10.1103/PhysRevB.104.L100502
S. Wolf, T.L. Schmidt, S. Rachel, Unconventional superconductivity in the extended Hubbard model: weak-coupling renormalization group. Phys. Rev. B 98(17), 174515 (2018). https://doi.org/10.1103/PhysRevB.98.174515
M. Abadi et al., TensorFlow: large-scale machine learning on heterogeneous systems. Software available from tensor ow.org. (2015). https://www.tensorflow.org/
T. Lewiner et al., Efficient implementation of marching cubes’ cases with topological guarantees. J. Graph. Tools 8(2), 1–15 (2003). https://doi.org/10.1080/10867651.2003.10487582
The CGAL Project. CGAL User and Reference Manual. 5.3.1. CGAL Editorial Board, (2021). https://doc.cgal.org/5.3.1/Manual/packages.html
L. Rineau, M. Yvinec, 3D Surface Mesh Generation, in CGAL User and Reference Manual. 5.3.1. CGAL Editorial Board, (2021). https://doc.cgal.org/5.3.1/Manual/packages.html#PkgSurfaceMesher3
F. Cacciola, M. Rouxel-Labbé, B. Şenbaşlar, Triangulated surface mesh simplification, in CGAL User and Reference Manual. 5.3.1. CGAL Editorial Board, (2021). https://doc.cgal.org/5.3.1/Manual/packageshtml#PkgSurfaceMeshSimplification
S. Loriot et al., Polygon Mesh Processing. In: CGAL User and Reference Manual. 5.3.1. CGAL Editorial Board (2021), https://doc.cgal.org/5.3.1/Manual/packageshtml#PkgPolygonMeshProcessing
M. I. Aroyo et al., Bilbao crystallographic server. II. Representations of crystallographic point groups and space groups. Acta Crystallogr. Sect. A 62(2), 115–128 (2006).https://doi.org/10.1107/S0108767305040286
S. A. Maier, C. Honerkamp, Q.- H. Wang, Interplay between Point-Group symmetries and the choice of the bloch basis in multiband models. Symmetry 5(4), 313–343 (2013). https://doi.org/10.3390/sym5040313. https://www.mdpi.com/2073-8994/5/4/313
L. Dalcin, Y.-L.L. Fang, mpi4py: status update after 12 years of development. Comput. Sci. Eng. 23(4), 47–54 (2021). https://doi.org/10.1109/MCSE.2021.3083216
L. D. Dalcin et al., Parallel distributed computing using Python. Adv. Water Resourc. 34(9), 1124–1139 (2011). https://doi.org/10.1016/j.advwatres.2011.04.013. https://www.sciencedirect.com/science/article/pii/S0309170811000777
L. Dalcín et al., MPI for Python: performance improvements and MPI-2 extensions. J. Parallel Distrib. Comput. 68(5), 655–662 (2008). https://doi.org/10.1016/j.jpdc.2007.09.005. https://www.sciencedirect.com/science/article/pii/S0743731507001712
L. Dalcín, R. Paz, M. Storti, MPI for Python. J. Parallel Distrib. Comput. 65(9), 1108–1115 (2005). https://doi.org/10.1016/j.jpdc.2005.03.010. https://www.sciencedirect.com/science/article/pii/S0743731505000560
X. Wu et al., Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A=K, Rb, Cs). Phys. Rev. Lett. 127(17), 177001 (2022). https://doi.org/10.1103/PhysRevLett.127.177001
S. Wolf et al., Triplet superconductivity from nonlocal coulomb repulsion in an atomic sn layer deposited onto a Si(111) substrate. Phys. Rev. Lett. 128(16), 167002.https://doi.org/10.1103/PhysRevLett.128.167002. Accessed 27 Apr 2022
A.T. Rømer et al., Pairing symmetry of the one-band Hubbard model in the paramagnetic weak-coupling limit: a numerical RPA study. Phys. Rev. B 92(10), 104505 (2015). https://doi.org/10.1103/PhysRevB.92.104505
R. Nandkishore, L.S. Levitov, A.V. Chubukov, Chiral superconductivity from repulsive interactions in doped graphene. Nature Phys. 8(2), 158–163 (2012). https://doi.org/10.1038/nphys2208, https://www.nature.com/articles/nphys2208. Accessed 14 Jan 2022
M.L. Kiesel et al., Competing manybody instabilities and unconventional superconductivity in graphene. Phys. Rev. B 86(2), 020507 (2012). https://doi.org/10.1103/PhysRevB.86.020507
W.-S. Wang et al., Functional renormalization group and variational Monte Carlo studies of the electronic instabilities in graphene near \(nfracf1gf4g\) doping. Phys. Rev. B 85(3), 035414 (2012). https://doi.org/10.1103/PhysRevB.85.035414
E. Rashba, Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 2, 1109–1122 (1960)
Acknowledgements
This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through Project-ID 258499086 - SFB 1170 and through the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter - ct.qmat Project-ID 390858490 - EXC 2147. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputer SuperMUC-NG at Leibniz Supercomputing Centre (www.lrz.de). We are extremely grateful for helpful discussions on related topics with Domenico di Sante, Mario Fink, Michael Klett, Stephan Rachel, Tobias Müller, Werner Hanke and Xianxin Wu.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
All the authors have contributed significantly to the development of the framework for wcRG calculations. M.D. and T.S. performed and analyzed all calculations for this publication. All authors were involved in the preparation of the manuscript and have approved the final version.
Corresponding author
Appendices
Appendix A: Decomposition of long range interactions
We show that a generic translationally invariant two particle interaction
involving a finite number of bonds can be rewritten in the direct particle–hole diagram representation
with a finite set of form factor functions \(f_i(\mathbf {k})\).
This is accomplished by first rewriting the exponent in Eq. (A.1) by using momentum conservation for \(\mathbf {k}_1\)
and introducing form factors
By shifting the summations via the use of translational invariance and defining
we can then simply rewrite Eq. (A.1)
The remaining interaction tensor can be identified as
Note that the summations over \(\mathbf {r}_g\) and \(\mathbf {r}_h\) involve a very limited number of terms for short range interactions and that the complete derivation does not necessitate any approximations.
Appendix B: Extensive dataset for the Rashba Hubbard model
We present four phase diagram scans for the Rashba Hubbard model at different values \(t'/t\). The \(\alpha _\text {R} = 0\) line in Fig. 9a/g coincides with Fig. 3a/Fig. 3c. We note, that in Fig. 9a particle–hole symmetry is present. Yet due to the small effective pairing strength depicted in b, which decreases for all hoppings as the spin orbit interaction is increased, the gap between leading and subleading instabilities drops beneath the numerical resolution of the applied scheme, which is a problem also present in other works (e.g. Ref. [19, 39]). The superconducting order is therefore only strictly reliable in phase space regions of sizable pairing strength. This is especially the case near van-Hove fillings, which manifests themselves as bright lines ranging out into regions with large spin orbit interaction. The fragmental coloring of these lines originates from the varying proximity of the discretized n to \(n_\text {vH}\). However, a match with previous studies by Wolf and Rachel [19] is also achieved in subtle regions of the phase diagram. A decrease of pairing strength with both \(\alpha _\text {R}\) and \(t^\prime \) can be stated, which was respected by adjusting the colormap accordingly from figure b to h. The phase diagram was calculated with \(N_{\mathbf{k}_F} = 120\) and \(N_\mathbf {l} = ( 640 \times 640)\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dürrnagel, M., Beyer, J., Thomale, R. et al. Unconventional superconductivity from weak coupling. Eur. Phys. J. B 95, 112 (2022). https://doi.org/10.1140/epjb/s10051-022-00371-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjb/s10051-022-00371-4