1 Introduction

Quantum anisotropic spin models, in several situations where strong quantum fluctuations and anisotropic parameters compete, are candidates to exhibit new quantum phases of different nature and hence possible quantum phase transitions (QPTs) driven by variation of appropriate non-thermal parameters [1,2,3,4,5,6,7]. Here, quantum fluctuations are generally introduced by the non-commutativity of quantum spin operators and their competitions with non-thermal parameters arise from different interactions in the Hamiltonian, as ferromagnetic bilinear and biquadratic exchange (BQE) couplings, external magnetic fields and crystal-field anisotropies [8,9,10,11].

The recent discovery of spin-1 magnetic compounds [12, 13] has led to a lot of experimental and theoretical studies involving also the effects of single-ion anisotropy (SIA). This feature has produced a strong interest in the study of quantum criticality in spin-1 models with easy-plane and easy-axis SIA (see, for instance, refs. [14] and [15]). Up to now, extensive studies have been devoted to the conventional situations where a single QCP takes place [16,17,18,19,20,21,22,23,24].

However, recent experiments on innovative materials have suggested the existence of two distinct QCPs driven, at \(T=0\), by variation of some non-standard control parameters [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. Nevertheless, the nature of quantum criticality between and beyond the two QCPs in these materials remains at present rather obscure and require further investigations. As a useful guide in this context, there is the evidence that also magnetic materials of this innovative class exhibit some aspects typical of spin-1 anisotropic magnetic models with XY symmetry [16, 40,41,42,43].

This relevant feature suggests that it may be very interesting to study analytically and numerically the thermodynamic of appropriate spin-1 models to provide insights into the basic physics for systems showing two QCPs. Bearing this in mind, in the present paper, we focus on a spin-1 ferromagnetic XY model described by the Hamiltonian

$$\begin{aligned} {\mathcal {H}}= & {} -\frac{1}{2} \sum _{<i,j>=1}^N \left[ J_{ij} (S_i^x S_j^x +S_i^y S_j^y) +I_{ij} \left( S_i^x S_j^x + S_i^y S_j^y\right) ^2\right] \nonumber \\&- D \sum _{i=1}^N(S_i^z)^2 - h \sum _i^N S_i^z, \end{aligned}$$
(1.1)

where \(\sum _{<i,j>}\) denotes a sum over nearest neighbor lattice sites, J and I are the ferromagnetic bilinear and biquadratic exchange interactions between nearest neighbor spins, h is the longitudinal magnetic field and D measures the intensity of a longitudinal crystal field that gives rise to an easy-axis \((D>0)\) or easy-plane \((D<0)\) SIA in the z-direction. In Eq. (1.1) \(\vec S_i\equiv (S_i^x,S_i^y,S_i^z)\) is the spin operator at site i with \(S_i^z\) taking the eigenvalues \(-1,0,1\).

To our knowledge, the thermodynamic properties of the Hamiltonian (1.1) have not been yet examined in their full aspects by variation of all the competing parameters (J, I, h, D). Several investigations have been performed only for particular values of the interaction parameters providing partial information about its thermodynamics. The simplest case with \(I = 0\) in the absence of SIA, i.e., the conventional transverse XY model [16, 18, 43] has been extensively analyzed in the context of magnetic-field-induced quantum criticality, where QPTs or QCPs are driven by the longitudinal magnetic field h, which activates quantum fluctuations in the low-temperature regime. In the last decade, a lot of interest has been attracted by the regimes with \(h\ge 0\) and different signs of the SIA parameter D. In this situation, it is found [15, 44, 45] that the nature of SIA has a significant effect on the h-induced phase diagram and quantum criticality in the (h, T)-plane. Specifically, in the easy-plane case the quantum critical lines have the conventional shape merging into a QCP (\(h_c(D), T=0\)) for appropriate values of D with a standard quantum critical thermodynamics. The situation appears quite different when easy-axis SIA is present. The easy-plane case (\(D< 0\)) is not so surprising, except for the existence of a h-induced QCP in a limited range of the SIA parameter, producing a quantum critical scenario qualitatively similar to that found in the absence of the crystal field anisotropy (of course, the non-universal critical quantities depend on the control parameter D). The easy-axis regime is certainly more interesting due to the emergent reentrant critical lines merging into a QCP for selected values of the SIA parameter [16,17,18]. The peculiar reentrant behavior in the phase diagram has been observed for superconducting vortices [46, 47], liquid crystals [48], polymeric materials [49], ferromagnetism in semiconductors [50], solid hydrogen [51], denaturation of DNA [52] and has stimulated several theoretical investigations [15,16,17, 20, 44, 53,54,55,56,57,58,59]. Therefore, a complete study of the paradigmatic model (1.1) with all competing interactions may be very interesting not only from a theoretical perspective.

The aim of the present paper is to investigate the structure of the phase diagram of the model (1.1) taking into account the competing effects of the crystal field and the BQE interaction by using the two-time Green functions framework according to the Devlin scheme [60] which is a reliable approach to treat the effects of SIA.

The paper is organized as follows. In Sect. 2, we present the basic equations obtained following the Devlin strategy for the spin-1 model (1.1) in the absence of the longitudinal magnetic field. Section 3 presents the stability conditions starting from the transverse susceptibility for paramagnetic phase. Analytical estimates for dimensionalities \(d \ge 3\) allow us to select two regimes of the BQE ratio \(\alpha = I/J\), where one or two D-induced QCPs occur in the (D, T)-plane. In the two-QCPs regime, low-temperature predictions suggest the possible occurrence of a dome-shaped phase diagram. Numerical results are reported in Section 4 which support the expected existence of two D-induced QCPs and related dome-shaped phase diagrams increasing the ratio \(\alpha \) above a well defined crossover value \(\alpha ^* \approx 1.8\) for cubic lattices. Section 5 closes the paper with concluding remarks.

2 Two-time Green functions framework

Although no ordering occurs in the z-axis, the Devlin scheme can be conveniently applied for a non conventional description of the magnetic properties of the model (1.1) in terms of the ensemble average of the operator \((S_i^z)^2\) even in the absence of the longitudinal magnetic field. To this aim, we put \(h=0\) in what follows and introduce the retarded Green functions (GFs)

$$\begin{aligned} \langle \!\langle S_i^+(t); S_j^-\rangle \!\rangle= & {} - i \theta (t) \langle [S_i^+(t), S_j^-]\rangle , \end{aligned}$$
(2.1)
$$\begin{aligned} \langle \!\langle A_i^+(t); S_j^-\rangle \!\rangle= & {} - i \theta (t) \langle [A_i^+(t), S_j^-]\rangle , \end{aligned}$$
(2.2)

where \(S_i^{\pm }=S_i^x\pm i S_i^y\) are the spin raising and lowering operators, \(\theta (x)\) is the step function, \(\langle X(t) \rangle \) stands for the equilibrium average at temperature T for a generic operator X, i.e.,

$$\begin{aligned} \langle X(t) \rangle = \frac{\text {Tr}[X(t)e^{-{\mathcal {H}}/T}]}{\text {Tr} e^{-{\mathcal {H}}/T}} \end{aligned}$$
(2.3)

with the Boltzman constant assumed equal to unity, and

$$\begin{aligned} A_i^{\pm } \equiv S_i^zS_i^{\pm } + S_i^{\pm }S_i^z. \end{aligned}$$
(2.4)

Following standard procedure, we obtain the equations of motion (EMs) for the time Fourier transform \(G_{ij}(\omega )=\int _{-\infty }^\infty dt\, e^{-i\omega t}\langle \!\langle S_i^+(t); S_j^-\rangle \!\rangle \equiv \langle \!\langle S_i^+|S_j^-\rangle \!\rangle _\omega \) and \(\Gamma _{ij}(\omega )=\int _{-\infty }^\infty dt\, e^{-i\omega t}\langle \!\langle A_i^+(t); S_j^-\rangle \!\rangle \equiv \langle \!\langle S_i^+|S_j^-\rangle \!\rangle _\omega \):

$$\begin{aligned} \omega G_{ij}(\omega )= & {} D\Gamma _{ij}(\omega ) -\sum _h \left\{ J_{ih}\langle \!\langle S_i^zS_h^+; S_j^-\rangle \!\rangle _\omega \right. \nonumber \\&+ \frac{1}{2} \left. I_{ih}\left[ \langle \!\langle (S_h^+)^2 A_i^-;S_j^-\rangle \!\rangle _\omega +2\Gamma _{ij}(\omega ) \right. \right. \nonumber \\&\left. \left. - \langle \!\langle (S_h^z)^2 A_i^+;S_j^-\rangle \!\rangle _\omega +\langle \!\langle S_h^z S_i^+;S_j^-\rangle \!\rangle _\omega \right] \right\} , \nonumber \\ \end{aligned}$$
(2.5)

and

$$\begin{aligned}&\omega \Gamma _{ij}(\omega )\nonumber \\&\quad = 2q \delta _{ij}- \sum _h\{J_{ih}\langle \!\langle q_i^zS_h^+;S_j^-\rangle \!\rangle _\omega +\frac{1}{2} I_{ih} [\langle \!\langle S_h^z A_i^+;S_j^-\rangle \!\rangle _\omega +\nonumber \\&\qquad - \langle \!\langle (S_h^z)^2S_i^+;S_j^-\rangle \!\rangle _\omega + 2 G_{ij}(\omega )]\} + D G_{ij}(\omega ). \end{aligned}$$
(2.6)

Here \(A_i^-\) is defined in equation (2.4), \(q=\langle q_i^z\rangle \) is the longitudinal quadrupolar parameter, where \(q_i^z=3(S_i^z)^2-2\). It is evident that the exact two coupled EMs (2.5) and (2.6) do not constitute a closed system of equations in the required GFs \( G_{ij}(\omega )\) and \(\Gamma _{ij}(\omega )\) due to the appearance of higher order exchange and crystal-field anisotropy-like GFs. Thus, one is forced to introduce appropriate decoupling schemes. Here, we follow the Devlin idea [60] using Random Phase Approximation (RPA)-like decouplings for the exchange GFs and treating exactly the crystal-field-like ones. Specifically, we adopt the following RPA scheme [10, 11]

$$\begin{aligned}&\langle \!\langle S_h^z S_k^+|S_j^-\rangle \!\rangle _\omega \simeq \langle S_h^z\rangle \langle \!\langle S_k^+|S_j^-\rangle \!\rangle _\omega = 0,\nonumber \\&\langle \!\langle (S_h^+)^2 A_i^-;S_j^-\rangle \!\rangle _\omega \simeq \langle (S_h^+)^2\rangle \langle \!\langle A_i^-;S_j^-\rangle \!\rangle _\omega = 0, \nonumber \\&\langle \!\langle (S_h^z)^2 A_i^+; S_j^-\rangle \!\rangle _\omega \simeq \langle (S_h^z)^2\rangle \langle \!\langle A_i^+;S_j^-\rangle \!\rangle _\omega =\langle (S_h^z)^2\rangle \Gamma _{ij}(\omega ),\nonumber \\&\langle \!\langle q_i^zS_h^+; S_j^-\rangle \!\rangle _\omega = q \langle \!\langle S_h^+;S_j^-\rangle \!\rangle _\omega = q G_{hj}(\omega ), \end{aligned}$$
(2.7)

which neglects the correlations between the transverse and longitudinal spin components at different lattice sites. In contrast the SIA-like terms will be treated exactly. Then, with the further Fourier transforms in space \(X_{ij}(\omega )=(1/N)\sum _{\vec k} e^{i\vec k\cdot (\vec r_i - \vec r_j)} X (\vec k,\omega )\), \((X = G, \Gamma )\) and \(Y(\vec k)= \sum _{\vec r} e^{i\vec k\cdot \vec r} Y(|\vec r|)\quad (Y = J, I)\), the wave-vector \(\vec k\) ranging in the first Brillouin zone (1BZ), the problem reduces to a simple closed set of two algebraic equations for \(G(\vec k,\omega )\) and \(\Gamma (\vec k,\omega )\) with solutions

$$\begin{aligned} G(\vec {k},\omega )= & {} \frac{2q{\mathcal {D}}}{\omega ^2-\omega ^2(\vec {k})}, \end{aligned}$$
(2.8)
$$\begin{aligned} \Gamma (\vec {k},\omega )= & {} \frac{2q\omega }{\omega ^2-\omega ^2(\vec {k})}, \end{aligned}$$
(2.9)

where

$$\begin{aligned} \omega (\vec {k})= \mid {\mathcal {D}}\mid \left( 1-{\frac{qJ(\vec {k})}{{\mathcal {D}}}}\right) ^{1/2} \end{aligned}$$
(2.10)

defines the dispersion relation of the spin excitations. In these equations, one must have \((1-{\frac{qJ(\vec {k})}{{\mathcal {D}}}})\ge 0\) for assuring the reality of \(\omega (\vec {k})\) and to simplify the notation we have defined

$$\begin{aligned} {\mathcal {D}}\equiv D-\frac{I(0)}{6}(4-q). \end{aligned}$$
(2.11)

Finally, the spectral theorem [10, 11] for two generic operators A and B

$$\begin{aligned}&\langle B A(t) \rangle \nonumber \\&\quad = \lim _{\varepsilon \rightarrow 0^+}\quad i \int _{-\infty }^{+\infty }\frac{d\omega }{2\pi }\frac{[\langle \langle A;B\rangle \rangle _{\omega +i\varepsilon }-\langle \langle A;B\rangle \rangle _{\omega -i\varepsilon }]e^{-i\omega t}}{e^{\omega /T}-1} \end{aligned}$$

allows to obtain the correlation functions \(\langle S_j^- S_i^+(t)\rangle \) and \(\langle S_j^- A_i^+(t)\rangle \).

With standard algebra one has, for instance,

$$\begin{aligned} \langle S_j^- S_i^+(t)\rangle= & {} q{\mathcal {D}}\frac{1}{N}\sum _{\vec {k}}\frac{e^{i\vec {k}\cdot (\vec {r}_i-\vec {r}_j})}{\omega (\vec {k})}\nonumber \\&\left[ \frac{e^{-i\omega (\vec k)t}}{e^{\omega (\vec k)/T}-1}-\frac{e^{i\omega (\vec k)t}}{e^{-\omega (\vec k)/T}-1}\right] . \qquad \quad \end{aligned}$$
(2.12)

In particular in the static case at the same site, one has

$$\begin{aligned} \langle S_i^- S_i^+\rangle =q {\mathcal {D}}\frac{1}{N}\sum _{\vec {k}}\frac{1}{\omega (\vec {k})}\coth \frac{\omega (\vec {k})}{2T}. \end{aligned}$$
(2.13)

From previous equations, it is evident that the unknown thermodynamic quantity \(q=\langle q^z\rangle \), as a function of the intensive parameters (T, D), plays a key role. Indeed, all the thermodynamic properties can be determined if \(q=q(T,D)\) is known, in analogy with the role played by the longitudinal magnetization \(m= \langle S^z\rangle \) in models where it is non-zero. A self-consistent equation for q can be derived combining the kinematic identity valid for spin \(S=1\)

$$\begin{aligned} S^-_i S^+_i = 2- S^z_i - (S^z_i)^2 \end{aligned}$$
(2.14)

and the spectral theorem. The result is the self-consistent equation

$$\begin{aligned} \frac{4}{3}-\frac{q}{3}= q {\mathcal {D}}\frac{1}{N}\sum _{\vec {k}}\frac{1}{\omega (\vec {k})}\coth \frac{\omega (\vec {k})}{2T}, \end{aligned}$$
(2.15)

in which q must satisfy the boundary condition \(-2\le q\le 1\). If in this equation we express \(\omega (\vec {k})\) and \({\mathcal {D}}\) in terms of q (see (2.10) and (2.11)) we obtain the required self-consistent “Devlin equation"

$$\begin{aligned} \frac{4-q}{3}= & {} q(\text {sign} {\mathcal {D}})\frac{1}{N}\sum _{\vec {k}}\frac{1}{\left( 1-Q\gamma (\vec {k})\right) ^{1/2}}\coth \nonumber \\&\left[ \frac{\mid {\mathcal {D}}\mid }{2T}\left( 1-Q\gamma (\vec {k})\right) ^{1/2}\right] , \end{aligned}$$
(2.16)

where \(1\le \frac{4-q}{3} \le 2\),    \(q(\text {sign} {\mathcal {D}})\ge 0\),    \(\gamma ({\vec k})=J(\vec {k})/J(0)\) is the “structure factor" and, for short notation,

$$\begin{aligned} Q\equiv \frac{qJ(0)}{D-\frac{I(0)}{6}(4-q)} = \frac{q J(0)}{{\mathcal {D}}}. \end{aligned}$$
(2.17)

At zero temperature Eq. (2.16) reduces to

$$\begin{aligned} \frac{4-q}{3}=q(\text {sign} {\mathcal {D}})\frac{1}{N}\sum _{\vec {k}}\frac{1}{\left( 1-Q\gamma (\vec {k})\right) ^{1/2}}, \end{aligned}$$
(2.18)

since the dispersion relation \(\omega (\vec {k})\) is always a non-negative quantity.

3 Transverse susceptibility, stability condition and crystal-field-induced quantum critical points

In our scheme, the physical solution q of the Devlin equation and the magnetic properties of the model can be obtained through the transverse susceptibility \(\chi _{\perp }=- G(\vec {k}=0, \omega =0)\) which is given by

$$\begin{aligned} \chi _{\perp }=\frac{2q{\mathcal {D}}}{\omega ^2(0)}=\frac{2}{J(0)}\frac{Q}{1-Q}, \end{aligned}$$
(3.1)

where

$$\begin{aligned} \omega (0)=\vert {\mathcal {D}}\vert \left( 1-q\frac{J(0)}{{\mathcal {D}}}\right) ^{1/2} \end{aligned}$$
(3.2)

provides the energy gap of the spin excitations. By inspection of Eq. (3.1), it is evident that the thermodynamic stability condition \(\chi _{\perp }^{-1}\ge 0\) is assured by the simple requirement \(0<Q\le 1\). From this condition the following basic features emerge:

  1. i)

    being Q a definite positive quantity, q and \({\mathcal {D}}\) must have always the same sign;

  2. ii)

    the reality condition for the energy spectrum is automatically satisfied through the stability condition, since \(\gamma (\vec {k})\le 1\);

  3. iii)

    the equation \(Q=1\) defines the phase boundary where \(\chi _{\perp } \rightarrow +\infty \) and the energy gap \(\omega (0)=\vert {\mathcal {D}}\vert (1-Q)^{1/2}\) vanishes. Thus, this criticality condition locates possible critical points for appropriate space dimensionalities.

It is important to emphasize that, in contrast to q and \({\mathcal {D}}\), the physical SIA parameters D and q do not have always the same sign and one can have a negative q even in the easy axis regime \((0<D<\frac{I(0)}{6}(4-q))\).

Exploiting the above feature (iii), the physical solution of the Devlin equation (2.16) at the criticality is determined setting \(Q=1\), thus yielding the self-consistent equation

$$\begin{aligned} \frac{4-q}{3}= & {} q(\text {sign} {\mathcal {D}})\frac{1}{N}\sum _{\vec {k}}\frac{1}{\left( 1-\gamma (\vec {k})\right) ^{1/2}}\coth \nonumber \\&\left[ \frac{\mid {\mathcal {D}}\mid }{2T}\left( 1-\gamma (\vec {k})\right) ^{1/2}\right] , \end{aligned}$$
(3.3)

that, at \(T=0\), reduces to

$$\begin{aligned} \frac{4-q}{3}=q(\text {sign} {\mathcal {D}})F\left( -\frac{1}{2}\right) . \end{aligned}$$
(3.4)

Here \(F(-1/2)=\frac{1}{N}\sum _{\vec {k}}1/(1-\gamma (\vec {k}))^{1/2}\) is the particular case \(n=-1/2\) of the so called “structure sums" \(F(n)=\frac{1}{N}\sum _{\vec {k}}(1-\gamma (\vec {k}))^{n}\). In the limit of infinite lattice (for \(N\rightarrow \infty \)) this sum reduce to an integral which converges for any space-dimensionality \(d>1\). For three-dimensional lattice: in the simple cubic (sc), \(F(-1/2))=1.11536\), in the body-centered cubic (bcc) it is \(F(-1/2))=1.08731\) and in the face-centered cubic (fcc), \(F(-1/2))=1.07341\).

Equation (3.4) can be simply solved yielding the global representation

$$\begin{aligned} q=\frac{4}{3F(-1/2)(\text {sign}{\mathcal {D}})+1} \end{aligned}$$
(3.5)

from which we see that q depends on the SIA parameter D and on the BQE interaction I(0) only through \(\text {sign} {\mathcal {D}}\). The solution corresponding to \(\text {sign}{\mathcal {D}}= +1\) is

$$\begin{aligned} q_{c1}=\frac{4}{3F(-1/2)+1}>0 \end{aligned}$$
(3.6)

that is a positive solution giving rise to the transverse autocorrelation function

$$\begin{aligned} \langle (S^z)^2\rangle = \frac{q+2}{3}=2\frac{F(-1/2)+1}{3F(-1/2)+1}, \end{aligned}$$
(3.7)

which measures the out-plane quantum spin fluctuations. Correspondingly, the \(T=0\) critical value of D is

$$\begin{aligned} D_{c1}=\frac{4J(0)}{3F(-1/2)+1}\left[ \frac{1}{2}\alpha F\left( -\frac{1}{2}\right) +1\right] , \end{aligned}$$
(3.8)

having defined \(\alpha \equiv \frac{I}{J}\) as the relative intensity of the BQE parameter. The other solution for q, corresponding to \(\text {sign} {\mathcal {D}}= -1\), is

$$\begin{aligned} q_{c2}=-\frac{4}{3F(-1/2)-1}<0, \end{aligned}$$
(3.9)

the out-plane quantum spin fluctuation now is

$$\begin{aligned} \langle (S^z)^2\rangle = 2\frac{F(-1/2)-1}{3F(-1/2)-1} \end{aligned}$$
(3.10)

and the related quantum D-coordinate is

$$\begin{aligned} D_{c2}= \frac{4J(0)}{3F(-1/2)-1}\left[ \frac{1}{2} \alpha F\left( -\frac{1}{2}\right) -1\right] . \end{aligned}$$
(3.11)

Notice that \(D_{c2}\) can be positive or negative depending on whether \(\alpha \) is greater or less than \(\alpha ^*\equiv 2F^{-1}(-1/2)\), respectively.

Previous \(T=0\) analysis suggests that, for \(\alpha < 2F^{-1}(-1/2)\), our spin model exhibits a D-induced QCP (\(D_{c1}\)) located in the easy-axis region \(D_{c1}>0\) and another QCP (\(D_{c2}\)) located in the easy plane region \(D_{c2}<0\). On the contrary, if \(\alpha >2F^{-1}(-1/2)\) both critical points are present in the easy axis region. Observe that \(D_{c2} < D_{c1}\) for all the allowed values of \(\alpha \) and at the crossover point \(\alpha ^*\) one has \(D_{c2}=0\) and \(D_{c1}=\frac{8J(0)}{3F(-1/2)+1} \).

The structure of the phase diagram of the model (1.1) at our level of approximation can be deduced inserting the low temperature solution q(T) of the Devlin equation (2.16) in the critical condition \(Q=1\) obtaining in this way the locus of critical points ending in \(D_{c1}\) and \(D_{c2}\). We find in this way a combination of two temperature depending branches, one driven by \(q(T)>0\) and the other by \(q(T)<0\), which merge at \(q=0\), corresponding to \(D=\frac{2}{3} I(0)\) for \(T_c/J(0) = (2/3) F(-1)\).

A conventional critical scenario is expected to occur for BQE ratio \(\alpha < 2F^{-1}(-1/2)\), when a single QCP exists in the D, T- plane. In this low-BQE regime, the solution \(q=q(T)\) close to the QCP \((D_{c1},T=0)\), with \(q_{c1}\) and \(D_{c1}\) given by Eqs. (3.6) and (3.8), can be determined setting \(\text {sign}{\mathcal {D}}=+1\) in Eq. (3.3). At low temperature, by iteration with initial point \(q_{c1}>0\), we get

$$\begin{aligned} q\simeq & {} q_{c1} \left\{ 1-\frac{3}{2} q_{c1} \int _{1BZ}\frac{d^dk}{(2\pi )^d}\frac{1}{(1-\gamma (\vec {k}))^{1/2}}\right. \nonumber \\&\left. \left[ e^{\frac{J(0)q_{c1}}{2T}(1-\gamma (\vec k))^{1/2}}-1\right] ^{-1}\right\} , \end{aligned}$$
(3.12)

where the integral can be estimated in a standard way for \(d>2\) assuming in the integrand a small-\(\vec k\) expansion depending on the coordination number z of the lattice \(\gamma (\vec k)\simeq 1- \frac{1}{z}k^2\), so the longitudinal quadrupolar parameter can be expressed as follows

$$\begin{aligned} q\simeq & {} q_{c1} \left\{ 1-\frac{3}{2} q_{c1} K_d \Gamma (d-1)\zeta (d-1) z^{d/2}\right. \nonumber \\&\left. \left( \frac{T}{J(0)q_{c1}}\right) ^{d-1}\right\} >0, \end{aligned}$$
(3.13)

where \(K_d=2^{1-d}\pi ^{-d/2}/\Gamma (d/2)\) and \(\Gamma (x)\) and \(\zeta (x)\) denote the Euler gamma and the Riemann zeta functions, respectively. With this ingredients, it is immediate to obtain the required asymptotic equation of the critical line using the criticality condition. We get

$$\begin{aligned} D_{c1}(T)\simeq & {} D_{c1} \left\{ 1-\frac{3}{2}\frac{q_{c1}}{D_{c1}}\left( D_{c1}- \frac{2}{3} I(0)\right) \right. \nonumber \\&\left. K_d \Gamma (d-1)\zeta (d-1) z^{d/2}\left( \frac{T}{J(0)q_{c1}}\right) ^{d-1}\right\} \nonumber \\ \end{aligned}$$
(3.14)

with \(D_{c1} -\frac{2}{3}I(0)>0\).

Let us consider now the high-BQE regime \(\alpha >2F^{-1}(-1/2)\) where two quantum critical points exist. Their \((T=0)\)-coordinates \(D_{c1}\) and \(D_{c2}\) are given by Eqs. (3.8) and (3.11) with correlated q values (3.6) and (3.9), respectively. For the branch of the critical line ending in the first QCP (\(D_{c1},T=0\)), we obtain the expression (3.14), as in the previous regime. Similar to this case, for the second QCP, the low-T longitudinal quadrupolar parameter reads

$$\begin{aligned}&q\simeq q_{c2} \left\{ 1-\frac{3}{2} \vert q_{c2}\mid K_d \Gamma (d-1)\right. \nonumber \\&\quad \times \left. \zeta (d-1) z^{d/2}\left( \frac{T}{J(0)|q_{c2}|}\right) ^{d-1}\right\} . \end{aligned}$$
(3.15)

Then, the critical line equation close to the QCP (\(D_{c2}, T=0\)) is

$$\begin{aligned} D_{c2}(T)= & {} D_{c2}\left\{ 1+\frac{3}{2} \frac{\vert q_{c2}\vert }{D_{c2}} \vert D_{c2} - \frac{2}{3} I(0)\vert \right. \nonumber \\&\left. K_d \Gamma (d-1)\zeta (d-1)z^{d/2}\left( \frac{T}{J(0)|q_{c2}|}\right) ^{d-1}\right\} , \nonumber \\ \end{aligned}$$
(3.16)

with \(D_{c2} - \frac{2}{3} I(0) < 0\). We observe that both the critical lines are characterized by the same shift exponent \(\psi =d-1\) typical of the continuous O(2)-vector TIM-like models [4, 5, 61] with dynamical critical exponent \(z=1\) as for the easy-plane and easy-axis SIA cases when \(\alpha <2F^{-1}(-1/2)\). More interestingly, they exhibit a different orientation of the curvature in the (D, T)-plane (on the right for \(D_{c2}(T)\), on the left for \(D_{c1}(T)\)). Previous estimates provide preliminary indications towards a peculiar phase diagram of the model when \(\alpha >\alpha ^*\).

To have additional information about the structure of the phase diagram we provide below analytical estimates of the critical temperature \(T_c\) as function of D for different values of the BQE coupling in some asymptotical regimes. As a first step, we solve by iteration the Devlin equation at criticality for \(D=0\) and therefore we must assume in (3.3) \(\text {sign} {\mathcal {D}}=-1\), hence \(q(T)<0\). So the equation to solve reads

$$\begin{aligned} \frac{4+\mid q\mid }{3}= & {} \mid q\mid \left\{ F\left( -\frac{1}{2}\right) +2 \frac{1}{N}\right. \nonumber \\&\left. \sum _{\vec {k}}\frac{1}{\left( 1-\gamma (\vec {k})\right) ^{1/2}}\frac{1}{e^{\frac{J(0) |q|}{2T}(1-\gamma (\vec k))^{1/2}}-1}\right\} . \nonumber \\ \end{aligned}$$
(3.17)

Focusing on the low-T regime a low-wave-vector expansion in the integrand of (3.17) yields

$$\begin{aligned}&\frac{4+\mid q\mid }{3} = \mid q\mid \left\{ F\left( -\frac{1}{2}\right) +2 K_d \Gamma (d-1)\right. \nonumber \\&\quad \times \left. \zeta (d-1)z^{d/2}\left( \frac{T}{J(0) |q|}\right) ^{d-1}\right\} \end{aligned}$$
(3.18)

except for an exponentially small term in T/J(0). By iteration with initial point \(q_0=-\frac{4}{3F(-1/2)+1}\le 0\) to leading order in \((T/J(0))^{d-1}\) we have the asymptotic solution

$$\begin{aligned}&q(T)=q_0\left\{ 1- \frac{3}{2} K_d \Gamma (d-1)\right. \nonumber \\&\quad \times \left. \zeta (d-1) z^{d/2}\mid q_0\vert ^{1-d}\left( \frac{T}{J(0)}\right) ^{d-1}\right\} . \nonumber \\ \end{aligned}$$
(3.19)

Then, the related equation of the critical line follows from the critical condition

$$\begin{aligned} q(T)=- \frac{(2/3)\alpha }{1-\alpha /6} \quad . \end{aligned}$$
(3.20)

Incidentally, we observe that, since it must be \(q(T)<0\) for internal consistency, this equation requires that \(\alpha /6<1\) at our level of approximation. Finally, the low-T estimate of the critical temperature as function of the biquadratic parameter is

$$\begin{aligned} \frac{T_c(\alpha )}{J}\simeq & {} \left[ \frac{2z^{d/2}-1}{3 K_d \Gamma (d-1)\zeta (d-1)\mid q_0\vert ^{2-d}}\right] ^{\frac{1}{d-1}}\nonumber \\&\left( \frac{1-\alpha /\alpha ^*}{1-\alpha /6}\right) ^{\frac{1}{d-1}}. \end{aligned}$$
(3.21)

Notice that this is a decreasing function that goes to zero as \(\alpha \rightarrow \alpha ^*\), with \(\alpha ^*\) the crossover value between the two BQE regimes. It is possible to estimate \(T_c(\alpha )\) also at finite temperature by applying to Eq. (3.3) the Laurent expansion

$$\begin{aligned} \coth (x)=\frac{1}{x} + \sum _{n=1}^{\infty }\frac{2^nB_{2n}}{(2n)!}x^{2n-1}, 0<\mid x\mid <\pi \nonumber \\ \end{aligned}$$
(3.22)

in terms of the Bernoulli numbers \(B_{2n}\). Bearing in mind the previous iterative procedure with starting point \(T_{c0}/J(0)=\frac{2}{3} F^{-1}(-1)\) and involving (3.20) the result for \(T_c(\alpha )\) is

$$\begin{aligned} \frac{T_c(\alpha )}{T_{0c}}\approx \frac{1}{1-\alpha /6}\left\{ 1 + \sum _{n=1}^{\infty }a_n\left( \frac{\alpha }{1-\alpha /6}\right) ^{2n}\right\} ^{-1}, \nonumber \\ \end{aligned}$$
(3.23)

where \(a_n=\frac{B_{2n}}{(2n)!}F(n-1)F(-1)^{2n-1}\).

In particular to second order in \(\alpha \), we have

$$\begin{aligned} \frac{T_c(\alpha )}{T_{0c}}\approx \left\{ 1 + \frac{\alpha }{6} - \left[ 2F(-1) - 1 \right] \left( \frac{\alpha }{6}\right) ^2 + ...\right\} , \nonumber \\ \end{aligned}$$
(3.24)

i.e., \(T_c\) first increases with \(\alpha \) (from \(\alpha =0\)) and then decreases. The behavior is confirmed by exact numerical calculations (see next section). Since \(T_c(\alpha )\) is the initial critical temperature of any critical line in the (D, T)-plane, its behavior with \(\alpha \) will play an important role to determine the structure of the phase diagram.

Finally, in this section, we obtain an estimate of the finite temperature \(T_c(D)\) when a single QCP exists. One first solves approximatively the Devlin equation (3.3) to obtain q(T) then, using the critical condition on q(T), a conventional iterative procedure leads to

$$\begin{aligned} \frac{T_c(D)}{T_{0c}}\simeq & {} \frac{1-D/(4J(0))}{1-\alpha /6}\left\{ 1 + \sum _{n=1}^{\infty }\right. \nonumber \\&\left. a_n\left( \frac{\alpha -\frac{3}{2} \frac{D}{J(0)}}{1-\alpha /6}\right) ^{2n}\right\} ^{-1}, \end{aligned}$$
(3.25)

with \(0\le D/J(0)<4\). Notice that at \(D=0\) this equation reproduces \(T_c(\alpha )\), i.e., the starting critical points in the absence of SIA. Previous analytical estimates do predict a structure of a phase diagram appearing as a sequence of “dome shaped" critical lines increasing \(\alpha \) and this is confirmed by numerical calculation.

4 Numerical data and dome-shaped structure of phase diagram

This section reports numerical data regarding the phase diagram of the spin-1 XY model with BQE interactions and easy-axis SIA obtained by means of the solution of the Devlin equation at criticality for the out-plane quadrupolar parameter q. Our primary interest is to derive a reliable numerical scenario about the structure of the phase boundary in the (D, T)-plane by variation of the reduced parameters D/J and \(\alpha =I/J\). In particular, we will focus on the appearance of partial and full dome-shaped critical lines increasing the BQE parameter \(\alpha \), as suggested by previous analytical estimates.

With this plan in mind, the starting step is to solve numerically the general Devlin equation (2.16) under the stability condition \(0 < Q = J(0)q/[ D-I(0)(4-q)/6]\le 1\) which is the basic ingredient to explore the thermodynamics of our spin model in the disordered phase.

Fig. 1
figure 1

Longitudinal quadrupolar parameter q as a function of reduced temperature T/J for several values of the crystal field D/J for \(\alpha = 0.5\) (panel a) and \(\alpha = 2\) (panel b). The black solid line, which encloses the shaded-gray ordered region, provides the phase boundary

Full size image
Fig. 2
figure 2

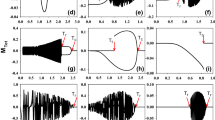
Evolution of the phase boundary in the (D/J; T/J)-plane upon variation of the biquadratic exchange coupling for a sc lattice. When \(\alpha > \alpha ^* \approx 1.8\) two quantum critical points occur with the related full dome-shaped critical lines and the amplitude of the domes decreases increasing \(\alpha \). It is worth emphasizing that the reduction of \(T_c(\alpha )\) increasing \(\alpha \ge 0\) is crucially involved in determining the structure of the phase diagram

Full size image

In Fig. 1, we have plotted the parameter q as a function of reduced temperature T/J by variation of D/J for \(\alpha = 0.5\) (panel a) and \(\alpha = 2\) (panel b), which are two representative values in the BQE regimes \(\alpha < \alpha ^*\) and \(\alpha > \alpha ^*\), where a single QCP and two QCPs are expected to occur, respectively. In this context, we have estimated analytically \(\alpha ^* =2F^{-1}(-1/2) = 1.793143\) for the simple cubic (sc) lattice. In both panels, the black solid line provides the parameter q evaluated on the phase boundary (where \(Q=1 (\chi ^{-1} = 0))\), which allows to analyze numerically the phase diagram of the system. From this figure it is evident that, consistently with the analytical estimates, the out-plane quadrupolar parameter q at the criticality depends only on temperature with negative values for \(D < I(0) (4-q)/6\), positive ones for \(D > I(0) (4-q)/6)\) and \(q=0\) at the crossover value \(D = I(0) (4-q)/6) = 2I(0)/3\). At our level of approximation in the criticality regime, these conditions become \(D/J(0) < (2/3) \alpha ^*\), \(D/J(0) > (2/3) \alpha ^*\) and \(D/J(0) = (2/3) \alpha ^*\) (\(=D^*/J(0))\), respectively. Notice that the single value (panel a) and the two values (panel b) of q at zero temperature correspond to the QCPs in the (D, T)-plane.

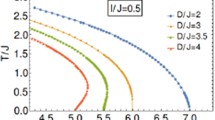
Figure 2 presents the critical lines in the (D, T)-plane by variation of the BQE ratio \(\alpha \) for simple cubic lattice. Here it is shown that, increasing \(\alpha \), a different structure of the phase boundaries takes place. For \(0 \le \alpha \le \alpha ^*\) (\(\alpha ^*\) depends on the coordination number) each critical line terminates in a single D-induced QCP with a incomplete dome-shaped behavior (see, for instance, panels a–d). Further increasing \(\alpha \), a non-conventional regime occurs with dome-shaped critical lines bounded by two QCPs (panels e–f). More specifically, for the BQE ratio in the interval \(0 \le \alpha \le 1\), usually studied in literature in the absence of SIA [23, 62,63,64], the cubic lattice exhibits a single QCP with conventional critical lines. However, our analysis indicates that this feature persists also for \(1 \le \alpha \le \alpha ^*\). The situation gradually changes in the BQE regime with \(\alpha \ge \alpha ^*\) displaying dome-structure critical lines bounded by two QCPs (panel f). It is also observed that the dome-amplitude of different critical lines decreases for increasing values of the BQE ratio \(\alpha \).

It is worth emphasizing that the reduction of \(T_c(\alpha )\) for increasing \(\alpha \ge 0\) is crucially involved in determining the structure of the phase diagram. In Fig. 3, we have plotted \(T_c\) as a function of \(\alpha \) for a sc lattice, for four values of the SIA parameter D. Here it is shown that, for \(D=0\), \(T_c(\alpha )\) vanishes exactly at \(\alpha = \alpha ^*\), which marks the crossover between the regimes with presence of one and two QCPs.

A scenario quite similar to the phase diagram found before for a sc lattice takes place also for bcc (z=8) and fcc (z=12) lattices.

To analyze the physical mechanism producing the dome-shaped phase diagram scenario in our anisotropic XY model beyond the Devlin-like framework is a prohibitive issue especially in the absence of reliable information about its ground state. However, at our level of approximation, the emerging dome-shaped phenomenon can be qualitatively traced back to the conflicting competition between the easy-plane BQE coupling and the transverse (out-plane) easy-axis SIA, where the latter tends to inhibit the in-plane ordering. Hence, some qualitative insights can be obtained analyzing the effects of the aforementioned competition. Increasing the crystal field, the z-component of the spins is enhanced implying a reduction of the in-plane order and hence a lowering of the transition temperature to disordered phase. The physical situation is drastically different from the case of an easy-plane crystal field which favors the in-plane order [18, 43, 44]. Here, the z-component of the spins decreases as the crystal field is enhanced implying a stronger ordering in the XY-plane and hence a higher transition temperature to disorder. Previous mechanism may provide a simple explanation of the appearance of disordered regions which are not present in the conventional phase diagrams in the absence of SIA [42, 65,66,67].

Bearing all this in mind, some insights can be provided on the possible physical origin of the domes in the phase diagram by observing the evolution in Fig. 2 from panel (a) to panel (f). Panel (a) depicts a typical critical line in the absence of BQE interaction \((\alpha = 0)\), which merges into a QCP arising from the quantum fluctuations produced by the presence of SIA. The BQE coupling starts to play a sensible role increasing the ratio \(\alpha \) as shown through the panels (b–e). As expected from the analytical estimates, for fixed \(\alpha <\alpha ^* \approx 1.8\) the critical lines exhibit a single D-induced QCP and a partial dome-shaped behavior which becomes more and more marked for small D from the panel (b) to panel (e). We argue that this feature is imputed to the more stabilized in-plane ordering produced by the increased BQE ratio up to the crossover value \(\alpha ^* = 1.8\) between the one-QCP regime and the two-QCPs one (panel e). When \(\alpha =\alpha ^*\), with \(T_c(D=0, \alpha ^*)=0\), the system is in a state with an incipient QCP \((D_{c2}=0)\) and an effective one \((D_{c1} \ne 0)\). In the panel (f), we present a full dome-shaped critical line typical of the regime \(\alpha > \alpha ^*\), where two D-induced QCPs occur. Here, the critical line shows a peculiar behavior which can be interpreted as follows. Since the easy-axis crystal field fluctuations tend to inhibit the in-plane ordering, it is reasonable to conjecture that for \(D_{c2}< D < D^*\) (\(q < 0\) ) the BQE coupling dominates and the in-plane ordering becomes active producing an increased critical temperature up to the a maximum \(T_c^* (D=D^*, q=0)\) signaling the balance of the two effects. For \(D^*< D< D_{c1} (q<0)\) quantum SIA fluctuations start to produce a sensible reduction of the XY order and increasing D the critical temperature decreases and vanishes at \(D = D_{c1}\). Finally, no critical singularity occurs for \(D > D_{c1}\).

Fig. 3
figure 3

Critical temperature as a function of the biquadratic–bilinear exchanges ratio \(\alpha =I/J\) for a sc lattice and for four different values of the single-ion-anisotropy parameter D

Full size image

We conclude this section showing some numerical data for thermodynamics of paramagnetic phase obtained using the solution of the general Devlin-like equation under stability condition \(0<Q<1\). In this context, the basic quantity is the transverse susceptibility \(\chi _{\perp } (T,D; \alpha )\).

Fig. 4
figure 4

Inverse susceptibility \(\chi ^{-1}\) as a function of the single-ion-anisotropy parameter D for different isotherms at fixed values of the biquadratic ratio \(\alpha \). In a, we have \(\alpha =0\), showing a conventional situation; in b, it is \(\alpha <\alpha ^*\), so we are in a regime with one-QCP, but the inverse susceptibility have a non-monotonic behavior; in c, we have \(\alpha >\alpha ^*\); hence, there is a characteristic dome-shaped critical line with two-QCPs

Full size image
Fig. 5
figure 5

Transverse susceptibility as a function of T at fixed D for three different values of the biquadratic exchange ratio \(\alpha =I/J\)

Full size image

In Fig. 4, we have plotted the inverse susceptibility in the paramagnetic phase as a function of the easy-axis SIA parameter D for different isotherms and three distinct values of the BQE ratio \(\alpha \). These figures show that, when two D-induced QCPs are present (see Fig. 4c) the transverse susceptibility has a non-standard behavior: at fixed temperature T it increases with \(D < D_{c2}(T)\) by approaching the low-D branch of the critical line and diverges as \(D\rightarrow D_{c2}^-(T)\) while along the high-D branch it diverges as \(D\rightarrow D_{c1}^+(T)\) and is a decreasing function of D for \(D > D_{c1}(T)\). Besides, along the D-axis it intercepts in two distinct critical values of D for \(T<T_c^*\), similarly to a typical reentrant phase diagram [15,16,17, 44]. Additional information can be extracted from Fig. 5, where the transverse susceptibility is plotted as a function of T at fixed D for selected values of \(\alpha \) in the paramagnetic phase around a typical critical line. It is evident that its behavior, as compared to the corresponding one in Fig. 4, appears more complex (panels b–c) especially in the regime where two QCPs are present (panel c). Notice that, in all cases (panels a–c), the susceptibility tends to zero increasing T and diverges at the QCP as \(T^{-1}\), as expected. Previous numerical data suggest also that, in all the regimes \(\chi _{\perp }\) decreases increasing the temperature at fixed D.

At this stage, using the general solution of the Devlin-like equation (2.16) and the numerical results for transverse susceptibility it is possible to derive information about other thermodynamic quantities in the paramagnetic phase (as internal energy, specific heat, and so on) by employing the basic formalism of the powerful two-time GF method and, in particular, the spectral theorem.

5 Concluding remarks

In this paper we have studied analytically and numerically the phase diagram of the spin-1 ferromagnetic XY model with BQE coupling (I) and longitudinal easy-axis crystal field (D) on cubic lattice. Following the Devlin strategy [60], in the EMs we have employed RPA decouplings for exchange higher-order GFs and treated exactly the crystal-field anisotropy terms. The main results are as follow: (i) for BQE ratio \(\alpha =I/J\) below a certain crossover value \(\alpha ^*\) a single D-induced QCP exists in the (D, T)-plane with a conventional phase diagram quite similar to that found in the absence of biquadratic interactions; (ii) increasing the BQE parameter the phase diagram is sensibly modified, with the appearance of critical lines showing a partial dome-like structure with a single QCP. Remarkably, with a further increase of the BQE ratio, above a threshold \(\alpha ^*\), two D-induced QCPs appear delimiting a full dome-shaped critical line. Notice that, although explicit numerical results were obtained for simple cubic lattices \((z=6)\), a similar scenario can be easily derived for bcc \((z= 8)\) and fcc \((z=12)\) lattices. To our knowledge, no theoretical studies have been performed in the past for investigating the non-conventional conflicting competition which may occur in simple anisotropic XY model between BQE and the quantum fluctuations induced by an easy-axis longitudinal SIA. At this stage, one can object that the above emerging non-conventional two-QCPs scenario is simply a product of the Devlin-like framework adopting the simple decoupling RPA scheme used in the EMs for the exchange higher-order GFs.

Theoretical improvements for testing this criticism can be obtained using Callen-like decouplings [68] for the exchange terms [21, 22, 24] providing an estimate of the correlation effects between spins in different sites. However, as suggested by previous general frameworks, this higher-order level of approximation, especially when in-plane BQE interaction and longitudinal easy-axis crystal field are simultaneously taken into account in the EMs, should complicate sensibly the mathematical treatment without a substantial change of the predictions arising from the simplest and controllable RPA scheme used through the present paper. So, we speculate that our approach is able to capture, at least qualitatively, the basic physics which governs the two-QCPs scenario with the related dome-shaped phase diagrams. In any case, the study of the competition between the contrasting BQE interaction and the longitudinal easy-axis SIA in our paradigmatic anisotropic spin-1 XY model (1.1) in \(h=0\) becomes, of course, a subject of experimental interest and may stimulate further theoretical, numerical and experimental researches.