1 Introduction

Piezoelectric ceramic materials are central to a wide range of technical devices, such as sensors, actuators, crystal oscillators, and ultrasonic transducers. The most common piezoelectric ceramic used for commercial purposes is lead zirconate titanate (PbZr\(_{x}\)Ti\(_{1-x}\)O\(_{3}\), PZT), which is favored due to its large piezoelectric coefficient, physical strength, and relatively low manufacturing costs [1]. However, its toxicity has prompted an increasingly urgent search for safer, lead-free alternatives [2]. Among the possible substitutes, potassium sodium niobate (K\(_{1-x}\)Na\(_{x}\)NbO\(_{3}\), KNN) is regarded as particularly promising owing to its excellent piezoelectric properties that are comparable with PZT [3, 4] and its high Curie temperature, which is a prerequisite for many applications.

The solid solution KNN is part of the perovskite family and exhibits a multitude of different phases depending on composition and temperature [5,6,7,8]. Therefore, elucidating the complex phase diagram has been a central thrust of numerous experimental investigations. At room temperature, pure potassium niobate (KNbO\(_{3}\)), corresponding to \(x=0\), has a ferroelectric orthorhombic crystal structure that originates from a symmetry-lowering distortion of the cubic aristotype. This configuration remains stable if up to 52.5 mole % of K are replaced by Na, but successive phase transitions occur at \(x=0.525\), 0.675, and 0.825 [6]. The resulting structures, originally assumed to be orthorhombic [5], are now identified as ferroelectric monoclinic [7, 8]. Finally, above \(x=0.98\), it changes into the antiferroelectric orthorhombic structure of sodium niobate (NaNbO\(_{3}\)). As a function of temperature, KNN undergoes a polymorphic phase transition to one of several ferroelectric tetragonal structures at about 220 \(^\circ \)C and further to a paraelectric cubic structure at about 430 \(^\circ \)C [7]. These transition temperatures are essentially independent of x in pure KNN, except for very Na-rich samples, but they can be tuned to a great extent by the addition of other elements [9], thus opening a route to design KNN-based piezoceramics with improved functional properties [10].

Although the symmetry of the crystal structure changes at certain values of the compositional parameter x in KNN, it is generally believed that these phase transitions are not accompanied by major alterations of the external lattice parameters, but chiefly reflect internal rearrangements of the atomic positions inside the existent unit cells, such as different tilt patterns of the oxygen octahedra and cation displacements [8]. In particular, although some experimental studies identified small irregularities in the lattice parameters of KNN in a very narrow compositional region around the supposed phase boundary near \(x=0.525\) [11], which are indicative of a structural transformation, no systematic trends are visible on a larger scale. For example, Tellier et al. [12], who used X-ray diffraction to measure the lattice parameters of KNN in the range \(0.4 \le x \le 0.6\) in steps of 0.02, observed that the three lattice constants of the rectangular orthorhombic unit cell increase linearly with the potassium content, with no discernible anomalies. Consequently, the variation of the unit-cell volume is also linear. In the alternative rhombic metric, which utilizes two length parameters and one angle \(\beta > 90^\circ \) instead, the latter decreases towards a more symmetrical orthorhombic unit cell with increasing potassium content. The relation between \(\beta \) and x is nonlinear, featuring a shallower slope on the sodium-rich side of the investigated compositional range, but the absolute variation is extremely small with an overall drop from \(90.34^\circ \) at \(x=0.6\) to \(90.32^\circ \) at \(x=0.4\). Very similar results were obtained by Wu et al. [13], who measured the lattice parameters over an even larger compositional range and likewise observed a continuous, linear behavior for \(0.4 \le x \le 0.6\); in addition, they pointed out that anomalies outside this interval, especially for large x, correlate with deviations in the grain-size distribution of the analyzed nanoparticles, a factor that may also play a role in other studies.

As the apparent inconsistencies between some of these experimental studies are still debated and may be linked to technical details of the sample fabrication, the expectation grows that numerical simulations might provide answers. In this respect, recent first-principles calculations for KNN have challenged the picture of weakly, monotonically varying lattice parameters. In particular, Liu et al. [14] investigated the geometric structure, total energy, and electronic properties of three competing phases based on density-functional theory (DFT) in the full range \(0 \le x \le 1\) and claimed that the variation of the lattice parameters of the orthorhombic structure is highly nonlinear. Most surprisingly, their results suggest that the volume of the unit cell is minimal at \(x=0.5\), where the compositional disorder is largest, and significantly smaller than either at \(x=0\) or at \(x=1\). This is accompanied by a large distortion, as \(\beta \) peaks at \(94^\circ \) for \(x=0.5\), although both pure potassium niobate and pure sodium niobate have angles close to \(90^\circ \). Furthermore, the electronic bandgap derived within DFT reaches 2.7 eV at \(x=0.5\), compared to 2.2 eV for both end members of the solid solution.

In another computational study of the orthorhombic and tetragonal phases in the interval \(0.540 \le x \le 0.570\), Yang et al. [15] found large, nonmonotonic changes of up to 0.1 Å in the lattice parameters between x values separated by merely 0.005, and overall variations of 0.05 eV in the bandgap across this narrow compositional range. This suggests an extreme sensitivity with respect to the K:Na ratio that not only contradicts the experimental evidence [12, 13] but also the slow, albeit large, variation predicted by Liu et al. [14] using very similar theoretical methods. These discrepancies remain as yet unresolved.

In general, DFT is regarded as a highly accurate computational scheme for predicting crystal structures from first principles, i.e., without any empirical parameters, and although it underestimates the absolute size of electronic bandgaps [16], trends with respect to structural or compositional variations are typically obtained reliably. However, the modeling of solid solutions like KNN, where the potassium and sodium atoms are distributed randomly, poses a special challenge, because most implementations require three-dimensional periodic boundary conditions. In this situation, DFT studies of disordered systems often resort to the virtual-crystal approximation (VCA), which was also employed in Refs. [14] and [15]. In this approach, the two distinct atomic species are replaced by merely one virtual atom type created by mixing the two pseudopotentials of the original elements in the required ratio [17]. A single primitive unit cell then suffices to represent the solid solution, making the calculations extremely efficient. While the VCA is generally trusted and often describes the properties of disordered solids, including perovskites [17, 18], correctly, it ignores the true local interactions that act between the real atoms, which may lead to deviations from supercell calculations [19]. The electronic properties, in particular, are very sensitive to this. The most serious possible pitfall of the VCA, however, is that the automatic mixing of pseudopotentials is prone to produce so-called ghost states [20], unphysical extra bound states, even if the underlying pure pseudopotentials are well behaved. This leads to incorrect orbital occupancies and hence to seemingly converged but false results. Therefore, the VCA must always be applied with caution and carefully validated.

To examine the VCA as a possible explanation for the discrepancy between the theoretical results by Liu et al. [14] as well as Yang et al. [15] on the one hand and the experimental measurements [12, 13] on the other hand, we avoid the VCA in this work and instead choose the supercell approach to calculate the lattice parameters and the electronic bandgap of KNN. We focus specifically on K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\), denoted as KNN50 in the following, which has an outstanding piezoelectric coefficient [5] due to its proximity to the morphotrophic phase boundary at \(x=0.525\) and is, therefore, of principal interest for technical applications. In addition, the discrepancy between the previously published experimental and theoretical results is largest at this point.

Compared to the VCA, the supercell approach is computationally more demanding, because it requires larger simulation cells containing the proper ratio of K and Na atoms, whose spatial distribution should ideally be as close as possible to the statistical average over all possible random structures [21]. To avoid an excessive computational cost, we follow a different, less expensive route in this work by selecting a set of six configurations that possess a high degree of periodic ordering and can be embedded in relatively small supercells but nevertheless span a wide variety of local chemical environments. This approach is validated a posteriori by the fact that our results for KNN50 turn out to be insensitive to the actual atomic arrangement and agree well for all configurations.

This paper is organized as follows. In Sect. 2, we give an overview of our computational method, including the selected supercell configurations that we use for KNN50. In Sect. 3, we then present our results and compare the calculated lattice parameters and electronic bandgaps with the available theoretical and experimental data. Finally, we summarize our conclusions in Sect. 4.

Fig. 1
figure 1

a Primitive unit cell of orthorhombic KNbO\(_{3}\), b c-stacked and c a-stacked unit cell for selected configurations of K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\) generated by doubling the primitive cell along \({\varvec{c}}\) or \({\varvec{a}}\) and replacing one of the two K atoms by a Na atom

Full size image

2 Computational method

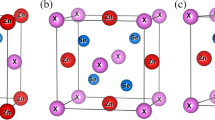
The solid solution K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\) crystallizes in the same perovskite structure as KNbO\(_{3}\) [7], which is shown in Fig. 1a. The perfect cubic aristotype is realized above 430 \(^\circ \)C and undergoes a succession of symmetry-lowering deformations as the temperature decreases, first to a tetragonal phase and then to the room-temperature orthorhombic phase. The orthorhombic geometry refers to a rectangular unit cell containing two formula units (10 atoms), which is characterized by three distinct edge lengths oriented along the symmetry axes of the crystal structure. Alternatively, it can also be described in terms of the primitive unit cell, which contains one formula unit (5 atoms) and exhibits a rhombic symmetry [12, 22]. It has the shape of a right prism with a rhombus as base and is characterized by two length parameters and one obtuse angle. Further adding to the confusion, different notation systems are in common use: if the axis perpendicular to the other two is designated as b, the space group is labeled Bmm2. This convention was adopted, e.g., in Ref. [12]. If this axis is chosen as a instead, the space group becomes Amm2. In this work, however, we follow yet another notation established in Refs. [14, 15] to facilitate a direct comparison. In this system, the axis perpendicular to the other two is c, the edges of the rhombic base are \(a=b\), and the angle between the a and b axes is \(\beta > 90^\circ \), as illustrated in Fig. 1a.

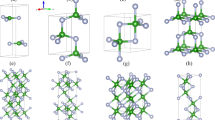
To model KNN50 in the orthorhombic phase, we adopt the supercell approach. The general recipe to set up supercells is to repeat the primitive unit cell of KNbO\(_{3}\) along one or more axes, so that one obtains a bigger cell with a larger number of atoms, and then replace half of the potassium atoms by sodium atoms. For large cell volumes, this leads to a vast number of possible configurations and hence to computational costs that are disproportionate in the context of this work, however. Instead, we only double the unit cell along one direction but use different combinations of lattice translation vectors to generate various possible crystal structures from these building blocks. In the example shown in Fig. 1b, the primitive unit cell is doubled along the c axis. After one of the two potassium atoms is substituted, this may be used to build a configuration where the K and Na atoms are stacked in layers perpendicular to the c axis. In Fig. 1c, the primitive unit cell is repeated along the a direction instead, which allows, for example, to construct layer structures perpendicular to this axis. We note that a repetition along the b direction need not be considered explicitly, because the a and b axes are equivalent in the rhombic symmetry.

By combining the c-stacked cell of Fig. 1b, where the K atom is positioned at \(\mathbf {0}\) and the Na atom at \({\varvec{c}}\), and the a-stacked cell of Fig. 1c, where the K and the Na atom are located at \(\mathbf {0}\) and \({\varvec{a}}\), respectively, with the sets of lattice translation vectors listed in Table 1, we arrive at a total of six configurations.

In the configurations 1 and 4, the K and Na atoms alternate along each of the three basis vectors \({\varvec{a}}\), \({\varvec{b}}\), and \({\varvec{c}}\) that define the edges of the primitive unit cell.

In the configurations 2 and 5, the K and Na atoms form chains along \({\varvec{a}}\) and \({\varvec{c}}\), respectively, but alternate along the other two directions.

In the configurations 3 and 6, the K and Na atoms are stacked in alternating layers perpendicular to \({\varvec{c}}\) and \({\varvec{a}}\), respectively.

Table 1 Position of the K and Na atoms inside the unit cell and choice of the lattice translation vectors for the six configurations used to model K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\) in this work. The vectors \({\varvec{a}}\), \({\varvec{b}}\), and \({\varvec{c}}\) span the primitive unit cell of KNbO\(_{3}\) as depicted in Fig. 1a
Full size table
Fig. 2
figure 2

Crystal structures of the six configurations of K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\) considered in this work. The color scheme is the same as in Fig. 1. The black lines indicate the unit cell spanned by the lattice translation vectors listed in Table 1. Configuration 4 represents the same physical system as configuration 1, differing only in the choice of the lattice translation vectors, and is not illustrated separately

Full size image

The configurations 1 and 4 actually correspond to the same physical system but are treated separately because the underlying unit cells exhibit different symmetries and thus allow a consistency check between calculations based on either the c-stacked or the a-stacked unit cell. The other configurations are physically distinct and visualized in Fig. 2. Instead of a single extensive supercell designed to model the solid solution KNN50 as realistically as possible, we thus have an ensemble of diverse but individually simpler structures covering a variety of local crystal environments, in which the six nearest alkali-metal neighbors of each K or Na atom comprise either six (configurations 1, 4), four (configurations 2, 5), or two (configurations 3, 6) members of the other species. Together with data of pure potassium and sodium niobate, these are expected to provide meaningful brackets for the lattice parameters of KNN50 that may be compared with experimental or other theoretical values. Indeed, as we show below, the results are remarkably insensitive to the actual configuration, which we take as further a posteriori justification for our approach.

The Vienna Ab initio Simulation Package (VASP) [23], a plane-wave implementation of DFT, is used to perform the calculations in this study. The electron–ion interaction is described within the projector-augmented-wave (PAW) scheme [24, 25]. The K 3s and 3p, Na 2s and 2p, and Nb 4s and 4p electrons from inner occupied shells are explicitly treated as valence states. For the parametrization of the exchange-correlation energy, we choose the PBEsol generalized gradient approximation [26], which we previously tested against a range of other functionals and found to be highly accurate for KNbO\(_{3}\) [22, 27] as well as other alkali-metal niobates [28]. Independently, a similar assessment was also reported specifically for NaNbO\(_{3}\) [29].

The electronic wave functions are expanded into plane waves up to a kinetic energy of 600 eV. For the optimization of the lattice parameters, we select a shifted regular mesh of 6 \(\times \) 6 \(\times \) 6 \({\varvec{k}}\) points to sample the Brillouin zone of pure KNbO\(_{3}\), corresponding to 6 \(\times \) 6 \(\times \) 3 (3 \(\times \) 6 \(\times \) 6) \({\varvec{k}}\) points for configurations based on the c-stacked (a-stacked) unit cell. All internal and external degrees of freedom are relaxed until the forces on each atom are smaller than 0.001 eV/Å. To determine the electronic bandgap, we switch to an unshifted 4 \(\times \) 4 \(\times \) 2 (2 \(\times \) 4 \(\times \) 4) \({\varvec{k}}\)-point mesh centered at \(\Gamma \), which includes the special high-symmetry \({\varvec{k}}\) points where the band edges are located. The bandgap is then obtained within DFT from the difference between the Kohn–Sham eigenvalues of the highest occupied valence-band state and the lowest unoccupied conduction-band state.

3 Results and discussion

3.1 Lattice parameters

Table 2 Calculated lattice parameters a, b, and c in Å, \(\beta \) in degrees, and equilibrium unit-cell volume V in Å\(^3\) for orthorhombic KNbO\(_{3}\), modeled using the six configurations considered in this work. The last row contains room-temperature experimental data for comparison. The calculated value of V is slightly smaller because it does not include thermal expansion
Full size table
Table 3 Optimized lattice parameters a, b, and c in Å, \(\beta \) in degrees, and equilibrium unit-cell volume V in Å\(^3\) for KNbO\(_{3}\), NaNbO\(_{3}\), and K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\) in the six configurations considered in this work, compared to experimental values
Full size table

To study the geometrical structure of the KNN50 solid solution, we consider the six different configurations described in the previous section. In a first step, we fill all alkali-metal positions with potassium atoms and perform a full structural relaxation. Although all configurations describe the same physical system in this case, pure KNbO\(_{3}\), the calculations themselves are technically not equivalent, because the distinct choices of primitive lattice translation vectors listed in Table 1 imply differing applicable symmetry operations. For example, configurations 4, 5, and 6 do not enforce \(b = a\), because the underlying a-stacked cell, in contrast to the c-stacked cell, lacks the appropriate mirror symmetry. Therefore, we take the average \((a+b)/2\) as the actual, physically meaningful value. The calculated lattice parameters a, b, c, and \(\beta \) as well as \((a+b)/2\) and the equilibrium unit-cell volume V are listed in Table 2. The fact that the results for all configurations are almost identical indicates a very small error bar due to the different geometrical setups and validates our computational scheme. Compared to the experimental values [30], which are measured at room temperature, the lattice parameters are underestimated, because our calculations refer to zero temperature and ignore the effects of thermal expansion. If the measured data are extrapolated to \(T=0\), then the quantitative agreement is indeed excellent [27].

Starting from the relaxed geometries, we next replace 50% of the K atoms with Na atoms, which yields the crystal structures illustrated in Fig. 2. For each configuration, we again reoptimize the lattice parameters and the atomic positions. The calculated results for a, b, c, and \(\beta \) as well as the equilibrium unit-cell volume V are listed in Table 3. The other angles of the unit cell are also allowed to vary but turn out numerically as 90\(^\circ \) and are not tabulated. As the spatial arrangement of the K and Na atoms reduces the symmetry with respect to the pure KNbO\(_{3}\), the a and b axes are not equivalent in most of the six configurations of KNN50 that we consider, and the different values of the lattice constants hence reflect true anisotropies. However, there is always a matching mirror system where the roles of a and b are reversed, which contributes equally to the solid solution. In the mirror system of configuration 2, for example, the K and Na atoms form chains along \({\varvec{b}}\) instead of \({\varvec{a}}\). To take the equal contribution of the mirror system into account, we again take the average \((a+b)/2\), which is also included in Table 3, as the actual prediction for the lattice parameter corresponding to the edge length of the rhombic base of the primitive unit cell. Compared to the experimental data [12] for \(x=0.5\) featured in Table 3, we note that our results are in very good agreement with the measured lattice constants.

In addition, Table 3 shows our results for the two end members KNbO\(_{3}\) and NaNbO\(_{3}\) of the solid solution in the orthorhombic phase. In the absence of atomic disorder, the primitive rhombic unit cell can be used in these cases. The values for KNbO\(_{3}\) equal those in Table 2.

Fig. 3
figure 3

Calculated lattice constants a and c, angle \(\beta \), and the unit-cell volume V, compared to experimental data by Fontana et al. [30] for \(x=0\) as well as Tellier et al. [12] and Wu et al. [13] for \(x>0\), and to theoretical results by Liu et al. [14] and Yang et al. [15]. Our values for a displayed in this figure are the averaged values listed as \((a+b)/2\) in Tables 2 and 3

Full size image

In Fig. 3, we display our calculated lattice parameters together with the experimental data by Fontana et al. [30] for \(x=0\) as well as Tellier et al. [12] and Wu et al. [13] for \(x>0\), and with the theoretical results by Liu et al. [14] and Yang et al. [15] as a function of the Na contents x. As explained before, our values for a shown in this figure are the averaged values listed as \((a+b)/2\) in Tables 2 and 3. No experimental results are available for NaNbO\(_{3}\), because the ferroelectric orthorhombic crystal structure considered here becomes energetically unstable for a high Na contents and can only be studied in theoretical simulations.

As an important observation, we note that our results for the six different configurations of KNN50 are all very similar, confirming that they are essentially insensitive to the detailed spatial arrangement of the alkali-metal atoms. Furthermore, our results for pure KNbO\(_{3}\) (\(x=0\)) as well as pure NaNbO\(_{3}\) (\(x=1\)) agree with those from Ref. [14], but there are significant deviations for solid solutions with intermediate x, especially at \(x=0.5\).

According to the experiments, the lattice constants a and c decrease linearly as x increases; the extra-polation to \(x=0\) coincides with the values from Ref. [30]. Our own results confirm this behavior: The calculated values are in very good agreement with the experiments, except for the small systematic underestimation, identical at \(x=0\) and \(x=0.5\), that stems from the neglect of thermal expansion in our computational scheme. On the other hand, we find no evidence for a strong variation of the lattice constants as observed in Ref. [14]. In particular, the large drop in c, whose minimum at \(x=0.5\) is 2.5% smaller than at \(x=0\), is not reproduced by our calculations. Besides, our results also contrast with the data from Ref. [15], which suggest a high sensitivity of the lattice constants with respect to the Na contents; however, the latter refer to slightly larger values \(0.540 \le x \le 0.570\) near the phase boundary and are hence not necessarily in conflict with our results, although they contradict the experimental measurements [12, 13].

For the angle \(\beta \), the experiments indicate only a minor increase from \(90.27^\circ \) at \(x=0\) [30] to \(90.33^\circ \) at x=0.5 [12]. Our results are in excellent quantitative agreement with the measured data and once more in stark contrast to Ref. [14], which predicted a huge increase of \(\beta \) at intermediate x with a maximum of \(94^\circ \) at \(x=0.5\). No evidence of such a large, nonmonotonic variation is found here.

The dependence of the unit-cell volume \(V = a^2 c \sin \beta \) on x shown in the bottom panel of Fig. 3 follows from that of the previously discussed lattice parameters. Except for the neglect of thermal expansion, our results are again in very good agreement with the experimental data, which exhibit an essentially linear decrease [12], whereas Ref. [14] found a minimum at \(x=0.5\) that is significantly smaller than the unit-cell volume of both end members.

Altogether, although our treatment of an ensemble of selected configurations is not designed to yield any definite values for the lattice parameters of KNN50, we suggest \(a = 3.994\) Å, \(c = 3.936\) Å, and \(\beta = 90.27^\circ \) here as the best zero-temperature estimates within DFT using the PBEsol exchange-correlation functional, obtained from a weighted average of the results in Table 3 where configurations with physically distinct mirror systems are counted twice.

3.2 Bandgap

Table 4 Fundamental bandgap of K\(_{0.5}\)Na\(_{0.5}\)NbO\(_{3}\), obtained within DFT using the PBEsol exchange-correlation functional, in eV for the six configurations considered in this work
Full size table

The electronic bandgap of a material is a key quantity for optical applications, another technological area where potassium sodium niobate is frequently employed due to its nonlinear optical properties, and therefore, of principal interest. Pure KNbO\(_{3}\) exhibits an indirect band gap where the valence-band maximum and the conduction-band minimum are located at T and \(\Gamma \) in the first Brillouin zone, respectively [22]. Consequently, the band gap of KNN50, which shares the same orthorhombic crystal structure, is also indirect. Table 4 contains our numerical results for the six configurations considered in this work. In each case, the fundamental (indirect) bandgap equals the energy difference between the Kohn–Sham eigenvalues of the highest valence-band and the lowest conduction-band state within DFT. Our results reveal that the bandgap is very similar for all six configurations of KNN50, which is plausible from the fact that the alkali-metal atoms do not contribute to the density of states near the band edges [22].

Fig. 4
figure 4

Calculated bandgap of K\(_{1-x}\)Na\(_{x}\)NbO\(_{3}\) within DFT as a function of x, compared to the results by Liu et al. [14] and by Yang et al. [15] at the same level of theory but with different exchange-correlation functionals. The observable optical bandgap, obtained by adding the quasiparticle correction of 1.64 eV and subtracting the exciton binding energy of 0.5 eV [27], is in good quantitative agreement with experimental measurements at \(x=0\) [35,36,37,38,39] and \(x=0.5\) [37, 40]

Full size image

In Fig. 4, we compare our numerical results with those by Liu et al. [14] and by Yang et al. [15]. All calculations are at the same level of theory but use different exchange-correlation functionals: PBEsol in this work, the Perdew–Burke–Ernzerhof parametrization [31] in Ref. [14], and the local-density approximation [32] in Ref. [15]. The absolute values of the Kohn–Sham eigenvalue gaps deviate for this reason, but as all of them ignore the derivative discontinuity [16] and hence underestimate the true electronic bandgap, only the relative variations within each dataset as a function of x should be considered significant. If we keep the lattice parameters fixed but derive the bandgap with PBE instead of PBEsol, then all of our values increase uniformly by 0.062 eV, and they increase even more if PBE is also employed for the structure optimization.

The qualitative differences in Fig. 4 are clearly visible; while Ref. [14] finds very similar bandgaps of about 2.2 eV for the end members KNbO\(_{3}\) and NaNbO\(_{3}\), it predicts a huge increase above 2.7 eV at intermediate x. In stark contrast, our own results indicate only a very small change in the DFT bandgap from \(x=0\) to 0.5 and 1. Finally, the values obtained by Yang et al. [15] for \(0.540 \le x \le 0.570\) are close to those of the end members in Ref. [14], but with strong oscillations for minor changes in the composition. In all cases, the evolution of the bandgap follows that of the lattice parameters discussed in the previous section.

Although no direct measurement of the electronic bandgap of KNN has been reported until now, the optical bandgap is often studied in experiments. The two quantities are related but distinct: the former is the minimum energy for independent electron and hole excitations, whereas the latter is the minimum energy for the excitation of bound electron–hole pairs, i.e., excitons. The optical bandgap is always smaller than the electronic bandgap; the difference is interpreted as the exciton binding energy.

Experimental values for optical bandgaps are typically deduced from Tauc plots [33], where the low-energy part of the measured absorption coefficient is fitted with a power function \(\alpha (E) \propto (E - E_\mathrm {gap})^r\). The bandgap \(E_\mathrm {gap}\) is then obtained from the extra polation of the fitting function to zero. The exponent depends on the nature of the transition with \(r=1/2\) for direct allowed transitions, the same value also used for amorphous semiconductors in Tauc’s original work [33], and \(r=2\) for indirect allowed transitions [34]. Since KNbO\(_3\) has an indirect electronic bandgap [22], it is clear that \(r=2\) should be selected in this case. Following this procedure, values of 3.2 eV [35], 3.15 eV [36], 3.18 eV [37], 3.25 eV [38], and 3.22 eV [39] have been reported. As the valence-band maximum is formed by O 2p states and the conduction-band minimum by Nb 4d states [22], the character of the electronic bandgap does not change if half of the K atoms are replaced by Na atoms. Hence, it seems natural to use \(r=2\) also for orthorhombic KNN50. The values of 3.15 eV [37] and 3.19 eV [40] derived in this way are essentially identical to those of KNbO\(_3\) and confirm that the optical bandgap does not depend strongly on x. In particular, Khorrami et al. [37], who analyzed samples with \(x=0\) and \(x=0.5\) using the same fabrication and measurement techniques, obtained nearly identical gaps of 3.18 eV and 3.15 eV, respectively. To enable a quantitative comparison, we add the quasiparticle correction of 1.64 eV [27], derived within the GW approximation for KNbO\(_3\), to the indirect Kohn–Sham eigenvalue gap and subsequently subtract the exciton binding energy of 0.5 eV [27], which equals the redshift of the absorption edge due to electron–hole attraction effects in the solution of the Bethe–Salpeter equation. The resulting optical bandgaps, displayed in the upper part of Fig. 4, are in very good agreement with the experimental data.

It should be noted that an extrapolation with \(r=1/2\) leads to substantially larger values for the optical bandgap if based on the same experimental data for the absorption coefficient [39, 40]. As a consequence, several experimental studies that falsely assumed a direct instead of an indirect transition between the valence and the conduction bands reported much larger optical bandgaps for KNbO\(_3\) [41] and KNN50 [42, 43] than the ones featured in Fig. 4, but these should be disregarded in the present context.

4 Conclusions

In this work, we conducted a new first-principles analysis of the structural and electronic properties of orthorhombic K\(_{1-x}\)Na\(_{x}\)NbO\(_{3}\) to resolve the strong discrepancy between the experimental lattice parameters [12, 13] and previous theoretical results [14, 15]. As a crucial difference, we avoid the virtual-crystal approximation, which sometimes yields incorrect results due to the appearance of unphysical ghost states, and instead adopt the supercell approach. For pure KNbO\(_{3}\), corresponding to \(x=0\), our results agree not only with those from Ref. [14], which are obtained at the same level of theory, but also with the experimental values [30]. For \(x=0.5\), our calculations are in equally good agreement with the experimental measurements [12, 13], whereas Ref. [14] predicts a large deviation from the lattice parameters of both KNbO\(_{3}\) and NaNbO\(_{3}\) in the orthorhombic phase, including a substantial volume contraction and a shearing that is effectuated by a strong increase of the obtuse angle \(\beta \) compared to the two end members of the solid solution. None of these could be observed in the present study. We attribute this to methodological differences, possibly the VCA that was employed in Ref. [14] but not in our work, and thus consider the discrepancy as resolved.

In conjunction with the experimental data [12, 13], our numerical results establish that the lattice constants a and c of orthorhombic K\(_{1-x}\)Na\(_{x}\)NbO\(_{3}\) decrease approximately linearly as the Na contents increases at least up to \(x=0.5\), whereas the angle \(\beta \) stays essentially constant. The volume reduction is consistent with the smaller atomic radius of sodium compared to potassium. Furthermore, our results reveal that the electronic bandgap is essentially identical for \(x=0\) and \(x=0.5\), which is confirmed by experimental measurements of the optical bandgap [37] and contradicts the surge at intermediate x observed in Ref. [14]. Although the electronic and optical bandgaps are distinct physical quantities, our results are in good quantitative agreement with the available experimental data [35,36,37,38,39,40] if we take the quasiparticle corrections to the DFT eigenvalues and the exciton binding energy [27] into account.