Abstract
The average energy and multiplicity of prompt \(\gamma \)-rays from slow neutron-induced fission of \(^{235}\)U have been measured using the STEFF spectrometer at the neutron time-of-flight facility n_TOF. The individual responses from 11 NaI scintillators were corrected for multiple \(\gamma \)-ray interactions, prompt fission neutrons and background counts before being deconvolved to estimate the emitted spectrum of prompt fission \(\gamma \)-rays. The results give an average \(\gamma \)-ray energy \({\bar{E}}_{\gamma }\) of 1.71(5) MeV and multiplicity \(\bar{\nu }_{\gamma }\) of 2.66(18) considering \(\gamma \)-rays emitted within the energy range 0.8–6.8 MeV. The n_TOF data has a slightly larger \({\bar{E}}_{\gamma }\) and smaller \(\bar{\nu }_{\gamma }\) than other recent measurements, however the product of the two is in agreement within quoted uncertainties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and motivation
Exploiting the energy released during thermal neutron-induced fission of \(^{235}\)U is fundamental to global energy production and forms a significant fraction of most developed countries’ low-carbon base-load electricity supply. As countries determine their future energy policy in order to meet the Paris agreement and thus a heavier reliance on low-carbon technologies, nuclear fission is often cited and depended upon as a reliable technology to complement and supplement other renewable energy sources.
Although nuclear reactors are a mature technology, supplying electricity to power grids since 1954, many of the precise details of the energy released in fission are still not known [1]. Alongside other physical quantities, which facilitate the calculations associated with nuclear technologies, nuclear fission observables fall under the blanket of nuclear data. The accuracy of these nuclear data underpins the feasibility, safety and efficiency of both present and future nuclear technologies. Fast reactors, which make up four of the six reactors considered within the generation IV (Gen-IV) international forum [2], are of particular interest for future technologies due to their benefits such as increased fuel burn-up efficiency and inherent safety. This increased efficiency and safety come at the cost of complexity and challenges in the design and operation of Gen-IV fast reactors. There is therefore an increased reliance on the accuracy of the associated nuclear data, such as the requirement for a maximum uncertainty of 7.5% on the energy deposition in non-fuelled zones such as the reactor core reflectors [3]. Heating in these zones is dominated by \(\gamma \)-rays, which typically constitute \(\sim \)10% of the total energy released in the reactor core. These \(\gamma \)-rays originate from radiative neutron capture, inelastic scattering, radioactive decay of fission products and prompt \(\gamma \)-rays emitted from fission products. The latter make up the largest contribution (\(\sim \)40%) and also dominate the uncertainty in the heating of the non-fuelled zones. A high priority request was issued in 2006 [4] to provide data on mean prompt fission \(\gamma \)-ray (PFG) energy \({\bar{E}}_{\gamma }\) and multiplicity \(\bar{\nu }_{\gamma }\) from neutron induced fission of \(^{235}\)U to meet application requirements. This request triggered investigations at different facilities into these quantities. The reported results show some differences (see Sect. 2).
The Spectrometer for Exotic Fission Fragments (STEFF) provides a powerful tool for measuring the properties of prompt fission \(\gamma \)-rays and has been utilised to study and measure the neutron-induced fission of \(^{235}\)U. This work describes the first measurement using STEFF at the neutron time-of-flight facility (n_TOF) at CERN, the results of which shall complement other recent measurements of mean prompt fission \(\gamma \)-ray energy and multiplicity.
The status of current data and recent measurements is discussed in Sect. 2, followed by a description of STEFF in Sect. 3. The details of the experimental campaign at n_TOF are provided in Sect. 4. The handling of the data analysis is addressed in Sect. 5, and the results are discussed in Sect. 6. Finally, some concluding remarks are provided in Sect. 7.
2 Current data
The aforementioned high priority request [4] has motivated multiple recent measurements of prompt fission \(\gamma \)-rays, which, when combined with older measurements from the 1970s, offer a large number of data sets. Table 1 summarises the data provided in EXFOR [5], with the mean quantities taken using the determined fission time window and lower and upper \(\gamma \)-ray energy limits \(E_{min}\) and \(E_{max}\) as stated in the respective reference.
A simple comparison of the mean energy is not intuitive as it is significantly affected by the choice of \(E_{min}\) and \(E_{max}\) in the measurement. In order to make direct comparisons, the chosen \(E_{min}\) and \(E_{max}\) must be the same and this is the approach used when comparing the results from this work with those in Table 1, as discussed in Sect. 7. To a lesser extent, the time window chosen relative to the time of fission also affects the measured quantities. This is however not expected to change \({\bar{E}}_{\gamma }\), but will be positively correlated with \(\bar{\nu }_{\gamma }\) [15].
The results of Oberstedt et al. [10], based on two LaBr\(_{3}\):Ce detectors of 50.8 mm diameter \( \times \) 50.8 mm thickness, exhibit unsurpassed PFG energy resolution for low-energy \(\gamma \)-rays, and the resulting data are in reasonable agreement with model codes such as CGMF [16]. As such, these data have been adopted by ENDF/B-VIII.0 [17], however, other experiments exhibit differences. Chyzh et al. [11] utilize a highly segmented and efficient \(\gamma \)-ray calorimeter, and large differences are apparent at low \(\gamma \)-ray energies. Further Makii et al. [14] used significantly larger scintillators (127 mm diameter \(\times \) 102 mm thick LaBr\(_{3}\):Ce) and the results show differences at higher \(\gamma \) energies (\(>5\) MeV); the detection of fission neutrons was cited as a possible reason.
The work of Murray et al. [12], which is an experiment using STEFF in the PF1b measurement station at the ILL high-flux research reactor, also showed significant differences from other measurements in the high-energy region of the prompt fission \(\gamma \)-ray spectrum. In practice, issues related to the electronics and initial data processing of this measurement have not been satisfactorily accounted for. Results from this experiment [12] list \(E_{min}=0\), as the data was interpreted based on a statistical model which fits the full energy spectrum [13].
In summary, many data-sets are available, which individually have very low uncertainties, however when comparing the spectra (see Fig. 8 below), discrepancies are still apparent, indicating possible underestimates of the various systematic errors, for example uncertainties from the unfolding procedure or neutron-induced signal subtraction. Complementary measurements utilising different experimental setups and analysis methods, such as those presented here, provide crucial checks of existing data and often additional information on various quantities.
3 STEFF
STEFF is a 2E2v device, where a combination of timing and energy detectors allow a simultaneous measurement of fission fragment (FF) energy (E) and velocity (v) for both fragments in binary fission. The combination of the kinetic energy and velocity of the fission fragments (FFs) allows the atomic masses of the post neutron evaporation fission products to be calculated. So-called 2E2v devices have historically been used to measure independent FF yields [18]. Moreover, there is a renewed interest in these detection systems [19,20,21,22] as detector technologies, electronics and analytical methods have advanced and new nuclear data requirements have become apparent.
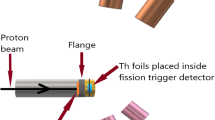
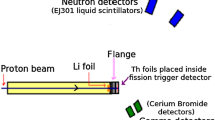
With STEFF, shown in Fig. 1, an actinide target is held in an evacuated central chamber where it is bombarded with neutrons from a collimated beam, which enters through a 50-\(\mu \)m thick Mylar window. Some FFs will be emitted in the direction of the two main arms of STEFF (marked Bragg 1 and 2 in Fig. 1), where they first pass through FF time-of-flight sections. The timing ‘start’ signal is taken from one of the arms with a thin secondary electron foil (\(\approx 200\) nm aluminium-coated Formvar) 152 mm away from the target center. Secondary electrons emitted backwards from the foil with respect to the fragment direction are reflected isochronously in a perpendicular direction to the FF axis using electrostatic mirror. The detection of deflected electrons is performed with a Micro Channel Plate (MCP) with sub-nanosecond timing resolution. The timing ‘stop’ signal is provided in each arm by Multi-Wire Proportional Counters (MWPC), based on the detection of secondary electrons from a second thin foil. The start and stop times, \(t_{\textrm{start}}\) and \(t_{\textrm{stop}}\), allow the velocities of both fragments to be determined based on the known flight path of 732 mm. The FFs then pass through a window made of 0.9 \(\mu \)m thick Mylar film with a 0.2 \(\mu \)g cm\(^{-2}\) aluminium layer where they are stopped in isobutane-filled Frisch-grid ionisation chambers with fifteen 10 cm \(\times \) 5 cm anode segments. This serves to measure the remaining kinetic energy of the FFs after passage through the foils and gas window and the direction \((\theta ,\phi )\) of the fission axis can be determined with a precision of \(\pm 2^{\circ }\). For the purposes of this work, the 2E2v capability of STEFF is used to provide a precise fission time \(t_{\textrm{fission}}\).
An array of eleven 127 mm diameter \(\times \) 102 mm thick NaI scintillator crystals surrounded the central chamber. NaI events occurring within a chosen coincidence window with respect to \(t_{\textrm{fission}}\) were selected for the prompt-fission \(\gamma \)-ray measurement. For the n_TOF experiment, there were two further FF time-of-flight arms (marked Bragg 3 and 4) at 45\(^{\circ }\) to the vertical, added to increase the solid angle coverage, and thus the efficiency, however these arms were not used as part of the present analysis as they cannot determine \(t_{\textrm{fission}}\) precisely.
4 n_TOF Experiment
STEFF was installed in the second experimental area (EAR2) of the neutron time-of-flight facility n_TOF at CERN [23, 24], which has an extensive programme of neutron-induced fission measurements [25]. The data presented here correspond to a 4-week experimental campaign in June 2016, measuring fission events induced in an 81-mm diameter 100 \(\upmu \)g cm\(^{-2}\) 93% enriched \(^{235}\)U target on a 2 \(\upmu \)g cm\(^{-2}\) Al backing. The n_TOF facility offers a high instantaneous flux of neutrons resulting from 20 GeV/c proton pulses with rms time width of \(\approx 7\) ns impinging on a fixed lead target. The subsequent spallation, evaporation and fission reactions produce high-energy neutrons which are, in the case of the vertical EAR2 beamline, moderated by a thin layer of water and thus leave the target with a broad neutron energy distribution from meV to GeV. As well as neutrons, a range of other particles are produced. The experimental area is shielded from charged particles by a permanent magnet. A high flux of relativistic neutral particles make up the so-called \(\gamma \)-flash, which arrives promptly after the proton beam impinges on the spallation target, and provide a reference for the time of neutron production. Neutrons that pass through the \(\approx 18.5\) m Experimental Area 2 (EAR2) beamline are collimated before arriving in the experimental area. The detection time of neutron-induced reactions relative to the \(\gamma \)-flash in the experimental area provides the corresponding neutron time-of-flight, from which the neutron energy can be determined, allowing measurement of fission events as a function of neutron energy.
The arrival of a proton bunch at the spallation target is used as a trigger for the n_TOF data acquisition which is composed of a series of flash ADC units. A secondary ‘fission’ trigger is generated from signals on any of the Frisch grids of the Bragg ionisation chambers, which opens an acquisition window, within which the detector outputs are stored digitally. The signal amplitude and timing information is extracted through the use of a pulse shape analysis routine [26], and the digitised ionisation chamber waveforms are saved for further offline analysis.
For the analysis in this work, a minimum threshold for \(\gamma \)-ray detection of \(E_{min}=0.8\) MeV and an upper neutron energy cut of 8 meV were adopted. These thresholds are both due to the response of the NaI detectors to the \(\gamma \)-flash. Although the detectors had a threshold set at 100 keV \(\gamma \)-ray energy, it was found after the processing that due to the baseline being incorrectly reconstructed after the \(\gamma \)-flash, a much higher 800 keV threshold had to be used for the beam-on data. Furthermore, the time it took the detectors to function without any severe gain and pile-up effects limited the maximum neutron energy to the subthermal region below 8 meV, based on an investigation of the NaI scintillator gain stability at various beam intensities at EAR2 at n_TOF.
A set of gain correction coefficients has been derived as a function of neutron energy in an effort to compensate for the \(\gamma \)-flash effects, however for neutron energies above the chosen 8 meV threshold, the magnitude of the correction factor rapidly exceeds 10% (for example, the magnitude of the gain correction is 7% for \(\approx \)10 meV neutron energy). Furthermore, changes in gain cause drift in the constant fraction discrimination of signals, affecting fission \(\gamma \)-ray timing resolution. The chosen neutron and \(\gamma \)-ray energy thresholds thus represent the most reliable segment of the collected data. Details of the gain investigation can be found in Ref. [27]. The investigation has also assessed the reliability of data collected with a LaBr\(_{3}\):Ce during the same measurement campaign, finding the detector to have been stable. Data extracted from this detector are expected to have a significantly lower threshold in \(\gamma \)-ray energy and provide information for more energetic neutrons. These data are presently undergoing analysis and are expected to be published at a later date.
5 Data analysis
5.1 Calibrations
The NaI detector signals were calibrated in time and energy using \(^{137}\)Cs, \(^{60}\)Co, \(^{88}\)Y and Am–Be sources. The digitised waveforms were fit with an average signal shape using a pulse-shape analysis routine described in Ref. [26]. The resulting timing resolution, energy calibration curves and energy resolution are given in Fig. 2. The NaI array timing resolution was 5 ns (FWHM). The mean FWHM energy resolution for the individual detectors was 8% for the 1173-keV \(^{60}\)Co \(\gamma \)-ray.
Top: The time \(\Delta t\) between signals in different detectors corresponding to detected photo-peak \(\gamma \)-rays from a \(^{60}\)Co source for a single NaI detector within the array. These \(\gamma \)-rays are emitted simultaneously, thus the measured distribution in time shows our intrinsic timing resolution. Bottom: Energy calibration for the same NaI detector. The quadratic fit is shown with a dashed line. The error bars on the data points represent full-width half-maxima of the \(\gamma \)-ray peaks
5.2 Fission event identification
The FF time-of-flight \(t_{\textrm{stop}}-t_{\textrm{start}}\) provides a clean fission event selection for analysis; the FF time-of-flight distribution is shown in Fig. 3. The FF velocity is thus calculated, and the time of fission \(t_{\textrm{fission}}\) is found from \(t_{\textrm{start}}-t_{\textrm{offset}}\), where \(t_{\textrm{offset}}\) is the time it takes the FF to reach the start detector based on the calculated velocity.
The mean detection time of prompt fission \(\gamma \)-rays is around 1 ns after \(t_{\textrm{fission}}\) corresponding to the \(\gamma \)-ray flight time to the NaI detectors from the target (\(\approx 20\) cm distance). Figure 4 shows the detected time versus deposited energy distribution of signals in the NaI detectors. The distribution of NaI signal times \(t_{\textrm{NaI}}\) relative to \(t_{\textrm{fission}}\) exhibits a peak corresponding to prompt fission \(\gamma \)-rays and a shoulder at later times corresponding to \(\gamma \)-rays originating from the interaction of prompt fission neutrons with the NaI detectors and surrounding materials (see Sect. 5.4 for details).
\(\gamma \)-ray detection time with respect to \(t_{fission}\) versus deposited \(\gamma \)-ray energy averaged over the 11 NaI detectors. The dashed boxes correspond to cuts that have been applied within the analysis. Box width corresponds to ±2\(\sigma \) window around the prompt fission \(\gamma \)-ray peak (as determined by fitting discussed in Sect. 5.4), and box height corresponds to the chosen \(\gamma \)-ray energy intervals, within which fits to the data were performed, also detailed in Sect. 5.4. The issues in the signal processing for lower energy \(\gamma \)-rays are clearly visible in the broadening of the peak in time
5.3 Multiple-hit subtraction
Due to multiple \(\gamma \)-rays being produced in a single fission event, there is a non-negligible probability that more than one prompt fission-related \(\gamma \)-ray will interact with the same detector crystal resulting in pile-up. Other sources of \(\gamma \)-rays can also lead to summation signals, such as those from two (or more) fission events, or background \(\gamma \)-rays uncorrelated to fission, although the latter events have a substantially lower probability due to the low background counting-rate, as shown by the counts outside the peak corresponding to fission-related \(\gamma \)-rays in Fig. 6. In all cases, the effect leads to an overestimation of the average \(\gamma \)-ray energy and underestimation of the deduced average multiplicity.
For an isotropic distribution of \(\gamma \)-rays, the probability of a pile-up event in one detector is the same as detecting two single \(\gamma \)-rays in two separate, but identical detectors with the same efficiency within a time window corresponding to the system dead-time. For this work, it is assumed that any two \(\gamma \)-rays that are detected in an individual detector within a 60 ns wide time range would not be resolved.
Each individual NaI detector in the array has the same total efficiency and our data is dominated by counts from prompt fission \(\gamma \)-rays (discussed further in Sect. 5.4), which are not emitted isotropically, however the anisotropy between the angles our detectors subtend is small and thus this technique is applicable and can be used to calculate a multiple-hit correction for the pile-up of \(\ge 2\) \(\gamma \)-rays. The correction is estimated on a detected \(\gamma \)-ray energy bin-by-bin basis, resulting in high statistical uncertainty at high \(\gamma \)-ray energies. The average correction from all eleven detectors in each energy bin is thus calculated and a fit was performed to obtain a smooth correction. This is shown in Fig. 5, where the number of counts at low energies (<1 MeV) is underestimated by up to 10%, whereas at high energies, the number of counts is overestimated by up to 40%. The uncertainty on the correction is estimated by the deviation between the results from individual detectors. The uncertainty is up to 10% below 5 MeV and up to 50% above. When weighted by the number of counts, the average uncertainty is around 15%, which propagates to a \(\sim \)2% and \(\sim \)3% uncertainty in the final mean energy and multiplicity values respectively.
Top: Average energy spectra from all 11 NaI detectors within a 60 ns time window shown in in Fig. 6 before and after the correction for multiple hits. Bottom: The magnitude of the multiple-hit correction (in %) as a function of \(\gamma \)-ray energy. All shown uncertainties are statistical only
5.4 Background structure
As well as prompt fission \(\gamma \)-rays, those originating from other sources are also detected and in order to differentiate between these, the expected time structure of the detector response to each source is utilized. A typical example of the experimental time response for the average of four of the NaI detectors for 1\(-\)1.5 MeV \(\gamma \)-ray energies is presented in Fig. 6. The time structure was assumed to comprise four parts:
-
1.
Counts from prompt fission \(\gamma \)-rays, showing a Gaussian distribution centered around the expected time relative to \(t_{fission}\) of \(\approx \)1 ns.
-
2.
Counts from the decay of isomeric states in FFs showing exponential decay after the arrival of prompt fission \(\gamma \)-rays.
-
3.
A random background constant in time, showing a constant level.
-
4.
Counts from the detection of \(\gamma \)-rays originating from the interaction of fission neutrons.
Over a time period corresponding to tens of ns after the fission event, these contributions are distinguishable. Relevant functions for these four sources can be fit to the data simultaneously. This is trivial for the first three sources but more complicated for the last one.
The detection of \(\gamma \)-rays from the interaction of fission neutrons originate primarily from capture and inelastic scattering reactions in the detectors themselves or the surrounding material. Neutrons emitted from the low-energy fission of \(^{235}\)U are assumed to follow the Watt distribution in energy [28]. Since the target-to-scintillator distance is known, the energy distribution can be converted to time-of-arrival at the centre of the scintillator with reference to the time of fission, \(t=t_{NaI}-t_{fission}\). The distribution of prompt fission \(\gamma \)-rays in time is expected to be closely related to this, therefore a function F(t) has been defined to estimate this distribution:
The constants in Eq. 1 have been derived from Ref. [29] and transformed into the corresponding time units for an estimated gamma-ray flightpath of 25 cm. Here, \(a_{n}\), \(\sigma _{n}\) and \(\upmu _{n}\) are free parameters to allow divergence from the Watt distribution. These free parameters are required, since the time spectra of detected events from fission neutrons will not follow the time distribution of a Watt spectrum exactly due a strong correlation between prompt fission neutron energy and angle of emission with respect to the fission axis, and due to the detector response to neutrons. This function has been summed along with a Gaussian representing prompt fission \(\gamma \)-rays and a constant component representing the non-fission correlated counts and then fit to the data in a time window of 10 ns before and 50 ns after \(t_{fission}\). The exponential component due to the decay of FF isomeric states is not included, since it is a minor contributor to the shape and was not required to find an adequate fit.
The angular distribution of fission neutrons with respect to the fission fragment axis is anisotropic, as is their distribution in energy, therefore it is expected that the measured neutron contribution varies with respect to the position of each NaI detector. The detectors position in the array with respect to the fission fragment axis have an angle \(\theta \) of either 45\(^{\circ }\) (4 detectors, on-axis) or at 69.3\(^{\circ }\) (7 detectors, off-axis), and it has been observed during fitting, that the measured neutron contribution is similar for all the detectors within their respective group. The respective magnitude of the various contributions will vary as a function of deposited \(\gamma \)-ray energy, therefore the sum of these three functions is fitted to the measured spectra for various deposited-energy regions, shown in Fig. 4. In order to use smaller \(\gamma \)-ray energy intervals, the on-axis and off-axis detector spectra were each averaged. This resulted in two sets of deposited-energy spectra subdivided into intervals increasing in width from 200 keV at low \(\gamma \)-ray energies, up to the final cut of all counts above 3 MeV. The boundaries in deposited \(\gamma \)-ray energy were chosen to be as small as possible whilst providing adequate statistics for the fits to be performed. An example fit for the on-axis detectors in the deposited energy range 1\(-\)1.5 MeV is shown in Fig. 6 indicating the goodness of the overall fit, therefore lending confidence to the assumptions made in accounting for the background.
The average spectrum of \(t_{NaI}-t_fission\) from on-axis detectors in the 1\(-\)1.5 MeV deposited \(\gamma \)-ray energy region. For description of fit components see Sect. 5.4. The counts above the total fit line at around 8 ns likely originate from isomeric contributions
This approach allows for an average total background contribution (Watt plus constant in the 10 ns before and 50 ns after \(t_{fission}\) time range) to be calculated for the on- and off-axis detectors. The background contribution for the on-axis detectors is larger in magnitude on average by \(\sim \) 50%, which is expected [30].
In order to minimise the contribution from background counts, a time window corresponding to ± 2 \(\sigma \) around the Gaussian mean has been applied. Whilst this reduces the PFG statistics, the chosen time window reduces any background counts to a negligible level (sub 1%) and therefore removes the need for background corrections a wider time window would require.
It is noted that if the full time window shown in Fig. 6 is used, then the contribution from background counts ranges from 8/15% at low energies up to 20/35% at high energies for on- and off-axis detectors respectively. While the method of background estimation used in this work is based on a mostly-empirical approach, and the full-window background contributions are substantial, background estimation quality was tested by subtracting the background from our results taken in the full-window shown in Fig. 6. The results agree with those using ±2\(\sigma \) time window within 1/2% for the average energy and multiplicity respectively, suggesting the background contributions are reasonably well-identified.
5.5 Deconvolution
The experimental response of the detectors to prompt fission \(\gamma \)-rays must be unfolded to obtain the energy spectrum of the emitted \(\gamma \)-rays and this is performed by iterations of applying the ‘Gold’ algorithm described in [31]. The response matrix for each detector was generated with GEANT4 [32] simulations of the mono-energetic detector responses, where the full detector array and the central chamber of STEFF were included in the geometry. The response matrix was validated by unfolding the detectors’ response to standard \(\gamma \)-ray calibration sources, which reproduced the emitted spectra well. Furthermore, the unfolded spectra reproduced the experimental data when the response was refolded in as shown in Fig. 7.
The efficiency of each individual detector was determined experimentally with a \(^{60}\)Co source and using the number of coincidences with reference to one of the two simultaneously emitted \(\gamma \)-rays. The measured photopeak efficiency was found to be on average 5% higher than that of the GEANT4 simulation, therefore the simulated responses were scaled to be in agreement with the experimentally measured values. The mean single-detector total photopeak efficiency of the 1.17 MeV \(\gamma \)-ray was determined to be 0.66(3)%.
After applying the multiple-hit correction and the background subtraction, one final correction must be performed due to the anisotropy of prompt fission \(\gamma \)-rays with respect to the fission axis angle, which for thermal neutron-induced fission on \(^{235}\)U exhibit an \([I(0)-I(90)]/I(90)\) of 0.13 [33] and thus the on-axis detectors overestimate \(\bar{\nu }_{\gamma }\) by 1.5% and the off-axis detectors underestimate \(\bar{\nu }_{\gamma }\) by 4.3%. The on- and off-axis energy spectra corresponding to a ±2\(\sigma \) cut around the Gaussian mean were averaged. Repeat iterations of the unfolding routine on this spectrum were performed until the chi-squared between the spectrum resulting from refolding of the unfolded spectrum and the measured spectrum was not changing. The resulting spectrum was then unfolded to generate the energy spectrum associated with the emitted prompt fission \(\gamma \)-rays.
The emitted energy spectrum can be used for an estimation of \(\gamma \)-ray Doppler shift and broadening. The former will be slightly different for the two different detector angles, however this systematic difference has been calculated to be negligible. Broadening arises due to the detected \(\gamma \)-ray originating from either a forward or backward moving FF with respect to the detector. This broadening is a maximum of \(\sim \)5% at the highest \(\gamma \)-ray energies, however since the spectrum being Doppler broadening is a continuum, it is not expected to affect the final results.
6 Results
The unfolded spectrum, normalised to the number of detected fissions and to the bin width in MeV is shown in Fig. 8 compared to the recent data sets of Chyzh et al. [11], Oberstedt et al. [10] and Makii et al. [14]. The data used for the Murray et al. measurement with STEFF at ILL [12] were also reanalysed with the full procedure used in the present work, however the results were not in agreement with the n_TOF data, due to the issues in the associated data set discussed in Sect. 2. The differences were particularly pronounced at high \(\gamma \)-ray energies, and it is assumed that the ILL data suffer from unresolved issues in this energy region such as ADC saturation, energy calibration and gain drift leading to problematic results, which are thus not included in the comparison.
Below 5 MeV, the n_TOF data is in good agreement with Oberstedt et al. and Makii et al. and the data of Chyzh et al. is systematically higher in \(\gamma \)-ray intensity/fission/MeV. The large detector volumes used in this work allow the measured spectrum to extend up to \(\sim \) 9.5 MeV providing data in this region. Here, the data of Chyzh et al. is in good agreement with this work, both of which measured more intensity at high energies than Makii et al.. However, in the higher-energy region, the data are particularly sensitive to the specifics of the deconvolution response matrix, detector calibration, and multiple-hit subtraction, which, combined with lower statistics, could account for the differences between the measurements.
The statistical uncertainty in average gamma-ray energy \({\bar{E}}_{\gamma }\) and average multiplicity \(\bar{\nu }_{\gamma }\) is given by the variation in the eleven individual detectors after the experimental effects and background have been subtracted. This is \(\approx \)2% for \({\bar{E}}_{\gamma }\) and \(\approx \)6% for \(\bar{\nu }_{\gamma }\). Further, there is a systematic uncertainty from the multiple-hit correction of 2% and 3% for \({\bar{E}}_{\gamma }\) and \(\bar{\nu }_{\gamma }\) respectively. The final uncertainty has been obtained from taking the statistical and systematic components in quadrature. A quantitative comparison of \({\bar{E}}_{\gamma }\) and \(\bar{\nu }_{\gamma }\) with those deduced from experiments available in EXFOR [5] was performed by calculating the two parameters within a common energy region of 0.8–6.8 MeV. These results, along with the product of the mean energy and multiplicity, are given in Table 2. The values of \({\bar{E}}_{\gamma }\) and \(\bar{\nu }_{\gamma }\) agree within two standard deviations with all data sets, as does the product of the two quantities.
7 Summary
STEFF has been used to measure the properties of prompt-fission \(\gamma \)-rays from thermal neutron induced fission of \(^{235}\)U at n_TOF. The analysis procedure involved identifying the time of fission and unfolding the \(\gamma \)-ray spectra from the corresponding time window after correcting for multiple hits and eliminating background contributions. A comparison of \({\bar{E}}_{\gamma }\) and \(\bar{\nu }_{\gamma }\) with other recent data sets shows the n_TOF results are in agreement with other recent measurements within three standard deviations but often not within one. Our final mean energy and multiplicity for the chosen energy range have a total uncertainty of 3% and 7% respectively. This uncertainty is larger than other measurements and mostly arises due to the differences from each individual NaI detector response.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data is available in the. EXFOR database.]
References
K.-H. Schmidt, B. Jurado, Review on the progress in nuclear fission-experimental methods and theoretical descriptions. Rep. Prog. Phys. 81(10), 106301 (2018). https://doi.org/10.1088/1361-6633/aacfa7
GenIV Internation Forum: GIF 2021 Annual Report (2021). https://www.gen-4.org/gif/
G. Rimpault, Nuclear data needs for the assessment of GEN IV systems. In: Nuclear Data Needs for Generation IV Nuclear Energy Systems, 18–31 (2006). https://doi.org/10.1142/9789812773401_0003
G. Rimpault, A. Courcelle, D. Blanchet, Needs for accurate measurements of spectrum and multiplicity of prompt \(\gamma \) emitted in Fission. In: NEA High Priority Request (2006)
N. Otuka, E. Dupont, V. Semkova, B. Pritychenko, A.I. Blokhin, M. Aikawa, S. Babykina, M. Bossant, G. Chen, S. Dunaeva, R.A. Forrest, T. Fukahori, N. Furutachi, S. Ganesan, Z. Ge, O.O. Gritzay, M. Herman, S. Hlavac, K. Kato, B. Lalremruata, Y.O. Lee, A. Makinaga, K. Matsumoto, M. Mikhaylyukova, G. Pikulina, V.G. Pronyaev, A. Saxena, O. Schwerer, S.P. Simakov, N. Soppera, R. Suzuki, S. Takács, X. Tao, S. Taova, F. Tárkányi, V.V. Varlamov, J. Wang, S.C. Yang, V. Zerkin, Y. Zhuang, Towards a more complete and accurate experimental nuclear reaction data library (exfor): international collaboration between nuclear reaction data centres (NRDC). Nucl. Data Sheets 120, 272–276 (2014). https://doi.org/10.1016/j.nds.2014.07.065
D.A. Brown, M.B. Chadwick, R. Capote, A.C. Kahler, A. Trkov, M.W. Herman, A.A. Sonzogni, Y. Danon, A.D. Carlson, M. Dunn, D.L. Smith, G.M. Hale, G. Arbanas, R. Arcilla, C.R. Bates, B. Beck, B. Becker, F. Brown, R.J. Casperson, J. Conlin, D.E. Cullen, M.-A. Descalle, R. Firestone, T. Gaines, K.H. Guber, A.I. Hawari, J. Holmes, T.D. Johnson, T. Kawano, B.C. Kiedrowski, A.J. Koning, S. Kopecky, L. Leal, J.P. Lestone, C. Lubitz, J.I. Márquez Damián, C.M. Mattoon, E.A. McCutchan, S. Mughabghab, P. Navratil, D. Neudecker, G.P.A. Nobre, G. Noguere, M. Paris, M.T. Pigni, A.J. Plompen, B. Pritychenko, V.G. Pronyaev, D. Roubtsov, D. Rochman, P. Romano, P. Schillebeeckx, S. Simakov, M. Sin, I. Sirakov, B. Sleaford, V. Sobes, E.S. Soukhovitskii, I. Stetcu, P. Talou, I. Thompson, S. van der Marck, L. Welser-Sherrill, D. Wiarda, M. White, J.L. Wormald, R.Q. Wright, M. Zerkle, G. Žerovnik, Y. Zhu, ENDF/B-VIII.0: The 8th major release of the nuclear reaction data library with cielo-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 148, 1–142 (2018). https://doi.org/10.1016/j.nds.2018.02.001 (Special Issue on Nuclear Reaction Data)
R.W. Peelle, F.C. Maienschein, Spectrum of Photons Emitted in Coincidence with Fission of \(^{235}{\rm U} \) by Thermal Neutrons. Phys. Rev. C 3, 373–390 (1971). https://doi.org/10.1103/PhysRevC.3.373
F. Pleasonton, R.L. Ferguson, H.W. Schmitt, Prompt gamma rays emitted in the thermal-neutron-induced fission of \(^{235}{\rm U} \). Phys. Rev. C 6, 1023–1039 (1972). https://doi.org/10.1103/PhysRevC.6.1023
V.V. Verbinski, H. Weber, R.E. Sund, Prompt gamma rays from \(^{235}{{\rm U}}(n, f)\), \(^{239}{{\rm Pu}}(n, f)\), and spontaneous fission of \(^{252}{{\rm Cf}} \). Phys. Rev. C 7, 1173–1185 (1973). https://doi.org/10.1103/PhysRevC.7.1173
A. Oberstedt, T. Belgya, R. Billnert, R. Borcea, T. Bryś, W. Geerts, A. Göök, F.-J. Hambsch, Z. Kis, T. Martinez, S. Oberstedt, L. Szentmiklosi, K. Takàcs, M. Vidali, Improved values for the characteristics of prompt-fission \(\gamma \)-ray spectra from the reaction \(^{235}\)U(\({n}_{\rm th }\),\(f\)). Phys. Rev. C 87, 051602 (2013). https://doi.org/10.1103/PhysRevC.87.051602
A. Chyzh, C.Y. Wu, E. Kwan, R.A. Henderson, T.A. Bredeweg, R.C. Haight, A.C. Hayes-Sterbenz, H.Y. Lee, J.M. O’Donnell, J.L. Ullmann, Total prompt \(\gamma \)-ray emission in fission of \(^{235}{{\rm U}}\), \(^{239,241}{\rm Pu}\), and \(^{252}\rm Cf \). Phys. Rev. C 90, 014602 (2014). https://doi.org/10.1103/PhysRevC.90.014602
E. Murray, A.G. Smith, A.J. Pollitt, J. Matarranz, I. Tsekhanovich, T. Soldner, U. Koster, D.C. Biswas, Measurement of gamma energy distributions and multiplicities using STEFF. Nucl. Data Sheets 119, 217–220 (2014). https://doi.org/10.1016/j.nds.2014.08.060
E. Murray, Measurement of prompt gamma-ray energy distribution and multiplicity of \(^{235}\)U following thermal fission using STEFF. PhD thesis, The University of Manchester (2015). https://pure.manchester.ac.uk/ws/files/54570082/FULL_TEXT.PDF
H. Makii, K. Nishio, K. Hirose, R. Orlandi, R. Léguillon, T. Ogawa, T. Soldner, U. Köster, A. Pollitt, F.-J. Hambsch, I. Tsekhanovich, M. Aïche, S. Czajkowski, L. Mathieu, C.M. Petrache, A. Astier, S. Guo, T. Ohtsuki, S. Sekimoto, K. Takamiya, R.J.W. Frost, T. Kawano, Effects of the nuclear structure of fission fragments on the high-energy prompt fission \(\gamma \)-ray spectrum in \(^{235}{{\rm U}}{({n}_{\rm th}}, f)\). Phys. Rev. C 100, 044610 (2019). https://doi.org/10.1103/PhysRevC.100.044610
A. Oberstedt, A. Gatera, A. Göök, S. Oberstedt, Time response and its impact on prompt fission \(\gamma \)-ray spectra characteristics. Eur. Phys. J. A 56(7), 196 (2020). https://doi.org/10.1140/epja/s10050-020-00209-6
P. Talou, T. Kawano, I. Stetcu, CGMF documentation. Tech. Rep. LA-UR-14-24031, Los Alamos National Laboratory (2014)
I. Stetcu, M.B. Chadwick, T. Kawano, P. Talou, R. Capote, A. Trkov, Evaluation of the prompt fission gamma properties for neutron induced fission of \(^{235,238}\)U and \(^{239}\)Pu. Nucl. Data Sheets 163, 261–279 (2020). https://doi.org/10.1016/j.nds.2019.12.007
A. Oed, P. Geltenbort, R. Brissot, F. Gönnenwein, P. Perrin, E. Aker, D. Engelhardt, A mass spectrometer for fission fragments based on time-of-flight and energy measurements. Nucl. Instrum. Methods Phys. Res. 219(3), 569–574 (1984). https://doi.org/10.1016/0167-5087(84)90232-1
K. Meierbachtol, F. Tovesson, D. Shields, C. Arnold, R. Blakeley, T. Bredeweg, M. Devlin, A.A. Hecht, L.E. Heffern, J. Jorgenson, A. Laptev, D. Mader, J.M. O’Donnell, A. Sierk, M. White, The SPIDER fission fragment spectrometer for fission product yield measurements. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerat. Spectromet. Detect. Assoc. Equip. 788, 59–66 (2015). https://doi.org/10.1016/j.nima.2015.02.032
D. Doré, F. Farget, F.-R. Lecolley, G. Lehaut, T. Materna, J. Pancin, S. Panebianco, T. Papaevangelou, FALSTAFF: a new tool for fission fragment characterization. Nucl. Data Sheets 119, 346–348 (2014). https://doi.org/10.1016/j.nds.2014.08.095
Q. Deshayes, B. Eric, D. Diane, T. Loic, C. Michel, K. Mariam, L. Philippe, M. Alain, M. Jean-Philippe, F. Marc-Olivier, H. Sébastien, L. Xavier, P. Julien, FALSTAFF, an apparatus to study fission fragment properties First arm results. EPJ Web Conf. 239, 05012 (2020). https://doi.org/10.1051/epjconf/202023905012
M.O. Frégeau S. Oberstedt, The fission-fragment spectrometer VERDI. In: Physics Procedia 64, 197–203 (2015). https://doi.org/10.1016/j.phpro.2015.04.027. (Scientific Workshop on Nuclear Fission Dynamics and the Emission of Prompt Neutrons and Gamma Rays, THEORY-3)
C. Guerrero, A. Tsinganis, E. Berthoumieux, M. Barbagallo, F. Belloni, F. Gunsing, C. Weiß, E. Chiaveri, M. Calviani, V. Vlachoudis, S. Altstadt, S. Andriamonje, J. Andrzejewski, L. Audouin, V. Bécares, F. Bečvář, J. Billowes, V. Boccone, D. Bosnar, M. Brugger, F. Calviño, D. Cano-Ott, C. Carrapiço, F. Cerutti, M. Chin, N. Colonna, G. Cortés, M.A. Cortés-Giraldo, M. Diakaki, C. Domingo-Pardo, I. Duran, R. Dressler, N. Dzysiuk, C. Eleftheriadis, A. Ferrari, K. Fraval, S. Ganesan, A.R. García, G. Giubrone, K. Göbel, M.B. Gómez-Hornillos, I.F. Gonçalves, E. González-Romero, E. Griesmayer, P. Gurusamy, A. Hernández-Prieto, P. Gurusamy, D.G. Jenkins, E. Jericha, Y. Kadi, F. Käppeler, D. Karadimos, N. Kivel, P. Koehler, M. Kokkoris, M. Krtička, J. Kroll, C. Lampoudis, C. Langer, E. Leal-Cidoncha, C. Lederer, H. Leeb, L.S. Leong, R. Losito, A. Manousos, J. Marganiec, T. Martínez, C. Massimi, P.F. Mastinu, M. Mastromarco, M. Meaze, E. Mendoza, A. Mengoni, P.M. Milazzo, F. Mingrone, M. Mirea, W. Mondalaers, T. Papaevangelou, C. Paradela, A. Pavlik, J. Perkowski, A. Plompen, J. Praena, J.M. Quesada, T. Rauscher, R. Reifarth, A. Riego, F. Roman, C. Rubbia, M. Sabate-Gilarte, R. Sarmento, A. Saxena, P. Schillebeeckx, S. Schmidt, D. Schumann, P. Steinegger, G. Tagliente, J.L. Tain, D. Tarrío, L. Tassan-Got, S. Valenta, G. Vannini, V. Variale, P. Vaz, A. Ventura, R. Versaci, M.J. Vermeulen, R. Vlastou, A. Wallner, T. Ware, M. Weigand, T. Wright, P. Žugec, Performance of the neutron time-of-flight facility n_TOF at CERN. Eur. Phys. J. A 49(2), 27 (2013). https://doi.org/10.1140/epja/i2013-13027-6
C. Weiß, E. Chiaveri, S. Girod, V. Vlachoudis, O. Aberle, S. Barros, I. Bergström, E. Berthoumieux, M. Calviani, C. Guerrero, M. Sabaté-Gilarte, A. Tsinganis, J. Andrzejewski, L. Audouin, M. Bacak, J. Balibrea-Correa, M. Barbagallo, V. Bécares, C. Beinrucker, F. Belloni, F. Bečvář, J. Billowes, D. Bosnar, M. Brugger, M. Caamaño, F. Calviño, D. Cano-Ott, F. Cerutti, N. Colonna, G. Cortés, M.A. Cortés-Giraldo, L. Cosentino, L. Damone, K. Deo, M. Diakaki, C. Domingo-Pardo, E. Dupont, I. Durán, R. Dressler, B. Fernández-Domínguez, A. Ferrari, P. Ferreira, P. Finocchiaro, R. Frost, V. Furman, S. Ganesan, A. Gheorghe, T. Glodariu, K. Göbel, I.F. Gonçalves, E. González-Romero, A. Goverdovski, E. Griesmayer, F. Gunsing, H. Harada, T. Heftrich, S. Heinitz, A. Hernández-Prieto, J. Heyse, D.G. Jenkins, E. Jericha, Y. Kadi, F. Käppeler, T. Katabuchi, P. Kavrigin, V. Ketlerov, V. Khryachkov, A. Kimura, N. Kivel, M. Kokkoris, M. Krtička, E. Leal-Cidoncha, C. Lederer, H. Leeb, J. Lerendegui, M. Licata, S. Lo Meo, D. López, R. Losito, D. Macina, J. Marganiec, T. Martínez, C. Massimi, P.F. Mastinu, M. Mastromarco, F. Matteucci, E. Mendoza, A. Mengoni, P.M. Milazzo, F. Mingrone, M. Mirea, S. Montesano, A. Musumarra, R. Nolte, R. Palomo Pinto, C. Paradela, N. Patronis, A. Pavlik, J. Perkowski, I. Porras, J. Praena, J.M. Quesada, T. Rauscher, R. Reifarth, A. Riego-Perez, M.S. Robles, C. Rubbia, J. Ryan, A. Saxena, P. Schillebeeckx, S. Schmidt, D. Schumann, P. Sedyshev, G. Smith, A. Stamatopoulos, P. Steinegger, S.V. Suryanarayana, G. Tagliente, J.L. Tain, A. Tarifeño-Saldivia, L. Tassan-Got, S. Valenta, G. Vannini, V. Variale, P. Vaz, A. Ventura, R. Vlastou, A. Wallner, S. Warren, M. Weigand, T. Wright, P. Žugec, The new vertical neutron beam line at the CERN n_TOF facility design and outlook on the performance. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerat. Spectromet. Detect. Assoc. Equip. 799, 90–98 (2015). https://doi.org/10.1016/j.nima.2015.07.027
N. Colonna, A. Tsinganis, R. Vlastou, N. Patronis, M. Diakaki, S. Amaducci, M. Barbagallo, S. Bennett, E. Berthoumieux, M. Bacak, G. Cosentino, S. Cristallo, P. Finocchiaro, J. Heyse, D. Lewis, A. Manna, C. Massimi, E. Mendoza, M. Mirea, A. Moens, R. Nolte, E. Pirovano, M. Sabaté-Gilarte, G. Sibbens, A.G. Smith, N. Sosnin, A. Stamatopoulos, D. Tarrío, L. Tassan-Got, D. Vanleeuw, A. Ventura, D. Vescovi, T. Wright, P. Žugec, the n_TOF collaboration: the fission experimental programme at the CERN n_TOF facility: status and perspectives. Eur. Phys. J. A 56(2), 48 (2020). https://doi.org/10.1140/epja/s10050-020-00037-8
P. Žugec, C. Weiß, C. Guerrero, F. Gunsing, V. Vlachoudis, M. Sabate-Gilarte, A. Stamatopoulos, T. Wright, J. Lerendegui-Marco, F. Mingrone, J.A. Ryan, S.G. Warren, A. Tsinganis, M. Barbagallo, Pulse processing routines for neutron time-of-flight data. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerat. Spectromet. Detect. Assoc. Equip. 812, 134–144 (2016). https://doi.org/10.1016/j.nima.2015.12.054
N.V. Sosnin, Atomic number and gamma-ray measurements from neutron-induced fission at the ILL and n_ToF. PhD thesis, The University of Manchester (2020). https://cds.cern.ch/record/2730110
B.E. Watt, Energy spectrum of neutrons from thermal fission of \(^{235}\)U. Phys. Rev. 87, 1037–1041 (1952). https://doi.org/10.1103/PhysRev.87.1037
R.B. Leachman, The world’s requirements for energy : the role of nuclear energy. In: Proc. Int. Conf. Peaceful Uses At. Energy 2, 193 (1956)
A.S. Vorobyev, O.A. Shcherbakov, Y.S. Pleva, A.M. Gagarski, G.V. Val’ski, G.A. Petrov, V.I. Petrova, T.A. Zavarukhina, Measurements of angular and energy distributions of prompt neutrons from thermal neutron-induced fission. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerat. Spectromet. Detect. Assoc. Equip. 598(3), 795–801 (2009). https://doi.org/10.1016/j.nima.2008.10.017
M. Jandel, M. Morháč, J. Kliman, L. Krupa, V. Matoušek, J.H. Hamilton, A.V. Ramayya, Decomposition of continuum \(\gamma \)-ray spectra using synthesized response matrix. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerat. Spectromet. Detect. Assoc. Equip. 516(1), 172–183 (2004). https://doi.org/10.1016/j.nima.2003.07.047
S. Agostinelli, J. Allison, K. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, D. Axen, S. Banerjee, G. Barrand, F. Behner, L. Bellagamba, J. Boudreau, L. Broglia, A. Brunengo, H. Burkhardt, S. Chauvie, J. Chuma, R. Chytracek, G. Cooperman, G. Cosmo, P. Degtyarenko, A. Dell’Acqua, G. Depaola, D. Dietrich, R. Enami, A. Feliciello, C. Ferguson, H. Fesefeldt, G. Folger, F. Foppiano, A. Forti, S. Garelli, S. Giani, R. Giannitrapani, D. Gibin, J.J. Gómez Cadenas, I. González, G. Gracia Abril, G. Greeniaus, W. Greiner, V. Grichine, A. Grossheim, S. Guatelli, P. Gumplinger, R. Hamatsu, K. Hashimoto, H. Hasui, A. Heikkinen, A. Howard, V. Ivanchenko, A. Johnson, F.W. Jones, J. Kallenbach, N. Kanaya, M. Kawabata, Y. Kawabata, M. Kawaguti, S. Kelner, P. Kent, A. Kimura, T. Kodama, R. Kokoulin, M. Kossov, H. Kurashige, E. Lamanna, T. Lampén, V. Lara, V. Lefebure, F. Lei, M. Liendl, W. Lockman, F. Longo, S. Magni, M. Maire, E. Medernach, K. Minamimoto, P. Mora de Freitas, Y. Morita, K. Murakami, M. Nagamatu, R. Nartallo, P. Nieminen, T. Nishimura, K. Ohtsubo, M. Okamura, S. O’Neale, Y. Oohata, K. Paech, J. Perl, A. Pfeiffer, M.G. Pia, F. Ranjard, A. Rybin, S. Sadilov, E. Di Salvo, G. Santin, T. Sasaki, N. Savvas, Y. Sawada, S. Scherer, S. Sei, V. Sirotenko, D. Smith, N. Starkov, H. Stoecker, J. Sulkimo, M. Takahata, S. Tanaka, E. Tcherniaev, E. Safai Tehrani, M. Tropeano, P. Truscott, H. Uno, L. Urban, P. Urban, M. Verderi, A. Walkden, W. Wander, H. Weber, J.P. Wellisch, T. Wenaus, D.C. Williams, D. Wright, T. Yamada, H. Yoshida, D. Zschiesche, Geant4-a simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerat. Spectromet. Detect. Assoc. Equip. 506(3), 250–303 (2003)
M.M. Hoffman, Directional correlation of fission fragments and prompt gamma rays associated with thermal neutron fission. Phys. Rev. 133, 714–723 (1964). https://doi.org/10.1103/PhysRev.133.B714
Acknowledgements
This work was supported by the UK Nuclear Data Network, the BEIS Advanced Fuel Cycle programme, the SANDA Nuclear Data Euratom Project and the funding agencies of the participating institutes.
Author information
Authors and Affiliations
Consortia
Corresponding author
Additional information
Communicated by Jose Benlliure.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
The n_TOF Collaboration (www.cern.ch/ntof)., Wright, T., Smith, A.G. et al. Measurement of the prompt fission \(\gamma \)-rays from slow neutron-induced fission of \(^{235}\)U with STEFF. Eur. Phys. J. A 60, 70 (2024). https://doi.org/10.1140/epja/s10050-024-01277-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-024-01277-8