1 Introduction

Nuclei around \(Z = 50\) continue to be an area of many experimental efforts, as they serve as an important testing ground for the shell structure of nuclei around \(N = Z = 50\) and the effective interaction. Experimental data for even–even Cd (\(Z = 48\)) [1,2,3,4,5,6,7] and even–even Sn (\(Z = 50\)) [8,9,10,11,12,13,14,15,16,17,18] isotopes have revealed an asymmetric behaviour with respect to the midshell in the trend of the \(B(\textrm{E2};2^+\rightarrow 0^+)\) values as a function of N for both these isotopic chains (see for example Fig. 1 in Ref. [2]). For the Sn isotopes, the experimental values indicate a shallow dip in the midshell. Two protons above the closed shell at Sn, in the Te isotopes, large-scale shell-model calculations indicate that this dip should be washed out due to enhanced neutron-proton interactions [19]. However, the exact shape of the theoretical curve around the midshell depends on the choice of the effective charges and single-particle energies, and it is interesting to note that a truncation of the model space around the midshell, as presented in Ref. [20], leads to a pronounced dip at the midshell. A comparison with available experimental data in this region does not provide a definite answer, mainly due to the large uncertainty associated with the \(B(\textrm{E2};2^+\rightarrow 0^+)\) measurement in 118Te and the missing value at 116Te. Therefore, obtaining more experimental data in this region would provide important and further constraints for theoretical models and allows for the testing of shell-model parameters.

Different experimental techniques have been employed for the determination of the transition probabilities in the tellurium isotopic chain. The three most commonly used methods to measure the \(B(\textrm{E2})\) of the \(2_1^+\rightarrow 0_{\text {g.s.}}^+\) transitions in this region are the Recoil Distance Doppler Shift (RDDS) technique, Coulomb excitation (CE) and fast-timing methods. The \(B(\textrm{E2};2^+\rightarrow 0^+)\) values in the Te isotopes with even mass numbers have previously been determined for the neutron-deficient isotopes with \(A =\) 108–114,118 using RDDS [20,21,22,23,24]. For the stable isotopes with \(A =\) 120–130 the \(B(\textrm{E2})\) values have been measured using CE [25,26,27,28,29], RDDS [30] and fast timing [31]. Finally, for the neutron-rich isotopes the \(B(\textrm{E2})\) values are known for \(A =\) 132–138 mostly through CE experiments [28, 29, 32, 33], but also via fast-timing measurements [31, 34].

Pasternak et al. [24] reported a value for the lifetime of the \(2^+\) state in 118Te of 8.8(14) ps, corresponding to \(B(\textrm{E2};2^+\rightarrow 0^+)\)\(=33^{+6}_{-5}\) W.u. This value suggests a drop as compared to the \(B(\textrm{E2};2^+\rightarrow 0^+)\) value at \(N=68\). However, due to the rather large experimental uncertainty of this value, and the still missing value for 116Te, it is difficult to identify a clear trend in the midshell region.

The challenge in measuring the \(B(\textrm{E2};2^+\rightarrow 0^+)\) of the midshell Te isotopes lies in the vibrational-like structure at low spins. This results in an overlap of the three lowest transitions in the ground-state band of 118Te [35, 36] and the two lowest transitions in 116Te [37]. In fact, apart from statistical considerations, the largest contribution to the uncertainty of the lifetimes of the \(2^+\) state in the measurement of Pasternak et al. was due to the uncertainty of the lifetimes of the \(6^+\) and \(4^+\) states. The reason for this is that in the data analysis the full group of overlapping peaks were fitted together, treating the lifetimes as line shape parameters. This resulted in the uncertainty of the lifetimes of the higher lying states propagating into the uncertainty of the lower lying states.

This work aims to reduce the uncertainty of the

\(B(\textrm{E2};2^+\rightarrow 0^+)\) value of 118Te, thereby better establishing the behaviour of the transition probabilities in the crucial midshell area. This is done by implementing the Differential Decay Curve Method (DDCM) in coincidence mode, with a gate on the direct feeding transition to reduce the interference of the higher lying states on the lifetime measurement of the \(2^+\) state.

2 Experimental details

An RDDS [38, 39] experiment was carried out at the JYFL accelerator laboratory in Jyväskylä, Finland. In the RDDS technique, a beam-induced reaction in a thin target creates an excited recoil travelling with a velocity v towards a thick stopper foil. Gamma-ray energies measured from the recoil will either be Doppler shifted, if the recoil decays in flight, or unshifted, if the decay occurs for recoils at rest in the stopper. Lifetime information is gathered from the change in intensity of the Doppler-shifted-energy peak and the unshifted-energy peak as the target-to-stopper distance x is varied.

The excited states of \(^{118}\)Te were populated in the \({}^{100}\textrm{Mo}({}^{22}\textrm{Ne}, 4\textrm{n})\) fusion-evaporation reaction at a beam energy of 75 MeV and beam current of 4 pnA. The detector setup consisted of the JUROGAM II \(\gamma \)-ray spectrometer [40, 41] in combination with the DPUNS plunger [42]. In JUROGAM II, 15 Compton suppressed Eurogam Phase-1 Ge detectors and 24 Compton suppressed Eurogam Ge clover detectors are arranged into four rings. Five of the Phase-1 detectors are placed in a ring at 157.6\(^{\circ }\) (ring 1) with respect to the beam axis, and the other ten detectors at 133.6\(^{\circ }\) (ring 2). Among the clovers, twelve are placed in a ring at 104.5\(^{\circ }\) (ring 3) and twelve at 75.5\(^{\circ }\) (ring 4). Rings 3 and 4 were not used for the lifetime analysis in this work, due to their angle being close to 90\(^{\circ }\), resulting in small separation of the shifted and unshifted components. For the plunger, a movable \(^{100}\textrm{Mo}\) target of 0.68 mg/cm\(^2\) thickness was mounted together with an Au stopper foil of 8 mg/cm\(^2\) thickness.

The Doppler-shifted energy will depend on the detector angle and on the velocity v of the recoil. This velocity was determined by fitting the shifted and unshifted component of a strong transition in 118Te at the smallest (\(x = 25\) \(\upmu \)m) and largest (\(x = 215\) \(\upmu \)m) distances in ring 1 and ring 2. The average velocity was found to be \(v/c = 1.3370(78)\%\), which results in the Doppler-shifted energies presented in Table 1. The small separation in energy between the three lowest transitions in the ground-state band of 118Te provides a challenge for the analysis, in particular for setting a clean gate on the feeding transition and achieving a good fit of the peak intensities.

Table 1 Unshifted (u) and Doppler-shifted (s) energies of the three lowest transitions in the ground-state band of 118Te. Unshifted energies are taken from Ref. [36] and shifted energies are calculated using the deduced recoil velocity
Full size table

3 Data analysis and experimental results

To extract the lifetime from the RDDS data, the Differential Decay Curve method (DDCM) [39, 43] was used in coincidence mode. This involves setting a gate on the Doppler-shifted component of a transition above the level of interest. The main advantage of using the coincidence mode is that the analysis is independent of other feeding paths than the one that is selected with the gate. This is helpful when dealing with complicated feeding patterns or unknown side-feeding. Furthermore, it has the advantage of simplifying the spectrum by removing the peaks not in coincidence with the gated peak. This is especially beneficial in the analysis of the \(2^+\) lifetime of 118Te, where the six partially overlapping peaks can be reduced to only three, by putting a gate on the shifted component of the direct feeding transition from the \(4^+\) state. Of the six peaks, this gate will leave only the shifted component of the decay of the \(6^+\) state, as well as the two peaks of interest; the unshifted and shifted components of the \(2^+\) decay.

Data were collected for eight different target-to-stopper distances, ranging from 25  to 215 \(\upmu \)m, covering a time of flight from approximately 6 ps to 54 ps. The events were sorted into 16 \(\gamma \gamma \) matrices, corresponding to ring 1 vs ring 2 and ring 1 vs ring 1 for each distance. These matrices will be denoted (R1, R2) and (R1, R1), respectively, where the gate will be set on the first component. Matrices (R2, R2) and (R2, R1) were not used during the data analysis of the \(2^+\) state lifetime. This is because neutron inelastic scattering on \(^{74}\)Ge results in a peak at 596 keV, with a tail on the high-energy side [44], in coincidence with both the shifted and unshifted components of the 118Te transitions. By gating only in R1 it was possible to avoid this distribution in the gate. The off-line data sorting and the analysis of the selected \(\gamma \gamma \) matrices were performed using the GRAIN [45] and RADWARE [46] software packages.

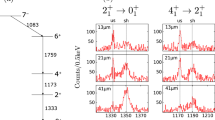
A carefully selected symmetric gate was set on the shifted component of the \(4^+\rightarrow 2^+\) transition for each target-to-stopper distance x. The gate had to be narrow to avoid overlapping with the shifted \(2^+ \rightarrow 0^+\) transition and the above mentioned neutron peak. A background spectrum was obtained by setting a gate on the Compton continuum close to the peaks of interest, with the same gate being used for all distances. After gating and subtracting the background, the intensities of the shifted and unshifted components of the \(2^+ \rightarrow 0^+\) transition were determined by fitting the background-subtracted spectrum, together with the shifted component of the \(6^+ \rightarrow 4^+\) transition. In the fit, both the widths and the positions of the three peaks were fixed. Examples of spectra obtained after the gate and the background subtraction are presented in Fig. 1.

The intensities were then normalised to the number of 118Te nuclei produced at each distance x. The normalisation constants were determined with two methods and checked for consistency. First, a gate was set on the shifted and unshifted components of the yrast \(8^+\rightarrow 6^+\) and the sum of the intensities of the shifted and unshifted components of two higher-lying transitions were determined. In the second method, that was used in the final lifetime analysis, the normalisation constants were determined by the total number of counts in each matrix. While it is important to note that the normalisation constants may be affected by the deorientation effect [39], the consistency of the two methods described above indicate a negligible effect, as was also concluded for the similar case of \(^{114}\)Te in Ref. [23].

Fig. 1
figure 1

Spectra of the \(2^+ \rightarrow 0^+\) transition in 118Te obtained by gating on the shifted component of the \(4^+\rightarrow 2^+\) transition for eight different target-to-stopper distances x in (R1, R2). The shifted component is shown in red, dashed line, while the stopped component is shown in blue, continuous line. The shifted component of the \(6^+ \rightarrow 4^+\) transition is shown in grey, continuous line. The sum of the three fitted peaks is shown in black, dotted line

Full size image

In DDCM the lifetime \(\tau (x)\), calculated for each distance x, is given by

$$\begin{aligned} \tau (x) = \frac{\{B_\textrm{s}, A_\textrm{u}\}(x)}{\frac{d}{dx}\{B_\textrm{s}, A_\textrm{s}\}(x)}\cdot \frac{1}{v}. \end{aligned}$$
(1)

Here, capital letters denote the populating transition (B) and the depopulating transition (A) of the level of interest. The indices s and u denote the shifted and unshifted components of a \(\gamma \)-ray transition, respectively. The curly braces \(\{X, Y\}\) denote the intensity of peak Y, while gating on peak X. The symbol v is the mean velocity of the 118Te recoils. Note that Eq. (1) is exact, even when the deorientation effect is present, as is shown in Ref. [47].

The derivative in Eq. (1) was calculated by fitting a piecewise continuously differentiable function to \(\{B_s, A_s\}(x)\) over the full range of x, using the software APATHIE [48]. The values where the derivative is within half of the maximum value constitutes the so-called region of sensitivity. The final value of \(\tau \) was taken as the weighted mean value of all \(\tau (x)\), where x was in the region of sensitivity.

The \(B(\textrm{E2})\) value can be calculated from the lifetime as

$$\begin{aligned} B(\textrm{E}2\downarrow ) = \frac{1.377\cdot 10^{4}}{E_\gamma ^5 A^{4/3} \tau (1+\alpha )} \quad [\mathrm{W.u.}], \end{aligned}$$
(2)

where \(E_\gamma \) is the energy of the transition in MeV, \(\tau \) is the lifetime in ps and \(\alpha \) is the internal conversion coefficient, for which the value \(\alpha = 4.836\cdot 10^{-3}\) from Ref. [49, 50] was used for the \(2^+ \rightarrow 0^+\) transition.

The DDCM analysis of the intensities from the matrix (R1, R2) can be seen in Fig. 2. The lifetime of the \(2^+\) state, averaged between the results of the matrices (R1, R2) and (R1, R1), is \(\tau =7.46(19)\) ps, which corresponds to

\(B(\textrm{E2};2^+\rightarrow 0^+)\) = 38.93(98) W.u.

Fig. 2
figure 2

Determination of the lifetime of the \(2^+\) state using the (R1, R2) matrix, with a gate on the \(4^+\rightarrow 2^+\) transition (B) resulting in intensities of the \(2^+\rightarrow 0^+\) transition (A). a Intensity of the shifted component. The solid line shows the fit performed in APATHIE. b Intensity of the unshifted component. The solid line is constructed by multiplying the deduced mean lifetime \(\tau \) with the derivative of the fitted line in a and mean velocity. c Lifetimes calculated in the region of sensitivity (35 \(\upmu \)m–95 \(\upmu \)m). The dashed lines mark the boundaries for the standard error of the weighted mean

Full size image

The analysis of the \(4^+\rightarrow 2^+\) transition followed a similar procedure as for the \(2^+\) state. However, a gate was not set on the shifted component of the direct \(6^+\rightarrow 4^+\) feeding transition of the \(4^+\rightarrow 2^+\) transition. Instead, an indirect gate was set on the shifted component of the \(8^+\rightarrow 6^+\) transition in the ground state band and the analysis was performed using DDCM with an indirect gate, as described in Ref. [39]. This was necessary in order to avoid the high-energy tail of the 596 keV peak from inelastic neutron scattering on \(^{74}\)Ge and to avoid overlap with the unshifted \(2^+\rightarrow 0^+\) transition. Using an indirect gate the expression for \(\tau \) becomes

$$\begin{aligned} \tau (x) = \frac{\{C_\textrm{s}, A_\textrm{u}\}(x)-\overline{\delta }\{C_s, B_u\}(x)}{\frac{d}{dx}\{C_\textrm{s}, A_\textrm{s}\}(x)}\cdot \frac{1}{v}, \end{aligned}$$
(3)

where \(\overline{\delta }\) is the mean value of \(\delta (x)\) with

$$\begin{aligned} \delta (x) = \frac{\{C_\textrm{s}, A_\textrm{u}\}(x)+\{C_s, A_s\}(x)}{\{C_\textrm{s}, B_\textrm{u}\}(x)+\{C_\textrm{s}, B_\textrm{s}\}(x)}. \end{aligned}$$
(4)

In Eq. (3) and (4), C denotes the indirect gate on the \(8^+\rightarrow 6^+\) transition, B denotes the direct feeding \(6^+\rightarrow 4^+\) transition and A denotes the depopulating \(4^+\rightarrow 2^+\) transition. This analysis, in contrast to the \(2^+\) state, is complicated by the fact that with a gate on the \(8^+\rightarrow 6^+\) transition, all six of the unshifted and shifted components of the lower lying states need to be fitted. The result for the (R2, R2) matrix is presented in Fig. 3, and the result averaged between matrices (R2, R2), (R2, R1) and (R1, R1) is \(\tau ~=~4.25(23)\) ps, corresponding to \(B(\textrm{E2};4^+\rightarrow 2^+)=71.3(38)\) W.u.

Fig. 3
figure 3

Determination of the lifetime of the \(4^+\) state using the (R2, R2) matrix. Region of sensitivity is 25 \(\upmu \)m–60 \(\upmu \)m. The details are the same as in Fig. 2, however here the transitions C, B and A are the \(8^+\rightarrow 6^+\), \(6^+\rightarrow 4^+\) and \(4^+\rightarrow 2^+\) transitions respectively

Full size image

Table 2 shows a summary of the measured lifetimes and transition probabilities obtained in this experiment. Only statistical uncertainties were considered in the analysis.

Table 2 Measured lifetimes and transition strengths obtained for 118Te in this experiment. Experimental \(B(\textrm{E2}\downarrow )\) values are compared to LSSM calculations [19] and IBM calculations from Ref. [24]
Full size table
Fig. 4
figure 4

(a) Reduced transition probabilities for even–even nuclei in the tellurium isotopic chain. Black points represent the adopted values taken from the evaluator Ref. [51], except for N = 58 which is taken from Ref. [22]. The black point at 118Te corresponds to the value proposed in Ref. [24], while the red point is the \(B(\textrm{E2};0^+\rightarrow 2^+)=0.669(17)~\textrm{e}^2\textrm{b}^2\) of 118Te obtained in the present work. Note that the red point has been shifted slightly horizontally for clarity. The solid and dashed lines are calculated values using full [19] and restricted [20] model space, respectively. See text for details. (b) Calculated proton and neutron matrix elements, \(M_p\) and \(M_n\), used to calculate the solid line in (a)

Full size image

4 Discussion

Both the new result for the \(2^+\) state and for the \(4^+\) state are in agreement with the previously published results in Ref. [24], but the new measurement of the \(2^+\) state lifetime reduces the relative uncertainty from 16 to 2.5%. The new result for \(B(\textrm{E2};0^+\rightarrow 2^+)\) of 118Te, with its significantly reduced uncertainty, is compared with the available experimental data for the Te isotopic chain in Fig. 4a. It is clear that the new value for 118Te does not represent any significant decrease in the trend, as compared to the nuclei with \(N > 66\).

In Fig. 4a two shell-model calculations are also presented, which differ significantly in the midshell. These calculations are at the very limit of the current computational capacity of the shell model, as the dimension of the shell-model space increases exponentially with increasing neutron and proton number and reaches \(2 \cdot 10^{10}\) at the midshell for the Te isotopes. In Ref. [19], the reduced transition probabilities were calculated for all Te isotopes in the full model space, involving the neutron and proton orbitals \(g_{7/2}, d_{5/2}, d_{3/2}, s_{1/2}\), and \(h_{11/2}\) with no truncation. It is plotted in Fig. 4a with a solid line. In earlier works [20, 21], truncated shell-model calculations were performed for the Te isotopes by limiting the maximal number of particles that can be excited to the \(h_{11/2}\) orbital to four. This truncated model space calculation is shown in Fig. 4a with a dashed line. The absolute amplitudes of the theoretical \(B(\textrm{E2})\) curves depend directly on the chosen neutron and proton effective charges, as B(E\(2; J\rightarrow J+2)=1/(2J+1)(e_nM_n+e_pM_p)^2\) where \(M_n\) and \(M_p\) are neutron and proton E2 matrix elements. Here they are calculated with the effective charges \(e_p=1.5e\) and \(e_n=0.8e\), as in Ref. [21]. The calculation with no truncation follows the parabolic trend of the experimental values approximately. In contrast, the truncated calculation illustrates how a dip in the midshell could be related to a suppressed contribution of the neutron excitation from the \(g_{7/2}\) and \(d_{5/2}\) orbitals, across the presumed \(N = 64\) subshell, to the \(h_{11/2}\) orbital.

The evolution of the B(E2) values shown in Fig. 4 may also be understood from a simple perspective based on the generalized seniority model [52]. If the neutron wave functions can be written as the product of \({\mathcal {N}}/2\) generalized seniority pairs, the neutron E2 matrix element can be calculated as

$$\begin{aligned} M_n=\sqrt{\frac{{\mathcal {N}}(2\Omega -{\mathcal {N}})}{4(\Omega -1)}}M_{n,0} \end{aligned}$$
(5)

where \(M_{n,0}\) is the E2 matrix element for the neutron generalised seniority pair, \(\Omega \) is the degeneracy of the model space and \({\mathcal {N}}\) is the number of valence neutrons. The \(M_n\) and the corresponding \(B(\textrm{E2})\) values will follow a parabolic curve as a function of valence neutron number between \(N = 50\) and 82 if the generalised seniority symmetry is conserved. The degeneracy will be reduced if the occupation of the \(h_{11/2}\) orbital is suppressed, leading to a dip in the midshell. It may be useful to mention that such a dip may appear in the evolution of the \(B(\textrm{E2})\) values in the midshell Sn isotopes in large-scale shell-model and generalised seniority model calculations if the \(N = 64\) subshell gap is made sufficiently large. However, in the full shell-model calculations, even if a shallow dip exists in the Sn midshell, it is expected to be washed out for the Te isotopes due to the existence of the two valence protons and consequently the enhanced neutron-proton interaction and quadrupole correlation. The new result presented here for the \(2^+\) state of 118Te gives support for this parabolic shape seen in the LSSM calculations.

A discrepancy between the data and the full model space shell-model calculation in Fig. 4a is the relatively large difference at \(N = 68,70\) and in general the model’s underestimation of the \(B(\textrm{E2})\) values for nuclei on the right side of the plot in Fig. 4a. In other words, the experimental \(B(\textrm{E2})\) values indicate an asymmetric pattern, with higher values observed for \(N > 66\) compared to the lighter ones. This asymmetric trend is not observed in the calculated values. To understand this phenomenon, in Fig. 4b, the \(M_n\) and \(M_p\) values extracted from the full-space shell-model calculation are plotted. An interesting feature is that the shape of the \(M_n\) curve deviates slightly from the parabolic behaviour expected from the generalised seniority framework, in reasonable agreement with the asymmetric shape of the experimental \(B(\textrm{E2})\) values. The reason why the total calculated \(B(\textrm{E2})\) values are less asymmetric is related to the fact that the calculated \(M_p\) values show a decreasing trend with increasing N due to the reduced neutron-proton interaction when moving away from \(N = Z\). From that perspective, it can be speculated that the underestimation of the \(B(\textrm{E2})\) values in the heavier Te isotopes indicates an underestimation of the neutron-proton correlation in those nuclei.

At low spins the level structure of even-A \(^{118-122}\)Te nuclei closely follow the one expected in the vibrator picture, with a \(0^+,2^+,4^+\) triplet of two-phonon states at roughly double the energy of the one-phonon \(2^+\) state [25, 36]. However, additional experimental observables are needed to get a complete picture of the collective behaviour. One such complementary observable is the spin dependence of the \(B(\textrm{E2})\) values. For the two yrast transitions this can be observed through the \(B_{4/2}\) ratio, defined as

$$\begin{aligned} B_{4/2} = \frac{B(\text {E}2;4^+\rightarrow 2^+)}{B(\text {E}2;2^+\rightarrow 0^+)}. \end{aligned}$$
(6)

For a vibrator this ratio is expected to be close to 2, but for \(^{120,122}\)Te the ratio has been found to be smaller than that, and in better agreement with the one of an asymmetric rotor [25]. In light of this, the \(B_{4/2}\) ratio for 118Te was calculated based on the new experimental results for the \(2^+\) and \(4^+\) states. The value is determined to be 1.83(11), providing evidence that it behaves as a near perfect harmonic vibrator at low spins. Furthermore, this measurement reaffirms that for 118Te there is no evidence for the so called \(B_{4/2}\) anomaly, which has recently been identified in several nuclei [53,54,55,56], including \(^{114}\)Te [23]. In fact, the \(B_{4/2}\) value of 118Te is among the highest known values in the Te isotopic chain, making the contrast against the unusually low \(B_{4/2}\) in \(^{114}\)Te even larger.

5 Conclusion

A Recoil Distance Doppler-shift measurement with the DPUNS plunger in combination with the JUROGAM II spectrometer has been performed in order to experimentally determine the lifetime of the yrast \(2^+\) and \(4^+\) states in 118Te. The lifetimes obtained using the Differential Decay Curve method in coincidence mode are \(\tau _{2^+}=7.46(19)\) ps and \(\tau _{4^+}=4.25(23)\) ps, corresponding to \(B(\textrm{E2};2^+\rightarrow 0^+)\) = 38.93(98) W.u. and \(B(\textrm{E2};4^+\rightarrow 2^+)=71.3(38)\) W.u., respectively. The new value with decreased uncertainty for the \(2^+\rightarrow 0^+\) transition indicates no significant drop in the \(B(\textrm{E2};0^+\rightarrow 2^+)\) value when going from \(N=68\) to \(N=66\), in agreement with the full model space large-scale shell-model calculations. The ratio between the two measured \(B(\textrm{E2})\) values, indicate that 118Te behaves as an almost perfect harmonic vibrator.