Abstract
Recent analysis of the viability of solid state-based relic neutrino detectors has revealed the fundamental necessity for the use of heavy, \(A>100\), \(\beta \)-decayers as neutrino targets. Of all heavy isotopes,  and
and  stand out for their sufficiently low decay energies, reasonable half-life times and stable daughter nuclei. However, the crucial bit of information, that is the soft neutrino capture cross-section is missing for both isotopes. The main reason for that is a particular type of \(\beta \)-decay, which precludes a simple link between the isotope’s half-life time and the neutrino capture rate. In light of the necessity for a reliable estimate of the capture rate – unimpeded by potentially devastating theoretical uncertainties – prior to using the isotope in a full-scale experiment, we propose an experimental method to bypass this difficulty and obtain the capture cross-section of a soft neutrino by a given isotope from the isotope’s \(\beta \)-spectrum.
stand out for their sufficiently low decay energies, reasonable half-life times and stable daughter nuclei. However, the crucial bit of information, that is the soft neutrino capture cross-section is missing for both isotopes. The main reason for that is a particular type of \(\beta \)-decay, which precludes a simple link between the isotope’s half-life time and the neutrino capture rate. In light of the necessity for a reliable estimate of the capture rate – unimpeded by potentially devastating theoretical uncertainties – prior to using the isotope in a full-scale experiment, we propose an experimental method to bypass this difficulty and obtain the capture cross-section of a soft neutrino by a given isotope from the isotope’s \(\beta \)-spectrum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The ambitious goal of detection [1] and the measurement of the mass [2] of the relic neutrino relies on the precise experimental knowledge of the \(\beta \)-spectrum of radioactive elements [3, 4]. Relic neutrinos, which fill the totality of space in the form of an almost ideal gas of temperature \(T_{\nu } \approx 1.95\,\hbox {K}\), are expected to manifest themselves in rare neutrino capture events. Such events involving cosmic neutrinos of mass \(m_\nu \) and a sample of radioactive atoms characterized by the \(\beta \)-decay energy Q would produce an extremely faint peak at the energy \(Q+m_\nu c^2\) in the \(\beta \)-spectrum of the sample. We recall that for all radioactive elements the overwhelming bulk of the \(\beta \)-spectrum arises from spontaneous \(\beta \)-decay and forms a continuum with the upper cutoff energy \(Q-m_{\nu }^0 c^2\) where \(m_{\nu }^0\) is the mass of the lightest neutrino. For this reason one expects the neutrino capture peak to be separated from the end of the spontaneous \(\beta \)-spectrum by an energy gap of at least one neutrino mass and for that reason to be discernible at least in principle.
Despite the simplicity of its theoretical premise, a neutrino capture experiment establishing the existence of relic neutrinos has not yet materialized. The reason for this is the weakness of the neutrino-matter interaction, which makes it difficult to achieve the sufficient number of capture events in a reasonably sized radioactive sample. The requirement of a large neutrino capture cross-section combined with other important considerations such as the manageable half-life time and the stability of the daughter isotope turn out to be so restrictive that only a handful of atoms can be viewed as viable candidates for the \(\mathrm C\nu B\) detection experiment. From this perspective, Tritium has long been regarded as the best candidate \(\beta \)-emitter [4,5,6,7,8,9,10,11], even though it was found that the workable sample of gaseous molecular Tritium falls short of the required activity levels by six orders of magnitude. Currently, the only viable alternative to the gas phase experiment is a solid state based architecture where the atomic tritium is adsorbed on a substrate [4].
The low event rate is not the only hindrance in the way of relic neutrino detection. The upper bounds on the neutrino mass [12] show that the energy gap between the signal from neutrino capture and the background is extremely small \(m_\nu /Q \ll 1\), therefore the detection of the \(\mathrm C\nu B\) requires extraordinary energy resolution. It has been demonstrated that the electromagnetic guidance system and the calorimetry module of the detection apparatus can be built to such stringent specifications [4]. However, solid-state interactions introduce additional complications [13,14,15,16,17]. In particular, it has been shown in [13] that deposition of \(\beta \)-emitters on a solid-state substrate produces a new fundamental limitation on the experimental resolution originating in the zero-point motion of the emitter’s centre of mass. For Tritium on solid surfaces, the best theoretical resolution is \(\varDelta E \sim 0.5\,\hbox {eV}\) which is an order of magnitude worse than what is required in order to see the relic neutrino peak. Furthermore, it was shown [13] that the main factor that determines this value is the ratio of the \(\beta \)-decay energy Q to the mass of the emitter nucleus \(m_{\text {nucl}}\), namely \(\gamma =[Q^2 m_{\text {e}}/ m_{\text {nucl}}^3]^{1/4}.\) This finding opens a new avenue to search for a possible alternative for Tritium that would have both a sufficient event rate and low enough energy uncertainty. In the same work [13], it was found that the two promising candidates that have low enough \(\gamma \)-values are Thulium ( ) and Samarium (
) and Samarium ( ) with
) with  and
and  respectively. This means that the intrinsic energy uncertainty for these isotopes is an order of magnitude smaller than that of Tritium. This value approaches the upper bound for the neutrino mass and therefore could, in principle, provide sufficient energy resolution for its detection.
respectively. This means that the intrinsic energy uncertainty for these isotopes is an order of magnitude smaller than that of Tritium. This value approaches the upper bound for the neutrino mass and therefore could, in principle, provide sufficient energy resolution for its detection.
The \(\gamma \)-value introduced in the previous paragraph is defined in terms of the simple intrinsic characteristics of a nucleus such as its mass and Q-value and therefore is straightforward to calculate. In contrast, the neutrino capture cross-section has not been calculated for every isotope. In particular, it is not known for either of the isotopes of interest,  and
and  .
.
The reason for this emanates from the complexity of the nuclear structure [18,19,20]. The \(n\leftrightarrow p\) conversion changes the nuclear state, introducing some unknown amplitudes of transition between the initial and final nuclear wave-functions. For some isotopes, there is a single dominant transition. This allows to extract the corresponding matrix element solely on the basis of the nucleus lifetime \(\tau \) of weak decay. Other isotopes undergo the so-called non-unique forbidden transition, which, as the name suggests, involves multiple possible configurations of the final nucleus with independent transition amplitudes. In this case, the direct link between the observed half-life time and the neutrino capture rate is generally absent.
A possible way to confront this difficulty relies on performing theoretical computations of the nuclear matrix elements. The list of nuclear models includes but is not limited to Nuclear Shell Model [21] and Interacting Boson-Fermion model [22, 23]. These have been employed in the work [24] to evaluate the relic neutrino capture cross-section for isotopes  ,
,  , and
, and  after the completion of this work.
after the completion of this work.
The goal of the present paper is to show how the neutrino capture cross section can be extracted from the experimentally accessible \(\beta \)-spectrum for a given radioactive isotope decaying through non-unique forbidden transitions.
2 Quantum mechanics of \(\beta \)-interaction and crude estimate of neutrino capture
Neutrino capture and \(\beta \)-decay are the same processes driven by the weak interaction; they differ only in whether the (anti)neutrino is in the initial or final state. To establish the exact connection between their respective rates, we start from briefly reminding the main concepts of \(\beta \)-decay theory. We consider the sibling processes of \(\beta \)-decay and neutrino capture by a generic nucleus
which are driven by the same weak \(\beta \)-decay Hamiltonian
where \(G_\beta = G_F\cos \theta _C\) and \(\theta _C\) is Cabbibo angle, \(\psi _e\), \(\psi _\nu \) are electron and neutrino fields and p, n being the proton and neutron fields respectively. The vector \(g_V\) and axial \(g_A\) coupling constants are renormalized by strong interactions with \(|g_A/g_V|\approx 1.27\) [25, 26].
The differential \(\beta \)-decay rate \(d\varGamma _\beta \) and the capture cross-section for spin-averaged neutrino are given by the Fermi Golden Rule and can be written as:Footnote 1
where \(p_{e(\nu )}\) and \(E_{e(\nu )}\) are the momenta and energies of the leptons, \(W_\beta (p_e, p_\nu )\) is the average transition rate for the decay of an atom into two lepton plane waves with momenta \(p_e, p_\nu ,\) and \(W_\nu (p_e,p_\nu )\) is the average transition rate for the capture of a neutrino having the momentum \(p_\nu \) and the emission of an electron with momentum \(p_e.\)
The average transition rates are expressed in terms of transition amplitudes by
Here \(\mathscr {M}_{\text {if}}\) is the quantum transition amplitude between the initial and the final state induced by the reduced weak interaction Hamiltonian [19, 20, 27]
which encapsulates all information about the changes in the internal nuclear structure in a function \(J^\mu _{\text {nuclear}}(\textbf{r}).\) This function cannot be calculated from first principles. However, its transformation properties under the symmetry group of space are known for each transition. The summation symbol in Eq. (4) is a shorthand for the sum over the spin quantum numbers of the out-states as well as averaging over the spins of the in-states. The averaging over the directions of \({\textbf{p}}_e\) and \({\textbf{p}}_\nu \) is shown explicitly. Two important remarks are in order
-
1
For an overwhelming part of the \(\beta \)-spectrum one can consider the neutrino as a massless (Weyl) particle in both the energy conservation law and the wave functions entering the transition amplitudes. There exists a tiny energy window on the order of \(m_\nu \) near the high-energy end of the \(\beta \)-spectrum where the neutrino mass plays a role. However, the resolution required for the observation of the \(\beta \)-spectrum inside that window is by far beyond the reach of the existing experimental technique. Since the existing \(\beta \)-decay experiment cannot distinguish between the massive and massless cases, we shall throughout this note discuss the function \(W_\beta (p_e, p_\nu )\) assuming the \(m_\nu \rightarrow 0 \) limit.
-
2
Our main focus is on neutrino capture processes involving the cosmic neutrino background. Relic neutrinos are non-relativistic \(p_\nu \ll m_\nu ,\) which is the opposite of the ultra-relativistic limit discussed in item 1. It is straightfoward to see that:
$$\begin{aligned} W_\nu (p_e, 0) = \frac{1}{2} \lim _{p_\nu \rightarrow 0} W_\beta (p_e, p_\nu ) \end{aligned}$$(6)for a left-handed particle with a Majorana mass term. Indeed, in the \(p_\nu \rightarrow 0\) limit the incoming massive neutrino is a superposition of a left-handed Weyl particle and a right-handed Weyl anti-particle
$$\begin{aligned} \vert \text {Majorana} \rangle = (\vert \nu \rangle + \vert {\bar{\nu }} \rangle )/\sqrt{2}. \end{aligned}$$In a process where an electron is created, the operator (5) only picks one term of the two, hence the corresponding transition rate is one half of the transition rate \(W_\beta \) of a Weyl neutrino.
2.1 Crude estimate of neutrino capture
In this subsection, we want to provide a simple order-of-magnitude estimate for neutrino capture cross-section. To this end, we assume that the matrix element has no dependence on the lepton energy and reduces to a constant encoding the information about the initial and final nuclear states
Such an approximation neglects the Coulomb interaction between the emitted electron and the nucleus.
In this case, all the structural information about the nuclei gets absorbed into a constant numerical factor, therefore the ratio of the \(\beta \) decay and the neutrino capture rates, Eq. (3), is completely determined by the phase volume factors \(p_\nu ^2p_eE_e\) and \(p_e E_e\) accordingly. Using Eq. (6), this gives rise to the following relationship between the capture cross-section \(\left( \sigma v\right) _\nu ,\) the total lifetime \(\tau = (\int d\varGamma _\beta )^{-1}\) of a \(\beta \)-decaying isotope, and the total kinetic energy Q released in the reaction:
with \(T_e = E_e-m_e\) being the kinetic energy of the electron, and neutrino momentum in \(\beta \) decay is \(p_\nu = Q-T_e\). In the particular case of nonrelativistic electron \(Q\ll m_e\), this relation gives the following simple scaling:
In order to quantify the error introduced by the simplifying assumptions leading up to Eq. (7), we introduce a correction factor \(\delta \) such that the actual cross-section is given by
The values of \(\delta \) for a number of elements where the exact results for the neutrino capture cross-section are known [6] are given in Table 1. One can see that in all those cases \(\delta \) is reasonably close to unity.
We are interested in neutrino capture by possible candidates for solid-state based C\(\nu \)B detection experiments —  and
and  . For these isotopes, the parameterization (10) reads
. For these isotopes, the parameterization (10) reads


However, unlike the isotopes listed in Table 1, the theoretical values of the \(\delta \) factors for  and
and  are not known. This is because both isotopes have a rather peculiar structure of the matrix element (5), as explained in the following paragraph.
are not known. This is because both isotopes have a rather peculiar structure of the matrix element (5), as explained in the following paragraph.
We follow the general formalism presented in [28, 29], see also [30] for a modern review. For purely illustrative purposes, we neglect the effect of the Coulomb attraction between the \(\beta \)-electron and the daughter nucleus, bearing in mind that in practice such an approximation may result in significant inaccuracy. We recall that the function \(J^\mu _{\text {nuclear}}(\varvec{r})\) is mainly localized inside the nucleus \(r<R,\) and decays rapidly with increasing r for \(r>R\), where \(R=A^{1/3} \times 1.2\times 10^{-13} \,\text {cm}\) is the radius of the nucleus. Since the typical lepton momentum is of the order \(1\,\hbox {MeV}\ll R^{-1}\), one can expand the matrix elements and the sum \(\sum |\mathscr {M}_{\text {if}}|^2\) as a series in small parameters \(p_{e/\nu } R \ll 1\)Footnote 2
The constants \(c_i\) in this expression are in essence combinations of the spherical multipole moments of \(J^\mu _{\text {nuclear}}({\textbf{r}})\) containing structural information about the many-body wave functions of the parent and daughter nuclei. The simplifying approximation (7) amounts to keeping only the leading-order term \(c_0\) in the expansion (13), which in many cases is well justified. For some isotopes, however, electroweak selection rules demand that \(c_0=0\). Indeed, if the mother and daughter isotopes have different spin and parity, at least one of the leptons is required to carry a non-vanishing orbital angular momentum. Since a lepton’s wave function corresponding to the orbital angular momentum l has the asymptotic form \((p r)^l\) at small r, the matrix element of such a transition, Eq. (5), will necessarily contain terms proportional to \(\left( p_{e} R\right) ^l(p_\nu R)^{l'}\) with \(l+l'>0.\) The worst case scenario, known as a forbidden non-unique transition, is when the selection rules admit for the presence of several commensurate leading-order terms on the right hand side of the asymptotic expansion Eq. (13). For such a transition the matrix element (13) contains several unknown constants \(c_i\), each multiplying its own unique function of energy. If that happens, the cancellation of the unknown constants, such as the one seen in Eq. (8), does not occur and the neutrino capture cross-section cannot be inferred from the isotope’s life time.
This conclusion may be relieved for heavy isotopes by the Coulomb attraction, which introduces two modifications. Firstly, the electronic wave-function are distorted by the presence of a “point charge”, resulting in additional known energy-dependent coefficients in the expansion (13). Secondly, the account for the non-zero size of the charge adds another dimensionless parameter \(\xi \cdot R \equiv \alpha Z/R \cdot R\) to \(p_{e,\nu } R\) in (13). For heavy nuclei one can expect this parameter to be dominant if \(\xi /Q\gg 1\). This motivates the so-called \(\xi \)-approximation, in which one keeps only expansion in the parameter \(\alpha Z\) and is left with a single nuclear constant. In this case, the spectrum of isotopes that undergo non-unique transitions has the allowed shape, and the usual technique of relating the neutrino capture cross-section to the half-life time of the isotope may be used.
The theoretical motivation of the \(\xi \)-approximation does not guarantee that the associated nuclear constant is not suppressed. This can abate the dominance of the corresponding term and break down the approximation. Such a situation requires some degree of fine-tuning, similar to the case of isotopes whose spectra deviate from the expected allowed shape due to the suppression of the leading order term. While it may seem unlikely, it further reinforces the necessity of a method that can establish the neutrino capture cross-section in a more direct way.
Given the high stakes of the PTOLEMY experiment, we require a method to estimate the neutrino cross-section without relying on the assumption of no-cancellation. At the same time, for the purposes of this paper, we do not seek high accuracy of the result. It is important to note that, if the \(\xi \)-approximation is experimentally established to be accurate for a particular isotope, the relation of the cross-section to the half-life time may give much more precise results.
3 Experimental determination of the neutrino capture rate from the end of the \(\beta \) decay spectrum
We have established that for isotopes such as  and
and  the knowledge of the lifetime and the Q-value is insufficient in order to predict the neutrino capture cross-section. Here, we discuss how the required cross-section can be inferred directly from the experimentally measured \(\beta \)-spectrum. Our approach is based on two key observations. Firstly, both the emission and capture processes are governed by the same unknown structure function \(W_\beta (p_e, p_\nu ),\) albeit taken at different values of arguments. Specifically, a capture process corresponds to the limit \(p_\nu \rightarrow 0 \) and
the knowledge of the lifetime and the Q-value is insufficient in order to predict the neutrino capture cross-section. Here, we discuss how the required cross-section can be inferred directly from the experimentally measured \(\beta \)-spectrum. Our approach is based on two key observations. Firstly, both the emission and capture processes are governed by the same unknown structure function \(W_\beta (p_e, p_\nu ),\) albeit taken at different values of arguments. Specifically, a capture process corresponds to the limit \(p_\nu \rightarrow 0 \) and
whilst in a spontaneous \(\beta \)-decay process
where \(p_\nu \) can take any value between 0 and Q, resulting in a broad \(\beta \)-spectrum. Secondly, the function \(W_\beta (p_e, p_\nu )\) is an analytic function of both arguments near the end point \(p_\nu =0\) of the \(\beta \)-spectrum. We recall that in our discussion \(W_\beta (p_e, p_\nu )\) is the rate involving transitions with massless neutrino states (see discussion at the end of Sect. 2).
Using the analyticity of \(W_\beta (p_e, p_\nu )\) and making use of equations (3) and (6) we write the following expansionFootnote 3 for the observable \(\beta \)-spectrum near the edge \(p_\nu = 0\)
where \(\alpha _1\) is a constant. The characteristic energy scale where the linear approximation is applicable can be estimated from the microscopic theory of \(\beta \) decay. For the purposes of the present work, we notice that the physics of \(\beta \) decay of heavy nuclei involves three important energy scales, that are Q, \(m_e,\) and 1/R. The smallest of the three defines the energy range where the expansion (14) works well. For  and
and  the smallest energy scale is Q.
the smallest energy scale is Q.
Now we are in position to discuss the experimental procedure. We assume a finite energy resolution \(\varDelta E \) of the experiment (say, \(1\,\hbox {keV}\)). We propose a way to deduce the neutrino capture rate of the  and
and  from the end of their experimentally measured \(\beta \) spectra:
from the end of their experimentally measured \(\beta \) spectra:
-
1.
Define some experimentally accessible energy resolution \(\varDelta E \ll Q\) and measure the number of \(\beta \) decay events N in several energy binsFootnote 4\(T_e \in [Q-(n+1)\varDelta E, Q-n\varDelta E]\) as a function of the electron energy residue \(\varepsilon _n = \varDelta E(n+1/2)\)
-
2.
We assume that all the decay events are detected. In this case, one can check whether the experimental points \(N(\varepsilon _n)\times (\varepsilon _n \,\hbox {in}\,\,\hbox {keV})^{-2}\) fit the linear curve. If so, continue the obtained fit up till the value \(\varepsilon _n = 0\).
-
3.
Assuming that the time of the measurement is \(T_{\text {m}}\ll \tau \) and there are \(N_{\text {at}}\) decaying atoms, the neutrino capture rate can be estimated as
$$\begin{aligned} \left( \sigma v\right) _\nu = \frac{7.0 \cdot 10^{-37}\,\hbox {cm}^{2}}{(T_{\text {m}} \text { in hours})(\varDelta E \text { in keV})}\nonumber \\ \times \frac{1}{N_{\text {at}}}\left( \dfrac{N(\varepsilon _n)}{(\varepsilon _n \,\hbox {in}\,\, \hbox {keV})^2}\right) \bigg |_{\varepsilon _n =0} \end{aligned}$$(15)
A remark should be made concerning the generality of (15). Until now we neglected possible contributions to the electron spectrum due to \(\beta \)-decay into excited states of daughter nuclear or/and electronic shell of the atom. Let us comment on these contributions:
-
1.
Excited nuclear states have typical energies \(E_{\text {ex}} \sim 10\,\hbox {keV}\), for instance, \(66.7\,\hbox {keV}\) for
 [31] (daughter isotope for
[31] (daughter isotope for  ) and \(21.5\,\hbox {keV}\) of
) and \(21.5\,\hbox {keV}\) of  [32] (daughter isotope of
[32] (daughter isotope of 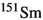 ). They do not contribute to the spectrum near the endpoint for \(T_e >Q-E_\text {ex}\). Therefore, they are not relevant for the measurement of the spectrum high-energy tail with resolution of order 1 keV.
). They do not contribute to the spectrum near the endpoint for \(T_e >Q-E_\text {ex}\). Therefore, they are not relevant for the measurement of the spectrum high-energy tail with resolution of order 1 keV. -
2.
Atomic excitations start to contribute to the spectrum from \(\sim 1\,\hbox {eV}\) and are expected to be too small to be resolved with a typical energy resolution of an experiment. If this is the case, Eq. (15) includes all these transitions and overestimates the actual cross-section. For \(Z\sim 60\), the probability to excite the electronic configuration is expected to be less than \(30\%\) [33, 34], which translates into the same possible error in the value of the cross-section. The account for this effect may be done with the use of the atomic mismatch correction [35, 36].
The corrections discussed above may only introduce a difference by a prefactor of order one and therefore are beyond our considerations.
4 Conclusion and discussion
The most promising route towards the relic neutrino detection is currently through the use of solid state based detectors where the \(\beta \) emitters are adsorbed on a substrate. Such a design has the potential to achieve sufficient density of emitters in a controllable way (such that electron scattering remains suppressed), and hence get a sufficient number of capture events. However, any \(\beta \) decay experiment that uses bound emitters (either in molecular form or adsorbed on a substrate) suffers from an irreducible intrinsic energy uncertainty due to the emitter’s zero-point motion. It was shown in [13] that such an uncertainty is proportional to the dimensionless parameter \(\gamma =[Q^2 m_{\text {e}}/ m_{\text {nucl}}^3]^{1/4}\), Q being the energy released in the \(\beta \) decay, \(m_e, m_{\text {nucl}}\) - masses of the electron and nucleus respectively. It was also shown that this parameter is too large for  , therefore Tritium-based detectors are unable to achieve the required energy resolution. Instead, the most promising candidates are
, therefore Tritium-based detectors are unable to achieve the required energy resolution. Instead, the most promising candidates are  and
and  as they have the intrinsic energy uncertainty that is an order of magnitude lower than that of
as they have the intrinsic energy uncertainty that is an order of magnitude lower than that of  .
.
However, contrary to the case of  for which the neutrino cross section is known [6, 10], theoretical calculation of \((\sigma v)_\nu \) for
for which the neutrino cross section is known [6, 10], theoretical calculation of \((\sigma v)_\nu \) for  and
and  poses a challenge. The quantum numbers (spin and parity) of the parent and daughter nuclei for these isotopes differ, hence the leptons are required to have a non-zero total orbital momentum. The latter can be composed in a non-unique way, which results in several different unknown nuclear constants entering the matrix element (5) that do not factor out.
poses a challenge. The quantum numbers (spin and parity) of the parent and daughter nuclei for these isotopes differ, hence the leptons are required to have a non-zero total orbital momentum. The latter can be composed in a non-unique way, which results in several different unknown nuclear constants entering the matrix element (5) that do not factor out.
We propose a way to estimate the relic neutrino capture cross section. Our proposal relies on the experimental measurement of the spectrum of \(\beta \)-decay near the endpoint. We show, that the extraction of the relic neutrino cross section can be achieved using the experimental data (via Eq. (15)) even if the energy resolution \(\varDelta E\) of the experiment that is much larger than neutrino mass \(\varDelta E \gg m_\nu \).
Finally, to get a rough idea of the feasibility of the relic neutrino capture experiment based on  (\(Q = 96.5\,\hbox {keV}\), \(\tau = 2.77\,\hbox {years}\)) or
(\(Q = 96.5\,\hbox {keV}\), \(\tau = 2.77\,\hbox {years}\)) or  (\(Q = 76.6\,\hbox {keV}\), \(\tau = 130\,\hbox {years}\)), we estimate the corresponding cross-sections using the \(\beta \)-decay spectra computed in BetaShape [30, 37]. For non-unique transitions, this software assumes that the \(\xi \)-approximation holds and evaluates the electromagnetic corrections to the spectrum.
(\(Q = 76.6\,\hbox {keV}\), \(\tau = 130\,\hbox {years}\)), we estimate the corresponding cross-sections using the \(\beta \)-decay spectra computed in BetaShape [30, 37]. For non-unique transitions, this software assumes that the \(\xi \)-approximation holds and evaluates the electromagnetic corrections to the spectrum.

The corresponding neutrino capture rates per single atom \(\varGamma _\nu = \eta _\nu (\sigma v)_\nu \) are:

for Majorana (Dirac) neutrino, where \(\eta _\nu \) is the local cosmic number density of one neutrino species. This density could be significantly larger than the average over the universe \(\langle \eta _\nu \rangle \sim 56\,\hbox {cm}^{-3}\) due to gravitational clustering. The corresponding cross-sections are in agreement with the crude estimate (\(\delta \approx 0.5\)).
Since the emitters in the solid-state based experiments are attached to the substrate atom by atom, the single event exposure based on the estimate (17) corresponds to \(2\cdot 10^{27}\,\hbox {atoms}\cdot \hbox {year}\) for  or \(10^{26}\,\hbox {atoms}\cdot \hbox {year}\) for
or \(10^{26}\,\hbox {atoms}\cdot \hbox {year}\) for  . For comparison, the same number of events can be achieved with \(2\cdot 10^{24}\,\hbox {atoms}\cdot \hbox {year}\) for
. For comparison, the same number of events can be achieved with \(2\cdot 10^{24}\,\hbox {atoms}\cdot \hbox {year}\) for  . According to this, using
. According to this, using  as \(\beta \) emitter in a full size C\(\nu \)B experiment is promising since it can provide with both sufficient event rate and energy resolution for the relic neutrino detection.
as \(\beta \) emitter in a full size C\(\nu \)B experiment is promising since it can provide with both sufficient event rate and energy resolution for the relic neutrino detection.
The estimates of the neutrino capture cross-section for  and
and  have been performed by two other theoretical groups after the completion of this work. In [38], the computation relies on the \(\xi \)-approximation accounting for possible deviations. In [24], the nuclear properties have been evaluated theoretically for
have been performed by two other theoretical groups after the completion of this work. In [38], the computation relies on the \(\xi \)-approximation accounting for possible deviations. In [24], the nuclear properties have been evaluated theoretically for  ,
,  , and another potential candidate isotope
, and another potential candidate isotope  . The latter was first analyzed in [39] with the method, proposed in this work. The results of all studies agree with each other. However, contrary to our O(1) precision, the results in [24, 38] are potentially more precise, with the claimed uncertainties of the percent and 10% level, respectively.
. The latter was first analyzed in [39] with the method, proposed in this work. The results of all studies agree with each other. However, contrary to our O(1) precision, the results in [24, 38] are potentially more precise, with the claimed uncertainties of the percent and 10% level, respectively.
Data availability statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: In this regard, there is no data, produced specifically by the Authors of the paper, to be submitted].
Notes
Here we use the fact that absorption of antineutrino with momentum \(p_\nu \) is equivalent to emission of neutrino with momentum \(-p_\nu \).
If Coulomb attraction is taken into account, the constants in this expansion get multiplied by correction factors \(F_i(p_e)\), which do not depend on unknown nuclear physics and can be computed explicitly.
Such a linear behaviour can be seen in the spectra generated by the BetaShape software, which predicts
 ,
, 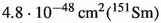 and
and 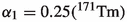 ,
,  . For further discussion see Sect. 4 and our accompanying paper.
. For further discussion see Sect. 4 and our accompanying paper.We note that the spectrum itself behaves as \(d\varGamma /dE_e \sim p^2_\nu \) and, therefore, events within a single bin are not uniformly distributed. Most of the events occur near the left side of a bin, which may introduce an additional systematic uncertainty. A possible way to avoid this problem and is to measure the integral number of events \(N(p_\nu ) = \int ^{Q}_{Q-p_\nu } \frac{dN}{dT_e} dT_e\) and consider the function \(N(p_\nu ) \cdot p_\nu ^{-3}\). This can be also fitted by a linear function and therefore used to extract \((\sigma v)_\nu \). In addition, this method allows to collect more statistics compared to the one with bins for sufficiently large \(p_\nu \).
References
S. Weinberg, Phys. Rev. 128, 1457 (1962). https://doi.org/10.1103/PhysRev.128.1457
J.A. Formaggio, A.L.C. de Gouvêa, R.G.H. Robertson, Phys. Rep. 914, 1 (2021). https://doi.org/10.1016/j.physrep.2021.02.002
C. Weinheimer, K. Zuber, Ann. Phys. 525(8–9), 565 (2013). https://doi.org/10.1002/andp.201300063
M.G. Betti et al., JCAP 07, 047 (2019). https://doi.org/10.1088/1475-7516/2019/07/047
J. Wolf, Nucl. Instrum. Methods A 623, 442 (2010). https://doi.org/10.1016/j.nima.2010.03.030
A.G. Cocco, G. Mangano, M. Messina, JCAP 06, 015 (2007). https://doi.org/10.1088/1475-7516/2007/06/015
R. Lazauskas, P. Vogel, C. Volpe, J. Phys. G 35, 025001 (2008). https://doi.org/10.1088/0954-3899/35/2/025001
M. Blennow, Phys. Rev. D 77, 113014 (2008). https://doi.org/10.1103/PhysRevD.77.113014
Y.F. Li, Z.Z. Xing, S. Luo, Phys. Lett. B 692, 261 (2010). https://doi.org/10.1016/j.physletb.2010.07.055
A. Faessler, R. Hodak, S. Kovalenko, F. Simkovic, (2011). https://doi.org/10.48550/arXiv.1102.1799
A.J. Long, C. Lunardini, E. Sabancilar, JCAP 08, 038 (2014). https://doi.org/10.1088/1475-7516/2014/08/038
A. Loureiro et al., Phys. Rev. Lett. 123(8), 081301 (2019). https://doi.org/10.1103/PhysRevLett.123.081301
Y. Cheipesh, V. Cheianov, A. Boyarsky, Phys. Rev. D 104(11), 116004 (2021). https://doi.org/10.1103/PhysRevD.104.116004
Z. Tan, V. Cheianov, (2022). https://doi.org/10.48550/arXiv.2202.07406
S. Nussinov, Z. Nussinov, Phys. Rev. D 105(4), 043502 (2022). https://doi.org/10.1103/PhysRevD.105.043502
A. Apponi et al., Phys. Rev. D 106(5), 053002 (2022). https://doi.org/10.1103/PhysRevD.106.053002
R. Catena, T. Emken, M. Matas, N.A. Spaldin, E. Urdshals, (2023). https://doi.org/10.48550/arXiv.2303.15497
K. Siegbahn, Indian J. Phys. 30, 47 (1955)
E. Konopinski, The Theory of Beta Radio Activity (Clarendon Press, Oxford, 1966)
H. Schopper, Weak Interactions and Nuclear Beta Decay (North-Holland Pub. Co., Amsterdam, 1966)
E. Caurier, G. Martínez-Pinedo, F. Nowacki, A. Poves, A.P. Zuker, Rev. Mod. Phys. 77, 427 (2005). https://doi.org/10.1103/RevModPhys.77.427
A. Arima, F. Iachello, Annu. Rev. Nucl. Part. Sci. 31, 75 (1981). https://doi.org/10.1146/annurev.ns.31.120181.000451
F. Iachello, P. Van Isacker, The Interacting Boson-Fermion Model (Cambridge Monographs on Mathematical Physics (Cambridge University Press, Cambridge, 2005). https://doi.org/10.1017/CBO9780511549724
J. Kostensalo, J.M. Kotila, J. Suhonen, Phys. Lett. B 840, 137894 (2023). https://doi.org/10.1016/j.physletb.2023.137894
M. Gell-Mann, M. Levy, Nuovo Cim. 16, 705 (1960). https://doi.org/10.1007/BF02859738
P.A. Zyla et al., PTEP 2020(8), 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
W. Bühring, Nucl. Phys. 40, 472 (1963)
H. Behrens, W. Bühring, Nucl. Phys. A 162, 111 (1971). https://doi.org/10.1016/0375-9474(71)90489-1
H. Behrens, W. Büring, Electron radial wave functions and nuclear beta decay. In: International series of monographs on physics. Clarendon Press (1982)
X. Mougeot, Phys. Rev. C 91(5), 055504 (2015). https://doi.org/10.1103/PhysRevC.91.055504. [Erratum: Phys. Rev. C 92, 059902 (2015)]
C.M. Baglin, E.A. McCutchan, Nucl. Data Sheets 151, 334 (2018). https://doi.org/10.1016/j.nds.2018.08.002
B. Singh, Nucl. Data Sheets 110, 1 (2009). https://doi.org/10.1016/j.nds.2008.11.035
T.A. Carlson, C.W. Nestor, T.C. Tucker, F.B. Malik, Phys. Rev. 169, 27 (1968). https://doi.org/10.1103/PhysRev.169.27
L. Hayen, N. Severijns, K. Bodek, D. Rozpedzik, X. Mougeot, Rev. Mod. Phys. 90(1), 015008 (2018). https://doi.org/10.1103/RevModPhys.90.015008
T.A. Carlson, C.W. Nestor, N. Wasserman, J.D. Mcdowell, Atom. Data Nucl. Data Tables 2, 63 (1970). https://doi.org/10.1016/S0092-640X(70)80005-5
J.P. Desclaux, Atom. Data Nucl. Data Tables 12, 311 (1973). https://doi.org/10.1016/0092-640X(73)90020-X
X. Mougeot, M.M. Bé, C. Bisch, Radioprotection 49(4), 269–273 (2014). https://doi.org/10.1051/radiopro/2014017
V. Brdar, R. Plestid, N. Rocco, Phys. Rev. C 105(4), 045501 (2022). https://doi.org/10.1103/PhysRevC.105.045501
N. de Groot, J. Phys. G 50(5), 055106 (2023). https://doi.org/10.1088/1361-6471/acc5fc
Acknowledgements
We would like to thank the theory group of PTOLEMY collaboration for many fruitful discussions. YC is supported by the funding from the Netherlands Organization for Scientific Research (NWO/OCW) and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme. AB is supported by the European Research Council (ERC) Advanced Grant “NuBSM” (694896). VC is grateful to the Dutch Research Council (NWO) for partial support, Grant no. 680-91-130. OM is supported by the funding from the NWO Physics Vrij Programme “The Hidden Universe of Weakly Interacting Particles” with project number 680.92.18.03 (NWO Vrije Programma), which is (partly) financed by the Dutch Research Council (NWO).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Vittorio Somà.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mikulenko, O., Cheipesh, Y., Cheianov, V. et al. Can we use heavy nuclei to detect relic neutrinos?. Eur. Phys. J. A 59, 216 (2023). https://doi.org/10.1140/epja/s10050-023-01121-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-023-01121-5




 [
[ ) and
) and  [
[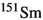 ). They do not contribute to the spectrum near the endpoint for
). They do not contribute to the spectrum near the endpoint for  ,
, 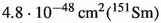 and
and 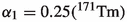 ,
,  . For further discussion see Sect.
. For further discussion see Sect.