1 Introduction

The extension of the nuclide chart in the region of heaviest elements is one of the major goals in low-energy nuclear physics. Of special interest is the synthesis of new superheavy elements (SHE) beyond oganesson (Z > 118) and the synthesis of new neutron-rich isotopes of known elements. To implement these goals, we have to abandon well established pathways.

To date, the heaviest elements were created in fusion-evaporation reactions with doubly magic projectile or target nuclei. The elements 107–112, bohrium, hassium, meitnerium, darmstadtium, roentgenium and copernicium were discovered at the GSI velocity filter SHIP (separator for heavy ion reaction products) in cold fusion reactions using targets of the doubly magic \(^{208}\)Pb and its neighbour \(^{209}\)Bi [23]. The cold fusion reaction method ended with the discovery of element 113, nihonium, at RIKEN, Japan. For the synthesis of three atoms a beam time of 553 days was applied, corresponding to a production cross-section of 22 fb [1]. This is the present limit for cold fusion.

The SHE with Z = (114–118), flerovium, moscovium, livermorium, tennessine, and oganesson were discovered at the Flerov Laboratory of JINR, Dubna. These elements were created in hot fusion reactions of doubly-magic \(^{48}\)Ca projectiles with actinide targets. The production cross-sections were of the order of picobarns. The series ends at oganesson, produced in the reaction \(^{249}\)Cf + \(^{48}\)Ca \(\rightarrow \) \(^{294}\)Og + 3n. This is the limit for SHE production with doubly magic nuclei because \(^{249}\)Cf is the heaviest target available at present. To synthesize new elements beyond oganesson, heavier beams such as \(^{50}\)Ti or \(^{54}\)Cr have to be applied. The question is, how small are the production cross-sections? Attempts to produce isotopes of elements 119 [2] and 120 [3] were made in the last decade in different labs, using various combinations of projectile and target nuclei. No events were observed. The smallest limit cross-sections were reached in the reaction \(^{50}\)Ti + \(^{249}\)Bk \(\rightarrow \) \(^{299}119^*\) (65 fb) [2] and in \(^{64}\)Ni + \(^{238}\)U \(\rightarrow \) \(^{302}120^*\) (90 fb) [3].

Also, the synthesis of new neutron-rich isotopes of already known heavy and superheavy elements requires new pathways for their production. Fusion reactions with stable projectile beams lead to evaporation residues on the neutron-deficient side of the stability valley. Fusion reactions with neutron-rich radioactive projectiles would help, but beam intensities of suitable projectiles are mostly far too small. The today most promising method for creating neutron-rich heavy nuclides is multinucleon transfer (MNT) reactions, which occur in deep inelastic binary collisions of heavy nuclei at Coulomb barrier energies. The study of MNT reactions with respect to nucleosynthesis is ongoing in many nuclear physics labs.

The cross-sections for new (super)heavy isotopes are expected to be very small. Model calculations as well as available experimental results indicate that they are reaching below picobarns. Beside an increase of beam intensities, efficient separation and detection techniques are needed which allow the detection of a single nucleus. Related activities are ongoing in laboratories worldwide.

In frame of our Manipal-GSI-Giessen collaboration we contribute to these activities with experimental investigations of MNT reactions and the design of a new-generation in-flight separator for heavy and superheavy fusion and MNT products. Our ideas are based on the long-term experience with SHIP which proved to be suitable for cold and hot fusion products as well as for MNT products. Motivated by these experiences, our design of a next-generation separator is a follow-up of the velocity filter SHIP. It is intended to meet the requirements of future experiments on SHE research.

In the first part of this article we will present the design of the new velocity filter named SuperSHIP. After, we will give a short overview on the state of the art in nucleosynthesis in MNT reactions. In the last part we will present our work on the statistical model code HIVAP which we modified such that it allows cross-section calculations of various (super)heavy fusion-evaporation residues by using a single set of paramters.

2 A next generation separator for SHE research

With the discovery of the chemical elements Z = (107–112), bohrium to copernicium, the SHIP concept has proven successful [4]. The tandem of two velocity filters [5], combined with a small magnetic deflection field at the exit provides an efficient and clean separation of fusion products with a suppression of scattered slow projectiles recoiling from the target with recoil velocity of SHE. The new SHE factories, progress in experimental techniques, the experience gathered from cold and hot fusion experiments, and the fact that the synthesis of new elements is at or even beyond the very limit of detection sensitivity present new challenges to develop a new generation of advanced separators and detection techniques. New developments and challenges may be itemized as follows:

  • SHE factories with high-current accelerators providing beam intensities of 10\(^{15}\)projectiles/s, a factor of 10–100 above the presently used beam intensities,

  • a new generation of in-flight separators with high transmission, optimized for cold and hot fusion including \(^{48}\)Ca beams,

  • direct measurement of masses with high resolution such as MRTOF or trap systems for direct mass identification, allowing to identify new elements and isotopes “still alive”.

In-flight separators used successfully for the discovery of new chemical elements include the velocity filter SHIP (GSI), and the gas filled separators DGFRS (JINR, Dubna) and GARIS (RIKEN). Both of the gas filled separators are followed by a new generation, at Dubna GFS 2 and GFS 3, and at RIKEN GARIS II and GARIS III. For the new generation the gain in transmission for \(^{48}\)Ca induced reactions is about a factor of two leading to an efficiency of about 60 % [6,7,8]. We decided to develop a follow-up of SHIP, a more compact design, also optimized for cold fusion and hot fusion with \(^{48}\)Ca. When SHIP was in the design stage, it was not at all clear which type of reaction would be successful for SHE production. Details can be found in [9]. The design limit was guided by the fusion of uranium with uranium at Coulomb barrier energy, which determined the voltage of 600 kV for the electric condenser. This required separated electric and magnetic fields. The acceptance was designed for a target-projectile combination with a projectile-to-target mass ratio of 1/3–2/3 which defined the aperture of the quadrupole lenses [5]. The new design will incorporate our experience gained from the synthesis of new elements at GSI and Dubna. It should in addition provide the option to investigate and apply MNT reactions for SHE production and make use of new developments including direct mass measurements with an ion-catcher-cooler system connected to a Penning trap or a high-resolving fast Multi-Reflection Time-Of-Flight Mass Spectrometer, MRTOF-MS.

2.1 General considerations for in-flight separators

Gas-filled separators separate the mass A with a small effect of the nuclear charge Z, according to A/Z\(^{1/3}\). They have low resolution, just sufficient to separate superheavy nuclei from the projectile beam. Transfer products or nuclei from incomplete fusion and \(\alpha \),xn channels cannot be separated. A problem is background from scattered filling gas atoms which becomes important for high beam intensities and \(\gamma \) radiation from the beam stopper.

Fig. 1
figure 1

Velocities of projectiles, fusion products, and target-like transfer products for the synthesis of element 114 depicting the dependence of velocity versus the projectile mass

Full size image
Fig. 2
figure 2

SuperSHIP with quadrupole focusing, two crossed-field Wien velocity filters in tandem, a small bending magnet at the exit, and detection systems for direct high resolution mass measurements and decay studies

Full size image

Our option is a follow-up of SHIP, a velocity filter using the reaction kinematics of complete fusion to separate the SHE from projectiles and other background. Figure 1 displays the velocities of projectiles, fusion products, target-like transfers, and fission products for the synthesis of element 114 plotted versus the projectile mass. SHE synthesis with actinide targets uses \(^{48}\)Ca projectiles. A cold-fusion projectile for this hypothetical case would be \(^{76}\)Ge. We see these projectiles are well separated from the SHE, suggesting that a velocity filter of moderate resolution separates the super-heavy nuclei from the projectile beam. A velocity resolution of about 30–50 is already sufficient. The momentum transfer of an \(\alpha \) particle emitted from the compound nucleus is already strong enough to drive the evaporation residue out of the accepted velocity window, such providing a clean separation of SHE from all other reaction products. The figure also shows that target-like transfer products can be selected if we set the velocity window to about twice the velocity of SHE. In summary:

  • Kinematic separation allows to define the type of reaction e.g. fusion or transfer,

  • The prediction of transmission and separation properties is more simple for vacuum separators as atomic interactions are not involved in separation and beam transport.

  • The recoils pass a stripper foil, their ionic charge state is close to 20, so we have a small beam rigidity and low magnetic field strength.

  • The disadvantage of a velocity filter is that in addition to the dipole magnets an electric deflection field is required.

In conclusion, the next generation velocity filter is optimized for cold fusion and for hot fusion with beams of \(^{48}\)Ca or heavier, and for transfer reactions [10,11,12]. We call it SuperSHIP as we discussed superconducting large-aperture quadrupole triplets. The voltage for the deflection condenser is maximum ±150 kV or 300 kV across the gap. This allows to place the electrostatic deflector inside the dipole magnet. We end up with a classical Wien Filter. This allows a more compact design as compared to SHIP. Similar to SHIP, the filter has two filter stages and a small dipole at the exit for good background suppression.

High transmission needs large-aperture quadrupole triplets. Large acceptance angles for beams with large velocity- and ionic charge spread create large chromatic aberrations. Consequently, the velocity resolution is moderate. Here we profit from the fact that the magnetic beam rigidity of the recoils and the projectiles is about the same. Both beams will be focused. The projectile beam with small emittance is well focused and well separated from the recoils, provided it has good quality and no energy tails or beam halos or scattered particles from bad spots of the target. In the velocity filter the beam is separated from the SHE recoils. That is why for a good background suppression excellent beam quality and targets without spots or folds are needed and why a moderate resolving power is sufficient. Comparatively small filters with a length of only 100 cm will be ideal as has been proven by SHIP.

2.2 SuperSHIP

Figure 2 shows SuperSHIP, two crossed-field velocity filters in tandem with a small bending magnet at its exit. A magnetic swinger in front of the target allows the investigation of transfer reactions. Large-aperture magnetic quadrupole triplets focus the beam onto the velocity slit and detector system. Two Wien Filters purify the SHE beams, and a small magnet at the exit deflects the beam to suppress scattered projectiles having SHE velocity, and in addition moves the detector system out of the zero degree direction, so it cannot see the target. This is important for \(\gamma \) spectroscopy, and in addition, to avoid neutron irradiation of the detector. The main parameters are listed in Table 2. Because of the low beam rigidity of less than 1 Tm, we do not need superconducting quadrupoles, but nevertheless decided to keep the name SuperSHIP (Table 1).

Table 1 Key parameters of Super SHIP, for details see reference [13]
Full size table

The transmission of SuperSHIP [13] compared to experimental and calculated [14] SHIP data are displayed in Fig. 3. We see a significant improvement of the transmission. For our benchmark reaction, \(^{48}\)Ca + \(^{208}\)Pb \(\rightarrow \) \(^{254}\)No + 2n, it is increased by a factor of almost two from 32 to 58%. The properties of SuperSHIP [13] were calculated with LISE++.

Fig. 3
figure 3

Experimental and calculated [14] transmissions of SHIP compared to Super SHIP plotted versus the ratio of projectile mass M\(_p\) to target mass M\(_t\) [13]

Full size image
Fig. 4
figure 4

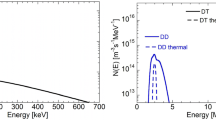
Left panel: calculated energy spread of a \(^{24}\)Ne rare isotope beam produced in projectile fragmentation and decelerated to an average energy of 6 MeV/u by degraders. Right panel: target-ioncatcher-MRTOF-MS system for SHE research at the SuperFRS low-energy branch at GSI. A stack of targets is used inside the ioncatcher. The energy range covered in the target stack to contribute to fusion is marked by dashed vertical lines

Full size image

2.3 Detection systems

SuperSHIP should be equipped with a multi-functional implantation detector for decay studies and an ion catcher system, see Fig. 2. An example of such a detector system is the GABRIELA \(\alpha \)-\(\beta \)-\(\gamma \) detector at SHELS, JINR Dubna [15]. An ion catcher connected to a high-resolution Multi-Reflection Time-of-Flight Mass Spectrometers (MRTOF - MS) or Penning Trap system allows direct A identification or mass measurements of highest precision. An MRTOF-MS is operated successfully at FRS [16] with a resolution of 500,000 [17]. Isobaric identification and separation of \(^{221}\)Ac was achieved. In addition, a special detector system allowed to measure the \(\alpha \)-decay of this nuclide. With this method in contrast to the presently used decay spectroscopy, SHE are directly identified “still alive”. This method works best far-off the minimum of the mass isobar curve. At RIKEN an MRTOF-MS system has been coupled to GARIS II. With this system the direct identification of astatine, polonium and bismuth isotopes has been achieved by isobaric mass analysis at a mass resolving power of more than 100,000 by measuring about 10 atomic nuclei [18].

At GSI, we investigate also the possibilities to apply rare-isotope beams produced in projectile fragmentation for SHE experiments. Fusion reactions with light neutron-rich RIBs such as \(^{22}\)O on \(^{248}\)Cm appear feasible because cross-sections are predicted on the order of (10–100) nb by some models. With predicted beam intensities of 10\(^{6}\) particles/s or more for light radioactive ion beams (RIBs) at SuperFRS [19] seizable count rates of reaction products can be expected.

Certainly, RIB facilities using the ISOL technique and post-accelerated beams, like e.g. FRIB or SPIRALII offer ideal conditions, however, our aim is to investigate, whether such experiments can be carried out with energy degraded RIBs at the low-energy branch at FRS and SuperFRS [20,21,22]. The simplest method to decelerate relativistic RIBs to Coulomb barrier einergies is with degraders which, however, lead to a relatively large energy spread of the decelerated beam (Fig. 4, left). To use the beam with large energy spread efficiently, a target stack can be used [20, 21, 23]. The reaction products recoiling from the targets are thermalized in a gas cell, extracted, and separated by an RFQ separation system, and finally transported to an MRTOF-MS where the isotopes are identified. Such scheme (Fig. 4, right) allows the identification of an atomic nucleus without knowing how it has been produced. It measures fusion and transfer products at the same time and can be combined with detector systems for alpha, beta and gamma spectroscopy.

3 Multinucleon transfer reactions as a possible pathway to new (super)heavy isotopes

As mentioned above, MNT reactions are currently studied as a possible pathway to still unknown heavy exotic nuclei. Here, we will give a short overview on the state-of-the-art in model calculations and experimental results, while for details we refer to our review article titled Nucleosynthesis in Multinucleon Transfer Reactions [24] which is also part of the collection Heavy and Super-Heavy Nuclei and Elements: Productions and Properties.

Multinucleon transfer reactions can lead to reaction products with neutron and proton numbers far from the entrance channel nuclei. After the discovery of MNT reactions in the late 1960s [25], many new neutron-rich isotopes up to \(_{89}^{232,234}\)Ac were discovered with this reaction type in the period from 1970 to 1995 [25,26,27,28,29,30,31,32,33,34]. Today, MNT reactions have become a topical subject again with regard to use them as a pathway to new isotopes in the region of heavy elements, where the following areas on the nuclide chart are in the focus of interest: (i) neutron-rich superheavy nuclei which are not reachable in fusion reactions, (ii) neutron-rich nuclei below Pb, located along the N = 126 shell and (iii) neutron-deficient transuranium isotopes. In the following we will summarize the present achievements and perspectives in that regions.

Fig. 5
figure 5

Langevin model calculations of MNT cross-sections for actinide and superheavy nuclei created in collisions of \(^{238}\)U + \(^{238}\)U (solid red line), \(^{238}\)U + \(^{248}\)Cm (dashed blue line) and \(^{238}\)U + \(^{254}\)Es (black solid line) [35]. The beam energy is (10–15)% above the respective Coulomb barrier. Experimental data for the U + U reactions (triangles) are taken from Ref. [36], and for U + Cm (circles) from Ref. [37]. The heaviest known isotopes of each given element are indicated by vertical dotted lines. The thick dashed curves in the lower part of the figure show primary (i.e. before neutron evaporation) isotopic distributions of Rf and Db from U + Es reactions

Full size image
Fig. 6
figure 6

Presently known MNT products in the uranium and transuranium region, observed in collisions of diverse projectile nuclei with U, Cm and Es targets. The nuclei were observed in radiochemical experiments and in experiments at the velocity filter SHIP. The five new neutron-deficient MNT products which were discovered at SHIP, are marked by dots

Full size image
Fig. 7
figure 7

Langevin model calculations of MNT cross-sections for isotopes of elements Z = (70–88) created in \(^{136}\)Xe + \(^{208}\)Pb collisions at E\(_{cm}\) = 450 MeV [38]. Available experimental cross-sections are represented by symbols

Full size image
Fig. 8
figure 8

Presently known MNT products in the region below Pb which were observed in different experiments. Gray squares represent MNT products from reactions of \(^{136}\)Xe beams on \(^{208}\)Pb and \(^{198}\)Pt targets [39, 40]. Small black squares represent MNT products from reactions of \(^{64}\)Ni + \(^{207,208}\)Pb [41, 42]. The limits of the chart on the neutron-rich side correspond to the limits of the current Karlsruhe chart of nuclides of 2022

Full size image

3.1 Neutron-rich superheavy nuclei

Neutron-rich isotopes of superheavy elements are not reachable in fusion reactions with stable projectile nuclei on actinide targets, because of the bending of the stability line toward the neutron axis. The application of neutron-rich radioactive projectile beams would help to overcome this bottleneck, but intensities of appropriate exotic beams are by far too small to synthesize isotopes of the heaviest elements. MNT reactions in heavy systems provide principally a sufficient number of neutrons to access neutron-rich SHE. Experimental [37, 43,44,45,46,47,48] and theoretical (see e.g. [35, 49] and references therein) MNT studies in the SHE region were to date performed with a large variety of collision systems, using heavy actinide targets and beams up to uranium.

As an example, Fig. 5 shows Langevin model calculations of MNT cross-sections from collisions of U beams with U, Cf and Es targets [35]. Accordingly, cross-sections drop below 1 pb for new isotopes of elements with Z > 106. Experimental MNT studies in the transuranium region were performed in early radiochemical experiments [37, 43,44,45,46] and in more recent experiments at the velocity filter SHIP of GSI [47, 48, 50]. For the latter, isotope identification was performed by \(\alpha \) decays.

The collection of up to date observed MNT products of elements from uranium to lawrencium is shown in Fig. 6. A total of 25 isotopes is from elements Z = (100–103). The most heavy and neutron-rich MNT products are to date \(^{260}\)Md, observed in radiochemical experiments, and \(^{260}\)No observed at SHIP. The so far smallest MNT cross-section of 0.5 nb we measured at SHIP for the isotope (\(^{260}\)No).

For future experiments, a decrease of the experimental sensitivity limit to the 1 pb level appears realistic, using a combination of increased irradiation time and increased experimental efficiency. Assuming a sensitivity of 1 pb, we could expect about 25 new MNT products of elements Z = (100–106) with neutron numbers N\(\le \)163. They include also the so far not directly produced endpoint nuclei of known hot fusion decay chains. However, neutron-rich MNT products around Z = 110, or even on the predicted island of stability at N = 184, Z = 114 or 120 appear to be far from feasibility.

3.2 Neutron-rich nuclei along N = 126

The largest still empty area on the nuclide chart is the region of neutron-rich nuclei below Pb (Z < 82). It comprises most of the isotopes which are expected to participate in the astrophysical r-process path. To date, fragmentation and fission reactions are used to produce nuclei in this area. Since uranium is the heaviest beam or target nucleus for these reactions, no fragments with more than 146 neutrons can arise. Model calculations suggest MNT reactions in heavy systems as an alternative to fragmentation [38, 51]. Figure 7 shows Langevin model calculations for MNT products with Z = (70–88) created in collisions of \(^{136}\)Xe + \(^{208}\)Pb [38]. Due to the large number of neutrons in such systems, MNT cross-sections overtake fragmentation cross-sections toward the neutron-rich side. This trend is also indicated by experimental data. It was first noticed by Watanabe et al. in collisions of \(^{136}\)Xe + \(^{198}\)Pt at the GANIL VAMOS spectrometer [52]. In that experiment, they measured the isotopic distributions of Xe-like MNT products and deduced from them the distributions of target-like nuclei. The data revealed that MNT cross-sections indeed overtake fragmentation cross-sections with decreasing proton number and increasing neutron number of the MNT products. The same trend is also indicated in \(^{64}\)Ni + \(^{207}\)Pb collisions at the velocity filter SHIP, where the target-like nuclei were detected directly [42].

Figure 8 shows all presently known MNT products in the region Z = (65–82) which were observed in different experiments [39, 41, 42]. The isotope identification was performed in all experiments by gamma spectroscopy, with a sensitivity limit between (1–10) \(\mu \)b. Many of the observed MNT products are on the neutron-rich side of the stability valley. But still, the present boarder of the nuclide chart is determined by isotopes from fragmentation reactions.

According to model calculations, a microbarn sensitivity principally would allow one to reach new neutron-rich isotopes in MNT reactions. However, the bottleneck in that region is rather the identification of the isotopes. As mentioned before, \(\beta \) emitters are presently identified via their gamma decays, which means serious restrictions. The method is only applicable if excited states in the daughter nucleus are populated with sufficient branching. Also, gamma transitions in the daughter nucleus must be already well known in order to attribute them correctly. Therefore, a universal and sensitive technique for isotope identification is needed, which is independent on the decay properties of the nuclei.

3.3 Neutron-deficient transuranium isotopes

Our experiments with \(^{238}\)U and \(^{248}\)Cm targets at SHIP revealed a large number of neutron-deficient MNT products in the uranium and transuranium region. Among them were five isotopes, which are so far the heaviest new isotopes produced in MNT reactions [47]. Normally, nuclei in that region are synthesised by fusion reactions. But a comparison of MNT and fusion cross-sections revealed that they become quite similar if one moves toward the neutron-deficient side [53]. Therefore, in the very neutron-deficient transuranium region, MNT might indeed become an attractive option to synthesize new isotopes. Here one can profit from the broad excitation functions of MNT products which leads to a wide-band population of many different nuclides with sizeable yields in the same experiment, while fusion reactions are only selective on very few specific isotopes.

Fig. 9
figure 9

Comparison of production cross-sections calculated with HIVAP [54] and the parameter set described in Ref. [13] (solid lines) with experimental data for the production of flerovium, livermorium, tennessine and oganesson isotopes in irradiations of \(^{244}\)Pu, \(^{245}\)Cm, \(^{248}\)Cm, \(^{249}\)Bk and \(^{249}\)Cf targets with \(^{48}\)Ca. The experimental cross-sections for the 3n and 4n reaction channels are represented by squares and circles, respectively. B\(_{Int}\) is the Bass interaction barrier. a, b The experimental data for \(^{244}\)Pu targets are from Oganessian [55] (solid symbols) and Gates [55] (open symbols), c, d for \(^{245}\)Cm targets from Oganessian [56] (solid symbols), e, f for \(^{248}\)Cm targets from Oganessian [57] (solid symbols) and Hofmann [58] (open symbols), g, h for \(^{249}\)Bk targets from Oganessian [59] (solid symbols) and Khuyagbaatar [60], (open symbols), i, j for \(^{249}\)Cf targets from Oganessian [56, 61] (solid symbol)

Full size image
Fig. 10
figure 10

Comparison of HIVAP [54] calculations using the set of parameters presented in [13] with the experimental data. Solid, dotted and dashed curves represent calculations, triangles, circles and squares represent measured data for 4n, 5n and 6n channels, respectively. The available experimental data from the following reactions are compared; a \(^{18}\)O+\(^{242}\)Pu [62] b \(^{15}\)N+\(^{249}\)Bk [63] c \(^{26}\)Mg+\(^{238}\)U [64] d \(^{22}\)Ne+\(^{244}\)Pu [65] e \(^{18}\)O+\(^{249}\)Bk [66] (solid symbols) [67] (open symbols) f \(^{22}\)Ne+\(^{248}\)Cm [68] (solid symbols) [69] (half filled symbols) [70] (open symbols) g \(^{22}\)Na+\(^{248}\)Cm [71] f \(^{22}\)Ne+\(^{249}\)Bk [72]

Full size image

4 HIVAP calculations

Model calculations of reaction product cross-sections are very important in the region of (super)heavy elements. Due to the tiny cross-sections they give important information about the expected yields and the feasibility of an experiment. There are different theoretical models to describe fusion-evaporation and MNT reactions in (super)heavy systems. Examples of some widespread models are the dinuclear system (DNS) model and the Langevin model. But also the statistical model code HIVAP [73] is used to calculate fusion-evaporation cross-sections in reactions of massive nuclear systems [54, 73]. The advantage of HIVAP is its widespread availability and even if it does not take into account the fine details like the more sophisticated reaction models, it delivers results with acceptable reliability.

Our aim was to modify the HIVAP code in such a way that only few paramters are required to describe the cross-sections of superheavy evaporation residues created in diverse reaction systems. The parameter set which describes the deexcitation process in HIVAP was determined such that it reproduces experimental excitation functions for superheavy isotopes created in reactions of \(^{48}\)Ca beams on actinide targets.

We intend to use the such modified code for the following applications:

  • the prediction of production cross sections for new isotopes of SHE produced in hot fusion

  • the prediction of production cross sections for SHE beyond oganesson

  • and, in view of the new generation rare-isotope facilities, the possibilities to create neutron-rich nuclides with exotic nuclear beams.

Table 2 Comparison of evaporation-residue cross-sections calculated with the HIVAP code, the dinuclear system model [74, 75] and the Langevin model [76,77,78] for various reactions leading to the synthesis of superheavy nuclei
Full size table

Figure 9 shows HIVAP calculations with our obtained parameter set for superheavy isotopes with Z = 114–118 created in reactions of \(^{48}\)Ca with actinide nuclei. The cross-sections for 3n evaporation channels are within less than one order of magnitude in agreement with experimental cross-sections in most of the cases. The calculated 4n evaporation residue cross-sections are by trend somewhat larger compared to their corresponding experimental values. The maximum discrepancies are less than a factor of ten. This level of agreement is quite fair, given that SHE synthesis is a complex process and that the HIVAP code cannot adequately take into account all the finer details. Moreover, experimental data have large error bars and also suffer from systematic errors, as seen e.g. in the figure for \(^{289}\)Fl. The cross-sections at higher excitation energies are overpredicted. Possibly the fission barriers used in the HIVAP code, adopted from ref. [79], are too high.

Excitation functions for nobelium, rutherfordium, dubnium, seaborgium and bohrium isotopes, produced with projectiles lighter than \(^{48}\)Ca on actinide targets \(^{238}\)U, \(^{242}\)Pu, \(^{244}\)Pu, \(^{248}\)Cm and \(^{249}\)Bk are shown in Fig. 10. The measured cross-sections for these reactions are in the range from 100 nb to 100 pb. Also these HIVAP calculations reproduce experimental cross-sections fairly well within maximum deviations of less than one order of magnitude.

In Table 2 we compare HIVAP cross-sections for several reaction systems and evaporation-residues with results of the DNS [74, 75] and Langevin model [76,77,78] which are available for the same systems. The cross-section values prodced by the three models compare well for most of the shown fusion products. A maximum deviation of less than a factor of five is observed for nine nuclei, and less than a factor of 10 for two nuclei presented in Table 2. A deviation of more than 2 orders of magnitude is observed only for the reaction \(^{48}\)Ca(\(^{257}\)Fm,3n)\(^{302}\)120 between the HIVAP estimate and the DNS model. More detailed information about the calculations and results can be found in [73].

5 Summary

In frame of our collaboration between the University of Manipal, GSI Helmholtz Centre, Darmstadt, and Justus-Liebig-University Giessen, we investigate new experimental pathways to the production, separation and identification of new heavy and superheavy nuclei. In the focus of our studies is the design of a next-generation velocity filter, named SuperSHIP. It is a follow-up version of the present GSI velocity filter SHIP. The SuperSHIP design is more compact, is aiming at higher transmission and better background suppression. It is applicable for (super)heavy fusion-evaporation resiudes and also for multinucleon transfer products. A magnetic swinger in front of the target allows the investigation of transfer products with their broad angular distributions. A multipurpose detection system is foreseen for isotope identification. The “conventional” method of (super)heavy isotope identification by alpha, beta and gamma decay tagging can be supplemented by high-precision mass measurements using a Multi-Reflection Time-Of-Flight Mass Spectrometer (MRTOF-MS).

Apart from these technical developments we are investigating multinucleon transfer reactions as a potential pathway to produce still unknown (super)heavy nuclei, mainly on the neutron-rich side of the nuclide chart (see also our contribution Nucleosynthesis in multinucleon transfer reactions). There we apply the method to separate very heavy target-like transfer products with a velocity filter. This technique allowed us to identify transfer products up to \(^{260}\)No and to reach the so far smallest experimental cross-section limit for transfer products of 0.5 nanobarns.