Abstract
Decays \(J/\psi \rightarrow B{\bar{B}}\) into octet baryon-antibaryons pairs are studied within the QCD factorisation framework. The next-to-leading power correction to the leading-order decay amplitude is calculated for the first time. The phenomenological analysis also includes the interference with the electromagnetic decay \(J/\psi \rightarrow \gamma ^*\rightarrow B{\bar{B}}\). The branching fractions and the angular coefficients \(\alpha _B\) are obtained with an accuracy of about \(20\%\). The obtained results allow us to conclude that the calculated amplitudes provide a dominant contribution and therefore QCD factorisation provides a suitable basis for understanding of these decays.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A systematic description of exclusive charmonia decays can be performed using QCD factorisation framework, see e.g. Refs. [1, 2] and references therein. Within this approach one constructs the expansion of an amplitude in inverse powers of \(1/m_c\) combining non-relativistic QCD and hard-collinear effective field theory. As a rule, most of these calculations are performed with leading power accuracy. In many cases this gives a reliable description, but in many cases this approximation is insufficient even for a good qualitative description of the data. Potentially such discrepancies can be associated with various large corrections and with a complicated underlying QCD dynamics. Therefore, a description of exclusive charmonia decays still includes many open questions, see, for example, reviews in Refs. [3, 4].
Decays of S-wave charmonia into proton-antiproton pairs have been discussed already long time ago within the QCD factorisation framework in Refs. [1, 5,6,7]. It was found that with the appropriate models of baryon matrix elements one can obtain a reasonable description of the branching ratio for \(J/\psi \rightarrow p {\bar{p}}\). This observation was further used in order to constrain the nucleon DAs in Refs. [8, 9]
In recent years, the BESII and BESIII collaborations have provided a lot of new and accurate data in Refs. [10,11,12,13,14,15]. The description of these data is a non-trivial task, since requires calculations beyond the leading-power approximation, which are often are very problematic. In addition, the phenomenological consideration suggested in Refs. [16, 17] indicates potential problems for the description based on QCD factorisation.
The new data provide not only the values of the cross sections, but also interesting information about the angular behaviour of the \(e^+e^-\rightarrow J/\psi \rightarrow B{\bar{B}}\) cross section. This behaviour is sensitive to the amplitude, which is power suppressed within the systematic QCD description. The contribution of this amplitude to the decay width is suppressed by additional factor \(1/m_c^2\) and therefore is expected to be a small correction. On the other hand, new data show that the effect of this amplitude on the description of the angular behaviour is very significant.
The various attempts to describe the angular coefficient \(\alpha _B\) have been considered in Refs. [18,19,20] using different phenomenological models and crude approximations. For the first time the power suppressed amplitude was calculated in the QCD factorisation framework in Refs. [21, 22]. The qualitative phenomenological analysis carried out in these works indicates that the corresponding description works sufficiently well. However, in order to better understand the role of the power corrections some theoretical uncertainties need to be clarified.
In this paper we continue the investigation of the decays into baryon-antibaryon pairs within the QCD factorisation framework. Two additional effects are included into phenomenological consideration, which was ignored in Ref. [22]. First, we calculate the next-to-leading power correction \(\sim \Lambda ^2/m^2_c\) to the dominant leading-power amplitude, where \(\Lambda \) is a typical hadronic scale. This correction is interesting because the mass of charm quark is not very large, and such contribution could provide rather large numerical effect. In addition, this correction is described by the same non-perturbative parameters as the subleading amplitude, which gives them better phenomenological constraints.
This power correction is closely associated with the higher Fock states of the baryon wave function and do not involve relativistic corrections with respect to the small heavy quark velocity in NRQCD. The decay mechanism associated with annihilation into the three hard gluons suggests that such contributions can also be described within the collinear factorisation framework that gives us an opportunity of a more detailed understanding of the systematic expansion in the inverse mass \(1/m_c\). The higher twist baryon light-cone distribution amplitudes (DAs), associated with the non-perturbative collinear matrix elements, have already been investigated in Refs. [23,24,25,26,27,28,29,30]. These results allows one to reduce theoretical uncertainties associated with the non-perturbative QCD input.
In this work we also discuss the effect that occurs due to the contribution of the electromagnetic amplitude \(J/\psi \rightarrow \gamma ^*\rightarrow B{\bar{B}}\). The given amplitude is sensitive to the baryon time-like electromagnetic form factors. For a given energy scale these form factors can not be computed within the QCD framework because of relatively large effect from the soft-overlap rescattering (or Feynman) mechanism. Time-like baryonic FFs are also poorly studied experimentally. Different cross sections for the \(e^+e^-\rightarrow B{\bar{B}}\) channels have been measured by BESIII recent years, and the so-called effective FFs are obtained from data fitting, see Refs. [31,32,33,34,35,36,37,38]. We use these results in order to estimate the numerical influence of the electromagnetic admixture in the angular distribution \(\alpha _B\).
Our paper is organised as follows. In Sect. 2 we discuss the higher twist baryon DAs and describe the models, which are used in our calculations. The calculation and the analytical expressions for the hard kernels and for the total amplitudes are discussed in the Sect. 3. The phenomenological analysis is presented in Sect. 4. In Sect. 5 we summarise our findings. In Appendix we provide additional useful details and a more detailed discussion of some technical issues.
2 Baryon light-cone distribution amplitudes
2.1 The basic set of the twist-5 DAs and their properties
In this section we describe the properties of twist-5 DAs and define the twist-5 auxiliary matrix elements, which are used in our calculation of the power corrections. We consider contributions with only three quark operators, which greatly simplifies the calculations. The total power correction is given by the sum of various contributions with the different combinations of DAs. The leading-power (lp) contribution to amplitude \(A_{1}\) only includes the integral with the twist-3 DAs \(\varphi _{3}\), schematically: \(A_{1}^{(\text {lp})}\sim \varphi _{3}*H*\varphi _{3}\), where the asterisk is used as a short notation for the convolution integral with respect to quark momentum fractions. The next-to-leading power (nlp) correction is more complicated, it depends on twist-4 \(\varphi _{4}\) and twist-5 \(\varphi _{5}\) DAs and can be represented as

where the last term can be associated with the kinematical contribution. The various higher twist DAs and their properties have been discussed in Refs. [25, 27,28,29] and we use these results in the present work.
Let us define the light-cone matrix elements, which define the light-cone DAs. The analysis of the twist-4 auxiliary DAs are given in Refs. [21, 22, 27]. Therefore, here we will focus only on the discussion of the twist-5 matrix elements.
We use the same notations as in Refs. [21, 22]. The light-like vectors \(n,\bar{n}\) ( \(n^{2}=\bar{n}^{2}=0\), \((n\bar{n})=2\) ) define the longitudinal and transverse components of a Lorentz vector \(V^{\mu }\)
In the following we also assume that the baryon momentum k is directed along z-axis and can be expanded as
For the baryon spinor N(k, s) we define the large and small components \(N_{\bar{n} }\) and \(N_{{n}}\), respectively:
The similar relations are also used for the antibaryon spinors.
The relevant three-quark light-cone operators are constructed from the QCD quark fields \(q=\{{u,d,s\}}\) and from the light-cone the Wilson lines
The basic operator can be written as
where we use the short notation \(q(x_{-})\equiv q(x_{-}n/2)\). Below, for brevity, we also simplify the notation of the Dirac indices setting \(\{\alpha _{1},\alpha _{2},\alpha _{3}\}\equiv \{1,2,3\}\) and we also will not show the colour structure. Following to Ref. [28] we assume the following flavour content of the operators \(\langle 0|q_{\alpha _{1}} q_{\alpha _{2}}q_{\alpha _{3}}|B\rangle \equiv \langle 0|q_{1}q_{2}q_{3}|B\rangle \):
For simplicity, this will not be shown explicitly.
Let us write the light-cone matrix element for the baryon state B as
where the subscript “tw3” indicate that we only count in this term the contributions of twist-3 and so on. The leading twist-3 contribution read
The twist-4 contribution is defined as
The twist-5 contribution read
where we always assume that \(\sigma _{\bar{n}n}=\sigma _{\alpha \beta }\bar{n}^{\alpha }n^{\beta }\) . The symbol “FT” denotes the Fourier transformation with respect to the quark momentum fractions
with the measure \(Du_{i}=du_{1}du_{2}du_{3}\delta (1-u_{1}-u_{2}-u_{3})\), the quark momenta in (14) are defined as
The DAs defined in Eqs. (11)–(13) are symmetric or antisymmetric with respect to interchange \(u_{1}\leftrightarrow u_{2}\)
with
The DAs in Eqs. (11)–(13) can be rewritten in terms of the basis light-cone DAs as [28, 29] ( below we use short notation \((x_i)\equiv (x_{123})\equiv (x_{1},x_{2},x_{3})\))
where
The coefficients \(c_{B}^{\pm }\) are chosen in such a way that these DAs satisfy the simple relations in the SU(3)-flavour symmetry limit, see e.g. Ref. [28].
For the nucleon state, the basic set of DAs can be further simplified by the isospin relationships, namely, it is sufficient to determine
The twist-4 and twist-5 DAs can be decomposed into components corresponding to the contributions of the light-cone operators of geometrical twist-3, twist-4 and twist-5. Let us write such decompositions in the following form
Here the superscript (i) indicates that the corresponding function is completely defined in terms of the moments of the light-cone operators of geometrical twist-i. The functions with the bar denote the genuine twist-4/5 contributions. The moments of genuine twist-5 DAs are not known. In the present work we assume that the corresponding matrix elements are sufficiently small and therefore be neglected that yields
The normalisation couplings \(f_{B},\ f_{\bot }^{B},\ \lambda _{1,2}^{B}\) and \(\lambda _{\bot }^{\Lambda }\) have dimension of GeV\(^{2}\) and their values will be discussed later.
The conformal expansion and evolution of the moments for different three-quark DAs was discussed in Refs. [24,25,26]. The explicit analytical expressions for the different terms in rhs in Eqs. (42)–(46) can be found in Refs. [25, 28, 29]. For convenience, in Appendix A we provide the explicit expressions for the models of basic DAs, which are used in present work.
2.2 Auxiliary DAs and their properties
Let us also consider the auxiliary set of the matrix elements, which is more convenient for the actual calculation of the hard kernels. More details about this calculation will be given in the next section. Here we only discuss the formal definition of the auxiliary matrix elements and their relations with the basic set of DAs.
The calculation of the decay amplitudes implies that the QCD fields can be splitted into sum of hard and collinear fields. The letter describe the non-perturbative overlap with the baryon-antibaryon state. Therefore performing a matching onto collinear operators one implies the effective field theory constructed from the hard (\(p_{h}\sim m_{Q}\), \(x\sim 1/m_{Q}\)) and collinear fields. Such theory provides a definite power counting, which is used for the ranging of the operators. The power counting of the collinear fields is associated with their momentum, if we assume the collinear sector associated with the momentum k in Eq. (3) then (\(\lambda ^{2}\sim \Lambda /m_{Q}\))
Performing the multipole expansions of collinear fields one also obtains derivatives of the collinear fields, which counts as
Remind, that we do not consider the contributions with the quark-gluon operators, therefore terms like \(A_{\bot }, A_{-}\) , \(\partial _{\bot }A_{+} \) and \((\bar{n}\partial )A_{+}\) will be excluded from our consideration.
The auxiliary DAs can be defined in terms of the matrix elements of 3-quark twist-5 operators with the transverse derivatives. These operators are defined using the gauge invariant collinear fields, which have a definite scaling behaviour within the effective field theory framework
Obviously
The most general 3-quark twist-3 operator is
where for simplicity we do not show the colour and flavour structure.
The 3-quark twist-4 operators include one transverse derivative
where the derivative is applied inside the brackets only. Notice that we do not need to write the covariant derivative because the field \(\chi (x_{-})\) is gauge invariant. The matrix elements of the twist-4 operators in (55) are considered in Ref. [21]. The results read
where the color and the flavour structure of the operators are the same as described before. The DAs in the rhs of these equations can be expressed in terms of DAs \(\{V_{i},A_{i},T_{i},S_{i},P_{i}\}^{B}\) using the Lorentz symmetry and QCD equations of motion. This givesFootnote 1 [21, 22, 27] .
where the quark masses \(m_{i}\) correspond to quarks \(q_{1}q_{2}q_{3}\) in the matrix elements in Eqs. (7)–(9), respectively. The relations (63) and (64) are obtained in [27] for the first time and without quark mass corrections, but their derivation is not given in this paper. In Ref. [21] these relations were rederived and the new relations for twist-4 DAs (65)–(68) are also derived. In Ref. [22] the quark mass corrections to (63)–(68) were calculated.
The additional relation is derived in Appendix B
Combining Eq. (69) with Eqs. (65), (66) and definitions in Eqs. (22) and (24) one finds for \(\Upsilon _{4}^{B}\) the following new relation
Therefore the DA \(\Upsilon _{4}^{B}\) is not an independent function in the 3-quark approximation.
The 3-quark twist-5 operators include two transverse derivatives
The longitudinal derivatives \((\bar{n}\partial )\chi \) can be excluded with the help of QCD equation of motion
Therefore the basis set of the 3-quarks operators can be defined as
The operators with \(\left[ \partial _{\bot }\chi _{3}\right] \) can be excluded because
where it is used that the matrix element from the operator with the total transverse derivative vanishes because the baryon momenta have longitudinal components only. The matrix elements of the three operators in Eq. (73) define the auxiliary set of the twist-5 DAs. It is convenient to write their definitions for the operators with projected Dirac indices \(\{12\}\). We introduce the following set of the matrix elements
with
where we use the short notaion for the following combination
This set of DAs can be splitted into two groups: chiral even and chiral-odd DAs defined in Eqs. (75)–(80) and Eqs. (81)–(83), respectively. These groups can be considered independently.
In order to establish relations of the auxiliary DAs with the basic ones, one needs to relate the operator \({\mathcal {O}}_{123}\) defined in Eq. (6) with the operators in Eq. (73). This can be done with the help of the QCD equations of motion. Let us write the quark field as a sum
where
The small field \(\eta (x_{-})\) can be written as, see e.g. Ref. [45]
where dots denote the terms with insertions of the transverse gluon components \(\left[ W^{\dag }(x_{-})i{\not {D} }_{\bot }W(x_{-})\right] \), which give the quark-gluon operators and therefore can be omitted. Hence
It is clear that each field \(\eta \) gives the one transverse drivative, therefore the twist-5 operators in the expansion of \({\mathcal {O}}_{123}\) in Eq. (6) have two fields \(\eta \)
The main idea is the following: we rewrite the terms in Eq. (90) using Eq. (89) in terms of the basis operators (73) and compute the matrix element using Eqs. (75)–(28). On the other hand, using the definitions (87) and one can express the \(\left[ {\mathcal {O}}_{123}\right] _{\text {tw5}}\) in terms of different projections of the three quark operator defined in Eq. (6) and use Eq. (10) in order to get the matrix element. Comparing the two results one finds the relations, which allows one to establish a connection of the auxiliary DAs with the basis ones. It is convenient to perform such calculations for the chiral-even and chiral-odd operators separately. Let us first consider the chiral-even sector, which includes 8 DAs:
Let us consider as example the following operator
where the Dirac indices \(\{12\}\) are contracted with the matrix  . Using Eq. (89) one finds
. Using Eq. (89) one finds
where we use the short notation
The matrix element of this operator can be computed with the help of Eqs. (77) and (80). One finds
where the factor \(1/(x_{1}x_{2})\) appears due to the inverse derivatives \(\left( in\partial \right) ^{-1}\) acting on the first and second fields. Remind, that the inverse derivatives \(\left( in\partial \right) ^{-1}\) must be undestood as nonlocal operator
On the other hand, using Eqs. (87) one finds
Computing the matrix element of this operator with the help of Eq. (13) one gets
Comparing Eqs. (97) and (101) one obtains
where, for simplicity, the arguments are not shown: \(F(x_{123})\equiv F\).
The similar consideration for the operators \(\eta C\gamma _{\bot }\xi \eta _{3}\) and \(\xi C\gamma _{\bot }\eta \eta _{3}\)Footnote 2 yields
respectively. The analysis for the axial operators \(\eta C\bar{n}\gamma _{5}\eta \xi _{3}\) gives
Two more equations can be obtained using the QCD EOM, which can be rewritten as
and describes the free collinear quark. Consider the following operator with the total derivative
Taking the matrix elements from the both sides one finds
The same consideration for the axial operator \(\chi C{\bar{\not {n}}}\gamma _{5} \chi \chi _{3}\) gives
Therefore we obtain six linear algebraic relations. The investigation of other possible 3-quark light-cone operators using the same technique does not provide any new information. We did not find any method in order to get two more pure algebraic equations. However one needs at least two more equations in order to express the eight auxiliary DAs (91) in terms of the basis ones. In order to derive these equations we introduce off light-cone correlation function (CF). Performing the expansion of this CF around the light-cone we derive two more equations, which allow us to solve the problem. However these relations are already not algebraic. The derivation of iii is more involved and the details are given in Appendix B. The obtained equations read
where the factors \(2(kx)=k_{+}x_{-}\), \(2(ky)=k_{+}y_{-}\) and the coordinates x and y enter in the definition of the FT in Eq. (14)Footnote 3. Remind, that the DAs \({\mathcal {V}}_{i}\) and \({\mathcal {A}}_{i}\) on the rhs denote the auxiliary twist-4 DAs from Eqs. (63)–(64). For instance, for the nucleon, taking the asymptotic contributions of twist-3 and twist-4 DAs one finds

Solving two Eqs. (110) and (111) one finds expressions for \(T_{xy}\) and \(G_{xy}\). Then one can easily solve the system of the linear equations.
The properties of Eqs. (110) and (111) imply that in case of \(x=0\) or \(y=0\) the one lhs vanishes and therefore must vanish the corresponding rhs. This gives two non-trivial conditions (\(x_3=1-x_1-x_2\))
These conditions allows one to perform the integrations by parts on rhs of Eqs. (110) and (111), that reduce these equations to a simple algebraic form. Notice, that the DAs on the rhs of Eqs. (113) and (114) depends on the twist-3 and twist-4 moments only. We have found that Eqs. (113) and (114) are satisfied if one uses for description of the DAs in Eqs. (113) and (114) the first moments (or equivalently the asymptotic contributions) for twist-3 and twist-4 DAs only. We believe that this observation is closely related to the disregard of the quark-gluon contributions and the genuine twist-5 moments Eq. (47). Such simple recipe does not work for the description of the twist-5 contributions associated with higher moments of the DAs and this makes such analysis to be more complicated in comparison with the twist-4 DAs. In order to illustrate this point we discuss a simple example, which is considered in the Appendix C.
Therefore in this work we only use the asymptotic expressions for the twist-3 and twist-4 DAs for the description of auxiliary twist-5 DAs. Let us also mention that obtained description of the twist-5 DAs ensures their proper normalisations, which are consistent with the Lorentz structure for the local matrix elements. This is automatically provided by the algebraic equations derived above.
It is convenient to solve the equations for twist-5 auxiliary DAs using the explicit expressions for the asymptotic DAs. Then the solutions are given by the simple analytical expressions. Assuming below \(B\ne \Lambda \) we write the final result as
The similar discussion also holds for the chiral-odd set of the auxiliary DAs. The details are given in Appendix B. The results read
For the nucleon set one has to substitute in the formulas \(f_{B}^{\bot }\rightarrow f_{N}\). The coefficients \(c_{\Lambda }^{\pm }\) are defined in Eq. (29). It is useful to note that all auxiliary DAs are proportional to the factor \(x_{1}x_{2}x_{3}\) that simplifies an investigation of analytic properties of the collinear integrals.
In addition to the identities, which follow from the Lorentz symmetry, one can also derive symmetry relations that follow from the condition that a baryon state has a certain isospin. For the auxiliary matrix elements this can be done in the same way as for the basis ones, see e.g. Ref. [23]. For instance, for the nucleon (\(I_N=1/2\)) this gives 15 different relations for the auxiliary DAs. We provide these relations in Appendix D. These relations can also be used for the finding of relations between the auxiliary and basic DAs. The problem is that different baryons has different isospin and this complicates such analysis. At the same time, the relations that follow from the Lorentz symmetry are universal and valid for all baryons. Nevertheless, the isospin relations provide a powerful check of the obtained result. We have verified that the obtained expressions for the auxiliary DAs in Eqs. (115)–(124) and (125)–(131) satisfy all 15 isotopic relations given in Appendix D.
3 Calculation of hard kernels
The decay amplitude can be written as [21]

where \(\epsilon _{\psi }\) is the charmonium polarisation vector, \(\bar{N}(k)\) and \(V(k^{\prime })\) denote baryon and antibaryon spinors, respectively. The scalar amplitudes \(A_{i}^{B}\) can be expanded within the effective field theory framework in small heavy quark velocity \(v^{2}\) (NRQCD) and in powers \(\lambda ^{2}\sim \Lambda /m_{c}\) (collinear factorisation), where \(\Lambda \) is the typical hadronic scale. In this work we consider the leading-oder contribution with respect to small velocity v and compute the next-to-leading power (NLP) correction to the amplitude \(A_{1}^B\), which is provided by the diagrams in Fig. 1a).
The expansion of the amplitudes \(A_{i}^B\) in powers of \(\lambda \) is associated with the power counting of the collinear matrix elements, which describe the overlap with outgoing baryons. The structure of the collinear expansion allows one to write the following expansions
The leading-power (LP) contribution scales as \(A_{1}^{\text {lp}}\sim {\mathcal {O}}(\lambda ^{8})\) because it is described by the two light-cone matrix elements, each of which is of order \({\mathcal {O}}(\lambda ^{4})\). The NLP correction \(A_{1}^{\text {nlp}}\) includes collinear operators, which are suppressed by the overall factor \(\lambda ^{4}\) and therefore \(A_{1}^{\text {nlo} } \sim {\mathcal {O}}(\lambda ^{12}).\) For the second amplitude one finds \(A_{2}^{\text {lp}}\sim {\mathcal {O}}(\lambda ^{12})\)Footnote 4.
The expansion in powers of \(1/m_c\) mixes up power corrections from the expansions of the scalar amplitudes \(A_{i}^B\) and from the baryon spinors. The calculation of the amplitude in the factorisation framework yields the result in the following form

where the coefficients \(\delta A_{i}\) scale as
The expressions for \(\delta A_{i} \) are given by the convolution integrals of the hard kernels with the different baryon DAs.
In order to perform the interpretation of \(\delta A_{i} \) in terms of the scalar amplitudes \(A_{1,2}^B\) one needs to perform the expansion of the rhs of Eq. (132). This gives

where we use that \(k_{+}\sim k_{-}^{\prime }\sim m_{c}\). Comparing Eqs. (134) and (136) one finds
The expressions for observables have a compact analytical form if we rewrite them in terms of the linear combinations \({\mathcal {G}}_{M}\) and \({\mathcal {G}}_{E}\), which read
Notice that the total power correction to \(A_{1}^{B}\) also includes the simple kinematical term \(\delta A_{1}^{\text {lo}}\times m_{B}^{2}/M_{\psi }^{2}\).
The LP term \(\delta A_{1}^{\text {lo}}\) is calculated long time ago, see e.g. Refs. [1, 5,6,7]. The contribution \(\delta A_{2}^{\text {lo}}\) is obtained in Ref. [21]. The correction \(\delta A_{1}^{\text {nlo}}\) will be considered for the first time. In this calculation we only consider the contributions of light-cone 3-quark operators and do not include the various quark-gluon matrix elements.
We use the same technique as in Ref. [21]. Here we just provide a schematic description and discuss some important points. The different contributions in \(\delta A_{1}^{\text {nlo}}\) can be divided into two groups, which are given by the product of the two twist-4 operators \( \left[ \chi _{1}\chi _{2}\chi _{3}\right] _{\text {tw4}}\otimes \left[ \bar{\chi }_{1^{\prime }}{\bar{\chi }}_{2^{\prime }}{\bar{\chi }}_{3^{\prime }}\right] _{\text {tw4}}\) or by the product twist-3 and twist-5 operators \(\left[ \chi _{1}\chi _{2}\chi _{3}\right] _{\text {tw3}}\otimes \left[ {\bar{\chi }}_{1^{\prime }}{\bar{\chi }}_{2^{\prime }} {\bar{\chi }}_{3^{\prime }}\right] _{\text {tw5}}\). Remind, \(\chi _{1}\) and \({\bar{\chi }}_{1^{\prime }}\) denote the collinear quark fields, see Eq. (52). Let us also remind that \(\chi _{1}\equiv \chi _{\alpha _{1}}\) and \({\bar{\chi }}_{1^{\prime }}\equiv {\bar{\chi }}_{\alpha _{1}^{\prime }}\). Each group can be further divided into two subgroups with respect to Dirac projections: \([\chi \Gamma _{even} \chi ]\chi _{3}\) and \([\chi \Gamma _{odd}\chi ]\chi _{3}\), where \(\Gamma _{even/odd}\) denote the chiral-even or chiral-odd Dirac matrices. The explicit definitions of the various operators and their matrix elements are discussed in Sect. 2.2.
The contribution of the sum of diagrams in Fig. 1 a) to \(\delta A_{1}^{\text {nlo}}\) can be written as

where \(D^i_{\left( 123\right) \left( 1^{\prime }2^{\prime }3^{\prime }\right) }\) denotes the analytical expression of the diagram i in momentum space. It can be written as
Here the matrices \(\gamma ^{\alpha }\otimes \gamma ^{\beta }\otimes \gamma ^{\gamma }\) corresponds to the light quark-antiquark vertices, \(D_{Q}^{(i)\alpha \beta \gamma }\) denotes the remnant part of the diagram, the trace in Eq. (140) is taken with respect of Dirac indices of the heavy quark fermion line. For simplicity, the colour structure of diagrams is not shown. The coupling \(f_{\psi }\) describes the matrix element in NRQCD and can be related with the radial wave function at the origin
The definition of the NRQCD matrix element is the same as in Ref. [21]. The expression  in the trace in Eq. (140) represent the Dirac part of the projector on the NRQCD matrix element, \(\omega =(1,0,0,0)\) and \(\varepsilon _\psi ^\mu \) denote the velocity and the polarisation vector of charmonium, respectively.
in the trace in Eq. (140) represent the Dirac part of the projector on the NRQCD matrix element, \(\omega =(1,0,0,0)\) and \(\varepsilon _\psi ^\mu \) denote the velocity and the polarisation vector of charmonium, respectively.
The operators \(P(x_{i})\) and \(\bar{P}(y_{i})\) describe the projections on the matrix elements of the light-cone 3-quark operators for baryon and antibaryon, respectively. For the twist-3 case these operators depend on the nucleon spinors, Dirac matrices and twist-3 DAs and can be obtained just from the definition in Eq. (11). For instance, for the matrix element \(\left\langle 0\right| {\mathcal {O}}_{123}\left| B(k)\right\rangle _{\text {tw3}}\) one easily obtains
For the higher twist matrix elements these projections also include the derivatives with respect to quark and antiquark momenta \(k_{i} \) and \(k_{i}^{\prime }\), which are assumed to be off-shell \(k_{i}^{2}\ne 0\), \(k_{i}^{\prime }\ne 0\). Only after the differentiations one can neglect the small momentum components and set \(k_{i}\simeq x_{i}k_{+}\bar{n}/2\) and \(k_{i}^{\prime }\simeq y_{i}k_{-}^{\prime }n/2\). The derivation of the twist-4 projections have been considered in Ref. [21] and here we follow the same technique. The analytical results for the different projectors are given in Appendix E. Substituting the various projectors in Eq. (140) one obtains the expression, which allows one to calculate the hard kernels. The analytical calculations were performed using the package FeynCalc [39, 40].
The obtained result can be written as
where the normalisation coefficient \(A_{0}\) read
The dimensionless integrals \(J_{ij}^{B}\) have subscripts “44” and “35” , which are related with the structure of the collinear matrix elements: twist-4\(\times \)twist-4 and twist-3\(\times \)twist-5. Each integral in Eq. (145) is given by the sum of simpler integrals J[X, Y] where X and Y denote the DAs, which are included in the integrand
where \(K_{XY}(x_{i},y_{i})\) is the universal hard kernel. The calculation of the traces in Eq. (140) gives the sum of the collinear integrals, which can be simplified using the symmetry properties of the DAs and the hard kernels with respect to interchange \(x_{1}\leftrightarrow x_{2}\) and \(x_{i}\leftrightarrow y_{i}\). Below we provide the analytical expressions for the integrals in Eq. (145), where such simplifications are taken into account. Let us write each term in Eq. (145) as
The subscript “even/odd” corresponds to the chiral-even and chiral-odd subsets of the DAs. Then
Each integral on the rhs of Eqs. (149)–(153) is IR-finite, i.e. does not have endpoint singularities. The integrals \(J_Z[X,Y]\) are given by the sum of singular integrals and read
where \(\delta _{B\Lambda }=1\) if \(B=\Lambda \) and 0 otherwise. Notice that expressions in Eqs. (154)–(158) include the integrals, which have twist-3 DAs only. These are contributions, which appears from twist-5 matrix elements with the total derivatives, see discussion in Appendix E. The Kronecker symbol \(\delta _{B\Lambda }\) appears in Eqs. (154) - (157) because we only use asymptotic twist-3 and twist-4 DAs for the evaluation of the twist-5 DAs. The integrals with the twist-3 DAs in Eqs. (154)–(158) are singular and they are included in the given expressions because they are required for the cancellation of the endpoint singularities in the integrals \(J_{Z}[X,Y]\).
The analytical expressions for the hard kernels \(K_{XY}(x_{i},y_{i})\), as defined in Eq. (147), are given in the Appendix F. It has been analytically verified that these kernels correctly describe the relations between the amplitudes in the SU(3) limit. The corresponding convolution integrals can be relatively easily calculated. Substituting the explicit expressions for DAs with arbitrary moments and summing the singular integrands gives analytical expressions with the well defined four-dimensional integrals. These integrals can be easily computed numerically using the standard mathematica packages for numerical integrations.
4 Phenomenology
A systematic numerical analysis of existing data is still very challenging due to various theoretical and experimental uncertainties. Therefore, the main goal of the following discussion is to understand how well the existing data can be described using plausible assumptions about various nonperturbative parameters.
In this analysis we take into account the electromagnetic amplitudes, which are shown by the diagram in Fig. 1b. With these contributions the decay amplitudes read

where \(F_{1,2}^{B}\) are the time-like e.m. form factors. Expression for the width reads
where \(\beta =\sqrt{1-4m_{B}^{2}/M_{\psi }^{2}}\),
The amplitudes \({\mathcal {G}}_{M}\) and \({\mathcal {G}}_{E}\) are defined in Eq. (139), the time-like Sachs form factors \(G^B_{E,M}\) read
The coupling \(\zeta \) in Eq. (161) is defined as
Therefore, the observables depend on the time-like form factors of baryons, which are still not well known. For the given value of the \(q^{2}=M_{\psi }^{2}\) their values are still depend on the large non-perturbative corrections and can not be sufficiently well estimated within the QCD factorisation framework. This introduces additional uncertainty into the phenomenological analysis.
The hadronic amplitudes calculated to this accuracy within the factorisation framework are real. The e.m. FFs have real and imaginary parts, therefore to this accuracy one finds
where \(\varphi _{M,E}\) are phases of the e.m. form factors. Let us rewrite the ratio as
with
where the factor \({\mathcal {R}}_{em}^{B}\) defines how the measured value \(\gamma _{B}\) depends on the interference with e.m. amplitude.
At present, the time-like baryon FFs are little known. The best experimental data for the proton can be found in Ref. [33]. For other baryons one can only find the data for the effective FF obtained from the analysis of the e.m. cross section under assumption \(G_{\text {eff}}^{B}=|G_{M}^{B}|=|G_{E}^{B}|\), see Refs. [31, 32, 34,35,36,37,38]. Therefore an estimation of \({\mathcal {R}}_{em}^{B}\) can not be done without assumptions. In the following we assume that \(0\ll \cos \varphi _{M,E}<1\)Footnote 5. The value of \(|G_{M}^{p}|\) we take from data in Ref. [33], the maximal value \(|G_{E}^{p}|\) is taken to be \(|G_{E}^{p}|\le 3.29\times 10^{-2}\) as it follows from analysis of data in Ref. [33]. In other cases we assume that \(|G_{M}^{B}|\approx G_{\text {eff}}^{B}\). The value of \(\cos \varphi _{M}\) can be estimated from the data for the width (160), where \(\gamma _{B}\) is fixed by the experimental value. An estimate of \(G_{E}^{B}\) is the most challenging point. We assume that \(\left| G_{E}^{B}\right| \le \)1.5 \(G_{\text {eff}}^{B}\), where the numerical coefficient 1.5 is our conservative estimate. Numerical value of \(\zeta ^{2}\left| G_{E}\right| ^{2}/\left| {\mathcal {G}}_{E}\right| ^{2}\) is quite small and can be neglected, which yields
Therefore, assuming the estimate
we get an interval, which is considered as an estimate of the possible numerical effect provided by \({\mathcal {R}}_{em}^{B}\).
Let us now discuss the non-perturbative input, which is used for calculation of the hadronic amplitudes. Recall that we consider only three-quark DAs. It is convenient to describe the non-perturbative input in terms of basic DAs as discussed in the Sect. 2.1. Analytical expressions for the corresponding models are described in Appendix A. The values of DAs parameters are summarised in Table 1.
The parameters of nucleon chiral-even DAs correspond to the model ABO-I from Ref. [27]. This set of parameters have beed obtained from the fit of the space-like electromagnetic FF data using the light-cone sum rules. The moments \(\lambda _{2}\) and \(\xi _{10}\) are evaluated in Ref. [23] using the QCD sum rule approach. Some twist-3 moments for different baryons are also obtained using QCD sum rules in Refs. [5,6,7]. Recently, the different twist-3 and twist-4 moments have also been computed on the lattice, see Ref. [30]. We use these results in order to fix parameter values in DA models. In particular, the values for the moments \(\phi _{10}^{B}, \phi _{11}^{B}\), \(\lambda _{1}^{B}\),\( \lambda _{\bot }^{B}\), \(\lambda _{2}^{B}, \pi _{10}^{B}\) and \(\pi _{11}^{B}\) (\(B\ne N\)) are fixed according to data in Ref. [30].
For the nucleon twist-3 normalisation coupling we take the value \(f_{N}(1\) GeV\()=5.5\times 10^{-3}\ \)GeV\(^{2}\), which is in agreement with the sum rule estimate \(f_{N}(1\) GeV\()=(5.3\pm 0.5)\times 10^{-3}\) GeV\(^{2}\) obtained in Refs. [5,6,7]. The other twist-3 normalisation couplings \(f_{B}\) are fixed from the fit of data. The values obtained in Ref. [30] were used as the first estimate and then changed if this improves the description of the data. Therefore the resulting value \(f_{\Lambda }\) in Table 1 is larger than the estimates in Refs. [5,6,7, 30], which read 0.50 and 0.48, respectively.Footnote 6 We also find a relatively small difference for values of \(f_{\Sigma }\) (0.54 [30] and 0.48 [5,6,7]) and \(f_{\bot }^{\Xi }\) (0.64 [30] and 0.50 [5,6,7]). The values for \(f_{\bot }^{\Sigma }\) and \(f_{\Xi }\) are the same as in Ref. [30].
The values of the twist-4 moments \(\eta _{10}^{B},\eta _{11}^{B}\), \(\zeta _{10}^{B}, \zeta _{11}^{B}\) and \(\xi _{10}^{B}\) are fixed from the data, assuming that their values are not significantly different from the nucleon ones because of approximate SU(3) symmetry.
In our calculation we fix relatively low renormalisation scale \(\mu ^{2}=1.5\,\)GeV\(^{2}\). This gives for the strong coupling \(\alpha _{s}(\mu ^{2})=0.35\). The twist-4 DAs include terms with the quark masses, see Eqs. (63)–(68). For these terms we set \(m_{u}\approx m_{d}\approx 0\), \(m_{s}\)(1.5 GeV\(^{2}\))=105 MeV. The value of \(J/\psi \) total width \(\Gamma _{tot}=93\,\)keV is taken from Ref. [41] .
For the value \(R_{10}(0)\) in Eq. (142) we use the estimate obtained for the Buchmuller-Tye potential [42]
which implies for the value of charm quark mass \(m_{c}=1.48\,\)GeV.
One of the elements of the current analysis is the estimation of the power-law correction to \({\mathcal {G}}_{M}^{B}\), see Eq. (139). In Table 2 we show the numerical results obtained for these corrections. The total effect of the power corrections is quite moderate due to the partial cancellation in the total sum, see Eq. (139). Therefore the total numerical effect from the next-to-leading power correction varies from \(1.7\%\) for \(\Xi \) up to \(16\%\) for nucleon.
The numerical results for branching fractions and ratios \(\gamma _{B}\) are presented in Table 3. The obtained values of \(\gamma _B\) include the error bars, which describe the estimate of the uncertainty occurring from to the interference with the electromagnetic FF’s as described by the coefficient \(R_{em}\).
The given choice of the different parameters for baryon DAs allows one to describe the data for the \(\gamma _B\) within the accuracy \(20\%\), which is sufficiently reasonable taking into account various higher order effects. The largest differences are obtained for neutron and for the \(\Sigma \) decay channels. In considered description, the neutron channel differs from the proton one only in the contribution of electromagnetic form factors. However this interference can not provide a sufficient numerical impact. On the other hand the neutron data in Ref. [11] have very large systematic error, which gives \(\gamma _n=0.95(6)\pm 0.27_{syst}\). Therefore the obtained value of \(\gamma _n\) can be accepted as quite reasonable result. For \(\Sigma \) decay channel, it is possible to obtain the larger value of \(\gamma _\Sigma \) but corresponding parameter set gives a worse description of the branching ratio because of relatively large and negative power correction.
Comparing the current analysis with that in Ref. [22] we conclude that the NLP corrections improve the phenomenological description and make it possible to better constrain the unknown parameters of baryon DAs. The negative effects of the power contribution reduces the absolute value of the amplitude \({\mathcal {G}}_M\) and increases the value of the ratio \(\gamma _B\) that improves the phenomenological description. However, this effect cannot be very large, since this can significantly worsen the description of the branching fractions.
5 Conclusions
In conclusion, in this work we continue to develop the analysis proposed in Ref. [22]. The decay amplitudes \(J/\psi \) into baryon-antibaryon pairs are considered within the NRQCD and collinear factorisation approach, power suppressed corrections and electromagnetic contributions are taken into account. This allows us to better appreciate some of the theoretical uncertainties.
The next-to-leading power correction, which is described by twist-4 and twist-5 three-quark baryon DAs is calculated and discussed for the first time. It is shown that this contribution is well defined and this allows one to study their effects in a more systematic way. From the phenomenological point of view the NLP correction allows to improve the description of the data and provide more rigorous constrains on the baryons DAs parameters.
In the given analysis we also take into account the interference with the electromagnetic amplitude, which depends on the time-like baryon form factors. Unfortunately, these values are little known due to the lack of experimental information. Therefore, an evaluation of their numerical impact can only be made under certain assumptions.
The existing experimental data for decays \(J/\psi \rightarrow B{\bar{B}}\) provide an interesting information about two observables: branching fractions and angular distribution coefficients \(\alpha _B\). The value of \(\alpha _B\) is determined by the ratio of the two independent decay amplitudes, which is especially interesting because it does not contain many theoretical uncertainties that are significant for the branching fractions. This also provides an attractive opportunity to study the baryon distribution amplitudes.
One of the main goal of the given phenomenological analysis is to verify that the current data can be described within the factorisation framework. In order to constrain the non-perturbative baryon DAs we use results obtained in the framework of QCD sum rules [5,6,7, 27] and from the lattice calculations [30]. Some of unknown moments have been estimated using flavour SU(3)-symmetry and from data fit. It is found that under reasonable assumptions about the non-perturbative parameters, the data can be described with an accuracy of 5%– 20%.
It is shown that the power corrections arising from higher twist baryonic DAs are moderate. This conclusion is, of course, sensitive to the models of baryonic DAs. The maximal numerical effect is about \( 16 \%\) is obtained for nucleon only. It is interesting to note that the model ABOI proposed in Ref. [27] for describing nucleon electromagnetic form factors also works well for describing charmonium decay, if we use the value for the normalisation couplings \(f_N\) obtained from the QCD sum rules [5,6,7]. The values of the branching fractions are very sensitive to the normalisation scale, a reliable description is obtained only for the relatively low scale \(\mu ^2=1.5\) GeV\(^2\).
Note also that a large value of \(\gamma _\Sigma \sim 2\) leads to a large numerical effect, which is crucially important for the correct estimate of the decay width. Unlike other baryons, in the case of \(\Sigma \) the contribution of the power suppressed term in the expression for the width, see the Eq. (160 ), is of the order of one, because it is enhanced by a factor of four due to large \(\gamma _\Sigma \).
The angular coefficient \(\gamma _B\) is quite sensitive to the interference with the electromagnetic decay amplitudes. Under the described assumptions, the corresponding numerical effect is estimated in the range of 10%–25%. This definitely reduces the accuracy in the constraining of DA parameters. Nevertheless, the obtained results allow us to conclude that the calculated hadronic amplitudes make a dominant contribution and therefore the QCD factorisation provides a suitable basis for understanding dynamics of these decays.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All experimental data used in the article are published in the form of scientific articles and are available at the specified references.]
Notes
If the all function in an equation have the same standard arguments \((x_i)\equiv (x_1,x_2,x_3)\) we use the simplification \(F(x_i)\equiv F\) to simplify the equations.
The Wilson lines are not shown for simplicity.
We also assume here that the argument of the third quark field is trivial: \(z=0\).
The additional power \(\lambda ^{2}\) appears due to the factor \(1/m_{B}\) in the definition in Eq. (132).
The small value of \(\cos \varphi _{M,E}\simeq 0\) implies that \(G_{M,E}\) dominates by imaginary part. We assume that such a scenario is unlikely.
For a convenience, these values are given in the same notation as in the Table 1.
References
S.J. Brodsky, G.P. Lepage, Phys. Rev. D 24, 2848 (1981). https://doi.org/10.1103/PhysRevD.24.2848
V.L. Chernyak, A.R. Zhitnitsky, Phys. Rept. 112, 173 (1984). https://doi.org/10.1016/0370-1573(84)90126-1
N. Brambilla et al. [Quarkonium Working Group], hep-ph/0412158
N. Brambilla et al., Eur. Phys. J. C 71, 1534 (2011). https://doi.org/10.1140/epjc/s10052-010-1534-9 [arXiv:1010.5827 [hep-ph]]
V. L. Chernyak, A. A. Ogloblin and I. R. Zhitnitsky, Z. Phys. C 42 (1989) 583
V.L. Chernyak, A.A. Ogloblin, I.R. Zhitnitsky, Yad. Fiz. 48, 1398 (1988)
V.L. Chernyak, A.A. Ogloblin, I.R. Zhitnitsky, Sov. J. Nucl. Phys. 48, 889 (1988). https://doi.org/10.1007/BF01557664
N.G. Stefanis, M. Bergmann, Phys. Rev. D 47, R3685–R3689 (1993). https://doi.org/10.1103/PhysRevD.47.R3685arXiv:hep-ph/9211250 [hep-ph]
J. Bolz, P. Kroll, Eur. Phys. J. C 2, 545–556 (1998). https://doi.org/10.1007/s100520050160arXiv:hep-ph/9703252 [hep-ph]
M. Ablikim et al., BES. Phys. Rev. D 78, 092005 (2008). https://doi.org/10.1103/PhysRevD.78.092005 [arXiv:0810.1896 [hep-ex]]
M. Ablikim et al., BESIII. Phys. Rev. D 86, 032014 (2012). https://doi.org/10.1103/PhysRevD.86.032014 [arXiv:1205.1036 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Rev. D 93 (2016) no.7, 072003 https://doi.org/10.1103/PhysRevD.93.072003 [arXiv:1602.06754 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Lett. B 770 (2017), 217-225 https://doi.org/10.1016/j.physletb.2017.04.048 [arXiv:1612.08664 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Rev. D 95 (2017) no.5, 052003 https://doi.org/10.1103/PhysRevD.95.052003 [arXiv:1701.07191 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Rev. Lett. 125 (2020) no.5, 052004 https://doi.org/10.1103/PhysRevLett.125.052004 [arXiv:2004.07701 [hep-ex]]
M. Alekseev, A. Amoroso, R.B. Ferroli, I. Balossino, M. Bertani, D. Bettoni, F. Bianchi, J. Chai, G. Cibinetto, F. Cossio et al., Chin. Phys. C 43(2), 023103 (2019). https://doi.org/10.1088/1674-1137/43/2/023103arXiv:1809.04273 [hep-ph]
R. Baldini Ferroli, A. Mangoni, S. Pacetti and K. Zhu, Phys. Lett. B 799 (2019), 135041 https://doi.org/10.1016/j.physletb.2019.135041 [arXiv:1905.01069 [hep-ph]]
M. Claudson, S.L. Glashow, M.B. Wise, Phys. Rev. D 25, 1345 (1982). https://doi.org/10.1103/PhysRevD.25.1345
C. Carimalo, Int. J. Mod. Phys. A 2, 249 (1987). https://doi.org/10.1142/S0217751X87000107
F. Murgia, M. Melis, Phys. Rev. D 51, 3487 (1995). https://doi.org/10.1103/PhysRevD.51.3487 [hep-ph/9412205]
N. Kivel, Eur. Phys. J. A 56 (2020) no.2, 64 [erratum: Eur. Phys. J. A 57 (2021) no.9, 271] https://doi.org/10.1140/epja/s10050-021-00575-9 [arXiv:1910.02850 [hep-ph]]
N. Kivel, Eur. Phys. J. A 58(2), 26 (2022). https://doi.org/10.1140/epja/s10050-021-00626-1arXiv:2109.05847 [hep-ph]
V. Braun, R. J. Fries, N. Mahnke and E. Stein, Nucl. Phys. B 589 (2000) 381 Erratum: [Nucl. Phys. B 607 (2001) 433] https://doi.org/10.1016/S0550-3213(00)00516-2, [hep-ph/0007279]
V. M. Braun, S. E. Derkachov, G. P. Korchemsky and A. N. Manashov, Nucl. Phys. B 553 (1999), 355-426 https://doi.org/10.1016/S0550-3213(99)00265-5 [arXiv:hep-ph/9902375 [hep-ph]]
V.M. Braun, A.N. Manashov, J. Rohrwild, Nucl. Phys. B 807, 89 (2009). https://doi.org/10.1016/j.nuclphysb.2008.08.012 [arXiv:0806.2531 [hep-ph]]
S. Krankl, A. Manashov, Phys. Lett. B 703, 519–523 (2011). https://doi.org/10.1016/j.physletb.2011.08.028arXiv:1107.3718 [hep-ph]
I.V. Anikin, V.M. Braun, N. Offen, Phys. Rev. D 88, 114021 (2013). https://doi.org/10.1103/PhysRevD.88.114021 [arXiv:1310.1375 [hep-ph]]
P. Wein, A. Schäfer, JHEP 05, 073 (2015). https://doi.org/10.1007/JHEP05(2015)073arXiv:1501.07218 [hep-ph]
I.V. Anikin, A.N. Manashov, Phys. Rev. D 93(3), 034024 (2016). https://doi.org/10.1103/PhysRevD.93.034024arXiv:1512.07141 [hep-ph]
G. S. Bali et al. [RQCD Collaboration], Eur. Phys. J. A 55 (2019) no.7, 116 https://doi.org/10.1140/epja/i2019-12803-6 [arXiv:1903.12590 [hep-lat]]
B. Aubert et al., BaBar. Phys. Rev. D 76, 092006 (2007). https://doi.org/10.1103/PhysRevD.76.092006 [arXiv:0709.1988 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Rev. D 97 (2018) no.3, 032013 https://doi.org/10.1103/PhysRevD.97.032013 [arXiv:1709.10236 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Rev. Lett. 124 (2020) no.4, 042001 https://doi.org/10.1103/PhysRevLett.124.042001 [arXiv:1905.09001 [hep-ex]]
M. Ablikim et al. [BESIII], Phys. Rev. D 103 (2021) no.1, 012005 https://doi.org/10.1103/PhysRevD.103.012005 [arXiv:2010.08320 [hep-ex]]
M. Ablikim et al., BESIII. Phys. Lett. B 814, 136110 (2021). https://doi.org/10.1016/j.physletb.2021.136110 [arXiv:2009.01404 [hep-ex]]
M. Ablikim et al. [BESIII], [arXiv:2103.12486 [hep-ex]]
M. Ablikim et al., BESIII. Phys. Lett. B 820, 136557 (2021). https://doi.org/10.1016/j.physletb.2021.136557 [arXiv:2105.14657 [hep-ex]]
M. Ablikim et al. [BESIII], [arXiv:2110.04510 [hep-ex]]
J. Kublbeck, H. Eck, R. Mertig, Nucl. Phys. B Proc. Suppl. 29, 204–208 (1992)
V. Shtabovenko, R. Mertig, F. Orellana, Comput. Phys. Commun. 256, 107478 (2020). https://doi.org/10.1016/j.cpc.2020.107478 [arXiv:2001.04407 [hep-ph]]
P.A. Zyla et al. [Particle Data Group], PTEP 2020 (2020) no.8, 083C01 https://doi.org/10.1093/ptep/ptaa104
E.J. Eichten, C. Quigg, Phys. Rev. D 52, 1726 (1995). ([hep-ph/9503356])
P. Ball, V.M. Braun, Nucl. Phys. B 543, 201–238 (1999). https://doi.org/10.1016/S0550-3213(99)00014-0arXiv:hep-ph/9810475 [hep-ph]
P. Ball, V.M. Braun, Y. Koike, K. Tanaka, Nucl. Phys. B 529, 323–382 (1998). https://doi.org/10.1016/S0550-3213(98)00356-3arXiv:hep-ph/9802299 [hep-ph]
M. Beneke, A.P. Chapovsky, M. Diehl, T. Feldmann, Nucl. Phys. B 643, 431–476 (2002). https://doi.org/10.1016/S0550-3213(02)00687-9arXiv:hep-ph/0206152 [hep-ph]
Acknowledgements
This work is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project-ID 445769443.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C.-M. Ko.
Appendices
Appendix
A Analytical expressions for the models of baryon DAs
In this Appendix we provide the explicit expressions for the models of the basic light-cone baryon DAs, which define the QCD nonperturbative input in the compact form. These DAs are used in order to compute the auxiliary DAs, which are convenient for the calculation of the decay amplitudes. Recall, that in this work we follow the definitions from Ref. [27].
The DAs for different baryons are related to each other by isospin symmetry. Following to definitions from Ref. [28] we define them as
and give results only for \( \text {DA}^N\), \(\text {DA}^\Sigma \), \(\text {DA}^\Xi \) and \(\text {DA}^\Lambda \).
We start from the description of the twist-3 DAs. For the nucleon DA introduced in Eq. (30) we use the following expression
For other baryons \(B\ne N\) the DAs are defined in Eqs. (19) and (20). Corresponding models read
The orthogonal polynomials \({\mathcal {P}}_{21}(x_{i})\) read
The moments \(\phi _{ik}^{B}\) are multiplicatively renormalisable and the corresponding anomalous dimensions can be found in Ref. [27].
The set of the models for the twist-4 DAs are defined as following. The nucleon DAs from Eqs. (31) and (32) have the following twist decomposition
The kinematical twist-3 contributions read
Notice that the differentiations must be computed with the unmodified expressions of the polynomials \({\mathcal {P}}_{nk}(x_{i})\) in Eqs. (A. 7)–(A. 10) and only after that one can apply the condition \( x_{1}+x_{2}+x_{3}=1\).
The genuine twist-4 DAs in Eqs. (A. 11), (A. 12) and (33) reads
where the orthogonal polynomials \({\mathcal {R}}_{1i}\) read
For other baryons we use definitions from Eqs. (37)–(40). Recall, that DA \(\Upsilon _4\) from Eq. (41) is not independent and can be obtained from Eq. (70 ). The kinematical twist-3 contributions in Eqs. (37)–(39) read
The genuine twist-4 contributions read
The basic twist-5 DAs are used in order to obtain the auxiliary DAs, which are discussed in Sect. 2.2. To obtain them, only the asymptotic expressions for DAs of twist-3 and twist-4 are used, i.e. all higher moments except \(f_B,\, f^B_\perp \), \(\lambda ^B_{1,2}\) and \(\lambda ^B_{\bot }\) are neglected in the above expressions. For the twist-5 basic DAs we used the following input
Numerical values of all moments are given in the Table 1. All these moments are multiplicatively renomalisable and the corresponding anomalous dimensions can be found in Refs. [25, 27].
B Relations between the twist-5 DAs
Here we discuss the technical details that clarify the derivation of relationships between the various DAs introduced in Sect. 2.
Let us start from discussion of the chiral even DAs. There are two ways to get additional equations, which relate the auxiliary and the basic DAs. One way is to consider the light-cone operator with one derivative and to repeat the same analysis as in Sect. 2. The second method is to use the off light-cone correlation function (CF). Below we use this one. For simplicity we consider the nucleon case. We also do not write explicitly the colour indices and the Wilson lines.
Consider the following CF (\(x^2\ne 0,\ y^2\ne 0\))
Performing the expansion of the operator in lhs of Eq. (B. 1) around the light-cone direction up to twist-5 terms and expanding the rhs of Eq. (B. 1) one obtains the set of relations.
The twist-5 operators resulting from the expansion can be divided into three groups. The first group includes the operators with two transverse derivatives, which arise from the expansion of the arguments of the fields
There second group includes the terms with one transverse derivative and one small field \(\eta \)
The third group includes the operators with two small fields \(\eta \)
All operators with fields \(\eta \) can be converted into the operators with two transverse derivatives using Eq. (88) and corresponding matrix elements can be obtained using Eqs. (75)–(77).
The matrix elements of the operators from the first group simply reproduce the definitions in Eqs. (75), (76) and (77).
The required relations can be obtained from the matrix elements of the operators from the second group (B. 4). Consider the terms with \(x_{\bot }\). There are three twist-5 light-cone operators, which appear in this case
where we assume \(qqq_{3}\equiv q(x_{-})q(y_{-})q_{3}(0)\). The matrix elements of these operators can be obtaned using QCD EOM (88) and definitions Eqs. (75), (76) and (77). On the other side the same matrix elements can be obtained from the expansion of rhs in Eq. (B. 1). Comparing these results one obtains
Excluding \(V^B_{x5}\) one obtains
where we assume \(2(ky)=k_{+}y_{-}\).
The similar analysis for the operators with \(y_{\bot }\)
allows one to obtain one more relation
Consider now the axial CF
The analogous consideration of terms with \(x_\bot \) and \(y_\bot \) yields the two relations
It is convenient to combine these two relations with ones in Eqs. (B. 9 ) and (B. 11) and simplify the obtained expressions using the relations (102)–(105). This gives the relations given in Eqs. (110) and (111).
Consider now the auxiliary chiral-odd DAs. The set of these functions is defined in Eqs. (81)–(83) and reads
The algebraic relations can be obtained in the same way as described for the chiral-even DAs in Sect. 2.2. Therefore we skip the details and only provide a schematical description. The consideration of the scalar operators \(\eta C\xi \eta _{3}\) and \(\xi C\eta \eta _{3}\) yields
respectively. From the analysis of the pseuvdoscalar operators \(\eta C\gamma _{5}\xi \eta _{3}\) and \(\xi C\gamma _{5}\eta \eta _{3}\) one finds
One more relation follows from the consideration of the tensor operator \(\eta C\bar{n}\gamma _{\bot }\eta \xi _{3}\):
Using the same consideration as in Eq. (107) we consider the matrix element of the operator \((\bar{n}\partial )\left[ \xi Cn\gamma _{\bot }^{\nu } \xi \xi _{3}\right] \). This yields
All other operators give the linear combinations of these six relations.
In order to get one more relation we use the method of CF, which is described above. Consider the following CF
where the rhs includes all terms up to twist-5 accuracy. Expanding the operator in the lhs we consider the following linear in \(x_{\bot }\) and \(y_{\bot }\) twist-5 terms
where
The consideration of the corresponding matrix elements yields
The sum of these two relations gives
Using Eqs. (B. 18) and (B. 19) one finds
The consideration of the matrix elements \(\ \left\langle 0\right| {\mathcal {O}}_{x}^{\alpha \sigma }\left| B(k)\right\rangle \) and \(\ \left\langle 0\right| {\mathcal {O}}_{y}^{\alpha \sigma }\left| B(k)\right\rangle \) yields
respectively. The sum of these two equations gives
where we used Eq. (B. 31). The rhs of this equation can be rewritten in terms of basic DAs. Combaining Eqs. (B. 16) and (B. 18) one finds
Similar combination Eqs. (B. 17) and (B. 19) gives
Substituting this into Eq. (B. 34) one obtains the relation, which allows one to find the DA \({\tilde{T}}_{2xy}\). The expressions for other DAs in the list (B. 15) can be derived from the linear relations (B. 16 )–(B. 21). The corresponding results are given in Eqs. (125)–(131).
Let us also notice that consistency of Eq. (B. 34) implies (setting \(x=y=0\))
where we assume \(x_3=1-x_1-x_2\). This provides a good check of the obtained expressions.
Finally, let us also mention that the additional relation for the twist-4 chiral-odd DAs given in Eq. (69), can be obtained from the consideration of the matrix element of the operator \(\xi (x_{-})C\sigma ^{\mu \nu }\xi (y_{-})\eta _{3}(0)\).
C On the determination of quark and quark-gluon contributions for the next-to-leading power correction
In this section, we discuss a simple example that demonstrates a difficulty in the determination of the pure quark contribution for the subleading power corrections. We assume the same kinematical notations as for the baryon with momentum k. Let us consider the light-cone matrix element for the vector meson state (\(J^{PC}=1^{--}\)), which can be parametrised as
where \(e_{\mu }\equiv e^\lambda _{\mu }(k)\) denotes the polarisation vector, FT denotes the appropriate Fourier transformation
All defined DAs are normalised to one
The twist-3 DA \(g_{v}\) and the twist-4 DA \(g_{3}\) in the rhs have been studied in Refs. [43, 44]. The obtained results read
where \(\bar{g}_{v}\) and \(\bar{g}_{3}\) denote the contributions of quark-gluon matrix elements.
The local limit in Eq. (C. 1) gives
where it is used that
The off light-cone CF can be written as [43]
The derivation of the expression for the DA \({\mathbf {A}}\) is given in Ref. [43], the result reads
where \(\bar{{\mathbf {A}}}\) again denotes the quark-gluon contributions. Such notation for the contributions of quark-gluon matrix elements is also accepted below. All results in Eqs. (C. 4),(C. 5) and (C. 10) are obtained with the help of differentiation of the CF, see details in Refs. [43, 44].
Let us now consider the twist-4 DAs with help of the technique discussed in this work. The twist-4 operators, which appear in the expansion of the off light-cone operator \({\bar{\psi }}(x)\gamma ^{\sigma }\psi (0)\) read
where, remind, the collinear fields \(\xi \) and \(\eta \) are defined in Eq. (87). The operator \({\mathcal {O}}_{4}^{\sigma }[{\mathcal {A}}]\) denotes the contribution of the quark-gluon operators.
The matrix element of the twist-4 operator with two derivatives can be obtained from the expansion of the CF
Consider now the operators with the longitudinal derivative \(i(\bar{n}\partial )\) in (C. 11). Using QCD EOM
where dots denote the quark-gluon contributions. Similarly
The sum of these terms gives the operator m.e. of the operator \(i(\bar{n}\partial )\left[ {\bar{\xi }}(x_{-}){\not {n}}\xi (0)\right] \) with the total derivative, which can be computed from Eq. (C. 9). This gives the following relation
where \(\bar{G}_{1}(u)\) again schematically denotes the contributions of quark-gluon DAs.
Consider now the m.e.
where we show the two-particle quark-antiquark operator only. On the other hand
Therefore this gives
where \(\bar{G}_{3}\) denotes a contribution from quark-gluon DAs. Using (C. 16) one obtains
Neglecting the quark-gluon terms \(\bar{G}_{1}\sim \bar{G}_{3}\rightarrow 0\) one finds the result
that agrees with Eq. (C. 5) assumming \(\bar{g}_{3}\rightarrow 0.\) At the same time the results for \({\mathbf {A}}\) in Eqs. (C. 10) and (C. 16) do not agree if one simply neglects the quark-gluon contributions
This result can be explained by the fact that the neglected quark-gluon contributions still implicitly depend on the twist-2 moments. For the local matrix elements this can be seen from the QCD equation of motions, see e.g. Ref. [43]. Therefore the simple recipe prescribing just to neglect the quark–gluon contributions, as for the twist-3 operators, is not applicable for the twist-4 calculations. Notice however that Eq. (C. 22) is valid for one particular case: for the asymptotic shape \(\phi ^{as}(u)=6u\bar{u}\). The corresponding local operator can not be related with any quark-gluon one.
This observation shows that consistent twist-4 calculation, which only account the two-particle quark operator requires some prescription, which makes it possible to unambiguously and systematically distinguish between the twist-4 quark and the quark-gluon contribution.
In fact, the Lorentz symmetry of the CF (C. 9) implies that DA \({\mathbf {A}}\) must satisfy to a certain condition. Let us briefly discuss this point. Consider the following matrix element
where we used Eq. (C. 1). Now the operator in lhs can be rewritten as
where we again skip the quark-gluon operators. The matrix element of this operator gives
where \({\mathbf {A}}_{\bar{q}q}\) denotes the pure quark part of the DA \({\mathbf {A}}\)
Therefore one finds
where \({\bar{G}}_{4}\) schematically denotes the quark-gluon contributions. Comparing with Eq. (C. 23) one finds the following relation
One can assume that consistently defined quark contribution \({\mathbf {A}}_{\bar{q}q}\) must satisfy
that ensures the correct Lorentz symmetry properties in the local limit, even if the quark-gluon contributions are not taken into account, see Eq. (C. 7). For instance, neglecting the quark-gluon contributions in Eq. (C. 16) one finds the expression
which satisfy to Eq. (C. 30).
In conclusion, the given consideration demonstrates that in general case the definition of the pure quark contribution for the twist-4 DAs is not universal due to the implicit contributions from the matrix element of the quark-gluon operators. In the given example the universal part can only be defined in terms of the asymptotic part of the twist-2 DA \(\phi \) because the corresponding local operator do not appear from the quark-gluon ones.
The similar arguments also applicable for the three-quark operators. Therefore in our calculations we only consider the asymptotic contributions of the twist-3 and twist-4 3-quark matrix elements in order to define the corresponding universal three-quark components of twist-5 DAs.
D Isospin relations between the auxiliary twist-5 DAs
The standard analysis of the light-cone matrix elements with two transverse derivatives allows one to obtain many relations between the auxiliary DAs defined in the Sect. 2.2. Here we consider such relations for a nucleon state. For simplicity, in this section we omit the baryon subscript “B=N” assuming for all DAs \(F^N\equiv F\). Let us define the operator basis as following
In these formulas we assume that each quark field \(q={u,d}\) is projected onto the large component \(\xi \) as defined in Eq. (87). Recall, that we use the short notation for the Dirac indices \(q_{\alpha _i}\equiv q_i\). From the technical point of view the derivation of such relations is the same as in Ref. [23] . This method gives the following three relations for the light-cone matrix elements of defined operators
Substituting in these equations the definitions of the auxiliary matrix elements from Sect. 2.2 and using the Fierz identities one derives various relations between the auxiliary DAs. It is convenient to divide the operators \(O_i^{\alpha \beta }\) in Eqs. (D.1)–(D.3) into three independent groups: symmetric (\(O_i^{\alpha \beta }=g_\bot ^{\alpha \beta }O_i\)), symmetric traceless \(g_\bot ^{\alpha \beta }O_i^{\alpha \beta }\) and and antisymmetric \(O_1^{\beta \alpha }=-O_1^{\alpha \beta }\). Each of these groups can be considered independently.
For simplicity, in what follow we use the following convenient notations
For the DAs, which describe the symmetric traceless matrix elements the set of relations read
For the DAs, which describe the antisymmetric matrix elements the set of relations read
The relations for the symmetric matrix elements are described by the matrix elements of the operators \(\left[ \partial _\bot ^{2}u\right] ud\), \(u\left[ \partial _\bot ^{2}u\right] d\) and \(\left[ \partial _\bot ^{\alpha }u\right] \left[ \partial _\bot ^{\alpha } u\right] d\). The analysis of the operator \(\left[ \partial _\bot ^{2}u\right] ud\) gives
The analysis of the operator \(u\left[ \partial _\bot ^{2}u\right] d\) gives
The analysis of the operator \(\left[ \partial _\bot u\right] \left[ \partial _\bot u\right] d\) gives
From these equations it follows that the relations between the chiral-odd and chiral-even auxiliary DAs have the following form
These equations are very helpful for the analytical check of the SU(3) limit for the calculated amplitudes.
E Expressions for the projections onto higher twist matrix elements
Here we give expressions for the projections P and \({\bar{P}}\) that enter Eq. (140). In the following we assume the matrix element with the baryon in the initial state as in the definitions in Sect. 2.1. This is convenient for a comparison of definitions of baryon DAs, which exist in the literature. This also implies that one calculates the amplitude of the time reversal process \(B+\bar{B}\rightarrow J/\psi \). Since the corresponding amplitude is real this also gives the correct result. The antibaryon projectors can be obtained from the baryon ones using the charge conjugation.
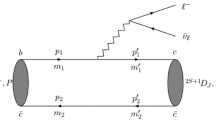
For partonic diagrams we assume the configuration of the external momenta as shown in Fig. 2.
After differentiations with respect to momenta \(k_{i}\) and \(k'_{i}\) we set
The derived projectors depend on the auxiliary DAs, which are defined in Sect. 2.2.
The twist-4 projectors have already been derived in Ref. [21]. The chiral-even projection reads
where (\(i=1,2\))



The chiral-odd projection reads
where



We assume that derivatives in these formulas are applied to the expressions on the right side, i.e. the derivatives are not applied to the momenta from the left side and therefore corresponding momenta can be simplified neglecting the power suppressed components. For a convenience, we also show the Dirac matrices in the square brackets: \([\not {k} ]\), \(\left[ \not {k} \gamma _{\bot }^{\alpha }\right] \) etc.
The expressions for the twist-5 projectors are more complicated and include some special contribution, which is completely defined in terms of twist-3 DAs.
The chiral-even projector is defined as
where


with


The terms in the second line of Eq. (E. 10) read




The terms from the third line of Eq. (E. 10)


with




with


The terms from the last line of Eq. (E. 10)
Notice that terms \(C_{V1}\) and \(C_{A1}\) include the derivatives with respect to initial momentum P, see a more detailed explanation below.
The twist-5 chiral-odd projector is defined as
where the coefficients read
‘



Below we use the short notation





where

The described projectors depend on the derivatives with respect to quark momenta \(\partial /\partial k_{1,2} \) and also include the terms with derivative with respect to charmonium momentum \(\partial /\partial P\). These terms only depend on the twist-3 DAs \(V_{1}^{B}\), \(A_{1}^{B}\) and \(T_{1}^{B}\) and they are related to the matrix element of the leading-twist operator with the total derivative
where \(({\bar{n}} k)\equiv k_{-}=2m_{B}^{2}/k_{+}\). This contribution does not vanish, in contrast to an operator with the total transverse derivative. It is clear that such contributions generate power corrections associated with the power suppressed component of the total baryon momentum k. Notice, that the calculation of the contributions with derivatives \(\partial /\partial k_{1,2}\) implies that \(k_{3}=k-k_{1}-k_{2}\) as it follows from the momentum conservation. The contributions with the matrix elements as in Eq. (E. 38) can be rewritten in a special way. This is related with the details of the Fourier transformation and with the derivation of the momentum conservation \(\delta \)-function.
Let us consider, as example, the contribution with \(V_{1}(x)\) and \(V_{1}(y_{i})\) and the diagram as in Fig. 1(a). The following discussion is also applicable for other cases. Performing the standard steps of the calculation one obtains the following result

where
where \({\tilde{D}}[z_{123},z_{123}^{\prime }]\) denotes the analytical expression for the diagram in the position space with the requiered operator vertices, \(z_{i}^{\prime }\) and \(z_{i}\) describe the coordinates of the QCD vertices, see Fig. 2. The various Fourier exponents in the lhs appear from the hadronic matrix elements. The quark momenta \(k_{i}^{\prime }\) and \(k_{i}\) in Eq. (E. 40) the same as in Eq. (E. 1).
In order to extract the momentum conservation \(\delta \)-function from the expression for \(T_{V1V1}\) one uses that \(x_{3}=1-x_{1}-x_{2}\), \(y_{3} =1-y_{1}-y_{2}\) and the translation invariance of the diagram \({\tilde{D}}[z_{123},z_{123}^{\prime }]\). Performing redefinition \(z_{i}\rightarrow z_{i}+z_{3}\) and \(z_{i}^{\prime }\rightarrow z_{i}^{\prime }+z_{3}^{\prime }\) for \(i=1,2\) one defines the Fourier exponent with the coordinate \(z_3\)
and
Therefore
The integrals over \(dz'_i dz_j\) in this expression can be understood as FT of the diagram \({\tilde{D}}\)
The first line in Eq. (E. 43) gives the \(\delta \)-function if the factor \(k_{-}(-iz_{3}\cdot n)\) is rewritten as
where l is just an auxiliary momentum. This gives
where one assumes that \(P^{2}\) is not fixed before the differentiation. This result explains the computational prescription for the terms with derivatives \(\partial /\partial P\).
Let us also to note that such terms also include the endpoint singularities, which cancel in the sum of the all twist-5 contributions. Therefore, it is important to take them into account properly.
F Analytical expressions for the hard kernels \(K_{XY}\)
In these section we provide the analytical expressions for the hard kernels \(K_{XY}(x_{i},y_{i})\) in the integrals J[X, Y] defined in Eq. (147). In the following we use convenient notation
The integrals, which describe twist-4\(\times \)twist-4 contribution read
where
where
The twist-3\(\times \)twist-5 integrals have the following kernels.
The first four integrals have relatively simple structure
The integrals \(J_{Z}\) defined in Eqs. (154)–(157) are also well defined, but they are given by the sum of the singular terms J[X, Y]. The analytical expression for the total sum is quite complicated and it is more constructive to describe the expressions for the individual kernels in J[X, Y] . Then
Each term in Eq. (F. 16) has the following kernel
where
where
where
The next integral reads
The kernels of the individual integrals read
where
where
where
The next integral reads
The kernels of the individual integrals read
The next integral reads
The kernels of the individual integrals read
The last integral reads
The kernels of the individual integrals read
where
where
where
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kivel, N. A description of charmonia decays \(J/\psi \rightarrow B\bar{B}\) within the QCD factorisation framework. Eur. Phys. J. A 58, 138 (2022). https://doi.org/10.1140/epja/s10050-022-00762-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-022-00762-2