Excitation functions of proton-induced nuclear reactions on $^{86}$Sr, with particular emphasis on the formation of isomeric states in $^{86}$Y and $^{85}$Y

Abstract

Cross sections of proton-induced nuclear reactions on enriched $^{\mathrm {86}}$Sr target were measured by the activation technique up to proton energies of 44  MeV. The isomeric cross-section ratios for $^{\mathrm {86m,g}}$Y and $^{\mathrm {85m,g}}$Y as a function of projectile energy were deduced from their measured data. The present experimental data for the nuclear reaction products, namely $^{\mathrm {86m}}$Y, $^{\mathrm {86g+xm}}$Y, $^{\mathrm {85m}}$Y, $^{\mathrm {85g}}$Y, $^{\mathrm {84}}$Rb and $^{\mathrm {83}}$Rb were compared with the results of nuclear model calculations using the code TALYS, which combines the statistical, precompound, and direct interactions. In general, the experimental cross-section data as well as the isomeric cross-section ratios are reproduced well by the model calculations, provided the input model parameters are properly chosen and the level structure of the product nucleus is thoughtfully considered. The quality of the agreement between experimental data and model calculations was numerically quantified. For products formed via emission of a light complex particle as well as multi-nucleons (e.g., $\alpha$ and 2p2n), the contribution of the latter process starts increasing when its energy threshold is crossed.

1 Introduction

Studies of excitation functions of charged-particle induced nuclear reactions on medium-mass target nuclei are of considerable significance for enhancing our understanding of nuclear theory as well as for practical applications. Regarding nuclear theory, several advanced nuclear model codes, incorporating mainly compound and precompound interactions, have been developed in recent years to describe the reaction cross section in the low to intermediate energy range. Precise experimental measurements allow one to test those model codes. Over the last two decades, extensive experimental and theoretical studies have been performed in many laboratories on reactions induced by protons, deuterons, $^{\mathrm {3}}$He-, and $\alpha$-particles, mainly up to energies of about 30  MeV, but also extending in some cases up to 100  MeV and beyond. The main aim of those studies was to measure or standardize reaction cross sections for medical applications. The results show that, in general, the experimental cross section for the total reaction channel is described fairly well by the model calculation up to the projectile energy of about 50  MeV, especially when a product is formed mainly by emission of nucleons (see as examples [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]). Some difficulty is observed in deuteron-induced reactions. More difficult to reproduce by the model calculation are, however, reactions leading to the formation of isomeric states of a product nucleus.

For experimental studies on isomer pairs, the activation technique is ideally suited. Through detailed investigations on $^{\mathrm {52m,g}}$Mn, $^{\mathrm {58m,g}}$Co, $^{\mathrm {73m,g}}$Se, $^{\mathrm {94m,g}}$Tc, $^{\mathrm {120m,g}}$I and some other isomer pairs, involving different combinations of target nucleus, incident charged projectile and various ejectiles, the dependence of the isomeric cross-section ratio on the excitation energy of the product nucleus, the nuclear spins of the two states concerned and the reaction channel involved has been amply demonstrated [1,2,3,4, 13, 16, 20]. Furthermore, in theoretical calculation of the isomer ratio in a charged-particle induced reaction, the effects of input level structure of the product nucleus, of the assumed angular momentum distribution in the preequilibrium decay and the spin distribution of the level density, have been elaborated [1,2,3,4, 21,22,23,24,25]. As it is well known [23,24,25], the isomeric cross-section ratio allows one to calculate the parameter $\eta$ which is defined as the ratio of the effective moment of inertia to the rigid body moment of inertia ($\Theta _{eff}/\Theta _{rig}$). This parameter is related to the spin distribution of the level density. In a recent extensive analysis of 61 nuclei [25], it has been shown that the $\eta$ value depends on the mass of the residual product nucleus. Whereas the $\eta$ values for the odd mass nuclei depict a characteristic exponential decrease as a function of the mass number, those for the even mass nuclei show a rather complicated behavior. Further studies on isomer pairs are thus needed to enhance our understanding of the various parameters affecting the isomeric state population with respect to the ground state. In particular, the postulated odd-even mass effect in the $\eta$ values [25] needs further substantiation.

As far as practical applications of excitation functions of charged-particle induced nuclear reactions are concerned, they allow one to optimize the production route of a radionuclide, i.e. the projectile energy range in a target that will lead to the maximum yield of the desired product and the minimum yield of undesired isotopic impurities. The cross-section data are of particular significance in the accelerator production of radionuclides of medical interest, for which high radionuclidic purity is demanded [26, 27]. Extensive experimental, theoretical, and evaluation studies in this direction have been performed over the last two decades, covering both diagnostic and therapeutic radionuclides. The results have been periodically reviewed [28,29,30,31,32,33]. Presently, the attention is on novel positron emitters [34, 35] for Positron Emission Tomography (PET) and on highly-ionizing radiation emitters (i.e. radionuclides emitting $\beta ^-$- and $\alpha$-particles) for internal targeted radionuclide therapy [31, 33]. The former are generally produced at low-energy cyclotrons (E < 20  MeV) and there is considerable need of accurate cross-section data measurements near the thresholds of the corresponding reactions, as demonstrated in the production of $^{\mathrm {124}}$I and $^{\mathrm {64}}$Cu [36, 37]. The production of therapeutic radionuclides, on the other hand, demands use of intermediate-energy accelerators, and the relevant data needs are rather extensive [31, 33, 38].

In the present study we chose to investigate the proton-induced reactions on highly enriched $^{\mathrm {86}}$Sr. One of the aims was to measure accurately the excitation function of the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86}}$Y reaction which is commonly used in the production of the novel positron-emitting radionuclide $^{\mathrm {86}}$Y (T$_{\nicefrac {1}{2}}$ = 14,7 h). It is applied as a marker to determine the distribution of the injected radioactivity in a tumor-bearing patient via PET, prior to medication with the $\beta ^-$-emitting therapeutic radionuclide $^{\mathrm {90}}$Y (T$_{\nicefrac {1}{2}}$ = 2.7 d) [39, 40]. This type of treatment is called “personalized medicine” and the concept is known as the “theranostic approach”. It is a rapidly developing methodology and several “matched-pairs” of radionuclides, i.e., one positron emitter and the other a therapeutic radionuclide, have been developed, such as $^{\mathrm {44g}}$Sc/$^{\mathrm {47}}$Sc, $^{\mathrm {64}}$Cu/$^{\mathrm {67}}$Cu and $^{\mathrm {86}}$Y/$^{\mathrm {90}}$Y [41]. Despite this successful use of $^{\mathrm {86}}$Y, the cross-section database for its production [42,43,44] has so far been weak and rather discrepant. We recently published a part of the results of this study [45] dealing with the production of $^{\mathrm {86}}$Y via the (p,n) reaction with protons of energies below the threshold of the (p,2n) reaction. Now we extend the investigation up to 44  MeV and also report the excitation functions of the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m,g}}$Y processes, for which the available information is scanty [43, 44]. The positron emitting isomers, $^{\mathrm {85m}}$Y (T$_{\nicefrac {1}{2}}$ = 4.86 h) and $^{\mathrm {85g}}$Y (T$_{\nicefrac {1}{2}}$ = 2.68 h) are formed as impurities in $^{\mathrm {86}}$Y production with incident proton energies above 14  MeV. If their amounts are large in comparison to $^{\mathrm {86}}$Y, the quantification of the PET scans of $^{\mathrm {86}}$Y would be adversely affected. The measured data should therefore be very useful in optimization of production conditions of $^{\mathrm {86}}$Y, if intermediate energy protons would be used.

Besides the practical application of the cross-section data mentioned above, two additional, rather theoretically-oriented, motivations existed for this investigation:

• Study of the isomeric cross-section ratios of both $^{\mathrm {86m,g}}$Y and $^{\mathrm {85m,g}}$Y. The spins of the nuclear levels concerned differ considerably from each other and the modes of decay of the isomeric states in the two cases are different. The two pairs could thus serve as interesting cases for a comparative investigation of the effects of various parameters on the isomer ratio. Furthermore, the even/odd mass effect on $\eta$, mentioned above, could be tested.

• Investigation of $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {83}}$Rb and $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {84}}$Rb processes; in the former case to analyse the relative contributions of the (p,$\alpha$) and multiple nucleon emission reactions, e.g. (p,2p2n), (p,$^3$He n), etc., to the formation of the residual product $^{\mathrm {83}}$Rb, and in the latter the contributions of the reactions (p,$^3$He), (p,2pn), and (p,pd) to the formation of the residual product $^{\mathrm {84}}$Rb.

The work described in this paper thus entails experimental determination of the excitation functions of the processes leading to the formation of the relevant radionuclides, and detailed nuclear model calculations to interpret and understand the reaction mechanisms involved. A special focus is on the isomeric cross-section ratios, studied over the proton energy range up to 44  MeV.

2 Experimental

2.1 Samples and irradiations

The stacked-foil activation method was used for cross-section measurements of proton-induced reactions on enriched $^{\mathrm {86}}$Sr. Thin strontium carbonate samples were prepared at the Forschungszentrum Jülich (FZJ) by the sedimentation technique using $^{\mathrm {86}}$Sr-enriched $^{\mathrm {86}}$SrCO$_3$ powder (isotopic composition: 96.4% $^{\mathrm {86}}$Sr; 1.33% $^{\mathrm {87}}$Sr; 2.26% $^{\mathrm {88}}$Sr; supplied by Eurisotop, France). Details are given in our earlier study on $^{\mathrm {86}}$Y-production cross sections [45]. Here only the salient steps are summarized. Al foils of 50 $\mu {\mathrm{m}}$ thickness and 13mm diameter (supplied by Goodfellow; chemical purity: 99.0%) were used as backing material of the sediments. A 0.75 mL portion of a suspension of 80mg of $^{\mathrm {86}}$SrCO$_3$ in 6 mL toluene, containing levapren-450 (1 mg/mL), which served as an excellent film forming additive, was transferred to a sedimentation cell with 10 mm diameter hole. The solvent was allowed to evaporate at room temperature for 2 days. The sedimented layers were examined under a microscope and only homogeneous and mechanically stable samples were selected. The weight and area of the sediment for each sample were determined. The netto weight of the sediments lay in the range of 5 to 7 mg, amounting to a thickness of 6 to 9 mg $^{\mathrm {86}}$SrCO$_3$/cm$^{\mathrm {2}}$. The sample was covered by a 10 $\mu {\mathrm{m}}$ thick Al foil of 16 mm diameter welted around the backing foil.

The $^{\mathrm {86}}$SrCO$_3$ sediment, sandwiched between two Al-foils, served as the target sample. Several such samples were stacked together with thin circular foils (diameter 13 mm) of Cu and Ti (supplied by Goodfellow; purity: Cu (99.9%); Ti (> 99.6%); thickness of both Cu and Ti foils: 25 $\mu {\mathrm{m}}$), serving as beam monitors to determine the proton flux and energy along the stack. In irradiations with 44.5  MeV protons, additional monitor foils of Al (supplied by Goodfellow; purity: 99.9%; thickness: 25 $\mu {\mathrm{m}}$) were inserted as beam monitors.

In total six stacks, each with five to nine target samples together with several monitor foils, were irradiated: three at the BC 1710 cyclotron at FZJ, Germany; one at the 88-Inch Cyclotron, Lawrence Berkeley National Laboratory (LBNL), USA; and two at the Jülich Isochronous Cyclotron (JULIC) at FZJ, Germany. The beam parameters are given in Table 1.

Table 1 Beam parameters of irradiations at BC 1710, JULIC and the 88-Inch cyclotron

The stacks irradiated at the BC 1710 were mounted in the screw-capped dummy target holder of the beam-line extension constructed a few years ago [46]. The JULIC is an established machine at FZJ. It has been in use for many years as the injector of the high-energy cooler synchrotron (COSY). Recently an external target station was constructed at JULIC with an adapter where several target holders can be fitted [47]. In the present measurements, the standard screw-capped dummy target holder, similar to the one at BC 1710 [46], was used to mount the samples and foils in a stacked-form. The irradiation at the 88-Inch Cyclotron at LBNL was carried out using a standard target holder [16].

2.2 Energy and flux of protons

The beam characterization and beam flux monitoring for the experiments with protons of primary energies of 16.7  MeV and 27.0  MeV (BC 1710 at FZJ and 88-Inch Cyclotron at LBNL, respectively), have already been reported in connection with the accurate determination of production data of the non-standard positron emitter $^{\mathrm {86}}$Y via the $^{\mathrm {86}}$Sr(p,n)-reaction [45]. The details of beam characterization and flux determination of the experiment with 44 and 44.5  MeV protons at JULIC at FZJ are given here. The extracted beam is of high precision with respect to energy and profile definition. Nevertheless, we checked the effective energy of the proton beam in a foil by the activity ratio method [48]. The $^{\mathrm {63}}$Zn/$^{\mathrm {62}}$Zn and $^{\mathrm {24}}$Na/$^{\mathrm {22}}$Na activities formed in Cu and Al monitor foils, respectively, mounted in front of the stack, were considered. The activities of the four products, viz. $^{\mathrm {63}}$Zn (T$_{\nicefrac {1}{2}}$ = 38.47 min), $^{\mathrm {62}}$Zn (T$_{\nicefrac {1}{2}}$ = 9.19  h), $^{\mathrm {24}}$Na (T$_{\nicefrac {1}{2}}$ = 14.997 h) and $^{\mathrm {22}}$Na (T$_{\nicefrac {1}{2}}$ = 2.60182 a), were determined non-destructively by $\gamma$-ray spectrometry, converted to decay rates with necessary corrections, and finally extrapolated to the end of bombardment (EOB). The mean energy of the proton beam in the front Cu foil as well as in the Al foil was determined by comparing the experimentally obtained ratios with the values calculated theoretically from the IAEA recommended excitation functions of the reactions $^{\mathrm {nat}}$Cu(p,x)$^{\mathrm {63}}$Zn, $^{\mathrm {nat}}$Cu(p,x)$^{\mathrm {62}}$Zn, $^{\mathrm {27}}$Al(p,x)$^{\mathrm {24}}$Na and $^{\mathrm {27}}$Al(p,x)$^{\mathrm {22}}$Na, respectively [49]. The deduced energy agreed well with the value derived from the accelerator parameters.

The effective proton flux was determined by using the reactions $^{\mathrm {nat}}$Cu(p,x)$^{\mathrm {62}}$Zn, $^{\mathrm {nat}}$Ti(p,x)$^{\mathrm {46}}$Sc and $^{\mathrm {27}}$Al(p,x)$^{\mathrm {22}}$Na induced in the Cu, Ti and Al foils, respectively, as monitors. Those monitor foils were placed in front of a stack as a Cu–Ti–Al arrangement during the irradiation. The monitor reactions were chosen owing to their nearly stable excitation function and better recommended precision for the proton energy range of this work. The proton flux was determined using the measured decay rates of $^{\mathrm {62}}$Zn, $^{\mathrm {46}}$Sc and $^{\mathrm {22}}$Na at EOB and the recommended cross-section values of the respective monitor reaction [49]. A simple average of the three individual fluxes obtained from the three monitor reactions was then taken and the value was used to determine the cross section of the investigated reaction. The proton flux values from the above three monitors agreed with the average value within 2–6%. Furthermore, we also determined the whole excitation function of each monitor reaction. Our data reproduced the recommended curves given by the IAEA [49] very well. This exercise provided additional confidence to the various techniques used in our measurements. The computer program, STACK, written at FZJ and based on the energy-range relation [50], was utilized to determine the beam energy degradation along the stack.

2.3 Radioactivity measurement

The radioactivity of the relevant radionuclides formed in $^{\mathrm {86}}$SrCO$_3$-samples and monitor foils was measured non-destructively using several high-purity germanium (HPGe) gamma-ray detectors, supplied by ORTEC, coupled with the necessary electronics and Maestro data acquisition software. The energy resolutions (FWHM) at 1332.5 keV of $^{\mathrm {60}}$Co of the detectors used were: 1.9 keV at FZJ and 2.5 keV at LBNL. The standard point sources $^{\mathrm {22}}$Na, $^{\mathrm {54}}$Mn, $^{\mathrm {57}}$Co, $^{\mathrm {60}}$Co, $^{\mathrm {88}}$Y, $^{\mathrm {137}}$Cs, $^{\mathrm {152}}$Eu, $^{\mathrm {226}}$Ra and $^{\mathrm {241}}$Am, supplied by Eckert & Ziegler, Berlin, were used for efficiency calibration of the $\gamma$-ray detectors at FZJ, and the $^{\mathrm {54}}$Mn, $^{\mathrm {133}}$Ba, $^{\mathrm {137}}$Cs and $^{\mathrm {152}}$Eu sources, supplied by Isotope Products Laboratories, were used for the detector at LBNL. The uncertainty in the activity of each source was specified as 3%. The $\gamma$-ray spectra measured were analyzed by both the GammaVision and FitzPeaks [51] software. A typical $\gamma$-ray spectum of a sample irradiated with 8 MeV protons has been recently reported [52]. At a higher incident proton energy, e.g. at 30 MeV, the $\gamma$-ray spectrum showed many more peaks but the main $\gamma$-rays of the products of interest could be conveniently analysed.

Samples were counted at various distances, viz. 10, 20, 30 and 50  cm from the surface of the detector depending on the half-life and activity of the irradiated sample. The dead time of the system was kept below 5%. The long-lived radionuclides $^{\mathrm {83}}$Rb (T$_{\nicefrac {1}{2}}$ = 86.2 d) and $^{\mathrm {84}}$Rb (T$_{\nicefrac {1}{2}}$ = 32.8 d) were measured at 5  cm from the detector surface to obtain good counting statistics. For all the above counting distances, the effect of the sample size on the efficiency and also the random coincidence loss became almost negligible. The correction for the true coincident $\gamma$-ray summing was, however, not negligible. The corrections were estimated with the TrueCoinc program [53] and the values obtained are given in Table 2 along with other related nuclear reaction and decay data [54,55,56,57,58,59,60]. The true coincidence losses for $^{\mathrm {83}}$Sr and $^{\mathrm {86}}$Y measurements were higher, because their decay schemes contain many cascade gamma transitions.

Table 2 Decay data including $\beta$ $^+$, EC branching [54,55,56,57,58,59,60], coincidence loss and production routes of the investigated radionuclides in irradiations of enriched $^{\mathrm {86}}$Sr with protons of energies up to 44  MeV

Measurements were carried out in four steps, depending on the half-life of the product. The short-lived $^{\mathrm {86m}}$Y (T$_{\nicefrac {1}{2}}$ = 47.4  min) activity was measured within 2 to 3 h after EOB at a distance of 50 cm. It was identified by its characteristic $\gamma$-ray of energy 208 keV. Special attention was paid to attenuation of that $\gamma$-ray as well as to detector efficiency for that gamma line. During the counting the Al-cover (10 $\mu {\mathrm{m}}$ thick) side of the $^{\mathrm {86}}$SrCO$_3$-sediment was always kept downward, i.e., facing the detector to minimize the absorption in Al. The absorption of the 208  keV gamma line in both the $^{\mathrm {86}}$SrCO$_3$ sediment and the Al-cover was estimated; it amounted to about 0.05% and 0.03%, respectively.

In the second step of counting, the radioactivity of each of the two radionuclides $^{\mathrm {85m}}$Y (T$_{\nicefrac {1}{2}}$ = 4.86 h) and $^{\mathrm {85g}}$Y (T$_{\nicefrac {1}{2}}$ = 2.68 h) was measured at a distance of 30 cm. The $^{\mathrm {85m}}$Y mainly decays directly to $^{\mathrm {85}}$Sr with a negligible isomeric transition branching (< 0.002%) to the ground state $^{\mathrm {85g}}$Y. The $^{\mathrm {85m}}$Y activity was assessed by its characteristic gamma line at 535.6 (3.46%) keV. It was also checked by measurement of other three weak gamma lines at 767.3 (3.6%), 768.6 (1.3%) and 769.7 (0.3%) keV as a triplet. For $^{\mathrm {85g}}$Y activity measurement, the 504 keV $\gamma$-line was used. It was located close to the 511 keV annihilation peak, with partial overlapping. Using the FitzPeak gamma analysis software [51], net peak area of the 504 keV line could be determined conveniently.

The third step of counting was devoted to the measurement of the $^{\mathrm {86g}}$Y (T$_{\nicefrac {1}{2}}$ = 14.7 h) radioactivity after the complete decay of $^{\mathrm {86m}}$Y (T$_{\nicefrac {1}{2}}$ = 47.4 min) to the ground state, i.e. about 12 h after EOB. The last step of measurement of each sample was related to the determination of radioactivity of the long-lived products $^{\mathrm {83}}$Rb (T$_{\nicefrac {1}{2}}$ = 86.2 d) and $^{\mathrm {84}}$Rb (T$_{\nicefrac {1}{2}}$ = 32.8 d). Counting was done about 10 d after EOB at a distance of 5 cm for 16–30 h. This provided good counting statistics for those radionuclides. The radionuclide $^{\mathrm {83}}$Rb was formed via the $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {83}}$Rb process. Above 32  MeV proton energy this radionuclide was also produced in the decay of $^{\mathrm {83}}$Sr. Its decay contribution to the formation cross section of $^{\mathrm {83}}$Rb was corrected from its individual production cross section measured in this work. It was observed that about 95–99% of the total $^{\mathrm {83}}$Sr formed decayed to $^{\mathrm {83}}$Rb before the measurement. The radionuclide $^{\mathrm {83}}$Sr was characterized by its three individual gamma rays at peak energies of 381.5 (14%), 418.3 (4.19%) and 762.6 (26.7%) keV. A weak gamma-line at 381.1 (1.79%) keV was not isolated from the neighboring peak at 381.5  keV. Therefore, the total net area of the doublet peak and sum of their intensities were used. The $\beta$ $^{+}$ branching was taken from the Table of Radioactive Isotopes [59], except for $^{\mathrm {86g}}$Y where the latest value was used [60]. The decay data used are collectively given in Table 2. The decay and production data of the monitor reaction products were taken from [49].

2.4 Cross sections (with corrections for subsidiary reactions)

The count rate of a characteristic $\gamma$-ray of a reaction product was converted to the decay rate by applying the necessary corrections for $\gamma$-ray intensity, efficiency of the detector and true coincidence losses, if any, and thereafter extrapolated to the end of bombardment (EOB). From the decay rate at EOB and the proton beam intensity measured by activation of the monitor foils, the cross section for the formation of the radioactive product was calculated using the well-known activation formula. For each radionuclide, generally a few repeated measurements with different detectors were carried out and several $\gamma$-rays were analysed to check the validity of results. Finally, an average of all the cross-section values was taken.

While measuring proton-induced reaction cross sections using a 96.4% enriched $^{86}$Sr target, some contributions to the reaction product from subsidiary reactions on the undesired target isotopes $^{\mathrm {87}}$Sr (1.33%) and $^{\mathrm {88}}$Sr (2.26%) present in the enriched $^{\mathrm {86}}$Sr were also expected. We estimated those contributions from model calculation using the TALYS code and the results are given in Table 3 for the radionuclides of interest. The calculated contribution was subtracted from the measured cross section of the radionuclide. The contribution was significant in the experiments with 44  MeV protons and amounted up to 37%. In the special case of $^{\mathrm {84}}$Rb, below 30  MeV the contribution from the subsidiary reactions was much higher than that from the $^{\mathrm {86}}$Sr target; at higher energies, however, it became negligible.

Table 3 Corrections for the contribution of the proton induced reactions on the impurities $^{87}$Sr and $^{88}$Sr target isotopes

2.5 Uncertainties

The overall uncertainty in the cross section was obtained by summing in quadrature the individual uncertainties involved in all parameters needed to calculate the cross section. The uncertainty of each cross-section value includes individual uncertainties in: counting statistics (1–5%), efficiency of the detector (5%), true coincidence correction (< 2%), decay data, especially $\gamma$-ray intensities (0.9–8.4%), proton flux (6%) and sample homogeneity (up to 5%). The uncertainty of the net peak area obtained from FitzPeaks analysis for the good Gaussian peaks was accepted. For weak and unsmooth peaks, the uncertainty associated with the peak area was calculated manually. The overall uncertainties of measured cross sections are between 8 and 16% (1$\sigma$), including 15% uncertainty in the contribution of the subsidiary reactions deduced from the nuclear model calculations.

The isomeric cross-section ratio was calculated as the ratio of $\sigma _m$/$\sigma _{g+xm}$ for the $^{\mathrm {86m,g}}$Y pair, because the isomeric state decays 99.31% to the ground state. The uncertainty of the isomeric ratio was estimated from the individual uncertainties in counting statistics, detector efficiency, $\gamma$-ray intensity and half-life of both the metastable state and the ground state, using the dividing formula for the cross sections of metastable state and ground state, thereby eliminating the common parameters [25]. The uncertainty in the isomeric cross-section ratio was thus smaller and amounted to 5–8%. For the $^{\mathrm {85m,g}}$Y pair we calculated $\sigma _m$/$\sigma _{g}$, i.e., the ratio of the directly measured values and not $\sigma _m$/$\sigma _{g+xm}$, because the two states decay independently to the daughter $^{\mathrm {85}}$Sr. The associated uncertainty was about 12% and thus comparatively higher due to uncertainty inferred from the gamma-ray intensity of $^{\mathrm {85m}}$Y.

3 Nuclear reaction model calculations

The reaction cross sections were calculated using the nuclear model code TALYS [61] version 1.9, adopting equidistant excitation energy grid. TALYS incorporates several nuclear models to analyze all the significant nuclear reaction mechanisms over the energy range of 1keV to 200  MeV. In the calculations, the particle transmission coefficients were generated via the spherical optical model using the ECIS-06 code [62] with global parameters: for neutrons and protons from Koning and Delaroche [63]; for the optical model parameters (OMP) of complex particles (d, t, $^3$He) the code made use of a folding approach, building up the OMPs from the neutron and proton potential. For OMP of alpha particles the TALYS default parameter set of Avrigeanu et al. was used [64]. The OM parameters for protons and neutrons were modified to get the best description of the experimental data. The gamma-ray transmission coefficients were calculated through the energy-dependent gamma-ray strength function according to Kopecky and Uhl [65] for E1 radiation, and according to Brink [66] and Axel [67] for all the other transition types. For the pre-equilibrium reactions, a two-component exciton model of the TALYS code was used. The energies, spins, parities, and branching ratios of the discrete levels were based on the RIPL-3 database [68]. In some cases, the energies, spins, parities, and branching ratios of the discrete levels were modified based on the information in Ref. [57]. In the continuum region, the level density was calculated by the back-shifted Fermi gas model (BSFG), using its slightly modified version in TALYS [69]. For the ratio of the effective moment of inertia to the rigid body moment of inertia parameter ($\eta$ = $\Theta _{eff}/\Theta _{rig}$) of the spin distribution of the level density, the systematics based on the evaluation by Sudár and Qaim [25] was used. Regarding discrete levels, it is known that their influence on the calculated isomeric cross-section ratio is very strong. In the case of $^{86}$Y some nuclear structure properties are either not known or known tentatively. Many of these missing/tentative data are assumed and available in the TALYS input based on RIPL [68]. Our initial attempt considering that input could not reproduce the measured isomeric-ratio data for the $^{\mathrm {86m,g}}$Y reaction. As a result, we examined the case with other possible spin-parity assignments within the limit of supporting arguments listed in Ref. [57] and references therein. Different assumptions were also made for depopulating transition and branching from levels, for which no experimental data are known. A summary of the final assumptions for all the low-lying excited levels of $^{\mathrm {86}}$Y to model the experimental ratio is described in Sect. 4.2.

4 Results and discussion

4.1 Reaction cross sections

The measured cross sections for the reactions $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m}}$Y, $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86g+xm}}$Y, $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m}}$Y, $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85g}}$Y, $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {83g}}$Rb and $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {84g}}$Rb are given in Table 4. The data for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86g+xm}}$Y reaction from threshold up to 25.4  MeV have been recently reported [45]. They are used here in nuclear model analysis together with the other data. It is pointed out that the cross sections for $^{\mathrm {83}}$Rb refer to its direct production from the $^{\mathrm {86}}$Sr target, since the contribution via the decay of $^{\mathrm {83}}$Sr was subtracted.

Table 4 Measured cross sections for the production of radionuclides via the $^{\mathrm {86}}$Sr+p process

4.2 Comparison of experimental data with model calculations

4.2.1 Effect of level scheme

The experimental data are generally compared with the calculated data obtained using a reaction code with default parameters implemented in the model. The parameter database of the code comes from other experiments. Unfortunately, only a few experiments are available, i.e. the OMPs of the proton-nuclei interaction are based on 26 measurements [63]; and for other nuclei, those data are extended by a fitted formula which is not theoretically proven. The original experiments also have experimental uncertainty and the fitted formula further increases the uncertainties of the implemented parameter set. It is therefore practically difficult to distinguish the origin of discrepancy between the experimental and model calculated data.

Fig. 1

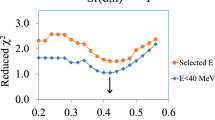
Effect of various assumed level transitions (A, B, C) on the calculated isomeric cross-section ratio of the pair $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y (for details see text). In this diagram the reduced $\chi ^2$ for each model calculation for each energy point is shown. Results based on our experimental data (from 8.3 to 14.7  MeV) are marked as A1, B1, and C1, and those on Levkovskii data [43] (from 9.5 to 14.8  MeV) as A2, B2 and C2. The assumption C, i.e., the transition 353 keV (3$^{+}$) $\longrightarrow$  303 keV (7$^{+}$) gives the best result

Before performing analysis on cross sections, we first investigated the isomeric cross-section ratios for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y and $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m,g}}$Y reactions. As mentioned in Sect. 3, the initial attempt considering the TALYS $^{86}$Y low-lying level input based on RIPL database [68] did not reproduce the measured isomeric-ratio data for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y reaction. From comparisons of the experimental and calculated level density for the low-lying states of $^{\mathrm {86}}$Y along with the isomeric cross-section ratio through the reduced $\chi ^2$ as a function of the number of discrete levels indicated that the first 10 (up to 476 keV) or 20 (up to 900 keV) discrete levels of $^{\mathrm {86}}$Y are important for the calculation. Among these, level 7 (353 keV: 3$^{+}$) shows a significant influence. It may be mentioned here that for this level no experimental data are available for connecting (population/depopulation) transitions and branching ratio with other levels. As a result, we performed calculations with three versions of the level/decay scheme considering different possible spins of the 353 keV level as one of the population routes for the isomeric state at 218 keV (8$^{+}$). For 536 and 643 keV levels also no experimental connecting transition with other levels are known.

The assumed transitions and branching (100% - when not listed above the arrow) were as follows:

(A)  643 keV (3$^{+}$) $\xrightarrow {\text { 50\% }}$ 536 keV (3$^{+}$) $\longrightarrow$

353 keV (5$^{+}$) $\longrightarrow$ 303 keV (7$^{+}$)

(B)  536 keV (3$^{+}$) $\xrightarrow {\text {90\%}}$  353 keV (4$^{+}$) $\longrightarrow$

303 keV (7$^{+}$)

(C)  353 keV (3$^{+}$) $\longrightarrow$   303 keV (7$^{+}$)

The results are shown in Fig. 1, calculating the reduced $\chi ^2$ for those measured data which have energy less than the given proton energy, comparing them with the different calculations for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y reaction. The calculation was done by the Eq. (1) using the parameter E$_i <~$E(p). We denote the results based on [45] and this work as A1, B1 and C1, and the Levkovskii data [43] as A2, B2 and C2. In these calculations, in all cases, the optimal $\eta$ and number of the discrete levels were used (see next section). The $\chi ^2$ values are high for the lowest energy data. This shows that the deviation originated from the low energy data for the level 353 keV using 5$^{+}$ and 4$^{+}$ spin parity values, and the best result for the model calculation is the 3$^{+}$ value, therefore the C branching scheme was used in all model calculations related to our experimental data.

The reduced $\chi ^2$ for Levkovskii data are smaller because of the 10% fictive uncertainties inserted by the compilers of those data. The lowest energy data point is higher, therefore the data start at higher energy. The level 353 keV 3$^{+}$ and 4$^{+}$ produce almost the same reduced $\chi ^2$ values and the best description of Levkovskii data is given by the level 353 keV 5$^{+}$ which is the best from the structural point of $^{\mathrm {86}}$Y. The best level scheme (C) from our data being different from (A) for Levkovskii data indicates that we are unable to decide between the level schemes of $^{86}$Y, and direct measurement of the branching ratios of the levels is needed.

In the case of $^{\mathrm {85}}$Y there was a similar problem (no experimental branching data) with the level 7 (752 keV: 3/2). It was set to decay to the ground state (0 keV: 1/2$^{-}$). We modified the branching to the level which has the same parity as level 7. The spin (9/2) of the isomeric state (19 keV) is not unambiguously defined and is indicated within parentheses [56]. A defined minimal value for the $\chi ^2$ was found only with a spin of (11/2). We used this value in the model calculation.

After proper choice of the level schemes of $^{\mathrm {86}}$Y and $^{\mathrm {85}}$Y, we investigated three items theoretically in detail: 1. $\eta$ values, to check the consistency of data, 2. isomeric cross-section ratios, and 3. excitation functions. A description of each item is given below.

4.2.2 Analysis of $\eta$ values

Since the covariance matrix of the isomeric cross-section ratio is usually not published, we used a simplified formula to calculate the $\chi ^2 (\eta ,N_d)$ which contains uncertainties of the experimental data.

$$\begin{aligned} {{\chi }^{2}}\left( \eta ,N_d \right) =\sum \limits _{i=1}^{N}{\frac{{{\left( \frac{{{\sigma }_{m}}{{\left( {{E}_{i}} \right) }_{\exp }}}{{{\sigma }_{g+xm}}{{\left( {{E}_{i}} \right) }_{\exp }}}-\frac{{{\sigma }_{m}}{{\left( {{E}_{i}},\eta ,N_d \right) }_{theo}}}{{{\sigma }_{g+xm}}{{\left( {{E}_{i},\eta ,N_d } \right) }_{theo}}} \right) }^{2}}}{{{\varepsilon }^{2}}{{\left( {{E}_{i}} \right) }_{\exp }}}}~~ \end{aligned}$$

(1)

where ${{E}_{i}}$ is the incident energy, $\varepsilon$ the uncertainty of the isomeric cross-section ratio, N$_d$ the number of discrete levels, and the indices refer to experimental data or theoretical calculation. The reduced chi-squared is defined as $\chi _\nu ^2$ = $\frac{\chi ^2(\eta ,N_d)}{\nu }$, where $\nu$ is the degree of freedom.

Fig. 2

Reduced $\chi ^2$ of the isomeric cross-section ratio as a function of the $\eta$ = $\Theta _{eff} /\Theta _{rig}$ parameter of the level density formula for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m+g}}$Y reaction

In Fig. 2 the reduced $\chi ^2$ is shown as a function of $\eta$ for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y reaction. Each point represents a different model calculation with a different $\eta$ parameter value and its comparison with the experimental data according to the above formula. It is summed for all energies for each experiment. The best $\eta$ value is determined by the minimal value of the reduced $\chi ^2$. Figure. 2 depicts that the isomeric cross-section ratios of this work and those of Levkovskii [43] have a definite minimum as a function of the $\eta$ parameter while the data by Rösch et al. [44] do not have a minimal value.

It should be mentioned that the data published by Levkovskii [43] are the ground state $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86g}}$Y and metastable $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m}}$Y cross sections. To make them comparable to the value in this experiment the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86g+xm}}$Y data were calculated using the formula $\sigma _{g+xm} = \left( \sigma _g+P_m\frac{\lambda _m}{\lambda _m-\lambda _g}\sigma _m\right)$ [70], where $P_m$ is the probability of the isomeric transition to the ground state and $\lambda _m$ and $\lambda _g$ are the decay constants of the metastable and ground states. The factor x describes the correction for the direct decay of m state to $^{\mathrm {86}}$Sr and is expressed as $x = P_m\frac{\lambda _m}{\lambda _m-\lambda _g}$. It was calculated as 1.055. The resulting cross sections were further modified by a reduction factor of 0.75 determined from the cross-section ratio of the monitor reaction $^{\mathrm {nat}}$Mo(p,x)$^{\mathrm {96}}$Tc value adopted now compared to the value used then by Levkovskii. The evaluated cross section at 30  MeV is 188 ± 2 mb [70]. Comparing this value with the value of 250 mb used by Levkovskii, a reduction factor of 0.75 ± 0.01 is obtained, i.e. 25% reduction [70]. This reduction factor, however, does not have any effect on the isomeric cross-section ratio because it is eliminated during the calculation of the ratio.

The evaluated $\eta$ value for the present measurement is $\eta$ = 0.63 ± 0.04 while that for the Levkovskii measurement [43] it is 0.69 ± 0.07. The results of the two evaluations thus agree within the uncertainty limits. But these data disagree with the systematics developed in Ref. [25]. The need for correction in the level scheme was discussed above through the calculation of the above measured data in the low energy range where only parameters of the discrete levels define the isomeric cross-section ratio. The data by Rösch et al. [44] are inconsistent.

Fig. 3

Reduced $\chi ^2$ of the isomeric cross-section ratio as a function of the $\eta$ = $\Theta _{eff} /\Theta _{rig}$ parameter of the level density formula for the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m,g}}$Y reaction

Figure 3 shows the reduced $\chi ^2$ values for the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m,g}}$Y reaction as a function of $\eta$ = $\Theta _{eff} /\Theta _{rig}$. In this case, the measured data are the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85g}}$Y and $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m}}$Y cross sections, therefore the ${\sigma _m}/{\sigma _g}$ ratio was analyzed. Using the ratio of the measured values is preferred because any other formulation will increase the uncertainty of the data.

The measurement by Rösch et al. [44] contains only a few points which show large scatter and are not suitable for the analysis. The best-fitted value of $\eta$ = $\Theta _{eff} /\Theta _{rig}$ for this work is $\eta$ = 0.57 ± 0.06, and for the Levkovskii data [43] it is $\eta$ = 0.69 ± 0.13. Although Levkovskii did not give any experimental details, his data overlap with the isomeric cross-section ratio from this work; it is thus possible to analyze them together. The result is $\eta$ = 0.60 ± 0.05. These data are near to the value of 0.67 deduced from the systematics [25]. The reduced $\chi ^2$ are 0.45, 1.05, and 0.64, respectively. These reduced values indicate that the isomeric cross-section ratios of the two measurements (this work and Ref. [43]) are consistent.

Comparing the results of the two investigated isomeric pairs ($^{\mathrm {86m,g}}$Y, $^{\mathrm {85m,g}}$Y), the odd/even effect in the $\eta$ value appears to be consistent, but for $^{\mathrm {86}}$Y it is not as pronounced as expected from the systematics [25].

Fig. 4

Comparison of experimental data with the model calculation for the isomeric cross-section ratio of the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y reaction. Plotted are $\sigma _m$/$\sigma _{g+xm}$ values against the proton energy

4.2.3 Isomeric cross-section ratios

(a) $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m,g}}$Y reaction. The experimental isomeric cross-section ratios obtained in this work as well as those reported in the literature [43, 44] are shown in Fig. 4 using the best $\eta$ values determined in Sect. 4.2.2.

As mentioned above, the data by Rösch et al. [44] are rather erratic, so they were not considered further. The other two sets of data agree fairly well till about 23  MeV; thereafter the Levkovskii data [43] are somewhat higher than our values. The increasing value of the isomeric cross-section ratio with the increasing proton energy is attributed to the higher spin of the metastable state (8$^{+}$) as compared to that of the ground state (4$^{-}$). The calculated isomeric cross-section ratio describes well the measured data, which are characterized by the reduced $\chi ^2$ value of 0.29 for the present data and 0.85 for the Levkovskii data. The two sets can be fitted by model calculated curves, adopting an $\eta$ value of 0.63 in the case of our data up to 44  MeV and 0.69 in case of Levkovskii data up to 30  MeV.

Fig. 5

Comparison of experimental data with the model calculation for the isomeric cross-section ratio of the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m,g}}$Y reaction. Plotted are $\sigma _m$/$\sigma _{g}$ values against the proton energy

(b) $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m,g}}$Y reaction. Fig. 5 shows the literature experimental data [43] as well as the data obtained in this work. A comparison of those data with the model calculation is also given. In this case we plotted the $\sigma _m$/$\sigma _{g}$values because they were directly measured and the uncertainty was smaller. The isomeric cross-section ratio again shows an increase up to 32  MeV and thereafter a slight decrease. The increase is due to the higher spin of the metastable state, (9/2$^{+}$) or (11/2$^{+}$), as compared to that of the ground state (1/2$^{-}$). A good agreement is found between the experimental data of this work and those of Levkovskii [43] up to 30  MeV, except for his two erratic values near the threshold. A comparison with the model calculation shows that in the energy range of 17 to 24  MeV the model systematically underestimates the experimental data. Since in this energy range mostly the contribution of the discrete levels is dominant, this may be an indication that the level scheme has some problems. Beyond 25  MeV, however, the experimental and model calculated results agree rather well.

4.2.4 Excitation functions

(a) $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86g+xm}}$Y reaction. The consistency of the nuclear reaction model calculation and the experimental data was checked by the reduced $\chi ^2$ analysis. In this case, the isomeric cross-section ratio is substituted in the Eq. 1 by $\sigma (E_i)_{exp}$ and $\sigma (E_i)_{model}$, respectively. During the calculation, the optical model parameters for proton and neutron were modified to get the best description of the experimental data. The present results together with the literature data are shown in Fig. 6, whereby our data up to 24.5  MeV are the same as reported earlier [45]. The experimental data of Rösch et al. [44] are significantly higher than the other two data sets. There is no clear explanation for the discrepancy. The Levkovskii data [43] were also too high but they have been reduced by the normalization factor of 0.75, as mentioned above. They are still higher than our data in the energy range up to 15  MeV; beyond that energy they are quite near to this measurement.

A reduced $\chi ^2$ value of 2.59 was achieved for our data for this reaction, which is quite far from the expected value of about 1.0. A significant deviation occurs only above 23  MeV where the scatter in the data is rather high. On the other hand, in that energy range this reaction becomes a rather weak channel compared to other nuclear processes like (p,xn), (p,pxn), etc. Keeping this in view, the agreement between the experimental data and the model calculation may be regarded as fairly good.

Fig. 6

Comparison of experimental data with the model calculation for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86g+xm}}$Y (color online). Our experimental data are based on measurements at three cyclotrons (88-Inch, BC1710 and JULIC)

Fig. 7

Comparison of experimental data with the model calculation for the $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m}}$Y reaction (color online); other details are the same as in Fig. 6

(b) $^{\mathrm {86}}$Sr(p,n)$^{\mathrm {86m}}$Y reaction. The measured and calculated cross-sections for this reaction are presented in Fig. 7. The reduced $\chi ^2$ value was 2.09 which is far from the expected value of about 1.0. Whereas the data by Rösch et al. [44] are rather erratic, between 23 and 30  MeV our data are significantly lower than the Levkovskii measurement [43]. Beyond 30 MeV no data exist in the literature. Our data set consists of two independent measurements. Each measurement with independent analysis is consistent with the model calculation but analyzing them together some inconsistency is observed, revealing some scatter in the results. Since the isomeric cross-section ratio is very good ($\chi ^2_{red}$ = 0.29) (see above), some experimental parameters affect the measured cross section, which are eliminated in the isomeric cross-section ratio (e.g., particle current, mass, etc.).

(c) $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85g}}$Y reaction. The experimental data and the model calculation for this reaction are depicted in Fig. 8. Our experimental data and the Levkovskii data [43] are in good agreement up to 25 MeV. The best approximation of the experimental data with the model calculation gives a reduced $\chi ^2$ value of 2.45. The experimental data are reproduced fairly well by the model calculation.

Fig. 8

Comparison of experimental data with the model calculation for the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85g}}$Y reaction (color online); other details are the same as in Fig. 6

(d) $^{\mathrm {86 }}$Sr(p,2n)$^{\mathrm {85m}}$Y reaction. Figure 9 presents a comparison of the experimental data from this work, Rösch et al. [44] and Levkovskii [43] with the model calculation. The few data points by Rösch et al. [44] for this reaction are also erratic; they were therefore not considered. Our data and the Levkovskii data are in good agreement up to 25 MeV; however, between 25 and 30  MeV our data are lower. Beyond that energy no data exist in the literature. The model calculation reproduces our data. The reported energy of the first data point is below the energy threshold of the reaction, therefore it was excluded from the reduced $\chi ^2$ calculation. In the full energy range, the model calculation gives a reduced $\chi ^2$ of 1.56. This indicates the consistency between the experimental data and the theory.

Fig. 9

Comparison of experimental data with the model calculation for the $^{\mathrm {86}}$Sr(p,2n)$^{\mathrm {85m}}$Y reaction (color online); other details are the same as in Fig. 6

Fig. 10

Comparison of experimental data with the model calculation for the $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {83}}$Rb reaction (color online); other details are the same as in Fig. 6

(e) $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {83}}$Rb reaction. The experimental cross-section data for the independent formation of $^{\mathrm {83}}$Rb from $^{\mathrm {86}}$Sr (i.e., after subtracting the decay contribution from $^{\mathrm {83}}$Sr), determined in this work, are shown in Fig. 10 together with the experimental data by Qaim et al. [71] and Levkovskii [43] as well as the results of the model calculation. The experimental data of this work and those by Qaim et al. [71] show quite a good agreement up to 18  MeV. The Levkovskii data [43] indicate an energy shift in the first two data points and the compound peak is much broader than in other works. Between 23 and 30  MeV the Levkovskii data are significantly higher than our data. It is not known whether he subtracted the $^{\mathrm {83}}$Sr feeding. The reduced $\chi ^2$ is 2.59 which indicates a relatively poor agreement of the experimental data with the model calculation.

It should be pointed out that the production cross section of the radionuclide $^{\mathrm {83}}$Rb measured by the activation method contains contributions from several different routes, as depicted in Fig 11. The most important reaction type is the (p,$\alpha$) which includes direct, compound, exciton model, pre-compound nucleon transfer (NT), and knock-out (KO) contribution too. Above 25  MeV, however, other important possible routes are (p,$^{\mathrm {3}}$He n) and (p,2n2p). The order of the other routes is: (p,npd), (p,pt) and (p,2d).

A comparison of Figs. 10 and 11 shows that up to about 33  MeV proton energy, the product $^{\mathrm {83}}$Rb is formed almost exclusively via the $^{\mathrm {86}}$Sr(p,$\alpha$)$^{\mathrm {83}}$Rb reaction. Beyond that energy, however, the contributions of multi-nucleon emission reactions (e.g. $^{\mathrm {3}}$He n, 2p2n, etc.) in comparison to a bound $\alpha$-particle emission start increasing, becoming dominant at the maximum energy of 44  MeV investigated in this work. This effect is, however, not uncommon. We mention three cases where the product nuclide is of medical interest: (a) $^{\mathrm {14}}$N(p,x)$^{\mathrm {11}}$C [72], (b) $^{\mathrm {58}}$Ni(p,x)$^{\mathrm {55}}$Co [73], (c) $^{\mathrm {70}}$Zn(p,x)$^{\mathrm {67}}$Cu [74]. In the low-energy range the (p,$\alpha$) reaction is important but at energies above about 30  MeV, multi-nucleon emission reactions have higher cross sections. A detailed theoretical analysis of those three cases was, however, not presented.

Fig. 11

Model calculations with TALYS showing contributions of different routes to the production of the radionuclide $^{\mathrm {83}}$Rb (color online)

Fig. 12

Comparison of experimental data with the model calculation (sum) for the $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {84}}$Rb reaction (color online)

(f) $^{\mathrm {86}}$Sr(p,x)$^{\mathrm {84}}$Rb reaction. This work describes the first experimental data on this reaction. The reduced $\chi ^2$ was found to be 0.49. The model calculation reproduces relatively well the experimental data (Fig. 12). Model calculations were also done on the various contributing processes, namely (p,$^{\mathrm {3}}$He), (p,pd) and (p,2pn) (Fig. 12 ). The cross section of the (p,$^{\mathrm {3}}$He) reaction is appreciably smaller than that of the multi-nucleon emission process. The relatively low emission probability of a $^{\mathrm {3}}$He-particle in comparison to an $\alpha$-particle may be understood in terms of its rather loosely bound character.

5 Concluding remarks

The cross-section data and the isomeric cross-section ratios of proton-induced reactions on $^{\mathrm {86}}$Sr, measured in this work and partly reported in the literature, were compared with nuclear model calculations. The isomeric cross-section ratios for $^{\mathrm {86m,g}}$Y and $^{\mathrm {85m,g}}$Y were described well by the theoretical models included in TALYS and the quality of the description was numerically quantified. The reduced $\chi ^2$ values were 0.29 and 0.96, respectively, which means that the model can describe on average the experimental data within their uncertainties (1$\sigma$) which is a statistically correct description. However, the cross sections themselves were not described well, despite a (partial) optimization of the parameters of the models. The reduced $\chi ^2$ values for the six reaction products ($^{\mathrm {86g}}$Y, $^{\mathrm {86m}}$Y, $^{\mathrm {85g}}$Y, $^{\mathrm {85m}}$Y, $^{\mathrm {83}}$Rb and $^{\mathrm {84}}$Rb) were 2.59, 2.09, 2.45, 1.56, 2.59, and 0.49, respectively, indicating that the quality of the description is between 1$\sigma$ and 2$\sigma$ (nearer to 1$\sigma$). The larger deviation may arise from partial optimization and some inconsistencies in the experimental data. This optimization procedure can allow to draw conclusion about the nuclear reaction models themselves and provide a possibility to improve the parameter database.

Besides experimental and theoretical studies on excitation functions and isomeric cross-section ratios discussed above, two other facets, namely, the even/odd mass effect on $\eta$ and the competition between a light complex particle and multi-nucleon emission, were also analyzed. Comparing the results of $^{\mathrm {86m,g}}$Y and $^{\mathrm {85m,g}}$Y the even/odd effect in the $\eta$ value appears to be confirmed, and modelling of excitation functions of $^{\mathrm {83}}$Rb and $^{\mathrm {84}}$Rb shows that, when energetically possible, the multi-nucleon emission process contributes more strongly to the product formation than the emission of a complex particle. A general remark could also be made about the practical use of the new data. Although $^{\mathrm {86g}}$Y is the main radionuclide of interest for theranostic studies, because of its shorter half-life $^{\mathrm {85g}}$Y is also of potential interest for some preclinical investigations. The optimum energy range for its production can be deduced from the cross-section data provided in this work.