Low lying particle-hole states in $^\mathbf{206 }$Pb and $^\mathbf{208 }$Pb and the shell model

Abstract

The nucleus $^{206}\mathrm{Pb}$ differs from the doubly magic nucleus $^{208}\mathrm{Pb}$ by two missing neutrons. In $^{208}\mathrm{Pb}$ most states at $E_x< 7.4$ MeV are described by one-particle one-hole configurations. The lowest configurations with a g $_{{ 9}/{2}}$ particle and dominant p $_{{ 1}/{2}}$, f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$ holes and admixtures from f $_{{ 7}/{2}}$ and a few more configurations build an ensemble of two dozen states at 3.2$<E_x< 4.9$ MeV. They are described by rather complete orthonormal transformation matrices of two dozen states with spins from 2$^-$ to 8$^-$ to configurations. In $^{206}\mathrm{Pb}$ a similar ensemble of states is deduced from the analysis of angular distributions measured in 1969 for the $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ reaction via the g $_{{ 9}/{2}}$ IAR in $^{207}\mathrm{Bi}$. An equivalent $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ experiment was performed in 1968 at the Max–Planck–Institut für Kernphysik at Heidelberg (Germany). New spins are determined for 32 states and 22 levels in $^{206}\mathrm{Pb}$. The comparison to corresponding states in $^{208}\mathrm{Pb}$ studied especially in 1982 yields both remarkable similarities and clear differences. Sizeable g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength found in 4$^-$ and 5$^-$ states is interpreted as admixtures of ${{\textit{p}}}{_{{ 3}/{2}}}^{-2}$ and ${{\textit{f}}}{_{{ 5}/{2}}}^{-2}$ components to the ground state of $^{206}\mathrm{Pb}$ with dominant ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$ character. The description of nuclear states by shell model particle-hole configurations in the lead region needs the inclusion of collective excitations at already very low excitation energies. For the two isotopes $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ a rather good agreement of excitation energies and configuration mixing is observed for states at 3.7$<E_x< 4.7$ MeV.

1 Introduction

Nuclei in the vicinity of the doubly magic $^{208}\mathrm{Pb}$ are an excellent playing ground for the examination of nuclear models. Different approaches use the schematic shell model without residual interaction (SSM) [1], the weak coupling model [2], shell model calculations with residual interactions derived in various ways [3,4,5,6,7,8,9,10,11] as well as combined models [12,13,14,15,16,17,18]. Shell model calculations around $^{208}\mathrm{Pb}$ investigate the interaction among nucleons spanning extended valence spaces $50 \le Z \le 126$ and $82 \le N \le 184$.

The comparison of the doubly magic $^{208}\mathrm{Pb}$ with two valence nucleons discussed recently [8, 9] may elucitate the successful description for $^{206}\mathrm{Pb}$ [19, 20] and $^{208}\mathrm{Pb}$ [1, 16, 21,22,23].

In order to study the residual interaction among particle-hole configurations [24] the proton decay of the g $_{{ 9}/{2}}$ isobaric analog resonance (IAR) in $^{207}\mathrm{Bi}$ [19, 20] and $^{209}\mathrm{Bi}$ [25,26,27,28,29,30] was studied at the Max-Planck-Institut für Kernphysik (MPIK) at Heidelberg (Germany) in 1968-1969.

The decisive tool for the analysis of nuclear states in lead isotopes is the inelastic proton scattering via an IAR [13, 31,32,33,34,35,36,37,38,39]. It is equivalent to a neutron pickup reaction on the ground state (g.s.) or excited states in the parent nucleus [40]. All fourty-three neutron one-particle one-hole configurations in the two major shells [6] were thus investigated. Only three out of thirty proton one-particle one-hole configurations are accessible by experiment.

The increasing fragmentation of nuclear matter starts with the breakup of two fragments in $^{208}\mathrm{Pb}$ at excitation energies of 3.2 MeV and at $0< E_x\le 1.8$ MeV for $^{206}\mathrm{Pb}$, $^{210}\mathrm{Po}$, $^{206}\mathrm{Tl}$, $^{210}\mathrm{Bi}$. The fragmentation into three parts starts at $E_x=5.8$ MeV and with four parts at $E_x\approx 10$ MeV. Fragmentation with more than four parts near $A= 208$ is not yet recognized. An open question is the starting energy for fission and ternary fission.

The most numerous type of excitations around the doubly magic nucleus $^{208}\mathrm{Pb}$ occurs with two valence nucleons, see Nuclear Data Sheets for A = 206–210 [21,22,23, 41,42,43,44] and [7,8,9, 16, 45, 46].

Pairing vibration starts with excitation energies of 4.8 MeV for the doubly magic nucleus [47, 48] and 0.2 MeV for semi-magic nuclei [48]. It became known with experiments studying triton beams and enumerate to a handful.

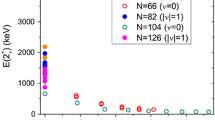
Collective excitations comprising the whole nucleus start to appear with spin 3$^-$ at $E_x=2.6$ MeV for the doubly magic nucleus [49] and semi-magic nuclei ($^{204}$Hg [50], $^{206}\mathrm{Pb}$ [41]).

Collective excitations with spin 2$^+$ start to appear for the doubly magic nucleus $^{208}\mathrm{Pb}$ at $E_x=4.1$ MeV and semi-magic nuclei at $E_x=0.2$ MeV. Collective excitations with spin 1$^-$, 2$^-$, 4$^+$, 6$^+$, 12$^+$ start to appear at higher excitation energies, but still less than 6 MeV.

Different types of collective excitations in $^{208}\mathrm{Pb}$ below 6 MeV have been observed at $E_x=2.6$ MeV [48, 56], 4.09 MeV [51], 4.14 MeV [51], 4.24 MeV [51], 4.44 MeV [52], 4.80 MeV [47], 5.77 MeV [53], 6.10 MeV [52], and at similar energies tentatively identified (5.44 MeV) [52, 54] or suggested [52, 55]. Only a handfull collective states excite the whole nucleus with excitation energies up to 8 MeV [51].

Coupling collective excitations to particle-hole configurations starts at excitation energies of $E_x=5.8$ MeV [17]. Coupling two different modes of collective excitations to particle-hole configurations starts at $E_x\approx 10$ MeV [18].

Large scale shell model calculations with residual interactions derived in various ways [3, 6, 7, 9,10,11] and spanning extended valence spaces are available. Alternative interpretations based on peculiar symmetries, such as pairing, tetrahedral and icosahedral with 2-, 4-, 5-fold symmetry are available [47, 51,52,53, 55,56,57,58,59].

The schematic shell model without residual interaction (SSM) explains most low lying one-particle one-hole (1p1h) states in $^{208}\mathrm{Pb}$ up to $E_x=7.0$ MeV with sufficient accuracy [1]. About 500 particle bound states ($S(n)=7368$ keV, $S(p)=8004$ keV) are known [23]. Among them most (about 300) negative parity states are known at $E_x< 7.5$ MeV [16, 23, 28,29,30, 46, 51, 60,61,62,63,64,65,66,67]. Also several positive parity states at $E_x< 6.3$ MeV are known [1, 23, 53, 68].

The splitting of particle-hole multiplets amounts up to one MeV in many cases [5, 17, 69, 70]. A refinement of the calculations is provided by including the surface $\delta$ interaction (SDI) [4, 5, 71]. The residual interaction in $^{208}\mathrm{Pb}$ is thus reduced to typically 50 keV [16].

Many nuclei in the lead region are well described by the coupling of two nucleons. Few states are described with difficulty. Especially higher lying states in $^{206}\mathrm{Pb}$ are not yet understood. A new theory based on SDI describes particle-hole states in $^{206}\mathrm{Pb}$ [72] but is not yet used. The concept of generalized neutron particle-hole (GNPH) configurations was introduced instead to describe states in the $N=82$ region [12,13,14,15, 36]. Levels described as GNPH configurations in $^{206}\mathrm{Pb}$ resemble one-particle three-hole configurations but also contain the coupling of particle-hole configurations to collective states.

Inelastic proton scattering via an IAR allows to determine amplitudes for all neutron particle-hole configurations [31, 32, 40]. The knowledge of relative signs allows to determine spins by using orthonormality and sum-rule relations [1, 12, 14, 61,62,63,64,65].

Two amplitudes with relative sign were first determined for the 4$^-$ yrast state by Bondorf [35] in 1968. Spin and configuration mixing for a dozen GNPH states in $N=82$ isotones were determined [13, 14, 36] in 1969. Several spins and the configuration mixing for negative parity states in $^{208}\mathrm{Pb}$ were determined [21, 22, 24, 26] in 1969–1973.

A new method described in [46] allows to determine up to five amplitudes of neutron configurations in each state. Angular distributions for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ and $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were thus studied.

Angular distributions for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were obtained by Solf et al. [19, 20] for twenty-two levels at $3.7< E_x <4.7$ MeV in $^{206}\mathrm{Pb}$. Original data are ready to be digitized for further reanalysis [73]. Angular distributions for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were obtained by Glöckner et al. [28, 29] for seventy-eight levels at $3.2< E_x <6.2$ MeV [16, 29] and for sixty levels at $5.8< E_x <7.0$ MeV [46] in $^{208}\mathrm{Pb}$. Original data were digitized [30] and partly analyzed.

In $^{206}\mathrm{Pb}$ new spins are determined for 32 states in twenty-two levels. Amplitudes of GNPH configurations are determined with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components and admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$.

In $^{208}\mathrm{Pb}$ two dozen particle-hole states with excitation energies $3.2<E_x< 4.7$ MeV were first identified in 1969–1973 [24]. States with spins from 2$^-$ to 7$^-$ at $E_x< 4.7$ MeV were described by rather complete orthonormal transformation matrices for two dozen states to configurations. A few spin assignments derived in 1973 needed to be exchanged. The reason for the exchanges in 1982 was the unknown role of the Coulomb interaction for the proton particle-hole configurations [74, 75].

Experiments with the $^{209}\mathrm{Bi}$ $({{\textit{d}}}, {^3\mathrm{He} })$ reaction revealed the correct spin assignments and state identifications [76, 77]. The wave functions deduced from $\gamma$-spectroscopy in 1999 [78] agree with the results from 1982. Amplitudes for positive parity configurations determined in 2010 [1] were found to agree similarily.

All states with spins from 1$^-$ to 7$^-$ in $^{208}\mathrm{Pb}$ at $E_x< 4.7$ MeV were identified in 1982. (The 8$^-$ yrast state was identified in 2006 [61]. The new analysis of the 1$^-$ yrast state was included in 2020 [67].) The exception is the collective state at $E_x= 4.14$ MeV recognized by Glöckner in 1972 [28, 79] but identified as the 2$^-$ yrast state only in 2017 [51].

Amplitudes of 1p1h configurations in $^{208}\mathrm{Pb}$ were determined with dominant g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components and admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$. In addition admixtures from 1p1h configurations with other particles than g $_{{ 9}/{2}}$ were determined. The results obtained in 1982 provided by Table 4 in [51] are sufficient for the comparison to the isotope $^{206}\mathrm{Pb}$. A refined analysis including admixtures from g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ is still awaited.

The nearly exhaustive identification of states in $^{208}\mathrm{Pb}$ at $E_x <6.2$ MeV [16] provides a basis for the comparison of states in $^{206}$Tl, $^{210}$Bi, and $^{206}\mathrm{Pb}$. The comparison of three dozen states in $^{206}\mathrm{Pb}$ and two dozen states in $^{208}\mathrm{Pb}$ reveals the strength distribution of particle-hole configurations in $^{208}\mathrm{Pb}$ and GNPH configurations in $^{206}\mathrm{Pb}$ at $3.7<E_x< 4.7$ MeV to be similar in a remarkable manner. Specific differences are related to two neutrons missing from the doubly magic nucleus $^{208}\mathrm{Pb}$.

Section 2 discusses the shell model description in the lead region. Section 3 reminds to theoretical descriptions used for the analysis of 1p1h states at $E_x <7.2$ MeV in $^{208}\mathrm{Pb}$ [46] and extends them to analyze GNPH states in $^{206}\mathrm{Pb}$ at $3.7<E_x< 4.7$ MeV. Section 4 shortly describes experimental data. Section 5 presents methods to identify states, assign spin and parity, and to determine amplitudes of particle-hole configurations. Section 6 discusses the structure differences of states in $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ at $3.7< E_x <4.7$ MeV.

2 Description of nuclei in the lead region by the shell model

Bromley and Weneser [80] pointed out that several nuclei in the lead region are extremely well described by the shell model. The comparison of particle-hole states in $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ allows to query this statement in detail.

The strong binding of nucleon pairs produces low lying 0$^+$ and 2$^+$ states in each even–even nucleus. They are well described by the pairing vibrational model [47, 53, 81, 82] introduced by Bohr and Mottelson [48].

Doubly magic nuclei have a simple structure described by the chain of spins $0^+, 2^+, 4^+, 6^+, 8^+, 10^+$ [4]. Calculations with SDI [71] explain excitation energies for many nuclear states quite well [4, 5, 17, 69, 70]. For one dozen states at $16\le A \le 210$ the deviation of the excitation energies from the description by SDI is less than 8% for protons and less than 15% for neutrons [70].

Excitation energies of 1p1h configurations in $^{208}\mathrm{Pb}$ are described with similar precision as calculations with realistic forces [9,10,11]. In $^{208}\mathrm{Pb}$ the SSM explains most low lying 1p1h states already with good reliability [1].

2.1 Composition of the ground state in lead isotopes

2.1.1 Ground states in $^{204,206,210}$Pb

The composition of the g.s. in $^{204,206,210}$Pb was investigated by Flynn et al. [82]. About 40%, 12%, 12% strength in the g.s. of $^{204}$Pb are attributed to ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}\otimes lj^{-2}$ with $lj={{\textit{f}}}{_{{ 5}/{2}}}, {{\textit{p}}}{_{{ 3}/{2}}}, {{\textit{i}}}{_{{13}/{2}}}$, respectively, and about 7% each to ${{\textit{f}}}{_{{ 5}/{2}}}^{-2}\otimes lj^{-2}$. About 55% and 20% strength in the g.s. of $^{206}$Pb are attributed to ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$ and ${{\textit{f}}}{_{{ 5}/{2}}}^{-2}$, respectively. Nearly the full strength in the g.s. of $^{210}$Pb is attributed to ${{\textit{g}}}{_{{ 9}/{2}}}^2$. The ${{\textit{g}}}{_{{ 9}/{2}}}^2$ multiplet with spins $0^+, 2^+, 4^+, 6^+, 8^+$ is perfectly described by the SDI [4, 70], especially for $^{210}$Po (see Eq. (9) in [5].) It yielded the single parameter to describe similar multiplets in one and a half dozen two-particle and two-hole nuclei from $^{ 16}O$ to $^{210}$Po [70].

2.1.2 Composition of the ground state in $^{208}\mathrm{Pb}$

Weak admixtures of the three lowest excited 0$^+$ states to the g.s. may be assumed. The 4868 0$^+$ state in $^{208}\mathrm{Pb}$ became known as neutron pairing vibrational configuration from $({{{\textit{t}}}, {{\textit{p}}} })$ and $({{{\textit{p}}}, {{\textit{t}}} })$ experiments [47, 48]. The 5666 0$^+$ state was recognized as proton vibrational configuration [53, 68]. The 5241 0$^+$ state was interpreted as tetrahedral vibration [51]. An interpretation as phonon excitation was given in 1968 [48, 56] and in 2000 [10, 11].

The weakness of admixtures to the g.s. in the doubly magic nucleus can be deduced from the interference pattern observed in the inelastic proton scattering via IARs observed at $19< E_p <21$ MeV [83] and described by the coupling of the g $_{{ 9}/{2}}$ particle to the three lowest excited 0$^+$ states in $^{208}\mathrm{Pb}$. The resonance energies in $^{209}\mathrm{Bi}$ are $E^{res}=19.8$, 20.2, 20.6 MeV.

The excitation functions of $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ for the 5$^-$ yrast and 5$^-$ yrare states indicate an enhancement near these three proton energies for the single scattering angle $\varTheta =165^\circ$ used in the $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ experiment (Fig. 2 in [83]). The structure of the 5$^-$ yrast and 5$^-$ yrare states is precisely described by orthonormal transformation matrices with rank 9 (Table 4 in [51]). The logarithmic dependence of the s.p. width on the proton energy [39] (Fig. 8 in [29]) enhances the cross section for the excitation of g $_{{ 9}/{2}}$ lj for $l2j= p1, p3, f5$ by a big factor with the differences in proton energy of 5-6 MeV. The analysis of the data provided by Fig. 2 in [83] yields an estimate for admixtures of the three lowest excited 0$^+$ states to the g.s. Less than 5% admixture are deduced. The absence of a resonant behaviour for the 4$^-$ yrast state is explained by the different composition [24, 51] and the different energy dependence of the s.p. widths [29].

Interference patterns near the same proton energies are observed in the excitation of the 3$^-$ yrast state (lower frame of Fig. 1 in [83] for $14.0<E_p<22.0$ MeV. Similar excitation functions are obtained for $14.3<E_p<18.3$ MeV in $^{208}\mathrm{Pb}$ [33].

Excitation functions for $14<E_p<20$ MeV in $^{205}$Tl are similar [84]. The coupling of the s $_{{ 1}/{2}}$ particle to the 3$^-$ yrast state is explained by the weak coupling model [2]. A ratio $6:8$ of the cross sections is observed [84].

Some interference patterns can be understood by the admixture of j $_{{15}/{2}}$ $\otimes |3^-_1\rangle$ to the 9/2$^+$ g.s. of $^{209}\mathrm{Pb}$ [56]. The additional pattern in the excitation of the 3$^-$ yrast state observed near $E_p=19.0$ MeV is interpreted by the coupling of the 4086 2$^+$ yrast state to the g $_{{ 9}/{2}}$ particle. (The resonance energy in $^{209}\mathrm{Bi}$ would be $E^{res}=19.01$ MeV.) It is interpreted by the primary excitation of the j $_{{15}/{2}}$ $\otimes |3^-_1\rangle$ component in the 9/2$^+$ IAR followed by the proton decay g $_{{ 9}/{2}}$ $\otimes |2^+_1\rangle \rightarrow$ g $_{{ 9}/{2}}$ $+$ $|3^-_1\rangle$. In the elastic scattering the raise and steep decrease across the resonance observed for the g $_{{ 9}/{2}}$ resonance at $E_p=14.92$ MeV [85] is visibly repeated near $E_p=19.0$ MeV (upper frame of Fig. 1 in [83]). It is typical for a resonance with spin $J=L+{\frac{ 1}{2}}$ [86, 87].

2.2 Hole states in ${^\mathbf{207 }}$Pb, $^\mathbf{207 }$Tl and particle states in $^\mathbf{209 }$Pb, ${}^\mathbf{209 }$Bi

The lowest states in $^{207}\mathrm{Pb}$ are well described by pure one-nucleon configurations in the hole orbits p $_{{ 1}/{2}}$, f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$, i $_{{13}/{2}}$, f $_{{ 7}/{2}}$, h $_{{ 9}/{2}}$, the lowest states in $^{207}\mathrm{Tl}$ by pure one-nucleon configurations in the hole orbits s $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$, h $_{{ 9}/{2}}$, d $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$, the lowest states in $^{209}\mathrm{Pb}$ by pure one-nucleon configurations in the hole orbits g $_{{ 9}/{2}}$, i $_{{11}/{2}}$, j $_{{15}/{2}}$, d $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$, the lowest states in $^{209}\mathrm{Bi}$ by pure one-nucleon configurations in the hole orbits h $_{{ 9}/{2}}$, f $_{{ 7}/{2}}$, i $_{{13}/{2}}$, f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$, p $_{{ 1}/{2}}$, respectively [88].

However the g $_{{ 9}/{2}}$ state in $^{209}\mathrm{Pb}$ is not quite pure, it contains a sizeable admixture from the coupling of the j $_{{15}/{2}}$ particle to the 3$^-$ yrast state [56].

2.3 Pairing vibrational states in ${}^{\mathbf{204,206,208,210 }}$Pb

Neutron pairing vibrational states in the lead region became known from $({{{\textit{t}}}, {{\textit{p}}} })$ and $({{{\textit{p}}}, {{\textit{t}}} })$ experiments [47, 82]. The three-phonon monopole state in $^{206}$Pb related to the two-phonon state in $^{208}\mathrm{Pb}$ and the g.s. of $^{210}\mathrm{Pb}$ was discovered in 1974 [82]: “$\cdots$ actually the 0$^+$ state at 5637 keV observed in the present experiment appears to be one of the purest three-phonon states seen in any region of the nuclides.”

The proton vibrational 0$^+$ state was recognized in 2015 [53, 68] based on the observation by $^{208}\mathrm{Pb}$ $({\alpha , \alpha '} )$ [89, 90].

2.4 Two-hole configurations in ${}^\mathbf{206 }$Pb

The lowest states in $^{206}\mathrm{Pb}$ at $E_x< 3.3$ MeV (Table 4) can be explained by the coupling of two of the first three neutron holes (p $_{{ 1}/{2}}$, f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$) to the 0$^+$ g.s.

First calculations by True and Ford [91] indicated admixtures of about 15% both of f $_{{ 5}/{2}}$ $^{-2}$ and p $_{{ 3}/{2}}$ $^{-2}$ to the dominant configuration p $_{{ 1}/{2}}$ $^{-2}$ in the g.s. of $^{206}\mathrm{Pb}$. Most states at $E_x{ {}^<\!\!\!\!_\sim }3.5$ MeV contain more than 80% of a single two-hole configuration. Calculations with the pairing model yielded similar wave functions [82].

Two-particle transfer experiments explain the lowest states in $^{206}\mathrm{Pb}$ [82] (Table 4). Two-neutron-hole configurations were also studied in low-lying states by $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ via IARs in $^{207}\mathrm{Bi}$ [92]. The calculated mixing of the two-hole configurations [41] is confirmed. The 2$^+$ yrast state is described by the dominant configuration p $_{{ 3}/{2}}$ $^{-1}$ f $_{{ 5}/{2}}$ $^{-1}$. It is also described as a (collective) pairing vibration (Sect. 2.3).

The g.s. of $^{206}\mathrm{Pb}$ is described by the dominant configuration $^{208}\mathrm{Pb}$ $\otimes {{\textit{p}}}{_{{ 1}/{2}}}^{-2}$. Yet strong admixtures of hole pairs ${{\textit{f}}}{_{{ 5}/{2}}}^{-2}$ and ${{\textit{p}}}{_{{ 3}/{2}}}^{-2}$ are present. Details are not discussed in this paper. The concept of generalized neutron particle-hole (GNPH) configurations is introduced instead (Sect. 3.2.1).

2.5 Two nucleon configurations in ${}^\mathbf{206, 208, 210 }{} \mathbf{Pb}$, ${}^{\mathbf{206 }}{} \mathbf{Tl}$, ${}^\mathbf{208, 210 }{} \mathbf{Bi}$

Two nucleon configurations in $^{210}\mathrm{Pb}$ are well described by the SDI [4, 5]. Two nucleon configurations in $^{206}\mathrm{Pb}$ are shortly discussed in Sect.  2.4.

The neutron pairing vibrational 0$^+$ state was discovered in 1970 [47], the proton vibrational 0$^+$ state in 2015 [53, 68]. The distance betwen the 4868 0$^+$ and the 4867 7$^+$ states is determined with 0.4$\pm 0.1$ keV [16, 23]. Two neutron pairing vibrational 2$^+$ states [47, 48] are mixed with 1p1h configurations coupled to the 3$^-$ yrast state [17] and 1p1h configurations at $5.0< E_x <6.2$ MeV [16].

Two nucleon configurations in the odd–odd $^{208}\mathrm{Bi}$ studied by Maier et al. [45] and in $^{210}\mathrm{Bi}$ studied by Cieplicka-Oryńczak et al. [8] revealed a rather simple structure for many multiplets at $E_x< 1.7$ MeV. An essay to describe the multiplet splitting of the lowest configurations by the SDI succeeded mostly rather well but fails for the two lowest states in $^{210}\mathrm{Bi}$. The inversion of the 0$^-$ and 1$^-$ yrast states was understood by the strong core-polarization [7].

Multiplets in the odd–odd $^{206}\mathrm{Tl}$ studied at $E_x< 1.6$ MeV revealed a large configuration mixing [9]. One reason is the small separation between the active orbitals.

2.6 Non-1p1h states in the lead region

In $^{208}\mathrm{Pb}$ more than fifty non-1p1h states among about 500 particle bound states are known [18, 93]. The 1$^-_1$, 2$^-_1$, 3$^-_1$, 2$^+_1$, 4$^+_1$, 6$^+_1$ yrast states, the 12$^+_2$ yrare state, and the 0$^+_{2,3,4}$ states build the lowest excitations not described as 1p1h configurations. The 4140 state was identified by the work of Glöckner [28, 79]. New data [94] confirm the excitation energy with $E_x= 4140$ keV. The residual interaction among 1p1h and non-1p1h is mostly weak. This is especially true for the 2$^-$ yrast state [51] and the 3$^-$ yrast state (Table 4 in [51]).

The SSM does not predict any excited 1p1h configuration with spin 0$^+$ in $^{208}\mathrm{Pb}$. However several low lying excited 0$^+$ states at $E_x<6$ MeV are observed. The 0$^+_{2,4}$ states are known as pairing vibrational states (Sect. 2.3). The 5241 0$^+_3$ state is interpreted as tetrahedral vibration [51]. The 2615 3$^-_1$, 4086 2$^+_1$, 4140 2$^-_1$, 4324 4$^+_1$, 4842 1$^-_1$, 5241 0$^+_3$, 5715 2$^+_{ 3}$, 7020 3$^-_{29}$, 7137 4$^+_{23}$, 7838 3$^-$ states could also be interpreted as tetrahedral configurations [51].

Coupling 1p1h configurations to the 3$^-$ yrast state creates several dozen states. Eighteen states of this type were described by g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 3^-_1$, i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 3^-_1$, and j $_{{15}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 3^-_1$ [17]. The 6$^+$ yrast [23], the 5444 state [54, 95] tentatively identified as the 10$^+$ yrare state, and the 12$^+$ yrare state [11, 16, 96] are suggested as members of an icosahedral rotational band [52]. The coupling of tetrahedral and icosahedral configurations to 1p1h configurations may explain high spin states up to excitation energies of 17 MeV [18, 97].

Finally the unusually long lifetime of the 10$^+$ yrast state with $0.5\upmu$s and the large $\gamma$-transition strength from the 10$^+$ yrast to the 7$^-$ yrast state together with the incomplete g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength in the 4037 7$^-$ state (with only about 70%, see Table If in [24]) may be related to the observation of three non-1p1h configurations with spin 3$^-$, 5$^-$ and 2$^-$ or 5$^-$ at $5.3< E_x< 6.0$ MeV. The 5318 3$^-$ and two 5$^-$ states (5705, 5993) are identified by complete spectroscopy as configurations of unknown type [93]. The 5993 state may have spin 2$^-$ [46] and not 5$^-$ [16].

2.6.1 Collective excitations of the whole nucleus

The 3$^-$ yrast state in $^{208}\mathrm{Pb}$ is rather unique among the whole nuclear chart. In a doubly magic nucleus another 3$^-$ state as the lowest excited state is known only in $^{146}$Gd [98]. Three low-lying states were identified in the 1920’s [99, 100]. The spins were determined in 1954 by the study of angular correlations. By assuming the g.s. to have spin 0$^+$, the lowest state in $^{208}\mathrm{Pb}$ was assigned spin 3$^-$ [49].

The high energy of the 3$^-$ yrast state was already noticed by Rutherford with the penetration of radioactivity for Thorium material being a factor 3 ${\frac{ 1}{2}}$ stronger than for Uranium material (Fig. 2 in [101]). In the 1920’s the excitation energy of 2.6 MeV for Thorium material was used as an etalon [102]. The energy calibration for the 2.6 MeV 3$^-$ yrast state changed by 8 keV after 1969 [21, 103]. Hence all energies determined by Moore et al. [34] had to be adjusted [63, 64], see Eq. (B.1) in [29]. The energy of the 2.6 MeV 3$^-$ yrast state is now known with an uncertainy of 10 eV [23].

The 3$^-$ yrast state in $^{208}\mathrm{Pb}$ is widely considered as an octupole phonon vibration of the entire $^{208}\mathrm{Pb}$ nucleus [56]. Besides the states in $^{208}\mathrm{Pb}$ and $^{206}\mathrm{Pb}$ other nuclei in the lead region are described with octupole phonons, too. The excitation energies with $E_x= 2.6$ MeV are similarily large for most nuclei in the lead region within 0.1 MeV. The reduced transition strength is very large (BE(E3)= 33.8 W.u. for $^{208}\mathrm{Pb}$ and 35.4 W.u. for $^{206}\mathrm{Pb}$). The strengths for other nuclei in the lead region ($^{198, 200, 202, 204}$Hg [50], $^{206}\mathrm{Pb}$ [104], $^{209}\mathrm{Bi}$ [104], $^{210}\mathrm{Po}$ [88]) are similar, too.

An alternate interpretation as a tetrahedral rotor was proposed [51]. Besides the knowledge of the charge radius for states in the lead region the algebraic cluster model [51, 105] needs no further parameters for an explanation of the large value BE(E3). The BE(E1) value for the 4.97 MeV 1$^-$ state in $^{206}\mathrm{Pb}$ [41] and for the 4841 1$^-$ state in $^{208}\mathrm{Pb}$ [23] is extremely small. The relation $P_1 -{\frac{ 1}{2}}= 0$ with the Legendre polynomial $P_1$ explains the vanishing strength [51, 105].

In $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ the reduced transition strengths BE(E$\lambda$) for the 4 MeV 2$^+$ and 4$^+$ states [23, 41] can be explained by tetrahedral configurations similarily.

With the 4$^+$ yrast states in $^{206,208}$Pb [23, 41] and the 4113 state in $^{204}$Hg [50] the second member of the assumed rotational vibrational g.s. band may be identified at $E_x=4.1$ MeV. Because of the poor knowledge of spin, parity and structure no other state in the lead region is identified as the tetrahedral member [88]. Solely in $^{208}\mathrm{Pb}$ ten tetrahedral states at $2< E_x< 8$ MeV were identified (Sect.  2.6).

The 6$^+$ 4424 state [23], (the tentatively identified 10$^+$ 5444 state [54]), and the 12$^+$ 6101 state [11, 16, 96] were identified as collective excitations. An icosahedral symmetry is suspected [52].

2.6.2 States coupled to non-1p1h configurations

The g $_{{ 9}/{2}}$ state in $^{209}\mathrm{Pb}$ is not pure (Sect. 2.2). Hamamoto and Siemens studied the coupling of the j $_{{15}/{2}}$ and g $_{{ 9}/{2}}$ particle to the 3$^-$ yrast state interpreted as octupole phonon [56]. (The similar coupling of the f $_{{ 7}/{2}}$ nucleon to the $3^-$ yrast state in the doubly magic $^{146}$Gd was studied by Kleinheinz et al. [106].) Two dozen states were found in $^{209}\mathrm{Pb}$ by the $^{207}\mathrm {Pb}(t,p)^{209}\mathrm {Pb}$ reaction with $E_t= 20$ MeV [107]. Some of them may be described by the coupling of the g $_{{ 9}/{2}}$ particle to $3^-$ yrast state.

The coupling of particles to the $3^-$ yrast state in $^{208}\mathrm{Pb}$ was studied by Rejmund et al. [108] for $^{207}\mathrm{Pb}$, $^{209}\mathrm{Pb}$, $^{207}\mathrm{Tl}$. They found out that the coupling is pronounced if two orbitals satisfy the $\varDelta j \equiv \varDelta l \equiv 3$ rule. This is the case for g $_{{ 9}/{2}}$ and j $_{{15}/{2}}$ in $^{209}\mathrm{Pb}$, f $_{{ 7}/{2}}$ and i $_{{13}/{2}}$ in $^{207}\mathrm{Pb}$, d $_{{ 5}/{2}}$ and h $_{{11}/{2}}$ in $^{207}\mathrm{Tl}$. Two states in $^{205}$Tl are described by the coupling of the s $_{{ 1}/{2}}$ particle to the 3$^-$ yrast state [84]. States in $^{207}\mathrm{Tl}$ were studied through $\beta$-decay [109]. An experiment at the ISOLDE Decay Station observed the population of a 17/2$^+$ state in $^{207}\mathrm{Tl}$ at $E_x=3813$ keV starting from $E_x=7.0$ MeV [110]. The $\gamma$-transition from the 3813 17/2$^+$ state to the 1348 11/2$^-$ state is determined as E3. The 3813 17/2$^+$ state may be described by the coupling of the h $_{{11}/{2}}$ proton to the 3$^-$ yrast state in $^{208}\mathrm{Pb}$.

Two-neutron states in $^{210}\mathrm{Pb}$ and the coupling to the collective 3$^-$ state was studied by Broda et al. [111]. The coupling of a nucleon to the 3$^-$ yrast state in $^{206 }$Hg, $^{206,207 }$Tl, $^{206,207,208,209}$Pb, $^{ 209}$Bi, $^{ 210 }$Po was studied by Broda et al. [112].

High-spin states up to 17 MeV in $^{208}\mathrm{Pb}$ were studied with deep inelastic scattering by Broda et al. [11]. The $\gamma$-transitions end intermediately in the 9091 17$^+$ state which transits by E3 to the 6744 14$^-$ state described by j $_{{15}/{2}}$ i $_{{13}/{2}}$ [113]. The spin of the 14$^-$ state is confirmed [11, 96]. The 9091 17$^+$ state may be described by the coupling of the stretched configuration j $_{{15}/{2}}$ i $_{{13}/{2}}$ to the 3$^-$ yrast state. The coupling of tetrahedral and other collective configurations to 1p1h states may explain most states populating the 9091 17$^+$ state at $E_x<17$ MeV [18].

Two dozen 1p1h configurations coupled to the ${3}^-$ yrast state in the doubly magic nucleus in $^{208}\mathrm{Pb}$ were identified [17]. Most of them have positive parity.

3 Two-nucleon states in the lead region

With the experiments performed in 1965-1969 at the MPIK on the inelastic proton scattering the comparison of particle-hole configurations in two heavy nuclei $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ can be achieved. Whereas about 250 states in $^{208}\mathrm{Pb}$ are well described by the SSM (Sect. 3.1) no particle-hole states were known in $^{206}\mathrm{Pb}$ before [41].

Methods for the study of inelastic proton scattering via an IAR in the doubly magic nucleus $^{208}\mathrm{Pb}$ (Sect. 3.1) and in $^{206}\mathrm{Pb}$ where two neutrons are missing from the doubly magic nucleus $^{208}\mathrm{Pb}$ (Sect. 3.2) allow to find spin, parity, and structure of particle-hole states. Inelastic proton scattering via an IAR is equivalent to a neutron pickup reaction on the g.s. or an excited state in the parent nucleus [40]. For $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ the parent states are in $^{207}\mathrm{Pb}$, for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ the parent states are in $^{209}\mathrm{Pb}$. Thirty-two particle-hole states in $^{206}\mathrm{Pb}$ are identified at $3.7<E_x<4.7$ MeV through the $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ experiment performed in 1969 at the MPIK [20]. In the same region $3.7<E_x<4.7$ MeV twenty-three 1p1h states were identified in $^{208}\mathrm{Pb}$. Thus 60% more states in $^{206}\mathrm{Pb}$ are identified and indications for possibly twice the number of states are given. Results from the prior $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ experiment performed for low lying particle-hole states in $^{208}\mathrm{Pb}$ discussed in 1973 [24] and after 1982 are refined and extended. Yet the results shown in Table 4 in [51] suffice for this work.

The lowest states in $^{208}\mathrm{Pb}$ and $^{206}\mathrm{Pb}$ $3.7<E_x<4.7$ MeV allow to discuss comparable shell model configurations in the lead region (Sect. 2) in a quantitative manner (Sect. 6.4).

3.1 Description of 1p1h states in ${}^\mathbf{208 }{} \mathbf{Pb}$

Most states in $^{208}\mathrm{Pb}$ are described as (1p1h) configurations

$$\begin{aligned} \left| \tilde{E}_x I^\pi _M \right\rangle= & {} \sum _{lj} c^{\tilde{E}_x I^\pi } _ {lj} \left| LJ\, lj \right\rangle + \sum _{i} c^{\tilde{E}_x I^\pi } _ {i} \left| {\mathrm{other}}_{I^\pi } \right\rangle . \ \ \ \ \end{aligned}$$

(1)

Here $\tilde{E}_x$ denotes the state in a unique manner by the known excitation energy rounded to 1-2 keV. $I^\pi$ is spin and parity. L, l are the angular momenta and J, j spin of particle and hole, respectively. Other than 1p1h configurations are discussed in Sect. 2.6.

3.1.1 States resonantly excited on IARs in $^{209}\mathrm{Bi}$

The proton decay of an IAR in $^{209}\mathrm{Bi}$ excites all neutron 1p1h configurations in each state [40]. All seven known IARs in $^{209}\mathrm{Bi}$ were investigated in much detail [1, 16, 60,61,62,63,64, 114].

The low lying states resonantly excited by the g $_{{ 9}/{2}}$ IAR were studied immediately after the first experiments on $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ in 1966 in the USA [33,34,35]. More experiments on $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ via the g $_{{ 9}/{2}}$ IAR were performed in 1968 at the MPIK. States resonantly excited by the d $_{{ 5}/{2}}$ IAR were also studied, at the Maier-Leibnitz-Laboratorium (Garching, Germany) after 2003 also the i $_{{11}/{2}}$, j $_{{15}/{2}}$, s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ IARs. They are not relevant to this work.

After the first attempts of an analysis of the resonant $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ reaction [24] a thorough analysis of the states with dominant 1p1h configurations involving the g $_{{ 9}/{2}}$ particle was not further pursued. Complementary data obtained in the USA were not used [115, 116]. Some of them were discussed later [29].

Table 4 in [51] yields results from an update done in 1982 and slightly improved in 2017. These data are used by this work in the comparison to $^{206}\mathrm{Pb}$. Essentially, similar wave functions (including signs of amplitudes) were obtained in 1999 [78].

3.2 Particle-hole states in ${}^\mathbf{206 }{} \mathbf{Pb}$

The lowest states in $^{206}\mathrm{Pb}$ at $E_x < 3.5$ MeV (Table 4) are well described by two-hole configurations (Sect. 2.4). Higher excited states have a more complex structure (Sect. 3.2.1).

The proton decay of the g $_{{ 9}/{2}}$ IAR in $^{207}\mathrm{Bi}$ strongly excites two dozen states in $^{206}\mathrm{Pb}$ at $3.7< E_x< 4.7$ MeV. The total mean cross section of two dozen states is 3 mb/sr. The value equals the total mean cross section found for the proton decay of the g $_{{ 9}/{2}}$ IAR in $^{209}\mathrm{Bi}$ into the states in $^{208}\mathrm{Pb}$ in the same range of excitation energies (Table 6). A reduction factor of $0.80\pm 0.02$ has to be included [29]. (Note that the correlation of configuration strength with the cross section is strongly distorted by the logarithmic dependence of the s.p. widths on the angular momentum and the bombarding energy [29, 39].)

The number of states in $^{206}\mathrm{Pb}$ is about twice the number of states in $^{208}\mathrm{Pb}$. The number may be even higher because of the insufficient resolution of about 15 keV [20]. The mean spacing of states is 9 keV in $^{208}\mathrm{Pb}$ [16] and estimated with about 4 keV in $^{206}\mathrm{Pb}$.

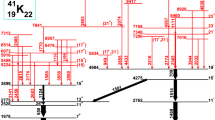
Twenty-two levels are observed in $^{206}\mathrm{Pb}$ (Tables 4, 5, 8). The analysis of angular distributions excited by the proton decay of the g $_{{ 9}/{2}}$ IAR in $^{207}\mathrm{Bi}$ identified thirty-two states in $^{206}\mathrm{Pb}$. In the following we denote a state by the excitation energy $\overline{E_x}$ varied within 4 keV ¹ from the value $E_x$ given by [20] for the level.

3.2.1 Generalized neutron particle-hole configurations

The concept of GNPH configurations was introduced by studying inelastic proton scattering via an IAR in $^{141}$Pr [12,13,14]. It explains several states in the $N=82$ isotones $^{136}$Xe, $^{138}$Ba, $^{140}$Ce, $^{142}$Ne, $^{144}$Sm [117]. The method of studying $({{{\textit{p}}}, {{\textit{p}}}' })$ via an IAR allowed to determine spin, parity, and structure of states [13, 14]. A theory explained the GNPH configurations by coupling a collective state to 1p1h configurations [15].

The model is used to explain the states observed by Solf et al. [19, 20, 73]. Negative parity states at $3.7< E_x< 4.7$ MeV are described by the coupling of 1p1h configurations to the 0$^+$ g.s. and the 2$^+$ yrast state as

$$\begin{aligned} \left| E_x I^- _M \right\rangle= & {} \sum _{lj} c^{E_x I^-_M} _ {lj} \left\{ \right. \alpha \left| ( LJ \, lj ) \otimes ( { 0\ 0^+_\mathrm{g.s.}} \right\rangle \nonumber \\&+\sum _K {\alpha _K} \left| \left( [LJ \, lj] _K \otimes { [803\ 2^+_1] } \right) _I \right\rangle \nonumber \\&+ \sum _{i} c^{E_x I^-_i} \left| { \mathrm other} _{I^-_i} \right\rangle , \nonumber \\ \mathrm{where }&0< \alpha ^2 + \sum _K {\alpha _K} ^2<1 , \nonumber \\&-1< c^{E_x I^-_M} _ {lj}<+1 , \quad -1< c^{E_x I^-_i} <+1 , \quad \mathrm{and } \nonumber \\&lj = {{\textit{p}}}{_{{ 1}/{2}}}, {{\textit{p}}}{_{{ 3}/{2}}}, {{\textit{f}}}{_{{ 5}/{2}}}, {{\textit{f}}}{_{{ 7}/{2}}}, {{\textit{h}}}{_{{ 9}/{2}}}. \end{aligned}$$

(2)

Here other configurations denoted as $\left| { \mathrm other} _{I^-_i} \right\rangle$ comprise especially the proton 1p1h configurations ${{\textit{h}}}{_{{ 9}/{2}}}{{\textit{s}}}{_{{ 1}/{2}}}\otimes {{\textit{p}}}{_{{ 1}/{2}}}^{-2}$ and ${{\textit{h}}}{_{{ 9}/{2}}}{{\textit{d}}}{_{{ 3}/{2}}}\otimes {{\textit{p}}}{_{{ 1}/{2}}}^{-2}$.

Only the configurations described by $LJ={{\textit{g}}}{_{{ 9}/{2}}}$ are exploited in this work. Another theory applying the surface $\delta$ interaction (SDI) is in preparation [72].

3.2.2 Orthonormality and sum-rule relations and center of gravity

The amplitudes $c_{LJ\,lj} ^{ E_x, I^-_M}$ in Eq. (1) and $c^{E_x, I^-_M} _ {lj}$ in Eq. (2) obey the orthonormality and sum-rule conditions,

$$\begin{aligned} \sum _{LJ\, lj} \sum _{L'J'\, l'j'} c_{LJ\,lj} ^{ E_x, I^-_M} c_{L'J'\, l'j'} ^{ E_x, I^-_M} = 0 ,&\quad \sum _{LJ\, lj} \left| c_{LJ\,lj} ^{ E_x, I^-_M} \right| ^2 = 1 , \nonumber \\ \sum _{ E_x} \sum _{ E'_x} c_{LJ\,lj} ^{ E_x, I^-_M} c_{LJ\,lj } ^{ E'_x, I^-_M} = 0 ,&\quad \sum _{ E_x} \left| c_{LJ\,lj} ^{ E_x, I^-_M} \right| ^2 = 1 .\nonumber \\ \end{aligned}$$

(3)

Here LJ describes a GNPH configuration with the parameter $\alpha$ [Eq. (2)]. The centroid energy is obtained as

$$\begin{aligned} \overline{ E_x} (LJ, lj, I^-)= & {} \sum _{lj} E_x \left| c_{LJ\,lj} ^{ E_x, I^-_M} \right| ^2 \Big / \sum _{lj} \left| c_{LJ\,lj} ^{ E_x, I^-_M} \right| ^2 \nonumber \\&\mathrm{for\ each\ GNPH\ configuration} . \end{aligned}$$

(4)

3.2.3 Number of states excited by $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$

The proton decay of the g $_{{ 9}/{2}}$ IAR in $^{207}\mathrm{Bi}$ is expected to populate negative parity GNPH states in $^{206}\mathrm{Pb}$ at excitation energies $3< E_x< 5$ MeV. The g.s. with dominant structure ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$ is assumed to contain admixtures of configurations $lj^{-2} \, {l'j'}^{-2}$. The coupling of the $0^+_\mathrm{g.s.}$ to the $803\ 2^+$ yrast and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ 1p1h configurations is interpreted as GNPH configurations.

The GNPH configurations are expected with four states at $E_x=4.4$ MeV with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and six states at $E_x=4.0$ MeV with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength in correspondence to 1p1h configurations in $^{208}\mathrm{Pb}$. In addition ten states with spins from 2$^-$ to 7$^-$ at $E_x=4.3$ MeV and structure $\left| {{\textit{g}}}{_{{ 9}/{2}}}\, {{\textit{p}}}{_{{ 1}/{2}}}\otimes {803\ 2^+_1} \right\rangle$ are expected (Table 2).

Thirty more states with spins from 0$^-$ to 8$^-$ structure $\left| ({{\textit{g}}}{_{{ 9}/{2}}}\, {{\textit{f}}}{_{{ 5}/{2}}}\otimes { 803\ 2^+_1 } \right\rangle$ at $E_x=4.8$ MeV and twenty more states with spins from 1$^-$ to 8$^-$ with the structure $\left| {{\textit{g}}}{_{{ 9}/{2}}}\, {{\textit{p}}}{_{{ 3}/{2}}}\otimes { 803\ 2^+_1 } \right\rangle$ at $E_x\approx 5.1$ MeV are predicted. Therefore in total about twenty states with a g $_{{ 9}/{2}}$ particle are expected in the region $4.0< E_x< 4.5$ MeV for $^{206}\mathrm{Pb}$ – twice the number as for $^{208}\mathrm{Pb}$. (Here the isospin is not considered.) The mixing with other configurations not containing the g $_{{ 9}/{2}}$ particle (i $_{{11}/{2}}$ $\,lj$, d $_{{ 5}/{2}}$ $\,lj$ and the proton configurations h $_{{ 9}/{2}}$ s $_{{ 1}/{2}}$, h $_{{ 9}/{2}}$ d $_{{ 3}/{2}}$) increases the number of GNPH configurations.

3.2.4 States resonantly excited on the g $_{{ 9}/{2}}$ IAR

Sixteen negative parity states exist at $3.9< E_x< 4.5$ MeV in $^{208}\mathrm{Pb}$ (Table 4 in [51]). Among them there are six states with dominant proton configurations h $_{{ 9}/{2}}$ s $_{{ 1}/{2}}$, h $_{{ 9}/{2}}$ d $_{{ 3}/{2}}$ and two states with i $_{{11}/{2}}$ p $_{{ 1}/{2}}$. Solf et al. [20] observe 27 levels at $3.7< E_x< 4.7$ MeV in $^{206}\mathrm{Pb}$ resonantly excited on the g $_{{ 9}/{2}}$ IAR.

Four levels resonantly excited by $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were observed with low resolution at $\varTheta =90^\circ$ [118]. The resolution in the experiment performed at the MPIK was 13–15 keV. The large ratio R of the on-to-off resonance cross sections at $3.7< E_x <4.7$ MeV proofs the presence of several unresolved states (Fig. 10).

The mean distance between any two states in $^{208}\mathrm{Pb}$ is 9 keV [16]. The number of states in $^{206}\mathrm{Pb}$ is certainly larger because of the two missing neutrons (Sect. 3.2.3). Therefore within 15 keV often more than one state is concealed. The result that 32 states are discerned in 22 observed levels [20] can be thus understood (Tables 4, 5, 8).

4 Experiments on the inelastic proton scattering via IARs

4.1 Experiments performed in 1968–1969

Experiments on the inelastic proton scattering performed in 1968-1969 at the MPIK are shortly described in [29]. Two targets of $^{208}\mathrm{Pb}$ and $^{206}\mathrm{Pb}$ isotopes were used with an enrichment of 99.98% and 97.38%, respectively. Protons were accelerated using the HVEC-MP Tandem in a scattering chamber equipped with 8–12 ion-implanted Si(II) detectors. The counters were cooled to 170$^\circ$ K in order to reduce the reverse current. A resolution of 13–15 keV was obtained for $^{208}\mathrm{Pb}$ [28,29,30] and for $^{206}\mathrm{Pb}$ [20, 73].

By turning the chamber different detectors were placed at the same scattering angle. By this means the solid angle for all 8–12 detectors was measured with a precision of 2%. Absolute and relative cross sections were determined by Rutherford scattering at $E_p=5$ MeV using the same experimental setup in the scattering chamber. Spectra for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were taken for $E_p =14.935$ (on g $_{{ 9}/{2}}$ IAR) and 14.40 MeV (off IAR) at $\varTheta =125^\circ$, see reproduction in Fig. 1. Additional spectra were taken for $E_p =14.935$ at $\varTheta =85^\circ$ and $110^\circ$. Spectra taken for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were used for the calibration of excitation energies [29]. The uncertainty of the excitation energies is 4 keV (Table 4).

Similar $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ spectra with low resolution were taken by Temmer and Lenz in 1968 at $\varTheta = 90^\circ$ (Fig. 18 in [118]). Levels observed off and on the g $_{{ 9}/{2}}$ IAR ($E_p=14.50$ and 14.97 MeV) correspond to the 27 levels determined by Solf et al. [20]. The cross section from the elastic scattering is a factor hundred larger than the group of four levels from the inelastic scattering. The ratio of the cross section on-resonance to off-resonance is about a factor twenty as expected (Fig.  10).

The levels at $E_x=3.68$, 3.90, 3.98, 4.17, 4.41 MeV may correspond to levels 23 and 25, 26 and 27, 28 and 34, 35 and 43 and 44 [20]. The unresolved level 32 at $E_x=4.21$ MeV is evident. Level 45 at $E_x=4.50$ MeV is near a contamination peak from $^{ 12}C$ $({{{\textit{p}}}, {{\textit{p}}}' })$.

Fig. 1

Spectra for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ taken at $E_p =14.935$ (on g $_{{ 9}/{2}}$ IAR) and 14.40 MeV (off IAR). Two peaks with about 2500 and 3500 counts stick out. They correspond to level 44 and 36 and are clearly associated with doublets. Namely in $^{208}\mathrm{Pb}$ no such large cross sections with about 400 and 300 $\upmu$b/sr observed. A ratio $R=20$ for the ratio on-resonance to off-resonance cross section is expected (Fig. 10)

4.2 Excitation functions

4.2.1 Excitation functions for $^{208}\mathrm{Pb}$

Excitation functions were measured for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ with the range $14.2<E_p< 18.2$ MeV [114, 119]. Four scattering angles ($\varTheta = 90^\circ$, $125^\circ$, $150^\circ$, $170^\circ$) [119] or two scattering angles ($\varTheta = 90^\circ$ or $100^\circ$ and $158^\circ$) were used [114]. Near the lowest IAR, the g $_{{ 9}/{2}}$ IAR, excitation functions were measured for $\varTheta = 90^\circ$ and $158^\circ$ [114].

The widest range of excitation functions covered the region $14.0<E_p< 21.8$ MeV [83]. The excitation function was measured for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ and $\varTheta =165^\circ$ (lower frame of Fig. 1 in [83]). Excitation functions for the 5$^-_1$ state at $E_x=3.20$, for the 4$^-_1$ state at 4.49, for the 5$^-_2$ state at 3.71 MeV covered the region $18.0<E_p< 21.8$ MeV [83]. Section 2.1.2 discusses the observations.

4.2.2 Excitation functions for other lead isotopes

Spectra for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ taken were taken for $E_p =14.935$ (on g $_{{ 9}/{2}}$ IAR) and 14.40 MeV (off IAR) at $\varTheta =85^\circ$, $110^\circ$ and $\varTheta =125^\circ$ (Figs. 1–3 in [20]). Fig. 2 in [20] is reproduced in Fig. 1. Fig. 3 in [20] exhibits the successful reproduction of the spectrum by the triangle method [28], see Fig. 1 in [29].

Excitation functions for the isotope $^{206}\mathrm{Pb}$ were taken for the region $11.5<E_p< 20.0$ MeV with $\varTheta =165^\circ$ and the excitation energies $E_x=0.803$ (upper frame) and 1.47 MeV (lower frame) [83]. Excitation functions for $({{{\textit{p}}}, {{\textit{p}}}' })$ with the isotopes $^{204,206,207}$Pb were measured in the energy range $13.5< E_p <18.0$ MeV for scattering angles $\varTheta = 140^\circ , 165^\circ$ [118, 120]. Excitation functions for the isotope $^{207}\mathrm{Pb}$ were measured in the energy range $13.5< E_p <18.0$ MeV for $\varTheta = 140^\circ$ and $160^\circ$ [121] and in the energy range $14< E_p <20$ MeV for $\varTheta = 120^\circ$, $125^\circ$, $150^\circ$, $170^\circ$ [122].

4.2.3 Excitation functions for $^{205}$Tl

Excitation functions were measured for $^{205}$Tl at the MPIK in 1969 [84]. Proton energies covering $13.8<E_p< 20.0$ MeV and scattering angle $\varTheta =160^\circ$ were used. Two states at $E_x=2.61$ and 2.69 MeV yielded two almost identical excitation functions.

The excitation functions resemble those measured for $^{208}\mathrm{Pb}$. Expecially the similarity to $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ taken for $\varTheta =165^\circ$ is striking (lower frame of Fig. 1 in [83]). The strong resonance at $E_p\approx 19.3$ MeV is observed both for $^{208}\mathrm{Pb}$ and $^{205}$Tl (Sect. 2.1.2). The region $19.5<E_p< 20.0$ MeV is insufficiently covered for $^{205}$Tl where two resonances for $^{208}\mathrm{Pb}$ are discerned.

Fig. 2

Twenty-two angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ fitted with Legendre polynomial $P_2 (\cos \varTheta )$. For each energy label shown at bottom up to three unresolved states are identified (Table  4). The thick line shows the best fit [19], the $1\sigma$ uncertainty is shown by dashed lines. The maximum is arbitrarily set to 1. The x-axis is given by the Legendre polynomial of second degree running from $P_2(\cos {90^\circ })$ to $P_2(\cos {180^ \circ })$; the values $P_2(\cos {120^\circ })$ and $P_2(\cos {140^ \circ })$ are marked at bottom

Fig. 3

Shape of pure 1p1h configurations $LJ\,lj$ for $LJ={{\textit{g}}}{_{{ 9}/{2}}}$ and $lj={{\textit{p}}}{_{{ 3}/{2}}}$ (f $_{{ 5}/{2}}$) with spins from 3$^-$ to 6$^-$ (2$^-$ to 7$^-$). The shape for $LJ=1$ and $lj=1$ is isotropic [Eq. (2a) in [13]]. For clarity the abscissa is omitted and the ordinate is shown only for the two leftmost panels. The strength normalized to unity is shown by a horizontal line. In each panel the function $P_2(\cos \varTheta )$ is used for $90^\circ<\varTheta <180^\circ$. Marks at $\varTheta =120^\circ$ and $140^\circ$ depict the non-linearity. At left a scale from 0 to 1.30 is shown. The angular distributions resemble those for $LJ={{\textit{d}}}{_{{ 3}/{2}}}, {{\textit{g}}}{_{{ 7}/{2}}}$ (Fig. 4e in [46])

4.3 Angular distributions for lead isotopes

Angular distributions for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ were measured at $E_p= 14.935$ MeV for twenty-two levels. Scattering angles from $\varTheta = 45^\circ$ to $165^\circ$ in $5^\circ$ steps were used. The maximum cross section was found at $E_p= 14.935\pm 0.005$ MeV.

For the study of the $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ reaction in 1968 six beam energies were used [29]. Among them the proton energy $E_p= 14.99$ MeV was used to measure angular distributions near the g $_{{ 9}/{2}}$ IAR [28,29,30]. The maximum cross section for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ on the g $_{{ 9}/{2}}$ IAR was later determined with $E_p= 14.918\pm 0.006$ MeV [114]. The reduction of the mean cross section from the maximum is calculated with $0.80\pm 0.02$ near $E_p= 14.99$ MeV [29, 114].

In comparing data for the two isotopes $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ only the angular distributions for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ measured at $E_p= 14.99$ MeV are of interest [29]. Here scattering angles from $\varTheta = 60^\circ$ to $165^\circ$ in $5^\circ$ steps were used. A full evaluation of the analysis of the angular distributions taken near the g $_{{ 9}/{2}}$ IAR in $^{209}\mathrm{Bi}$ is still awaited. The results obtained in 1982 provided by Table 4 in [51] however are sufficient for the comparison to the isotope $^{206}\mathrm{Pb}$.

Complementary data obtained in the USA were not used [115, 116]. They were discussed later [29].

Angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ are presented in Figs. 2, 11, 12, 13, 14, and 15 in a special manner using the Legendre polynomial $P_2(\cos \varTheta )$ as abscissa (see Fig. 3 in [46]). Calculated angular distributions shown in Figs. 6, 7, 8, and 9 and fits of experimental data (Figs. 11, 12, 13, 14, 15) are displayed.

4.4 Identification of states in ${}^\mathbf{206 }{} \mathbf{Pb}$ and ${}^\mathbf{208 }{} \mathbf{Pb}$

Experimental data for the inelastic proton scattering via IARs in $^{207}\mathrm{Bi}$ and $^{209}\mathrm{Bi}$ still exists [30, 73]. Here we use the evaluated data [19] for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ and the data reconstructed from scans of spectra [29, 46] for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$. Tables 4, 5, 8 present the data analyzed by this work for $^{206}\mathrm{Pb}$.

Information about identified states in $^{206}\mathrm{Pb}$ and angular distributions from the $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ reaction via the g $_{{ 9}/{2}}$ IAR is shown in Sect.  4.5. Comparative data for $^{208}\mathrm{Pb}$ are cited in Sect. 4.6. Tables 6 and 7 compare the results from this work to $^{208}\mathrm{Pb}$ (Table 4 in [51]).

4.5 States in ${}^\mathbf{206 } \mathbf{Pb}$

4.5.1 Tables

The most recent source of information about states in $^{206}\mathrm{Pb}$ derives from Nuclear Data Sheets [41]. The discussion of negative parity states at $3.7<E_x< 4.7$ MeV in $^{206}\mathrm{Pb}$ is a main topic of this work.

• Table 1 shows positive parity states at $E_x< 1.7$ MeV discussed in Sect. 2.

• Table 2 shows calculations of 1p1h configurations by SDI [4, 5, 69]. Excitation energies calculated by the SSM [16] for states expected by the coupling to the $2^+$ yrast state are included. Cross sections for 1p1h configurations near the g $_{{ 9}/{2}}$ IAR both in $^{207}\mathrm{Bi}$ and $^{209}\mathrm{Bi}$ are shown.

• Table 3 characterizes each angular distribution in order to allow the comparison of the shape with calculated angular distributions of various configuration mixings (Figs. 6, 7, 8, 9).

• Finally determined spin assignments are given in Tables 4, 5, 8. The correspondence of known states [41] to states identified by this work is discussed in Sect. 6.2.1.

• A detailed comparison of calculated angular distributions to best fits is done in Table 5.

• Table 6 compares the strength distribution for three ranges of excitation energies ($3.0<E_x< 3.7$, $3.7<E_x< 4.17$, $4.17<E_x< 4.7$ MeV) in the two lead isotopes (Sect.  6.4).

• Table 7 compares the results from this work to $^{208}\mathrm{Pb}$ in detail (Sect. 6.4).

• Table 8 tabulates the amplitudes of the fit ordered by the assigned spin and the excitation energy. The finally accepted spin (Sect. 6.2.9) is printed bold face, discarded spins italic. For states within doublets (Sect. 6.2.6) or with alternate spin assignments (Sect. 6.2.7) the other spin assignments are shown, too, printed bold face or italic as discussed in Sect. 6.2.9.

  The amplitudes are given as obtained from the fit, especially for states with unique spin assignments

  (Sect. 6.2.5) and for doublet states (Sect. 6.2.6). For states with alternate spin assignments (Sect. 6.2.7) the amplitudes refer to the shown cross section.

  Sect. 6.2.8 discusses the discrimination of spins. For a discarded spin (Sec. 6.2.9) the strength is shown in parentheses. For each level the mean cross section is given as used for determining the amplitudes. For recognized doublets (Sect. 6.2.6) the division into two or three parts is indicated by the factor 1/2 and 1/3.

  For each spin the centroid energy $\overline{ E_x}$ [Eq. (4)] is printed bold face. The sum of the strength $\sum c^2$ for the configurations g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ is determined for two ranges of excitation energies, $E_x< 4.17$ MeV and $E_x> 4.17$ MeV.

4.5.2 Angular distributions for $^{206}\mathrm{Pb}$

• Figures 4a–c in [19] show angular distributions for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ fitted by Legendre polynomial $P_K$ with $K=0,2,4$ [19]. In total 29 angular distributions were measured.

• An excerpt from Fig. 4a in [20] displays angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ for levels 27–26/29 (Fig. 4).

• Angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ are presented in Fig. 2 for 20 levels in $^{206}\mathrm{Pb}$ (Table  4). A special method uses the Legendre polynomial $P_2(\cos \varTheta )$ as abscissa (see Fig. 3 in [46]). The level number is shown at top, the excitation energy in units of keV at bottom.

• Figure 5 shows as an example the angular distribution for level 23 in two variants

  • (top frame) the best fit [20] and the uncertainties of the fit by Legendre polynomials $P_K$, $K=0$, 2, 4 in relative units. The maximum is arbitrarily set to 1.

  • (bottom frame) a fit with Legendre polynomials $P_2(\cos \varTheta )$; the mean cross section is normalized to unity (dotted line).

• Figure  3 displays the shape of pure 1p1h configurations $LJ\,lj$ for LJ=g $_{{ 9}/{2}}$ and $lj={{\textit{p}}}{_{{ 3}/{2}}}$, f $_{{ 5}/{2}}$.

• Figures 6, 7, 8, and 9 show calculated angular distributions for configurations g $_{{ 9}/{2}}$ lj for $l2j=p1$, p3, f5, f7.

• Figures 11, 12, 13, 14, 15, 16, 17 and 18 show the fit of the angular distribution by Eq. (6) with the configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$. The unity value representing the mean cross section is shown by a dotted line, a scale is drawn at right.

In order to linearize the angular distributions as much as possible [46], in Figs. 11, 12, 13, 14, 15, 16, 17 and 18 the x-axis is given by the Legendre polynomial of second degree running from $P_2(\cos {90^\circ })$ to $P_2(\cos {180^ \circ })$. The values $P_2(\cos {120^\circ })$ and $P_2(\cos {140^ \circ })$ are marked at bottom. The ordinate is given in values relative to the mean cross section shown by a dotted line. The scale runs up to a maximum of 3.0; the values 0.5, 1.0, 1.3, 1.5, 2.0 are shown at right. The line at left shows the range up to 1.5 thus illustrating extremely large slopes. The description of the x-axis is omitted for clarity.

In Figs. 11, 12, 13, 14, 15, 16, 17 and 18 the thick drawn curve shows the fit by Eq. (6). (The thin dotted curve shows the fit with one reversed sign of the amplitudes thus illustrating the sensitivity on the value of one weak amplitude. This choice is discarded.)

The legend of Figs. 11, 12, 13, 14, 15, 16, 17 and 18 shows the excitation energy $E_x$ and the mean cross section $\sigma$ [Eq. (5)] in units of $\mu$b/sr. It slightly deviates from Table  4 because of rounding uncertainties. For recognized doublets (Sect. 6.2.6) each member is assumed to contribute equally ($\sigma /2$ or $\sigma /3$). For accepted doublets (Sect. 6.2.5) the factor 2 or 3 is included. In a next line the amplitudes multiplied by a factor hundred are given for the GNPH configuration g $_{{ 9}/{2}}$ $l\,2j$ with $lj={{\textit{p}}}{_{{ 1}/{2}}}$, p $_{{ 3}/{2}}$, f $_{{ 5}/{2}}$, f $_{{ 7}/{2}}$, h $_{{ 9}/{2}}$. The amplitudes for the levels recognized as doublets (Sect. 6.2.6) are already multiplied by the factor $\sqrt{1/2}$ or $\sqrt{1/3}$.

Table 1 Known states in $^{206}\mathrm{Pb}$ at $E_x< 1.8$ MeV including the 3$^-$ yrast state

Table 2 Excitation energies $E_x^{SSM}$ calculated by SSM [1] and SDI [5, 69] and calculated mean cross section of pure 1p1h configurations in $^{208}\mathrm{Pb}$ up to $E_x^{SSM}=4.8$ MeV. The spins of the GNPH configurations are shown for $E_x^{SSM} + E_x(2^+_1)$. Cross sections for states with other spins but $2\le I\le 7$ are expected to be unobservable

Table 3 Character ${d \sigma _{rel}} / {d \Omega }$ [Eq. (7)] of observed angular distributions. For most levels fits with 2–3 different spins were done. The bending of the angular distributions is indicated by giving the minimum, maximum and its range for $\varTheta \approx 140^\circ$

Table 4 States with negative parity at $3.7< E_x< 4.7$ MeV in $^{206}\mathrm{Pb}$ numbered $i_s$. The sum of the cross sections at $3.7< E_x$ MeV and $4.17<E_x< 4.7$ MeV are almost equal (printed bold face). Each level $n_l$ contains up to three unresolved states (Sect. 6.2.9). For each level $N_{s}$ states with different spins are identified (Sect. 6.2.9). The cross section is assumed to be evenly distributed with $\sigma / N_{s}$. In total 15 states are discarded by regarding orthonormality and sum-rule relations [Eq. (3)]. For $N_{R}$ states the ratio $R\gg 20$ with $R\ne N_{s}$ indicates additional doublets (Fig. 10). Several of the $N_{dscd}$ and $N_{R}$ states need to be identified in third iteration (Sect.  6.2.10)

Table 5 Comparison of calculated angular distributions to best fit. Discarded assignments are denoted by overlined figure numbers (a)–(h). For details see Sect.  6.3.2 and Tables 4, 8

Table 6 Centroid energies, sum rules, and integral cross sections for (top) $^{206}\mathrm{Pb}$ and (bottom) $^{208}\mathrm{Pb}$. Two ranges of excitation energies (a) $3.7<E_x <4.17$ MeV and (b) $4.17<E_x <4.7$ MeV are considered. Table 8 shows results for $^{206}\mathrm{Pb}$, see also Table 5. Table 4 in [51] and Table 2 in [29] are used to summarize results for $^{208}\mathrm{Pb}$

Table 7 Comparison of configuration strength given in percent for states of $^{206}\mathrm{Pb}$ with state number $i_s$ (Table 8) and $^{208}\mathrm{Pb}$ (Table 4 in [51])

4.5.3 Extended description of Figs. 11, 12, 13, 14, 15, 16, 17 and 18

An extended description of Figs. 11, 12, 13, 14, 15, 16, 17 and 18 is provided, see also Fig. 5 above. It includes remarks on discarded assignments (Tables 4, 5, 8).

In the angular distributions the differential cross section is linearized by choosing the abscissa as the Legendre polynomial $P_2(\cos \varTheta )$ (see Fig. 3 in [46]).

For spins 3$^-$, 4$^-$, 5$^-$, 6$^-$ with dominant configuration g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ the linearization enhances variations by admixtures of configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$. Thick marks at $\varTheta =120^\circ$ and $140^\circ$ depict the non-linearity.

The ordinate is omitted for clarity. Scales from 0 to 1.0 and values 1.3, 1.5, 1.8, 2.0 are shown at right. A scale from 0 to 1.5 allows to estimate the steepness of the angular distribution.

For each frame the uniquely defined energy label $\overline{E_x}$, spin $I^\pi$ and mean cross section $\sigma$ in units of $\mu$b/sr normalized to unity by $\sum c^2 =1$ are shown in the first line of the legend. Because of rounding in the calculations the displayed value $\sigma$ for the cross section deviates from the value in Table 8. The value ${d \sigma _{rel}} / {d \Omega }=1$ [Eq. (7)] is shown by the dotted line.

The next line in the legend shows the configuration mixing g $_{{ 9}/{2}}$ lj, $l2j=$p1, p3, f5, f7, h9. The third line shows the amplitudes l2j multiplied by a factor 100. In each case two configurations differing by one sign are depicted, one amplitude is given in parentheses.

For each frame five curves are shown. The drawn curve shows the angular distribution with the amplitudes g $_{{ 9}/{2}}$ l2j yielding a best fit. The dotted curve the shows the fit with one reverse sign, the amplitude with the reverse sign is given in parentheses. The three doubly-dash-dotted curves show the angular distribution measured by Solf et al. and fitted by Legendre polynomials of even order $K=0,2,4$ and $1\sigma$ deviations. Figures 11, 12, 13, 14, 15, 16, 17 and 18 show the fit for 46 states in 22 levels.

Figure 11 shows the fit for one state with unique spin assignment but different configurations (a) with two similar amplitudes p $_{{ 3}/{2}}$ and f $_{{ 5}/{2}}$, (b) with a strong f $_{{ 5}/{2}}$ component (Sect. 6.2.5). The fit shown at right (b) is discarded by considering the orthonormality and sum-rule relations [Eq. (3)]. Fig. 12 show the fit for four states with unique spin assignments.

Figures 13, 14 and 15 show the fit for eleven levels with different spin assignments in each pair from (a, b) to (g,h). In Figs. 13a, f, g, 14a, e, g, 15a, c, the spin assignment is discarded by regarding the orthonormality and sum-rule relations [Eq. (3)].

Figures 16, 17, 18 show the fit for six doublets or triplets. Figure 16a–c for a triplet with different spins, Fig. 18d–f for a triplet with different spins, Fig. 16d–f for two states with same spin and different configuration mixing and a third state.

Tables 4, 5, 8 show the assumed and discarded spin assignments.

Fig. 4

An excerpt from Fig. 4a in [20] for levels 27–26/29 displays three angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$. The symmetry for $|90^\circ -\varTheta |$ is mostly rather well realized. The fits shown in Fig. 2 use only the range $90^\circ<\varTheta < 180^\circ$

Fig. 5

An excerpt from Fig. 4a in [20] displays the angular distribution of levels 23 for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ in two variants (Sect. 4.5.2), (top) displayed with the usual linear scaling and error bars with uncertainties of about 5%, (bottom) with the fit by Legendre polynomials $P_2(\cos \varTheta )$, see Fig. 12 (a) for the fit with five GNPH configurations. The angular distribution is predicted to be symmetric for $|90^\circ -\varTheta |$ because of time reversal. Therefore only the scattering angles $90^\circ< \varTheta <180^\circ$ are displayed. The values for the scattering angles are not equidistant, see Fig. 3 in [46]. The differential cross section with dominant configuration g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ is linearized by the fit with Legendre polynomials $P_2(\cos \varTheta )$. Deviations from the linearity by admixtures of configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ thus become more pronounced, see Fig.  12 (c) 13 (b,c,e,f,h) 14 (b,e,f,g,h) 15 (c,f) 16 (a,b,d,f) 17 (d,f) 18 (c,e,f), and especially Fig. 14 (g). The uncertainty of the fit increases with the scattering angle; the thick line shows the fit, thin lines the $1\sigma$ uncertainty. Thick marks at $\varTheta =120^\circ$ and $140^\circ$ depict the non-linearity. Here, the mean cross section is normalized to unity (dotted line).

Fig. 6

Calculated angular distributions for mixed configurations g $_{{ 9}/{2}}$ lj with $l2j= f5, f7$ fo spins 2$^-$ (a,b), 7$^-$ (c,d) with an arbritrary excitation energy of 4401 keV. They are linearized with the function $P_2(\cos \varTheta )$. Marks at $\varTheta =120^\circ$ and $140^\circ$ depict the non-linearity. For each spin (2$^-$ and 7$^-$) two sets are given. The drawn line shows the calculation for one sign. The calculation with the reverse sign is shown with dotted lines and the amplitudes are given in parentheses. The strong energy dependence of the s.p. widths on the proton energy leads to subtle changes of the cross sections because of rounding. The ratio ${d \sigma _{rel} } /{d \Omega } (\varTheta , I^-)$ [Eq. (7)] is shown for $90^\circ< \varTheta < 180^\circ$. The abscissa omitted for clarity is chosen as the Legendre polynomial $P_2(\cos \varTheta )$. The ordinate is shown on right. The left axis shows the range 0-1.5 thus illuminating the large range of ratios of relative cross sections. The value ${d \sigma _{rel}} / {d \Omega }=1$ [Eq. (7)] is shown by the dotted line . The amplitudes $LJ\,lj$ for $l2j= p1,p3,f5,f7,h9$ are multiplied by 100 with the sum of the strength normalized to unity, $\sum c^2 =1$. The name of the particle $LJ={{\textit{g}}}{_{{ 9}/{2}}}$ is omitted because we consider only the proton decay of the g $_{{ 9}/{2}}$ IAR.

Fig. 7

Similar to Fig. 6 but for mixed configurations g $_{{ 9}/{2}}$ lj for $l2j= p3, f5, f7$ with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components and spin 3$^-$ and 6$^-$. The angular distributions differ by the choice of one sign. The differential cross section is linearized and variations become more pronounced

4.6 States in ${}^\mathbf{208 }{} \mathbf{Pb}$

Information about identified states in $^{208}\mathrm{Pb}$ may be obtained from [16, 23, 46, 51, 60,61,62,63,64].

In this work only states at $3.1<E_x< 4.7$ MeV are mentioned. Table 4 in [51] and Table 6 show the data used in this paper. The evaluation is based on experimental data for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ taken in 1968 at the MPIK [28, 46] and reconstructed in 2017 [29, 30].

5 Methods of analysis

The main tool to assign a spin to a state in $^{206}\mathrm{Pb}$ or $^{208}\mathrm{Pb}$ and determine amplitudes of particle-hole configurations is the inelastic proton scattering via an isolated IAR. In the analysis of $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ other available experimental data is used, see especially [23, 76, 77].

Yet the primary tool is the resonant proton scattering because of its high sensitivity and the opportunity to determine relative signs of amplitudes on each IAR [31, 40].

5.1 Theory of the inelastic proton scattering via an IAR

Here a short reminder to the theory of the inelastic proton scattering via an IAR is given. It is described in detail in [1, 13, 36, 38]. Eqs. 7–10 in [46] are adapted to describe needed qualities for the analysis of the angular distributions for $({{{\textit{p}}}, {{\textit{p}}}' })$ taken on an IAR.

The mean (angle integrated) cross section for a configuration $LJ\,lj$ is determined by

$$\begin{aligned} \sigma ^{calc} (lj, I^-) = (2 I +1) \varGamma ^{s.p.}_{LJ} \varGamma ^{s.p.}_{lj} a_{ lj} . \end{aligned}$$

(5)

Here the factor $a_{ lj}$ describes the IAR [13]. The single particle widths $\varGamma ^{s.p.}_{LJ}$ and $\varGamma ^{s.p.}_{lj}$ are taken from [29].

Table 4 shows the excitation energies of the configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ predicted by the SDI together with the mean cross sections $\sigma ^{calc}$. The angular distribution near the g $_{{ 9}/{2}}$ IAR are described by a series of Legendre polynomials $P_K$

$$\begin{aligned}&\frac{d \sigma }{d \Omega } ( \varTheta , E_x, I^-_M, LJ, E_p ) = \varLambda ( LJ, E_p ) (2 I + 1) \sum _{\mathrm{even}\,K} P_K ( \varTheta ) \nonumber \\&\quad \sum _{lj} \sum _{l'j'} a_K(I, LJ, lj, l'j') \phi (lj, l'j') \nonumber \\&\quad \sqrt{ \varGamma ^{s.p.}_{lj} } \sqrt{ \varGamma ^{s.p.}_{l'j'} } c_{lj} ^{ E_x, I^-_M} c_{l'j'} ^{ E_x, I^-_M} . \end{aligned}$$

(6)

The parameter $\varLambda$ describes the population of the resonance [46].

The shape is given by the ratio of $\frac{d\sigma }{d\Omega }$ [Eq. (6)] to $\sigma ^{calc}$ [Eq. (5)]

$$\begin{aligned} \frac{d \sigma ^{rel} }{d \Omega } (LJ\,lj, I^-_M) = \frac{d \sigma }{d \Omega } (\varTheta , E_x, I^-_M, LJ, E_p) \big / \sigma ^{calc} (lj, I^-) \end{aligned}$$

(7)

with the given proton energy $E_p$, $LJ={{\textit{g}}}{_{{ 9}/{2}}}$, and state energy $E_x$.

Figures 6, 7, 8, and 9 show the shape of angular distributions for mixed configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with large admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$.

Fig. 8

Similar to Fig. 6 but for mixed configurations g $_{{ 9}/{2}}$ lj for $l2j= p1, p3, f5$ with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components and spin 4$^-$. The angular distributions differ by the choice of two sets of configuration mixing and two signs. The differential cross section is linearized and variations become more pronounced

Fig. 9

Similar to Fig. 6 but for mixed configurations g $_{{ 9}/{2}}$ lj for $l2j= p1, p3, f5$ with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components and spin 5$^-$. The angular distributions differ by the choice of two sets of configuration mixing and two signs. The differential cross section is linearized and variations thus become more pronounced

5.2 Methods of spin assignment to states in $^\mathbf{206 }$Pb

Because of the two neutrons missing from the doubly magic nucleus $^{208}\mathrm{Pb}$ admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ to GNPH configurations are expected to be weak. The excitation energies of the configurations g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ are expected to be about 300 keV higher than for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. Calculations of excitation energies by SDI [5, 69] and mean cross sections are shown in Table 2. The spin assignment and the determination of GNPH amplitudes are strongly correlated across all states. The fit of an angular distribution of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ via the g $_{{ 9}/{2}}$ IAR in $^{207}\mathrm{Bi}$ is done in several major steps. The following assumptions are regarded.

• 1. The slope and the curvature of the angular distribution of a state with a dominant GNPH configuration is related to the spin; for low admixtures of other GNPH configurations slight changes are expected (Figs. 3, 4, 5, 6, 7, 8, and 9). Some spin assignments can be ruled out by the slope and the bending.

• 2. The cross section is much higher for g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ than for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ whereas strengths of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ are similar. Here the interference pattern allows to distinguish the two configurations.

• 3. The distant configurations g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ contribute less than about one percent in strength. Yet the interference pattern is sensitive to such low admixtures. In cases where three small amplitudes admix to one dominant configuration even a fifth particle-hole configuration distorts the calculated shape of the angular distribution more than only marginally, especially at scattering angles $\varTheta { {}^>\!\!\!\!_\sim }160^\circ$ where the Legendre polynomials $P_K$ differ most [Eq. (6)].

• 4. The excitation energies predicted by the SDI for $^{208}\mathrm{Pb}$ are assumed to be valid for $^{206}\mathrm{Pb}$. States with dominant configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ are expected to be absent because in the SSM the p $_{{ 1}/{2}}$ orbits are empty. Because of the low orbital momentum ($l=0$) in the $({{{\textit{p}}}, {{\textit{p}}}' })$ reaction considerable cross sections for a weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture may be expected. In $^{206}\mathrm{Pb}$ additional GNPH configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 2^+_1$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 2^+_1$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ $\otimes 2^+_1$, and h $_{{ 9}/{2}}$ s $_{{ 1}/{2}}$ $\otimes 2^+_1$, h $_{{ 9}/{2}}$ d $_{{ 3}/{2}}$ $\otimes 2^+_1$ are expected to be present. Their excitation energies are higher² by 803 keV than the excitation energies calculated by the SDI for 1p1h configurations [5, 69].

5.2.1 Sequence of iterations

The study of angular distributions in twenty-two observed levels yields good fits in a few major steps by guessing spin assignments and varying configuration amplitudes (Sects. 6.2.5–6.2.7). In another (not consecutive) step the presence of more than one state in each level is discussed (Sects. 6.2.6, 6.2.9).

Categorizing the shape of the angular distribution. In a first step the shape of the angular distribution with relative values of 1–3 major configurations is investigated (Table 3). For spin 2$^-$ and 7$^-$ weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ are added to the major configuration g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, for spins 3$^-$ and 6$^-$ weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ to major configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$.

For spins 4$^-$ and 5$^-$ a sizeable admixture of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ to major g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ components and weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ are used. Here four dimensions were considered. A fifth dimension (given by g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$) improves the fit marginally.

Adjusting the mean cross section. In a second step the measured mean cross section is adapted by applying a common factor to all amplitudes. Because of numerics the cross section shown in Figs. 11, 12, 13, 14, 15, 16, 17 and 18 slightly differs from the measured value shown in Tables 4, 8.

Comparing the mean cross section and the excitation energy to calculations. In a third step the mean cross sections and the excitation energies are compared to calculations of GNPH configurations (Table 2).

Investigating sum rules and centroid energies. In a fourth step spins for alternate assignments (Sect.  6.2.7) or alternate particle-hole compositions (Sects. 6.2.5–6.2.7) are chosen which approximate the unity value of the sum rules for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and assume the sum rule for g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ to be much below unity. Many iterations were tried until reasonable results were obtained.

Section 6.2.9 discusses the arguments for the final choice of spins. Table 6 summarizes the results. The final spin assignment for the 32 states in the 22 levels shown in Table 8 may need in future another explanation. The cross sections for the doublets $N_s$ certainly are not evenly distributed, the ratio $R\gg 20$ hints to more unresolved doublets, some discarded assignments $N_{dscd}$ have to be changed.

5.2.2 Major steps in determining spin and structure of states

Fig. 10

Ratio of cross section on-to-off IAR for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$. A ratio $R=20$ is expected for a Lorentzian with $\varGamma ^{tot}_{{{\textit{g}}}{_{{ 9}/{2}}}}=250$ keV [114] and the two proton energies $E_p=14.935, 14.40$ MeV. Up to three states (marked bold face) are discerned in each level (Tables 4, 5, 8). A ratio larger than 20 suggests unresolved states in the level. Apparently more unresolved states are present (Table   4). The ratio $R=9$ for level 24 may be explained by assuming the triplet to consist of the 5$^-$, 6$^-$, 7$^-$ members with cross sections $\sigma /2, \sigma /4, \sigma /4$ (denoted by dotted lines)

Using Table 2 and Figs. 6, 7, 8, and 9 the shape alone allows to exclude certain spins for many states. The minimum and maximum or the relative cross section ${d\sigma ^{rel} }/{d\Omega }$ [Eq. (7)] is important. Table 3 shows characterizing values. In the following, conditions are enumerated which allow to find possible spin assignments.

• 1. For states with spin 2$^-$ the bending is upwards. The maximum reaches 2.0-3.0 at $\varTheta =180^\circ$.

• 2. For states with spin 3$^-$ and dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component the shape of the angular distribution could have an extraordinary bending different from all other spins.

• 3. For states with spin 3$^-$ and dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component a steep slope with upward bending is expected differing from the downward bending for spin 6$^-$.

• 4. For states with spin 4$^-$ or 5$^-$ the shape may have many different shapes because of the possibly mixing among three configurations (g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$) and additional weak admixtures from a fourth configuration g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$. Because of the weak s.p. width contributions from g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ can be neglected.

• 5. For states with spin 4$^-$ and 5$^-$ admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ may be sizeable because of the impurity of the g.s. (Sect.  2.1.2).

• 6. For states with spin 4$^-$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components the slope is rather flat and the bending is upwards (downwards) for a negative (positive) sign for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and positive sign of the g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ amplitude.

• 7. For states with spin 4$^-$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components the slope is rather flat and the upward bending becomes increasingly more expressive with negative sign of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ amplitude and for each sign of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$.

• 8. For states with spin 5$^-$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components the slope is downwards and the bending is straight (upwards) for a negative (positive) sign for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with a positive sign of the g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ amplitude.

• 9. For states with spin 5$^-$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components the slope is rather flat and the upward bending is downward (upward) for a positive (negative) sign for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with a negative sign of the g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ amplitude.

• 10. For states with spin 6$^-$ and a dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components the bending is nearly straight until the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ amplitude becomes large and if the signs differ. The maximum reaches 1.3-1.7 at $\varTheta =180^\circ$.

• 11. For states with spin 6$^-$ and a dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component the bending is downward with a weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ admixture of positive sign.

• 12. For states with spin 7$^-$ the bending is upwards and the maximum is about 1.5 at $\varTheta =180^\circ$. There is a high sensitity to g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures.

• 13. For all states admixtures of the distant configurations g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ should be negligible.

• 14. The total strength $c^2$ should not approach unity because proton particle-hole configurations and neutron configurations with another particle are certainly present in each state [Eq. (3)].

• 15. The sum rule $c^2$ for the GNPH configurations g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ should not exceed unity [Eq. (3)]. However the uncertainties of the parameters (especially $\varGamma ^{s.p.}_{lj}$) [29] allow for deviations in the order of several percent.

Fig. 11

Angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ observed by Solf [19] and fitted with five GNPH configurations given in the legend. For extended details see Sect. 4.5.3

6 Discussion

In Sect. 6.1 results for $^{208}\mathrm{Pb}$ at shortly cited.

In Sect. 6.2 results for $^{206}\mathrm{Pb}$ are summarized as they are obtained from the analysis of the angular distributions (Sects. 6.2.4, 6.2.9, 6.3).

In Sect. 6.4 states in $^{206}\mathrm{Pb}$ are compared to states in $^{208}\mathrm{Pb}$ for the region at $3.7<E_x< 4.7$ MeV.

6.1 Results for ${}^\mathbf{208 }{} \mathbf{Pb}$

First results for $^{208}\mathrm{Pb}$ discussing orthogonal ensembles of 1p1h configurations were presented in 1973 [24]. All of the thirty-four lowest particle-hole negative parity particle-hole states at $E_x<5.2$ MeV in $^{208}\mathrm{Pb}$ were investigated after 1982. Results are shown in Table 4 in [51]. An update is being done but still awaited. Only results for the 1$^-$ yrast state are included [67].

Twenty states at $3.2< E_x4.7$,MeV build an orthogonal ensemble of states with spins from 2$^-$ to 7$^-$ (one 2$^-$, three 3$^-$, five 4$^-$, six 5$^-$, four 6$^-$, one 7$^-$ states). Orthonormality and sum-rules are fulfilled with deviations less than 5% [24], see Table 4 in [51]. Seven non-1p1h configurations at $2.6< E_x4.9$ MeV are observed [47, 51, 52, 54, 56, 67].

Figure 20 displays the results for the strength distribution with g $_{{ 9}/{2}}$ lj configurations in $^{208}\mathrm{Pb}$. Figure 21 complements it for other configurations than g $_{{ 9}/{2}}$ lj (h $_{{ 9}/{2}}$ lj, i $_{{11}/{2}}$ lj). The results for $^{208}\mathrm{Pb}$ can be compared to Fig.  19 for $^{206}\mathrm{Pb}$ where the GNPH configurations $2^+_1\otimes$ g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ are included (Fig. 20). Calculations for both nuclei $^{206}\mathrm{Pb}$,$^{208}\mathrm{Pb}$ are illustrated in Fig.  22.

Fig. 12

Figure 11 continued

Fig. 13

Figure 11 continued. Spin assignment for 3833 4$^-$, 4040 5$^-$, 4061 4$^-$ (Fig. 13a, f, g) discarded, see Table 8

Fig. 14

Figure 11 continued. Spin assignment for 4161 4$^-$, 4321 4$^-$, 4341 4$^-$ (Fig. 14f, g) discarded, see Table 8

Fig. 15

Figure 11 continued. Spin assignment for 4430 4$^-$, 4499 4$^-$ (Fig. 15a, c) discarded, see Table 8

Fig. 16

Figure 11 continued

Fig. 17

Figure 11 continued. Spin assignment for 4051 5$^-$, 4095 5$^-$ (Fig. 17c, e) discarded, see Table 8

Fig. 18

Figure 11 continued. Spin assignment for 4240 5$^-$ (Fig. 18c) discarded, see Table 8

6.2 Results for ${}^\mathbf{206 }{} \mathbf{Pb}$

6.2.1 Comparison to nuclear data sheets

The correspondence of known states [41] to the states determined from the measured levels [20] by this work is discussed in the following. In view of the resolution of 15 keV equal to four times the mean distance of states at any spin (about 4 keV) the correspondence is rather uncertain.

The excitation energies agree within the uncertainties for all states except for the 4094, 4096 states in the 4094 level. They were not observed before. Note that in order to obtain uniqueness the excitation energies differ from the experimental values [20] by up to two keV and some values in [41] are reported without an uncertainty. An agreement of the excitation energy given in Table 4 with excitation energies from [41] is found for the 3713, 3771, 3772, and 3774, 3832, 3961, 3977 and 3778, 3993 and 3994, 4011, 4040, 4050, 4160, 4214 and 4215, 4239 and 4241, 4292, 4340, 4431, 4452, 4453, and 4454, 4500, 4540, 4592 and 4593, and 4680 states.

The assignments of spin 5$^-$ are confirmed for the 3772, 4060, and 4452 states corresponding to $E_x=3776.1\pm 0.09, 4066 \pm 3, 4459 \pm 3$ keV. A tentative assignment of spin 6$^-$ is confirmed for the 4500 state corresponding to $E_x=4496 \pm 5$ keV.

6.2.2 Starting point to identify particle-hole states in $^{206}\mathrm{Pb}$

The starting point to identify particle-hole states in $^{206}\mathrm{Pb}$ is the observation that the total sum of the cross sections for 22 levels at $3.7<E_x< 4.7$ MeV in $^{206}\mathrm{Pb}$ excited by $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ via the g $_{{ 9}/{2}}$ IAR in $^{207}\mathrm{Bi}$ is 2.7 mb/sr. It corresponds to 2.4 mb/sr found for 20 states at $3.7<E_x< 4.7$ MeV in $^{208}\mathrm{Pb}$ excited by $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ via the g $_{{ 9}/{2}}$ IAR in $^{209}\mathrm{Bi}$. Note that the chosen proton energy for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ was $E_p=14.99$ MeV which is 20% off the resonance maximum [29]. The agreement with the total sum calculated for the configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with 2.1 mb/sr (Table  2) indicates that little g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength is present as expected if the p $_{{ 1}/{2}}$ orbit is empty. (In $^{208}\mathrm{Pb}$ little g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength is located at $3.7<E_x< 4.7$ MeV.)

The maximal cross sections are 0.30 and 0.41 mb/sr in $^{206}\mathrm{Pb}$ but only 0.24 and 0.33  mb/sr in $^{208}\mathrm{Pb}$ (Fig. 1). Hence obviously some levels in $^{206}\mathrm{Pb}$ are doublets. Indeed 32 states are strongly suggested in the 22 observed levels.

6.2.3 Major steps of iterations

Two major iterations allow to identify 32 states in 22 levels.

In a first iteration only the shape ${d\sigma ^{rel} }/{d\Omega }$ [Eq. (7)] is considered (Sects. 6.2.5, 6.2.6, 6.2.7). The levels are discussed within each subsection in consecutive order. In Sect. 6.2.9 the levels are finally discussed by considering the orthonormality and sum-rule relations [Eq. (3)] and the expectation from calculations by SDI (Table 2).

First iteration. A few steps lead to rather convincing spin assignments with the assistance of Table 3 and Figs. 11, 12, 13, 14, 15, 16, 17 and 18.

The high sensitivity of the $({{{\textit{p}}}, {{\textit{p}}}' })$ reaction via an IAR needs to include admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$.

(i) The shape of the angular distribution (Fig. 2) in comparison to calculations (Figs. 6, 7, 8, 9) is considered in the beginning. Often two or three spin assignments are similarly probable.

(ii) Admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ should be less than one percent in strength because of the large distance of the configurations from g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ (Table 2).

(iii) Admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ should be less than half the strength if the g.s. of $^{206}\mathrm{Pb}$ is rather pure (Sect. 2).

Second iteration.

(i) The sum rule [Eq. (3)] should approach unity for states with a certain spin and dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength at $E_x{ {}^<\!\!\!\!_\sim }4.17$ MeV.

(ii) The sum rule [Eq. (3)] should approach unity for states with a certain spin and dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength at $E_x{ {}^>\!\!\!\!_\sim }4.17$ MeV.

(iii) The centroid energies for states with dominant configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ should be close to the energy $E_x^{SDI}(I^\pi ,lj)$ for $lj={{\textit{f}}}{_{{ 5}/{2}}}$, p $_{{ 3}/{2}}$, respectively (Table 2).

(iv) The spacing between any two states of the same spin should be larger than 20 keV. The minimum distance between any two states of the same spin in $^{208}\mathrm{Pb}$ is about 35 keV [16, 46]. It is explained by the level repulsion in the theory of chaotic spacing [123, 124]. The level density in $^{206}\mathrm{Pb}$ is twice larger as shown by this work (Sect.  6.4).

This argument is not used explicitly, arguments (i)–(iii) suffice. The final result shows that the minimal spacing between any two states of the same spin in $^{206}\mathrm{Pb}$ with 15 keV is half of the corresponding value for $^{208}\mathrm{Pb}$ [16]. Note that the uncertainties of the excitation energies are 4 keV [20].

Tables 4, 5, 8 show the final spin assignments. Figures 11, 12, 13, 14, 15, 16, 17 and 18 (Sect.  4.5.2) the amplitudes. In the following, the spin assignments and the identification of states are discussed.

6.2.4 Shape of the angular distribution

Figures 6, 7, 8, and 9 show the shape of the angular distributions for mixtures of the configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. Table 3 characteristizes the angular distributions. In many cases admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ turn out to be sensitive, too. The method described in Sect.  5.2 allows to find solutions in a 4- or even 5-dimensional space.

In first iteration considering the shape of the angular distribution alone, some levels contain one state with a unique shape of the angular distribution (Sect.  6.2.5). Some levels are shown to certainly contain two or three states (Sect. 6.2.6). Some levels may contain two or three states (Sect. 6.2.7).

In a second iteration, other considerations discard some spin assignments (Sect. 6.2.9).

This work tries to decipher the experimental data with the utmost accuracy. However Fig. 10 together with Table 4 points to possibly more unresolved states.

A triplet with spins 5$^-$, 6$^-$, 7$^-$ is deduced for level 24. The assumption of equal cross sections for the three members yields an extremely low ratio R. The 6$^-$ member contains a large g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixture which is unlikely; the cross section of the 7$^-$ member may be weaker, and the five amplitudes in the 5$^-$ member may lead to a mixture with less g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$. By assuming the cross section for the 5$^-$ member to be twice as large as for the 6$^-$, 7$^-$ members the ratio R would assume a ratio nearer to $R=20$ expected for the on-to-off resonance cross section (Fig. 10).

A third iteration is needed in future (Sect. 6.2.10) after the first and second iteration (Sect. 6.2.9).

6.2.5 Unique spin assignments

Some angular distributions have a unique shape ${d\sigma ^{rel} }/{d\Omega }$ [Eq. (7)] thus firmly assigning a certain spin and a major GNPH configuration to the state. Nevertheless the level may indicate the presence of another unresolved state covered by the level because of discrepancies of the angular distribution at scattering angles $\varTheta { {}^<\!\!\!\!_\sim }130^\circ$ or $\varTheta { {}^>\!\!\!\!_\sim }160^\circ$.

• The 3960 level is assumed to contain a 4$^-$ state (Fig.  11). The shape of the angular distribution steeply decreases from 1.4 at $\varTheta =90^\circ$ to 0.7 at $\varTheta =180^\circ$ with a slight upward bending. The curvature clearly differs from the shape for spin 6$^-$ with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. Spin 5$^-$ is excluded because of the different bending at $\varTheta { {}^>\!\!\!\!_\sim }160^\circ$. The fit with four configurations yields either a strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component with unique signs (3960) or an even mixture of g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with admixtures from g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ (3961).

• The 3713 level is assumed to contain a 2$^-$ state (Fig.  12). The shape of the angular distribution is extremely steep raising from 0.7 to 2.0 with a slight upward bending. The deviation from the factor 2.6 at $\varTheta =180^\circ$ for a pure g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ configuration yields an admixture of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ with a unique sign; admixtures of g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ are weak.

• The 4011 level is assumed to contain a 6$^-$ state (Fig.  12). The shape of the angular distribution is very peculiar; it raises from $\varTheta = 90^\circ$ to 1.2 at $\varTheta =130^\circ$ and then decreases to 0.25 at $\varTheta =180^\circ$. The shape excludes all other spins but 6$^-$. The coincidence with the characteristic bending for a pure g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ configuration yields weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ with unique signs.

• The 4540 level is assumed to contain a 5$^-$ state (Fig.  12). The shape of the angular distribution is peculiar, it raises from a minimum of 0.8 with a slight upward bending to a maximum of 1.5. Spin 3$^-$ is excluded because the slope is much smaller. Spin 7$^-$ is excluded because the pronounced down-bending near $\varTheta =140^\circ$ cannot be fitted.

• The 4680 level is assumed to contain a 6$^-$ state (Fig.  12). The shape of the angular distribution is rather straight. The angular distribution resembles that for the 4453 level with 10% of its strength. The slope is larger favoring assignment of spin 6$^-$. In view of the weak cross section no other spin assignment was tried.

6.2.6 Doublets

The cross section of some levels exceeds the value calculated for a single state (Table 2). Clearly a doublet with two or three states with different spins is present.

Table 8 indicates doublets by including the factor 1/2 or 1/3 to the cross section for the two or three members. The amplitudes and strength are determined with the reduced cross section.

States with spin 4$^-$ or 5$^-$ may contain weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixtures because of the impurity of the g.s. (Sect. 2.1.2). Therefore angular distributions of 4$^-$ or 5$^-$ states are difficult to fit because at least three configurations admix rather strongly; in a few cases even five configurations contribute.

Because of the wide range of shapes angular distributions of 4$^-$ or 5$^-$ states sometimes resemble that with another spin.

• The 3773 level has the large cross section of 154$\mu$b/sr. It is assumed to consist of the 3772 5$^-$, 3771 6$^-$, 3774 7$^-$ states (Fig. 16). The shape of the angular distribution has a strong bending starting from about 1.0 at $\varTheta =90^\circ$ up to 1.3 at $\varTheta =180^\circ$. Spins 2$^-$ and 3$^-$ are excluded because the slope is too low. The fit assuming spin 5$^-$ or 6$^-$ reproduces the bending. For spin 6$^-$ the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ amplitude is much larger than g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, the g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ admixtures are negligible. For spin 5$^-$ the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ amplitudes are equal, admixtures from g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ are negligible. Assuming spin 7$^-$ the angular distribution deviates largely at $\varTheta <130^\circ$ but the fit at $\varTheta >130^\circ$ is reasonable. The excitation energy is not far from the prediction by SDI.

• The 3977 level has the large cross section of 191$\mu$b/sr. It is assumed to consist of the 3977 4$^-$ and 3978 5$^-$ states. The fit of the level yields similar results for spin 4$^-$ and 5$^-$ (Fig. 13). The angular distribution decreases from 1.2 at $\varTheta =90^\circ$ to 0.5 at $\varTheta =180^\circ$ with a slight downward bending. A fit with spin 4$^-$ alone needs a g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ amplitude larger than unity violating the sum rule relation [Eq. (3)]. A fit with spin 5$^-$ alone needs large g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ amplitudes. The normality relation is nearly violated [Eq. (3)]. A doublet with equal cross sections is assumed. For spin 4$^-$ a dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component with strong g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, and weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures are determined. For spin 5$^-$ g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components of similar size with weak admixtures from g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ are determined.

• The 3993 level is assumed to consist of the 3992 3$^-$ and 3992 or 3994 6$^-$ states (Fig. 16). The shape of the angular distribution is rather steep; it raises by from 0.9 at $\varTheta =90^\circ$ to 1.5 at $\varTheta =180^\circ$ without a bending. The fit assuming spin 3$^-$ and dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength reproduces the angular distribution quite reasonable at $130^\circ< \varTheta <180^\circ$ with a maximum of 1.35 at $\varTheta =180^\circ$. Weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and a negligible g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ admixture are derived. The straight increase starting with 0.9 at $\varTheta =90^\circ$ is better fitted by assuming spin 6$^-$, either the 3992 state with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ or the 3994 state with mixed g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$.

• The 4214 level has the large cross section of 410$\mu$b/sr. It is assumed to consist of the 4214 4$^-$ and 4215 5$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 14). The shape of the angular distribution is steep starting from 1.3 at $\varTheta =90^\circ$ down to 0.3 at $\varTheta =180^\circ$ with a slight bending. The fit for spin 4$^-$ with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component with unique signs and weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. The fit for spin 5$^-$ with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component with unique signs, a considerable g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ contribution and weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures.

• The 4240 level has the large cross section of 136$\mu$b/sr. It is assumed to consist of two states, the 4239 3$^-$ and 4241 4$^-$ states (Fig. 18). The angular distribution starts from 1.0$\pm 0.1$ at $\varTheta =90^\circ$ ending with 1.4$\pm 0.2$ at $\varTheta =180^\circ$ with a clear upward bending. The spin assignments 4$^-$ and 5$^-$ yield a reasonable interpretation of the angular distribution. The 5$^-$ state alone would contain half of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength and a strong g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture. By assuming spin 4$^-$ the bending is well fitted. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures of similar size. The fit for spin 3$^-$ with a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component and weak g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures reproduces the steep raise at $\varTheta >140^\circ$ rather well but fails at $\varTheta \approx 90^\circ$ by a factor two.

• The 4453 level has the large cross section of 297$\mu$b/sr. It is assumed to contain the 4454 4$^-$, 4452 5$^-$, 4453 6$^-$ states (Fig. 18). Spin 2$^-$ is excluded because of the large cross section and because the slope is not very steep. Spin 3$^-$ is excluded because of the large cross section and because there is no bending. Spin 7$^-$ is excluded because of the large cross section. The shape of the angular distribution is straight. It raises from 0.8 at $\varTheta =90^\circ$ to 1.3 at $\varTheta =180^\circ$ in near coincidence with the factor 1.35 for pure g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ for spin 6$^-$. It thus yields weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ with unique signs.

• The 4500 level is assumed to consist of the 4499 4$^-$ and 4500 6$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 15). For spin 4$^-$ a dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component with a strong g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, and weak g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures are determined. For spin 6$^-$ a dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component with weak g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ admixtures are determined.

6.2.7 Alternate spin assignments

Several levels can be fitted with two alternate spin assignments. A level may contain two states, either the first or the second energy label or the first and the second energy label is assumed, in few cases even three energy labels. Table 8 indicates spins discarded by further reasoning (Sect. 6.2.9). The strength is given in parentheses, in Table 4 the discarded assignments are denoted by $N_{dscd}$, see also Table  5.

A factor ${ 1}/{2}$ is included in the strength if two spins are assumed to be valid. The amplitudes are calculated with the full cross section.

• The 3833 level is assumed to consist of the 3832 6$^-$ and 3833 4$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 13). For spin 4$^-$ a dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component with weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, and g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures are determined. For spin 6$^-$ a dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component with weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ admixtures are determined.

• The 4040 level is assumed to consist of the 4040 5$^-$ and 4041 4$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 13). The angular distribution has an expressive upward bending starting from 1.0 at $\varTheta =90^\circ$ to 0.8 at $\varTheta =180^\circ$ with a maximum of 1.1. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 4$^-$ state with a weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 5$^-$ state with a considerable g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and a weak g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures.

• The 4050 level is assumed to consist of the 4049 4$^-$ and 4051 5$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution, for spin 4$^-$ two different sets of amplitudes are possible (Fig. 17). The angular distribution smoothly decreases from 1.2 at $\varTheta =90^\circ$ to 0.5$\pm 0.2$ at $\varTheta =180^\circ$ without a bending; the uncertainty at $\varTheta >160^\circ$ however is large. An assignment of spin 6$^-$ is excluded because the slope is straight and not large. The fit for spin 4$^-$ with five configurations yields either a strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with a weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ or a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with a weak g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component with negligible admixtures from g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$. The fit for spin 5$^-$ with four configurations yields similar amplitudes for the configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and a weak g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixture.

• The 4060 level is assumed to consist of the 4060 5$^-$ and 4061 4$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 15). The angular distribution decreases from 1.2 at $\varTheta =90^\circ$ to 0.7 at $\varTheta =180^\circ$ without a bending. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 4$^-$ state with weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component in the 5$^-$ state with considerable g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and a weak g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures.

• The 4094 level is assumed to consist of the 4094 4$^-$, 4095 5$^-$, and 4096 6$^-$ states. The spin assignments yield a reasonable interpretation of the angular distribution (Fig. 15), however among all angular distributions these fits are worst. The shape of the angular distribution is very steep starting from 1.4 at $\varTheta =90^\circ$ down to 0.3 at $\varTheta =180^\circ$ with a peculiar double bending. The fit with four configurations for spin 4$^-$ yields strong g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ components and weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. For spin 5$^-$ the fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component, admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with unique signs are weak, with g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ negligible. The fit with three configurations for spin 6$^-$ yields a strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component and weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. The fit assuming spin 4$^-$ does not reproduce the rather straight angular distribution. The fit assuming spin 5$^-$ reproduces the data at $\varTheta < 130^\circ$ even worse. The fit assuming spin 6$^-$ reproduces the data at $\varTheta > 140^\circ$ best but completely fails for lower scattering angles.

• The 4160 level is assumed to consist of the 4161 4$^-$ and 4160 5$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 15). The angular distribution decreases from 1.2 at $\varTheta =90^\circ$ to 0.4 at $\varTheta =180^\circ$ without bending. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 4$^-$ state with weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. Similarly, the fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 5$^-$ state with weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures.

• The 4320 level is assumed to consist of the 4321 4$^-$ and 4320 6$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 15). The angular distribution raises from 0.8 at $\varTheta =90^\circ$ to 1.2 at $\varTheta =180^\circ$ with a slight downward bending. The fit with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 4$^-$ state with a weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture. The fit with two configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component in the 6$^-$ state.

• The 4340 level is assumed to consist of the 4341 4$^-$ and 4340 5$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 16). The angular distribution smoothly decreases from 1.2 at $\varTheta =90^\circ$ to 0.5 at $\varTheta =180^\circ$ without a bending. The shape of the 4340 level is similar to shape of the 4050 level. The fit for spin 4$^-$ with four configurations yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component and weak g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. The fit for spin 5$^-$ with four configurations yields similar amplitudes for the configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and weak g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures. A fit with similar relative amplitudes as for the 4050 level fails for spin 4$^-$ because of the large cross section whereas for spin 5$^-$ the ratio of the amplitudes is about a factor two.

• The 4430 level is assumed to consist of the 4430 4$^-$ and 4431 6$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 16). For spin 4$^-$ a dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component with a considerable g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, and weak g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures are determined. For spin 6$^-$ a dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component with a considerable g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, and weak g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ admixtures are determined.

• The 4592 level is assumed to consist of the 4592 7$^-$ and 4593 6$^-$ states. Both spin assignments yield a reasonable interpretation of the angular distribution (Fig. 16). The shape of the angular distribution is extremely steep; it raises from 0.8 at $\varTheta =90^\circ$ to 1.5 at $\varTheta =180^\circ$. The coinciding factor 1.55 for a pure g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with spin 7$^-$ yields weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ with unique signs. The fit for spin 6$^-$ yields a strong g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component with a considerable g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixture and a weak g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixture.

6.2.8 Discrimination of spins

Two or three spins can be assigned to an unresolved doublet. The clearest example is the level number 33 with $E_x=4094$ keV. The shapes of Fig. 17 d-f differ considerably. The spin 5$^-$ is discarded because the excitation energy is low and the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength is large (Fig. 17 e, Sect. 6.2.9). The fit of the 4094 level with even order Legendre polynomials (Figs. 2, 17) deviates at $\varTheta >140^\circ$ by 20% for spin 4$^-$ (d) and at $\varTheta <120^\circ$ by 50% for spin 6$^-$ (f).

In other cases the deviations are smaller but still significant. In Fig. 13 the fit with Legendre polynomials deviates by 20% at $\varTheta <120^\circ$ for spin 4$^-$ by 10% at $\varTheta { {}^>\!\!\!\!_\sim }160^\circ$ both for (e) and (f). In Fig. 16 the fit with Legendre polynomials deviates by 20% at $\varTheta <120^\circ$ and for spin 7$^-$ (c); for spin 3$^-$ the bending matches badly throughout (f); especially the deviations at $\varTheta <120^\circ$ are large. The deviations for spin 3$^-$ in Fig. 18a are similar to Fig. 14f. In both cases the bending is typically for the low spin.

Two levels are assumed to contain three states with equal cross sections for each pair. Six levels are assumed to contain two states with equal cross sections for each triple.

For five levels two different spin assignments (from 3$^-$ to 7$^-$), for one level two different configuration mixings with spin 4$^-$ are deduced (Fig. 17a, b). In one case a triplet with two different configuration mixings and spin 6$^-$ and a third state with spin 3$^-$ are deduced (Fig. 16d–f). In two cases a triplet with different spins (4$^-$, 5$^-$, 6$^-$ and 5$^-$, 6$^-$, 7$^-$) are deduced (Figs. 16a–c, 18d–f).

6.2.9 States identified in $^{206}\mathrm{Pb}$ in first and second iteration

In the following the identification of GNPH states in $^{206}\mathrm{Pb}$ is discussed. Some spin assignments compatible with the shape (Sects. 6.2.5, 6.2.6, 6.2.7) have to be discarded in second iteration (Sect. 6.2.3) alternating with the first iteration.

Table 2is used as a guide for the discussion. Tables 4, 5, 8assist in locating the levels and states. For each level dominant configurations are mentioned (Table 5).

• Level 23 (Fig. 12) can be fitted assuming the presence of the 2$^-$ 3713 state (Sect. 6.2.5). The slope of the angular distribution is extremely steep. The state contains 60% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength, the excitation energy is 0.5 MeV lower than expected.

• Level 24 (Fig. 16) can be fitted assuming the presence of three states with equal cross sections, the 3772 5$^-$, 3771 6$^-$, and 7$^-$ 3774 states (Sect. 6.2.6). The large cross section clearly indicates the presence of more than one state. The fit assuming spin 7$^-$ reproduces the data at $\varTheta >130^\circ$, especially the steep raise. The state contains 21% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The splitting of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength for spin 7$^-$ is discussed in Sect. 6.3.1. The bending of the angular distribution is better fitted with a 5$^-$ and a 6$^-$ state. The 5$^-$ state contains 14% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength besides 4% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and a negligible g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component. The 6$^-$ state contains 14% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and 3% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The excitation energies of the 5$^-$ and 6$^-$ states agree with the prediction for a strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component (Table 2).

• Level 25 (Fig. 13) can be fitted assuming the presence of the 4$^-$ 3833 and 6$^-$ 3832 states (Sect. 6.2.7). The 4$^-$ state alone would contain 8% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with weak admixtures from g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. The low excitation energy disfavores a large g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The assignment of spin 6$^-$ is chosen. The 6$^-$ state contains 10% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and 3% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 26 (Fig. 13) can be fitted assuming the presence of the 4$^-$ 3960 state (Sect. 6.2.5). The shape of the angular distribution leads to a unique spin assignment however with two different compositions. The solution with a strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component is excluded by considering the sum rule; especially the 3980 already contains 49% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. The 3961 state contains 10% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with 8% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and 4% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture.

• Level 27 (Fig. 13) can be fitted assuming the presence of two states with equal cross sections, the 4$^-$ 3977 and 5$^-$ 3978 states (Sect. 6.2.6). The cross section is larger than for any state in $^{208}\mathrm{Pb}$. The large cross section clearly indicates the presence of two states. The 4$^-$ state contains half of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength with a 9% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ component and 1% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ admixture. The excitation energies of the 4$^-$ state agrees with the prediction by SDI (Table 2). The 5$^-$ state contains 12% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 10% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength and 3% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture.

• Level 28 (Fig. 16) can be fitted assuming the presence of two states, the 3$^-$ 3993, and 6$^-$ 3994 states(Sect. 6.2.6). The steep slope of the angular distribution strongly suggests the presence of a 3$^-$ state, the large deviation at $\varTheta <130^\circ$ indicates the doubleting with another state. The 3$^-$ state contains one third g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength with 1% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ admixture. The excitation energy agrees with the expectation from SDI (Table 2). The 6$^-$ 3992 state with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength is discarded because such a large component is disfavored because of the low excitation energy. The 6$^-$ 3994 state contains a stronger g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component filling the sum rule to 91%.

• Level 29(Fig. 12) can be fitted assuming the presence of the 6$^-$ 4011 state (Sect. 6.2.5). The shape of the angular distribution is peculiar. The state contains 30% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength with a negligible g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ admixture. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 30(Fig. 13) can be fitted assuming the presence of the 4$^-$ 4039 and 5$^-$ 4040 states (Sect. 6.2.7). The assignment of spin 4$^-$ is excluded. The 4$^-$ state alone would contain 23% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with negligible g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixtures. The low excitation energy disfavores a large g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The assignment of spin 5$^-$ is chosen. The 5$^-$ state contains 17% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with 8% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 31 (Fig. 17) can be fitted assuming the presence of the 4$^-$ 4049 or 4$^-$ 4050 and 5$^-$ 4051 states (Sect. 6.2.7). The assignment of spin 5$^-$ is excluded because of the worse fit. With an assignment of spin 4$^-$ there are two solutions. A 8% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component is excluded because of the low excitation energy. The 4$^-$ state contains 38% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength with negligible admixtures from g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$. The excitation energy agrees with the expectation from SDI.

• Level 32(Fig. 13) can be fitted assuming the presence of the 4$^-$ 4061 and 5$^-$ 4060 states (Sect. 6.2.7). The 4$^-$ state alone would contain 8% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with negligible g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixtures. The low excitation energy disfavores a large g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The assignment of spin 5$^-$ is chosen. The 5$^-$ state contains 42% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with 6-7% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 33 (Fig. 17) can be fitted assuming the presence of the 4$^-$ 4094 and 6$^-$ 4096 states (Sect. 6.2.7). The assignment of spin 5$^-$ is excluded. The 5$^-$ state alone would contain 25% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 4% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength and a negligible g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture. The low excitation energy disfavors a large g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength (Table 2). In contrast the 4$^-$ state alone would contain 14% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and 32% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength with 1% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ admixture. The low excitation energy favors a large g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The fit assuming spin 6$^-$ is best at $\varTheta >140^\circ$. A strong g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component is expected near this excitation energy (Table  2).

• Level 35 (Fig. 14) can be fitted assuming the presence of the 4$^-$ 4161 state and 5$^-$ 4160 states (Sect. 6.2.7). The assignment of spin 4$^-$ is excluded. The 4$^-$ state alone would contain 70% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with less than 1% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. The low excitation energy disfavores such a large g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength by observing the sum rule and the centroid energy. The assignment of spin 5$^-$ is chosen. The 5$^-$ state contains 34% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with less than 1% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 36 (Fig. 14) can be fitted assuming the presence of two states with equal cross sections, the 4$^-$ 4214 and 5$^-$ 4215 states (Sect. 6.2.6). The cross section of 400 $\mu$b/sr is larger than for any state in $^{208}\mathrm{Pb}$. The extremely large cross section clearly indicates the presence of two states. The fit with spin 4$^-$ alone would need a g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ amplitude larger than unity violating the orthonormality and sum-rule relations [Eq. (3)]. Hence by assuming spin 4$^-$ no reasonable interpretation of the angular distribution can be found. The 5$^-$ state alone would contain 80% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 12% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength with 2% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture. The normality relation [Eq. (3)] approaching unity is unlikely. Hence by assuming spin 5$^-$ no reasonable interpretation of the angular distribution can be found. The 4$^-$ state contains half of the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 3% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength and a negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixture. The 5$^-$ state contains 40% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 6% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength with 1% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixture. The excitation energies agree with the expectation from SDI (Table 2).

• Level 37 (Fig. 18) can be fitted assuming the presence of three states with equal cross sections, the 3$^-$ 4239, 4$^-$ 4241, and 5$^-$ 4240 states (Sect. 6.2.6). The large cross section clearly indicates the presence of more than one state. A doublet with spins 3$^-$, 4$^-$ and equal cross sections is assumed, spin 5$^-$ is discarded. Assuming the spin 5$^-$ the state would contain 34 and 12% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength with a negligible g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component. For g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ the sum rule would exceed unity and the centroid could be energy higher than expected. The fit assuming spin 3$^-$ reproduces the data at $\varTheta >130^\circ$, especially the steep raise. The state contains 15% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2). The bending of the angular distribution is better fitted with a 4$^-$ and 5$^-$ state. The 4$^-$ state contains 10% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength besides 3% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and a negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component. The excitation energies of the 4$^-$ state agrees with the prediction (Table 2).

• Level 39 (Fig. 14) can be fitted assuming the presence of the 4$^-$ 4321 and 6$^-$ 4320 states (Sect. 6.2.7). The assignment of spin 4$^-$ is excluded. The 4$^-$ state alone would contain 31% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with 1% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixtures. The sum rule would exceed unity because 49% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength is located in the 4214 state (see level 36 above) and 27% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength in the 4454 state (see level 44 below). The assignment of spin 6$^-$ is chosen. The 6$^-$ state contains 24% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 1% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 40 (Fig. 14) can be fitted assuming the presence of the 4$^-$ 4341 and 5$^-$ 4340 states (Sect. 6.2.7). The assignment of spin 4$^-$ is excluded. The 4$^-$ state alone would contain 26% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 1% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength. The sum rule would exceed unity similarly as discussed for level 39 before. The 5$^-$ state contains 21% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with 17% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and % g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 43 (Fig. 15) can be fitted assuming the presence of the 4$^-$ 4430 and 6$^-$ 4431 states (Sect. 6.2.7). The assignment of spin 4$^-$ is excluded. The 4$^-$ state alone would contain 26% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 1% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength. The sum rule would exceed unity similarly as discussed for level 39 before. The 6$^-$ state contains 27% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with 3% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$. The excitation energy agrees with the expectation from SDI (Table 2).

• Level 44 (Fig. 18) can be fitted assuming the presence of three states with equal cross sections, the 4454 4$^-$, 4452 5$^-$, and 4453 6$^-$ states (Sect. 6.2.6). The large cross section of 300 $\mu$b/sr clearly indicates the presence of more than one state. The 4$^-$ state contains 27% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixture. The 5$^-$ state contains 14% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and 14% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength with negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixture. The 6$^-$ state contains 21% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength with 2% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixture. The excitation energies agree with the expectation from SDI (Table 2).

• Level 45 (Fig. 15) can be fitted assuming the presence of a doublet with equal cross sections, the 4$^-$ 4499 and 6$^-$ 4500 states (Sect. 6.2.7). The large cross section clearly favors the presence of more than one state. The 4$^-$ state contains 14% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with 2% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and a negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ admixture. The 6$^-$ state contains 11% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ with negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ admixtures. The excitation energies agree with the expectation from SDI (Table 2).

• Level 46 (Fig. 12) can be fitted assuming the presence of the 5$^-$ 4540 state (Sect. 6.2.5). The shape of the angular distribution is peculiar. The state contains an even mixture of three configurations (5% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, 6% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, 2% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength).

• Level 47 (Fig. 15) can be fitted assuming the presence of states with equal cross sections, the 6$^-$ 4593 and 7$^-$ 4592 states (Sect. 6.2.7). The 6$^-$ state contains 7% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ || 2% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The excitation energy agrees with the expectation from SDI (Table 2). The 7$^-$ state contains 28% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The splitting of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength for spin 7$^-$ is discussed in Sect. 6.3.1.

• Level 48 (Fig. 11) can be fitted assuming the presence of the 6$^-$ 4680 state (Sect. 6.2.5). The shape of the angular distribution is straight and steep. The state contains 9% g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength and a negligible g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component. The excitation energy agrees with the expectation from SDI (Table 2).

6.2.10 Possible identification of more states in $^{206}$Pb in third iteration

Figures 1 and 10 shows the ratio of the on-to-off resonance cross section for twenty levels in $^{206}\mathrm{Pb}$. A ratio $R=20$ is expected with a total width $\varGamma ^{tot}_{{{\textit{g}}}{_{{ 9}/{2}}}}=250$ keV [114] for a Lorentzian and two proton energies $E_p=14.935, 14.40$ MeV, see also Fig. 2 in [46].

Three levels are recognized as triplets with two or three different spins, six levels as doublet with two states (Table  4); they are marked in Fig.  10. Six levels have a ratio $R\approx 50$, three levels a ratio of around $R\approx 35$. Without almost any exception all these levels were recognized as doublets which were discarded by the investigation of the orthonormality and sum-rules [Eq. (3)] (Sect. 6.2.7).

Obviously some spin assignments (Sect. 6.2.9) must be revised by a third major reconsideration. 15 states are discarded by regarding orthonormality and sum-rule relations [Eq. (3)] ($N_{dscd}$ in Table  4). 15 additional states are suggested to be identified from the ratio $R\gg 20$ with $R\ne N_{s}$ shown in Fig. 10 ($N_{R}$ in Table 4). The number of discarded states $N_{dscd}$ is underestimated and $N_{R} - N_s$ more states are suggested.

In third iteration the number of identified states at $3.7<E_x <4.7$ MeV in $^{206}\mathrm{Pb}$ may thus increase to twice the number of states in $^{208}\mathrm{Pb}$.

6.3 Strength distribution

In order to check the strength distribution for the configurations g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ in $^{206}\mathrm{Pb}$ the states are divided into two groups with excitation energies less and larger than $E_x=4.17$ MeV, a boarder dividing the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength from the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength (Table 2).

The g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength for spins from 2$^-$ to 7$^-$ is located in the lower part with a center of gravity of $E_x\approx 4.10$ MeV close to the prediction $E_x^{SDI}=4.00$ keV. The sum of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength for spins 2$^-$, 3$^-$, 4$^-$, 5$^-$, 6$^-$, 7$^-$ is about 60, 30, 40, 40, 40, 30%, respectively. At $E_x>4.17$ MeV less than 6% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength is found except for spin 5$^-$. However about 60% g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength is observed for spin 7$^-$ at $E_x>4.17$ MeV. The major g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ component in the 4592 7$^-$ state is interpreted by the configuration ${{\textit{g}}}{_{{ 9}/{2}}}\, {{\textit{f}}}{_{{ 5}/{2}}}\otimes { 803\ 2^+_1}$. The energy difference between the two 7$^-$ states with 818 keV well corresponds to the excitation energy of the 2$^+$ yrast state.

The g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength for spins from 3$^-$ to 6$^-$ is located in the upper part with a center of gravity of $E_x\approx 4.25$ MeV close to the prediction $E_x^{SDI}=4.33$ keV The sum of the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength for spins 3$^-$, 4$^-$, 5$^-$, 6$^-$ is 22, 84, 77, 111% and at $E_x<4.17$ MeV 1, 43, 33, 6% is found, respectively. In contrast to the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength is wider distributed especially for spins 4$^-$ and 5$^-$.

Admixtures from g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ are less than about one percent in the 32 states. However the g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength for spins 4$^-$ and 5$^-$ does not vanish as expected, 35% and 33% g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength for spin 4$^-$ and 5$^-$ are found. The centroid energy of the g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength is $E_x\approx 4.2$ MeV. It well corresponds to $E_x =4.23$ keV predicted by the weak coupling model [2] for $2^+_1\otimes {{\textit{g}}}{_{{ 9}/{2}}}{{\textit{p}}}{_{{ 1}/{2}}}$. It thus shows the g.s. of $^{206}\mathrm{Pb}$ to contain weak ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$ admixtures with dominant ${{\textit{p}}}{_{{ 3}/{2}}}^{-2}, {{\textit{f}}}{_{{ 5}/{2}}}^{-2}$ components.

6.3.1 Distribution of configurations with the g $_{{ 9}/{2}}$ particle in $^{206}\mathrm{Pb}$

Table 8 shows the strength distribution for the configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ in $^{206}\mathrm{Pb}$. Most spin assignments are considered to be valid. Yet some results are problematic. In the following we discuss the results in detail.

Figures 19 and 20 compare the distribution of the GNPH configurations in $^{206}\mathrm{Pb}$ to 1p1h configurations in $^{208}\mathrm{Pb}$, both excited near the g $_{{ 9}/{2}}$ IAR. Fig. 21 show the 1p1h configurations complementing the configuration strength in the states at $E_x<4.8$ MeV in $^{208}\mathrm{Pb}$. Fig. 22 shows excitation energies calculated by SDI for the 1p1h configurations in $^{208}\mathrm{Pb}$; the GNPH configuration g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 2^+_1$ is included. In Sect. 6.3 details of the comparison are discussed. As a general result the strength distribution for GNPH configurations in $^{206}\mathrm{Pb}$ (Fig. 19) is found to be similar to the well known distribution for 1p1h configurations in $^{208}\mathrm{Pb}$.

• One 2$^-$ state is observed in $^{206}\mathrm{Pb}$. The 3713 state contains about half of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The excitation energy being 0.5 MeV lower may be explained by a strong mixing between the 1p1h configuration g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $E_x^{SDI}=4304$ and $2^-_1\otimes$ g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ $E_x^{calc}=4230$ (Table 2).

• Two 3$^-$ states are observed in $^{206}\mathrm{Pb}$. They contain 60% of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and 90% of the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength. The excitation energies are similar to $E_x^{SDI}$.

• Ten 4$^-$ states are observed in $^{206}\mathrm{Pb}$. The 4050 state contains the major g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ fraction, the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength is widely distributed. The centroid energies [Eq. (4)] agree with $E_x^{SDI}$.

• Seven 5$^-$ states are observed in $^{206}\mathrm{Pb}$. Both the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength is widely distributed. The 4215 state contains a major g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ fraction. The centroid energies agree with SDI.

• Five 6$^-$ states are observed in $^{206}\mathrm{Pb}$. The 4011 state contains a major g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ fraction, the 4453 state contains a major g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ fraction. The centroid energies agree with SDI.

• Two 7$^-$ states are observed in $^{206}\mathrm{Pb}$, each states contains about 30% of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength. The centroid energy roughly agrees with the SDI calculation. The splitting is explained by a strong mixing between g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 0^+_\mathrm{g.s.}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 2^+_1$.

6.3.2 Comparison of calculated angular distributions to best fits

Table 5 compares calculated angular distributions for configurations g $_{{ 9}/{2}}$ lj with $l2j= p1, p3, f5 ,f7$ to best fits. It shows calculated angular distributions with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and spin 2$^-$ and 7$^-$ and weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ in Fig. 6, for spin 3$^-$ and 6$^-$ with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ in Fig. 7, for dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ with spin 4$^-$ with in Fig. 8 and with spin 5$^-$ in Fig. 9, for dominant g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with spin 4$^-$ with in Fig. 6e and with spin 5$^-$ in Fig. 6f.

Best fits with spins and configuration mixing derived by investigating sum rules and orthogonality relations are printed bold face in Table  8. Best fits of angular distributions for spin 4$^-$ and two different sets of amplitudes are shown in Fig. 11, for unique spin assignments in Figs. 12 and 13, for different sets of amplitudes but similar shapes of angular distributions in Figs. 14, 15, 16, 17 and 18. Spins in parentheses denote assignments which are discarded by the investigation of sum rules and orthogonality relations [Eq. (3)]. In Table 4 discarded assignments are denoted by $N_{dscd}$. The dominant configuration or the two major configurations out of the three configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ are shown in Cols. 9–11.

The shape of angular distributions varies with spin and amplitudes of particle-hole configurations in a charactistic manner. The relative cross sections vary by factors from about 0.2 to 3 for configurations with amplitudes near one (pure configurations). Figure 4 in [46] shows examples. The mixing of several configurations varies the relative maxima and minima even more (Table 3). The shape of configurations with one dominant amplitude and admixtures of less than about 10% strength already vary the relative cross section by factors up to 2.

In order to reduce the variation a linearization is introduced with the function $P_2(\cos \varTheta )$, see Fig. 3 in [46]. By this means the cross sections near $\varTheta =120^\circ$ and $140^\circ$ change less, marks indicate the introduced non-linearity in Figs. 3 and 4 in [46] and in Figs. 6, 7, 8, 9, 14, 15, 16, 17 and 18.

Admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ to states with dominant configuration g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and spin 2$^-$ or 7$^-$ change the shape of the angular distribution sensitivily. The change is more pronounced for spin 7$^-$ than for 2$^-$. Variations of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures to states with dominant configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ for spin 3$^-$ or 6$^-$ follow the ratio of the two amplitudes from $-1$ to $+1$ in charactistic manner. The change is more pronounced for spin 3$^-$ than for 6$^-$. Variations of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ admixtures to states with an already strong g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ component and dominant configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ for spin 4$^-$ or 5$^-$ follow the ratio of the three amplitudes from $-1$ to $+1$ in a systematic manner which however leads to extreme changes.

In addition to the variation of the shape of the angular distributions the strong dependence of the s.p. width $\varGamma ^{s.p.}_{LJ}, \varGamma ^{s.p.}_{lj}$ on the proton energy enhances the cross with decreasing proton energy [39] (Fig. 8 in [29]). The change of the s.p. phase $\xi ^{s.p.}_{lj}$ with the proton energy is weak [13] and ignored for the lead isotopes. For $\xi ^{s.p.}_{{{\textit{h}}}{_{{ 9}/{2}}}}$ a crude guess is sufficient because admixtures from g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ are relevant only in few cases.

In Table 5 Col. 5 shows the number of the calculated angular distribution in Figs.  6, 7, 8 and 9. The drawn curve is denoted by the figure number, the dotted curve by the overlined figure number (Cols. 5-7). In several cases two or three calculations are similar. For spin 4$^-$ and 5$^-$ often no good agreement is found. Only the nearest approximation is shown.

6.4 Comparison of particle-hole configurations in ${}^\mathbf{206 }$Pb and ${}^\mathbf{208 }$Pb

Table 4 shows excitation energies calculated by SSM and SDI and calculated mean cross sections.

The range of excitation energies is limited to $3.7<E_x <4.7$ MeV.

• Table 4 in [51] shows amplitudes of 28 negative parity states at $2.6<E_x <5.2$ MeV in $^{208}\mathrm{Pb}$. The results from an update done in 1982 were slightly improved in 2017. Among the 43 neutron 1p1h configurations most larger amplitudes were measured for all IARs ($LJ={{\textit{g}}}{_{{ 9}/{2}}}$, i $_{{11}/{2}}$, j $_{{15}/{2}}$, d $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$). Amplitudes for g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ may be determined from data taken in 1968 [30] but are not yet evaluated except for the admixture in the 1$^-$ yrast state [67]. Cross sections involving the intruder i $_{{13}/{2}}$ are vanishingly small.

• Sect. 6.3 discusses the strength distribution in $^{206}\mathrm{Pb}$. The expected absencs of the configuration g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ is proven by spectra taken at $2.6<E_x<6.0$ MeV [20, 73]. The 2648 3$^-$ yrast state is weakly excited. Half a dozen weak levels show up at $3.0<E_x<3.7$ MeV and $4.7<E_x { {}^<\!\!\!\!_\sim }5.6$ MeV.

6.4.1 Global comparison

Energies near 3.5 MeV predicted for dominant g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ components are expected to be absent in $^{206}\mathrm{Pb}$. Configurations g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ are observed at $E_x\approx 5.7$ MeV [65]. They contribute weak admixtures to states at $3.7<E_x <4.7$ MeV.

Table 6 shows the sum rules for the three configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ in (top) $^{206}\mathrm{Pb}$ and (bottom) $^{208}\mathrm{Pb}$. Three ranges of excitation energies are chosen, $E_x< 3.7$ MeV, $3.7<E_x< 4.17$ MeV, $E_x>4.17$ MeV. In $^{208}\mathrm{Pb}$ the full sum rules are observed within the uncertainties of the IAR parameters. The only exception is found for the 7$^-$ state (Sect. 2.6). Note that part of this achievement is obtained by the orthonormality and sum-rule relations as a constraint [24]. The splitting of the g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ multiplets is rather well reproduced by SDI calculations.

The analysis of angular distributions for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ started with the finding of similar sums of cross sections for $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ (Sect.  3.2). Indeed the total cross sections for spins from 2$^-$ to 7$^-$ agree for $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ in detail (Cols. 19, 20 in Table 6). The sum rules for $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ and spins from 2$^-$ to 7$^-$ agree mostly. Yet there are clear differences.

In $^{206}\mathrm{Pb}$ the sum rules for g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ are overestimated for spins 4$^-$, 6$^-$ and for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ underestimated for spins 2$^-$, 3$^-$, 6$^-$. One reason is the arbitrary partitioning of doublets by assuming equal cross sections for each spin. For spin 2$^-$ and 3$^-$ another reason is the low cross section because of the spin factor. The g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ sum rule is a measure of the impurity of the g.s. (Sect. 2).

The centroid energies for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ in the two chosen energy ranges and in total are reproduced by the SDI calculations (Table 2) in a reasonable manner.

The comparison of particle-hole configurations in $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ show remarkable similarities and clear differences as shown in the following. The correspondence of levels observed in $^{206}\mathrm{Pb}$ to non-1p1h states in $^{208}\mathrm{Pb}$ may be given for a few states. The 4110 level is identified with the 4116.7$\pm 1.8$ keV 2$^+$ state (Table 4). It apparently corresponds to the 4086 2$^+$ state with tetrahedral configuration [51]. The 4340 level may contain besides the 5$^-$ state a 4$^+$ state corresponding to the 4324 4$^+$ state with tetrahedral configuration [51]. The 4500 level may contain besides the 6$^-$ state a 6$^+$ state corresponding to the 4424 6$^+$ state with suggested icosahedral configuration [52].

6.4.2 Detailed comparison

Figures 19 and 20 compare the strength distribution for configurations with the g $_{{ 9}/{2}}$ particle in $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$. Fig. 21 shows the distribution for the other configurations in $^{208}\mathrm{Pb}$, especially the proton configurations and configurations excited on the i $_{{11}/{2}}$ IAR. Fig. 22 displays distributions calculated by SDI and weak coupling. Table 8 gives excitation energies and configuration strengths for $^{206}\mathrm{Pb}$, Table 4 in [51] for $^{208}\mathrm{Pb}$. Finally assumed spin assignments are shown in Tables 4, 5, 8.

Table 7 correlates specific states in $^{206}\mathrm{Pb}$ to states in $^{208}\mathrm{Pb}$ with similar excitation energies and similar relative strengths for g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$.

Similarities and differences are discussed in the following.

• 1. The number of states differs for $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ in the region $3.7<E_x< 4.7$ MeV.

  • (a) One 2$^-$ state is observed in $^{206}\mathrm{Pb}$ at $E_x=3.7$ MeV. The excitation energy is 0.5 MeV lower than predicted by SDI. The down shift may be explained by the mixing among the configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 0^+_{g.s.}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 2^+_{1}$. Apparently higher 2$^-$ states are not observed because of the weak cross section. Two 2$^-$ states are known at $E_x=4.2$ MeV in $^{208}\mathrm{Pb}$, the 4140 2$^-$ state interpreted as tetrahedral configuration and the 4230 2$^-$ state with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ and sizeable d $_{{ 5}/{2}}$ p $_{{ 1}/{2}}$ admixture. The 5038 state is the next one with major d $_{{ 5}/{2}}$ p $_{{ 1}/{2}}$ and f $_{{ 7}/{2}}$ d $_{{ 3}/{2}}$.

  • (b) Two 3$^-$ states are observed in $^{206}\mathrm{Pb}$ at $4.0<E_x<4.3$ MeV. Apparently more 3$^-$ states are not observed because of the weak cross sections. The same number of 3$^-$ states is observed in $^{208}\mathrm{Pb}$. The next 3$^-$ state contains a major g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ component.

  • (c) Seven 4$^-$ states are observed in $^{206}\mathrm{Pb}$ at $3.9<E_x< 4.5$ MeV but only four ones in $^{208}\mathrm{Pb}$.

  • (d) Nine 5$^-$ states are observed in $^{206}\mathrm{Pb}$ at $3.7<E_x< 4.6$ MeV but only five ones in $^{208}\mathrm{Pb}$.

  • (e) Eleven 6$^-$ states are observed at $3.7<E_x< 4.5$ MeV in $^{206}\mathrm{Pb}$ but only four ones in $^{208}\mathrm{Pb}$.

  • (f) Two 7$^-$ states are observed in $^{206}\mathrm{Pb}$ at $3.7<E_x< 4.7$ MeV similar to $^{208}\mathrm{Pb}$.

  Summing up, for spins 4$^-$, 5$^-$, and 6$^-$ the number of states in $^{206}\mathrm{Pb}$ is about twice the number of states in $^{208}\mathrm{Pb}$. The additional states are explained by the GNPH configurations at $E_x= 4.23$ MeV. For spin 2$^-$ the excitation energy of the single observed state and for spin 7$^-$ the two excitation energies differ much from $^{208}\mathrm{Pb}$.

• 2. The summed g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength differs for $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ in the region $3.7<E_x< 4.7$ MeV for some spins.

  • (a) No g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength is expected for $^{206}\mathrm{Pb}$ if the g.s. is entirely ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$. Yet 40% 4$^-$ g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and 60% 5$^-$ g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength with the centroid energy $E_x=4.2$ MeV are found. Clearly the g.s. has an admixture from ${{\textit{p}}}{_{{ 3}/{2}}}^{-2}, {{\textit{f}}}{_{{ 5}/{2}}}^{-2}$ to dominant ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$. The centroid energy agrees with the expectation by the weak coupling of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ to the 2$^+_1$ state.

  • (b) The summed g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength for spins 3$^-$, 4$^-$, 5$^-$, 6$^-$ is 22%, 104%, 123%, 124%, respectively. The respective summed g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength in $^{208}\mathrm{Pb}$ is 84%, 102%, 108%, 94%. The missing g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength for spin 3$^-$ in $^{206}\mathrm{Pb}$ is explained by the low cross section. It may be concealed within the strong excitations at $E_x\approx 4.4$ MeV with higher spins. The overestimate for spins 5$^-$ and 6$^-$ is explained by the incomplete separation and the arbitrary division of the cross section into doublets. The centroid energies $E_x=4.2$, 4.3, 4.3, 4.4 MeV agree with the expectation by SDI within 0.1 MeV. The slight overestimate for spins 4$^-$ and 5$^-$ in $^{208}\mathrm{Pb}$ may be related to the uncertainty of the s.p. widths [29].

  • (c) The summed g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength for spins 2$^-$, 3$^-$, 4$^-$, 5$^-$, 6$^-$, 7$^-$ is 58%, 33%, 102%, 113%, 124%, 50%, respectively. Again the overestimate for spins 4$^-$, 5$^-$, and 6$^-$ is explained by the incomplete separation and the arbitrary division of the cross section into doublets. The centroid energies agree with the expectation by SDI except for spin 2$^-$. The respective summed g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength in $^{208}\mathrm{Pb}$ is 96%, 91%, 95%, 97%, 105%, 65%. The lower strength for spin 7$^-$ is discussed in Sect.  2.6.

  The reason for the missing strength for spins 2$^-$, 3$^-$, 7$^-$ is related to the difficulty to find levels with weak cross sections and the difficult separation of doublets. The total g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strengths approach unity for spins 4$^-$, 5$^-$, 6$^-$.

• 3. A close correspondence between $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ is found for several states. The energy difference $\varDelta E_x =E_x(^{206}\mathrm{Pb})- E_x(^{206}\mathrm{Pb})$ is sometimes remarkably small.

  • (a) The 3993 3$^-$ state with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength corresponds to the 4051 3$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 58$ keV.

  • (b) The 4239 3$^-$ state corresponds to the 4256 3$^-$ state in $^{208}\mathrm{Pb}$with $\varDelta E_x=+ 16$ keV.

  • (c) The 3977 4$^-$ and 4050 4$^-$ states with dominant g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength correspond to the 3996 4$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+37$ keV at average. The sum of the g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength in the two 4$^-$ states agrees exactly with the strength in the 3995 4$^-$ state in $^{208}\mathrm{Pb}$.

  • (d) The 3772 5$^-$ state with mixed g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength corresponds to the 3708 5$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 64$ keV.

  • (e) The 4040 5$^-$ and 4060 5$^-$ states with mixed g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ strength corresponds to the 4125 5$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 75$ keV at average.

  • (f) The 4160 5$^-$ and 4215 5$^-$ states with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength correspond to the 4180 5$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 8$ keV at average.

  • (g) The 4340 5$^-$ state corresponds to the 4297 5$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 44$ keV.

  • (h) The 3832 6$^-$ state corresponds to the 3920 6$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+88$ keV.

  • (i) The 4320 6$^-$ and 4431 6$^-$ states with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength correspond to the 4383 6$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 8$ keV at average.

  • (j) The 4431 6$^-$ and 4453 6$^-$ states with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength correspond to the 4383 6$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=+ 4$ keV at average.

  • (k) The 4453 6$^-$ state with dominant g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength corresponds to the 4481 6$^-$ state in $^{208}\mathrm{Pb}$ with $\varDelta E_x=- 28$ keV.

  • (l) In $^{208}\mathrm{Pb}$ two configurations rather completely describe the 4383 6$^-$ and 4481 6$^-$ states with the proton configuration h $_{{ 9}/{2}}$ d $_{{ 3}/{2}}$ and the neutron configuration g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$. In $^{206}\mathrm{Pb}$ the g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ strength is distributed across four states with similar sizes.

  Summing up, small energy differences $\varDelta E_x$ are found in astonishingly many pairs of states in the two lead isotopes. Several times the correspondence to some state in $^{208}\mathrm{Pb}$ is given by two states in $^{206}\mathrm{Pb}$.

• 4. Several states with spins 4$^-$, 5$^-$, 6$^-$ in $^{206}\mathrm{Pb}$ have no correspondence in $^{208}\mathrm{Pb}$.

  • (a) The configurations g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ and i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ are expected to be absent; only by admixtures of ${{\textit{p}}}{_{{ 3}/{2}}}^{-2}$ and ${{\textit{f}}}{_{{ 5}/{2}}}^{-2}$ to the g.s. some strength is expected. The 5$^-$ state with dominant i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ strength at $E_x= 4.1$ MeV should be absent; the configuration i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 2^+_{1}$ is expected 0.8 MeV higher. The mixing between the configurations g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 0^+_{g.s.}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ $\otimes 2^+_{1}$ separated by 0.8 MeV creates GNPH configurations at $E_x= 4.23$ MeV. Indeed at $3.9<E_x< 4.6$ MeV seven states are found whereas in $^{208}\mathrm{Pb}$ four states are known.

  • (b) The 4206 6$^-$ state in $^{208}\mathrm{Pb}$ with almost the complete i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ strength has no correspondence in $^{206}\mathrm{Pb}$.

  • (c) The absence of the configuration i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ for spin 6$^-$ and the additional GNPH configurations at $E_x= 4.23$ MeV explain the observation of nine 6$^-$ states at $3.8<E_x< 4.7$ MeV. In $^{208}\mathrm{Pb}$ only four states are known.

  Summing up, the number of states in $^{206}\mathrm{Pb}$ being larger than in $^{208}\mathrm{Pb}$ is explained by the appearance of the configuration g $_{{ 9}/{2}}$ $lj\otimes 2^+_{1}$ for $lj={{\textit{p}}}{_{{ 1}/{2}}}$ amidst the region $E_x\approx 4.17$ MeV which divides g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ from g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$. The missing correspondence to 4206 state in $^{208}\mathrm{Pb}$ with the complete i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ strength is expected by the two missing p $_{{ 1}/{2}}$ neutrons in $^{206}\mathrm{Pb}$. The g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength for spins 4$^-$ and 5$^-$ amounts to about one half.

7 Summary and conclusion

The proton decay of the $\frac{9}{2}^+$ IAR in $^{207}\mathrm{Bi}$ at $E_p=14.935$ MeV populates 22 levels in $^{206}\mathrm{Pb}$ [19, 20, 73]. Thirty-two states in $^{206}\mathrm{Pb}$ are identified at $3.7<E_x< 4.7$ MeV in 22 levels (Tables 4, 7, 8). Two levels contain three states, six levels two states. The cross sections are assumed to be equal for each pair or triple of the states.

The proton decay of the $\frac{9}{2}^+$ IAR in $^{209}\mathrm{Bi}$ populates 24 states in $^{208}\mathrm{Pb}$ at $3.7<E_x< 4.7$ MeV [25,26,27, 29, 30, 114,115,116]. They resonate on the g $_{{ 9}/{2}}$ IAR at $E_p=14.99$ MeV [28,29,30] and at $E_p=14.92$ MeV [114,115,116].

The total mean cross section for the levels at $3.7<E_x< 4.7$ MeV on top of the $\frac{9}{2}^+$ IAR in $^{207}\mathrm{Bi}$ is 2.7 mb/sr for $^{206}\mathrm{Pb}$. The total mean cross section for the levels at $3.7<E_x< 4.7$ MeV near the $\frac{9}{2}^+$ IAR in $^{209}\mathrm{Bi}$ is 2.4 mb/sr for $^{208}\mathrm{Pb}$ in agreement with reduction by a factor 0.80 from $E_p=14.99$ MeV to $E_p=14.92$ MeV.

Four states in $^{208}\mathrm{Pb}$ at $3.1<E_x<4.9$ MeV are identified to not exhibit a resonant excitation on the g $_{{ 9}/{2}}$ IAR in $^{209}\mathrm{Bi}$. They are recognized as collective excitations of the entire nucleus.

Angular distributions taken at $E_p=14.99$ MeV were discussed in detail in 1969–1982 and 2003–2019 [28,29,30, 51]. The results obtained in 1969-1982 are not discussed in detail (Table 4 in [51]).

Angular distributions taken at $E_p=14.918\pm 0.006$ MeV in 1968 [114,115,116] show a good agreement with those analyzed in 1969. Wave functions deduced from $\gamma$-spectroscopy in 1999 [78] were found to agree perfectly.

The comparison of angular distributions of the inelastic proton scattering via an IAR for the two isotopes $^{206}\mathrm{Pb}$ and $^{208}\mathrm{Pb}$ is more interesting than details for $^{208}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$.

On the $\frac{9}{2}^+$ IAR in $^{207}\mathrm{Bi}$ with the dominant structure $0^+_{g.s.} \otimes {{\textit{g}}}{_{{ 9}/{2}}}$ levels are recognized to contain states with spins from 2$^-$ to 7$^-$. The states contain major strengths of the particle-hole configurations g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ with admixtures of g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$, and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$. Weak admixtures of g $_{{ 9}/{2}}$ f $_{{ 7}/{2}}$ and g $_{{ 9}/{2}}$ h $_{{ 9}/{2}}$ with less than 1% strength influence the interference pattern of the angular distributions of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ sensitively.

The strength distribution for the configurations g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ determined for 32 states in $^{206}\mathrm{Pb}$ (Fig.  19) resembles the corresponding strength distribution for 24 states in $^{208}\mathrm{Pb}$ (Fig.  20). In both nuclei almost the complete 1p1h strength for g $_{{ 9}/{2}}$ p $_{{ 3}/{2}}$ and g $_{{ 9}/{2}}$ f $_{{ 5}/{2}}$ is localized except for some spins (2$^-$ and 3$^-$ in $^{206}\mathrm{Pb}$ and 7$^-$ in $^{208}\mathrm{Pb}$). The 1p1h strength is distributed in $^{206}\mathrm{Pb}$ among twice the number of states than in $^{208}\mathrm{Pb}$.

The g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ strength in $^{206}\mathrm{Pb}$ is found to be weak but not absent. The g.s. of $^{206}\mathrm{Pb}$ is shown to contain sizeable ${{\textit{p}}}{_{{ 3}/{2}}}^{-2}$ and ${{\textit{f}}}{_{{ 5}/{2}}}^{-2}$ admixtures to the dominant ${{\textit{p}}}{_{{ 1}/{2}}}^{-2}$.

The detailed comparison of three dozen states in $^{206}\mathrm{Pb}$ and two dozen states in $^{208}\mathrm{Pb}$ at excitation energies of $3.7<E_x< 4.7$ MeV yields remarkable similarities and clear differences. In a few cases one state with a dominant 1p1h configuration in $^{208}\mathrm{Pb}$ corresponds to a close pair of states in $^{206}\mathrm{Pb}$ with similar excitation energies and similar configuration mixings. In other cases the presence of a low lying 2$^+$ at $E_x=803$ keV in $^{206}\mathrm{Pb}$ state splits one state with a dominant 1p1h configuration in $^{208}\mathrm{Pb}$ into two largely separated GNPH states in $^{206}\mathrm{Pb}$.

The mixing of three hole pairs in the g.s. of $^{206}\mathrm{Pb}$ explains the appearance of states with considerable g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ components not expected in the simple schematic shell model.

Appendices

Appendix A

See Figs. 19, 20, 21, 22.

Fig. 19

Distribution of GNPH configuration strengths with the g $_{{ 9}/{2}}$ particle at $3.1<E_x<4.9$ MeV in states of $^{206}\mathrm{Pb}$ involving holes $lj={{\textit{p}}}{_{{ 1}/{2}}},$ f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$. See Sects. 6.3, 6.4 for details

Fig. 20

Distribution of 1p1h configuration strengths with a g $_{{ 9}/{2}}$ particle at $3.1<E_x<4.9$ MeV in states of $^{208}\mathrm{Pb}$ involving holes $lj={{\textit{p}}}{_{{ 1}/{2}}},$ f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$. See Sect. 6.4 and Table 4 in [51] for details

Fig. 21

Complement to Fig. 20 for other 1p1h configurations but ${{\textit{g}}}{_{{ 9}/{2}}}\,lj$ with $lj={{\textit{p}}}{_{{ 1}/{2}}},$ f $_{{ 5}/{2}}$, p $_{{ 3}/{2}}$ (see Table 4 in [51]). Admixtures from d $_{{ 5}/{2}}$ p $_{{ 1}/{2}}$ in the 2$^-$ and 3$^-$ states are not shown for clarity. The 4230 2$^-$ state contains 4% d $_{{ 5}/{2}}$ p $_{{ 1}/{2}}$ strength. The 4051, 4255, 4698 3$^-$ states contain 0%, 1%, 21% d $_{{ 5}/{2}}$ p $_{{ 1}/{2}}$ strengths

Fig. 22

Calculated strength distribution for 1p1h configurations in $^{208}\mathrm{Pb}$ and GNPH configurations in $^{206}\mathrm{Pb}$ at $E_x^{SSM}< 4.7$ MeV (Sect. 6.4). Table 2 shows 1p1h configurations in $^{208}\mathrm{Pb}$ and all GNPH configurations in $^{206}\mathrm{Pb}$ at $E_x^{SSM}< 4.8$ MeV. Vertical lines delineate the region 3.7$<E_x< 4.7$ MeV discussed in this work. The GNPH configurations $2^+_1\otimes {{{\textit{g}}}{_{{ 9}/{2}}}} p_{1/2}$, $2^+_1\otimes$ h $_{{ 9}/{2}}$ s $_{{ 1}/{2}}$, $2^+_1\otimes$ i $_{{11}/{2}}$ p $_{{ 1}/{2}}$ are shown in a simplified manner by including calculations with SDI. They lie mostly outside the discussed region. The interference pattern observed for $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$ on the g $_{{ 9}/{2}}$ IAR in $^{209}\mathrm{Bi}$ does not allow to distinguish configurations g $_{{ 9}/{2}}$ $\,lj\otimes 2^+_1$ from g $_{{ 9}/{2}}$ $\,lj\otimes 0^+_{g.s.}$. Only configurations involving the g $_{{ 9}/{2}}$ particle are discussed in the analysis of $^{206}\mathrm{Pb}$ $({{{\textit{p}}}, {{\textit{p}}}' })$. The twelve configurations i11/2 p $_{{ 1}/{2}}$ and g $_{{ 9}/{2}}$ p $_{{ 1}/{2}}$ $\otimes 2^+_1$ at 4.115, 4.290 and 4.918, 5.093 MeV, respectively, are expected to not exist in the simplified model but seven of them are shown

Appendix B

See Table 8.

Table 8 Amplitudes and strengths for 32 states $i_s$ in 22 levels $n_l$ in $^{206}\mathrm{Pb}$. Excitation energies given by [20] are varied within 4 keV in order to achieve uniqueness for doublets ($\overline{E_x}$). Finally accepted assignments are printed bold face. Discarded assignments are printed italic. For further details see Sect. 6.2