1 Introduction

The phase diagram of QCD has received a lot of attention since the first ideas appeared in the 1970s. At that time, it was thought that QCD has two phases, a hadronic phase at low temperatures and a deconfined phase of quarks and gluons at high temperatures. In 1984, Bailin and Love [1] suggested that at high density, quark matter should be a color superconductor. The ideas are analogous to those of ordinary superconductivity and BCS theory [2], namely the instability of the Fermi surface to form Cooper pairs under an attractive interaction. In QCD, an attractive interaction is provided by one-gluon exchange in the triplet channel. Since then, there have been large efforts to map out the phase diagram of QCD and study the properties of its different phases [3,4,5]. The phase diagram has shown to be surprisingly rich at high baryon density and low temperatures. It includes a quarkyonic phase [6] as well as a number of superconducting phases, some of them being inhomogeneous. Most of these results have been obtained using low-energy models of QCD, notably the quark-meson (QM) model and the Nambu–Jona-Lasinio (NJL) model, with or without coupling to the Polyakov loop. The reason is that lattice simulations are notoriously difficult to perform at finite baryon chemical potential \(\mu _B\) due to the sign problem, so that one cannot use techniques involving importance sampling.

The temperature T and baryon chemical potential \(\mu _B\) are not the only relevant parameters of QCD. For example, one can introduce a separate chemical potential \(\mu _f\) for each quark flavor f. For two flavors, this leads to another independent chemical potential besides \(\mu _B\), namely the isospin chemical potential \(\mu _I\). For the three flavors, \(\mu _S={1\over 2}(\mu _u+\mu _d-2\mu _s)\) is added. The addition of these chemical potentials gives rise to pion and kaon condensation. At \(T=0\), pion condensation occurs for \(\mu _I>m_{\pi }\), while kaon condensation takes place for \(|\pm {1\over 2}\mu _I+\mu _S|>m_K\) (upper sign for charged kaons and lower sign for neutral kaons). The former is particularly interesting since finite \(\mu _I\) and vanishing \(\mu _B\) has no sign problem and is therefore amenable to lattice simulations.

The final example of an external parameter, which is the topic of this review, is a (constant) magnetic background. There are several areas of high-energy physics, where such a background is relevant. One is non-central heavy-ion collisions, where large, time-dependent fields are generated. These fields are short-lived and have a maximum value of approximately \(eB=6m_{\pi }^2\) [7]. The basis mechanism is simply that (in the center-of mass frame) the two nuclei represent electric currents that according to Maxwell’s equations generate a magnetic field. Another example where strong magnetic fields appear, are magnetars [8]. This is a special class of neutron stars with relatively low rotation frequencies. It is believed that the magnetic fields on the surface are \(10^{14}\)–\(10^{15}\) Gauss, while in the interior they can be as strong as \(10^{16}\)–\(10^{19}\) Gauss.

We consider QCD with an SU(3) gauge group, a global \(SU(N_f)\) vector symmetry and quark masses \(m_f\). The QCD Lagrangian is

$$\begin{aligned} {\mathcal {L}}_{\mathrm{QCD}}= & {} -{1\over 4}F_{\mu \nu }^aF_a^{\mu \nu } +i\bar{\psi }_f\gamma ^{\mu }D_{\mu }\psi _f-m_f\bar{\psi }_f\psi _f\nonumber \\&+{\mathcal {L}}_{\mathrm{gf}}+{\mathcal {L}}_{\mathrm{ghost}}\;, \end{aligned}$$
(1)

where the gluon field strength tensor is \(F^a_{\mu \nu }=\partial _{\mu }A_{\nu }^a-\partial _{\nu }A^a_{\mu } -gf^{abc}A_{\mu }^bA_{\nu }^c\), \(f^{abc}\) are the structure constants the covariant derivative in the presence of an abelian background field \(A_{\mu }^{\mathrm{EM}}\) is

$$\begin{aligned} D_{\mu }=\partial _{\mu }+iq_fA_{\mu }^{\mathrm{EM}}+igA_{\mu }\;. \end{aligned}$$
(2)

Moreover, \(m_f\) is the mass of a quark of flavor f and there is a sum of flavors in Eq. (1). The nonabelian gauge field is \(A_{\mu }=t_aA_{\mu }^a\), \(t_a={1\over 2}\lambda _a\), and \(\lambda _a\) are the Gell-Mann matrices. Finally \({\mathcal {L}}_{\mathrm{gf}}\) and \({\mathcal {L}}_{\mathrm{ghost}}\) are the gauge-fixing and ghost part of the Lagrangian, respectively.

The partition function in QCD can be written as

$$\begin{aligned} {\mathcal {Z}}= & {} \int {\mathcal {D}}A_{\mu }{\mathcal {D}}\bar{\psi }_f{\mathcal {D}}\psi _f\, e^{-S_{\mathrm{QCD}}}\nonumber \\= & {} \int {\mathcal {D}}A_{\mu }e^{-S_g}\det (/\!\!\!\!D(B)+m_f)\;, \end{aligned}$$
(3)

where \(S_{\mathrm{QCD}}\) is the Euclidean action for QCD. In the second line, we have integrated over the fermions which can be done exactly since \({\mathcal {L}}_{\mathrm{QCD}}\) is bilinear in the quark fields. Moreover, \(S_g\) is the Euclidean action for the gluons and

$$\begin{aligned} /\!\!\!\!D(B)= & {} \begin{pmatrix} 0&{} \quad iX\\ iX^{\dagger }&{} \quad 0 \end{pmatrix}\;, \end{aligned}$$
(4)
$$\begin{aligned} iX= & {} D_0+i{\varvec{\sigma }}\cdot \mathbf{D}\;. \end{aligned}$$
(5)

This yields

$$\begin{aligned} \det \left( /\!\!\!\!D(B)+m_f\right)= & {} \det \left[ X^{\dagger }X+m_f^2\right] \;. \end{aligned}$$
(6)

The last equation shows that the fermion determinant is manifestly positive. As in the case of finite isospin chemical potential, QCD in a magnetic field is also free of the sign problem, and one can therefore carry out lattice simulations. Interestingly, the combination of finite isospin and magnetic field is free of the sign problem only if the charges of the u and d-quark are the same. This is of course not real QCD, but it offers the possibility to compare lattice predictions with those of low-energy effective theories and models.

In this review, we will discuss (inverse) magnetic catalysis and the phase diagram of QCD in a strong magnetic background, paying attention to recent developments. There are other reviews [9,10,11,12] focusing on different aspects of the field. The paper is organized as follows. In the next section, we discuss the physics of magnetic catalysis at \(T=0\). In Sect. 3, we introduce the Polyakov loop and discuss magnetic catalysis in model calculations at nonzero temperature. In Sect. 4, we review inverse magnetic catalysis on the lattice focusing on the competing sea and valence effects. In Sect. 5, the improvement of models to incorporate inverse magnetic catalysis is discussed and in Sect. 6, we summarize. In Appendix A, we discuss renormalization of the quark-meson model in the on-shell scheme, while in Appendix B, we show how the parameters of the model are fixed.

2 Magnetic catalysis at zero temperature

Magnetic catalysis can be defined as

  1. 1.

    The magnitude of a condensate is enhanced by the presence of an external magnetic field B if the condensate already is present at vanishing field.

  2. 2.

    An external magnetic field induces symmetry breaking and a nonzero value of a condensate when the symmetry is intact for \(B=0\).

The condensate is the expectation value of a field, which can be either fundamental or composite. The expectation of a scalar field \(\phi \) in low-energy models is an example of the former, while \(\bar{\psi }\psi \) is the chiral condensate in e.g. the NJL model or QCD is an example of the latter. One refers to the second case as dynamical symmetry breaking by a magnetic field. We will discuss both cases below. The first papers on magnetic catalysis at \(T=0\) appeared three decades ago in the study of the NJL model in three dimensions [13]. Shortly thereafter in the linear sigma model [14] and the NJL model in two dimensions [15,16,17]. Since then it has been demonstrated in QED [18], chiral perturbation theory [19,20,21], in the Walecka model in nuclear physics [22], and also on the lattice, see e.g. [23,24,25,26,27].

In this section, we will use the two-flavor quark-meson model as an explicit example of a low-energy effective model of QCD that displays magnetic catalysis. The Lagrangian is

$$\begin{aligned} {\mathcal {L}}= & {} -{1\over 2}B^2+{1\over 2}\left[ (\partial _{\mu }\sigma )(\partial ^{\mu }\sigma ) +(\partial _{\mu }\pi _0)(\partial ^{\mu }\pi _0)\right] \nonumber \\&+D_{\mu }^*\pi ^-D^{\mu }\pi ^+-{1\over 2}m^2(\sigma ^2+\pi _0^2+2\pi ^+\pi ^-)\nonumber \\&-{\lambda \over 24}(\sigma ^2+{\pi }_0^2+2\pi ^+\pi ^-)^2+h\sigma \nonumber \\&+\bar{\psi }\left[ i\gamma ^{\mu }D_{\mu } -g(\sigma +i\gamma ^5\mathbf{\tau }\cdot {\varvec{\pi }})\right] \psi \;, \end{aligned}$$
(7)

where \(D_{\mu }=\partial _{\mu }+iqA_{\mu }\) is the covariant derivative \(\sigma \), \({\varvec{\pi }}=(\pi _0,\pi _1,\pi _2)\) are the meson fields, \(\pi ^{\pm }={1\over \sqrt{2}}(\pi _1\mp i\pi _2)\) , \(\tau _a\) are the Pauli matrices, \(\psi \) is a color \(N_c\)-plet, a four-component Dirac spinor as well as a flavor doublet

$$\begin{aligned} \psi= & {} \left( \begin{array}{c} u\\ d \end{array}\right) \;. \end{aligned}$$
(8)

In the absence of an abelian gauge field in Eq. (7), the symmetry is \(SU(2)_L\times SU(2)_R\) for \(h=0\), otherwise it is \(SU(2)_V\). In its presence, the Lagrangian Eq. (7) has a \(U(1)_L\times U(1)_R\) symmetry for \(h=0\), otherwise it is \(U(1)_V\). The reason is that one cannot transform a u-quark into a d-quark due to their different electric charges. Defining \(\varDelta ^{\pm }={1\over \sqrt{2}}(\sigma \pm i\gamma ^5\pi _0)\), the two sets of transformations are 1) \(u\rightarrow e^{-i\gamma ^5\alpha }u\), \(d\rightarrow e^{i\gamma ^5\alpha }d\), \(\varDelta ^{\pm }\rightarrow \varDelta ^{\pm }e^{\pm 2i\gamma ^5\alpha }\), and \(\pi ^{\pm }\rightarrow \pi ^{\pm }\), and 2) \(u\rightarrow e^{i\alpha }u\), \(d\rightarrow e^{-i\alpha }d\), \(\varDelta ^{\pm }\rightarrow \varDelta ^{\pm }\), and \(\pi ^{\pm }\rightarrow \pi ^{\pm }e^{\pm 2i\alpha }\).

After symmetry breaking, the sigma field has a nonzero expectation value \(\phi _0\). The classical potential is

$$\begin{aligned} V_0={1\over 2}B^2+{1\over 2}m^2\phi _0^2+{\lambda \over 24}\phi _0^4-h\phi _0\;. \end{aligned}$$
(9)

The tree-level relations between the parameters of the Lagrangian \(m^2\), \(\lambda \), g, and h and the physical masses \(m_{\sigma }\) and \(m_{\pi }\), the pion decay constant \(f_{\pi }\), and the quark mass \(m_q\) are

$$\begin{aligned} m^2&=-{1\over 2}\left( m_{\sigma }^2-3m_{\pi }^2\right) \;, \quad \lambda =3{(m_{\sigma }^2-m_{\pi }^2)\over f_{\pi }^2}\;, \end{aligned}$$
(10)
$$\begin{aligned} g^2&={m_q^2\over f_{\pi }^2}\;, \quad h =m_{\pi }^2f_{\pi }\;. \end{aligned}$$
(11)

Using the relations (10)–(11), we obtain

$$\begin{aligned} V_0= & {} {1\over 2}B^2+\frac{3}{4}m_{\pi }^2 f_{\pi }^2\frac{\varDelta ^2}{m_q^2} -\frac{1}{4}m_{\sigma }^2 f_{\pi }^2\frac{\varDelta ^2}{m_q^2} + \frac{1}{8}m_{\sigma }^2 f_{\pi }^2\frac{\varDelta ^4}{m_q^4}\nonumber \\&- \frac{1}{8}m_{\pi }^2 f_{\pi }^2\frac{\varDelta ^4}{m_q^4} -m_{\pi }^2f_{\pi }^2\frac{\varDelta }{m_q}\;, \end{aligned}$$
(12)

where we have introduced \(\varDelta =g\phi _0\). The minimum of the classical potential is given by \(\varDelta =gf_{\pi }\).

The classical potential has by construction its minimum at \(\varDelta =m_q\) or \(\phi _0=f_{\pi }\). In the large-\(N_c\) limit, the mesons are included at tree level, while we include the Gaussian fluctuations of the fermions. Including the one-loop corrections from the fermions using a minimal subtraction scheme, leaves a renormalized one-loop effective potential that depends on the renormalization scale \(\varLambda \). The minimum of the effective potential therefore depends on \(\varLambda \). In order to ensure that the one-loop effective potential has its minimum at \(\phi _0=f_{\pi }\) for zero magnetic field B, several methods have been used in the literature. One method is simply to subtract the one-loop contribution to the effective potential for \(B=0\). Then the renormalization scale dependence drops out and the correction to Eq. (12) is a finite B-dependent term that vanishes for \(B=0\). However this is inconsistent since one includes fermion fluctuations in the effective potential at finite magnetic field, but not for \(B=0\). Moreover, it is also incorrect since Eqs. (10)–(11) are tree-level relations that receive radiative corrections. One can also choose a specific value for \(\varLambda \) such that the one-loop correction to the position of the minimum of the effective potential vanishes. In this case, one has included quantum fluctuations also for \(B=0\), but again, the tree-level relations between the parameters of the Lagrangian and physical quantities receive loop corrections. In order to be consistent, the parameters of the Lagrangian must be determined to the same order in the loop expansion as one calculates the effective potential. The solution to the problem is to combine the minimal subtraction scheme with the on-shell scheme [28,29,30,31]. In this way one includes loop corrections to Eqs. (10)–(11), while at the same time ensures that the effective potential has its minimum at \(\varDelta = gf_{\pi }\). Details of the renormalization of the one-loop effective potential in the large-\(N_c\) limit can be found in Appendix A and the parameter fixing in Appendix B. It reads

$$\begin{aligned} V_{0+1}&=\frac{3}{4}m_{\pi }^2 f_{\pi }^2 \left\{ 1-\frac{4 m_q^2N_c}{(4\pi )^2f_{\pi }^2} m_{\pi }^2F^{\prime }(m_{\pi }^2) \right\} \frac{\varDelta ^2}{m_q^2}\nonumber \\&\quad -\frac{1}{4}m_{\sigma }^2 f_{\pi }^2 \left\{ 1 +\frac{4 m_q^2N_c}{(4\pi )^2f_{\pi }^2}\right. \nonumber \\&\quad \left. \left[ \left( 1-4m_q^2\over m_{\sigma }^2\right) F(m_{\sigma }^2) +\frac{4m_q^2}{m_{\sigma }^2}-F(m_{\pi }^2)-m_{\pi }^2F^{\prime }(m_{\pi }^2)\right] \right\} \nonumber \\&\quad \frac{\varDelta ^2}{m_q^2}+ \frac{1}{8}m_{\sigma }^2 f_{\pi }^2 \left\{ 1 -\frac{4 m_q^2 N_c}{(4\pi )^2f_{\pi }^2} \left[ \frac{4m_q^2}{m_{\sigma }^2} \left( \log \frac{\varDelta ^2}{m_q^2} \frac{-3}{2}\right) \right. \right. \nonumber \\&\quad \left. \left. -\left( 1 -4m_q^2\over m_{\sigma }^2\right) F(m_{\sigma }^2) +F(m_{\pi }^2)+m_{\pi }^2F^{\prime }(m_{\pi }^2)\right] \right\} \nonumber \\&\quad \frac{\varDelta ^4}{m_q^4}- \frac{1}{8}m_{\pi }^2 f_{\pi }^2\left[ 1-\frac{4 m_q^2N_c}{(4\pi )^2f_{\pi }^2} m_{\pi }^2F^{\prime }(m_{\pi }^2)\right] \frac{\varDelta ^4}{m_q^4}\nonumber \\&\quad -m_{\pi }^2f_{\pi }^2\left[ 1-\frac{4 m_q^2 N_c}{(4\pi )^2f_{\pi }^2} m_{\pi }^2F^{\prime }(m_{\pi }^2) \right] \frac{\varDelta }{m_q}\nonumber \\&\quad +{1\over 2}B^2 -{8N_c\over (4\pi )^2}\sum _f(q_fB)^2\nonumber \\&\quad \left[ {\zeta ^{(1,0)}(-1,x_f)}+{1\over 4}x_f^2 -{1\over 2}x_f^2\log x_f\right. \nonumber \\&\quad \left. +{1\over 2}x_f\log x_f -{1\over 12}\log \frac{m_q^{2}}{2|q_{f}B|}-{1\over 12}\right] \;, \end{aligned}$$
(13)

where \(x_f={\varDelta ^2\over 2|q_fB|}\) and \(\zeta (a,x)\) is the Hurwitz zeta-function. Here and in the remainder of the paper, \(\zeta ^{(1,0)}(n,x_f)={\partial \zeta (n+\epsilon ,x_f) \over \partial \epsilon }|_{\epsilon =0}\), in Eq. (13), \(n=-1\). Finally, \(F(p^2)\) and \(F^{\prime }(p^2)\) are defined in Eqs. (B.29)–(B.30).

The first four lines of the one-loop effective potential are independent of the magnetic field and this part was first calculated in Ref. [32]. The last line is the B-dependent correction to \(V_{0+1}\). Note also that final result is independent of the renormalization scale \(\varLambda \).

In Fig. 1, we show the effective potential divided by \(f_{\pi }^4\) at \(T=0\). The black line is the tree-level potential Eq. (12), while the green and blue lines are the one-loop effective potential Eq. (13) for \(|eB|=0\) and \(|eB|=10 m_{\pi }^2\), respectively. We have used \(m_{\sigma }=600\ \hbox {MeV}\), \(m_{\pi }=140\ \hbox {MeV}\), \(f_{\pi }=93\ \hbox {MeV}\), and \(m_q=300\ \hbox {MeV}\). The classical potential as well the one-loop effective potential with \(|eB|=0\) have a minimum at \(\varDelta =gf_{\pi }\) by construction. Notice, however, that the latter is significantly deeper. The blue line with \(|eB|=10 m_{\pi }^2\), shows that the minimum of the effective moves to a larger value, i. e. the system exhibits magnetic catalysis.

Fig. 1
figure 1

Effective potential as a function of \(\varDelta \) normalized by \(f_{\pi }^4\) at \(T=0\). The black line is the tree-level result, the green and blue lines are the one-loop result for zero magnetic field and for \(eB=10m_{\pi }^2\). See main text for details

Full size image

While the above clearly demonstrates magnetic catalysis numerically, we would like to gain insight in the mechanism behind the effect. Instead of analyzing Eq. (13), we will discuss the gap equation in the NJL model.

In order to simplify the discussion, we will consider the NJL model with a single quark flavor and color, \(N_f=N_c=1\) with electric charge \(q_f\). In the chiral limit, the Lagrangian is [33]

$$\begin{aligned} {\mathcal {L}}=\bar{\psi }i\gamma ^{\mu }\partial _{\mu } \psi +{G\over 2}\left[ (\bar{\psi }\psi )^2+(\bar{\psi }i\gamma ^5\psi )^2\right] \;. \end{aligned}$$
(14)

This Lagrangian has a \(U(1)_V\times U(1)_A\) symmetry. We introduce the gap \(M=-G\langle \bar{\psi }\psi \rangle \) and linearize the interaction terms, writing \((\bar{\psi }\psi )^2\approx \langle \bar{\psi }\psi \rangle ^2+2\langle \bar{\psi }\psi \rangle \bar{\psi }\psi \) and \((\bar{\psi }i\gamma ^5\psi )^2\approx 0\). M is now an effective quark mass arising after breaking the axial symmetry spontaneously, i.e. when \(\langle \bar{\psi }\psi \rangle \ne 0\). In the mean-field approximation, we perform the Gaussian integral over the fermion field giving rise to the following one-loop effective potential,

$$\begin{aligned} V_{0+1}={M^2\over 2G}-2\int {d^4p\over (2\pi )^4}\log \left[ p^2+M^2\right] \;. \end{aligned}$$
(15)

The gap equation for M is found by extremizing \(V_{0+1}\) which yields

$$\begin{aligned} {M\over 4G}=M\int {d^4p\over (2\pi )^4} {1\over p^2+M^2}\;. \end{aligned}$$
(16)

Conventionally, since the NJL model is non-renormalizable, one has used a three-dimensional or a four-dimensional momentum cutoff \(\varLambda \) to regulate divergences. If \(\varLambda \) is a four-dimensional cutoff, the gap equation (16) reads for \(M\ll \varLambda \)

$$\begin{aligned} M\left[ {4\pi ^2\over G}-\varLambda ^2+M^2\log {\varLambda ^2\over M^2}\right] =0\;. \end{aligned}$$
(17)

\(M=0\) is always a solution, however for \(G>G_c={4\pi ^2\over \varLambda ^2}\) there is also a nontrivial solution. Thus for G larger than the critical value \({4\pi ^2\over \varLambda ^2}\), quantum fluctuations induce symmetry breaking in the model.

At finite magnetic field, the partial derivative in Eq. (14) is replaced by the covariant derivative and we add a term \({1\over 2}B^2\) to the effective potential. The gap equation becomes

$$\begin{aligned} {M\over 2G}=M{|q_fB|\over 2\pi } \sum _{s=\pm 1}\sum _{k=0}^{\infty }\int {d^2p_{\parallel }\over (2\pi )^2} {1\over p_0^2+p_z^2+M_B^2}\;, \end{aligned}$$
(18)

where \(M_B^2=M^2+|q_fB|(2k+1-s)\), \(p_{\parallel }^2=p_0^2+p_z^2\) and \(q_f\) is the charge. The divergences in Eq. (18) can be isolated by adding and subtracting the right-hand side of Eq. (16). The right-hand side of Eq. (18) minus the subtracted term is finite and is conveniently evaluated using dimensional regularization in the same way as done Appendix A [34, 35]. Finally, we impose a four-dimensional cutoff on the added term as in Eq. (16). Factoring out the trivial solution \(M=0\), this yields the regularized gap equation

$$\begin{aligned}&{4\pi ^2\over G}-\varLambda ^2+M^2\log {\varLambda ^2\over M^2} -{2|q_fB|}\nonumber \\&\quad \times \left[ \zeta ^{(1,0)}(0,x_f)+x_f -{1\over 2}(2x_f-1)\log {x_f}\right] =0\;, \end{aligned}$$
(19)

where \(x_f={M^2\over 2|q_f|B}\). This equation has only a nonzero M as solution. For \(G<G_c\), the solution is [33, 36]

$$\begin{aligned} M^2={|q_fB|\over \pi }\exp \left[ {-{1\over |q_fB|}} \left( {4\pi ^2\over G} -\varLambda ^2\right) \right] \;. \end{aligned}$$
(20)

In the limit \(|q_fB|\rightarrow 0\), this solution connects to the trivial solution \(M=0\). In lowest Landau level approximation, the gap equation has solution \(M^2=\varLambda ^2e^{-4\pi ^2/G|q_fB|}\), which is reminiscent of Eq. (20) if we identify the cutoff \(\varLambda \) with \(\sqrt{|q_fB|}\). We can then think of magnetic catalysis as a 1 + 1 dimensional phenomenon, i.e. a dimensional reduction from 3+1 dimensions has taken place. The functional form of the gap equation is the same as for the gap equation in BCS theory of superconductivity as well as the gap equation found in the large-N limit of O(N)-symmetric nonlinear sigma model in 1 + 1 dimensions. The 1 + 1 dimensional nature of magnetic catalysis raises the question of whether this phenomenon is in conflict with the Coleman theorem, which forbids spontaneous symmetry breaking in less than two spatial dimensions at zero temperature [37]. As pointed out in Ref. [36], the field \(\bar{\psi }\psi \) is neutral with respect to the magnetic field. The neutral pion is the associated Goldstone boson that appears after breaking the U(1) symmetry. The charged pions are now massive even in the chiral limit.

There are other ways of regularizing the gap equation (18) or the fermion contribution to the one-loop effective potential (A.1), for example Schwinger’s proper time method [38]. Let us illustrate this by computing the corresponding bosonic functional determinant, which shows up in chiral perturbation theory. It is based on the representation in Euclidean space

$$\begin{aligned} V_1= & {} \log \det (-D_{\mu }D^{\mu }+m^2) \nonumber \\= & {} -\int _0^{\infty }{ds\over s}\mathrm{Tr}\,e^{-s(-D_{\mu }D^{\mu }+m^2)}\nonumber \\= & {} -{|qB|\over 2\pi }\sum _{k=0}^{\infty }\int _{p_{\parallel }} \int _0^{\infty }{ds\over s} e^{-s(p_{\parallel }^2+|qB|(2k+1)+m^2)}\;,\nonumber \\ \end{aligned}$$
(21)

where the sum over Landau levels k as well the momentum integral over \(p_{\parallel }\) is convergent. The result is

$$\begin{aligned} V_1=-\frac{(e^{\gamma E}\varLambda ^{2})^{\epsilon }}{(4\pi )^{2}}\int _0^{\infty }{ds\over s^{3-\epsilon }}e^{-m^2s} {|qB|s\over \sinh (|qB|s)}\;. \end{aligned}$$
(22)

For \(\epsilon =0\), the integral is divergent for small s, i.e. for large momentum. By adding and subtracting the divergent terms, we can isolate the divergences. One finds

$$\begin{aligned} V_1&=-\frac{(e^{\gamma E}\varLambda ^{2})^{\epsilon }}{(4\pi )^{2}}\int _0^{\infty }{ds\over s^{3-\epsilon }}e^{-m^2s} +{(qB)^2\over 6(4\pi )^2}\int _0^{\infty }{ds\over s^{1-\epsilon }}e^{-m^2s}\nonumber \\&\quad -\frac{(e^{\gamma E}\varLambda ^{2})^{\epsilon }}{(4\pi )^{2}}\int _0^{\infty }{ds\over s^{3-\epsilon }}e^{-m^2s} \left[ {|qB|s\over \sinh (|qB|s)}-1+{(qBs)^2\over 6}\right] \;. \end{aligned}$$
(23)

The integrals in the first line are divergent for \(\epsilon =0\), while the last integral is convergent. The divergences show up as poles in \(\epsilon \). The first term in Eq. (23) is a vacuum energy counterterm while the second term corresponds to charge and wavefunction renormalization [38]. The last integral in Eq. (23) can be calculating exactly and involves the Hurwitz zeta function. Using the proper time method with the momentum integrals evaluated in \(d=2-2\epsilon \) dimensions yields the same results as those obtained by combining dimensional regularization and zeta-function regularization, as done in Appendix A. Alternatively, one can evaluate Eq. (23) with \(\epsilon =0\) using a cutoff \(1/\varLambda ^2\) as the lower limit of the s-integration in the divergent integrals.

The regularization methods discussed so far separates in clean way the B-independent divergences from the B-dependent terms whether they are finite or divergent. Footnote 1 There are other regularization methods that do not separate this contributions, for example a sharp cutoff imposed directly on the integral in Eq. (22) or a form factor that is a function of e.g. \(p_z^2+2k|qB|(2k+1-s)\). One has to be careful choosing such regulators since nonphysical oscillations may result [39, 40].

The on-shell scheme used to obtain the final result Eq. (13) has two important virtues as first pointed out in Ref. [41]. By considering the small-B (large-\(x_f\)) behavior of the Hurwitz zeta-function, one finds that the only contributions at order \(B^2\) comes from the renormalized magnetic field term \({1\over 2}B^2\),

$$\begin{aligned} {\zeta ^{(1,0)}(-1,x_f)}= & {} -{1\over 4}x_f^2 +{1\over 2}x_f^2\log x_f-{1\over 2}x_f\log x_f \nonumber \\&+{1\over 12}\log x_f +{1\over 12}+{1\over 720}{1\over x_f^2}+ \cdots \;. \end{aligned}$$
(24)

It also ensures that the magnetic-field contribution to the effective potential and the magnetization vanishes in the limit \(m_q\rightarrow \infty \). Both properties are expected from a physical point of view. It leads to a paramagnetic vacuum, in agreement with the hadron resonance gas model calculations [41] and lattice QCD lattice simulations [42]. Other renormalization schemes, such as the (modified) minimal subtraction scheme are connected to the above by a finite renormalization. However, the effective potential and the magnetization then grow logarithmically in the limit \(m_q\rightarrow \infty \). Similar remarks apply to the (P)NJL model. Regularizing the model by imposing a UV cutoff \(\varLambda \) on the divergent integrals in the fermionic version of Eq. (23), the authors of [43] show that it predicts diamagnetic behavior for low values of B and paramagnetic behavior for large magnetic fields. By defining a subtraction procedure that resembles the renormalization of the magnetic field in the on-shell scheme, their effective potential leads to paramagnetic behavior as seen on the lattice.

After having discussed magnetic catalysis in models, we now turn to lattice gauge theory. The first lattice simulations were carried out for an SU(2) gauge group for magnetic field strengths up to \(\sqrt{eB}\sim 3\ \hbox {GeV}\) in the quenched approximation, i.e. setting the quark determinant to unity [23]. The simulations confirmed that the quark condensates is enhanced by the magnetic field and that the enhancement is qualitative linear with eB. The quark condensate itself was calculated using the Banks–Casher relation [44], which relates the density of eigenvalues close to zero of the Dirac operator and the condensate. Their calculations showed a monotonic increase of the spectral density for typical gauge field configurations. This enhancement induced by the magnetic field can be considered the basic mechanism behind magnetic catalysis. Below, we will discuss this mechanism further, here it suffices to add that the enhancement of the spectral density as a function of B for typical gauge configuration is also seen in full QCD [45]. Even in the free case, there is a proliferation of small eigenvalues due to the degeneracy of states, which in a constant magnetic field is proportional to |qB| [19].

3 Magnetic catalysis at nonzero temperature

In the previous section, we reviewed magnetic catalysis at \(T=0\) in some detail. A survey of the literature shows that it is a robust feature of lattice simulations as well model calculations: magnetic catalysis does not depend on particular values of the masses or couplings. Since the condensate increases as a function of the magnetic field, it should raise the transition temperature for the chiral transition. This expectation was made explicit a long time ago in Ref. [19]. A number of model calculations have confirmed this expectation, e.g. [13, 46,47,48,49,50,51,52], although some of them suggest that the chiral and deconfinement transition split for larger values of eB.

The effective potential of the quark-meson model in the large-\(N_c\) approximation at finite temperature is

$$\begin{aligned} V_{0+1}^T&=V_{0+1}-\sum _f{2N_c|q_fB|\over 2\pi }T\sum _{s=\pm 1}\nonumber \\&\qquad \sum _{k=0}^{\infty } \int _{p_{z}} \log \left[ 1+e^{-\beta E_f}\right] \;, \end{aligned}$$
(25)

where \(E_f=\sqrt{p_z^2+\varDelta ^2+|q_fB|(2k+1-s)}\) and \(V_{0+1}\) is given by Eq. (13). In Fig. 2, we show the results of a typical calculation where the quark-meson model was used. The curves show the transition temperature for the chiral transition as a function of \(|qB|/m_{\pi }^2\) in the chiral limit (green points) and at the physical point (red points). At \(B=0\), the gap between the two critical temperatures is approximately 10 MeV, which decreases as |qB| grows. In both cases, it is clear that the transition temperature increases with the magnetic field. Here the transition temperature was defined as the inflection point of the curve \(\phi _0(T)\) at the physical point and \(\phi _0(T)=0\) in the chiral limit. An alternative definition of the critical temperature is the peak of the chiral susceptibility  Footnote 2

$$\begin{aligned} \chi ={\partial \langle \bar{\psi }\bar{\psi }\rangle \over \partial T}\;. \end{aligned}$$
(26)
Fig. 2
figure 2

Figure taken from Ref. [11]

\(T_{pc}(B)\) as a function of |qB| in units of \(m_{\pi }^2\) in the quark-meson model. The green points are in the chiral limit and the red points are at the physical point. See main text for details

Full size image

In QCD, two transitions take place as one increases the temperature, namely the chiral transition and the deconfinement transition. Lattice calculations suggest that chiral symmetry is restored at a temperature of approximately \(T^{\chi }_c= 155\ \hbox {MeV}\) [53,54,55,56,57] though strictly speaking the transition is only a crossover. The crossover temperature is defined by the peak of the chiral susceptibility. This temperature is slightly less than the crossover temperature for the deconfinement transition, \(T_c^{\mathrm{dec}}=170\ \hbox {MeV}\). However this temperature difference is observable dependent. In most cases, \(T_c^{\mathrm{dec}}\) has been determined by the behavior of the Polyakov loop. Recently, it has been defined by the behavior of the quark entropy and in this case the two crossover temperatures agree within errors [57].

We will next discuss the Polyakov loop and how it can be incorporated in model calculations. The Wilson line is defined as

$$\begin{aligned} L(\mathbf{x})={\mathcal {P}}\exp \left[ i\int _0^{\beta }d\tau A_4(\mathbf{x},\tau )\right] \;, \end{aligned}$$
(27)

where \({\mathcal {P}}\) denotes path ordering, \(A_4=iA_0\) and \(A_0=t_aA_0^a\). The Polyakov loop operator l is the trace of the Wilson line (27). Together with its Hermitian conjugate, it is defined as

$$\begin{aligned} l={1\over N_c}\mathrm{Tr}L\;, \qquad l^{\dagger }={1\over N_c}\mathrm{Tr}L^{\dagger }\;, \end{aligned}$$
(28)

where \(N_c\) is the number of colors. The expectation values of l and \(l^{\dagger }\) are denoted by \(\varPhi \) and \(\bar{\varPhi }\). Under the center group \(Z_{N_c}\) of the gauge group \(SU(N_c)\), the Polyakov loop transforms as \(\varPhi \rightarrow e^{2\pi in\over N_c}\varPhi \) with \(n=0,1,2 \ldots N_c-1\). In pure-glue QCD it is an order parameter for confinement, while for QCD with dynamical fermions it is only an approximate order parameter [58, 59]. Note also that \(\varPhi =\bar{\varPhi }\) at zero density, i.e. for \(\mu _f=0\).

For \(N_c=3\) and in the Polyakov gauge, one can write a nonabelian background gauge field as

$$\begin{aligned} A_4=t_3A_4^{3}+t_8A_4^{8}\;. \end{aligned}$$
(29)

Introducing the fields \(\phi _1={1\over 2}\beta A_4^{3}\) and \(\phi _2={1\over 2\sqrt{3}}\beta A_4^{8}\), the thermal Wilson line reads for constant gauge fields

$$\begin{aligned} L=\left( \begin{array}{ccc} e^{i(\phi _1+\phi _2)}&{}0&{}0\\ 0&{}e^{i(-\phi _1+\phi _2)}&{}\\ 0&{}0&{}e^{-2i\phi _2}\\ \end{array}\right) \;. \end{aligned}$$
(30)

Since the Polyakov loop is an approximate order parameter for deconfinement, the strategy put forward in Ref. [60] is to write down a phenomenological effective potential for \(\varPhi \), \(\bar{\varPhi }\) and the chiral condensate that describes the thermodynamics of the system. This potential consists of a gluonic part \(U(\varPhi ,\bar{\varPhi })\) as well as a matter part. The term \(U(\varPhi ,\bar{\varPhi })\) is constructed such that it reproduces the pure-glue pressure calculated on the lattice [61]. A number of different forms of \(U(\varPhi ,\bar{\varPhi })\) have been proposed [62,63,64,65]. In Ref. [62], they used a Polynomial expansion incorporating the \(Z_3\) center symmetry,

$$\begin{aligned} {{ U}\over T^4}=-{1\over 2}b_2(T)\varPhi \bar{\varPhi }-{1\over 6}b_3(T) \left[ \varPhi ^3+\bar{\varPhi }^3\right] +{1\over 4}b_4(\varPhi \bar{\varPhi })^2.\nonumber \\ \end{aligned}$$
(31)

Here the coefficients are

$$\begin{aligned}&b_2(T)=6.75 -1.95\left( {T_0\over T}\right) +2.625\left( {T_0\over T}\right) ^2-7.44\left( {T_0\over T}\right) ^3, \nonumber \\\end{aligned}$$
(32)
$$\begin{aligned}&b_3=0.75\;, \end{aligned}$$
(33)
$$\begin{aligned}&b_4=7.5\;, \end{aligned}$$
(34)

and \(T_0=270\ \hbox {MeV}\), the transition temperature for pure-glue QCD [61]. A drawback of the proposed pure-glue potentials is that they are independent of the number of flavors \(n_f\). The transition temperature for \(B=0\) depends on the number of flavors and one should incorporate the back-reaction from the fermions to the gluonic sector [63]. This is done by using an \(n_f\)-dependent \(T_0\). Once the coupling between the gluonic sector and the matter sector has been implemented, the two transitions take place at approximately the same temperature: The chiral transition moves to larger temperatures, while the deconfinement transition moves to lower temperatures. Finally, the Polyakov-loop potential is coupled to the matter sector via replacing the partial derivatives in the fermionic part of the Lagrangian by covariant ones including the constant background gauge field. This is implemented by making the substitution

$$\begin{aligned}&\log \left[ 1+e^{-\beta E_f}\right] \nonumber \\&\quad \rightarrow {1\over 6}\log \left[ 1+3\varPhi e^{-\beta E_f} +3\bar{\varPhi }e^{-2\beta E_f}+e^{-3\beta E_f}\right] \nonumber \\&\qquad +{1\over 6}\log \left[ 1+3\bar{\varPhi } e^{-\beta E_f}+3{\varPhi } e^{-2\beta E_f}+e^{-3\beta E_f}\right] \end{aligned}$$
(35)

in Eq. (25). In the same way, the Fermi-Dirac distribution function is generalized,

$$\begin{aligned} n_F(\beta E_f)={1+2\bar{\varPhi }e^{\beta E_f}+\varPhi e^{2\beta E_f} \over 1+3\bar{\varPhi }e^{\beta E_f}+3\varPhi e^{2\beta E_f}+ e^{3\beta E_f}}\;. \end{aligned}$$
(36)

For small values of the Polyakov loop, \(\varPhi \approx 0\), \(\bar{\varPhi }\approx 0\) Eq. (36) reduces to a Fermi-Dirac distribution with excitation energy \(3E_f\), i.e. that of three quarks. For large temperatures, when \(\varPhi \approx 1\), \(\bar{\varPhi }\approx 1\), the excitation energy is \(E_f\), which is the distribution function of deconfined quarks.

To the best of our knowledge, there are no systematic studies of the transition temperature as a function of the magnetic field B in various approximations. However, some interesting results using the quark-meson model exist.

Fig. 3
figure 3

Figure taken from Ref. [50]

\(T_{\mathrm{pc}}(B)/T_{\mathrm{pc}}\) as a function of \(eB/m_{\pi }^2\) in the quark-meson model. Solid line is the mean-field result and the dashed line is the result from the functional renormalization group. See main text for details

Full size image

Figure 3 shows the normalized transition temperature from Ref. [50] in two approximations using the functional renormalization group (FRG) [66]. In this approach, one solves a flow equation for the effective potential numerically by lowering a sliding scale k from an initial UV cutoff \(k=\varLambda \) (where the effective potential is equal to the classical potential) down to \(k=0\). The bare parameters at \(k=\varLambda \) are tuned such that one obtains the physical values of the masses and the pion decay constant in the vacuum (i. e. for \(k=0\)). In this way, all quantum and thermal fluctuations are included. The black solid line is the mean-field result, i.e. the bosons are excluded from the flow equation, whereas the brown line is the result using the functional renormalization group. Clearly, the addition of bosonic fluctuations increases the transition temperature significantly.

Fig. 4
figure 4

Figure taken from Ref. [52]

Normalized chiral transition temperature \(T_{\phi }(B)\) as a function of |qB| in units of \(m_{\pi }^2\) in the quark-meson model. The green points are without the Polyakov loop and the blue points are with the Polyakov loop. See main text for details

Full size image

In Fig. 4, we show the transition temperature at the physical point using the functional renormalization group [52]. The green points are the results without the Polyakov loop, whereas the blue points are the results including it. Clearly, the Polyakov loop lowers the transition temperature for fixed B, but it is still increasing as we increase the magnetic field. The above FRG results are obtained in the so-called local-potential approximation. In Ref. [67], the authors added the effects of wavefunction renormalization and the curve for the critical temperature lies between the mean-field approximation and the local-potential approximation. Thus the coupling of the Polyakov loop to the chiral sector is not sufficient to reproduce (qualitatively) the results seen on the lattice.

4 (Inverse) Magnetic catalysis on the lattice

After having discussed magnetic catalysis in low-energy models and theories of QCD, we next consider QCD lattice simulations. In the past decade, there have been a number of lattice calculations of QCD in a magnetic field [23,24,25,26,27, 45, 68,69,70,71,72,73,74], which have improved our understanding of QCD in a magnetic background.

In order to discuss (inverse) magnetic catalysis as seen on the lattice, it is advantageous to take a look at the path-integral representation of a number of expectation values. The QCD Lagrangian is bilinear in the quark fields \(\psi _f\) and so one can integrate over them, giving for the partition function as a path integral over gauge configurations \(A_{\mu }\)

$$\begin{aligned} {\mathcal {Z}}(B)=\int d{A}_{\mu }e^{-S_g}\det (/\!\!\!\!D(B)+m)\;, \end{aligned}$$
(37)

where \(S_g\) is the Euclidean gluon action and \(\det (/\!\!\!\!D(B)+m)\) is the fermion functional determinant (suppressing flavors). The operator \(/\!\!\!\!D(B)\) contains the nonabelian gauge field, which we have suppressed, as well as the abelian background B that we have indicated. The quark condensate is given by

$$\begin{aligned} \langle \bar{\psi }\psi \rangle&={\partial \over \partial m}\log {\mathcal {Z}}(B)\nonumber \\&={1\over {\mathcal {Z}}(B)}\int d{A}_{\mu }e^{-S_g}\det (/\!\!\!\!D(B)+m) \nonumber \\&\quad \times \mathrm{Tr} (/\!\!\!\!D(B)+m)^{-1}\;. \end{aligned}$$
(38)

We can think of \(P={1\over {\mathcal {Z}}(B)}e^{-S_g}\det (/\!\!\!\!D(B)+m)\) as a measure that depends on the gauge-field configuration \(A_{\mu }\), the magnetic field, and the quark masses. Note that the B-dependence is in the functional determinant as well as the trace of the propagator. In order to study the contributions to the quark condensate coming separately from the change of the operator and the change of the measure, it is convenient to introduce the valence and sea contributions defined as

$$\begin{aligned} \langle \bar{\psi }\psi \rangle ^{\mathrm{val}}&={1\over {\mathcal {Z}}(0)}\int d{A}_{\mu } e^{-S_g}\det (/\!\!\!\!D(0)+m)\mathrm{Tr}(/\!\!\!\!D(B)+m)^{-1}\;, \end{aligned}$$
(39)
$$\begin{aligned} \langle \bar{\psi }\psi \rangle ^{\mathrm{sea}}&={1\over {\mathcal {Z}}(B)}\int d{A}_{\mu } e^{-S_g}\det (/\!\!\!\!D(B)+m)\mathrm{Tr}(/\!\!\!\!D(0)+m)^{-1}\;. \end{aligned}$$
(40)

This can be thought of as an expansion of the quark condensate around \(B=0\). A priori, the sum of the two contributions needs not add up to the total quark condensate unless we are at small fields. However, it turns out that writing the condensate as a sum of the valence and sea contribution is remarkably good. This is clearly demonstrated in Fig. 5 from Ref. [26], which shows the relative increment r of the valence and sea contributions, their sum as well as the complete results for the quark condensate as a function of a dimensionless quantity b. The relative increment is defined as

$$\begin{aligned} r={\langle \bar{\psi }\psi \rangle _B\over \langle \bar{\psi }\psi \rangle }-1\;, \end{aligned}$$
(41)

where \(\langle \bar{\psi }\psi \rangle \) is the average of the u and d quark condensates. Within error, the additivity is confirmed for values of b up to 8, which corresponds to magnetic fields up to \(eB=(500\;\mathrm{MeV})^2\) [26]. It is also of interest to notice that both contributions work in the same direction, namely to increase the quark condensate as B grows. This is unlike what happens at temperatures around the critical temperature \(T_c\), as we shall see below. As pointed out in Ref. [45], \(\langle \bar{\psi }\psi \rangle ^{\mathrm{sea}}\) can be thought of as the quark condensate of an electrically neutral fermion flavor coupled to an electrically charged fermion flavor, since the magnetic field only appears in the functional determinant and not in the propagator. On the other hand, \(\langle \bar{\psi }\psi \rangle ^{\mathrm{val}}\) is reminiscent of the expression of the quark condensate in model calculations, except in models one does not integrate over gauge-field configurations.

Fig. 5
figure 5

Figure taken from Ref. [26]

Relative increment of the average of the u and d quark condensates as a function of b. Valence (red points) and dynamical (sea) (blue points) contributions, the sum of them (open circles), and the full quark condensate as a function of the dimensionless quantity b. See main text for details

Full size image

Let us now turn to finite temperature. Inverse magnetic catalysis seems to have two somewhat different meanings in the literature. The first meaning corresponds directly to the concept magnetic catalysis discussed above: it simply means that a condensate, for example \(\langle \bar{\psi }\psi \rangle \), decreases with the magnetic field at a fixed temperature. The second meaning is that the transition temperature itself is a decreasing function of the magnetic field.

The first finite-temperature lattice simulations were carried out in [23, 24] for SU(2) gauge theory in the quenched approximation, focusing on the B-dependence of the chiral condensate for temperatures below the transition. In two-flavor QCD, simulations at finite temperature were carried out for pion masses in the range 200–480\(\ \hbox {MeV}\) in Ref. [26] and it was concluded that the chiral and deconfinement transitions take place at the same temperature and that they increase slightly with the external magnetic field. The increase of the transition temperature with B is, at least qualitatively, in agreement with model calculations. Bali et al [27, 69] carried out lattice simulations at the physical point with 2 + 1 flavors, i.e. for quark masses that correspond to \(m_{\pi }=140\ \hbox {MeV}\), and the result was somewhat surprising: The transition temperature turned out to be decreasing as B increases. The different behavior of \(T_c\) is not a consequence of the different pion masses, rather it results from lattice artefacts and that the results of  [26] were not continuum extrapolated. Today there is consensus that the chiral transition temperature is a decreasing function of the magnetic field. This behavior is illustrated in Fig. 6, which shows the results of a recent lattice simulation [71], namely the transition temperature in MeV as a function of the magnetic field eB in GeV for three different pion masses. The pion mass is 343 MeV (red points), 440 MeV (blue points), and 664 MeV (green points), which is much larger than the physical pion mass of 140 MeV. The transition temperature increases as a function of the pion mass for fixed value of B, which is also known from \(B=0\) calculations.

Fig. 6
figure 6

Figure taken from Ref. [71]

Transition temperature in GeV for the chiral transition as a function of eB for different values of the pion mass. See main text for details

Full size image

In Ref. [45], the authors carried out a thorough analysis of the quark condensate around the critical temperature to understand the behavior of the transition temperature, focusing on disentangling the valence and sea effects. The valence contribution Eq. (39) can also be written as

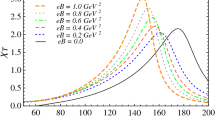
$$\begin{aligned} \langle \bar{\psi }\psi \rangle ^{\mathrm{val}}=\langle \mathrm{Tr}(/\!\!\!\!D(B)+m)^{-1}\rangle _0\;, \end{aligned}$$
(42)

where the subscript indicates that the quark determinant is without a magnetic field. The spectral density of the quark operator for different values of the magnetic field is shown in Fig. 7. From the figure, it is evident that there is an increase in the spectral density around zero with increasing magnetic field. The corresponding ensemble was generated at finite temperature, \(T=142\ \hbox {MeV}\) and for vanishing magnetic background [45]. The Banks-Casher relation [44] then implies an increase of the valence contribution.

Fig. 7
figure 7

Figure taken from Ref. [45]

Spectral density of the Dirac operator for three different values of the magnetic field. See main text for details

Full size image

Defining the quantity

$$\begin{aligned} -\varDelta S_f(B)=\log \det (/\!\!\!\!D(B)+m)-\log \det (/\!\!\!\!D(0)+m),\nonumber \\ \end{aligned}$$
(43)

the full condensate can be written as

$$\begin{aligned} \langle \bar{\psi }\psi \rangle = {\langle e^{-\varDelta S_f(B)}\mathrm{Tr} (/\!\!\!\!D(B)+m)^{-1}\rangle _0\over \langle e^{-\varDelta S_f(B)}\rangle _0}\;. \end{aligned}$$
(44)

Note that Eq. (44) reduces to the valence contribution Eq. (42) if one replaces \(\varDelta S_f(B)\) by unity. Figure 8 from Ref. [45] shows a scatter plot of the condensate as a function of the change in the action \(\varDelta S_f(B)\) due to the magnetic field. In this plot, the magnetic field strength is \(eB\approx 5\ \hbox {GeV}^2\) and T close to the transition temperature. Each point represents a gauge configuration and they were generated at vanishing magnetic field. The plot suggests that larger values of the condensates correspond to larger values of the weight \(e^{-\varDelta S_f(B)}\) and therefore suppresses the weight of the associated gauge configuration. As a result, this counteracts the valence effect, and leads to a decrease in the critical temperature. For pion masses that are not too large, it also leads to a decrease of the condensate itself (see discussion below).

Fig. 8
figure 8

Figure taken from Ref. [45]

Scatter plot of the down-quark condensate as a function of \(\varDelta S_f(B)\). See main text for details

Full size image

In Refs. [71, 72], the effects of varying the pion mass on the quark condensate as a function of the temperature have been studied in detail (again 2 + 1 flavors). Figure 9 from [71] shows the difference between the quark condensates as a function of the temperature at \(B=0\) and \(eB=0.425\ \hbox {GeV}^2\) (blue data points) and \(eB=0.85\ \hbox {GeV}^2\) (red points) for three values of the pion mass. The authors find that the sea contribution is a decreasing function of B around \(T_c\) for the different values of the pion masses, while the valence contribution is on the other hand an increasing function of the magnetic field for all temperatures and pion masses. In the upper panel it is clear that the sea contribution wins the competition around the transition temperature implying inverse magnetic catalysis in the strict sense of the word. This effect can barely been seen in the middle panel and is completely absent in the lower panel. In other words, a decreasing function of the transition temperature does not imply that the chiral condensate decreases as a function of temperature and it is therefore not clear that the latter is the driving mechanism of the former [71]. This nontrivial behavior was also demonstrated in [72], where the authors fixed the magnetic field to \(eB=0.6\ \hbox {GeV}^2\) and varied the pion mass. In QCD, there is inverse magnetic catalysis for pion masses up to 500 MeV, and magnetic catalysis for larger values Footnote 3

Fig. 9
figure 9

Figure taken from Ref. [71]

Difference between the quark condensates at zero magnetic field and non-vanishing B for three different values of the pion mass. See main text for details

Full size image

We finally comment on the nature of the chiral transition and the temperature as a function of B. The simulations have been done with magnetic fields up to \(eB=1\ \hbox {GeV}^2\). They all show an analytic crossover and that the transition temperature is a decreasing function of B. However, it has been conjectured that the transition would start increasing again for sufficiently large temperatures, a phenomenon dubbed delayed magnetic catalysis. In Ref. [70] the author went as high as \(eB=3.25\ \hbox {GeV}\) in the simulations. The transition remains a crossover (albeit sharper), there is no sign of delayed magnetic catalysis, and the chiral and deconfinement transitions coincide. The sharper crossover suggests that there may be a critical point for even larger values of the magnetic field. For asymptotically large fields, QCD can be mapped onto an anistropic pure-glue theory. This theory was simulated on the lattice and strong evidence for a first-order transition was found [70]. This implies the existence of a critical point and its position was estimated to be at \(eB\simeq 10\ \hbox {GeV}^2\).

5 Improvements of models

The failure of models to correctly describe the behavior of QCD around the critical temperature, even after the introduction of the Polyakov loop, has lead to significant efforts to improve them, see e.g. [75,76,77,78,79,80,81,82,83,84,85]. The temperature \(T_0\) that enters the Polyakov-loop potential depends on the number of flavors, it is therefore a reasonable assumption that it also depends on the magnetic field. In Ref. [75], the authors fitted the strange-quark susceptibilities from their calculations in the entangled PNJL model to the lattice results of Ref. [69]. Their ansatz for the field dependence was a simple polynomial in \((eB)^2\) up to quadratic order, giving two fitting parameters,

$$\begin{aligned} T_0(eB)=T_0(0)+\zeta (eB)^2+\xi (eB)^4\;. \end{aligned}$$
(45)

An interesting feature here is that the model predicts a first-order transition for magnetic fields larger than approximately \(eB=0.25\ \hbox {GeV}^2\). As mentioned above, such a critical point is expected in QCD, albeit at much larger magnetic fields [70].

The crossover nature of the chiral transition was a guide for the authors of Ref. [76], trying to incorporate the decreasing behavior of the transition temperature in the (Polyakov-loop extended) two-flavor quark-meson model. In their mean-field analysis, they allowed the Yukawa coupling to vary with the magnetic field, \(g=g(B)\) using the boundary value \(g(0)=3.3\). This value is indicated by the vertical dotted line in Fig. 10 and corresponds to a fixed quark mass in the vacuum. The critical temperature as a function of the Yukawa coupling for three values of the magnetic field is also shown in Fig. 10. The region to the right of the vertical solid line indicates the values of g for which the transition is first order.

Fig. 10
figure 10

Figure taken from Ref. [76]

\(T_c\) as a function of the Yukawa coupling g for various values of the magnetic field. See main text for details

Full size image

However, to obtain a transition temperature which is decreasing with the magnetic field any curve g(B) must start at \(g(0)=3.3\) and successively cross the dashed (red) and solid (black) curves. One therefore soon enters the region of a first-order transition in the QM model. Thus a function g(B) can simply not describe the correct B-dependence of the transition temperature, while at the same time having a crossover transition.

Similar approaches have been used in the NJL model allowing the coupling G to depend on both T and B. For example, in Ref. [77], the authors fix a set of parameters to get a reasonable fit to the lattice data for the sum of the light quark condensates. The form of the B-dependent coupling was motivated by the running of the coupling in QCD for strong magnetic fields [86].

One particular appealing idea was recently put forward in Ref. [87] (see also Refs. [88, 89]). Only \(T=0\) physics from the lattice is used as input to improve the model. In other words, there is no fitting to lattice data for \(T_c\) or a coupling that depends both upon B and T. The authors first performed a determination of the baryon spectrum at the physical point as a function of magnetic field using lattice simulations. The authors focused on strong magnetic fields, which are relevant for the phase diagram. Making the simple assumption that the baryon masses can be written as the sum of the masses of their constituents, they derived B-dependent constituent quark masses. This was used as input in the PNJL model at zero temperature: Using the gap equation with the B-dependent quark masses, a B-dependent four-fermion coupling was obtained. The B-dependent constituent quark masses as well as G(B) are decreasing functions of the magnetic field. For \(B=0\), \(M^2=0.097\ \hbox {MeV}^2\) and \(G(0)=12.8\ \hbox {GeV}^{-2}\) and for the largest magnetic field used (\(|eB|=0.6\ \hbox {GeV}^2\)), \(M^2=0.079\ \hbox {MeV}^2\) and \(G(B)=6.7\ \hbox {GeV}^{-2}\).

Fig. 11
figure 11

Figure taken from Ref. [87]

Normalized average quark condensate in the PNJL model as a function of eB. See main text for details

Full size image

Figure 11 shows the normalized average quark condensate at \(T=0\) as a function of the magnetic field. The dashed black line is obtained from a next-to-leading order (one-loop) calculation in chiral perturbation theory [19, 20], the light-blue points are obtained from the standard PNJL model, while the green points are obtained from the lattice-improved PNJL model. Finally, the red band shows the results from lattice simulations including errors. The plot has several interesting features. Firstly, all low-energy approaches are in good agreement with lattice results for low values of the magnetic field. For larger values, both \(\chi \)PT and PNJL underestimate the quark condensate. This is in contrast with the lattice-improved PNJL model, which is in quantitative very good agreement with the simulations. It would be of interest to see the predictions if one would include the effects of the s-quark in the model calculations.

We next consider the finite-temperature calculations of Ref. [87]. Figure 12 shows the quark condensate as a function of T for different strengths of the magnetic field. The dashed lines are the predictions from the standard PNJL model without error bands, while the solid bands are the lattice-improved PNJL model predictions. We first note that quark condensate at \(T=0\) for fixed magnetic field is higher for the lattice-improved PNJL model in agreement with Fig. 11. This behavior persists for low temperature, for larger temperatures, however, the condensate drops faster compared to that calculated using the standard PNJL model. Thus for fixed magnetic field, the transition temperature defined as the inflection point of the quark condensate moves to a lower value of T compared to the PNJL model. This in itself is not enough to conclude that we have inverse magnetic catalysis, but the effect is so strong that the inflection point moves to the left as a function of B so the transition temperature decreases.

Fig. 12
figure 12

Figure taken from Ref. [87]

Quark condensate in the PNJL model as a function of T for different values of the magnetic field. See main text for details

Full size image

Figure 13 shows the normalized transition temperature for the chiral transition, as defined by the inflection point of the quark condensate, as a function of eB in units of \(\hbox {GeV}^2\). The pink band is from the lattice results of Ref. [69]. The width of the band indicates the errors of the simulations. The light-blue points are the results of a calculation from the standard PNJL model showing that the transition temperature increases as the magnetic field grows. This is in sharp contrast to the lattice-improved PNJL model, where the results are shown by the green points including uncertainties coming from the lattice determination of the baryon masses. Given the large uncertainties, the results for the transition temperature are in good agreement with the simulations. Similarly, the analytic crossover found also agrees with lattice results.

Fig. 13
figure 13

Figure taken from Ref. [87]

Normalized transition temperature from the lattice and in the PNJL model as a function of eB. See main text for details

Full size image

6 Summary and final remarks

The idea of magnetic catalysis at zero temperature has been around for 3 decades after its discovery in the NJL model. It is a robust phenomenon. For large values of the magnetic field, it can be understood in terms of dimensional reduction from \(3+1\) to \(1+1\) dimensions (or from 2 + 1 to 0 + 1 dimensions). Lattice simulations in the last decade have improved our understanding of the effect significantly by showing that both the valence and sea effect contribute in a nontrivial way. Since the discovery of the the decrease of the chiral transition temperature with increasing magnetic field, a lot of work has been devoted to incorporate this feature in models. This includes T- and B-dependent couplings and Polyakov-loop potentials. Fitting parameters can be considered an indirect way of incorporating the sea effect and requires input from lattice simulations at finite temperature. In our opinion, a cleaner approach is provided by the work [87], which uses lattice input at \(T=0\) only. In much the same way as one uses experimentally measured meson masses in the vacuum, they use B-dependent baryon masses measured on the lattice as input in their PNJL-model calculations, although assuming that the baryon mass is the sum of its constituents perhaps is somewhat simplistic.