1 Introduction

Lifetime measurements play a crucial role in furthering our understanding of the nuclear force at the very edges of stability and have shed light on a number of nuclear structure phenomena, including shape coexistence, proton-neutron correlations, and the role of three-body forces [1,2,3,4]. Plunger techniques have been often employed for lifetime measurements of excited nuclear states [5]. The most common plunger method is the recoil distance Doppler-shift (RDDS) technique based on the detection of \(\gamma \)-ray transitions between excited states in recoiling nuclei [6]. However, the method is not applicable for measuring the lifetime of excited states that de-excite predominantly by the internal conversion process.

Two methods to extract the lifetime of nuclear states that de-excite via strong internal conversion are the charge plunger, the focus of this work, and the recoil shadow method [7]. The recoil shadow method uses an electron spectrometer to detect electrons from the internal conversion of excited states that de-excite in flight after the target foil. The target is “shadowed” from the spectrometer using a longitudinal semi-cylindrical baffle which suppresses the large \(\delta \)-electron background originating from reactions in the target. Lifetime measurements are then possible by varying the target position.

The charge plunger method is based on an analysis of the changes in the charge-state distribution (CSD) of ions caused by a cascade of Auger electrons that follow internally converted transitions [8]. As shown in Fig. 1, it utilises a thin reset foil placed downstream at a distance from the target. The recoils produced at the target pass through the foil and their ionic charges are reset to a value dependent on their velocity. Thus the distribution of ionic charge states after the reset foil should reflect the proportion of internal conversions occurring before or after the reset foil. In Ref. [8] the authors used a tabletop magnetic deflector after the reset foil to separate ions by charge and deposit them on to a catcher foil. The distribution of recoils along the catcher foil was then measured offline. This was done for several target-to-reset foil distances, measured using a micrometer, to determine the change in intensity of high-charge components in the CSD with distance. Lifetime information was then obtained through either an integral or differential analysis. In the integral analysis the overall de-excitation of a sequence of states such as a rotational band is measured using the total yield of highly charged recoils as a function of target-to-reset foil distance. The differential analysis uses the decay curve of the different components in the CSD corresponding to 1, 2, 3 etc. internal conversions after the reset foil to measure the lifetime of individual states in a rotational band. Using this method the authors determined the lifetime of excited states in fission isomers for uranium and plutonium isotopes [9, 10].

More recently the charge plunger method has been developed further in order to extend studies to nuclear states produced with low-production cross sections in nuclear reactions [11]. Here, the DPUNS plunger device [12] was used for improved control of the distance between the target and reset foils. The recoils of interest are separated from the beam like and fissioning reaction products according to their mass/charge (m/q) ratio by the MARA recoil separator [13] and are transported to the focal plane for their detection by a multiwire proportional counter (MWPC) and a double-sided silicon strip detector (DSSSD). Nuclei of interest are then identified either by employing the recoil-decay tagging technique, i.e. using coincidences between the recoil implanted in the DSSSD and the subsequent particle decay [14], or by using \(\gamma \)-ray-recoil coincidences between the prompt \(\gamma \) rays detected at the target position using the JUROGAM 3 spectrometer [15] and the recoils detected in the MWPC and DSSSD.

In ref. [11], the CSD of ions detected in coincidence with the \(\gamma \)-ray de-excitation from the \(4_1^+\) state occurring before the reset foil were influenced only by the de-excitation from the \(2_1^+\) state via the internal conversion process. An analysis within the differential decay curve method (DDCM) [16] framework was performed to obtain the lifetime of the \(2_1^+\) state in \(^{180}\)Pt. In the present work, we obtained the lifetime of the \(2_1^+\) state in \(^{178}\)Pt using the same method. As in Ref. [11], it was not possible to resolve the Doppler-shifted components of the \(4_1^+\rightarrow 2_1^+\) \(257\,\,\)keV feeding transition occurring before and after the reset foil, therefore the analysis was restricted to data points taken at longer distances where the \(\gamma \)-ray de-excitation from the \(4_1^+\) state always occurs before the reset foil.

Fig. 1
figure 1

Schematic diagram of the charge plunger method (upper) at target-to-reset foil distance x. An internal conversion and subsequent Auger cascade will cause the ionic charge to increase. If the transition occurs before the plunger foil the charge will be reset. If the transition occurs after the reset foil, and proceeds by internal conversion, the ion remains in a high charge state. A \(\gamma \)-ray transition does not create a vacancy in the atomic shell configuration and therefore does not affect the charge state of the ion. The charge state distribution after the plunger foil will therefore contain two components (lower)

Full size image

It is beneficial to develop an analysis procedure for charge plunger experiments which is not dependent on observing the \(\gamma \)-ray emission of the feeding transition. This would be especially important for cases where the DDCM is unsuitable due to either low production cross-sections, where coincidence analyses are limited due to low statistics, or the presence of multiple highly converted transitions in a band. This can be achieved by fitting experimental data to the Bateman equation, which takes into account the de-excitation properties of higher energy states feeding the level of interest. Therefore, an additional analysis was performed whereby an alpha particle of \(\sim 5.5\,\)MeV energy from the ground state decay of \(^{178}\)Pt, with branching ratio \(\sim 7.5\)%, was used to obtain recoil-alpha tagged CSD spectra [17]. These are influenced by the internal conversion of transitions other than the \(2_1^+\rightarrow 0_1^+\) \(170\,\,\)keV transition. The lifetime of the \(2_1^+\) and \(4_1^+\) states were then obtained using the Bateman equation, accounting for the de-excitation of two states.

2 Charge plunger method

A description of the principle of the charge plunger method can be found in Ref. [8]. The method relies on the large increase in ionic charge (\(\sim 5-10\)e) due to the Auger cascade that follows from the internal conversion of an electromagnetic transition from an excited nuclear state [18]. Nuclei are created via fusion–evaporation reactions in a target and recoil away from the target with a mean velocity v. If a charge reset foil is placed at a distance x after the target, then the distribution of charge states after this foil will depend on whether or not the de-excitation of the excited state occurs before or after the foil, and if it proceeds by internal conversion. This is demonstrated in Fig. 1, for the simple example of a nucleus with one excited state that can de-excite either by \(\gamma \)-ray transition or internal conversion. The CSD after the reset foil will contain a low charge component (\(Q_L\)) and a high charge component (\(Q_H\)). The intensities of these two components (\(I_L\) and \(I_H\)) will depend on the time taken for recoils to traverse the distance x, the internal conversion coefficient of the transition and the lifetime of the excited state.

The next two sub-sections describe two methods of analysis that can be used to obtain the lifetime of an excited nuclear state. A \(\gamma \)-ray-recoil coincidence gate can be placed on a feeding transition to combine the charge plunger technique together with the DDCM (2.1). Alternatively a fit can be made to the intensities of the different components in the CSD using the Bateman equation (2.2).

Fig. 2
figure 2

a Example level scheme to demonstrate how the DDCM and Bateman analysis can be applied to the charge plunger method to deduce lifetimes in a band. b The CSD will now contain higher charge components corresponding to two and three internal conversions after the reset foil

Full size image

2.1 DDCM coincidence analysis

As shown in Ref. [11], it is possible to use \(\gamma \)-ray coincidences with the charge plunger method and analyse the data in a DDCM framework. Figure 2a shows a rotational band level scheme. As well as containing \(Q_L\) and \(Q_H\), the CSD will now contain higher charge components (\(Q_{2H}, Q_{3H}\), etc.) due to successive internal conversions after the reset foil, Fig. 2b. These higher charge components have intensities (\(I_{2H}, I_{3H}\), etc.). For the \(N^\mathrm {th}\) level shown in Fig. 2a, the lifetime is found using,

$$\begin{aligned} \tau _N = \frac{I_{\{M_B, N_A\}}(x)}{d(I_{\{M_B, N_B\}}(x))/dx} \cdot \frac{1}{v} \end{aligned}$$
(1)

where \(I_{\{M,N\}}\) is the number of \(T_N\) transitions that are in coincidence with a measured \(\gamma \) ray from the \(T_M\) transition. The subscript B and A refer to the transition occurring before or after the reset foil, respectively [6].

The discussion of physical processes benefits from focussing on the number of nuclei that de-excite after or before the reset foil, whereas the experimental observables are the intensity of charge components in the CSD (\(I_L, I_H, I_{2H}\), etc). For the specific case where a coincidence gate is set on transitions between levels 2 and 1 \((T_2)\) occurring before the reset foil then only transitions between level 1 and the ground state \((T_1)\) can occur after the foil. The mapping of the experimental observables to the number of \(T_1\) transitions occurring after and before the reset foil is developed in Ref. [11] and the result is given here.

The intensity of the high charge component in the CSD is related to the number of de-excitations occurring after the reset foil that proceed by internal conversion. Similarly the intensity of low charge ions is found from the number of de-excitations that occur either before the reset foil, or after the foil proceeding by \(\gamma \)-ray emission,

$$\begin{aligned} I_{H}(x)= & {} P_{\mathrm {ic}} I_{A}(x) \end{aligned}$$
(2)
$$\begin{aligned} I_{L}(x)= & {} I_{B}(x) + P_{\mathrm {\gamma }} I_{A}(x) \end{aligned}$$
(3)

where \(P_{\mathrm {ic}}\) and \(P_{\gamma }\) are the probabilities that the transition proceeds via internal conversion or \(\gamma \)-ray emission respectively. By rearranging Eqs. 2 and 3 one obtains,

$$\begin{aligned} I_{A}(x)= & {} \left( \frac{1+\alpha _1}{\alpha _1}\right) I_{H}(x) \end{aligned}$$
(4)
$$\begin{aligned} I_{B}(x)= & {} I_{L}(x) - \frac{I_{H}(x)}{\alpha _1} \end{aligned}$$
(5)

where \(\alpha _1\) is the internal conversion coefficient of transition \(T_1\). By measuring the charge state of ions in coincidence with the \(T_2\) transition occurring before the charge reset foil, one can use Eqs. 5 and 4 together with Eq. 1 to find the lifetime of level 1.

2.1.1 Transition \(T_2\)

For example, to find the lifetime of level 2, \(\tau _2\), a gate is placed on \(T_3\) transitions occurring before the reset foil. There are now two internal conversions that can occur after the reset foil. The possible combinations of \(\gamma \)-ray transitions and internal conversions that can occur after the reset foil are shown in Fig. 3. The number of \(T_2\) transitions occurring after and before the foil are given by,

$$\begin{aligned} I_{\{3_B,2_A\}}= & {} \left( \frac{1+\alpha _2}{\alpha _2}\right) \left( \frac{1+\alpha _1}{\alpha _1}\right) I_{\{3_B,2H\}} \end{aligned}$$
(6)
$$\begin{aligned} I_{\{3_B,2_B\}}= & {} I_{\{3_B,L\}} + I_{\{3_B,H\}} - I_{\{3_B,2H\}}\left[ \frac{1}{\alpha _1}+\frac{1}{\alpha _2}+\frac{1}{\alpha _2\alpha _1}\right] \nonumber \\ \end{aligned}$$
(7)

where the extra terms result from the different combinations of two transitions that can proceed by either \(\gamma \)-ray emission or internal conversion after the reset foil.

2.1.2 Transition \(T_N\)

When using coincidences to measure the lifetime of the \(N^{\mathrm {th}}\) level in the band, which is fed by the transition \(T_M (M \rightarrow N)\), the number of \(T_N\) transitions occurring after or before the foil are given by,

$$\begin{aligned} I_{\{M_B,N_A\}}= & {} \left( \prod _{i=1}^{N}\frac{1+\alpha _i}{\alpha _i}\right) I_{\{M_B,NH\}} \end{aligned}$$
(8)
$$\begin{aligned} I_{\{M_B,N_B\}}= & {} I_{\{M_B,L\}} + \left( \sum _{i=1}^{N-1} I_{\{M_B,iH\}}\right) \nonumber \\&- I_{\{M_B,NH\}}\left[ \sum _{i=1}^{N} C_i(\alpha _1,\alpha _2,...,\alpha _N)\right] \end{aligned}$$
(9)

where the function \(C_i(\alpha _1,\alpha _2,...,\alpha _N)\) is defined as,

$$\begin{aligned} C_1(\alpha _1,\alpha _2,&...,\alpha _N) = \sum _{j_1=1}^{N} \left( \frac{1}{\alpha _{j_1}} \right) \nonumber \\ C_2(\alpha _1,\alpha _2,&...,\alpha _N) = \sum _{j_1=1}^{N-1} \sum _{j_2=j_1 + 1}^{N} \left( \frac{1}{\alpha _{j_1} \alpha _{j_2}} \right) \nonumber \\ C_i(\alpha _1,\alpha _2,&...,\alpha _N) = \sum _{j_1=1}^{N-(i-1)} \sum _{j_2=j_1+1}^{N-(i-2)} ... \sum _{j_i=j_{i-1}+1}^{N} \nonumber \\&\qquad \times \left( \prod _{j=j_1}^{j_i} \frac{1}{\alpha _j}\right) \nonumber \\&...\nonumber \\ C_N(\alpha _1,\alpha _2,&...,\alpha _N) = \frac{1}{\alpha _1 \alpha _2 \cdot \cdot \cdot \alpha _N} \end{aligned}$$
(10)

and describes the different combinations of N transitions that can proceed by either \(\gamma \)-ray emission or internal conversion after the foil. In Eqs. 8 and 9 it is important to note that for a lifetime measurement of a state where there are N possible internal conversions occurring after the reset foil, then all N components of the CSD must be measured.

2.2 Bateman analysis

To illustrate how one may solve the Bateman equation in order to retain the lifetime of a state, consider a level scheme similar to the one shown in Fig. 2a, with just two excited states. There are three components in the CSD; \(Q_L\), \(Q_H\) and \(Q_{2H}\). This is a similar scenario to the one described in Sect. 2.1.1, and the possible combinations that make up each component of the CSD are shown in Fig 3.

Fig. 3
figure 3

Schematic diagram to show the possible combinations that make up the different components in the CSD when there are two transitions that can occur after the reset foil

Full size image

The intensity of the second-high charge component, \(Q_{2H}\) is the probability that both states proceed by internal conversion after the reset foil,

$$\begin{aligned} I_{2H}(x) = P_{2_A}(x) \cdot P_{2, \mathrm {ic}} \cdot P_{1, \mathrm {ic}} \end{aligned}$$
(11)

where \(P_{1(2), \mathrm {ic}}\) is the probability that transition \(T_{1(2)}\) proceeds by internal conversion. \(P_{2_A}(x)\) is the probability that transition \(T_2\) occurs after the reset foil at target-to-reset foil distance x. Since \(T_2\) is not fed by any higher transition the probability it occurs after the reset foil is given by,

$$\begin{aligned} P_{2_A}(x) = \mathrm {exp}\left( -\lambda _2 \cdot \frac{x}{v}\right) \end{aligned}$$
(12)

where \(\lambda _2\) is the decay constant of level 2. A measurement of \(I_{2H}\) is therefore sensitive to the lifetime of level 2.

The intensity of the first-high charge component, \(Q_H\), is the probability that only one internal conversion occurs after the reset foil. By considering the possible combinations shown in Fig. 3, this intensity is given by,

$$\begin{aligned} I_{H}(x)= & {} P_{2_A}(x) \left[ P_{2, \mathrm {ic}} \cdot P_{1, \gamma } + P_{2, \gamma } \cdot P_{1, \mathrm {ic}} \right] \nonumber \\&+P_{2_B,1_A}(x) \cdot P_{1, \mathrm {ic}} \end{aligned}$$
(13)

where \(P_{1(2), \gamma }\) is the probability that transition \(T_{1(2)}\) proceeds by \(\gamma \)-ray emission. \(P_{2_B,1_A}(x)\) is the probability that transitions \(T_2\) and \(T_1\) occur before and after the reset foil respectively. An expression for \(P_{2_B,1_A}(x)\) can be found from the Bateman equation and is given by,

$$\begin{aligned} P_{2_B,1_A}(x)= & {} \frac{\lambda _{2}}{\lambda _{1}-\lambda _{2}} \left[ \mathrm {exp}\left( -\lambda _{2} \cdot \frac{x}{v} \right) \right. \nonumber \\&\left. - \mathrm {exp}\left( -\lambda _{1} \cdot \frac{x}{v}\right) \right] \end{aligned}$$
(14)

where \(\lambda _1\) is the decay constant of level 1. \(I_H(x)\) is sensitive to the lifetime of both levels 2 and 1. Similarly, the intensity of the low charge component with respect to target-to-reset foil distance x, is also sensitive to the lifetime of both levels and is given by,

$$\begin{aligned} I_{L}(x)= & {} P_{1_B}(x) + P_{2_A}(x) \cdot P_{2, \gamma } \cdot P_{1, \gamma }\nonumber \\&+ P_{2_B,1_A}(x) \cdot P_{1, \gamma } \end{aligned}$$
(15)

where \(P_{1_B}(x)\) is the probability that both transitions \(T_2\) and \(T_1\) occur before the reset foil and is given by,

$$\begin{aligned} P_{1_B}(x)&= 1 - P_{2_A}(x) - P_{2_B,1_A}(x) \nonumber \\&= \frac{1}{\lambda _{2}-\lambda _{1}} \left[ \lambda _{1}\mathrm {exp}\left( -\lambda _{2} \cdot \frac{x}{v} \right) - \lambda _{2}\mathrm {exp}\left( -\lambda _{1} \cdot \frac{x}{v}\right) \right] . \nonumber \\ \end{aligned}$$
(16)

By fitting functions of the form described above to the intensities of the relevant components in the CSD it is possible to find the lifetime of levels 2 and 1 shown in Fig. 2a.

The model given here assumes no side feeding into the first-excited state, i.e. the population of level 1 is solely due to the transition \(T_2\). Side feeding can be accounted for within the model by varying the initial population of each state within the band.

Some consideration must be given to estimating the effect of unknown internal conversion coefficients in a cascade. Good knowledge of the conversion coefficient for the transition depopulating the level of interest is imperative, however for transitions from higher-lying states the effect may not be so large. The conversion coefficient for transition \(T_2\) only becomes important when \(T_2\) occurs after the foil. If there is a significant difference in the lifetime of levels 1 and 2 then the obtained lifetime for level 1 has only a weak dependence on the conversion coefficient of \(T_2\). For example, it is estimated for the case presented in this paper (\(\tau _1 \approx 8\cdot \tau 2\)) that the systematic error in the obtained lifetime of level 1 is \(\sim 3.7\%\) when varying the conversion coefficient for transition \(T_2\) between 0 and \(\infty \).

3 Experimental method

An experiment was performed at the accelerator laboratory of the University of Jyväskylä, Finland to measure the lifetime of excited states in \(^{178}\)Pt. The experiment was performed during the same experimental run as Ref. [11] and a description of the setup can also be found there. The lifetime of the \(2_1^+\) has been previously measured to be \(412(30)\,\)ps [19]. Two previous RDDS measurements of the lifetime of the \(4_1^+\) state give \(41(2)\,\)ps [20], measured using \(\gamma \)-ray coincidences, and \(54(5)\,\)ps [21], measured using \(\gamma \)-ray singles. The internal conversion coefficient taken from BrIcc for the \(2^+\rightarrow 0^+\) \(170\,\,\)keV transition is 0.63(1), and is 0.1578(23) for the \(4^+\rightarrow 2^+\) \(257\,\,\)keV transition [22]. A \(2\,\)pnA beam of \(^{32}\)S from the K130 cyclotron was used to bombard a 1 mg/\(\hbox {cm}^2\) \(^{152}\)Sm target with an upstream 1.5 mg/\(\hbox {cm}^2\) Ta backing at an energy of 192 MeV over a period \(\sim \)2 days. For this asymmetric reaction at such a beam energy, recoils are expected to be created with relatively small kinetic energy. A thin stretched 0.29 mg/\(\hbox {cm}^{2}\) Ni charge reset foil was therefore used to maintain good resolution and efficiency in MARA. Due to imperfect alignment of the target and reset foil, and additional surface effects, there was an offset between electrical contact of the foils and true zero separation distance which was measured to be 8(1) \(\upmu \)m. To maximise transmission of \(^{178}\)Pt recoils, MARA settings were tuned for a reference particle of mass \(M_\mathrm {ref} = 178\) u and energy \(E_\mathrm {ref} = 23\) MeV. Data was collected for 12 plunger distances that were chosen to be sensitive to the lifetime of the \(2_1^+\) excited state.

The vacuum separator MARA was used to separate ions by their mass/charge (m/q) ratio [13]. The ions were detected at the focal plane of MARA using a suite of detectors starting with a MWPC. The position of the ion in the MWPC is related to its m/q value. After the MWPC, ions are implanted into a DSSSD which reads out the energy of the implantation. A 300 \(\upmu \)m thick BB20 DSSSD was used to detect recoils at the focal plane. The DSSSD had dimensions 128\(\times \)48 \(\hbox {mm}^2\) with a pixel size of 0.69\(\times \)0.69 \(\hbox {mm}^2\). Two Si veto detectors were employed behind the DSSSD and events were discarded if the signals from the DSSSD and veto detectors were recorded in coincidence.

Prompt \(\gamma \) rays were detected with the JUROGAM 3 spectrometer [15], an array of 39 Compton-suppressed HPGe detectors, on loan from GAMMAPOOL. The total data readout (TDR) [23] data acquisition system was employed to record the events from all detectors and the GRAIN [24] software package was used to perform offline analysis.

An initial scan of the CSD was taken at the start of the beam time to identify the regions of the low and high charge components, \(Q_{\mathrm {L}}\) and \(Q_{\mathrm {H}}\) respectively. The scan was taken at a reset foil distance of \(x=1542\,\upmu \)m and is shown in Fig. 4. At this distance only the first-high charge and reset components should be present in the CSD. \(^{178}\)Pt recoils were identified using their characteristic alpha decays in the DSSSD. The two charge components \(Q_{\mathrm {L}}\), \(Q_{\mathrm {H}}\) are shown. Due to beam time restrictions it was not possible to collect the entire CSD for each plunger distance. Instead, two charge states (indicated in Fig. 4) were chosen to represent \(Q_{\mathrm {L}}\) (\(q_{\mathrm {ref}} =17\)e) and \(Q_{\mathrm {H}}\) (\(q_{\mathrm {ref}} =25\)e) respectively. These charge states were chosen to maximise intensity and to minimise the intensity from overlapping charge components. For each plunger distance, two sets of data were collected for MARA settings corresponding to \(q_{\mathrm {ref}} =17\)e, 25e. Coulomb excitation population of the \(2^{+}_{1}\) in the \(^{152}\)Sm target was used to normalise the charge states intensity across all data sets.

Fig. 4
figure 4

Recoil CSD when gating on \(^{178}\)Pt alpha decays for reset foil distance \(x=1542\,\upmu \)m. The different components that make up the CSD are shown including \(Q_{\mathrm {L}}\), \(Q_{\mathrm {H}}\). Two charge states were chosen to represent the intensities of \(Q_{\mathrm {L}}\) and \(Q_{\mathrm {H}}\), these are also shown as \(q_{\mathrm {L}}\) and \(q_{\mathrm {H}}\) respectively. Instead of measuring the entire CSD, it was the intensity of these charge states that were measured for each plunger distance

Full size image

4 Results

Figure 5 shows part of the JUROGAM 3 spectrum for \(\gamma \)-ray-recoil coincidences. Yrast transitions in \(^{178}\)Pt are labelled. The spectrum is the result of a combination of all plunger distances to illustrate the quality of the data. The greatest contaminant came from Coulomb excitations in the target and backing materials. The mean velocity of \(^{178}\)Pt recoils after the target was measured to be \(\beta =\) 1.77(2)% using the Doppler-shift of the \(4_1^+\rightarrow 2_1^+\), \(6_1^+\rightarrow 4_1^+\) and \(8_1^+\rightarrow 6_1^+\) transitions at a plunger distance of \(x=5061\,\upmu \)m. At this distance all these transitions are expected to occur before the reset foil.

Fig. 5
figure 5

Part of the JUROGAM 3 spectrum for \(\gamma \)-ray-recoil coincidences. Yrast transitions for the \(^{\mathrm {178}}\)Pt ground-state rotational band are labelled. This spectrum is a summation of all distances. The \(4_1^+\rightarrow 2_1^+\) (257 keV) transition shown inset for reset foil distances of \(x = 43\,\upmu \)m (all transitions occur after reset foil) and \(x = 5061\,\upmu \)m (all transitions occur before reset foil)

Full size image
Fig. 6
figure 6

Charge spectra at the focal plane of MARA when gating on the \(4_1^+\rightarrow 2_1^+\) transition at 257 keV. In each spectrum counts have been normalised using coulomb excitation in the target. The central peaks lie at 17e and 25e. The evolution with distance of low and high charge components is shown for five distances. The integration limits of the central charge peaks are shown as blue (\(q=17\,\)e) and red (\(q=25\,\)e) dotted lines

Full size image

4.1 DDCM coincidence analysis

A gate was set on the \(4_1^+\rightarrow 2_1^+\) feeding transition, and the intensity of low and high charge ions (\(I_{L}\) and \(I_{H}\) respectively) were measured from the resulting normalised charge state spectra, shown in Fig. 6 for five distances. The transmission through MARA is largest for the reference charge state, \(q_{\mathrm {ref}}\), therefore \(I_{L}\) and \(I_{H}\) were measured by integrating the counts in the normalised charge spectra for the central charge state only. The limits for the integration are shown in Fig. 6 as dotted lines. The values \(R_{L}=\frac{I_{L}}{I_{L}+I_{H}}\) and \(R_{H}=\frac{I_{H}}{I_{L}+I_{H}}\) were used in Eqs. 4 and 5 to find the relative intensity of \(2_1^+\rightarrow 0_1^+\) transitions before (\(R_{B}\)) and after (\(R_{A}\)) the reset foil respectively.

The DDCM lifetime Eq. (1) requires that the coincidence gate is set on feeding transitions occurring before the reset foil. The \(4_1^+\rightarrow 2_1^+\) transition at 257 keV is shown in Fig. 5 inset for reset foil distances \(x=43\,\upmu \)m and \(x=5061\,\upmu \)m. At these distances all the transitions are expected to occur after and before the charge reset foil respectively. As recoils pass through the reset foil they will slow down resulting in a smaller Doppler shift in \(\gamma \)-ray energy, and thus a different energy centroid. The change in the energy centroid (\(\Delta E = 0.2\) keV) is much smaller than the resolution of the detectors (\(\delta E \sim 2\,\)keV), due to how thin the reset foil was. This meant that it was not possible to set a gate on feeding transitions occurring before the reset foil. However, using the unresolved Doppler-shifted components method (UDCM) [25] it was possible to measure the proportional intensity of \(4_1^+\rightarrow 2_1^+\) transitions occurring before and after the foil. This uses the change in the measured centroid of the transition to find the relative intensities of the unresolved Doppler-shifted components of the transition. The relative intensity of \(4_1^+\rightarrow 2_1^+\) transitions occurring after the reset foil is shown in Fig. 7 against target-to-reset foil distance. At distances \(x\ge 1223\,\upmu \)m the proportion of \(4_1^+\rightarrow 2_1^+\) transitions occurring after the reset foil is consistent with 0 to within \(1\sigma \) and the requirement for using the DDCM coincidence analysis is satisfied.

Fig. 7
figure 7

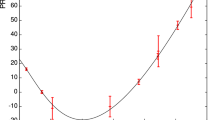
Proportional intensity of \(4_1^+\rightarrow 2_1^+\) transitions occurring after the reset foil for each target-to-reset foil distances. This was measured by applying the unresolved Doppler-shifted components method (UDCM) [25]. At distances longer than \(x=1223\,\upmu \)m the proportion of \(4_1^+\rightarrow 2_1^+\) transitions occurring after the reset foil is consistent with 0 to within \(1\sigma \)

Full size image

The program NAPATAU was used to extract the lifetime of the \(2_1^+\) state [26]. NAPATAU uses Eq. 1 to extract lifetime information from the data. A second degree polynomial, f(x), was fit to the values of \(R_{B}\) in the range of distances sensitive to the lifetime of the \(2_1^+\) state. The differential of this function is used in the form \(\tau \cdot v \cdot \frac{df(x)}{dx}\) to describe the values \(R_{A}\). A common \(\chi ^2\) minimisation of f(x) and \(\frac{df(x)}{dx}\) is used to find a value for the lifetime at each distance [16]. The values \(R_{B}\) along with the fit f(x) are shown in Fig. 8a, and \(R_{A}\) is shown in Fig. 8b with the function \(\tau \cdot v \cdot \frac{df(x)}{dx}\). Figure 8c shows the resulting \(\tau \)-curve for the \(2_1^+\) state in \(^{178}\)Pt. Data points at \(x\le 1223\, \upmu \)m were not included in the fit, since at these distances the proportion of \(4_1^+\rightarrow 2_1^+\) occurring after the foil are not consistent with 0 (see Fig. 7). A weighted average gives a lifetime of \(\tau (2_1^+) = 430(20)\) ps.

Fig. 8
figure 8

Results from the analysis of the normalised charge spectra shown in Fig. 6 using the program NAPATAU [26]. a The values \(R_{B}\) are shown with a second degree polynomial f(x) (solid green line) which is fit to the data. b The values \(R_{A}\) are shown along with a function of the form \(\tau \cdot v \cdot \frac{df(x)}{dx}\) (solid orange line). c The \(\tau \)-curve of the \(2_1^+\) state in \(^{\mathrm {178}}\)Pt. The weighted average (solid line) of the lifetime found for each distance is shown. The error on the weighted mean is also shown (dashed line)

Full size image
Fig. 9
figure 9

Part of the DSSSD energy spectrum for recoil-decay coincidences. This spectrum is an summation of all distances. The prominent peaks originate from the alpha decays of \(^{178}\)Pt and \(^{177}\)Pt recoils. The parent nucleus is labelled for each peak

Full size image

4.2 Bateman analysis

An alternative method of analysing the CSD spectra that result from the internal conversion of transitions from excited states in \(^{178}\)Pt is to use recoil-alpha coincidences in the DSSSD. The half-life of the \(^{178}\)Pt ground state is 20.7(7) s [27]. A time window of 200 seconds was used to search for recoil-alpha coincidences originating from \(^{178}\)Pt. Fig. 9 shows part of the DSSSD spectrum for recoil-decay coincidences with an enlargement of the prominent alpha-decay lines shown in the inset. The strongest peak represents the \(^{178}\)Pt alpha decay. There is also a weaker peak resulting from the alpha decay of \(^{177}\)Pt recoils.

Recoils were selected in coincidence with \(^{178}\)Pt alpha decays and the resulting normalised charge spectra are shown in Fig. 10 for five distances. Once again the intensities of the low (\(I_{L}\)) and high (\(I_{H}\)) charge states were measured by integrating the counts in the central charge peak. The limits of integration are shown in Fig. 10 as dotted lines.

Fig. 10
figure 10

Charge spectra at the focal plane of MARA in coincidence with an alpha decay of \(^{178}\)Pt. Normalization is the same as in Fig. 6. The evolution with distance of low and high charge components is shown for five distances. The integration limits of the central charge peaks are shown as blue (\(q=17\,\)e) and red (\(q=25\,\)e) dotted lines

Full size image

Figure 11 shows proportional intensity of the high charge state \(R_H=\frac{I_{H}}{I_{L}+I_{H}}\) against target-to-reset foil distance. At the distances \(x \le 264\,\upmu \)m the proportion of high charge ions increases rapidly. There are two possible explanations for this. Firstly, at low distances there will be a significant intensity of a second-high charge component (2 internal conversions after the reset foil). As only the intensity of charge states corresponding to the low and first-high charge component were measured, the effect of this second-high charge component is ignored. The second possibility is that there could be highly converted side-feeding transitions that populate the ground state band. In this case the change in intensity of highly charge ions detected after the reset foil will reflect the lifetime of these side feeding transitions. For this reason the data points at distances \(x \le 264\,\upmu \)m are left out of the Bateman analysis. A two-state fit of the form described in Eq. 13 is made to the data points at distances \(x\ge 264\,\upmu \)m. In this model the first excited level corresponds to the \(2_1^+\) state; the second excited level accounts for the average de-excitation properties of all higher energy states but is dominated by the lifetime of the \(4_1^+\) state. Intensities for the \(170\,\,\)keV and \(257\,\,\)keV transitions were compared using the data set for target-to-reset foil distance \(x=5061 \upmu \)m and found to be the same to within \(1\sigma \). This confirms that there is negligible side-feeding directly into the \(2_1^+\) state, thus the equations given in Sect. 2.2 are suitable. To minimise the number of free parameters in the fit, the assumption is made that the rotational band is described by a single quadrupole moment \(Q_0\), with units eb, and the lifetime of each state is defined by,

Fig. 11
figure 11

The relative intensity of highly charged ions detected at the focal plane as a function of target-to-reset foil distance. The solid (blue) line is the result of fitting a two-state model described in Eq. 13 to the data (circles). The lifetimes of the two states are described by a single quadrupole moment, as defined in Eq. 17. Data points below \(264\, \upmu \)m (squares) were left out of the fit (see text). The dashed (red) and dot-dashed (green) lines represent the contribution to the high charge component from internal conversion of the \(2^+\rightarrow 0^+\) or \(4^+\rightarrow 2^+\) transition respectively. The dotted line (blue) is the \(1\sigma \) error on the fit

Full size image
$$\begin{aligned} \tau (J_i) = \frac{0.826}{E_{\gamma }^5 Q_0^2 \langle J_i\; 020 | J_f\; 0 \rangle ^2 (1 + \alpha )}\;\;\;(\mathrm {ps}) \end{aligned}$$
(17)

where the \(E_\gamma \) is the transition energy in MeV, \(\alpha \) is the internal conversion coefficient and \( \langle J_i\; 020 | J_f\; 0 \rangle \) is the Clebsch–Gordon coefficient for the E2 transition \(J_i \rightarrow J_f\). This assumption is justified by the experimental results in Ref. [20] which show a constant quadrupole moment within the yrast band down to the ground state for \(^{178}\)Pt.

Table 1 Contributions from different sources of systematic error to final uncertainty in \(\tau (2^+)\) and \(\tau (4^+)\) for the Bateman analysis. Each error contribution was varied by \(\pm 1\sigma \)
Full size table

The fit gives a quadrupole moment of \(Q_0 = 6.4(4)\,\)eb which corresponds to lifetime values of \(\tau (2^+) = 430(50)\,\)ps and \(\tau (4^+) = 54(6)\,\)ps. Table 1 shows the uncertainty contribution from systematic errors in internal conversion coefficients, average velocity of recoils and absolute distance values. The total systematic error contribution amounts to \(1.2\%\) for \(\tau (2^+)\) and \(1.3\%\) for \(\tau (4^+)\), whilst the statistical error is \(11\%\). The systematic error arising from having no knowledge of the \(4^+\rightarrow 2^+\) internal conversion coefficient \((0 \le \alpha (4^+\rightarrow 2^+) \le \infty )\) amounts to \(\sim 3.7\%\). The values for lifetime of the \(2_1^+\) and \(4_1^+\) states from previous measurements and from this work for both the DDCM coincidence and Bateman analysis are summarised in Table 2.

5 Discussion

We have shown through both a DDCM and Bateman analysis that the charge plunger method is able to measure the lifetime of low-lying states in \(^{178}\)Pt. It is difficult to perform a lifetime measurement on the \(2_1^+\) state in \(^{178}\)Pt using the standard RDDS technique due to both a relatively large internal conversion coefficient and unfavourable kinematics for asymmetric reactions which produce recoiling nuclei at a slow mean velocity.

Table 2 Lifetime of excited states in \(^{178}\)Pt deduced from the DDCM coincidence analysis described in Sect. 4.1, and from the Bateman fits described in Sect. 4.2. The lifetime of the \(2_1^+\) and \(4_1^+\) states measured in Refs. [19,20,21] are also given
Full size table

Whilst the value for the \(2_1^+\) lifetime obtained from the Bateman analysis is consistent to within \(1\sigma \) of the result obtained using the DDCM coincidence analysis and the value given in Ref. [19], the uncertainty is more than twice that in the DDCM. This is because a DDCM coincidence analysis has significant advantages over a Bateman analysis for retrieving lifetime information. The DDCM is independent of absolute distances between the target and reset-foil, and instead only the relative distances are needed. This means the method is independent of the offset between the foils which can cause an error when analysing the data using a Bateman fit. Additionally, when applying a Bateman fit to the data, there is a dependence on the lifetime of states feeding the level of interest (directly or indirectly). If the lifetime of these transitions are unknown then they must be included in the fit as free parameters which will introduce more uncertainty in to the final result. In this work it was possible to reduce the number of free parameters by assuming a rigid-rotor model for the nucleus, however this assumption may not always be valid. The DDCM becomes independent of these lifetimes when a \(\gamma \)-ray coincidence is required on the feeding transition occurring before the reset foil.

A lifetime is also obtained for the \(4_1^+\) state using the Bateman analysis. The true lifetime of the \(4_1^+\) state will in fact be shorter than the value given here since only a two-state system is used and the lifetime of higher energy excited states are not considered. The value is also dependent on the assumption of a rigid-rotor model for \(^{178}\)Pt which allows for the lifetime of excited states in the rotational band to be contained within a single parameter, the quadrupole moment. Since more data points were taken at longer target-to-reset foil distances, the fit of the quadrupole moment will be more sensitive to the lifetime of the \(2_1^+\) state. However, the lifetime given here agrees to within 3\(\sigma \) of the value given in Ref. [20], which is an independent lifetime measurement obtained using the DDCM coincidence method, and is exactly the same as that obtained using \(\gamma \)-ray singles, given in Ref. [21], with a similar error. This suggests that the charge plunger method is vulnerable to the same effects as \(\gamma \)-ray singles measurements.

There are drawbacks to performing the DDCM coincidence analysis with the charge plunger method. In both this work and in ref. [11], a recoil was required to be detected in coincidence with the \(\gamma \)-ray emission of the feeding transition occurring before the reset foil. Due to the inability to resolve between different Doppler-shifted peaks in the \(\gamma \)-ray spectrum, this limited the available data to distances where the feeding transition always occurred before the reset foil.

The need for \(\gamma \)-ray detection also reduces the available data. The JUROGAM 3 spectrometer has an absolute efficiency of 5.2% at 1.3 MeV [15]. Using this efficiency, the available statistics in an experiment are reduced by a factor of \(\sim 20\) when one requires a \(\gamma \)-ray-recoil condition. The data is then further split between the number of measured charge states and target-to-reset foil distances. Comparatively, the detection efficiency of recoiling ions in the DSSSD after separation in MARA is \(\sim 100\%\). Subsequent alpha decays, which either travel out of or further into the DSSSD, then have a detection efficiency of \(\sim 50\%\). This value can be increased by using box detectors or, in the case of an alpha-decay chain, searching for child alpha decays [28]. For future experiments using the charge plunger, the use of \(\gamma \)-ray-recoil coincidences will depend heavily on the specific case.

The charge plunger method has been suggested as a possible means of extracting lifetime information in transfermium nuclei, where, at present, \(\tau (2^+)\) and \(\beta _2\) (quadrupole deformation parameter) values are determined using empirical formulas [29, 30] and any direct lifetime measurements would be invaluable. In this region, production cross sections are low (\(\sigma (^{254}No) \le 3\,\mu \)b [31]) and internal conversion coefficients for low energy transitions are extremely high, for example the \(2_1^+\rightarrow 0_1^+\) \(44\,\)keV transition in \(^{254}\)No has an internal conversion coefficient of \(\alpha =1510\) [22].

Due to low \(\gamma \) ray statistics, a DDCM coincidence analysis will be unsuitable and instead it will be more efficient to require recoil detection only and retain lifetimes using a Bateman analysis. Identification would have to be done using the alpha decay of the recoiling nucleus. This would not be a problem for many nuclei in the transactinide and transfermium regions of the chart where alpha decay channels are typically very strong with branching ratios \( \simeq 100\%\). It may also be possible to reduce the number of free parameters in a Bateman fit by considering a rotational band that is described by a single quadrupole moment, and determining the lifetimes of individual states according to the rotational model, as has been shown here. The fit is then sensitive to only one free parameter, the quadrupole moment. This assumption is valid for transfermium nuclei where ground state bands match closely to the rigid rotor model [32].

6 Conclusion

The charge plunger method has been used at the accelerator laboratory at the University of Jyväskylä to measure the lifetime of the \(2_1^+\) and \(4_1^+\) states in \(^{178}\)Pt which de-excite through either internal conversion or \(\gamma \)-ray emission. The recoil separator MARA was used to select ions by their charge state and ions were implanted into a DSSSD at the focal plane. Identification of \(^{178}\)Pt recoils was done using prompt \(\gamma \)-ray-recoil coincidences with the JUROGAM 3 spectrometer and the resulting CSD spectra were analysed in a DDCM framework, with a \(\gamma \)-ray-recoil coincidence gate set on the \(4_1^+\rightarrow 2_1^+\) \(257\,\)keV feeding transition. This yielded the lifetime for the \(2_1^+\) state in \(^{178}\)Pt of \(\tau = 430(20)\,\)ps. CSD spectra were also obtained by identifying \(^{178}\)Pt ions using recoil-alpha coincidences in the DSSSD. The de-excitation of states were modelled by fitting a two-state Bateman equation to the relative intensity of high charge ions against distance. The lifetime of states in this fit were determined using a single quadrupole moment for the rotational band. This gave the lifetime of the \(2_1^+\) state as \(\tau = 430(50)\,\)ps and \(\tau = 54(6)\,\)ps for the \(4_1^+\) state. These values agree with both previous results and the measurement made using a DDCM coincidence analysis. The development of a Bateman analysis and its application here is crucial for a thorough understanding of the how the charge plunger method can be used with a recoil separator to perform lifetime measurements of excited states in nuclei at the spectroscopic boundary of the nuclear chart.