Lifetime measurement of excited states in $^{116}$Xe

Abstract

Lifetimes of excited states in $^{116}$Xe were measured using the recoil-distance Doppler-shift technique. Excited $^{116}$Xe nuclei were populated in the fusion-evaporation reaction $^{102}$Pd($^{16}$O,2n)$^{116}$Xe. Lifetimes of the 2$^+_1$ and 4$^+_1$ states were evaluated using the differential decay-curve method with $\gamma$-$\gamma$-coincidence data as well as lifetimes of the 6$^+_1$ and 7$^-_1$ states using simulations of spectra considering Doppler-shift attenuation effects.

1 Introduction

Previous measurements of transition strengths in the neutron-deficient even-even Te and Xe nuclei have unveiled an interesting behavior. Following the $N_\pi N_\nu$ scheme [1], an increase in the reduced transition strength of the ground state transition, $B(E2; 2^+_1 \rightarrow 0^+_1)$, is expected from the shell closures at $N=50$ and $N=82$ towards neutron mid-shell. This behavior is qualitatively very well reproduced by the experimental data for the Te and Xe isotopes, as can be seen in Fig. 1.

For further information on the nuclear structure, the ratio $B_{4/2}=B(E2;4^+_1\rightarrow 2^+_1)/B(E2;2^+_1\rightarrow 0^+_1)$ is a key observable (see, for example, Ref. [45]). For nuclei far away from closed shells, a collective behavior is expected, indicated by a $B_{4/2}$ ratio in between the value of a rotor ($B_{4/2} \approx 1.43$) and a vibrator ($B_{4/2}=2$). Typically, nuclei at mid-shell for both protons and neutrons are expected to be deformed and thus show a rotor-like behavior, while nuclei closer to the shell closures are expected to behave vibrator-like. Any $B_{4/2}$ ratio outside this range can not be explained with a collective model. Especially ratios $\lesssim 1$ are usually interpreted as indicators for a non-collective behavior or shape coexistence as discussed in, e.g., Ref. [46].

In Fig. 2 the $B_{4/2}$ ratios for the Xe and Te isotopes are shown. While it is not surprising that the very simple collective approach can not perfectly describe the Te and Xe isotopes lying close in Z to the magic Sn nuclei, the values of $B_{4/2} \lesssim 1$ in nuclei near neutron mid-shell and the non-smooth behavior are still very surprising. It can be seen in Fig. 2 that the $B_{4/2}$ ratios for $^{114}$Xe [2, 3] and $^{114}$Te [4] have been measured to be $<1$. A comparison with the Te isotopes is made difficult by the fact that for $^{116}$Te no $B_{4/2}$ ratio is known, which would be a crucial data point neighboring the nucleus $^{114}$Te with $B_{4/2}<1$.

In the Sn isotopic chain, a similar behavior can be seen exhibiting a drop in $B_{4/2}$ ratios between $^{116}$Sn and $^{114}$Sn with values of $B_{4/2} \lesssim 1$ for $^{108-114}$Sn. Unlike in the Te and Xe isotopes however, this is not only due to a lowering of the $B(E2; 4^+_1 \rightarrow 2^+_1)$ values, but also an increase in $B(E2; 2^+_1 \rightarrow 0^+_1)$ values (see Fig. 1 in Ref. [5]). The latter could be explained with Monte Carlo shell model calculations in Ref. [48]. In these calculations, an increase in $B(E2; 2^+_1 \rightarrow 0^+_1)$ strengths from $^{116}$Sn towards lower neutron numbers is explained by the number of proton holes in the 1$g_{9/2}$ orbit. The breaking of the magic $Z=50$ core and excitation of protons from the 1$g_{9/2}$ to the 2$d_{5/2}$ orbit are associated with a stronger quadrupole deformation caused by the proton-neutron interaction [48]. For the lowering of the $B(E2; 4^+_1 \rightarrow 2^+_1)$ values, however, no conclusive theoretical explanation exists for the Sn, Te or Xe isotopes. While the increase in $B(E2; 2^+_1 \rightarrow 0^+_1)$ strengths seems to be limited to the semi-magic Sn nuclei, the decrease in $B(E2; 4^+_1 \rightarrow 2^+_1)$ strengths seems to represent an unexpected structural change that appears also in the Te and Xe nuclei. $^{116}$Xe is in this regard a key nucleus as the current data suggest a sharp drop of the $B_{4/2}$ ratios between $^{116}$Xe and $^{114}$Xe.

The only previous evaluation of transition strengths in $^{116}$Xe was performed in a lifetime measurement employing the recoil-distance Doppler-shift (RDDS) technique [2]. The lifetimes were analyzed from $\gamma$-ray singles spectra for which the relative feeding intensities and lifetimes of all feeding states—direct as well as indirect feeding—have to be taken into account. Especially in the case of fusion-evaporation reactions like the one used in Ref. [2], the feeding history is usually complex and the higher-lying states are often populated to a significant fraction via unobserved feeding. For this unobserved feeding, an effective lifetime has to be assumed, which is derived from the same fit as the lifetimes of interest, resulting in a larger number of degrees of freedom. Thus an analysis in singles spectra is prone to errors in the accounting of feeding.

Fig. 1

Evolution of $B(E2;2^+_1\rightarrow 0^+_1)$ values for the even Te, Xe isotopes between the shell closures at N = 50 and N = 82. Different values for the same neutron number have been slightly shifted horizontally to sustain readability. Experimental data taken from Refs. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]

Fig. 2

Evolution of B$_{4/2}=\text {B(E2};4^+_1\rightarrow 2^+_1) / \text {B(E2};2^+_1\rightarrow 0^+_1)$ values for the even Te, Xe isotopes between the shell closures at N = 50 and N = 82. Different values for the same neutron number have been slightly shifted horizontally to sustain readability. The values for the collective models of the rotor and vibrator are marked. Experimental data taken from Refs. [2,3,4,5, 8,9,10, 19, 22,23,28, 30, 33,34,35, 38, 39, 41, 42, 47]

In this work, lifetimes in $^{116}$Xe were also evaluated from an RDDS experiment. For the lifetime analysis of the $2^+_1$ and 4$^+_1$ states, the differential decay-curve method (DDCM) with data from $\gamma$-$\gamma$-coincidence matrices was used for the first time in this nucleus. By setting $\gamma$ gates on the shifted component of a directly feeding transition, the necessity for any assumptions on feeding conditions can be eliminated as described in Ref. [49]. Furthermore, when applying the DDCM, only relative target-to-stopper distances are needed, which can be measured far more precisely than absolute distances. The level lifetimes of the 6$^+_1$ and 7$^-_1$ states were also evaluated using simulations of spectra considering Doppler-shift attenuation effects, since the lifetime results from a DDCM analysis were of the order of the stopping time of the recoiling nuclei.

2 Experimental setup

The RDDS experiment to measure lifetimes in $^{116}$Xe was conducted at the FN-tandem accelerator at the University of Cologne, Germany, using the Cologne coincidence plunger device [49]. Excited states in $^{116}$Xe were populated in the fusion-evaporation reaction $^{102}$Pd($^{16}$O,2n)$^{116}$Xe at a beam energy of 62 MeV. The $^{102}$Pd target foil had a thickness of 1.0 mg/cm$^2$ with an enrichment of 69%. A Ta foil with a thickness of 3.1 mg/cm$^2$ was used to stop the recoiling nuclei. For detection of $\gamma$ rays, 11 high-purity germanium (HPGe) detectors were used arranged in two rings at angles of 45$^{\circ }$ (ring 1, 6 detectors) and 142.3$^{\circ }$ (ring 2, 5 detectors) with respect to the beam axis. The measurement was performed at ten different target-to-stopper distances ranging from 1 µm to 150 µm with respect to the electrical contact point between the target and stopper foils. Fluctuations in the distance were compensated by an automatic feedback control system using the capacitance between the two foils as a measure for the distance.

3 Data analysis and results

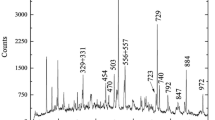
For the analysis, the data from the HPGe detectors were sorted in $\gamma$-$\gamma$-coincidence matrices using the sort code SOCOv2 [50]. The matrices were sorted ring-wise giving four possible ring-ring combinations N_M where the gate is set on events in ring M and the resulting spectrum shows coincident events in ring N. A projection of the $\gamma$-$\gamma$ matrix 1_1 for a target-to-stopper distance of 1 µm can be seen in Fig. 3. Since other reaction channels are also populated with large cross sections, it is very difficult and for some transitions even impossible to avoid contaminations in the $\gamma$ gates. These contaminations however, are only a problem if they have a coincident transition with a similar energy as the transition of interest. Thus it is very important to carefully check for any contaminations and their coincident transitions that may appear in a gated spectrum. To give an impression of the available $\gamma$-ray statistics per distance in the gated spectra, a spectrum resulting from a gate on both components of the $2^+_1 \rightarrow 0^+_1$ transition in $^{116}$Xe for the 1 µm distance can be seen in Fig. 4.

Fig. 3

Projection of the $\gamma$-$\gamma$ matrix 1_1 for 1 µm distance. For each of the strong channels of the fusion-evaporation reaction, the $\gamma$ peak with the highest intensity is labeled. Also the $e^+e^-$-annihilation line is labeled. The non-labeled peaks correspond to less intense $\gamma$ transitions in the reaction products. The background mostly consists of Compton background

Fig. 4

$\gamma$-ray spectrum resulting from a gate on both components of the $2^+_1 \rightarrow 0^+_1$ transition in $^{116}$Xe for the 1 µm distance. The peaks from transitions in $^{116}$Xe that are visible in the spectrum are labeled. The spectrum results from a gate in detector ring 1 (forward angle) and also shows events from detector ring 1, so the shifted component of each peak has a higher energy than the unshifted component

For the lifetime analysis, the differential decay-curve method (DDCM) was used in $\gamma$-$\gamma$-coincidence mode as described in Ref. [49]. It has the advantages that only relative target-to-stopper-distances are needed, which can be measured far more precisely than absolute distances, and that no assumptions on feeding conditions are needed. To determine the lifetime of a state, a gate was set on the Doppler-shifted component of a feeding transition. In the resulting spectrum, the Doppler-shifted and unshifted components of a depopulating $\gamma$-ray transition were fitted by Gaussian functions. For very small and very large distances, the intensity of one of the two peaks is very small. To ensure a reliable fit of the peak intensities also for these distances, the degrees of freedom in the fit were reduced by fixing the peak width and position. The lifetime for the measurement at distance x was then deduced from the intensities of the shifted/unshifted component $I_\text {sh/un}$ and the mean recoil velocity v with the formula

$$\begin{aligned} \tau (x) = \frac{I_\text {un}}{v\cdot \frac{d}{dx}I_\text {sh}} \end{aligned}$$

(1)

for a gate on a direct feeder. In case of a gate on an indirect feeder, i.e. a higher-lying transition that is not directly populating the level of interest, the intensity of the unshifted component has to be corrected for the direct feeder.

The recoil velocity v was determined from the energy shift between the shifted and unshifted peaks of different $\gamma$-ray transitions in $^{116}$Xe. From this a mean recoil velocity of $v=0.99(3)\,\%\, c$ was derived. The relative distances as well as the offset distance for absolute foil separation were determined with the capacitance method as first introduced by Alexander and Bell [51] and described in more detail in Ref. [52]. To correct for differences in beam intensity and run time between the different distance runs, a normalization factor was determined for every distance.

The gates were set separately for the two detector rings, since the gate has to be set on the shifted component and the energy shift depends on the detection angle. For every distance, this results in one spectrum for each of the four ring-ring combinations N_M. To increase the statistics in the spectra, the two gated spectra of the same ring, i.e. spectra with same N, were summed into one spectrum. Thus, for each distance, two statistically independent spectra were used for the lifetime analysis. In Fig. 5 the evolution of the shifted and unshifted intensities of the $2^+_1 \rightarrow 0^+_1$ transition can be seen for different distances.

Fig. 5

Fitted peaks of the shifted and unshifted component of the $2^+_1 \rightarrow 0^+_1$ transition. The spectra are from detectors at 142.3$^{\circ }$ for distances 10, 60 and 150 µm gated on the shifted component of the $4^+_1 \rightarrow 2^+_1$ transition. In blue the gaussian functions describing each respective peak are shown. The position and width of each function are held constant for all distances. In red the total fit functions are shown consisting of the sum of both peaks and a linear background function

For the DDCM analysis, the program Napatau [53] was used. In this program a lifetime curve is fitted simultaneously to the normalized intensities of the shifted and unshifted component, where the shifted component is described by continuously connected second-order polynomials and the unshifted component is described by the derivative of these polynomials multiplied by a proportionality factor following Eq. (1). In this step, the proportionality factor is however only treated as a fit parameter of the curve and is not directly used to determine the lifetime. The lifetime is extracted in a second step for each distance separately using again Eq. (1) where for $\frac{d}{dx}I_\text {sh}(x)$ the derivative of the polynomial fit function is used. The error calculation takes the covariance between the function $I_\text {sh}(x)$ and the measured value $I_\text {un}(x)$ into account. From all measurement points inside the sensitive region, where the derivative $\frac{d}{dx}I_\text {sh}(x)$ is larger than half of its maximum value, the weighted average is taken as the resulting lifetime. Exemplary lifetime fits from Napatau for the $2_1^+$ and $4_1^+$ states can be seen in Figs. 6 and  7, respectively.

Fig. 6

Exemplary lifetime curve fit from Napatau for the $2^+_1$ state. From bottom to top, the intensities of the unshifted components, intensities of the shifted components and resulting lifetimes are shown. The lifetime value in the top-right corner is the weighted average of the values from the different distances

Fig. 7

Same as Fig. 6 but for the $4^+_1$ state

The lifetimes of the 2$^+_1$ and 4$^+_1$ states were determined using this method. For each of the states, results could be obtained using spectra from a gate on a direct feeder as well as an indirect feeder. Since the results from an indirect gate are dependent on data used also in the direct gate, the indirect gates were only used for a consistency check. The weighted average of the results from the direct gate from different detector rings is taken as the adopted lifetime value for each state as listed in Table 1. The results from the respective indirect gates are consistent within the uncertainty range.

For the 6$^+_1$ and 7$^-_1$ states, lifetimes were at first also obtained in the same manner. However, the lifetimes resulting from the DDCM analysis for these states are of the order of the expected stopping time inside the stopper foil. Thus Doppler-shift attenuation effects have to be taken into account. When decays occur inside the stopper but before the nucleus is fully stopped, the $\gamma$ energy is shifted but not as much as the fully shifted peak. When the stopping time is not negligible compared to the level lifetime, this leads to a deviation from the Gaussian shape of the $\gamma$ peaks resulting in a wrong evaluation of the lifetime.

To evaluate the lifetimes of the short-lived 6$^+_1$ and 7$^-_1$ states, simulated spectra were used from the Geant4-based simulation code PTBG4 [54], which accounts for the stopping power of the stopper foil material. Input parameters of the code are positions, materials and thicknesses of the target and stopper foils, efficiency and positions of the detectors, material and energy of the beam and the simulated cascades of excited states with assumed lifetimes of the respective states. Unlike in the DDCM analysis, absolute target-to-stopper distances are needed. Reaction events with these parameters were simulated with the code and then sorted into $\gamma$-$\gamma$-coincidence matrices similar to the experimental data. The simulation was repeated for various lifetimes of the level of interest. The level lifetime was then deduced from the minimization of

$$\begin{aligned} \chi ^2 = \sum _{i=j}^{k} \left( \frac{n_{i,\text {exp}} - n_{i,\text {sim}}}{\Delta n_{i,\text {exp}}} \right) ^2 \end{aligned}$$

(2)

where $n_{i,\text {exp/sim}}$ is the number of counts in the i-th bin of the experimental/simulated spectrum and the bins j to k are taken into account for the $\chi ^2$ minimization.

Table 1 Lifetime results of the DDCM analysis for the 2$^+_1$ and 4$^+_1$ states

The relative intensities of the shifted and unshifted components in the resulting simulated spectra depend on the lifetime of the state of interest as well as the feeding conditions. In order to fix the feeding cascade and make a comparison to the experimental spectra possible, a gate was set on the shifted component of a feeding transition in the simulated matrices and the exact same gate was set in the matrices from the experimental data. To simplify the feeding conditions in the simulation, an effective lifetime was simulated as the lifetime of the feeder on which the gate was set. The effective lifetime of the feeding state was obtained from the experimental data prior to running the simulation by gating from below and extracting $\tau$ from the decay equation

$$\begin{aligned} R(x) = \frac{I_\text {un}(x)}{I_\text {un}(x)+I_\text {sh}(x)} = \exp \left( \frac{-x}{v\cdot \tau } \right) . \end{aligned}$$

(3)

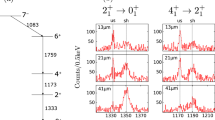
This simulation was performed for the 6$^+_1$ and 7$^-_1$ lifetime separately with the 7$^-_1$ and 9$^-_1$ as simulated feeder, respectively. The uncertainty of the results was estimated by the variation between the results from different spectra and by varying the most crucial input parameters of the simulation inside their uncertainty range. In Fig. 8 the experimental spectrum from detector ring 1 for the 15 µm distance showing the $7_1^- \rightarrow 6^+_1$ transition and the respective spectrum simulated for lifetimes of $\tau (7_1^-)=0.7,\,2.3$ and 5.0 ps are shown. The respective $\chi ^2$ distribution is also shown in the inset. The results of the simulations are listed in Table 2 together with the results from the DDCM analysis.

Table 2 Lifetime results for the 6$^+_1$ and 7$^-_1$ states from the DDCM analysis as well as from the simulations. Note that the results from the DDCM analysis of the 6$^+_1$ and 7$^-_1$ states were not taken for the final results. See text for detail

The adopted lifetime values for all states are listed again in Table 3 together with the respective reduced transition strengths.

Fig. 8

Experimental spectrum of the $7^-_1 \rightarrow 6^+_1$ transition for detectors at 45$^{\circ }$ in comparison to the respective spectra simulated for lifetimes of $\tau (7^-_1)=0.7,\,2.3,\,5.0$ ps. The spectra correspond to the 15 µm distance with a gate on the shifted component of the $9^-_1 \rightarrow 7^-_1$ transition. The experimental spectrum is corrected for background with a linear function. The region considered in the $\chi ^2$ minimization is marked with blue lines. The spectra are normalized, so that the number of counts in the considered region is equal. The inset shows the $\chi ^2$ distribution for different simulated lifetimes of the $7^-_1$ state

Table 3 Final lifetime results and extracted reduced transition strengths

4 Conclusion

In summary, reliable lifetimes of the 2$^+_1$, 4$^+_1$, 6$^+_1$ and 7$^-_1$ states in $^{116}$Xe were measured and the resulting reduced transition strengths were determined. The lifetime values of the 6$^+_1$ and 7$^-_1$ states previously measured in Ref. [2] could be confirmed within the margin of uncertainty. The relatively large $B(E1;7^-_1 \rightarrow 6^+_1)$ value suggests a discussion in the framework of octupole correlations, considering the exceptionally large E3 transition strengths of $B(E3) \approx 70$ W.u. that have been measured in neighboring $^{114}$Xe [3]. However, no E3 transitions are known in $^{116}$Xe, which would be a crucial indicator for the investigation of octupole correlations. Furthermore, calculations from Nomura et al. [55] suggest octupole deformations only in the very neutron-deficient Xe isotopes with $A \approx 108-112$, while for $^{116}$Xe a pronounced quadrupole collectivity is suggested.

The lifetime results of the 2$^+_1$ and 4$^+_1$ states are only overlapping with the values previously measured in Ref. [2] within the 2$\upsigma$  range. One possible explanation for this could be errors in the accounting for the complex feeding conditions in the calculations of lifetimes in Ref. [2]. In this work the lifetimes of the 2$^+_1$ and 4$^+_1$ states were determined using the DDCM in $\gamma$-$\gamma$-coincidence mode avoiding the need for any feeding assumptions for the first time. However, the $B_{4/2} = 1.70(7)$ ratio extracted from this work confirms the value from Ref. [2] and thus the sharp drop in transition strength of the $4^+_1 \rightarrow 2^+_1$ transition between $^{116}$Xe and $^{114}$Xe. While the cause for this lowering of $B_{4/2}$ ratios remains unexplained, this strengthens the picture of a very abrupt change in $B(E2;4^+_1 \rightarrow 2^+_1)$ transition strengths that is seen in the Sn, Te and Xe isotopic chains and suggests a connection between these.

Further investigations on transition strengths in this region are needed to enhance the picture, especially in more neutron-deficient Xe isotopes and $^{116}$Te. For the latter, the determination of a $B_{4/2}$ ratio is difficult due to the fact that the $4^+_1 \rightarrow 2^+_1$ and $2^+_1 \rightarrow 0^+_1$ transitions form a doublet. The lighter ($A\le 114$) Xe isotopes on the other hand are difficult to reach experimentally since they are very far away from the valley of stability and can thus only be produced with very low cross sections or from radioactive ion beams.

To explain the general structure in this region and the evolution of transition strengths in particular, an extension of the aforementioned Monte Carlo shell model calculations from Togashi et al. [48] to the neighboring Te and Xe isotopic chains, especially including transition strengths for the $2^+$ and $4^+$ yrast states, would be highly desirable. These calculations were done in Ref. [48] for the $2^+_1$ states in Sn isotopes solely. This extension could provide a fundamental understanding of the structural evolution from “regular” collectivity of the lowest states towards $B_{4/2}<1$ that cannot be understood so far.