Appendix 1: The Faddeev equation of the particle-dimer scattering process in \(nn\alpha \) system
Since \({}^{6}\text {He}\) nucleus has spin-parity \(J^{P}=0^{+}\) in the ground state, we apply the Faddeev equation (T-matrix) of the particle-dimer scattering process in \(nn\alpha \) system with \(J^{P}=0^{+}\). This integral equation is shown in Fig. 8. According to Lagrangian in Eq. (4) we use two different dimers, \(d_{0}\) and \(d_{1}\), so there are four possible transitions between particle-dimer states
$$\begin{aligned} n+d_{1}\longrightarrow & {} n+d_{1},\;\;\;\;\;\;\;\; n+d_{1}\longrightarrow \phi +d_{0},\nonumber \\ \phi +d_{0}\longrightarrow & {} n+d_{1},\;\;\;\;\;\;\;\phi +d_{0}\longrightarrow \phi +d_{0}. \end{aligned}$$
(A.1)
In the c.m. frame, on-shell T-matrix depends on the total energy E and the incoming (outgoing) three-momentums of the \(\phi +d_{0}\) and \(n+d_{1}\) systems which indicated by \(k_{1}\;(p_{1})\) and \(k_{2}\;(p_{2})\) respectively.
In the cluster-configuration space, the projection operator of \({}^{6}\text {He}\) channel is obtained by
$$\begin{aligned} ({\mathcal {P}}_{0^{+}}){}^{\beta _{1},\beta _{2}}_{{\bar{\alpha }},\alpha }=\left( \begin{array}{c@{\quad }c} \mathbf {1}{}^{\beta _{1}}_{\alpha } &{} 0 \\ 0 &{} \sqrt{\frac{3}{2}}\Big (\sigma _{2}{\hat{e}}\cdot \mathbf {S}\Big ){}^{\beta _{2}}_{{\bar{\alpha }}}\\ \end{array} \right) , \end{aligned}$$
(A.2)
where \(\mathbf {1}\) is the \(2\times 2\) unit matrix and \({\hat{e}}\) denotes the unit vector of c.m. momentum of the \(n+d_{1}\) system [28]. Applying the projection operator according to Eq. (A.2), the resulting \(2\times 2\) T-matrix integral equation can be given by
$$\begin{aligned}&T(E,k_{1},p_{1},k_{2},p_{2})=\Big [R(E,k_{1},p_{1},k_{2},p_{2})+ H(k_{2},p_{2},\varLambda )\Big ]\nonumber \\&\qquad -\frac{1}{2\pi ^{2}}\int _{0}^{\varLambda }q^{2}dq\Big [\Big (R(E,k_{1},q,k_{2},q)+ H(k_{2},q,\varLambda )\Big )\nonumber \\&\quad \cdot D(E,q)\cdot T(E,q,p_{1},q,p_{2})\Big ], \end{aligned}$$
(A.3)
where \(\varLambda \) is an ultraviolet cutoff. The kernel \(R(E,k_{1},q_{1},k_{2},q_{2})\) is a \(2\times 2\) matrix introduced by [28]
$$\begin{aligned} R(E,k_{1},q_{1},k_{2},q_{2})\equiv \left( \begin{array}{c@{\quad }c} 0 &{} R_{10}(E,k_{2},q_{1}) \\ R_{01}(E,k_{1},q_{2}) &{} R_{11}(E,k_{2},q_{2}) \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(A.4)
that
$$\begin{aligned}&R_{11}(E,k,q)=-\frac{g_{1}^{2}m_{\alpha }}{6}\Big [2(1-r)\frac{k^{2} +q^{2}}{k q}Q_{1}(\varepsilon _{11}(E,k,q))\nonumber \\ \nonumber \\&\quad +\frac{8}{3}Q_{2}(\varepsilon _{11}(E,k,q))+\left( \frac{4}{3}+(1-r)^{2})Q_{0}(\varepsilon _{11}(E,k,q)\right) \Big ], \end{aligned}$$
(A.5)
$$\begin{aligned} R_{10}(E,k,q)= & {} -\frac{ g_{0} g_{1}m_{n}}{4\sqrt{3}}\Big [\frac{2}{k}Q_{1}(\varepsilon _{10}(E,k,q)) \nonumber \\&\qquad \quad +\frac{1+r}{q}Q_{0}(\varepsilon _{10}(E,k,q))\Big ], \end{aligned}$$
(A.6)
$$\begin{aligned} R_{01}(E,k,q)= & {} -\frac{g_{0} g_{1}m_{n}}{4\sqrt{3}}\Big [\frac{2}{q}Q_{1}(\varepsilon _{01}(E,k,q)) \nonumber \\&\qquad \quad +\frac{1+r}{k}Q_{0}(\varepsilon _{01}(E,k,q))\Big ]. \end{aligned}$$
(A.7)
The relation between the \(L-th\) Legendre function of the first kind \(P_{L}(z)\) and the second kind \(Q_{L}(z)\) is written by \(Q_{L}(z)=\frac{1}{2}\int _{-1}^{1}dt\frac{P_{L}(t)}{z-t}\), therefore
$$\begin{aligned} Q_{0}(z)= & {} \frac{1}{2}\mathrm {ln}\Big (\frac{z+1}{z-1}\Big ),\nonumber \\ Q_{1}(z)= & {} \frac{1}{2}z \mathrm {ln}\Big (\frac{z+1}{z-1}\Big )-1,\nonumber \\ Q_{0}(z)= & {} -\frac{3}{2}z+\frac{1}{4}(3z^{2}-1)\mathrm {ln}\Big (\frac{z+1}{z-1}\Big ). \end{aligned}$$
(A.8)
The functions of \(\varepsilon _{11}\), \(\varepsilon _{10}\), and \(\varepsilon _{01}\) in the above equation are defined by [28]
$$\begin{aligned} \varepsilon _{11}(E,k,q)= & {} \frac{m_{\alpha }\;E - \frac{m_{\alpha }}{2\mu }(k^{2}+q^{2})}{k q},\nonumber \\ \varepsilon _{10}(E,k,q)= & {} \frac{m_{n}\;E - k^{2} - \frac{m_{n}}{2\mu }q^{2}}{k q},\nonumber \\ \varepsilon _{01}(E,k,q)= & {} \frac{m_{n}\;E - \frac{m_{n}}{2\mu }k^{2} - q^{2}}{k q}. \end{aligned}$$
(A.9)
In Eq. (A.3), the three-body force H shown by a bare trimer with external particle-dimer lines in Fig. 8 is given by the following relation
$$\begin{aligned} H(k,q,\varLambda )\equiv \left( \begin{array}{c@{\quad }c} 0 &{} 0 \\ 0 &{} -\frac{m_{n}\;g_{1}^{2} k q H_{0}(\varLambda )}{\varLambda ^{2}}\\ \end{array} \right) , \end{aligned}$$
(A.10)
which connects only the incoming and outgoing \(n+d_{1}\) channels [25, 28, 30]. The bound state equation is written as
$$\begin{aligned} T_{{}^{6}He}(p)= & {} \!-\!\frac{1}{2\pi ^{2}}\int _{0}^{\varLambda }q^{2}dq \Big [R(-B_{2n},k,q,k,q)\!+\! H(k,q,\varLambda )\Big ] \nonumber \\&\qquad \cdot D(-B_{2n},q)\cdot T_{{}^{6}He}(q), \end{aligned}$$
(A.11)
The transition \(xX\rightarrow yY\) \((x,y = \phi , n\) and \(X, Y = d_{0}, d_{1})\) contributes to construction of \({}^{6}\text {He}\) such that
$$\begin{aligned} \!\!\!\!\!T_{{}^{6}He}(q)\!\equiv \!\left( \! \begin{array}{c@{\quad }c} T_{{}^{6}He,\;\phi d_{0}\rightarrow \phi d_{0}}(q) &{} T_{{}^{6}He,\;n d_{1}\rightarrow \phi d_{0}}(q) \\ T_{{}^{6}He,\;\phi d_{0}\rightarrow n d_{1}}(q) &{} T_{{}^{6}He,\;n d_{1}\rightarrow n d_{1}}(q)\\ \end{array} \!\right) . \end{aligned}$$
(A.12)
For the incoming \(\phi +d_{0}\) channel, the proper normalization condition for the solution of Eq. (A.11) is [45]
$$\begin{aligned} \Big (D\mathbf {{\mathcal {B}}}\Big )^{T}\otimes \left. \frac{d}{dE}\Big (I-K\Big )\right| _{E=-B_{2n}}\otimes \Big (D\mathbf {{\mathcal {B}}}\Big )= \mathbf {1}, \end{aligned}$$
(A.13)
where D matrix is given by Eq. (19), \(\mathbf {{\mathcal {B}}}=T_{{}^{6}He}{1\atopwithdelims ()0}={{\mathcal {B}}_{0}\atopwithdelims (){\mathcal {B}}_{1}}\) is the bound state vector, and K is given by \(K(E,q,q')=R(E,q,q',q,q')+ H(q,q',\varLambda )\). We must define the inverse propagators matrix \(I=\mathrm {diag}(I_{0},I_{1})\) with
$$\begin{aligned} I_{0,1}= \frac{2\pi ^{2}}{q^{2}}\;\delta (q-q')\; {\overline{D}}_{0,1}(E,q)^{-1}. \end{aligned}$$
(A.14)
We have defined here the short notation [45]
$$\begin{aligned} A\otimes B \equiv \frac{1}{2 \pi ^{2}} \int _{0}^{\varLambda } q^{2} dq\; A(\cdots , q) B(q,\cdots ). \end{aligned}$$
(A.15)
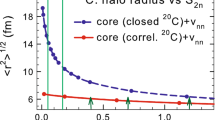
Therefore for each cutoff \(\varLambda \), we have fixed the \(H_{0}(\varLambda )=\frac{h^{2}}{\varOmega }\) parameter such that Eq. (A.11) is satisfied at experimental value of \(E=-B_{2n}=-0.97 \;\text {MeV}\).
Appendix 2: the contribution of diagrams \((\text {a})\), \((\text {b})\), \((\text {c})\) and \((\text {d})\) to charge form factor
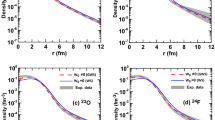
In this appendix, we introduce explicitly the relations of four different diagrams (a–d) that contribute to the charge form factor as shown in Fig. 5.
1.1 B.1 Contribution \({\mathcal {F}}_{E}^{(a)}\)
After performing the energy integral analytically, using Eqs. (4), (22)–(24) and Feynman rules, the contribution of diagram (a) in Fig. 5 is given by
$$\begin{aligned} {\mathcal {F}}^{(a)}(Q^{2})= & {} \int _{0}^{\varLambda } \frac{p^{2}}{2\pi ^{2}}\;dp\;\int _{0}^{\varLambda } \frac{k^{2}}{2\pi ^{2}}\;dk\;\mathbf {{\mathcal {G}}}^{irr}(p)^{T} \nonumber \\&\times D(p)\;\varUpsilon ^{(a)}(Q,p,k) D(k)\;\mathbf {{\mathcal {G}}}^{irr}(k), \end{aligned}$$
(B.1)
where the components of \(2\times 2\) matrix \(\varUpsilon ^{(a)}(Q,p,k)\) are given by
$$\begin{aligned}&\varUpsilon ^{(a)}_{ij}(Q,p,k)=\frac{g_{1}^{2}}{4}\;\frac{(2\mu )^{2}}{8\pi }\int _{-1}^{1}dx\int _{-1}^{1}dy\int _{0}^{2\pi }d\phi \nonumber \\&\times \bigg \{p^{2}+k^{2}+r'^{2}-2(ky+\frac{m_{n}}{M_{1}}px)r' \nonumber \\&\quad +\frac{2m_{n}}{M_{1}}k p(\sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy)+2\mu B_{2n}\bigg \}^{-1}\nonumber \\&\times \bigg \{p^{2}+k^{2}+r'^{2}+2(px+\frac{m_{n}}{M_{1}}ky)r' \nonumber \\&\quad +\frac{2m_{n}}{M_{1}}k p(\sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy)+2\mu B_{2n}\bigg \}^{-1}\nonumber \\&\times U(p, k, Q, x, y, \phi )\;\delta _{i1}\;\delta _{j1}, \end{aligned}$$
(B.2)
where \(\mathbf {r'}=\frac{m_{n}}{M_{tot}}\mathbf {Q}\), \(\mu =\frac{m_{n}m_{\alpha }}{m_{n}+m_{\alpha }}\), the polar angles \(x=\cos (\angle (\mathbf {Q},\mathbf {p}))\), \(y=\cos (\angle (\mathbf {Q},\mathbf {k}))\), \(\cos (\angle (\mathbf {p},\mathbf {k}))=\sqrt{(1-x^{2})}\sqrt{(1-y^{2})}\cos \phi +xy\) and
$$\begin{aligned}&U(p, k, Q, x, y, \phi )=-4 r'^{2}x y+\frac{4}{3}p y r'\Big (1+\frac{4 m_{n}}{M_{1}}\Big ) \nonumber \\&-\frac{4}{3}k x r'\Big (1+\frac{4 m_{n}}{M_{1}}\Big )\nonumber \\&\quad -\frac{20}{3}p x r'\left( \sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy\right) \nonumber \\&\quad +\frac{20}{3}k y r'\left( \sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy\right) \nonumber \\&\quad +\frac{16}{3}\frac{m_{n}}{M_{1}}\;p^{2}\left( \sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy\right) \nonumber \\&\quad +\frac{16}{3}\frac{m_{n}}{M_{1}}\;k^{2}\left( \sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy\right) \nonumber \\&\quad -\frac{4}{3}\;r'^{2}\left( \sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy\right) \nonumber \\&\quad +\frac{20}{3}\;k p\left( \sqrt{1-x^{2}}\sqrt{1-y^{2}}\cos \phi +xy\right) ^{2} \nonumber \\&\quad -\frac{4}{3} p k\Big (1-\frac{4 m_{n}^{2}}{M_{1}^{2}}\Big ). \end{aligned}$$
(B.3)
1.2 B.2 Contribution \({\mathcal {F}}_{E}^{(b)}\)
For the contribution of the diagram (b) in Fig. 5, calculating the energy integral analytically, applying Eqs. (4), (22)–(24) and Feynman rules lead to the following relations
$$\begin{aligned} {\mathcal {F}}^{(b)}(Q^{2})= & {} \;\int _{0}^{\varLambda } \Big (-\frac{p^{2}}{2\pi ^{2}}\Big )\;dp\;\int _{0}^{\varLambda } \Big (-\frac{k^{2}}{2\pi ^{2}}\Big )\;dk \nonumber \\\times & {} \mathbf {{\mathcal {G}}}^{irr}(p)^{T}\;D(p) \;\varUpsilon ^{(b)}(Q,p,k)\;D(k)\;\mathbf {{\mathcal {G}}}^{irr}(k), \nonumber \\ \end{aligned}$$
(B.4)
where
$$\begin{aligned} \varUpsilon ^{(b)}_{ij}(Q,p,k)=\!\frac{m_{\alpha }}{2}\!\int _{0}^{\varLambda } \!\Big (\frac{q^{2}}{2\pi ^{2}}\!\Big )\!\frac{d q}{q}\!\int _{-1}^{1}\!\frac{d x'}{x'}\chi ^{(b)}_{ij}(r', q, x',p,k), \nonumber \\ \end{aligned}$$
(B.5)
so that
$$\begin{aligned}&\chi ^{(b)}_{ij}(r', q, x', p, k)=\;\frac{1}{Q}\;\Big \{R_{i0}\Big (-B_{2n}, p, d(q, r', x')\Big )\nonumber \\&\quad \times {\overline{D}}_{0}\Big (-B_{2n}\;-\;\frac{m_{n}}{4m_{\alpha }M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 m_{\alpha }}, q\Big )\nonumber \\&\quad \times R_{0j}\Big (-B_{2n}\;-\;\frac{q Q x'}{m_{\alpha }}, d(q, r', -x'), k\Big )\nonumber \\&-R_{i0}\Big (-B_{2n}\;+\;\frac{q Q x'}{m_{\alpha }}, p, d(q, r', x')\Big )\nonumber \\&\quad \times {\overline{D}}_{0}\Big (-B_{2n}\;-\;\frac{m_{n}}{4m_{\alpha }M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 m_{\alpha }}, q\Big )\nonumber \\&\quad \times R_{0j}\Big (-B_{2n}, d(q, r',-x'), k\Big )\Big \}\;\delta _{i1}\;\delta _{j1}, \end{aligned}$$
(B.6)
with \( d(q, r', \pm x')=\sqrt{q^{2}+r'^{2}\pm 2qr'x'}\).
1.3 B.3 Contribution \({\mathcal {F}}_{E}^{(c)}\)
The leading contribution to charge form factor in the \({}^{6}\text {He}\) halo nucleus comes from diagram (c) in Fig. 5 by coupling the photon to \(\alpha \) core inside a \(n\alpha \) bubble.
For calculating the contribution of the form factor presented in Fig. 9, we start with the four-momentum integration as
$$\begin{aligned}&{\mathcal {F}}^{(c)}(Q^{2})=(-ie{\mathcal {Z}})^{-1}\;\int _{k<\varLambda }\frac{d^{4}k}{(2\pi )^{4}} \;\int _{p<\varLambda } \frac{d^{4}p}{(2\pi )^{4}}\;(2\pi )^{4} \nonumber \\&\times \delta (k_{0}-p_{0})\delta ^{(3)}(\mathbf {k}-\mathbf {p}-\frac{m_{n}}{M_{tot}}\mathbf {Q}) \nonumber \\&\times (-ie{\mathcal {Z}})\; \Big \{i\;{\mathcal {G}}_{1}^{irr}(P_{0},\mathbf {P},p_{0},\mathbf {P})^{T} \nonumber \\&\qquad \qquad \times \frac{i}{\frac{m_{n}}{M_{tot}}P_{0}-p_{0}-\frac{(\frac{m_{n}}{M_{tot}}\mathbf {P}-\mathbf {p})^{2}}{2m_{n}}+i\varepsilon } \nonumber \\&\qquad \qquad \times \Big [-i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{p}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{k}}\Big )\Big ] \nonumber \\&\qquad \qquad \times i D_{1}\Big (\frac{M_{1}}{M_{tot}}K_{0}+k_{0},\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {k}\Big )\nonumber \\&\qquad \qquad \times i D_{1}\Big (\frac{M_{1}}{M_{tot}}P_{0}+p_{0},\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {p}\Big ) \nonumber \\&\qquad \qquad \times i\;{\mathcal {G}}_{1}^{irr}(K_{0},\mathbf {K},k_{0},\mathbf {k})\Big \}, \end{aligned}$$
(B.7)
where \(\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{p}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{k}}\Big )\) is the \(n\alpha \) bubble contribution in Fig. 9. One of the two four-momentum integrations in Eq. (B.7) is absorbed by a delta-function, so we obtain
$$\begin{aligned} {\mathcal {F}}^{(c)}(Q^{2})= & {} \int _{p<\varLambda }\frac{d^{4}p}{(2\pi )^{4}}\; \Big \{{\mathcal {G}}_{1}^{irr}(P_{0},\mathbf {P},p_{0},\mathbf {P})^{T} \nonumber \\\times & {} \frac{i}{\frac{m_{n}}{M_{tot}}P_{0}-p_{0}-\frac{(\frac{m_{n}}{M_{tot}}\mathbf {P}-\mathbf {p})^{2}}{2m_{n}}+i\varepsilon } \nonumber \\\times & {} \Big [-i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{p}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{k}}\Big )\Big ] \nonumber \\\times & {} D_{1}\Big (\frac{M_{1}}{M_{tot}}K_{0}+p_{0},\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {p}+\frac{m_{n}}{M_{tot}}\mathbf {Q}\Big ) \nonumber \\\times & {} D_{1}\Big (\frac{M_{1}}{M_{tot}}P_{0}+p_{0},\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {p}\Big ) \nonumber \\\times & {} {\mathcal {G}}_{1}^{irr}(K_{0},\mathbf {K},p_{0},\mathbf {p}+\frac{m_{n}}{M_{tot}}\mathbf {Q})\Big \}. \end{aligned}$$
(B.8)
Using the rescaled four-momentum \({\bar{s}}=\frac{m_{n}}{2M_{tot}}{\bar{Q}}\) and the shifted loop momentum according to \({\bar{p}}\mapsto {\bar{q}}-{\bar{s}}\), we have
$$\begin{aligned} {\mathcal {F}}^{(c)}(Q^{2})= & {} \int _{q<\varLambda }\frac{d^{3}\mathbf {q}}{(2\pi )^{3}}\int _{-\infty }^{+\infty }\frac{d q_{0}}{2\pi }\; \Big \{{\mathcal {G}}_{1}^{irr}(P_{0},\mathbf {P},{\bar{q}}-{\bar{s}})^{T} \nonumber \\\times & {} \frac{i}{\frac{m_{n}}{M_{tot}}P_{0}-q_{0}-\frac{(\frac{m_{n}}{M_{tot}}\mathbf {P}-\mathbf {q}+\mathbf {s})^{2}}{2m_{n}} +i\varepsilon } \nonumber \\\times & {} \Big [-i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big )\Big ] \nonumber \\\times & {} D_{1} \Big (\frac{M_{1}}{M_{tot}}K_{0}+q_{0},\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {q}+\mathbf {s}\Big )\nonumber \\\times & {} D_{1}\Big (\frac{M_{1}}{M_{tot}}P_{0}+q_{0},\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {q}-\mathbf {s}\Big ) \nonumber \\\times & {} {\mathcal {G}}_{1}^{irr}(K_{0},\mathbf {K},{\bar{q}}+{\bar{s}})\Big \}. \end{aligned}$$
(B.9)
After performing the \(q_{0}\) integration according to the pole \(q_{0}=\frac{m_{n}}{M_{tot}}P_{0}-\frac{(\frac{m_{n}}{M_{tot}}\mathbf {P}-\mathbf {q}+\mathbf {s})^{2}}{2m_{n}}+i\varepsilon \), we obtain
$$\begin{aligned} {\mathcal {F}}^{(c)}(Q^{2})= & {} \int _{q<\varLambda }\frac{d^{3}\mathbf {q}}{(2\pi )^{3}}\; \Big \{{\mathcal {G}}_{1}^{irr}(P_{0},\mathbf {P},{\bar{q}}-{\bar{s}})^{T}\; \nonumber \\\times & {} \Big [-i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big )\Big ] \nonumber \\\times & {} D_{1}\Big (\frac{M_{1}}{M_{tot}}K_{0}+q_{0},\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {q}+\mathbf {s}\Big )\nonumber \\\times & {} D_{1}\Big (\frac{M_{1}}{M_{tot}}P_{0}+q_{0},\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {q}-\mathbf {s}\Big ) \nonumber \\\times & {} {\mathcal {G}}_{1}^{irr}(K_{0},\mathbf {K},{\bar{q}}+{\bar{s}})\Big \}. \end{aligned}$$
(B.10)
Considering Eq. (24) and by substituting the pole \(q_{0}\), we have
$$\begin{aligned} {\mathcal {G}}_{1}^{irr}(P_{0},\mathbf {P},{\bar{q}}-{\bar{s}})^{T}= & {} \frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\;\left| \beta \;H_{0}(\varLambda )\right| \;d(q, s, -x')\nonumber \\- & {} \sum _{i=0}^{1}\int _{0}^{\varLambda }dp\frac{p^{2}}{2\pi ^{2}}\;{\mathcal {G}}_{i}^{irr}(E,p)\;{\overline{D}}_{i}(E,p) \nonumber \\&\quad \times R_{i1}\Big (E,p,d(q, s, -x')\Big ), \end{aligned}$$
(B.11)
$$\begin{aligned} {\mathcal {G}}_{1}^{irr}(K_{0},\mathbf {K},{\bar{q}}+{\bar{s}})= & {} \frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\;\left| \beta \;H_{0}(\varLambda )\right| \;d(q, s, x')\nonumber \\- & {} \sum _{j=0}^{1}\int _{0}^{\varLambda }dk\frac{k^{2}}{2\pi ^{2}}\;R_{1j}\Big (E,d(q, s, x'),k\Big )\nonumber \\&\quad \times {\overline{D}}_{j}(E,k)\;{\mathcal {G}}_{j}^{irr}(E,k), \end{aligned}$$
(B.12)
with \(d(q, s, \pm x')=\sqrt{q^{2}+s^{2}\pm 2qsx'}\) and the polar angle \(x'=\cos (\angle (\mathbf {Q},\mathbf {q}))\). Using Eq. (9), Eq. (19) and inserting the pole \(q_{0}\), we can redefine the two propagators in Eq. (B.9) as
$$\begin{aligned}&D_{1}\Big (\frac{M_{1}}{M_{tot}}K_{0}+q_{0},\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {q}+\mathbf {s}\Big ) \nonumber \\&\qquad \quad \qquad ={\overline{D}}_{1}\Big (E-\frac{m_{n}}{8M_{1}M_{tot}}Q^{2}-\frac{q Q x'}{2M_{1}},q\Big ), \end{aligned}$$
(B.13)
$$\begin{aligned}&D_{1}\Big (\frac{M_{1}}{M_{tot}}P_{0}+q_{0},\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {q}-\mathbf {s}\Big ) \nonumber \\&\quad \qquad ={\overline{D}}_{1}\Big (E-\frac{m_{n}}{8M_{1}M_{tot}}Q^{2}+\frac{q Q x'}{2M_{1}},q\Big ). \end{aligned}$$
(B.14)
1.3.1 B.3.1 Bubble diagram
We now calculate the term \(-i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big )\) for the bubble diagram depicted in Fig. 10. For general incoming (outgoing) four-momenta \({\bar{p}}\;({\bar{k}})\) and according to Eq. (4), we obtain
$$\begin{aligned} -i\varSigma ({\bar{p}},{\bar{k}})= & {} -\int \frac{d^{3}\mathbf {q'}}{(2\pi )^{3}}\Big (i\frac{g_{1}}{2}\Big )^{2} \nonumber \\\times & {} \Big [\frac{1}{\frac{q'^{2}}{2m_{n}}+\frac{(\mathbf {k}+\mathbf {q'})^{2}}{2m_{\alpha }}-k_{0}}\times \frac{1}{\frac{q'^{2}}{2m_{n}}+\frac{(\mathbf {p}+\mathbf {q'})^{2}}{2m_{\alpha }}-p_{0}}\nonumber \\\times & {} (\mathbf {k}(1-r)+2\mathbf {q'})_{j}(\mathbf {p}(1-r)+2\mathbf {q'})_{i}\;\text {Tr}(S^{\dag }_{j}S_{i})\Big ].\nonumber \\ \end{aligned}$$
(B.15)
According to Eq. (6), we derive \(\text {Tr}(S^{\dag }_{j}S_{i})=\frac{4}{3}\delta _{ij}\). Furthermore, using the relation \(\frac{1}{a_{1}a_{2}}=\int _{0}^{1}\frac{dx}{[a_{1}x+a_{2}(1-x)]^{2}}\) and defining the rescaled loop momentum \(\mathbf {b}:=\frac{\mathbf {q'}+\frac{\mu }{m_{\alpha }}[x\mathbf {p}+(1-x)\mathbf {k}]}{\frac{\mu }{m_{\alpha }}Q}\) and replacing our kinematics \({\bar{p}}\mapsto \frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}}\) and \({\bar{k}}\mapsto \frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\) in Eq. (B.15), we can obtain the following relation for the bubble contribution, \(\varSigma \), as
$$\begin{aligned}- & {} i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big ) \nonumber \\&=\frac{4}{3}\frac{\mu \;m_{\alpha }}{Q}g_{1}^{2}\int _{0}^{1}dx\int \frac{d^{3}\mathbf {b}}{(2\pi )^{3}} \Bigg \{\frac{1}{(b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x))^{2}} \nonumber \\&\times \Bigg [\Big (\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {q}+\mathbf {s}\Big )(1-r) \nonumber \\&\qquad + \frac{2\mu }{m_{\alpha }}\Big (Q\mathbf {b}-\Big [x\Big (\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {q}-\mathbf {s}\Big ) \nonumber \\&\qquad +(1-x)\Big (\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {q}+\mathbf {s}\Big )\Big ]\Big )\Bigg ]_{i} \nonumber \\&\times \Bigg [\Big (\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {q}-\mathbf {s}\Big )(1-r) \nonumber \\&\qquad + \frac{2\mu }{m_{\alpha }}\Big (Q\mathbf {b}-\Big [x\Big (\frac{M_{1}}{M_{tot}}\mathbf {P}+\mathbf {q}-\mathbf {s}\Big ) \nonumber \\&\qquad +(1-x)\Big (\frac{M_{1}}{M_{tot}}\mathbf {K}+\mathbf {q}+\mathbf {s}\Big )\Big ]\Big )\Bigg ]_{i}\Bigg \}, \nonumber \\ \end{aligned}$$
(B.16)
where
$$\begin{aligned} A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)=x^{2}- x\Big (1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}- C_{{\overline{K}},{\overline{q}}+{\overline{s}}}\Big )-C_{{\overline{K}},{\overline{q}}+{\overline{s}}}, \nonumber \\ \end{aligned}$$
(B.17)
with
$$\begin{aligned}&C_{{\overline{P}},{\overline{q}}-{\overline{s}}}=2\mu \Big [B_{2n}+\frac{(\mathbf {q}-\mathbf {s})^{2}}{2{\tilde{\mu }}}\Big ]\Big (\frac{M_{1}}{2M_{tot}}\Big )^{2}\frac{1}{s^{2}},\nonumber \\&\quad C_{{\overline{K}},{\overline{q}}+{\overline{s}}}=2\mu \Big [B_{2n}+\frac{(\mathbf {q}+\mathbf {s})^{2}}{2{\tilde{\mu }}}\Big ]\Big (\frac{M_{1}}{2M_{tot}}\Big )^{2}\frac{1}{s^{2}}, \nonumber \\ \end{aligned}$$
(B.18)
and \({\tilde{\mu }}=\frac{m_{n} M_{1}}{M_{tot}}\). Finally, after some derivations, the relation of the bubble contribution in Eq. (B.16) converts to
$$\begin{aligned}- & {} i\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big ) \nonumber \\= & {} \frac{4}{3}\frac{\mu m_{\alpha }}{Q}g_{1}^{2}\int _{0}^{1}dx\Bigg \{4\frac{\mu ^{2}}{m_{\alpha }^{2}}Q^{2} \int \frac{d^{3}\mathbf {b}}{(2\pi )^{3}}\frac{b^{2}}{[b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)]^{2}} \nonumber \\&+16Qs\Big (\frac{\mu ^{2}}{m_{\alpha }^{2}}\frac{M_{1}}{M_{tot}}\Big )\!(x^{2}\!-\!x)\!\int \!\frac{d^{3}\mathbf {b}}{(2\pi )^{3}} \frac{1}{\left[ b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)\right] ^{2}} \nonumber \\&+ 16\frac{\mu ^{2}}{m_{\alpha }^{2}}s^{2}(\!x^{2}\!-x\!)\!\int \!\frac{d^{3}\mathbf {b}}{(2\pi )^{3}} \frac{1}{[b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)]^{2}} \nonumber \\&+4\Big (\frac{\mu ^{2}}{m_{\alpha }^{2}}\frac{M_{1}^{2}}{M_{tot}^{2}}\Big )Q^{2}(\!x^{2}\!-\!x\!)\!\int \!\frac{d^{3}\mathbf {b}}{(2\pi )^{3}} \frac{1}{\left[ b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)\right] ^{2}}\Bigg \} \nonumber \\= & {} \frac{2i}{3\pi }\frac{\mu ^{3}}{m_{\alpha }}g_{1}^{2}Q[-3I_{4}+I_{3}-I_{2}], \nonumber \\ \end{aligned}$$
(B.19)
where the functions \(I_2\), \(I_3\) and \(I_4\) in the last line are given using the relations
$$\begin{aligned} \int \frac{d^{3}\mathbf {b}}{(2\pi )^{3}} \frac{1}{[b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)]^{2}}= \frac{i}{8\pi }\frac{1}{\sqrt{A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)}}, \nonumber \\ \end{aligned}$$
(B.20)
and
$$\begin{aligned} \int \frac{d^{3}\mathbf {b}}{(2\pi )^{3}} \frac{b^{2}}{[b^{2}-A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)]^{2}}= \frac{3i}{8\pi }\sqrt{A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)}, \nonumber \\ \end{aligned}$$
(B.21)
as
$$\begin{aligned} I_{2}= & {} \int _{0}^{1}dx\frac{x}{\sqrt{A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)}} \nonumber \\= & {} i\left( \sqrt{C_{{\overline{P}},{\overline{q}}-{\overline{s}}}}-\sqrt{C_{{\overline{K}},{\overline{q}}+{\overline{s}}}}\right) \!+\!\frac{\left( 1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}-C_{{\overline{K}},{\overline{q}}+{\overline{s}}}\right) }{2}I_{1}, \nonumber \\ I_{3}= & {} \int _{0}^{1}dx\frac{x^{2}}{\sqrt{A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)}} \nonumber \\= & {} \frac{1}{4}\Big [\left( 1+C_{{\overline{K}},{\overline{q}}+{\overline{s}}}-C_{{\overline{P}},{\overline{q}}-{\overline{s}}}\right) i\sqrt{C_{{\overline{P}},{\overline{q}}-{\overline{s}}}} \nonumber \\&+\left( 1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}-C_{{\overline{K}},{\overline{q}}+{\overline{s}}}\right) i\sqrt{C_{{\overline{K}},{\overline{q}}+{\overline{s}}}}\;\Big ] \nonumber \\&+\frac{1}{2}\Big (C_{{\overline{K}},{\overline{q}}+{\overline{s}}}+\frac{(1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}} -C_{{\overline{K}},{\overline{q}}+{\overline{s}}})^{2}}{4}\Big )I_{1} \nonumber \\&+\left( 1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}-C_{{\overline{K}},{\overline{q}}+{\overline{s}}}\right) i\Big (\sqrt{C_{{\overline{P}},{\overline{q}}-{\overline{s}}}}-\sqrt{C_{{\overline{K}},{\overline{q}}+{\overline{s}}}}\;\Big ) \nonumber \\&+\frac{\left( 1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}-C_{{\overline{K}},{\overline{q}}+{\overline{s}}}\right) ^{2}}{4}I_{1}, \end{aligned}$$
(B.22)
$$\begin{aligned} I_{4}= & {} \int _{0}^{1} dx \sqrt{A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)}\nonumber \\= & {} \frac{1}{4}\Big [\left( 1+C_{{\overline{K}},{\overline{q}}+{\overline{s}}}-C_{{\overline{P}},{\overline{q}}-{\overline{s}}}\right) i\sqrt{C_{{\overline{P}},{\overline{q}}-{\overline{s}}}} \nonumber \\&+\left( 1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}-C_{{\overline{K}},{\overline{q}}+{\overline{s}}}\right) i\sqrt{C_{{\overline{K}},{\overline{q}}+{\overline{s}}}}\;\Big ]\nonumber \\&-\frac{1}{2}\left( C_{{\overline{K}},{\overline{q}}+{\overline{s}}}+\frac{(1+C_{{\overline{P}},{\overline{q}}-{\overline{s}}}-C_{{\overline{K}},{\overline{q}}+{\overline{s}}})^{2}}{4}\right) I_{1}. \nonumber \\ \end{aligned}$$
(B.23)
The \(I_1\) function in Eqs. (B.22)–(B.23) is defined by the expression
$$\begin{aligned} I_{1}= & {} \int _{0}^{1}\frac{dx}{\sqrt{A_{\left| {\overline{q}}-{\overline{s}}\right| ,\left| {\overline{q}}+{\overline{s}}\right| }(x)}}\nonumber \\= & {} -i\left[ \arctan \left( \frac{\frac{M_{tot}}{M_{1}}s+\frac{m_{\alpha }}{M_{1}}qx'}{\sqrt{2\mu \left( B_{2n}+\frac{(\mathbf {q}-\mathbf {s})^{2}}{2{\tilde{\mu }}}\right) }}\right) \right. \nonumber \\&\left. \qquad +\arctan \left( \frac{\frac{M_{tot}}{M_{1}}s-\frac{m_{\alpha }}{M_{1}}qx'}{\sqrt{2\mu \left( B_{2n}+\frac{(\mathbf {q}+\mathbf {s})^{2}}{2{\tilde{\mu }}}\right) }}\right) \right] . \end{aligned}$$
(B.24)
1.3.2 3.3.2 Final representation of \({F}^{(c)}(Q^{2})\)
In the final step, by inserting Eqs. (B.11)–(B.14) into Eq. (B.10), we find
$$\begin{aligned}&{\mathcal {F}}^{(c)}(Q^{2})=\;\int _{0}^{\varLambda } \left( -\frac{p^{2}}{2\pi ^{2}}\right) \;dp\;\int _{0}^{\varLambda } \left( -\frac{k^{2}}{2\pi ^{2}}\right) \;dk\;\mathbf {{\mathcal {G}}}^{irr}(p)^{T} \nonumber \\&\times D(p)\;\varUpsilon ^{(c)}(Q,p,k)\;D(k)\;\mathbf {{\mathcal {G}}}^{irr}(k)\nonumber \\&+2\int _{0}^{\varLambda } \left( -\frac{p^{2}}{2\pi ^{2}}\right) dp\mathbf {{\mathcal {G}}}^{irr}(p)^{T}D(p)\mathbf {\varUpsilon }^{(c)}(Q,p)+\varUpsilon ^{(c)}_{0}(Q), \nonumber \\ \end{aligned}$$
(B.25)
where
$$\begin{aligned} \varUpsilon ^{(c)}_{ij}(Q,p,k)= & {} \frac{1}{(2\pi )^{3}}\;\int _{0}^{\varLambda }q^{2}\;dq\;\int _{-1}^{1}dx'\;\int _{0}^{2\pi }d\phi \nonumber \\&\times \chi ^{(c)}_{ij}(\frac{m_{n}}{2M_{tot}}Q, p, k, q, x', \phi ),\nonumber \\ \varUpsilon ^{(c)}_{i}(Q,p)= & {} \frac{1}{(2\pi )^{3}}\;\int _{0}^{\varLambda }q^{2}\;dq\;\int _{-1}^{1}dx'\;\int _{0}^{2\pi }d\phi \nonumber \\&\times \chi ^{(c)}_{i}(\frac{m_{n}}{2M_{tot}}Q, p, q, x', \phi ),\nonumber \\ \varUpsilon ^{(c)}_{0}(Q)= & {} \frac{1}{(2\pi )^{3}}\int _{0}^{\varLambda }q^{2}dq\int _{-1}^{1}dx'\int _{0}^{2\pi }d\phi \nonumber \\&\times \chi ^{(c)}_{0}(\frac{m_{n}}{2M_{tot}}Q, q, x', \phi ), \nonumber \\ \end{aligned}$$
(B.26)
with the following relations
$$\begin{aligned}&\chi ^{(c)}_{ij}(\frac{m_{n}}{2M_{tot}}Q, q, x, p, k)=R_{i1}\left( -B_{2n}, p, d(q, s, -x')\right) \nonumber \\&\qquad \times {\overline{D}}_{1}\left( -B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 M_{1}}, q\right) \nonumber \\&\qquad \times \left[ -i\;\varSigma \left( \frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\right) \right] \nonumber \\&\qquad \times {\overline{D}}_{1}\left( -B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 M_{1}}, q\right) \nonumber \\&\qquad \times R_{1j}\left( -B_{2n}, d(q, s, x'), k\right) , \nonumber \\ \end{aligned}$$
(B.27)
$$\begin{aligned}&\chi ^{(c)}_{i}(\frac{m_{n}}{2M_{tot}}Q, p, q, x', \phi ) =\frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\left| \beta H_{0}(\varLambda )\right| d(q, s, x') \nonumber \\&\qquad \times R_{i1}\left( -B_{2n}, p, d(q, s, -x')\right) \nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times \Big [-i\;\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big )\Big ]\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 M_{1}}, q\Big ), \end{aligned}$$
(B.28)
$$\begin{aligned}&\chi ^{(c)}_{0}(\frac{m_{n}}{2M_{tot}}Q, q, x', \phi )=\frac{1}{\sqrt{3}}\frac{m_{n}g_{1}^{2}}{\varLambda ^{2}}\left| \beta H_{0}(\varLambda )\right| d(q, s, -x')\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times \Big [-i\;\varSigma \Big (\frac{M_{1}}{M_{tot}}{\bar{P}}+{\bar{q}}-{\bar{s}},\frac{M_{1}}{M_{tot}}{\bar{K}}+{\bar{q}}+{\bar{s}}\Big )\Big ]\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times \frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\;\left| \beta \;H_{0}(\varLambda )\right| \;d(q, s, x'). \nonumber \\ \end{aligned}$$
(B.29)
As it mentioned all calculations have been performed in Breit frame, so we have substituted \(E= -B_{2n}\) in Eqs. (B.27)–(B.29) and drop this energy variable in \(\mathbf {{\mathcal {G}}}^{irr}\) and matrix D in Eq. (B.25).
1.4 B.4 Contribution \({\mathcal {F}}_{E}^{(d)}\)
Diagram (d) in Fig. 5 is the same as diagram (c) by converting the \(n\alpha \) bubble to the vertex of photon-\(d_{1}\) coupling, therefore the contribution of the diagram (d) is given by
$$\begin{aligned} {\mathcal {F}}^{(d)}(Q^{2})= & {} \;\int _{0}^{\varLambda } \left( -\frac{p^{2}}{2\pi ^{2}}\right) \;dp\;\int _{0}^{\varLambda } \Big (-\frac{k^{2}}{2\pi ^{2}}\Big )\;dk \nonumber \\&\quad \times \mathbf {{\mathcal {G}}}^{irr}(p)^{T}\;D(p)\;\varUpsilon ^{(d)}(Q,p,k)\;D(k)\;\mathbf {{\mathcal {G}}}^{irr}(k)\nonumber \\&+2\int _{0}^{\varLambda } \Big (-\frac{p^{2}}{2\pi ^{2}}\Big )\;dp\;\mathbf {{\mathcal {G}}}^{irr}(p)^{T}\;D(p)\;\mathbf {\varUpsilon }^{(d)}(Q,p) \nonumber \\&+\varUpsilon ^{(d)}_{0}(Q), \end{aligned}$$
(B.30)
where
$$\begin{aligned} \varUpsilon ^{(d)}_{ij}(Q,p,k)= & {} \frac{1}{(2\pi )^{3}}\;\int _{0}^{\varLambda }q^{2}\;dq\;\int _{-1}^{1}dx'\;\int _{0}^{2\pi }d\phi \nonumber \\&\quad \times \chi ^{(d)}_{ij}\left( \frac{m_{n}}{2M_{tot}}Q, p, k, q, x', \phi \right) ,\nonumber \\ \mathbf {\varUpsilon }^{(d)}_{i}(Q,p)= & {} \frac{1}{(2\pi )^{3}}\;\int _{0}^{\varLambda }q^{2}\;dq\;\int _{-1}^{1}dx'\;\int _{0}^{2\pi }d\phi \nonumber \\&\quad \times \chi ^{(d)}_{i}\left( \frac{m_{n}}{2M_{tot}}Q, p, q, x', \phi \right) ,\nonumber \\ \varUpsilon ^{(d)}_{0}(Q)= & {} \frac{1}{(2\pi )^{3}}\;\int _{0}^{\varLambda }q^{2}\;dq\;\int _{-1}^{1}dx'\;\int _{0}^{2\pi }d\phi \nonumber \\&\quad \times \chi ^{(d)}_{0}\left( \frac{m_{n}}{2M_{tot}}Q, q, x', \phi \right) , \nonumber \\ \end{aligned}$$
(B.31)
with the following relations
$$\begin{aligned}&\chi ^{(d)}_{ij}\left( \frac{m_{n}}{2M_{tot}}Q, q, x', p, k\right) =R_{i1}\Big (-B_{2n}, p, d(q, s, -x')\Big )\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times R_{1j}\Big (-B_{2n}, d(q, s, x'), k\Big ),\nonumber \\&\chi ^{(d)}_{i}\left( \frac{m_{n}}{2M_{tot}}Q, p, q, x', \phi \right) =\frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\;\left| \beta \;H_{0}(\varLambda )\right| \nonumber \\&\qquad \times d(q, s, x')\;R_{i1}\Big (-B_{2n}, p, d(q, s, -x')\Big )\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 M_{1}}, q\Big ),\nonumber \\&\chi ^{(d)}_{0}\left( \frac{m_{n}}{2M_{tot}}Q, q, x', \phi \right) =\frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\;\left| \beta \;H_{0}(\varLambda )\right| \nonumber \\&\qquad \times d(q, s, -x')\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;-\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times {\overline{D}}_{1}\Big (-B_{2n}\;-\;\frac{m_{n}}{8M_{1}M_{tot}}\;Q^2\;+\;\frac{q Q x'}{2 M_{1}}, q\Big )\nonumber \\&\qquad \times \frac{1}{\sqrt{3}}\;\frac{m_{n}\;g_{1}^{2}}{\varLambda ^{2}}\;\left| \beta \;H_{0}(\varLambda )\right| \;d(q, s, x'). \end{aligned}$$
(B.32)