Feasibility studies for the measurement of time-like proton electromagnetic form factors from $\bar{p}p \rightarrow \mu ^+\mu ^-$ at $\overline{\text {P}}\text {ANDA}$ at FAIR

Abstract

This paper reports on Monte Carlo simulation results for future measurements of the moduli of time-like proton electromagnetic form factors, $|G_{E}|$ and $|G_{M}|$, using the $\bar{p} p \rightarrow \mu ^{+} \mu ^{-}$ reaction at $\overline{\text {P}}\text {ANDA}$ (FAIR). The electromagnetic form factors are fundamental quantities parameterizing the electric and magnetic structure of hadrons. This work estimates the statistical and total accuracy with which the form factors can be measured at $\overline{\text {P}}\text {ANDA}$, using an analysis of simulated data within the PandaRoot software framework. The most crucial background channel is $\bar{p} p \rightarrow \pi ^{+} \pi ^{-}$, due to the very similar behavior of muons and pions in the detector. The suppression factors are evaluated for this and all other relevant background channels at different values of antiproton beam momentum. The signal/background separation is based on a multivariate analysis, using the Boosted Decision Trees method. An expected background subtraction is included in this study, based on realistic angular distributions of the background contribution. Systematic uncertainties are considered and the relative total uncertainties of the form factor measurements are presented.

1 Introduction

Electromagnetic form factors (FFs) are fundamental quantities, which describe the internal structure of hadrons. The proton structure at leading order in $\alpha$ ($\alpha$, being the electromagnetic fine structure constant), can be described by the electric ($G_E$) and the magnetic ($G_M$) FFs. Experimental access to these FFs is possible via the measurement of differential and total cross sections for elastic electron-proton scattering in the space-like region (momentum transfer squared $q^2 < 0$ (GeV/c)$^2$), while in the time-like region ($q^2>0$ (GeV/c)$^2$) proton FFs can be accessed in annihilation processes of the type $\bar{p} p \rightarrow \ell ^{+} \ell ^{-}$ with $\ell =$ $e,\mu , \tau$ (or the time-reversed process in case of electrons). Here the interaction takes place through the exchange of a single virtual photon, carrying a momentum transfer squared $q^2$.

Although the space-like FFs have been studied since the 1950’s [1], the recent application of the polarization transfer method [2, 3] triggered new efforts in the field of electromagnetic proton FFs. Precise data on polarised elastic electron-proton scattering up to $Q^2=-q^2 \approx 8.5$ (GeV/c)$^2$ [4,5,6,7,8] are in tension with the existing results obtained with the well-established Rosenbluth method [9]. The polarization transfer method showed that the ratio $\mu _p G_E$/$G_M$ (where $\mu _p$ stands for the proton magnetic moment) decreases linearly from unity to zero with increasing values of $Q^2$. The recent experiments from the OLYMPUS [10], CLAS [11] and VEPP [12] as well as the GEp2gamma [13] collaborations did not show evidence of a two photon exchange contribution at the level needed to explain the discrepancy (6$\%$ relative). A common analysis of these experiments shows that the difference between the cross sections of electron and positron elastic scattering on protons – when consistently corrected by radiative corrections – remains within the uncertainty of the radiative correction calculation [14].

At low momentum transfer, space-like FFs provide information on the distributions of the electric charges and magnetization within the proton. The proton charge radius is related to the derivative of the electric FF at $Q^2=0$ (GeV/c)$^2$. It has been determined from electron-proton scattering measurements and hydrogen spectroscopy [15,16,17] but the results are not totally in agreement. Future experiments, e.g. the MUon proton Scattering Experiment (MUSE) at Paul Scherrer Institute (PSI) [18], aim to extend the current studies by determining the proton radius using both muon and electron scattering measurements. In the time-like region, the proton FFs have been measured in electron-positron annihilation $e^+e^-\rightarrow {\bar{p}} p$ and proton-antiproton annihilation ${\bar{p}} p\rightarrow e^+e^-$ [19,20,21,22,23,24,25,26,27,28,29,30,31]. In addition, the radiative return process $e^+e^-\rightarrow {\bar{p}} p \gamma$, where $\gamma$ is a hard photon emitted by initial state radiation (ISR), has been used by the BaBar and the BESIII collaboration to measure the modulus of the time-like proton FF ratio $|G_E|/|G_M|$ and the effective FF $|F_p|$ in a continuous range of $q^2$ [32,33,34]. The data show a strong energy dependence near threshold and some regular oscillations in the measured $|F_p|$, which have been the subject of several theoretical studies [35,36,37,38]. The precision of the measurements of the proton FFs $|G_E|$ and $|G_M|$ (and their ratio) in the time-like region has been limited over the past decades by poor statistics [39, 40], in contrast to the space-like region measurements. In 2019 the BESIII collaboration measured the Born cross section of the $e^+e^-\rightarrow {\bar{p}} p$ process and the proton FFs at 22 center-of-mass (CM) energy points from $q^2=4$ (GeV/c)$^2$ to $q^2=9.5$ (GeV/c)$^2$ [41]. The FF ratio was determined with total uncertainties around $10\%$, comparable to the data in the space-like region at the same $|q^2|$ values.

Proton FFs in the space-like and time-like regions are connected via dispersion relations. Therefore, a precise determination of the time-like FFs over a large $q^2$ range using different electromagnetic processes can help to constrain the theoretical models and shed light on the discrepancies which have been found in the space-like region. The situation in the time-like region will be improved even more in the future by the data which will be collected with the $\overline{\text {P}}\text {ANDA}$ (antiProton ANnihilation at DArmstadt) detector.

The modulus of the time-like proton FFs will be measured at $\overline{\text {P}}\text {ANDA}$ in the ${\bar{p}} p \rightarrow e^+ e^-$ and ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ annihilation processes [42, 43]. It will be the first time that muons in the final state will be used to measure the modulus of the time-like FFs of the proton. In contrast to the $\bar{p}p \rightarrow e^+e^-$ process, the ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ reaction has the advantage that corrections due to final state radiation are expected to be smaller. Measuring both channels should therefore allow the formalism for radiative corrections to be tested. Moreover, a test of lepton universality at a few percent level could be possible at $\overline{\text {P}}\text {ANDA}$, based on the determination of the effective FF of the proton with both channels.

Fig. 1

The proposed $\overline{\text {P}}\text {ANDA}$ detector

The possibility to access the proton FFs in the region below the kinematic threshold of the proton antiproton production through the measurement of the ${\bar{p}} p \rightarrow \ell ^+ \ell ^- \pi ^0$ process [44,45,46] is under investigation. This region below ($2M_p$)$^2$ is called the unphysical region and it has never been experimentally accessed. Feasibility studies of exploiting the ${\bar{p}} p \rightarrow e^+ e^-$ reaction at $\overline{\text {P}}\text {ANDA}$ were addressed in Refs. [47, 48]. It has been shown that a separate measurement of $|G_E|$ and $|G_M|$ can be performed up to $q^2 \sim 14$ (GeV/c)$^2$. In this paper, the results of a feasibility study to extract the modulus of the time-like proton FFs using the ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ process at $\overline{\text {P}}\text {ANDA}$ are presented.

2 The $\overline{\text {P}}\text {ANDA}$ experiment at FAIR

The $\overline{\text {P}}\text {ANDA}$ experiment [49] will be located at the Facility for Antiproton and Ion Research (FAIR), which is currently under construction in Darmstadt (Germany). The $\overline{\text {P}}\text {ANDA}$ experiment will measure annihilation reactions induced by a high-intensity antiproton beam covering a wide range of momenta between 1.5 GeV/c and 15 GeV/c. The physics program includes hadron spectroscopy in the charmonium, hyperon and light quark sectors, hypernuclear physics, and studies of hadron properties in a nuclear medium. An important part of the $\overline{\text {P}}\text {ANDA}$ physics program will be dedicated to the investigation of the nucleon structure. It is planned to measure nucleon-to-meson transition distribution amplitudes (TDAs) through the measurements of the exclusive processes ${\bar{p}} p \rightarrow \gamma ^* \pi ^0 \rightarrow e^+ e^- \pi ^0$ [50] and ${\bar{p}} p \rightarrow J/\varPsi \pi ^0 \rightarrow e^+ e^- \pi ^0$ [51]. The generalized distribution amplitudes (GDAs) of the proton can be also accessed with the large angle production of the neutral states $\gamma \gamma$ and $\pi ^0 \gamma$ [49]. In addition, a Drell-Yan physics program to access transverse momentum dependent (TMD) parton distribution functions (PDFs), using the inclusive production of lepton pairs in proton-antiproton annihilations, is also foreseen [49].

2.1 The FAIR accelerator complex

The FAIR accelerator complex will extend the existing facilities of the GSI Helmholtzzentrum für Schwerionenforschung in Darmstadt [52]. It will deliver antiproton and ion beams for four main experimental projects that aim to provide fundamental insights into the structure of matter and the evolution of the universe. FAIR will use a new large synchrotron ring, named SIS100, with a circumference of 1.1 km and a bending power of 100 Tm to accelerate protons up to 30 GeV/c. The accelerated protons will hit a copper target to produce antiproton beams with a time-averaged production rate in the $5.6\times 10^6$ to $10^7$ per second range. The antiprotons will be collected and cooled in the collector ring (CR), followed by their accumulation in the recycled experimental storage ring (RESR). Finally, the antiprotons will be injected in the high energy storage ring (HESR), where the induced antiproton annihilation reactions will be studied by the $\overline{\text {P}}\text {ANDA}$ fixed-target experiment.

This setup is designed to provide a beam of up to $10^{11}$ antiprotons per filling and peak instantaneous luminosities up to $2 \times 10^{32}$ $\hbox {cm}^{-2}$ $\hbox {s}^{-1}$. However, in the initial start-up phase of the FAIR operation without the RESR, the HESR will be used as an accumulator, resulting in a luminosity about a factor of 20 lower than the nominal design value. In the present study, the results are obtained assuming an integrated luminosity of 2 $\hbox {fb}^{-1}$, which can be accumulated in 4 to 5 months of data taking at the maximum design luminosity.

2.2 The $\overline{\text {P}}\text {ANDA}$ detector

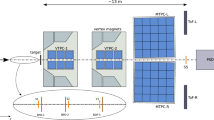
The proposed $\overline{\text {P}}\text {ANDA}$ detector [49], shown in Fig. 1, will be located at the HESR. It is divided into a target spectrometer surrounding the target area and a forward spectrometer designed to detect particles in the forward rapidity region. The two spectrometers have a solid angle acceptance of almost $4\pi$.

The antiproton beams at the HESR will interact with a fixed proton target at CM energies between 2.2 and 5.5 GeV. A frozen pellet and a cluster-jet are two alternative hydrogen targets foreseen for the $\overline{\text {P}}\text {ANDA}$ ${\bar{p}} p$ annihilation studies [53]. In addition, internal targets filled by heavier gases and non-gaseous nuclear targets will be available for the ${\bar{p}} A$ studies and hypernuclear experiments, respectively.

The target spectrometer is equipped with a superconducting solenoid magnet with a maximum magnetic field of 2 T [54]. The innermost tracking system of the target spectrometer is the Micro Vertex Detector (MVD) [55]. It is based on radiation-hard silicon strip and pixel sensors and is optimized for the detection of secondary decay vertices of short lived particles such as D-mesons and hyperons. The MVD will provide precise vertex position measurements with a resolution of about 100 $\upmu$m along the beam axis and 30 $\upmu$m in the perpendicular plane. The Straw Tube Tracker (STT) is the central tracking detector in the target spectrometer [56]. It encloses the MVD and is followed by three planar stations of Gas Electron Multipliers (GEM) downstream of the target. The MVD, the STT and the GEM will provide momentum measurement of charged particles with a transverse momentum resolution better than $1\%$. In addition, the measurement of the energy loss by the STT and the MVD will be used for particle identification. A barrel and an end-cap Detection of Internally Reflected Cherenkov light (DIRC) detectors will be used to separate pions from kaons at polar angles between $5^{\circ }$ and $140^{\circ }$, and momenta up to 4 GeV/c [57]. A time-of-flight (TOF) system, made of small plastic scintillator tiles (SciTil), will be also employed for particle identification of pions, protons and kaons.

The energy of photons and electrons will be measured by an electromagnetic calorimeter (EMC), consisting of lead tungstate ($\hbox {PbWO}_4$) crystals operated at a temperature of $-25\,^{\circ }$C to improve the light yield [58]. Muon PID will be provided by the Muon Detectors (MD), which surround the solenoid magnet in the target spectrometer (Muon System) and are additionally located in the forward spectrometer (Forward Range System (FRS)) [59]. For the separation of muons from other particles, the range measurement technique is used, which is based on a sampling structure of active and passive layers in all subsystems of the Muon Detectors (MD). The MD are the most relevant components for this analysis and are described in detail in Ref. [59].

The forward spectrometer [49, 54, 60] with a 2 Tm dipole magnet will detect particles with polar angles below the end cap coverage of the target spectrometer. It comprises a forward tracking system (FTS), an Aerogel Ring Imaging Cherenkov Counter (FRICH), a Forward TOF system (FTOF), a Shashlyk calorimeter and the Forward Range System (FRS). The forward spectrometer is completed by the Luminosity Monitor Detector (LMD) for precise determination of the absolute and the relative time integrated luminosities. A detailed overview of the $\overline{\text {P}}\text {ANDA}$ detector can be found in Ref. [49].

In order to reach the physics goals of the experiment, operation at high annihilation rates exceeding 20 $\cdot$ 10$^{6}$ per second is expected. This requires a novel approach to data acquisition and real-time event selection. After a full online reconstruction of the events, an event filtering procedure based on a preliminary selection of the physics channels of interest will be performed.

3 Reaction kinematics and cross sections

The lowest-order QED contribution to the amplitude of the $\bar{p}p \rightarrow {\ell }^+{\ell }^-$ $({\ell } = e, \mu )$ annihilation reaction is shown in Fig. 2. The four momenta of the involved particles are written in parentheses. Four-momentum conservation at the hadronic vertex implies that $q^2$ is equal to the $\bar{p}p$ CM energy squared s:

$$\begin{aligned} q^2 = (p_1 + p_2)^2 = s. \end{aligned}$$

(1)

Fig. 2

Lowest-order QED diagram contributing to the reaction amplitude of antiproton-proton annihilation into $\ell ^{+}\ell ^{-}$ final states

In the Born approximation, which assumes one photon exchange, the differential cross section in the $\bar{p}{p}$ CM system of the annihilation of $\bar{p}p$ into a lepton pair can be written as a function of the Sachs FFs [43, 61] as

$$\begin{aligned} \frac{d\sigma }{d\cos {\theta _{CM}}}= & {} \frac{\pi {\alpha }^2}{2s} \frac{\beta _{\ell }}{\beta _{p}} \bigg [ \frac{1}{\tau } \bigg (1- {{\beta }_{\ell }}^2 \cos ^{2}\theta _{CM}\bigg ) {|G_E|}^2 \nonumber \\&+ \bigg (2 - {\beta }_{\ell }^2 + {{\beta }_{\ell }}^2 \cos ^{2}\theta _{CM}\bigg ) {|G_M|}^2\bigg ], \end{aligned}$$

(2)

where $\theta _{CM}$ is the polar angle of the negative charged lepton $\ell ^-$ and is measured with respect to the antiproton direction in the $\bar{p}p$ CM frame. $\alpha \approx$ 1/137 is the fine structure constant and the kinematic factors are

$$\begin{aligned}&\beta _{\ell ,p} = \sqrt{1-4M^2_{\ell ,p}/s},\\&\tau = \frac{q^2}{4M_p^2}, \end{aligned}$$

where $\beta _{\ell ,p}$ is the velocity of the lepton or the proton in the CM frame, respectively. The measurement of the angular distribution of the charged leptons at a fixed energy requires a high luminosity in order to collect enough statistics over the whole angular range. With the precise knowledge of the luminosity, the absolute value of the cross section can be determined and an individual extraction of the modulus of the time-like electromagnetic proton FFs, $|G_E|$ and $|G_M|$, is possible.

Fig. 3

The proton effective FF values measured by: E835 [20, 21], Fenice [22], PS170 [23], E760 [24], DM1 [25], DM2 [26, 27], BES [28], BESIII [29, 34, 41], CLEO [30], BABAR [32, 33], and ADONE73 [19]. The blue dashed curve shows the QCD inspired parametrization [36, 62] based on Eq. (5). The solid black curve shows the parametrization [Eq. (6)] suggested in Ref. [66]

The effective proton FF is a quantity which can be determined even at low statistics experiments. It is a linear combination of the $|G_E|$ and $|G_M|$ FFs, and can be obtained by the measurement of the integrated cross section ($\sigma (q^2)$) via

$$\begin{aligned} \sigma (q^2) = \frac{4\pi {\alpha }^{2}}{q^2} \bigg (1 - \frac{ {\beta }_{\ell }^{2}}{3} \bigg ) \; \frac{\beta _{\ell }}{\beta _{p}} \bigg (1 + \frac{1}{2\tau } \bigg ) |F_{p}|^2, \end{aligned}$$

(3)

being

$$\begin{aligned} |F_{p}| = \sqrt{\frac{2\tau {|G_{M}|^{2}}+|G_{E}|^{2}}{2\tau + 1}}. \end{aligned}$$

(4)

The world data on the proton effective FF are shown in Fig. 3. Different parametrizations of the proton FFs can be found in literature [62,63,64,65,66,67,68]. For example, the blue dashed curve in Fig. 3 represents the quantum chromodynamics (QCD) inspired $|F_{p}|$ parametrization from Refs. [36, 62]:

$$\begin{aligned} |F_{p}|=\frac{\mathcal{{A_\mathrm{QCD}}}}{q^4 (\log ^2(q^2/\varLambda _\mathrm{QCD}^2)+\pi ^2)}, \end{aligned}$$

(5)

where the parameters $\mathcal{{A_\mathrm{QCD}}}=72~(\text{ GeV/ }c)^4$ and $\varLambda _\mathrm{QCD}=0.52~(\text{ GeV/ }c)$ are obtained from a fit to the experimental data [36]. The data on the time-like effective FF can also be reproduced by the function proposed in Ref. [66],

$$\begin{aligned} |F_{p}|=\frac{{{\mathcal {A}}}}{(1+q^2/m_a^2)(1+q^2/q_0^2 )^2}, \end{aligned}$$

(6)

where the fit parameters are ${{\mathcal {A}}}=22.5$, $m_a^2=3.6~(\text{ GeV/ }c)^2$, and $q_0^2=0.71~(\text{ GeV/ }c)^2$. This model is illustrated in Fig. 3 by the solid black curve. The two functions (Eqs. 5 and 6) reproduce the behavior of $|F_p|$ over a wide $q^2$ range. For the current studies, Eq. 6 is used to parametrize the proton electric and magnetic FFs assuming their ratio, $R=|G_E|/|G_M|$, is equal to one. The region between $q^2$ = 5.1 (GeV/c)$^2$ (laboratory beam momentum $p_{beam}$ = 1.5 GeV/c) and 8.2 (GeV/c)$^2$ ($p_{beam}$ = 3.3 GeV/c), where $\overline{\text {P}}\text {ANDA}$ is expected to provide the first data on the modulus of the time-like proton FFs using the process $\bar{p} p \rightarrow \mu ^{+} \mu ^{-}$, will be examined in this paper.

Table 1 Number of expected events $N_{int}$ and integrated cross-sections $\sigma _{int}$ based on Eq. 2 in the |cos($\theta _{CM}$)| < 0.8 angular range. For the calculations, the FF parametrization of Eq. 6 is used for the $\bar{p} p \rightarrow {\mu }^{+} {\mu }^{-}$ signal reaction. At 1.5 GeV/c and 1.7 GeV/c, a cross-section is used for $\bar{p} p \rightarrow {\pi }^{+} {\pi }^{-}$ based on a fit of available data from [69] with Legendre polynomials. The 2.5 and 3.3 GeV/c beam momentum values correspond to the interpolation region of the pion cross section model. A time-integrated luminosity of $\mathcal {L}$ = 2 $\hbox {fb}^{-1}$ is assumed for each $N_{int}({\mu }^{+} {\mu }^{-})$ and $N_{int}({\pi }^{+} {\pi }^{-})$ kinematic point

4 Monte Carlo simulation with PandaRoot

The offline software for the $\overline{\text {P}}\text {ANDA}$ detector simulation and analysis, PandaRoot [70], has been developed within the framework for the future FAIR experiments, FairRoot [71]. The PandaRoot software encompasses full detector simulation and event reconstruction. In order to investigate the feasibility to use the $\bar{p} p \rightarrow \mu ^{+} \mu ^{-}$ process for the measurement of the proton time-like FFs at $\overline{\text {P}}\text {ANDA}$, Monte Carlo (MC) simulation studies based on PandaRoot are performed.

4.1 Generation of the $\bar{p} p \rightarrow {\mu }^{+} {\mu }^{-}$ signal events

The signal event generation at different beam momenta values, $p_{beam} \in$ (1.5, 1.7, 2.5, 3.3) GeV/c, is based on the expression of the differential cross-section (Eq. 2) as a function of the time-like electromagnetic proton FFs. Equation 6 is used for the parametrization of $|G_{E}|$ and $|G_{M}|$. For each value of beam momentum, the number of expected signal events is extracted (see Table 1), assuming a time-integrated luminosity of 2 $\hbox {fb}^{-1}$. The MC sample denoted as S1 is produced at each value of the beam momentum with a large amount of events to determine the signal efficiency; as a result, the statistical uncertainty on the efficiency is negligible. Additional MC samples (S2) are generated based on the numbers of expected signal events for a proper consideration of the statistical fluctuations and uncertainties. The samples S2 represent the signal events that will be collected in the future at the $\overline{\text {P}}\text {ANDA}$ experiment. The dependence of the expected number of signal events on cos($\theta _{CM}$) is illustrated in Fig. 4 at beam momenta of 1.5 GeV/c, 1.7 GeV/c, 2.5 GeV/c, and 3.3 GeV/c.

4.2 Largest background sources

The suppression of the hadron background is one of the main experimental challenges for the measurement of the modulus of the time-like proton FFs in the muon channel. The possible background channels with the largest cross sections (see also [47, 72,73,74,75]) are

• $\bar{p}p \rightarrow \pi ^+\pi ^-$;

• $\bar{p}p \rightarrow K^+K^-$;

• $\bar{p}p \rightarrow K^+K^-{\pi }^0$;

• $\bar{p}p \rightarrow \pi ^+\pi ^-{\pi }^0$;

• $\bar{p}p \rightarrow \pi ^+\pi ^-\omega$;

• $\bar{p}p \rightarrow \pi ^+\pi ^-{\rho }^0$;

• $\bar{p}p \rightarrow n\pi ^+ n\pi ^- m{\pi }^0$ with n $\ge$ 2 and m $\ge$ 0.

The main background source is the production of two charged pions ($\bar{p} p \rightarrow \pi ^{+} \pi ^{-}$). Its total cross section is estimated to be a factor of $10^{5}$-$10^{6}$ larger than the signal, depending on the beam energy [69, 74, 76]. Therefore, an efficient background suppression together with a sufficient signal efficiency is required to extract the desired signal. Furthermore, due to their similar masses, it is difficult to distinguish between muons and pions, especially at higher particle momenta, where they show a quite similar behavior inside the $\overline{\text {P}}\text {ANDA}$ MD.

Fig. 4

Angular distribution of the MC generated $\mu ^-$ in the $\bar{p}p$ CM frame for the $\bar{p}p \rightarrow {\mu }^+{\mu }^-$ process (sample S2) for $p_{beam}$ = 1.5 GeV/c (green), 1.7 GeV/c (blue), 2.5 GeV/c (red) and 3.3 GeV/c (magenta) (color online). Due to the $\overline{\text {P}}\text {ANDA}$ detector acceptance the events are generated in the |cos(${\theta }_{CM}$)|< 0.8 angular range

4.3 $\bar{p}p \rightarrow \pi ^{+}\pi ^{-}$ background generation

For the simulation of the main background channel $\bar{p}p \rightarrow \pi ^{+}\pi ^{-}$ (referred in the following as pion background), a dedicated event generator has been developed [77] based on two phenomenological parameterizations in different beam momentum ranges. For antiproton momenta in the $0.79\le p_{beam}\le 2.43$ GeV/c range, the “low energy region”, a combination of Legendre polynomials reproduces the data well and is used to fit the available data (see [69]). The oscillating behavior of the angular distribution at lower momentum (see Fig. 5) is due to contributions of higher L waves in the relative motion in the di-pion system.

Fig. 5

Angular distribution of the generated $\pi ^{-}$ in the $\bar{p}p$ CM frame for the $\bar{p}p \rightarrow {\pi }^+{\pi }^-$ process (sample B1) for $p_{beam}$ = 1.5 GeV/c (green), 1.7 GeV/c (blue), 2.5 GeV/c (red) and 3.3 GeV/c (magenta)

For $5.0 \le p_{beam} \le 12.0$ GeV/c beam momenta, the so-called “ high energy region”, a Regge-inspired parametrization from [76] is tuned to the data from [78,79,80,81]. The angular distribution of the $\pi ^-$ loses its oscillating behavior, becoming forward or backward peaked. This corresponds to small values of the Mandelstam variables t or u, respectively, to which different exchange particles contribute.

For momenta in the $2.43< p_{beam} < 5.0$ GeV/c intermediate region, an interpolation is used since there are no available data or valid models providing a reliable description.

A data sample (B1) consisting of $10^{8}$ background events, is simulated in the $|\cos (\theta _{CM})| < 0.8$ range at each value of the beam momentum. The angular distribution of the generated $\pi ^{-}$ is depicted in Fig. 5 at $p_{beam}$ = 1.5 GeV/c (green), 1.7 GeV/c (blue), 2.5 GeV/c (red) and 3.3 GeV/c (magenta).

5 Analysis of the simulated event samples

After event generation, the particles are propagated through the material of the $\overline{\text {P}}\text {ANDA}$ detector using the GEANT4 software package. The digitization of the detector analog signals is then simulated, followed by the event reconstruction. At this step the reconstruction of the trajectories in the sub-detectors is done by fitting the charged particle tracks. Finally, particle identification and the analysis of the reconstructed data are performed.

5.1 Event reconstruction

The events for the signal and background reactions are reconstructed based on the following conditions:

• events with at least one positive and one negative track are selected. If more than one positive–negative track pair can be combined, the pair with the ${(\theta ^{+}+\theta ^{-})}_{CM}$ closest to 180$^\circ$ is selected;

• both particle candidates must have at least one hit each in the MD.

5.2 Kinematic and PID variable information

Kinematic selections can be used to suppress contributions from hadronic channels with more than two particles in the final states, as well as events with secondary particles originating in the interaction with the detector materials. One of the kinematic variables is the sum of the polar angles of both charged tracks in the CM frame. The angles are derived from the three-momenta at the vertex, which are based on the reconstructed trajectory using the information of both STT and MVD. The particle’s energy at the production vertex is calculated assuming the muon mass hypothesis. The total polar production angle is depicted in Fig. 6 (a, c). One can see that the peak of the background distribution is shifted to smaller angles in comparison to the signal peak, due to assigning the background pions the muon mass hypothesis. Therefore this variable can be used for the signal-background separation. In addition, both tracks are ideally emitted back-to-back in the lab frame in a plane perpendicular to the beam so the azimuthal angle difference ${(|\phi ^{+}-\phi ^{-}|)}_{lab}$ is ideally peaked at 180$^\circ$. From the 4-momenta of both tracks, the invariant mass is calculated:

$$\begin{aligned} M_{inv}=\sqrt{{(p_{\ell ^+}+p_{\ell ^-})}^2}. \end{aligned}$$

(7)

The corresponding $M_{inv}$ distributions are shown in Fig. 6 (b, d). The invariant mass spectrum shows a hump at the region around 1.8 GeV/$c^2$ at $p_{beam}$ = 1.5 GeV/c and 1.7 GeV/c, which is caused by the decay of a single pion ($\pi \rightarrow \mu \nu$). For $p_{beam}$ = 2.5 GeV/c and 3.3 GeV/c, this hump starts around 2.0 GeV/$c^2$ and 2.2 GeV/$c^2$, respectively, due to the higher beam momentum.

Fig. 6

Left column: Distribution of the kinematic variable ${(\theta ^{+}+\theta ^{-})}_{CM}$ for the signal (blue) and the background (red) reconstructed events. The plots describe the S1 and B1 samples at a $p_{beam}$ = 1.5 GeV/c and c $p_{beam} =$3.3 GeV/c. Due to the muon mass hypothesis, the peak of the background distribution is shifted to slightly smaller angles. Right column: Distribution of the invariant mass $M_{inv}$ of the particles final state for the signal (blue) and the background reconstructed events (red) at b $p_{beam} =$1.5 GeV/c and d $p_{beam} =$3.3 GeV/c

The most important subdetector for the $\mu$/$\pi$ separation is the MD. Its sandwich structure consists of alternating active and passive layers, which allow the different behavior of $\mu$ and $\pi$ inside the detector to be distinguished. Pions interact via both ionization energy loss and hadronic showering, while muons interact only through ionization.

A highly energetic pion is misidentified as a muon when (a) it undergoes only ionization processes inside the MD material and (b) it decays into a muon and the corresponding (anti-)neutrino. After the $\mu$-selection, also muons from pion decay can enter in the pionic background.

The momenta of the produced particles decrease with increasing values of ${\theta }_{CM}$. Hence, most of the particles are absorbed by the MD at large backward angles ${\theta }_{CM}$. As an example, at $p_{beam}$ = 1.5 GeV/c this behavior can be seen at angles approximately bigger than 100 degrees. Particles which are produced under smaller angles are able to cross through the MD due to their higher momenta.

Fig. 7

Angular dependence of the number of fired detection layers in the MD for negatively charged particles for the signal (left column) and the background (right column) reconstructed events at $p_{beam}$ = 1.5 GeV/c. The different behavior of muons and pions in the MD is crucial for an efficient $\mu /\pi$ separation. From the differences in the detector response, one can deduce that the number of fired detection layers has a strong separation power for muons and pions

Fig. 8

Dependence of the path length in the iron absorber of the MD on the incident particle momentum , for negatively charged particles for the signal (left column) and background (right column) reconstructed events at $p_{beam}$ = 1.5 GeV/c. This variable has a strong separation power and is used, in combination with $p_{layer zero, MDT}$, for the determination of the identification probability for muons, named P($\mu$), by the MD

Figure 7 shows the number of fired detection layers versus the reconstructed polar angle for negatively charged tracks from the signal (left column) and the background (right column). Most of the $\pi ^-$’s from the pion background sample are absorbed within the first layers of the MD at $p_{beam}$ = 1.5 GeV/c. At this momentum, about 7$\%$ of all the tracks cross 11 detection layers or more. Of that fraction, the MC truth information shows that about 9$\%$ are decay muons ($\mu ^{-}$) and the rest of the particles are $\pi ^{-}$. A negligible fraction (at the level of a few per mille) consists of misidentified particles of opposite charge ($\mu ^{+}$ and $\pi ^{+}$).

Another important variable for signal-background separation is the path length of the trajectories inside the MD. The dependence of this path length on the track momentum at the entrance of the MD is shown in Fig. 8 for reconstructed negatively charged particles in the high statistics signal samples (left) and the background sample (right). Note that the expected path length for a given incident particle momentum is strongly correlated with the incident polar angle.

The observables measured in the STT and EMC are generally less powerful for $\mu /\pi$ separation, as both detectors respond in a very similar way to these particles. The relevant variables are the deposited energy inside the electromagnetic calorimeter ($E_{EMC}$/p, with p the magnitude of the reconstructed particle 3-momentum at the interaction vertex), the EMC lateral moment and the mean energy loss per unit of length in the Straw Tube Tracker (dE/dx STT). The EMC lateral moment is defined as:

$$\begin{aligned} LAT = \frac{\sum _{i=3}^{N} {E}_{i}{r_{i}}^{2}}{\sum _{i=3}^{N} {E}_{i}{{r}_{i}}^2+{E}_{1}{r_{0}}^{2}+{E}_{2}{{r}_{0}}^{2}}, \end{aligned}$$

(8)

where N is the number of crystals hit by the shower and $E_{i}$ is the deposited energy in the i-th crystal in the shower, with $E_1$ $> E_2> \cdots > E_N$. The lateral distance between the central and the i-th crystal is given by $r_i$. Here $r_0$ stands for the fixed average distance between two crystals. Since the numerator does not contain the three highest energy depositions, the ratio will be smaller for electromagnetic showers in comparison to hadronic showers.

Despite the low separation power of the EMC and STT variables by themselves, they can help to improve the signal-background separation when multivariate data classification is used to optimize the $\mu /\pi$ separation.

The identification probability for being a muon, named P($\mu$), is determined based on two variables from the MD; the path length inside the iron absorber of the MD, denoted as the iron depth, and the initial particle momentum $\hbox {p}_{layer zero, MDT}$ measured at the detector entrance. Threshold values are defined for both of them and depend on the MD module. Further studies based on measurements using a real MD prototype are planned and will help to achieve a marginal improvement of the PID capability for muons.

5.3 Optimizing the $\mu$/$\pi$ separation by using boosted decision trees

The analysis of the simulated data aims to achieve the best possible background suppression while keeping a sufficient signal efficiency. Multivariate data classification is used to optimize the signal-background separation. Signal efficiency and background suppression studies are based on the high statistics $\mu ^{+}\mu ^{-}$ sample (S1) and the high statistics $\pi ^{+}\pi ^{-}$ sample (B1). After the event reconstruction, the full analysis based on multivariate data analysis (MVA) is carried out. Different methods of multivariate data classification are investigated using the Root-integrated software package Toolkit For Multivariate Data Analysis with ROOT (TMVA) [82, 83].

For MVA, a set of input variables is needed. The most important detector related to the $\mu$/$\pi$ separation is the MD, as discussed in the previous section.

5.3.1 MVA analysis

To summarize, for the analysis the following input variables are considered:

• the path length inside the iron absorber of the MD, denoted as “iron depth”;

• the number of fired layers in the MD;

• the initial momentum at MD layer zero: $\hbox {p}_{layer zero, MDT}$;

• the normalized path length of the tracklet inside the MD to $\hbox {p}_{layer zero, MDT}$;

• the identification probability for being a muon based on MD observables: P($\mu$);

• the ratio of the deposited energy inside the EMC to the reconstructed momentum of the associated track: $E_{EMC}$/p;

• the lateral moment of the EMC;

• the deposited energy inside a $3 \times 3$ crystal clusters, the central cluster being defined by the maximum energy deposition;

• the mean energy loss per unit of length inside STT, ${(dE/dx)}_{STT}$;

• the number of hits inside STT.

Kinematic variables are used as input variables as well, although they are, generally less powerful, and are mainly used for data selection after MVA:

• the sum of the polar angles in the CM system: ${({\theta }^{+}+{\theta }^{-})}_{CM}$;

• the invariant mass of the final state particles: $M_{inv}$.

The following “spectator variables” are not used for the training, but are stored into the output tree together with the response of the multivariate classifiers:

• the azimuthal angle ${(|\phi ^{+}-\phi ^{-}|)}_{lab}$ difference;

• the CM polar angle of the negative final state particle: cos(${\theta _{CM}}$);

• the CM polar angle of the positive final state particle.

Two different data sets feed the selected classifiers, both containing the reconstructed events together with the MC truth information. For the training, the classifiers use 50$\%$ of the input events, the remaining amount serving as test data for the trained classifiers. On the basis of these studies, different classification methods like Fisher Discriminants, Neural Networks or Boosted Decision Trees are trained, tested and their separation performance evaluated. The trained classifiers are stored as weight files and can be used afterwards to classify sets of unknown data. A helpful criterion to evaluate the performance of the different classifiers is the Receiver Operating Characteristics curve (ROC curve) which shows the achievable background rejection as a function of the corresponding signal efficiency.

Fig. 9

The classifiers ROC curves deliver information on the performance of each classification method (for $p_{beam}$ = 1.5 GeV/c). The bigger the area underneath each curve, the higher is the quality of the classifiers performance. Here the performance of boosted decision trees (BDT) is compared to an artificial neural network (CFMlpANN) and a method based on boosted Fisher discriminants. The curves in this figure are based on training data samples for signal and background containing $2 \times 10$ $^5$ events

In this work, Boosted Decision Trees (BDT) show the best performance for $\mu$/$\pi$ separation. Figure 9 reports the performance of different multivariate classifiers, which are applied on signal and background data sets after reconstruction, which have been generated only for the training of the classifiers. Each of those data samples contains $2 \times 10^{5}$ events. The area below each classifier curve can be used to judge on the quality of the classifiers performance. A high signal purity demands a very high background rejection which on the other hand implies small signal efficiencies.

The BDT response for the signal and background samples is shown in Fig. 10. A classifier must be checked for overtraining to reject cases of overfitting the classifier parameters to statistical fluctuations in the training data set. TMVA does this by comparing the event distributions from the training data and the values predicted by the classifiers. If the event selections ($2.1< M_{inv} < 2.4$ GeV/$\hbox {c}^2$) as well as the ${({\theta ^{+}}+{\theta ^{-}})}_{CM}>178.0^\circ$ cut are applied to the training data, the quality of the training data and the classification performance is improved. In the current studies an amount of $2 \times 10$ $^5$ events used in the TMVA procedure produced the best results. Half of the event sample is used to train the classifier, and the other half are used for testing.

Fig. 10

Output distributions of the BDT classifier using adaptive boosting (“BDT response”) after the training for the signal events (blue) and the background events (red) from the training data sample ($2 \times 10^5$ events each). Due to the overlap of both distributions it is not possible to fully reject the background while keeping an acceptable signal efficiency

Table 2 Criteria used to select the signal ($\mu ^+ \mu ^-$) and suppress the background ($\pi ^+\pi ^-$) events for each $p_{beam}$ value. The criteria are chosen in order to keep enough signal events in each bin of the reconstructed angular distribution histogram and at the same time to suppress as many background events as possible. The last columns list the values of the signal efficiency, background efficiency and signal-to-background ratio (S-B ratio)

The event selections considered in this work are summarized in Table 2. Selections are applied on the BDT outputs and on the distributions of the kinematic variables.

The signal and background efficiencies are mainly affected by the cuts on the BDT values. Sufficient signal statistics in each histogram bin of the reconstructed angular distribution is crucial to avoid uncertainties in the final result, therefore the event selections with loose requirements on the BDT output at each value of $p_{beam}$ are preferred. However, this should be balanced against the need to suppress the large background contribution. Stricter requirements on the BDT output led to strong increases in the uncertainty of the final signal angular distribution and are therefore not preferred. The final selection criteria are chosen at each $p_{beam}$ value in order to minimize the statistical uncertainty on the determined proton form factors.

Fig. 11

Angular dependance of the signal efficiency $\epsilon$ (blue dots, scale on the right side) after applying the event selection conditions (Table 2), the MC generated signal (red open up triangles) and the selected signal events (green open circles) from sample S1 at antiproton momentum of a 1.5 GeV/c, b 1.7 GeV/c, c 2.5 GeV/c, d 3.3 GeV/c

5.4 Angular distribution of the signal efficiency

Figure 11 shows the angular dependence of the signal efficiency ($\epsilon$) (blue dots), the MC generated signal events (red open up triangles) and the selected signal events (green open circles) from sample S1 at different beam momenta. The shape of the signal efficiency distribution is determined by the selections on the BDT response. Especially at $p_{beam}$ = 3.3 GeV/c, the signal efficiency drops strongly in the $0.4<$cos($\theta _{CM}$)$<0.8$ polar angle range. This is caused by the high values of the pion differential cross section in this range, which overwhelms the ability to separate signal from background. Therefore, these histogram bins will be excluded in further steps.

5.5 Background contamination from $\bar{p}p \rightarrow \pi ^+\pi ^-$

From the obtained background suppression factors, it follows that a high pion contamination, including muons from pion decay, will be expected in the $\mu$-selected data. In order to correct for it, a background subtraction procedure will be applied to the experimental data, which will introduce an additional statistical uncertainty. The influence of this procedure on the precision of the extracted FF values is considered in this feasibility study. In the experiment, the measured pion contamination of the $\bar{p}p \rightarrow \pi ^+\pi ^-$ background reaction and the pion contamination in the $\mu$-selected signal data will not exhibit identical statistical fluctuations due to the different procedures used to extract them. Therefore, two statistically independent angular distributions of the pion contamination are required to assess the background subtraction performance in this study.

Fig. 12

a Source histogram obtained with the adapted fit function $f_1$ within $\pm 1\sigma$ error band. A reduced $\chi ^2$ for the fit of $\chi ^2/ndf$ = 1.59 is obtained. The function $f_1$ is used for the generation of the two statistically independent target histograms, shown in Fig. (b) (black open squares and red dots). b Also shows the signal distribution after $\mu$-selection (blue squares)

A background suppression factor ($\epsilon _{B}$) of the order of $10^{-5}$ is typically achieved (see Table 2). The expected number of produced $\bar{p}p \rightarrow \pi ^+\pi ^-$ background events is on the order of $10^{9}-10^{11}$ (exact numbers are listed in Table 1) assuming a time-integrated luminosity of 2 $\hbox {fb}^{-1}$. From that, the expected numbers of background events after $\mu$-selection are calculated. They include also the events with muons in the final state such as $\pi ^{-}\mu ^{+}$, $\mu ^{-}\pi ^{+}$ and $\mu ^{-}\mu ^{+}$, in which one or both the pions decay.

The angular distribution of the pion contamination must contain the expected statistics in each bin. In this method, the $\mu$-selection is applied to the $\bar{p}p\rightarrow \pi ^+ \pi ^-$ reconstructed background sample and the obtained angular distribution acts as a source histogram, which contains a few thousand entries. The source histogram is fitted by a polynomial of the form

$$\begin{aligned} f(x) = \sum _{n=0}^{n_{max}} a_n x^n, \end{aligned}$$

(9)

where the maximum power is chosen in order to achieve an optimal value of reduced $\chi ^2$. For beam momenta of 1.5 GeV/c and 1.7 GeV/c, $n_{max}$ = 8 is chosen. At the largest beam momentum values, 2.5 GeV/c and 3.3 GeV/c, a fit function with $n_{max}$ = 9 is optimal. This function serves as an input for a random number generator, which is used to fill a new histogram (target histogram). The integral of the target histogram corresponds to the expected statistics. Two target histograms are created starting from different seeds. The first target histogram corresponds to the pion contamination in the selected data sample, and the second one is used for background subtraction. The obtained angular distribution in the target histograms not only contains the expected statistics, but also possess the most realistic shape, and a possible systematic uncertainty due to limited MC statistics in the background subtraction can be neglected. An example of the fit function $f_1$ is shown in Fig. 12a for the case of $p_{beam}=1.5$ GeV/c. Figure 12b shows the obtained target histograms, which contain the angular distribution of the pion contamination, together with the signal distribution after $\mu$-selection.

5.6 Suppression of other relevant background channels

Due to the high momentum and spatial resolution as well as the nearly $4\pi$ acceptance of the $\overline{\text {P}}\text {ANDA}$ detector, it will be possible to very efficiently suppress reactions of the type $\bar{p}p \rightarrow n\pi ^+ n\pi ^- m{\pi }^0$ with $n \ge$ 2 and $m \ge$ 0, $\bar{p}p \rightarrow \pi ^+\pi ^-\omega$, $\bar{p}p \rightarrow \pi ^+\pi ^-{\rho }^0$ ($\omega$ and $\rho ^0$ decay into pions at a rate of nearly $100\%$). This can be done by counting the detected charged particles in the final states and utilizing kinematic cuts.

In the beam momentum range considered for this work, the total cross section of the $\bar{p}p \rightarrow \pi ^{+} \pi ^{-} \pi ^{0}$ reaction is about seven orders of magnitude larger than the signal [72, 73]. In order to reach a signal contamination < 1$\%$ from this channel, a rejection factor of the order of 10$^{-9}$ must be achieved. Compared to the channel with $\pi ^+\pi ^-$ final state, the invariant mass of the $\pi ^+\pi ^-$ system in the $\pi ^{+} \pi ^{-} \pi ^{0}$ final state is expected to be shifted drastically to smaller values and broadened because of the additional $\pi ^0$. Therefore, one gains an additional rejection factor of at least of $10^{-1}$. The $\bar{p}p \rightarrow K^{+} K^{-} \pi ^{0}$ reaction can be easily identified for the same reason and also due to the high rest mass of the kaon compared to the muon mass.

5.6.1 $\bar{p}p \rightarrow K^{+} K^{-}$ background

Kaons from $\bar{p}p \rightarrow K^{+} K^{-}$ constitute a strong background source as well, whose cross section is of the same magnitude as the $\bar{p}p \rightarrow \pi ^{+} \pi ^{-}$ reaction. Therefore it is necessary to investigate if a strong enough suppression for this channel is possible.

The differential cross section of the $\bar{p}p \rightarrow {K}^{+} {K}^{-}$ reaction was measured in 1975 by Eisenhandler et al. [69]. Figure 13 shows the CM differential cross section as a function of cos($\theta _{CM}$) for the negative kaon from the $\bar{p}p \rightarrow {K}^{+} {K}^{-}$ process.

Fig. 13

Differential cross section for the $\bar{p}p \rightarrow K^{+} K^{-}$ process as a function of the $K^{-}$ CM emission angle from Ref. [69]

For the estimation of the rejection factor, the EvtGen generator [84] is used to produce phase space (PHSP) angular distributions. This estimation is assessed at the lowest value of beam momentum, where the highest precision of the FFs is achieved, as well as at the highest beam momentum, 3.3 GeV/c.

At 1.5 GeV/c, the integration over the possible angular range leads to a total cross section of 53.38 $\mu$b. Assuming a time-integrated luminosity of 2 $\hbox {fb}^{-1}$, this corresponds to 1.07 $\cdot$ 10$^{11}$ expected kaon events at this value of beam momentum. The total cross section of the $\bar{p}p \rightarrow K^{+} K^{-}$ channel decreases with increasing beam momentum. In total, more than $1.05 \cdot 10^8$ events are generated in the |cos($\theta _{CM}$)| < 0.8 angular range. Since the masses of the charged kaons are larger by a 4.7 factor than the muon rest mass, the misidentification probability for kaons is expected to be much smaller than the pion case. Hence, the kinematic cuts are much more powerful for the suppression of this process. Applying the event selection conditions reported in Table 2, a suppression factor better than 10$^{-8}$ is achieved for this background channel with a confidence level of 95$\%$. This corresponds to a signal pollution < 1$\%$ with a total signal efficiency of 31.5$\%$, therefore the contamination from this channel can be neglected. Also at $p_{beam}$ = 3.3 GeV/c, a signal pollution < 1$\%$ is achieved, with a total signal efficiency of 29.5$\%$.

6 Results for feasibility at $\overline{\text {P}}\text {ANDA}$

This section describes the extraction of the modulus of the time-like electromagnetic proton FFs, $|G_E|$ and $|G_M|$, and their ratio R = $|G_E|$/$|G_M|$, from the efficiency-corrected angular distributions of the reconstructed and selected simulated data. A background subtraction is always included in these studies based on the reconstructed pion contamination distributions, as discussed in the previous section. A fit is used for the extraction of the different physics quantities and their uncertainties. At this level of the simulation, systematic uncertainties can already be estimated and included into the calculation of the total uncertainties. The proton effective FF and the total ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ signal cross section with their uncertainties are extracted from the selected and efficiency corrected simulated data.

After the background subtraction, the signal efficiency correction is applied in each i-th bin of the angular distribution of the selected simulated data:

$$\begin{aligned} N^{corr}_{i} = \frac{N^{reco}_{i, fluc}}{\epsilon _{i}}, \end{aligned}$$

(10)

with $N^{corr}_{i}$ being the efficiency corrected number of signal events, $N^{reco}_{i, fluc}$ the number of reconstructed and selected signal events after background subtraction and $\epsilon _{i}$ the signal efficiency. For the determination of the physics quantities, the angular distribution of efficiency-corrected signal events is fit to a function based on the differential cross section (Eq. 2):

$$\begin{aligned} f(\cos \theta )= & {} C_{1} W_i \Biggl [ \frac{4{M_p}^2}{q^2} (1- {\beta _{l}}^2 \cos ^2\theta ) P_{1} \nonumber \\&+ (1 + \frac{4{m_{\mu }}^2}{q^2}+ {\beta _{l}}^2 \cos ^2\theta ) P_{0} \Biggr ]. \end{aligned}$$

(11)

The values of $|G_E|$, $|G_M|$ and $R=|G_E|/|G_M|$ can be obtained, from the fit parameters $P_{1}$ = $\mathcal {L} \cdot {|G_{E}|}^2$, $P_{0}$ = $\mathcal {L} \cdot {|G_{M}|}^2$ and their ratio. Here, $\mathcal {L}$ stands for the time-integrated luminosity, for which 2 $\hbox {fb}^{-1}$ is assumed. $C_{1}$ is a $q^2$-dependent constant and contains the rest masses of proton and muon:

$$\begin{aligned} C_{1} = \frac{{(\hbar c)}^2 \alpha ^2 \pi }{2q^2} \sqrt{\frac{q^2 - 4{{m}_{\mu }}^2}{q^2 - 4{{M}_{p}}^2}}. \end{aligned}$$

(12)

$W_{i}$ corresponds to the width of the i-th histogram bin of the $\cos (\theta _{CM})$ angular distribution.

Figure 14 shows the resulting angular distributions for the signal after the efficiency correction along with the corresponding fit.

Fig. 14

$\cos (\theta _{CM})$ distributions for the beam momentum values indicated in each panel. The green squares with error bars represent the selected signal yields after background subtraction, corrected by the signal efficiency. The fit function (Eq. 11) (red solid line) is used to extract the proton FFs and their uncertainties

Table 3 Extracted value and statistical precision of $R=|G_{E}|/{|G_{M}|}$ at each considered value of beam momentum ($p_{beam}$ = 1.5, 1.7, 2.5 and 3.3 GeV/c). The studies are based on the assumption of R = 1

Table 4 Extracted value and statistical precision of $|G_{E}|$ and ${|G_{M}|}$ at each value of beam momentum ($p_{beam}$ = 1.5, 1.7, 2.5 and 3.3 GeV/c). The theoretical values of the magnetic FF, $|G_M|$ (model), which are based on the FF model for the parameterization of $|G_M|$ from Ref. [66] are shown for comparison

Tables 3 and 4 show the extracted values of R, ${|G_{E}|}$ and ${|G_{M}|}$ with their uncertainties at each value of beam momentum ($p_{beam}$ = 1.5, 1.7, 2.5 and 3.3 GeV/c). The results are consistent with the corresponding theoretical values used as input to the simulations within one sigma. The 4${M_{p}}^2/q^2$ factor in the differential cross section formula suppresses the $|G_E|$ term, so that at larger values of $q^2$ the cross section is dominated by $|G_M|$, which also leads to a larger uncertainty in the measured values of $|G_E|$.

6.1 Integrated cross section and the effective proton FF

The integrated cross section of the $\bar{p}p \rightarrow \mu ^+\mu ^-$ process is calculated for each value of $q^2$ as

$$\begin{aligned} {\sigma }_{int} = N^{corr}/\mathcal {L}, \end{aligned}$$

(13)

with $\mathcal {L}$ = 2$\hbox {fb}^{-1}$. Table 5 shows the obtained values of the integrated cross section at each considered value of beam momentum.

Table 5 Extracted statistical precisions of the integrated cross section of the $\bar{p}p \rightarrow \mu ^+\mu ^-$ signal process together with the calculated values based on Eq. 2, in -0.8 < cos($\theta _{CM}$) < 0.8 angular range

From the results one can conclude that the integrated cross section of the signal process can be determined with high accuracy at $\overline{\text {P}}\text {ANDA}$. The proton effective FF can be determined from the integrated cross section in the |cos($\theta _{CM}$)| < $\bar{a}$ range ($\bar{a}$ = 0.8) using

$$\begin{aligned} |F_{p}| = \sqrt{\frac{\sigma _{int}(q^2)}{\frac{\pi {\alpha }^{2}}{2q^2} \frac{\beta _{\ell }}{\beta _{p}} \bigg [ (2 - {\beta }_{\ell }^{2}) + \frac{1}{\tau } \bigg ] \; \bigg [2 \bar{a} + \frac{2}{3} A_0 \; \bar{a}^3 \bigg ]} }, \end{aligned}$$

(14)

with

$$\begin{aligned} A_{0}={\beta }_{\ell }^{2} \; \frac{1-{\frac{1}{\tau }}}{2-{{\beta }_{\ell }}^{2}+\frac{1}{\tau }}, \end{aligned}$$

being $\tau = q^2/4M^2_p$ , $\beta _{\ell ,p} =\sqrt{1-4M^2_{\ell ,p}/q^2}$.

Table 6 Extracted values and statistical precisions of the effective proton FF, ${|F_{p}|}$. The third column is the theoretical value (simulation input)

The extracted relative statistical uncertainty of the effective FF (Table 6) ranges between 0.33$\%$ and 1.39$\%$ for beam momenta between 1.5 and 3.3 GeV/c. As a systematic uncertainty, the contribution from the luminosity measurement can be calculated as $\varDelta |F_p|/ |F_p|$ (syst.) = ± 2$\%$, assuming a relative uncertainty of the luminosity of 4$\%$ at all values of $q^2$.

6.2 Systematic uncertainties

Since only MC simulated data are currently available, naturally a precise estimation of the systematic uncertainties is not possible at the present time. However, several sources of systematic uncertainties can already be estimated based on the MC study and will be discussed in the following.

6.2.1 Luminosity measurement

$\overline{\text {P}}\text {ANDA}$ will determine the luminosity $\mathcal {L}$ exploiting the well known elastic $\bar{p}p$ scattering. $\mathcal {L}$ will be measured with a relative systematic uncertainty from 2.0$\%$ to 5.0$\%$, depending on the beam momentum, the knowledge of the differential cross section parameters and the $\bar{p}p$ inelastic background contamination [85]. In this estimation, a relative uncertainty of $\varDelta \mathcal {L}/\mathcal {L}$ = 4.0$\%$ is assumed at all beam momenta. This corresponds to a relative uncertainty on the determination of the proton FFs of 2.0$\%$.

6.2.2 Choice of event selections

The signal and background efficiencies are mainly affected by the selections on the BDT outputs. The contribution from the choice of event selections to the total systematic uncertainty is determined at each beam momentum by varying the value of the BDT output selection around the reference value. The spread of the values of the proton FFs using different BDT selections is taken as the systematic uncertainty due to this source.

6.2.3 Choice of histogram binning

The $\cos (\theta _{CM})$ distributions binning has an effect on the values of the extracted quantities and their uncertainties. In order to compare to the results determined for the $\bar{p}p \rightarrow e^+e^-$ reaction from Ref. [48], the same binning (16 bins) is chosen at beam momenta $p_{beam}$ = 1.5, 1.7 and 2.5 GeV/c. At $p_{beam}$ = 3.3 GeV/c, wider bins are chosen (12 bins) since the data points show larger statistical fluctuations. The difference between the results obtained with the different binning is calculated at 3.3 GeV/c and is used for the determination of the uncertainty due to this source.

Table 7 Statistical and systematic uncertainties, which contribute to the relative total uncertainty of ${|G_{E}|}$, ${|G_{M}|}$ and of the ratio $R=|G_E|/|G_M|$

Fig. 15

Values, with total uncertainties, obtained for the $R = |G_{E}|/|G_{M}|$ ratio for the $\bar{p}p \rightarrow \mu ^+\mu ^-$ channel at different values of $q^2$ (red points). R = 1 is the simulation input. Also shown are the currently existing data from Ref. [23] (green squares), from Ref. [32] (open black triangles), from Ref. [29] (open orange circles), from Ref. [90] (magenta down triangle), from Ref. [34] (open green squares), and from Ref. [41] (open blue crosses)

6.2.4 Asymmetry contributions to cos($\theta _{CM}$)

In this work, no radiative corrections are included, since no calculations for the muon channel exist. A symmetric angular distribution in cos($\theta _{CM}$) is assumed in this work as a consequence of the one-photon exchange approximation.

In Ref. [48] two-photon exchange for the electron channel is discussed, which introduces asymmetry contributions to the angular distribution [86, 87]. The contribution of the two-photon exchange to the cross section for the electron channel is expected to be negligible, being less than 1$\%$ [88]. The contribution of the interference term between one- and two-photon-exchange is symmetric under interchange of electron and positron and can be removed from the angular distribution by adding both angular distributions [89]. This strategy will be also applied for the muon channel.

6.2.5 Pion background

The cross section of the background channel ${\bar{p}} p \rightarrow \pi ^+ \pi ^-$ will be measured at $\overline{\text {P}}\text {ANDA}$ with a very high precision due to its large cross section (see Table 1). The same data samples will be used to extract the signal and background processes. Therefore, systematic uncertainties due to the modeling of the differential cross section of this process used in simulations or due to the detector performance are expected to be negligible. In addition, the influence of the shape of the pion background distribution on the extracted precision of the form factors is investigated and found to be also negligible.

The contributions to the systematic uncertainties of the proton FFs are summarized in Table 7.

6.3 Total relative uncertainties

An overview of the statistical and systematic contributions to the relative total uncertainty of the FFs and the ratio R is given in Table 7. The largest sources of systematic uncertainties are related to the choice of histogram binning, the event selections and the luminosity measurement. The total uncertainty is listed for all the considered beam momenta.

The results show that the total relative uncertainty, $\varDelta R$/R, ranges between 5$\%$ and 37$\%$ for $q^2$ between 5.08 and 8.20 (GeV/c)$^2$. The estimated values of the total relative uncertainty $\frac{\varDelta |G_{M}|}{|G_{M}|}$ lie between 2.5$\%$ and 10$\%$, while those for $\frac{\varDelta |G_{E}|}{|G_{E}|}$ between 3.7$\%$ and 27.0$\%$. Figure 15 shows the final results obtained for $R \pm \varDelta R$, including all considered statistical and systematic uncertainties. The results show that $|G_{E}|$, $|G_{M}|$ and their ratio are expected to be measured with high precision at $\overline{\text {P}}\text {ANDA}$. At lower beam momenta, the statistical precision increases due to the increasing cross section of the signal reaction; therefore, the highest precision of the modulus of the time-like proton FFs will be obtainable at the lowest possible value of $q^2$ = 5.1 (GeV/c)$^2$.

7 Test of lepton universality

Since the lepton universality is a fundamental feature part of the Standard Model, a violation of this universality would be a sign for new physics beyond the Standard Model. The only hints for the violation of lepton universality exist so far from experiments such as BaBar, Belle and recently LHCb (CERN) [91]. The LHCb experiment measured the ratio of the branching fractions of the $B^+ \rightarrow K^+\mu ^+\mu ^-$ and $B^+ \rightarrow K^+e^+e^-$ decays using proton-proton collision data. The ratio of the branching fractions, denoted as $R_K$, within a fixed range of the di-lepton mass squared from $q^2_{min}$ to $q^2_{max}$ is given by

$$\begin{aligned} R_K [q^2_{min}, q^2_{max}] = \frac{\int ^{q^2_{max}}_{q^2_{min}} dq^2 \frac{d\varGamma (B^+\rightarrow K^+ \mu ^+\mu ^-)}{dq^2}}{\int ^{q^2_{max}}_{q^2_{min}}dq^2 \frac{d\varGamma (B^+\rightarrow K^+ e^+e^-)}{dq^2}}, \end{aligned}$$

(15)

where $\varGamma$ stands for the $q^2$-dependent partial width of the B meson decay. Details of the measurement can be found at Ref. [91].

A calculation of the Standard Model prediction for $R_{K}$ predicted a value of unity within an uncertainty of $\mathcal {O}$($10^{-3}$) by Ref. [92, 93]. More recent calculations, which have been performed by [94] showed that the largest theoretical uncertainty of $R_K$ is due to QED corrections, and result in a relative uncertainty of $\approx$ 1-2$\%$.

In the LHCb measurement, a time-integrated luminosity of 3 $\hbox {fb}^{-1}$ was achieved at center of mass energies between 7 and 8 TeV. The measurement was performed in the 1 < $q^2$ < 6 (GeV/c)$^2$ range, where $q^2$ corresponds to the di-lepton invariant mass squared. The ratio of branching fractions was

$$\begin{aligned} R_K = 0.745^{+0.09}_{-0.074} (stat.) \pm 0.036 (syst.), \end{aligned}$$

(16)

which is compatible with the value predicted by the Standard Model within 2.6 standard deviations, and is the most precise measurement of this ratio of branching fractions to date. Further data from an upgrade of the LHCb and from Belle-II are expected within the next years.

Assuming that all radiative corrections are well known, the ratio of the effective FF evaluated with the $\bar{p}p \rightarrow \ell ^+\ell ^-$ process with $\ell$ = $e, \mu$, could be used to perform a test of the lepton universality at $\overline{\text {P}}\text {ANDA}$ at a few percent level:

$$\begin{aligned} \mathcal {R}_{e\mu } = \frac{|F_p(\bar{p}p \rightarrow \mu ^+\mu ^-)|}{|F_p(\bar{p}p \rightarrow e^+e^-)|}. \end{aligned}$$

(17)

The estimation of the expected precision of this ratio depends on the expected precision of the effective FF in each of the channels. The studies for the $\bar{p}p \rightarrow \ell ^+\ell ^-$ reaction were performed at $q^2$ = 5.4 (GeV/c)$^2$ ($p_{beam}$ = 1.7 GeV/c) and can be found in Ref. [48]. The effective FF is expected to be [95]

$$\begin{aligned}&|F_p(\bar{p}p \rightarrow e^+e^-)| = 0.1216 \pm 0.0004 \; \text{(stat.) }\nonumber \\&\quad \pm 0.0024 \; \text{(syst.) }. \end{aligned}$$

(18)

From that, the total relative uncertainty is obtained as

$$\begin{aligned} \varDelta |F_p(\bar{p}p \rightarrow e^+e^-)| / |F_p(\bar{p}p \rightarrow e^+e^-)| \sim 2.02\%. \end{aligned}$$

(19)

For the muon channel, the effective proton FF value

$$\begin{aligned}&|F_p(\bar{p}p \rightarrow \mu ^+\mu ^-)| \nonumber \\&\quad = 0.1210 \pm 0.0009 \; \text{(stat.) } \; \pm 0.0024 \;\text{(syst.) } \end{aligned}$$

(20)

is obtained, so one gets for the ratio

$$\begin{aligned} \mathcal {R}_{e\mu } = 0.99 \pm 0.03, \end{aligned}$$

(21)

which corresponds to a relative total uncertainty of $\sim 3\%$. An even better precision would be expected for the lowest $q^2$ = 5.1 (GeV/c)$^2$ value ($p_{beam}$ = 1.5 GeV/c), since the signal cross section has higher values.

From these results, it can be concluded that $\overline{\text {P}}\text {ANDA}$ will be able to perform a test of a possible violation of the lepton universality (e-$\mu$) with a good precision, provided the QED radiative corrections are precisely known for both channels. This calls for a new set of calculations.

8 Summary

A thorough feasibility study for the measurement of the modulus of the time-like proton FFs in the ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ reaction is performed within the PANDARoot framework at four beam momenta between 1.5 and 3.3 GeV/c. A method based on multivariate data classification (BDT) is used to optimize the separation of the signal from the main background channel ${\bar{p}} p \rightarrow \pi ^+ \pi ^-$. Signal to background ratios between 1:5 and 1:13 (background rejection factor of $\sim 10^{-5}$) are achieved. A subtraction of the residual background events is performed. Assuming an integrated luminosity of 2 $\hbox {fb}^{-1}$ per beam momentum setting, the statistical precisions of ${|G_{E}|}$, ${|G_{M}|}$ and $R=|G_{E}|/|G_{M}|$ are determined by fitting the angular distributions of the ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ signal reaction. The main contributions to the systematic uncertainties are studied, determining the precisions of the integrated cross section of the ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ reaction and the proton effective FF. The results of the simulations show that a first time measurement of the proton FFs exploiting the ${\bar{p}} p \rightarrow \mu ^+ \mu ^-$ reaction will be possible at $\overline{\text {P}}\text {ANDA}$ and a good precision is expected: for instance, a total relative uncertainty on the measurement of the proton FF ratio between $5\%$ at 1.5 GeV/c and $37\%$ at 3.3 GeV/c. Since the measurement of the muon channel is very challenging due to the overwhelming pion background, the precision of the proton FFs determined in these feasibility studies provides an exciting opportunity for the experiment and the measurement of this channel will offer a very promising contribution to the rich $\overline{\text {P}}\text {ANDA}$ physics program.